Abstract
Recently developed cameras in the low-cost sector exhibit lens distortion patterns that cannot be handled well with established models of radial lens distortion. This study presents an approach that divides the image sensor and distortion modeling into two concentric zones for the application of an extended radial lens distortion model. The mathematical model is explained in detail and it was validated on image data from a DJI Mavic Pro UAV camera. First, the special distortion pattern of the camera was examined by decomposing and analyzing the residuals. Then, a novel bi-radial model was introduced to describe the pattern. Eventually, the new model was integrated in a bundle adjustment software package. Practical tests revealed that the residuals of the bundle adjustment could be reduced by 63% with respect to the standard Brown model. On the basis of external reference measurements, an overall reduction in the residual errors of 40% was shown.
1. Introduction
1.1. Pinhole Model
In photogrammetry and computer vision, the pinhole camera model is frequently used to describe the mapping of an object point with world coordinates onto the camera sensor, i.e., the image plane. Figure 1 shows the pinhole model with an image, a camera and the world coordinate system.
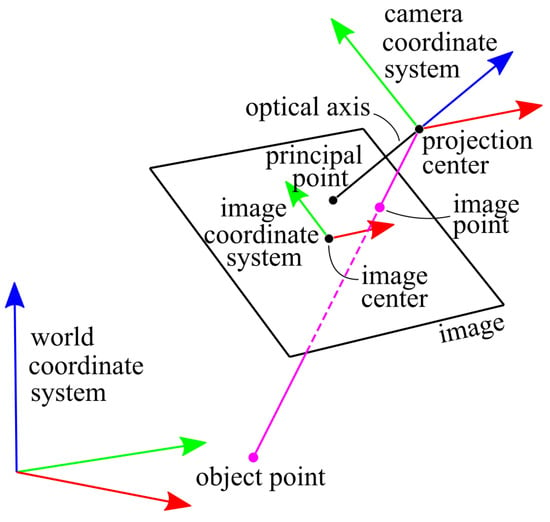
Figure 1.
Pinhole model. The corresponding X axis is colored red, Y in green and Z in blue. The ray from the object point into the image is depicted in magenta. The principal point is the perpendicular foot of the projection center onto the image.
Model A describes the corresponding transformation of the object point vector from the world coordinate system into the camera coordinate system (step 1). This is followed by the projection into the image (perspective division, step 2), resulting in the image point given in the camera coordinate system. Afterwards, the image point is shifted into the image coordinate system defined by the image center (step 3).
| Model A: Pinhole model |
| Step 1: Step 2: Step 3: |
| where = center of projection coordinates in world coordinate system |
| R = rotation matrix of the camera coordinate system |
| = (Xw, Yw, Zw)T = object point in world coordinate system |
| c = principal distance |
| = (Xc, Yc, Zc)T = object point in camera coordinate system |
| = (xc, yc, −c)T = image point in camera coordinate system |
| xi, yi = image point in image coordinate system |
| xp, yp = principal point in image coordinate system |
These steps are often summarized in the collinearity equations [1], see Equation (1).
where rkl = elements of the rotation matrix R.
1.2. Lens Distortion
There are several influences that lead to a deviation of the pure pin hole model due to different lens distortions, which are depicted in detail in the following.
1.2.1. Symmetric Radial Lens Distortion
Seidel aberrations [2] of spherical lenses cause symmetric radial image distortions centered around the principal point. This effect leads to different image scales that depend on the distance to the optical axis due to the changing refractive power of the lens. There are two main types of radial distortions that are observable in practice: barrel and pincushion distortion. Brown [3] introduced a correction term, which is a power series applied to the radial distance from the principal point r:
where = distance from the principal point;
Δr = correction term at the distance from the principal point;
A1, A2, A3 = parameters of radial distortion.
The corrections applied to the coordinates are:
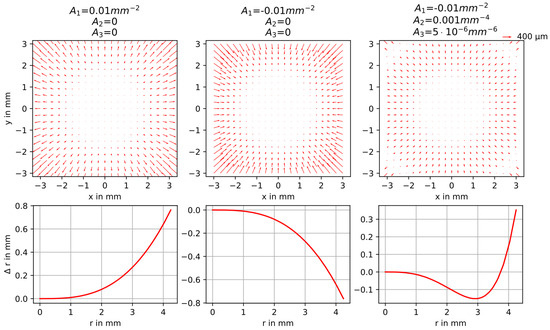
Figure 2.
Upper part: Correction vectors for symmetric radial lens distortion for different parameter examples of a virtual camera. Lower part: Corresponding radial corrections as a function of the image radius.
1.2.2. Decentering Lens Distortion
The decentering of the lens, i.e., due to the misalignment of individual elements of the lens system, also leads to distortions in the image. Conrady [4] analyzed this effect mathematically and could thereby show that there is a tangential as well as an asymmetric radial component, where the latter is three times larger than the former. Therefore, Brown [5] proposed the well-known parameterization that considers four parameters:
where xc, yc = camera coordinates centered at the principal point;
B1, B2, B3, B4 = parameters of decentering distortion.
Corrections are often not required in case of high-quality camera systems, and often the model is reduced to two parameters [6] (Equation (5)). Luhmann et al. [6] recommend the decentering distortion model mainly for low-cost or mobile phone cameras.
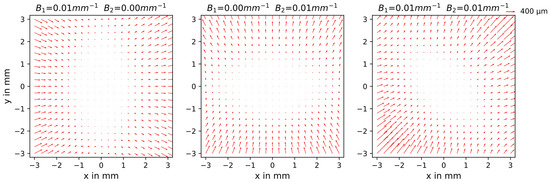
Figure 3.
Correction vectors for decentering lens distortion of a virtual camera for different parameter examples.
1.2.3. Affinity and Non-Orthogonality
In addition to the radial and decentering lens distortions, affine parameters for non-orthogonality and shear are often integrated in standard camera models to overcome effects from camera electronics [7].
Equation (6) shows the correction terms with the two parameters and :
1.2.4. Pinhole Model Including Distortion
Eventually, all the previously explained corrections for distortion and affinity can be summarized:
Consideration of these corrections leads to an extension of the pure pinhole model (model A). The extended model (here called model B) is a widely used model [8].
| Model B: Pinhole model including distortion |
| Step 1: |
| Step 2: |
| Step 3: |
| with and |
| Step 4: |
The corrections can also be integrated into the collinearity equations:
1.3. Non-Physical Models for Distortion Corrections
There are distortions that may not be described fully by physically motivated parameters. For this purpose, correction approaches based on mathematical functions only can be used. Thereby, distortion can be, for instance, approximated by polynomials up to a certain order. Mathematical correction approaches with orthogonal, bivariate polynomials of second and fourth order were first presented by Ebner [9] and Grün [10], respectively. These models were mainly intended for application in aerial photogrammetry. More recent approaches are based on polynomial series such as Chebychev polynomials [11], Legendre polynomials [12], or considering Fourier series [13]. A combination of physical and mathematical models is possible as well [14,15]. Some of these approaches consist of a large number of polynomials or parameters and not all of them might be significant. Furthermore, correlations among them may appear, which can lead to a poor convergence behavior of the bundle adjustment.
Physical and mathematical approaches are usually well suited to correcting global distortion patterns. However, local effects may also occur, which can be corrected using the finite element method [14,16] or considering a local distortion model [17]. Luhmann et al. [8] give an overview of the mathematical models and calibration techniques for a wide range of cameras.
1.4. Motivation of This Work
UAV photogrammetry with low-cost cameras is used in a wide range of applications such as archaeology, building modeling, ecology, forestry, hydrology or geomorphology [18]. Some of these low-cost cameras revealed to be challenging to model with the standard distortion models. For instance, Eltner et al. [19] applied the 10-parameter model (model B, based on [3,7]) to a DJI Mavic Pro camera and showed that large errors remained after bundle adjustment, which was indicated by large residuals. Figure 4 visualizes the corresponding residual plot for the residual vectors of all image points that were included in the self-calibration during bundle adjustment. There were unusually large radial deviations around the image center and a clear systematic pattern remained.
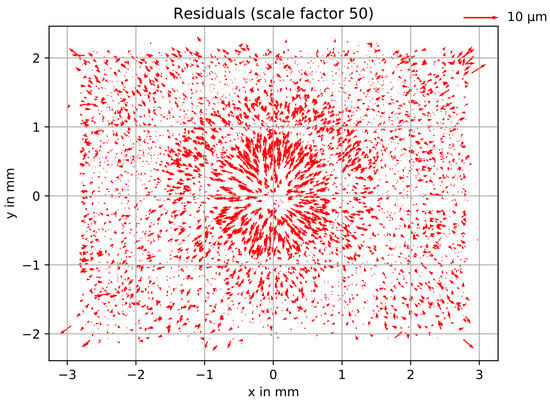
Figure 4.
Residual plot after free net bundle adjustment using model B.
Hastedt et al. [15] also studied this type of camera. They suspected that some UAV camera lenses constructed from aspheric lenses may not be made of glass and that there is some internal black box image pre-processing, such as filtering and other corrections, that could lead to this behavior. In addition, ref. [20] highlighted that image pre-processing by the UAV camera manufacturer can result in physically based lens distortion models no longer being valid for actual bundle adjustment because only residual distortion is modeled. Hastedt et al. [15] proposed an extended Brown polynomial to overcome the effects shown in Figure 4.
The article at hand presents an alternative parametrization for radial distortion that is called the bi-radial model. In contrast to existing correction models, the bi-radial approach divides the sensor into two concentric zones in which independent Brown polynomials are applied. Our approach is compared with the method of [15].
The article is structured as follows: First, we analyze the special residual patterns. Thus, the radial components of the residuals are computed and appropriate models are proposed. The results of this analysis are then integrated into a bundle adjustment. Afterwards, the new models are validated. Finally, the results are discussed and concluded.
2. Methods and Results
In this section, we first analyze the results of a bundle adjustment with fixed object coordinates and without considering the distortions of the tested DJI Mavic Pro camera, i.e., by using model A. Then, we introduce a new distortion model (bi-radial distortion correction, Section 2.3), which we integrated in an extended bundle block adjustment to calibrate the DJI Mavic Pro camera (Section 2.4). The results reveal an improved removal of systematic residuals (Section 2.5). To further enhance the bi-radial correction, we also present an automated segmentation of the distortion zones (Section 2.6) and eventually validate the bi-radial distortion correction approach (Section 2.7).
2.1. Analysis of the Residual Patterns
We used a reference target field (Figure 5) to analyze the DJI Mavic Pro camera (see Table 1). The target field has a size of approximately 7 m × 3 m × 1 m. The reference coordinates of the target field were determined photogrammetrically using an image block captured by a high-quality camera (Panasonic Lumix DMC-GX80 camera (from company Panasonic) with a lens with a focal length of 20 mm) and performing a free bundle adjustment with model B (standard model).

Figure 5.
(a) Reference target field used for bundle adjustments. (b) Orientation of the images of the Panasonic Lumix DMC-GX80 camera and locations of the object points. The schematic illustration was created with the software package AICON 3D Studio (version 12.50.03).

Table 1.
Sensor specifications for the DJI Mavic Pro camera.
The coordinates, obtained photogrammetically by the data from the Panasonic Lumix DMC-GX80 camera, were used as control points, i.e., they were kept fixed for a second bundle adjustment using an image data set of the reference target field acquired with the DJI Mavic Pro camera (from company DJI). Model A (pinhole model without distortion correction) was applied in the bundle adjustment with the DJI data. This approach was chosen to retrieve the full distortion pattern to identify systematics. The residuals of the image points after the bundle adjustment are depicted as a vector field in Figure 6a, revealing a similar behavior as already shown in Figure 4.
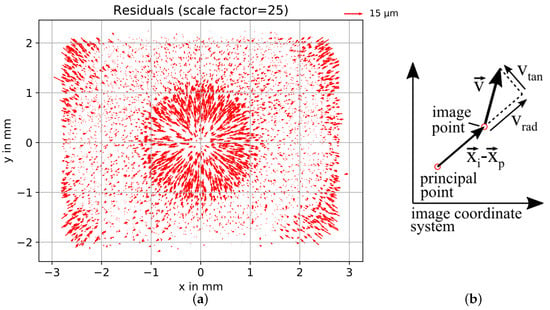
Figure 6.
(a) Residual plot after bundle adjustment using model A (i.e., pure pinhole model) with fixed object coordinates. (b) Decomposition of the residual vector into radial and tangential components.
The residual vectors were decomposed into a radial and tangential part (Figure 6b). The radial component was computed by projecting the residual vector onto the difference vector between the principal point and the image point:
where = residual vector of the image point;
= image coordinate vector;
= principal point coordinate vector
The tangential component was calculated by the projection of the residual’s normal onto the difference vector:
where vx = x component of the residual vector;
vy = y component of the residual vector.
Both components are visualized as a function of the image radius r and as a function of the azimuth of the image point in Figure 7. In addition, the moving median is depicted in red, which was computed using the neighbors around the measurement point in a distance of 0.1 mm. The radial component (over r) shows a strong systematic behavior (Figure 7a), whereas the tangential component appears to be randomly distributed (Figure 7b). Figure 7c,d further reveal a systematic effect for both components regarding the azimuth that may show radial asymmetric effects. However, the radial component also shows a high scattering when considering the azimuth (Figure 7c). Figure 7c also show four vertical tails with larger radial components around the azimuth abscissae of about ±45° and ±135°. These values are caused by the residuals of the image corner points as visible in Figure 6a. In the following, we concentrate on the radial component versus the image radius.
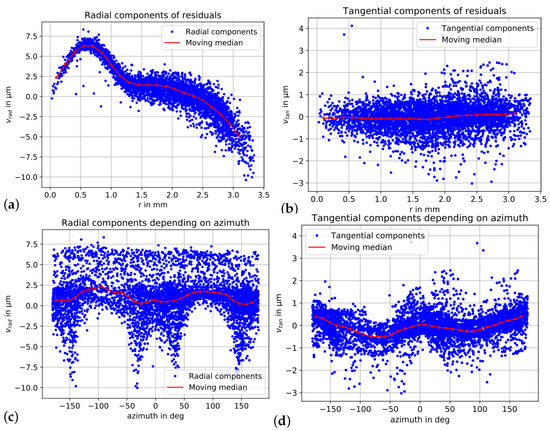
Figure 7.
(a) Radial components of the residuals plotted against the image radius. (b) Tangential components of the residuals plotted against the image radius. (c) Radial components plotted against the azimuth of the image point. (d) Tangential components plotted against the azimuth of the image point. For all subplots, the moving median is shown in red.
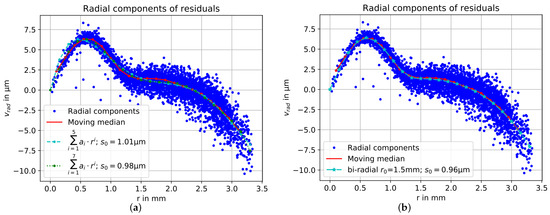
Polynomial fits for the radial components versus image radius shown in Figure 7a were computed using the radial Brown polynomials and . In contrast to the bundle adjustment, the term was included in the polynomial fit to take the influence of the principal distance into account. However, the linear term had to be omitted in the bundle adjustment because it cannot be separated from the principal distance [6]. To evaluate the quality of the polynomial fit, the standard deviation of the unit weight was computed as (where n = number of points and u = number of unknowns).
Figure 8 displays the fitted Brown polynomials. Significant deviations of the polynomial to the points in the left part of the curve (corresponding to the central part of the image format) become obvious, explaining the behavior noticed in [19], which is also visible in Figure 6a. The Brown polynomials do not model the behavior of this lens well. The standard deviations of the unit weights of the polynomial fits considering three and four parameters are 1.78 µm (1.15 px) and 1.52 µm (0.98 px), respectively.
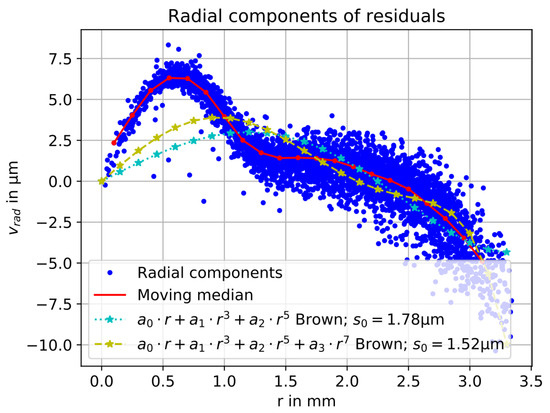
Figure 8.
Radial components and fitted Brown polynomials with standard deviations of the unit weight of the polynomial fit.
2.2. Extended Brown Polynomial Model
The extension of the radial function with even coefficients corresponds to the extended radial polynomial of [15]. We fitted this extended model (Equations (11) and (12)) to our data:
and
The extended polynomials are displayed in Figure 9a. With the adapted Brown model, the standard deviation of the unit weight (polynomial fit) can be decreased to 1.01 µm (0.65 px) and 0.98 µm (0.63 px) when using five or seven parameters, respectively.
2.3. Bi-Radial Polynomial Model
In our new approach, we combine two Brown polynomials. This approach was inspired by the residual plots shown in Figure 4 and Figure 6a. The image space is divided into two concentric radial zones with a separate set of radial distortion parameters defined and determined for each zone, i.e., a bi-radial approach. The polynomials are then applied as follows:
Initially, the value was manually set to 1.5 mm. The standard deviation of the unit weight after the polynomial fit was = 0.96 µm (0.62 px). Figure 9b shows the fitted bi-radial function as well as the radial components as a function of r.
Both extended polynomials fit much better to the radial components than the standard Brown polynomial. This holds especially for the center region of the image, which is most relevant for tasks such as orthophoto mosaic generation. Note that the bi-radial model performs slightly better, which can also be seen in the graphs in Figure 9.
2.4. Bundle Adjustment with the Extended Radial Correction Functions
Both extended functions of Section 2.2 and Section 2.3 for the radial distortion correction were implemented in bundle adjustments. The model in [15], with addition of additional even coefficients () to the Brown model and hence in total using six parameters for the radial distortion description, is included in model C. Thus, the corresponding radial correction function was used:
| Model C: Full polynomial radial distortion model |
| Step 1: |
| Step 2: |
| Step 3: |
| with and |
| Step 4: |
Model C was applied to the image data of the DJI Mavic Pro camera. Again, the object coordinates of the reference target field (obtained photogrammetically using the Panasonic Lumix DMC-GX80 camera) were kept fixed during the bundle adjustment. The computed parameters with their standard deviations and significance values are summarized in Table 2.

Table 2.
Interior orientation parameters of Model C, their standard deviation and significance.
Table 3 shows the correlations between the parameters of model C. The radial distortion parameters (, , , , , ) reveal high correlation values between each other, partly almost 100%. High correlations between radial distortion parameters are a typical phenomenon, even for model B.

Table 3.
Correlations between the parameters of model C.
In model D, the second extension option, i.e., the bi-radial radial distortion correction, was integrated (see Equation (15)).
| Model D: Bi-radial distortion model |
| Step 1: |
| Step 2: |
| Step 3: |
| with and |
| Step 4: |
The estimated parameters of the interior orientation with their standard deviations and significance values are summarized in Table 4. Note that the standard deviation of the camera constant is ca. five times smaller in model D due to a more relaxed correlation situation.

Table 4.
Interior orientation parameters of Model D, their standard deviation and significance.
Table 5 shows the correlations between the parameters of model D. The parameter groups for the radial distortion correction (group 1: , , , and group 2: , , ) reveal high correlation values between each other within the groups, sometimes almost 100%. However, the correlations between groups are close to zero.

Table 5.
Correlations between the parameters of model D.
Table 6 depicts the standard deviations of the unit weights of the bundle adjustments of the different models applied to the data of the DJI Mavic Pro camera to enable a first assessment of differences between different approaches. It already becomes obvious that models C and D reveal a similar performance and that they seem to be significantly better than Model B. A further accuracy analysis is shown in Section 2.7.

Table 6.
Standard deviation of the unit weight after the bundle adjustment with fixed object coordinates and considering different models describing lens distortions.
2.5. Systematic Effects in the Residual Errors of the Extended Distortion Models
Residual plots were computed to give a visual impression of potential remaining systematic residual errors (Figure 10 for model C and Figure 11 for model D, i.e., bi-radial). Both plots show randomly distributed residuals that have much smaller magnitudes compared to those in model B (see Figure 4).
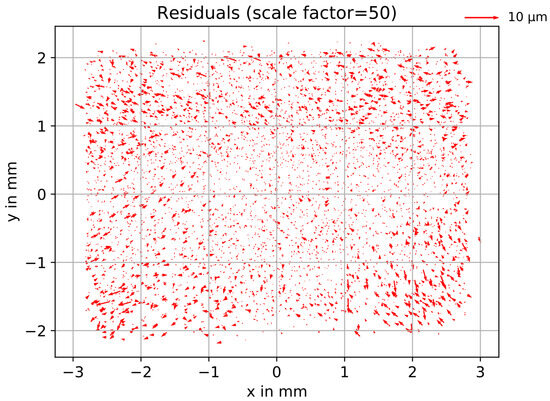
Figure 10.
Residual plot after bundle adjustment with fixed object coordinates using model C.
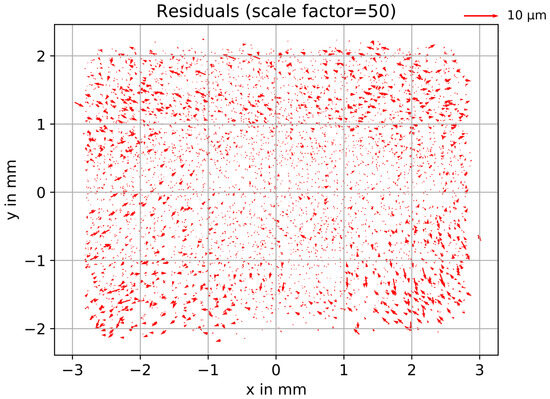
Figure 11.
Residual plot after bundle adjustment with fixed object coordinates using model D.
Again, the residuals were decomposed into a radial and tangential part. Figure 12 shows the result for model C, whereas Figure 13 depicts the components for the bi-radial model (D). For model C, an oscillation in the radial components becomes obvious (Figure 12a). This effect could be caused by the high correlations between the radial distortion parameters of model C. The correlations between the parameter groups for radial distortion of model D are close to zero. However, this effect does not influence the standard deviation of the unit weight significantly. The components reveal the aspired non-systematic behavior for the bi-radial model D (Figure 13a).
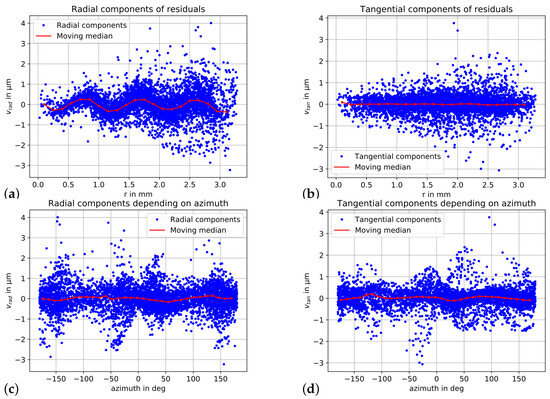
Figure 12.
Residuals after bundle adjustment using model C. (a) Radial components versus image radius. (b) Tangential components versus image radius. (c) Radial components versus the azimuth of the image point. (d) Tangential components versus the azimuth of the image point. For all subplots, the moving median is shown in red.
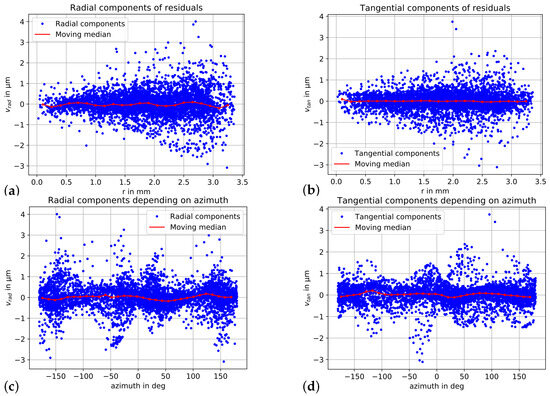
Figure 13.
Residuals after bundle adjustment using model D: (a) Radial components versus image radius. (b) Tangential components versus image radius. (c) Radial components versus the azimuth of the image point. (d) Tangential components versus the azimuth of the image point. For all subplots, the moving median is shown in red.
2.6. Strategy for Automatic Zone Segmentation of the Bi-Radial Model
To date, the radial zone segmentation radius of the bi-radial model had been manually set to 1.5 mm. In general, the optimal value should be determined automatically. However, cannot be estimated in bundle adjustment due to its discrete nature. An obvious first approach is an iterative (brute force) computation of the bundle adjustment with different values of , where the best corresponds to the lowest standard deviation of the unit weight. Accordingly, Figure 14a shows the standard deviation of the unit weight as a function of the limit value . In the range of 1.3 mm 1.8 mm, does not change significantly, indicating that the selection of the segmentation value for the concentric zones is rather uncritical.
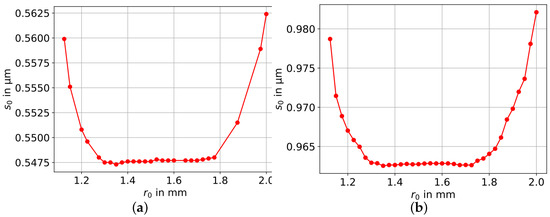
Figure 14.
(a) Standard deviation of the unit weight of the bundle adjustment as a function of . (b) Standard deviation of the unit weight of the polynomial fit as a function of .
A much less computationally intensive approach is the brute force computation of the polynomial fit introduced in Section 2.1. Only one bundle adjustment using model A is performed for the polynomial analysis. Then, the radial components of the residuals are calculated (Equation (9)). Afterwards, a polynomial fit in the residual data is performed by a step-wise increase in the values of . The standard deviation of the unit weight of the polynomial fit as a function of is displayed in Figure 14b. The behavior coincides with the former approach (shown in Figure 14a), and therefore the polynomial analysis is recommended.
2.7. Validation
The aim of this subsection is to evaluate the accuracy of the proposed extended models C and D. Their validation was performed by comparing the object coordinates, which were calculated in a free net adjustment (self-calibration) using images captured with the UAV camera, to the reference coordinates, which were independently obtained by a second camera with a significantly higher accuracy potential (Nikon D300 camera (from company Nikon) with a Nikkor lens with a focal length of 20 mm). The same target field as in Section 2.1 was used (Figure 5; 7 m × 3 m × 1 m), this time with four additional scale bars of superior precision included. Figure 15 shows the object points and the position of the scale bars as well as the image network geometry used for both cameras.
Figure 15.
Object points and scale bars as well as the image orientations (illustration created with AICON 3D Studio (version 12.50.03)).
Figure 16 shows the combined violin plots (including extreme values, blue) and box plots (including outliers in magenta) of the standard deviations (, , ) of the object point coordinates from the bundle adjustment. The standard deviations of the unit weights are also listed below the plots. The Nikon D300 camera revealed the smallest values for the standard deviations (left side of Figure 16). The standard deviations of the DJI Mavic Pro camera—computed with the different models B, C and D - highlight that the errors could be reduced using models C and D. The median of was reduced by two thirds in the case of model D when compared to model B. Models C and D (bi-radial) showed a similar behavior, with model D indicating slightly better values. However, both models still exhibited higher standard deviations compared to the values obtained with the Nikon camera data (using model B).
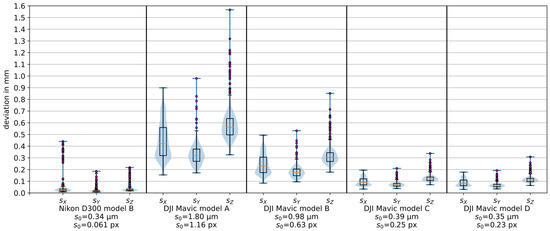
Figure 16.
Combined violin and box plots of the object coordinates’ standard deviations computed in the bundle adjustment and corresponding standard deviation of the unit weight () in mm and in px.
In order to evaluate the accuracy of the different models, the object coordinate sets obtained from the image bundles of both cameras (DJI Mavic Pro and Nikon D300) were compared, with the latter camera providing the reference coordinates. Therefore, the parameters of a least-squares rigid transformation were computed to align the coordinates to the reference. The rigid body transform was chosen because the bundle adjustment was performed with scale bars so that the scale is comparable between the coordinate sets. The distribution of the residual vectors is visualized on the left side of Figure 17. The estimation of the parameters was performed between the data sets of the Nikon D300 using model B and the DJI Mavic Pro using different models (i.e., model B in Figure 17a, model C in Figure 17b, model D in Figure 17c). Model C and model D show significantly smaller residual vectors than model B. Differences between model C and D are hardly noticeable. The standard deviations of the unit weights of the parameter determination of the rigid body transformation were 0.39 mm for the first case (DJI model B), 0.23 mm for the second (DJI model C), and 0.24 mm the third case (DJI model D).
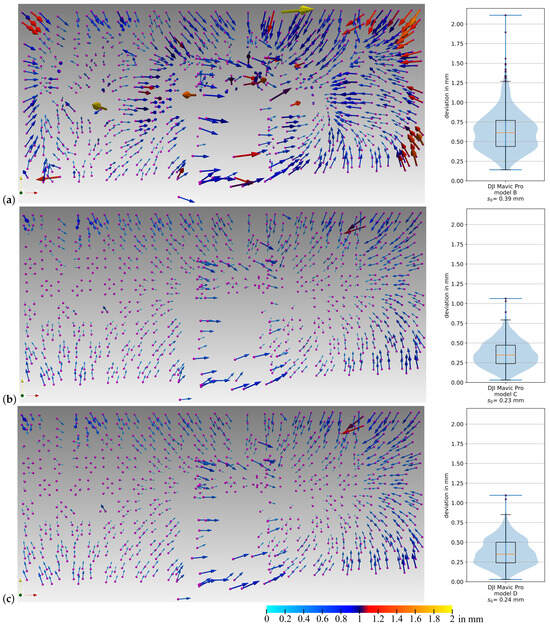
Figure 17.
Residuals (left side, scale factor 300) and combined violin and box plots (right side) for the residuals’ lengths of the rigid body transformation between: (a) DJI Mavic Pro camera (model B) and Nikon D300 camera (model B), (b) DJI Mavic Pro camera (model C) and Nikon D300 camera (model B), (c) DJI Mavic Pro camera (model D) and Nikon D300 camera (model B).
Residual systematics are still visible in Figure 17 and deviations, especially of the points in the foreground, are noticeable. Due to their smaller number, these foreground points have a smaller effect on the transformation parameter computation than the many more points on the wall in the background. This circumstance may lead to higher residuals.
Figure 17 also shows the combined violin and box plots for the residual vector lengths of the rigid body transform using the different models for the DJI Mavic Pro camera. The median residual vector length is 0.62 mm for the first case (standard Brown model B) and the maximum amounts to 2.1 mm. For models C and D, the median residual vector length is 0.35 mm and the maximum deviations are 1.1 mm. These (standard) deviations are considered as accuracy values.
3. Discussion
Based on the results presented, the following conclusions were drawn:
- In this study, we could demonstrate that the estimation of a bi-radial distortion model can decrease the errors during bundle adjustment when using low-cost UAV cameras that might be difficult to model with standard, physics-based models such as the Brown model. The unusual systematic errors of the DJI Mavic Pro camera could be reduced using the proposed bi-radial model (model D) as well as model C (extended polynomial of radial distortion). The standard deviations of the unit weights of the bundle adjustment could be significantly reduced (60% for model C and 64% for model D). The improvement was also recognizable visually in the residual vector plots. The improvement was most evident in the center of the images.
- In contrast to model C, a segmentation zone radius has to be determined for our proposed model D. Our experiments revealed that there was a range, between 1.3 mm and 1.8 mm, in which the results did not change significantly. Furthermore, an automatic determination method is possible (as shown in Section 2.6). The additional step of the determination of requires a higher computing effort compared to model C.
- For the accuracy evaluation, the object coordinates computed via free bundle adjustment of the DJI Mavic Pro camera with the different models were compared to the reference coordinates obtained by a well-known camera. The residuals of a rigid body transformation were analyzed, where the standard deviation of the unit weight of the transformation was reduced by 40% using models C and D compared to the standard Brown model (model B). Model C and model D showed similar residuals and the differences were hardly noticeable.
- Future work could concentrate on a constraint in which the polynomials of the bi-radial model fit together at the transition point between both zones concerning function value and the derivative similar to spline constraints.
4. Conclusions
Popular low-cost UAV-based cameras such as the very widespread DJI Mavic Pro camera often show unusual lens distortion patterns, which cannot be handled well by standard camera modeling and calibration approaches. We introduce a novel bi-radial lens distortion model consisting of separate polynomials for two concentric image zones. While standard models show clear systematic effects in residual plots after bundle adjustment, the new model provides significantly better precision values and leaves no systematic effects in the residual plot, with the most evident improvement at the image center. The segmentation of the image space into the two zones can be performed automatically and this turned out to be rather uncritical. The model may also be useful for modeling mobile phone imaging devices and other similar low-cost cameras. It may also be easily extended to a segmentation of the image into more than two concentric zones.
Author Contributions
Conceptualization, F.L., D.M. and H.S.; methodology, F.L.; software, F.L.; validation, F.L., D.M. and H.S.; formal analysis, F.L.; investigation, F.L. and D.M.; data curation, F.L. and D.M.; writing—original draft preparation, F.L.; writing—review and editing, D.M., H.S., A.E. and H.-G.M.; visualization, F.L.; supervision, H.-G.M.; project administration, H.-G.M.; funding acquisition, H.-G.M. All authors have read and agreed to the published version of the manuscript.
Funding
A part of this work has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation–SFB/TRR 280; Projekt-ID: 417002380 and Projekt-ID: 405774238).
Data Availability Statement
The authors are willing to share the experimental data upon personal request.
Acknowledgments
We thank Michael Gebhardt for their preliminary analyses of a low-cost UAV camera and Christian Mulsow for their discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schmid, H.H. Eine allgemeine analytische Lösung für die Aufgabe der Photogrammetrie. Bildmess. Luftbildwes. 1958, 4/58, 103–113. [Google Scholar]
- von Seidel, P.L. Ueber die Theorie der Fehler, mit welchen die durch optische Instrumente gesehenen Bilder, behaftet sind, und über die mathematischen Bedingungen ihrer Aufhebung. In Abhandlungen der Naturwissenschaftlich-Technischen Commission bei der Königl; Bayerischen Akademie der Wissenschaften in München: Munich, Germany, 1857; Volume 1, Chapter 10; pp. 227–267. [Google Scholar]
- Brown, D.C. Close-Range Camera Calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Conrady, A.E. Decentred Lens-Systems. Mon. Not. R. Astron. Soc. 1919, 79, 384–390. [Google Scholar] [CrossRef]
- Brown, D.C. Decentering distortion of lenses. Photogramm. Eng. 1966, 32, 444–462. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; De Gruyter: Berlin, Germany; Boston, MA, USA, 2020. [Google Scholar] [CrossRef]
- El-Hakim, S.F. Real-Time Image Metrology with CCD Cameras. Photogramm. Eng. Remote Sens. 1986, 52, 1757–1766. [Google Scholar]
- Luhmann, T.; Fraser, C.; Maas, H.G. Sensor modelling and camera calibration for close-range photogrammetry. Isprs J. Photogramm. Remote Sens. 2016, 115, 37–46. [Google Scholar] [CrossRef]
- Ebner, H. Self calibrating block adjustment. In Proceedings of the XIII ISP Congress, Helsinki, Finland, 11–23 July 1976; pp. 540–558. [Google Scholar]
- Grün, A. Experiences with the self-calibrating bundle adjustment. In Proceedings of the ACSM-ASP Convention, Washington, DC, USA, 3 March 1978. [Google Scholar]
- Abraham, S.; Förstner, W. Zur automatischen Modellwahl bei der Kalibrierung von CCD-Kameras. In Mustererkennung 1997; Paulus, E., Wahl, F.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 147–155. [Google Scholar] [CrossRef]
- Tang, R. New mathematical self-calibration models in aerial photogrammetry. In Proceedings of the DGPF-Tagungsband, Potsdam, Germany, 14–17 March 2012; Volume 21, pp. 457–469. [Google Scholar]
- Tang, R. A rigorous and flexible calibration method for digital airborne camera systems. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, 39, 153–158. [Google Scholar] [CrossRef]
- Richter, K.; Mader, D.; Seidl, K.; Maas, H.G. Development of a geometric model for an all-reflective camera system. ISPRS J. Photogramm. Remote Sens. 2013, 86, 41–51. [Google Scholar] [CrossRef]
- Hastedt, H.; Luhmann, T.; Przybilla, H.J.; Rofallski, R. Evaluation of interior orientation modelling for cameras with aspheric lenses and image pre-processing with special emphasis to SFM reconstruction. Int. Arch. Photogramm. Remote Sens. Spat. 2021, 43, 17–24. [Google Scholar] [CrossRef]
- Reznicek, J.; Luhmann, T. Finite-Element Approach to Camera Modelling and Calibration. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2019, 87, 1–17. [Google Scholar] [CrossRef]
- Detchev, I.; Lichti, D. Calibrating a lens with a local distortion model. Int. Arch. Photogramm. Remote Sens. Spat. 2020, 43, 765–769. [Google Scholar] [CrossRef]
- Eltner, A.; Karrasch, P.; Stoecker, C.; Klingbeil, L.; Hoffmeister, D.; Kaiser, A.; Rovere, A. UAVs in Environmental Sciences—Methods and Applications; WBG Academic: Darmstadt, Germany, 2022. [Google Scholar] [CrossRef]
- Eltner, A.; Bertalan, L.; Grundmann, J.; Perks, M.T.; Lotsari, E. Hydro-morphological mapping of river reaches using videos captured with UAS. Earth Surf. Process. Landf. 2021, 46, 2773–2787. [Google Scholar] [CrossRef]
- James, M.R.; Antoniazza, G.; Robson, S.; Lane, S.N. Mitigating systematic error in topographic models for geomorphic change detection: Accuracy, precision and considerations beyond off-nadir imagery. Earth Surf. Process. Landf. 2020, 45, 2251–2271. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).