Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest
Abstract
:1. Introduction
- (i)
- to evaluate and compare the effectiveness of the random forest (RF) and extreme gradient boosting (XGBoosting) ensemble regression methods in estimating AGB with different predictor sets;
- (ii)
- to evaluate the potential of Sentinel-1 (SAR) texture and Sentinel-2 (MSI) for AGB mapping in TDF;
- (iii)
- to identify the optimal variables to predict AGB; and
- (iv)
- to create a prediction map of the forest AGB within the research zone using the most suitable model.
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.2.1. Field Dataset and Allometric Equation Estimation
2.2.2. Remote Sensing Data Acquisition
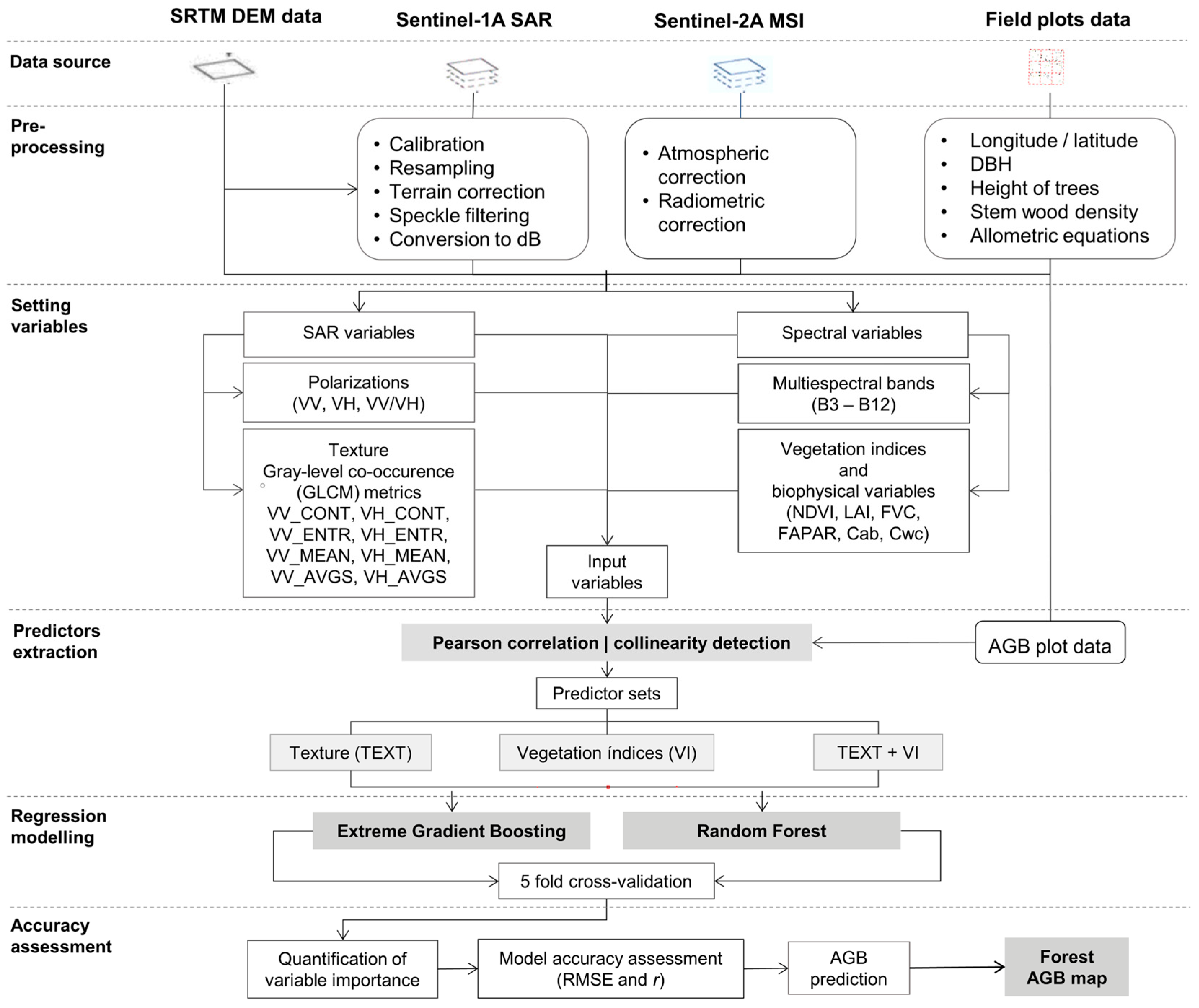
2.3. Data Pre-Processing and Setting Variables
2.3.1. SAR Texture Data Processing
2.3.2. Multispectral Data Processing
2.4. Extraction of Predictor Variables (Plot-Level Variable Extraction from Remotely Sensed Data)
2.5. Predictor Variable Reduction and Selection
2.6. Data Analysis (Statistical and Regression Algorithms for Modeling AGB)
2.6.1. Random Forest Regression Model
2.6.2. Extreme Gradient Boosting Model
- For nrounds = from (245 to 420);
- For learning_rate values, eta = (0.009 to 0.03);
- For max_depth = from (3 to 5).
- For min_child_weight = from (0.4 to 0.9);
- For subsample = from (0.3 to 0.8);
- For colsample_bytree = from (0.3 to 0.7).
- For gamma = from (0 to 10).
2.7. Model Accuraccy Assessment of Estimated AGB
3. Results
3.1. Selection of Variables
| (S-1) SAR Texture Set | (S-2) MSI Set | ||||
|---|---|---|---|---|---|
| Variable | Coefficient | Correlation with AGB. r | Variable | Coefficient | Correlation with AGB. r |
| Intercept | 2.20 | ------ | Intercept | −12.61 | ------ |
| D_VH_GLCMMean | −8.341 | −0.28 *** | D_B3 | 168.29 | −0.07 *** |
| D_VH_GLCMCorr | 1.92 | −0.22 ** | D_B7 | −39.79 | 0.12 ** |
| D_VV_Cont | −3.83 | 0.10 *** | D_lai | 9.69 | 0.23 * |
| D_VV_GLCMMean | −5.12 | −0.11 *** | W_B6 | 224.54 | 0.32 *** |
| D_VV_GLCMVari | −4.90 | −0.12 *** | W_B7 | −61.56 | 0.40 ** |
| D_VH_ASM | 8.52 | −0.16 ** | W_B8A | −301.76 | 0.42 *** |
| D_VH_Dis | 2.20 | 0.15 ** | W_B11 | 389.02 | −0.20 *** |
| D_VV_Ent | −3.28 | 0.15 ** | W_cab | 0.13 | 0.48 *** |
| D_VV_MAX | 5.13 | −0.13 * | W_cw | 469.03 | 0.50 *** |
| D_VV_Ene | 3.52 | −0.14 * | |||
| W_VV_GLCMMean | −8.45 | −0.20 ** | |||
| W_VV_GLCMVari | 4.25 | −0.21 ** | |||
| W_VH_Dis | 4.90 | 0.12 * | |||
| W_VH_GLCMCorr | 3.19 | −0.18 * | |||
| W_VV_Hom | 7.75 | −0.19 * | |||
| W_VV_Ent | 3.39 | 0.19 * | |||
3.2. Comparison Analysis of the AGB Models
3.2.1. RF and XGBoost Regression Model Performance
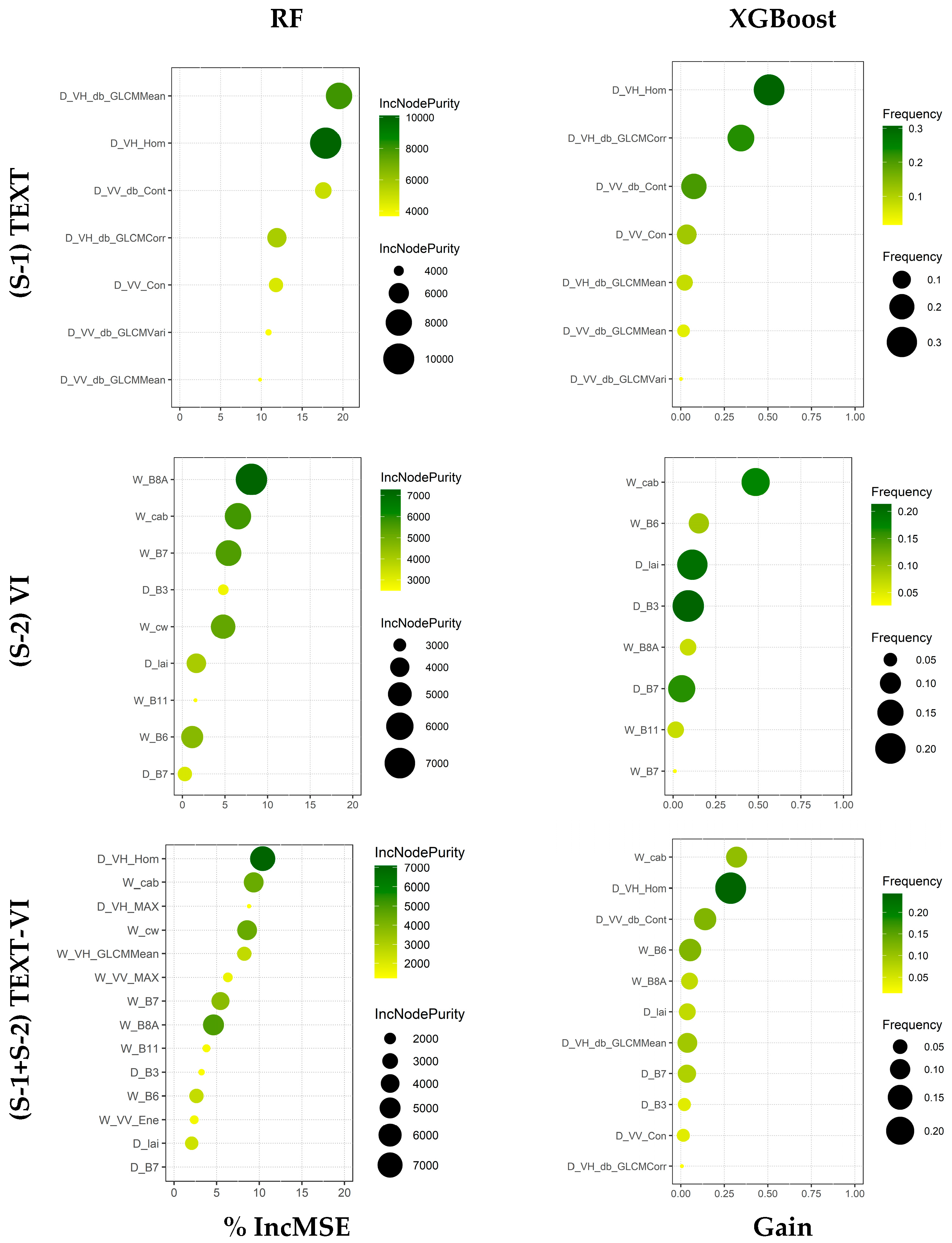
3.2.2. Ranking of Variable Importance for AGB Estimation
3.3. Mapping of Estimated Forest AGB
4. Discussion
4.1. Model Performance: Efficiency of the RF and XGBoost Using Predictor Set
4.2. Potential of Sentinel Imagery Combination for Estimating AGB
4.3. Important RS Predictor Variables
4.4. Forest AGB Map
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonan, G.B. Forests and climate change. Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Mitchard, E.T.A. The tropical forest carbon cycle and climate change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef] [PubMed]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2007, 27, 1297–1328. [Google Scholar] [CrossRef]
- Goetz, S.J.; Hansen, M.; Houghton, R.A.; Walker, W.; Laporte, N.; Busch, J. Measurement and monitoring needs, capabilities and potential for addressing reduced emissions from deforestation and forest degradation under REDD+. Environ. Res. Lett. 2015, 10, 123001. [Google Scholar] [CrossRef]
- West, P.W. Tree and Forest Measurement; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Bustamante, M.M.C.; Roitman, I.; Aide, T.M.; Alencar, A.; Anderson, L.O.; Aragão, L.; Asner, G.P.; Barlow, J.; Berenguer, E.; Chambers, J.; et al. Toward an integrated monitoring framework to assess the effects of tropical forest degradation and recovery on carbon stocks and biodiversity. Glob. Chang. Biol. 2016, 22, 92–109. [Google Scholar] [CrossRef] [PubMed]
- Corona, P. Consolidating new paradigms in large-scale monitoring and assessment of forest ecosystems. Environ. Res. 2016, 144, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Waring, R.H.; Way, J.; Hunt, E.R.; Morrissey, L.; Ranson, K.J.; Weishampel, J.F.; Oren, R.; Franklin, S.E. Imaging Radar for Ecosystem Studies. BioScience 1995, 45, 715–723. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height estimation from Shuttle Radar Topography Mission and National Elevation Datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Rosenqvist, A.; Shimada, M.; Igarashi, T.; Watanabe, M.; Tadono, T.; Yamamoto, H. Support to multi-national environmental conventions and terrestrial carbon cycle science by ALOS and ADEOS-II-the Kyoto & carbon initiative. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2015, 9, 63–105. [Google Scholar]
- Kumar, L.; Sinha, P.; Taylor, S.; Alqurashi, A.F. Review of the use of remote sensing for biomass estimation to support renewable energy generation. J. Appl. Rem. Sens. 2015, 9, 97696. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Fremout, T.; Cobián-De Vinatea, J.; Thomas, E.; Huaman-Zambrano, W.; Salazar-Villegas, M.; la Fuente, D.L.-D.; Bernardino, P.N.; Atkinson, R.; Csaplovics, E.; Muys, B. Site-specific scaling of remote sensing-based estimates of woody cover and aboveground biomass for mapping long-term tropical dry forest degradation status. Remote Sens. Environ. 2022, 276, 113040. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above ground biomass across different fertilizer treatments. ISPRS J. Photogramm. Remote Sens. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Relationships between forest stand parameters and Landsat TM spectral responses in the Brazilian Amazon Basin. For. Ecol. Manag. 2004, 198, 149–167. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS J. Photogramm. Remote Sens. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2010, 25, 3999–4014. [Google Scholar] [CrossRef]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2007, 26, 2509–2525. [Google Scholar] [CrossRef]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle. A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Drake, J.B.; Knox, R.G.; Dubayah, R.O.; Clark, D.B.; Condit, R.; Blair, J.B.; Hofton, M. Above-ground biomass estimation in closed canopy Neotropical forests using lidar remote sensing. Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests—The potential of combined X- and L-band SAR data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Le Toan, T. L- and P-band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
- Santos, J. Airborne P-band SAR applied to the aboveground biomass studies in the Brazilian tropical rainforest. Remote Sens. Environ. 2003, 84, 482–493. [Google Scholar] [CrossRef]
- Joshi, N.; Mitchard, E.T.A.; Brolly, M.; Schumacher, J.; Fernández-Landa, A.; Johannsen, V.K.; Marchamalo, M.; Fensholt, R. Understanding ‘saturation’ of radar signals over forests. Sci. Rep. 2017, 7, 3505. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Goetz, S.J.; Baccini, A.; Laporte, N.T.; Johns, T.; Walker, W.; Kellndorfer, J.; Houghton, R.A.; Sun, M. Mapping and monitoring carbon stocks with satellite observations. A comparison of methods. Carbon Balance Manag. 2009, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Cutler, M.E.J.; Boyd, D.S.; Foody, G.M.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data. An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Tien Bui, D. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning. A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 red-edge bands for empirical estimation of green LAI and chlorophyll content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Wan, R.; Li, B. Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms. A Case Study of the Dabie Mountain Region, China. Remote Sens. 2022, 14, 176. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Xi, Y. Estimation of Forest Above-Ground Biomass by Geographically Weighted Regression and Machine Learning with Sentinel Imagery. Forests 2018, 9, 582. [Google Scholar] [CrossRef]
- Laurin, G.V.; Balling, J.; Corona, P.; Mattioli, W.; Papale, D.; Puletti, N.; Rizzo, M.; Truckenbrodt, J.; Urban, M. Above-ground biomass prediction by Sentinel-1 multitemporal data in central Italy with integration of ALOS2 and Sentinel-2 data. J. Appl. Rem. Sens. 2018, 12, 1. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Askar, A.; Stratoulias, D.; Wicaksono, P. Combined use of Sentinel-1 and Sentinel-2 data for improving above-ground biomass estimation. Geocarto Int. 2022, 37, 366–376. [Google Scholar] [CrossRef]
- Spracklen, B.; Spracklen, D.V. Synergistic Use of Sentinel-1 and Sentinel-2 to Map Natural Forest and Acacia Plantation and Stand Ages in North-Central Vietnam. Remote Sens. 2021, 13, 185. [Google Scholar] [CrossRef]
- David, R.M.; Rosser, N.J.; Donoghue, D.N.M. Improving above ground biomass estimates of Southern Africa dryland forests by combining Sentinel-1 SAR and Sentinel-2 multispectral imagery. Remote Sens. Environ. 2022, 282, 113232. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; López-Sánchez, C.A.; Álvarez-González, J.G.; García-Gutiérrez, J. A Comparison of Machine Learning Techniques Applied to Landsat-5 TM Spectral Data for Biomass Estimation. Can. J. Remote Sens. 2016, 42, 690–705. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Le, N.N.; Bui, D.T. Estimating aboveground biomass of a mangrove plantation on the Northern coast of Vietnam using machine learning techniques with an integration of ALOS-2 PALSAR-2 and Sentinel-2A data. Int. J. Remote Sens. 2018, 39, 7761–7788. [Google Scholar] [CrossRef]
- Liu, J.; Yue, C.; Pei, C.; Li, X.; Zhang, Q. Prediction of Regional Forest Biomass Using Machine Learning. A Case Study of Beijing, China. Forests 2023, 14, 1008. [Google Scholar] [CrossRef]
- Wu, C.; Shen, H.; Shen, A.; Deng, J.; Gan, M.; Zhu, J.; Xu, H.; Wang, K. Comparison of machine-learning methods for above-ground biomass estimation based on Landsat imagery. J. Appl. Rem. Sens. 2016, 10, 35010. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, H.; Ma, K.; Fu, L.; Tang, J. Improving aboveground biomass estimation of natural forests on the Tibetan Plateau using spaceborne LiDAR and machine learning algorithms. Ecol. Indic. 2022, 143, 109365. [Google Scholar] [CrossRef]
- Labrecque, S.; Fournier, R.A.; Luther, J.E.; Piercey, D. A comparison of four methods to map biomass from Landsat-TM and inventory data in western Newfoundland. For. Ecol. Manag. 2006, 226, 129–144. [Google Scholar] [CrossRef]
- Fuchs, H.; Magdon, P.; Kleinn, C.; Flessa, H. Estimating aboveground carbon in a catchment of the Siberian forest tundra. Combining satellite imagery and field inventory. Remote Sens. Environ. 2009, 113, 518–531. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Optimizing the k-Nearest Neighbors technique for estimating forest aboveground biomass using airborne laser scanning data. Remote Sens. Environ. 2015, 163, 13–22. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Wan, R.; Wang, P.; Wang, X.; Yao, X.; Dai, X. Mapping Aboveground Biomass of Four Typical Vegetation Types in the Poyang Lake Wetlands Based on Random Forest Modelling and Landsat Images. Front. Plant Sci. 2019, 10, 1281. [Google Scholar] [CrossRef]
- Wu, C.; Tao, H.; Zhai, M.; Lin, Y.; Wang, K.; Deng, J.; Shen, A.; Gan, M.; Li, J.; Yang, H. Using nonparametric modeling approaches and remote sensing imagery to estimate ecological welfare forest biomass. J. For. Res. 2018, 29, 151–161. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J. Estimating forest aboveground biomass using temporal features extracted from multiple satellite data products and ensemble machine learning algorithm. Geocarto Int. 2023, 38, 98. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction. The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef] [PubMed]
- Pizano, C.; García Martínez, H. El Bosque Seco Tropical en Colombia. Bogotá: Ministerio de Ambiente y Desarrollo Sostenible; Instituto de Investigación de Recursos Biológicos Alexander von Humboldt: Bogotá, Colombia, 2014; 349p. [Google Scholar]
- Espinal, S. Zonas de Vida o Formaciones Vegetales de Colombia. Memoria Explicativa Sobre el Mapa Ecologico. Vol. XIII, No. 11. (+Maps, Scale 1. 500,000); Subdireccion Agrologica, Bogotá, Instituto Geografico “Agustin Codazzi”: Bogotá, Colombia, 1977.
- Santoro. Estudios de Caracterización Biofísica y Socioeconómica de la Ecorregión Estratégica del Valle del Alto Magdalena; (2002–Report); Componente Aguas, Ministerio de Ambiente, CORTOLIMA, CAM, Universidad del ToIima and Universidad Surcolombiana: Ibagué, Colombia, 2002.
- Norden, N.; González-M, R.; Avella-M, A.; Salgado-Negret, B.; Alcázar, C.; Rodríguez-Buriticá, S.; Aguilar-Cano, J.; Castellanos-Castro, C.; Calderón, J.J.; Caycedo-Rosales, P.; et al. Building a socio-ecological monitoring platform for the comprehensive management of tropical dry forests. Plants People Planet 2020, 2, 228. [Google Scholar]
- Condit, R.; Lao, S.; Singh, A.; Esufali, S.; Dolins, S. Data and database standards for permanent forest plots in a global network. For. Ecol. Manag. 2014, 316, 21–31. [Google Scholar] [CrossRef]
- Carreiras, J.; Melo, J.; Vasconcelos, M. Estimating the Above-Ground Biomass in Miombo Savanna Woodlands (Mozambique, East Africa) Using L-Band Synthetic Aperture Radar Data. Remote Sens. 2013, 5, 1524–1548. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.; Nezry, E.; Touzi, R.; Laur, H. Maximum a Posteriori Speckle Filtering and First Order Texture Models in Sar Images. In Proceedings of the 10th Annual International Symposium on Geoscience and Remote Sensing, Washington, DC, USA, 20–24 May 1990; pp. 2409–2412. [Google Scholar] [CrossRef]
- Huang, Y.; van Genderen, J.L. Evaluation of several speckle filtering techniques for ERS-1 & 2 imagery. Int. Arch. Photogramm. Remote Sens. 1996, 31, 164–169. [Google Scholar]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Richter, R.; Schlapfer, D.; Muller, A. Operational Atmospheric Correction for Imaging Spectrometers Accounting for the Smile Effect. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1772–1780. [Google Scholar] [CrossRef]
- Ramsey, P.H. Critical Values for Spearman’s Rank Order Correlation. J. Educ. Stat. 1989, 14, 245–253. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal. Coupling In Situ Measurements with Landsat 8 Satellite Data. Remote Sens. 2018, 10, 1848. [Google Scholar] [CrossRef]
- Bourgoin, C.; Blanc, L.; Bailly, J.-S.; Cornu, G.; Berenguer, E.; Oszwald, J.; Tritsch, I.; Laurent, F.; Hasan, A.F.; Sist, P.; et al. The Potential of Multisource Remote Sensing for Mapping the Biomass of a Degraded Amazonian Forest. Forests 2018, 9, 303. [Google Scholar] [CrossRef]
- Dang, A.T.N.; Nandy, S.; Srinet, R.; Luong, N.V.; Ghosh, S.; Kumar, A.S. Forest aboveground biomass estimation using machine learning regression algorithm in Yok Don National Park, Vietnam. Ecol. Inform. 2019, 50, 24–32. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2007, 26, 217–222. [Google Scholar] [CrossRef]
- Freeman, E.A.; Moisen, G.G.; Coulston, J.W.; Wilson, B.T. Random forests and stochastic gradient boosting for predicting tree canopy cover. Comparing tuning processes and model performance. Can. J. For. Res. 2016, 46, 323–339. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; 426p. [Google Scholar]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Adv. Neural Inf. Process. Syst. 2013, 26, 431–439. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost. A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates. A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.I.; Hurtt, G.C.; Thomas, R.Q.; Chambers, J.Q. Clustered disturbances lead to bias in large-scale estimates based on forest sample plots. Ecol. Lett. 2008, 11, 554–563. [Google Scholar] [CrossRef]
- Forkuor, G.; Zoungrana, J.-B.; Dimobe, K.; Ouattara, B.; Vadrevu, K.P.; Tondoh, J.E. Above-ground biomass mapping in West African dryland forest using Sentinel-1 and 2 datasets—A case study. Remote Sens. Environ. 2020, 236, 111496. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Puletti, N.; Hawthorne, W.; Liesenberg, V.; Corona, P.; Papale, D.; Chen, Q.; Valentini, R. Discrimination of tropical forest types, dominant species, and mapping of functional guilds by hyperspectral and simulated multispectral Sentinel-2 data. Remote Sens. Environ. 2016, 176, 163–176. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Abdel-Rahman, E.M.; Ismail, R. Estimating standing biomass in papyrus (Cyperus papyrus L.) swamp. Exploratory of in situ hyperspectral indices and random forest regression. Int. J. Remote Sens. 2014, 35, 693–714. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Liesenberg, V.; Chen, Q.; Guerriero, L.; Del Frate, F.; Bartolini, A.; Coomes, D.; Wilebore, B.; Lindsell, J.; Valentini, R. Optical and SAR sensor synergies for forest and land cover mapping in a tropical site in West Africa. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 7–16. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]



| Forest Stand Plot ID | Forest Stratum | Stage of Recovery | Number of Subplots | # of Trees > 15 cm DBH | Mean AGB (Mg/ha−1) |
|---|---|---|---|---|---|
| C-Plana | Degraded | >30 Yr. | 25 | 205 | 63.21 |
| C-Loma | Low degraded | >40 Yr. | 25 | 302 | 92.21 |
| Tambor | Low degraded | >60 Yr. | 25 | 185 | 133.65 |
| Jabiru | Degraded | >30 Yr. | 25 | 324 | 77.39 |
| Mission | Observation Date/Season | Cloud Cover (%) | Cell Size (m) | Unit Resource Identifier (URI) |
|---|---|---|---|---|
| S-1A | 19 May 2015 Dry | - | 10 | S1A_IW_GRDH_1SDV_20150519T231327_20150519T231352_005997_007BAA_3573 |
| S-1A | 27 November 2015 Wet | - | 10 | S1A_IW_GRDH_1SDV_20151127T231352_20151127T231417_008797_00C8C4_2024 |
| S-2A | 21 December 2015 Wet | 7 | 10 | S2A_MSIL1C_20151221T153112_N0201_R025_T18NWL_20151221T153112 |
| S-2A | 18 June 2016 Dry | 5 | 10 | S2A_MSIL1C_20160618T152642_N0204_R025_T18NWL_20160618T153021 |
| Model Abbrev. | Predictor Sets | Training Dataset | Testing Dataset | |||
|---|---|---|---|---|---|---|
| R2 Observed vs. Estimated | Cross-Validation RMSE (Mg/ha−1) | R2 Observed vs. Estimated | Cross-Validation RMSE (Mg/ha−1) | |||
| RF | (S-1) | TEXT | 0.83 | 31.03 | 0.64 | 46.10 |
| (S-2) | VI | 0.79 | 40.30 | 0.70 | 45.44 | |
| (S-1 + S-2) | TEXT-VI | 0.81 | 38.60 | 0.78 | 42.25 | |
| XGBoost | (S-1) | TEXT | 0.71 | 41.75 | 0.43 | 50.53 |
| (S-2) | VI | 0.62 | 45.90 | 0.57 | 52.95 | |
| (S-1 + S-2) | TEXT-VI | 0.73 | 40.60 | 0.60 | 48.41 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salazar Villegas, M.H.; Qasim, M.; Csaplovics, E.; González-Martinez, R.; Rodriguez-Buritica, S.; Ramos Abril, L.N.; Salazar Villegas, B. Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest. Remote Sens. 2023, 15, 5086. https://doi.org/10.3390/rs15215086
Salazar Villegas MH, Qasim M, Csaplovics E, González-Martinez R, Rodriguez-Buritica S, Ramos Abril LN, Salazar Villegas B. Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest. Remote Sensing. 2023; 15(21):5086. https://doi.org/10.3390/rs15215086
Chicago/Turabian StyleSalazar Villegas, Mike H., Mohammad Qasim, Elmar Csaplovics, Roy González-Martinez, Susana Rodriguez-Buritica, Lisette N. Ramos Abril, and Billy Salazar Villegas. 2023. "Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest" Remote Sensing 15, no. 21: 5086. https://doi.org/10.3390/rs15215086
APA StyleSalazar Villegas, M. H., Qasim, M., Csaplovics, E., González-Martinez, R., Rodriguez-Buritica, S., Ramos Abril, L. N., & Salazar Villegas, B. (2023). Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest. Remote Sensing, 15(21), 5086. https://doi.org/10.3390/rs15215086







