The Selection of Basic Functions for a Time-Varying Model of Unmodeled Errors in Medium and Long GNSS Baselines
Abstract
:1. Introduction
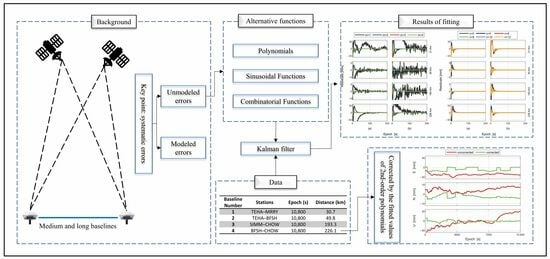
2. Data and Methodology
2.1. Unmodeled Error Data
2.1.1. Baseline Data
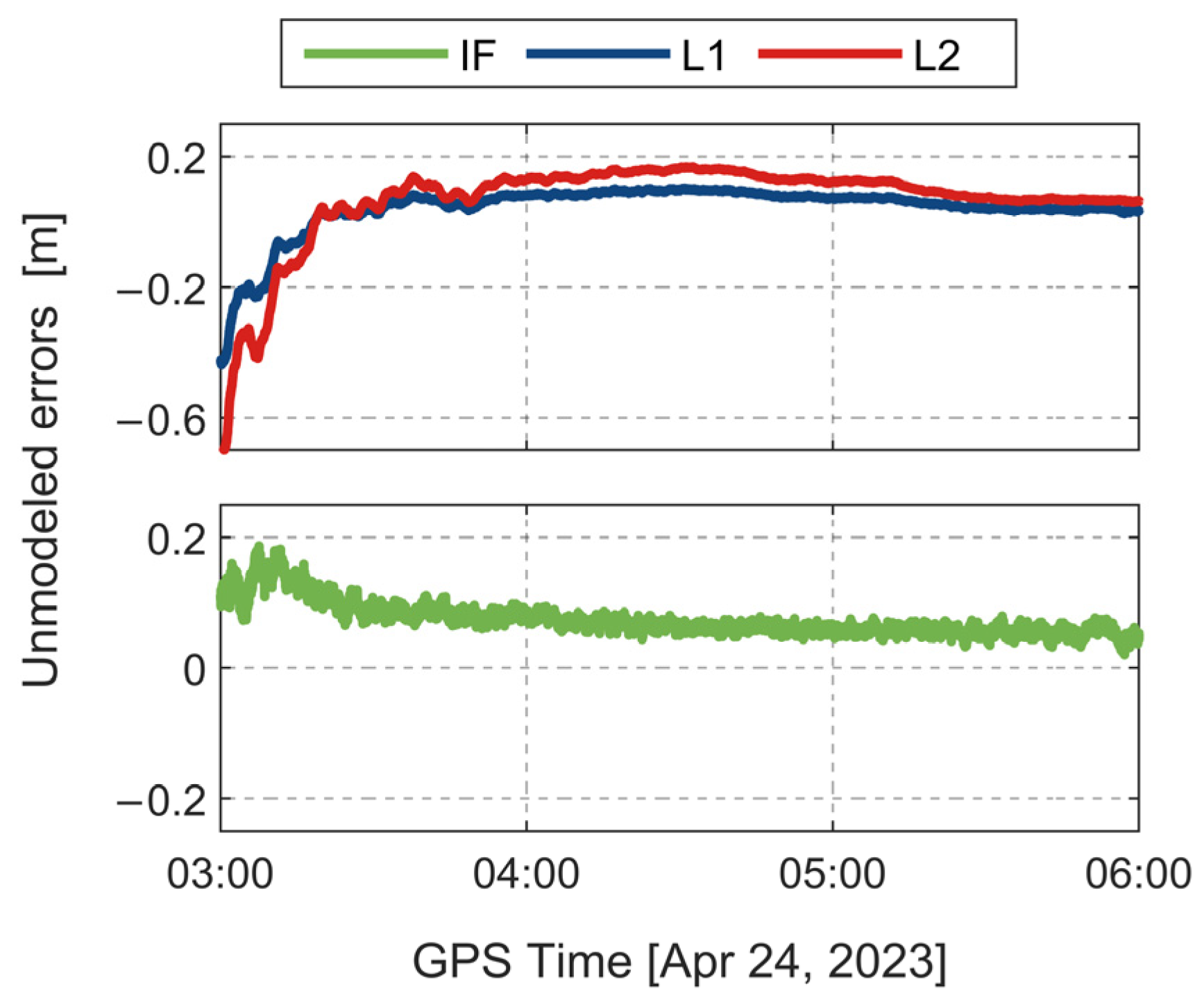
2.1.2. Inversion of Unmodeled Errors
2.2. Methodology
2.2.1. Alternative Basic Functions
2.2.2. Model Testing and Evaluation
2.2.3. Positioning Verification
3. Results
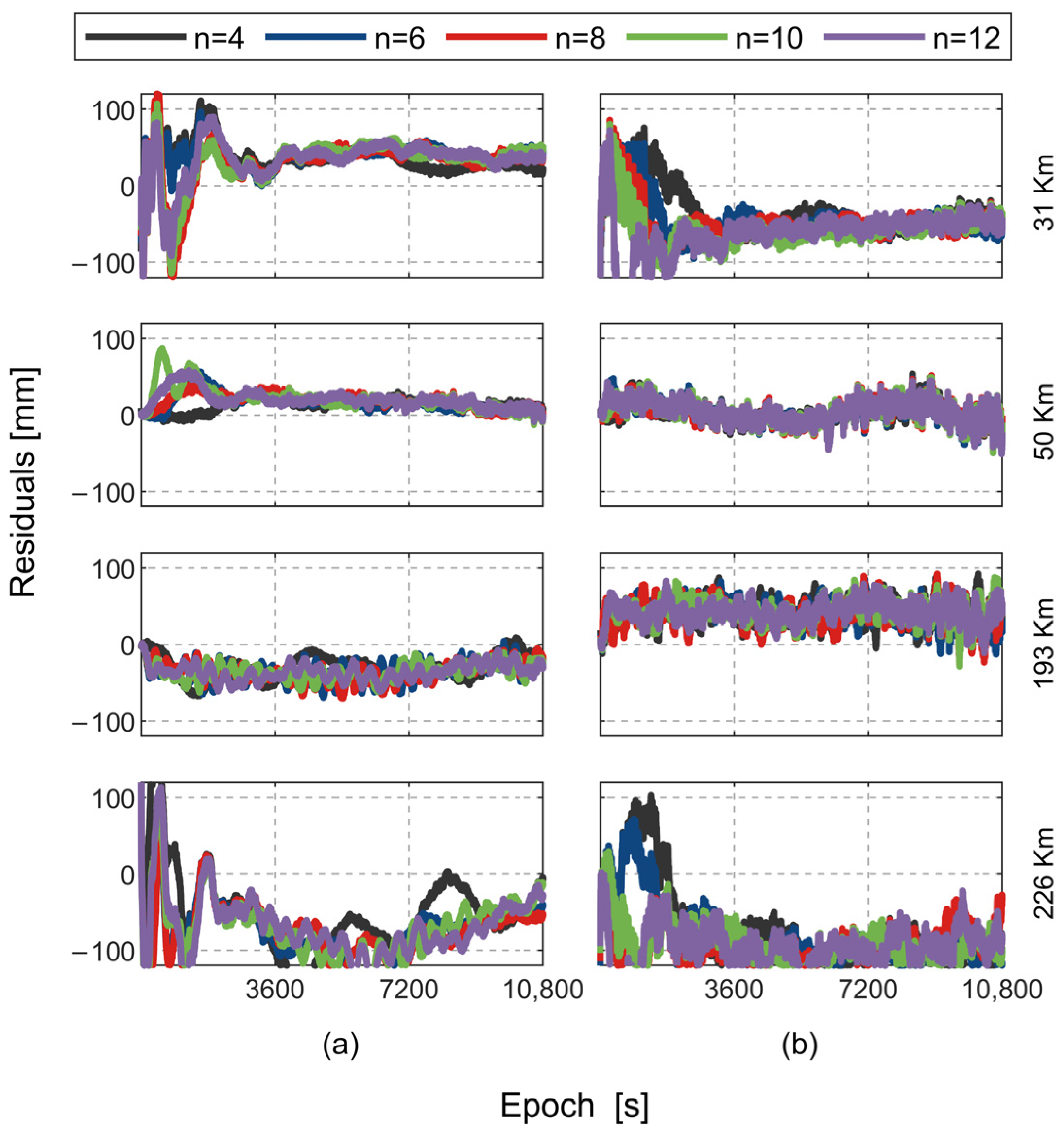
3.1. Fitting Experiments
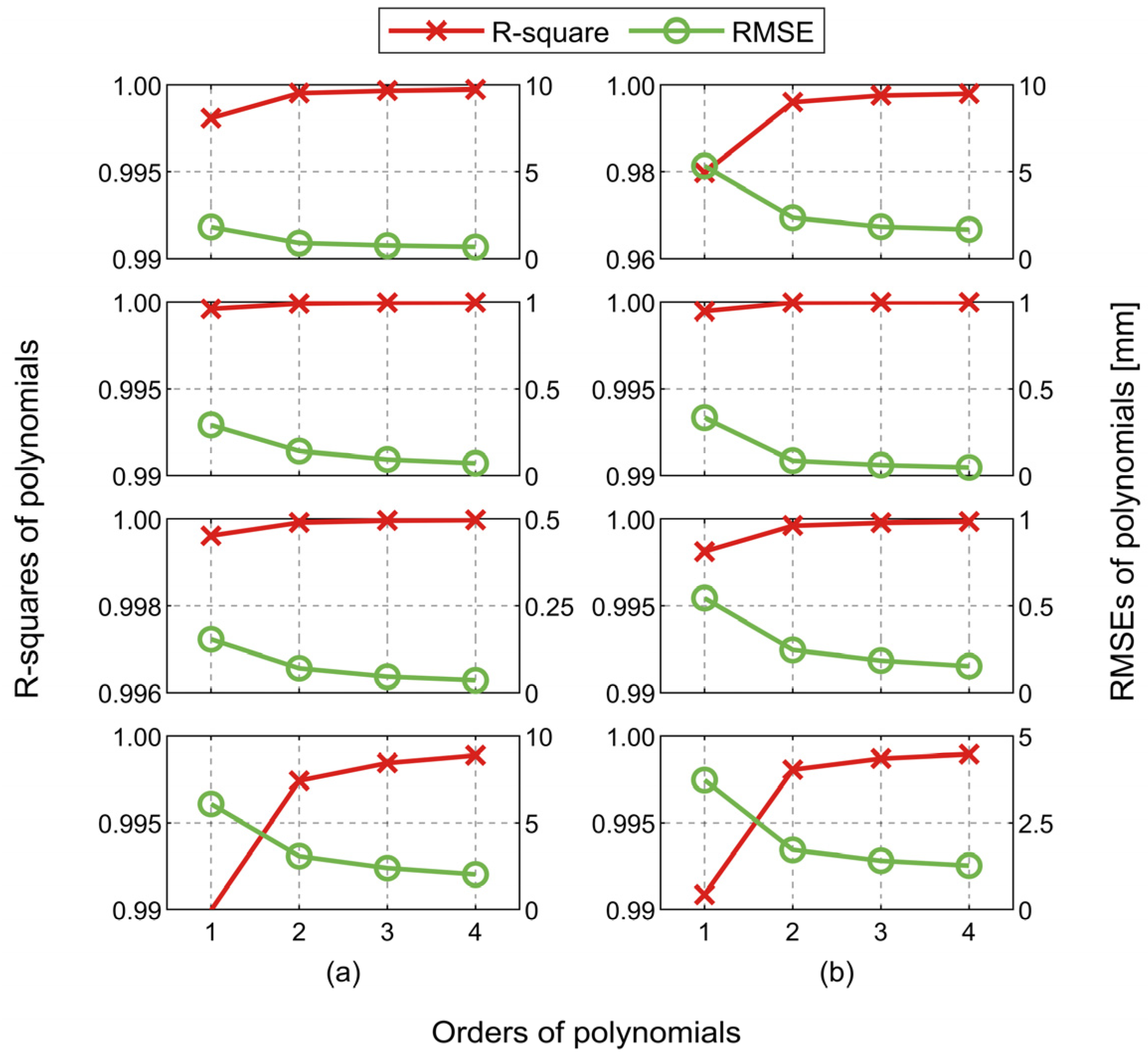
3.1.1. Polynomials
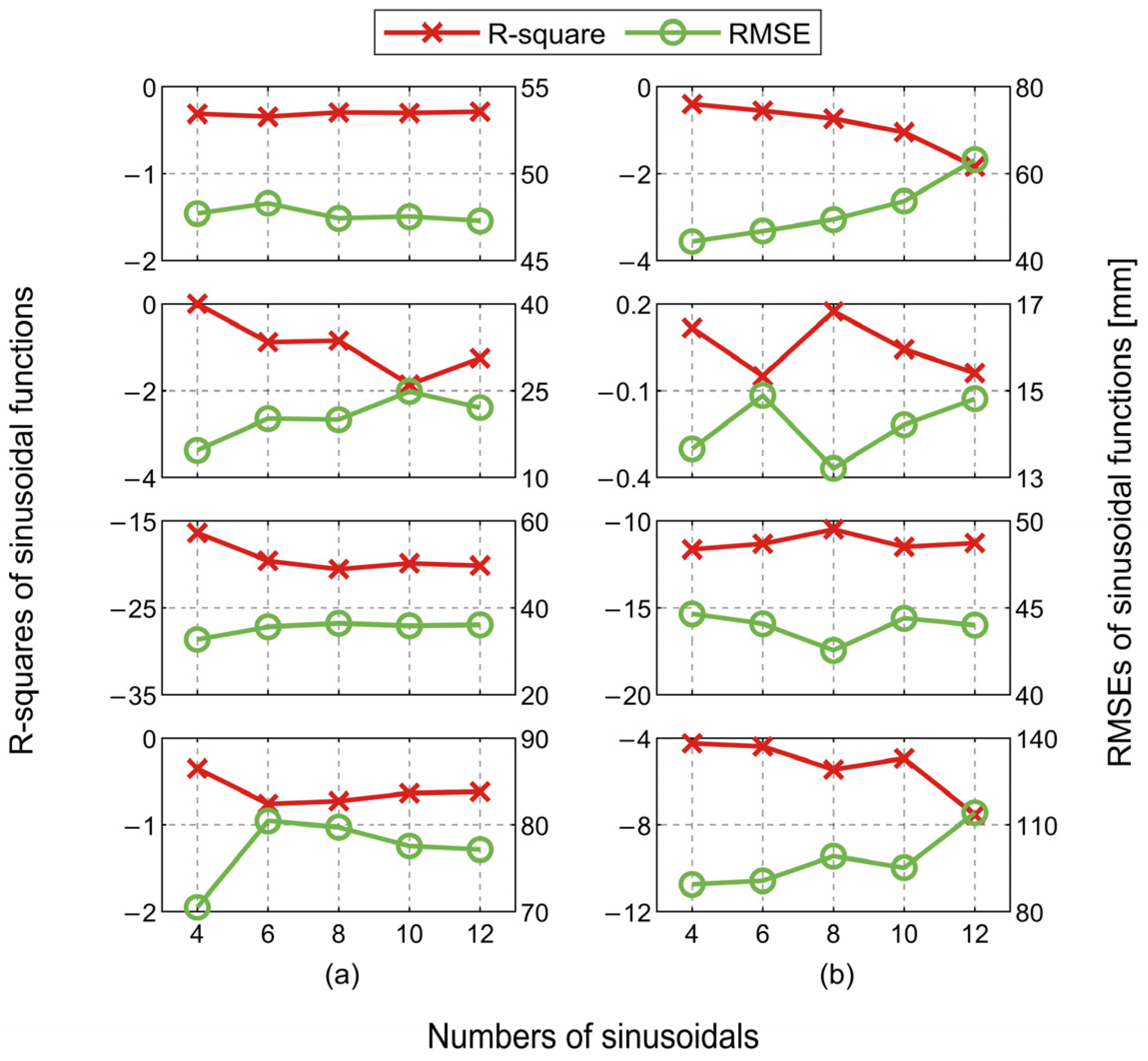
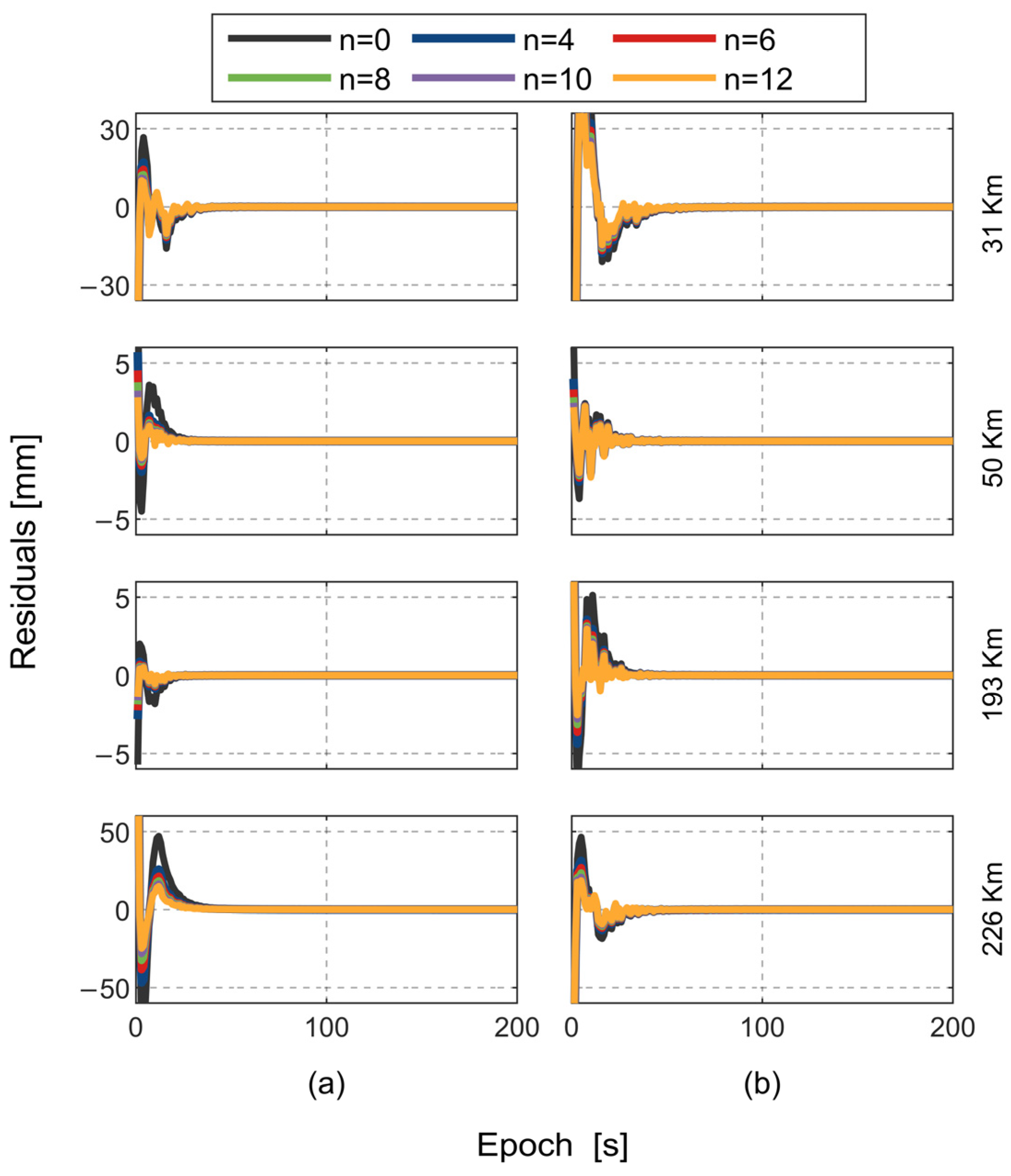
3.1.2. Sinusoidal Functions
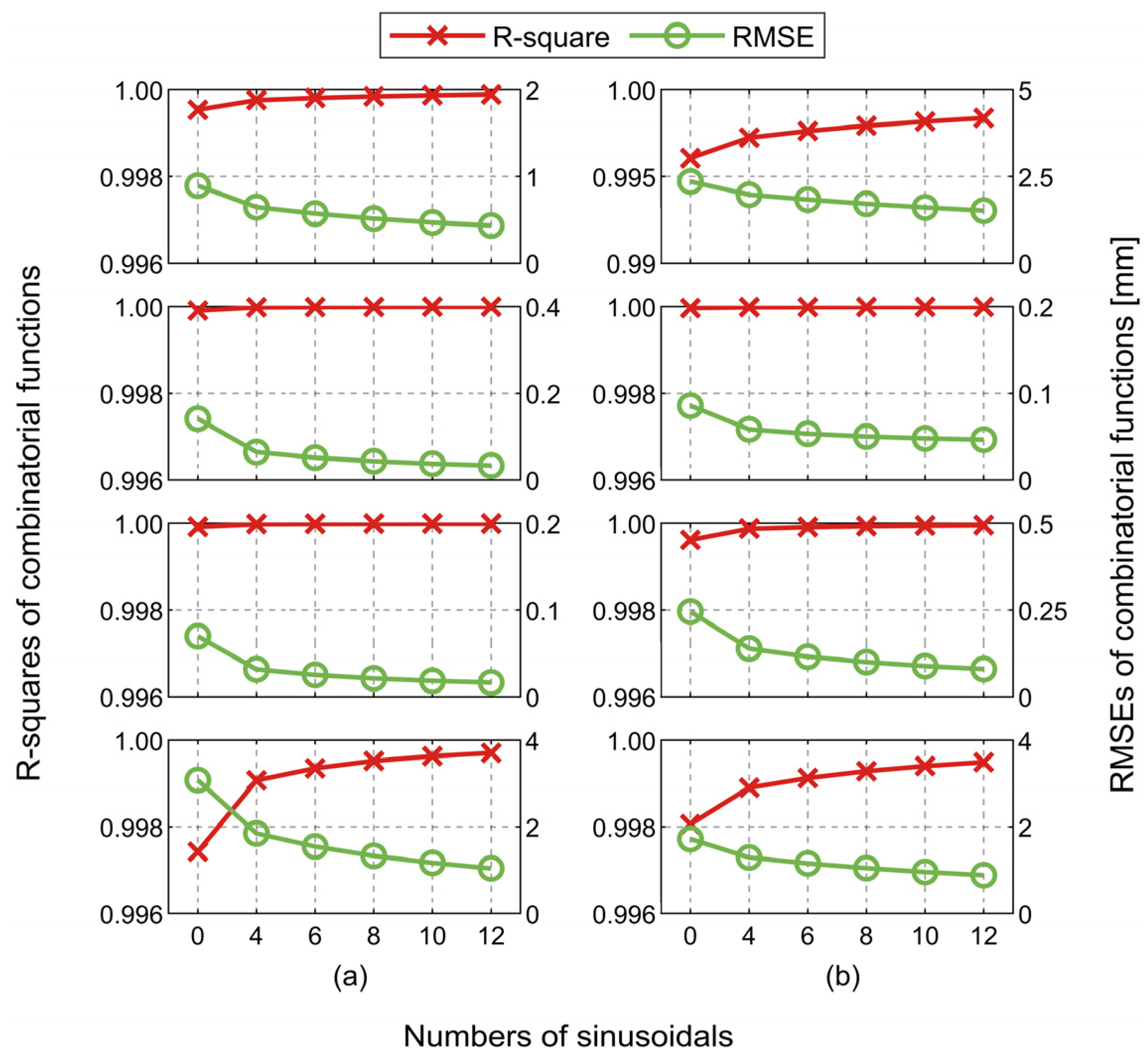
3.1.3. Combinatorial Functions
3.2. Positioning Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, N.; Chen, L.; Wang, L.; Chen, R. GNSS Site unmodeled error prediction based on machine learning. GPS Solut. 2023, 27, 77. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Shen, Y. Comparison and analysis of unmodelled errors in GPS and BeiDou signals. Geod. Geodyn. 2017, 8, 41–48. [Google Scholar] [CrossRef]
- Wang, J.; Yu, X.; Guo, S. Inversion and characteristics of unmodeled errors in GNSS relative positioning. Measurement 2022, 195, 111151. [Google Scholar] [CrossRef]
- Klobuchar, J. Ionospheric time-delay algorithms for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Giovanni, G.D.; Radicella, S.M. An analytical model of the electron density profile in the ionosphere. Adv. Space Res. 1990, 10, 27–30. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Liu, G.; Feng, G.; Yuan, Y.; Zhang, K.; Ren, X. Triple-frequency PPP ambiguity resolution with multi-constellation GNSS: BDS and Galileo. J. Geod. 2019, 93, 1105–1122. [Google Scholar] [CrossRef]
- Hopfield, H. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Geod. 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B.; Xu, C.; He, C.; Yu, C.; Yan, F. A global empirical model for estimating zenith tropospheric delay. Sci. China Earth Sci. 2016, 59, 118–128. [Google Scholar] [CrossRef]
- Marini, J.W. Correction of Satellite Tracking Data for an Arbitrary Tropospheric Profile. Radio Sci. 1972, 7, 223–231. [Google Scholar] [CrossRef]
- Böhm, J.; Schuh, H. Vienna mapping functions in VLBI analyses. Geophys. Res. Lett. 2004, 31, L01603. [Google Scholar] [CrossRef]
- Yuan, L.; Huang, D.; Ding, X.; Xiong, Y.; Zhong, P.; Li, C. On the influence signal multipath effects in GPS carrier phase surveying. Acta Geod. Cartogr. Sin. 2004, 33, 210–215. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.; Zheng, D.; Chen, W. An adaptive wavelet transform based on crossvalidation and its application to mitigate GPS multipath effects. Acta Geod. Cartogr. Sin. 2007, 36, 279–285. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Aragón-Ángel, À.; Defraigne, P.; Bergeot, N.; Prieto-Cerdeira, R.; García-Rigo, A. Distribution and mitigation of higher-order ionospheric effects on precise GNSS processing. J. Geophys. Res. Solid Earth 2014, 119, 3823–3837. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B. Unmodeled error mitigation for single-frequency multi-gnss precise positioning based on multi-epoch partial parameterization. Measur. Sci. Technol. 2020, 31, 025008. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; He, X.; Hsu, L. Resilient GNSS real-time kinematic precise positioning with inequality and equality constraints. GPS Solut. 2023, 27, 116. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Z.; Shen, Y.; Yang, L. A procedure for the significance testing of unmodeled errors in GNSS observations. J. Geodesy 2018, 92, 1171–1186. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Shen, Y.; Gao, Y.; Wang, M. Site-specific unmodeled error mitigation for GNSS positioning in urban environments using a real-time adaptive weighting model. Remote Sens. 2018, 10, 1157. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Z.; He, X.; Li, G.; Wang, S. Stochastic model assessment of low-cost devices considering the impacts of multipath effects and atmospheric delays. Measurement 2022, 188, 110619. [Google Scholar] [CrossRef]
- Zhang, Z.; Yuan, H.; He, X.; Chen, B.; Zhang, Z. Unmodeled-error-corrected stochastic assessment for a standalone GNSS receiver regardless of the number of tracked frequencies. Measurement 2023, 206, 112265. [Google Scholar] [CrossRef]
- Takasu, T. RTKLIB: Open Source Program Package for RTK-GPS, FOSS4G 2009, Tokyo, Japan, 2 November 2009. Available online: https://gpspp.sakura.ne.jp/rtklib/rtklib.htm (accessed on 17 January 2023).
- Hawkes, A.G. Statistical Models in Applied Science; Bury, K.V., Ed.; Wiley: London, UK, 1975; ISBN 0-471-12590-3. [Google Scholar] [CrossRef]



| Baseline Number | Base Station–Rover Station | Observation Type | Receiver Type at the Base Station | Antenna and Radome Types at the Base Station | Epoch (s) | Distance (km) |
|---|---|---|---|---|---|---|
| 1 | TEHA–MRRY | L1C, L2W | TRIMBLE NETR9 | TRM57971.00 NONE | 10,800 | 30.7 |
| 2 | TEHA–BFSH | L1C, L2W | TRIMBLE NETR9 | TRM57971.00 NONE | 10,800 | 49.8 |
| 3 | SIMM–CHOW | L1C, L2W | TRIMBLE NETR9 | TRM57971.00 NONE | 10,800 | 193.3 |
| 4 | BFSH–CHOW | L1C, L2W | TRIMBLE NETR5 | TRM57971.00 NONE | 10,800 | 226.1 |
| Categories | Settings | |
|---|---|---|
| Estimating Atmospheric Delays | Using IF Combination | |
| Observations | Uncombined L1, L2 | |
| Stochastic model | ||
| Cut-off angle | 10 degrees | 10 degrees |
| Parameter estimation | Extended Kalman filter | Extended Kalman filter |
| Satellite orbit | Precise ephemeris | Precise ephemeris |
| Clock bias | DD | DD |
| Ionospheric delay | DD + Parameter estimation | DD + IF combination |
| Tropospheric delay | DD + Parameter estimation | DD + Parameter estimation |
| Relativistic effect | Model correction | Model correction |
| Earth Solid Tide | IERS 2010 | IERS 2010 |
| Ambiguity resolution | Continuous | Continuous |
| Positioning Mode | Baseline Number | Convergence Time (s) | |||
|---|---|---|---|---|---|
| Estimating atmospheric delays | 1 | 319 | 25 | 9 | 5 |
| 2 | 68 | 11 | 5 | 1 | |
| 3 | 12 | 3 | 3 | 3 | |
| 4 | 146 | 30 | 11 | 6 | |
| Using the IF combination | 1 | 720 | 39 | 14 | 8 |
| 2 | 243 | 4 | 1 | 1 | |
| 3 | 223 | 12 | 6 | 1 | |
| 4 | 597 | 35 | 11 | 6 | |
| Positioning Mode | Processing Time (s) | |||
|---|---|---|---|---|
| Estimating atmospheric delays | 0.467 | 0.592 | 0.739 | 0.875 |
| Using the IF combination | 0.430 | 0.586 | 0.729 | 0.855 |
| Positioning Mode | Baseline Number | Convergence Time (s) | |||||
|---|---|---|---|---|---|---|---|
| Estimating atmospheric delays | 1 | 25 | 21 | 19 | 18 | 18 | 18 |
| 2 | 11 | 7 | 7 | 7 | 7 | 7 | |
| 3 | 3 | 2 | 2 | 2 | 2 | 2 | |
| 4 | 30 | 25 | 23 | 23 | 23 | 20 | |
| uUsing IF combination | 1 | 39 | 39 | 35 | 35 | 35 | 35 |
| 2 | 4 | 1 | 1 | 1 | 1 | 1 | |
| 3 | 12 | 8 | 8 | 8 | 8 | 8 | |
| 4 | 35 | 31 | 26 | 26 | 26 | 26 | |
| Positioning Mode | Processing Time (s) | |||||
|---|---|---|---|---|---|---|
| Estimating atmospheric delays | 0.592 | 1.306 | 1.595 | 1.909 | 2.068 | 2.531 |
| Using IF combination | 0.586 | 1.284 | 1.598 | 1.905 | 2.214 | 2.533 |
| Positioning Mode | Directions | RMSEs of Uncorrected Positioning (m) | RMSEs of Corrected Positioning (m) | Improvement (%) |
|---|---|---|---|---|
| estimating atmospheric delays | E | 0.0224 | 0.0080 | 64.29 |
| N | 0.0051 | 0.0031 | 39.22 | |
| U | 0.0165 | 0.0033 | 80.00 | |
| using IF combination | E | 0.0115 | 0.0109 | 5.22 |
| N | 0.0088 | 0.0053 | 39.77 | |
| U | 0.0184 | 0.0066 | 64.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yu, X.; Aragon-Angel, A.; Rovira-Garcia, A.; Wang, H. The Selection of Basic Functions for a Time-Varying Model of Unmodeled Errors in Medium and Long GNSS Baselines. Remote Sens. 2023, 15, 5022. https://doi.org/10.3390/rs15205022
Wang J, Yu X, Aragon-Angel A, Rovira-Garcia A, Wang H. The Selection of Basic Functions for a Time-Varying Model of Unmodeled Errors in Medium and Long GNSS Baselines. Remote Sensing. 2023; 15(20):5022. https://doi.org/10.3390/rs15205022
Chicago/Turabian StyleWang, Jiafu, Xianwen Yu, Angela Aragon-Angel, Adria Rovira-Garcia, and Hao Wang. 2023. "The Selection of Basic Functions for a Time-Varying Model of Unmodeled Errors in Medium and Long GNSS Baselines" Remote Sensing 15, no. 20: 5022. https://doi.org/10.3390/rs15205022
APA StyleWang, J., Yu, X., Aragon-Angel, A., Rovira-Garcia, A., & Wang, H. (2023). The Selection of Basic Functions for a Time-Varying Model of Unmodeled Errors in Medium and Long GNSS Baselines. Remote Sensing, 15(20), 5022. https://doi.org/10.3390/rs15205022