Ionosphere Total Electron Content Modeling and Multi-Type Differential Code Bias Estimation Using Multi-Mode and Multi-Frequency Global Navigation Satellite System Observations
Abstract
:1. Introduction
2. Methods and Data
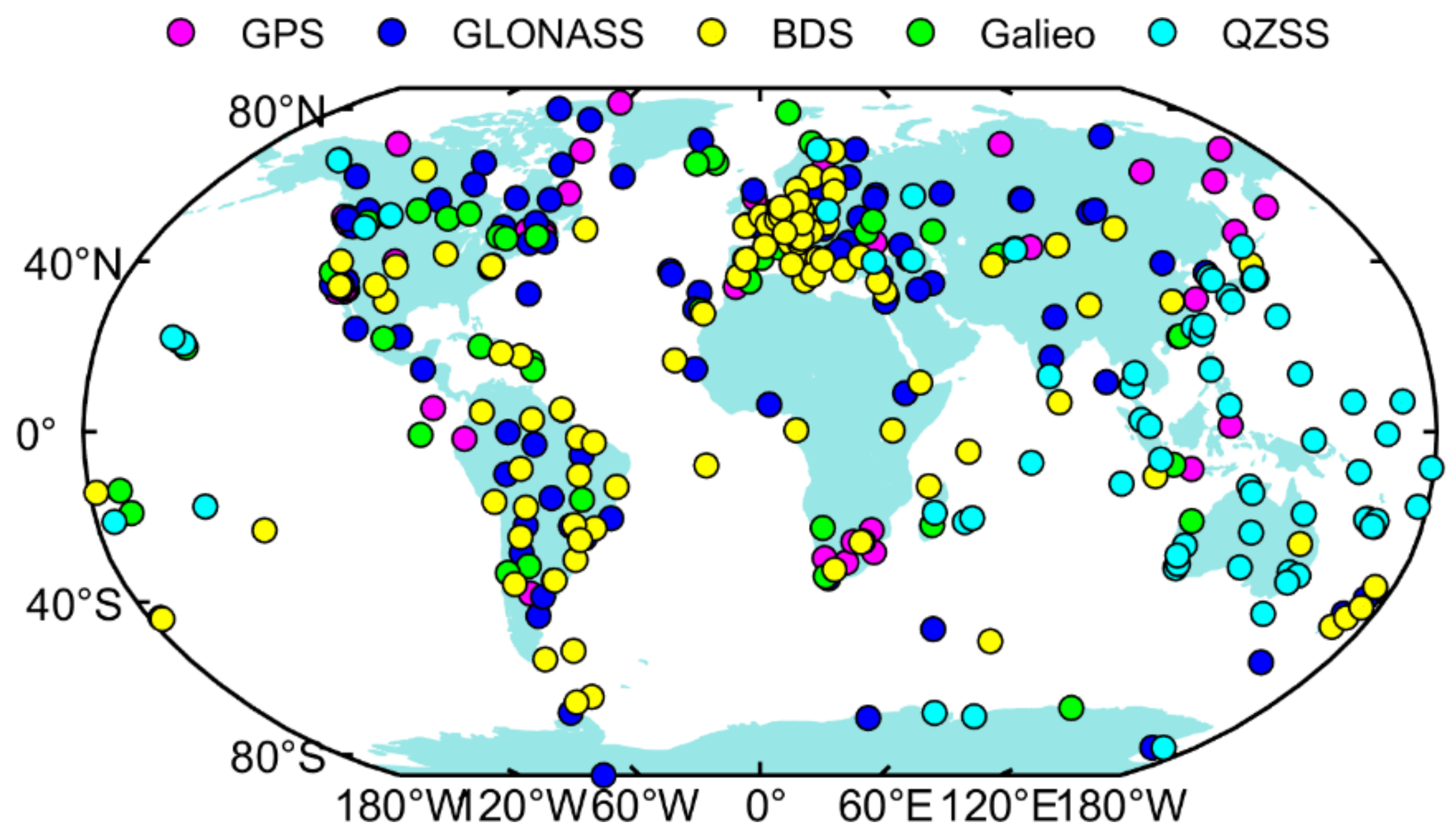
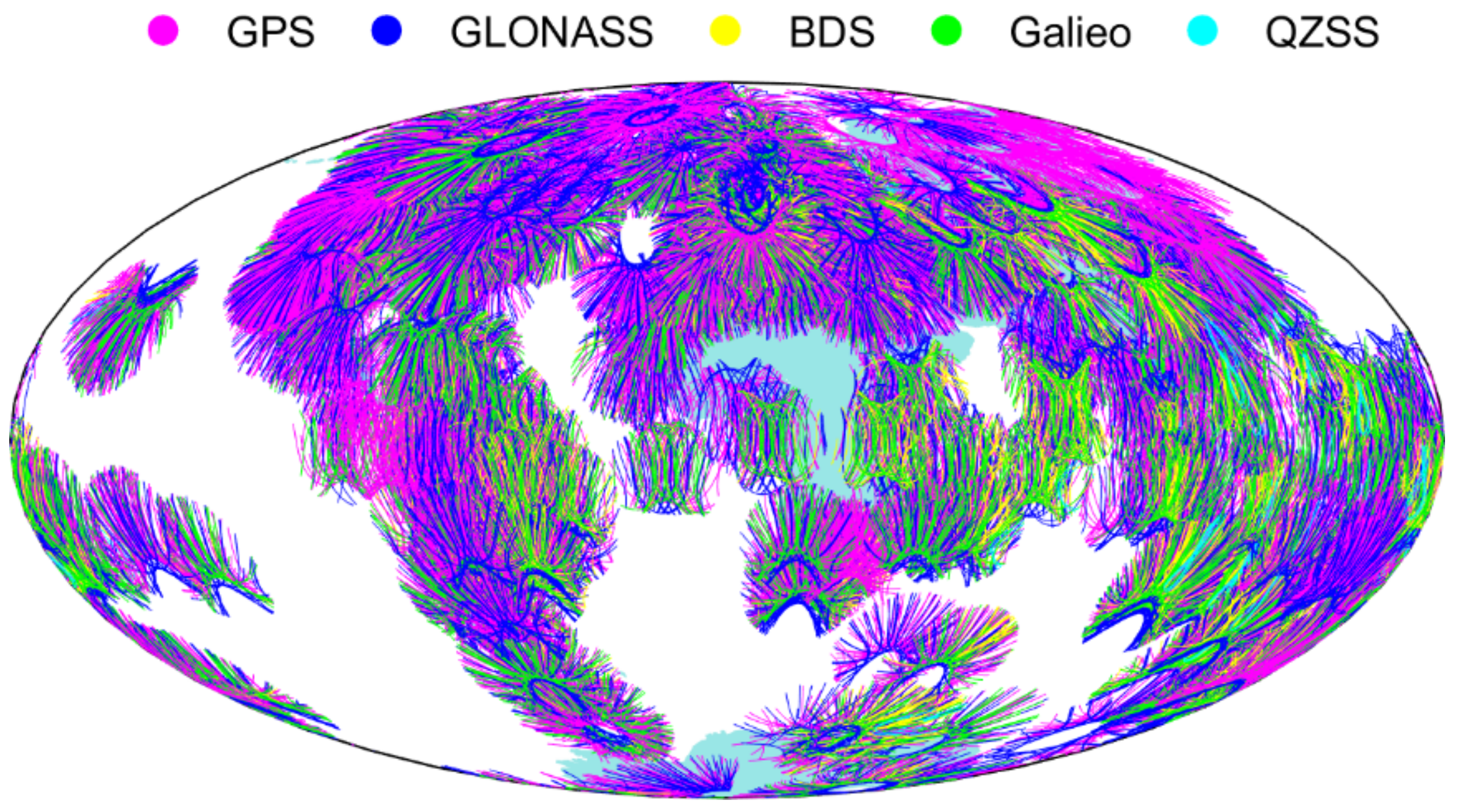
2.1. Ionospheric Observations
2.2. Ionospheric TEC Modeling and DCB Estimation
2.3. Data
3. Results
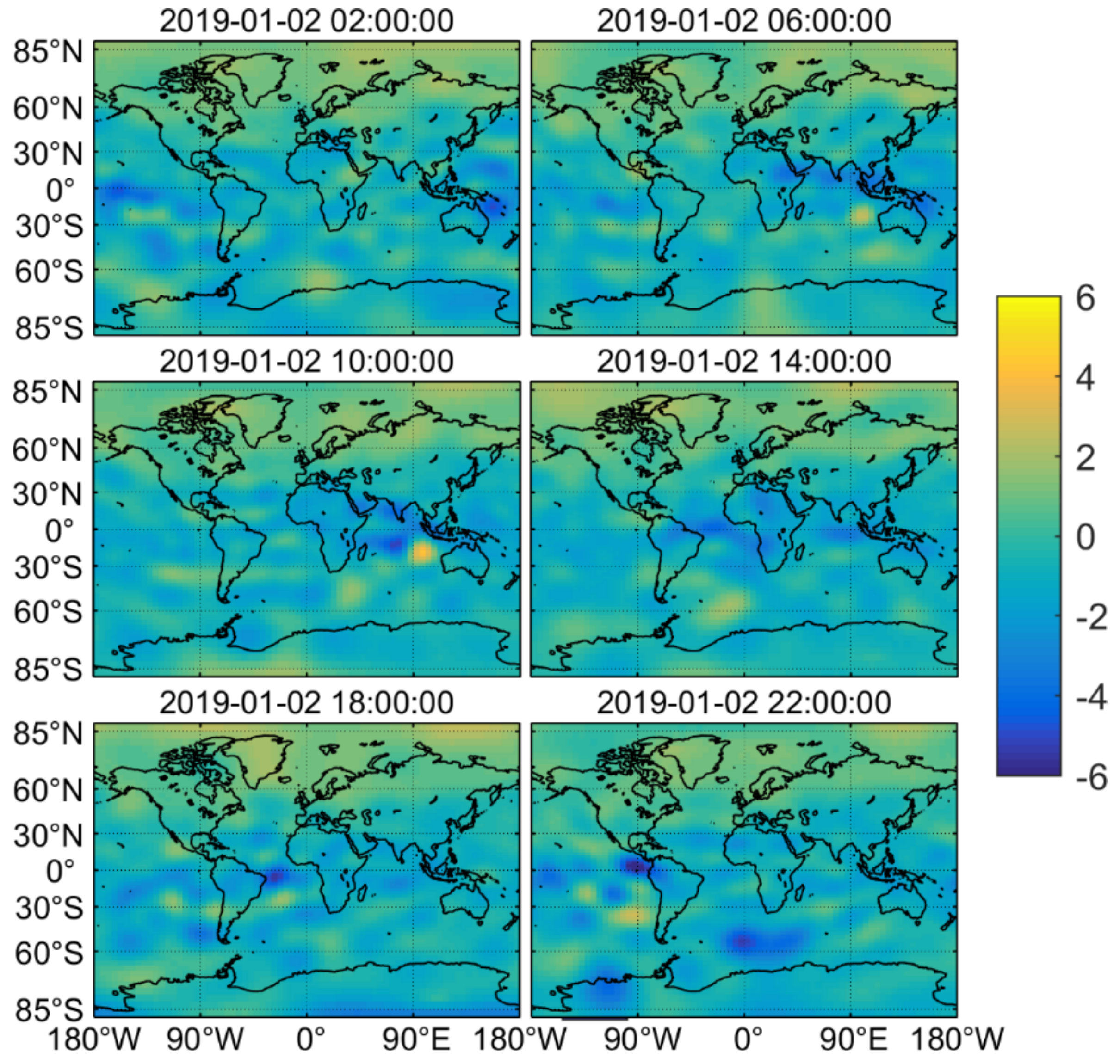
3.1. Ionospheric TEC Modeling
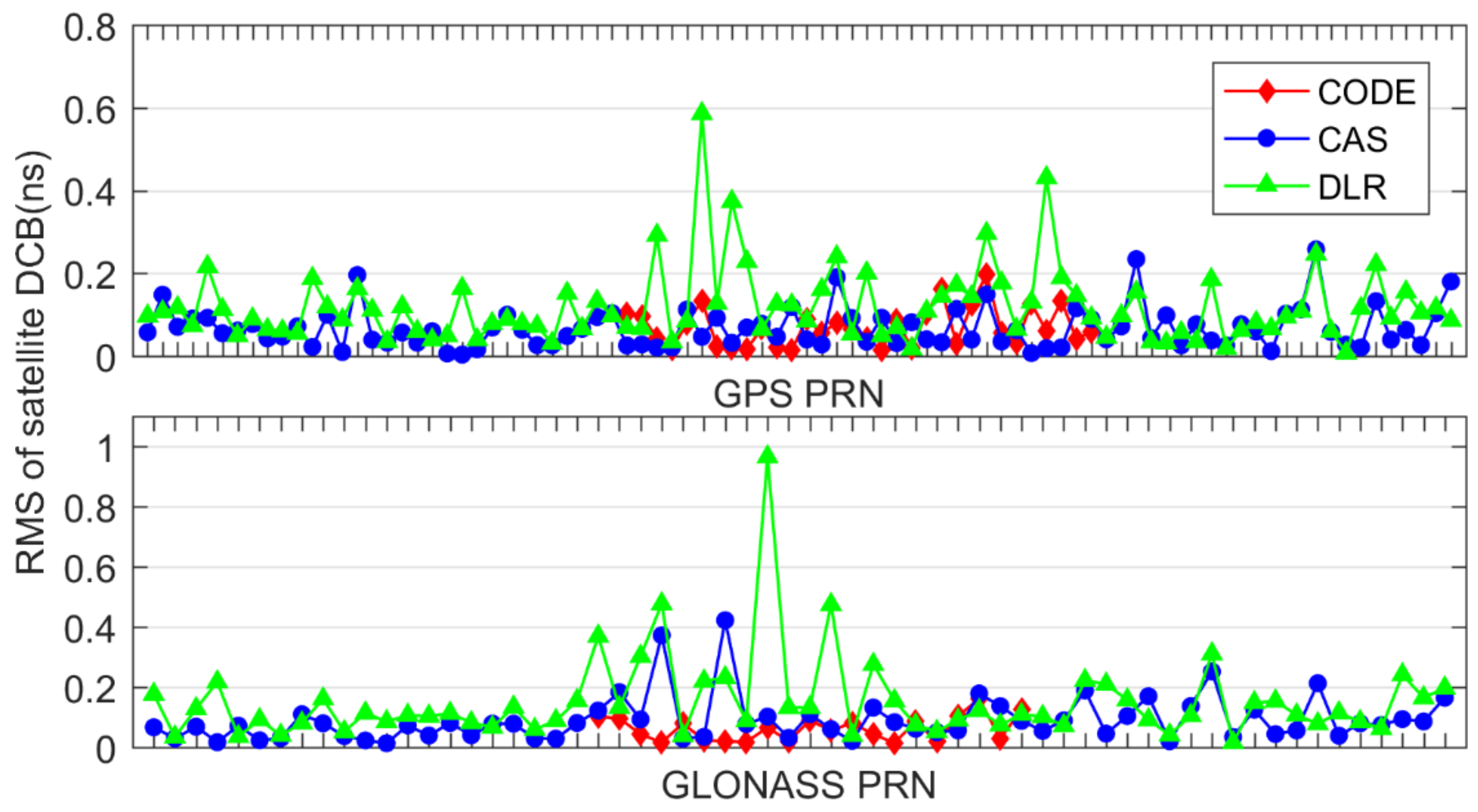
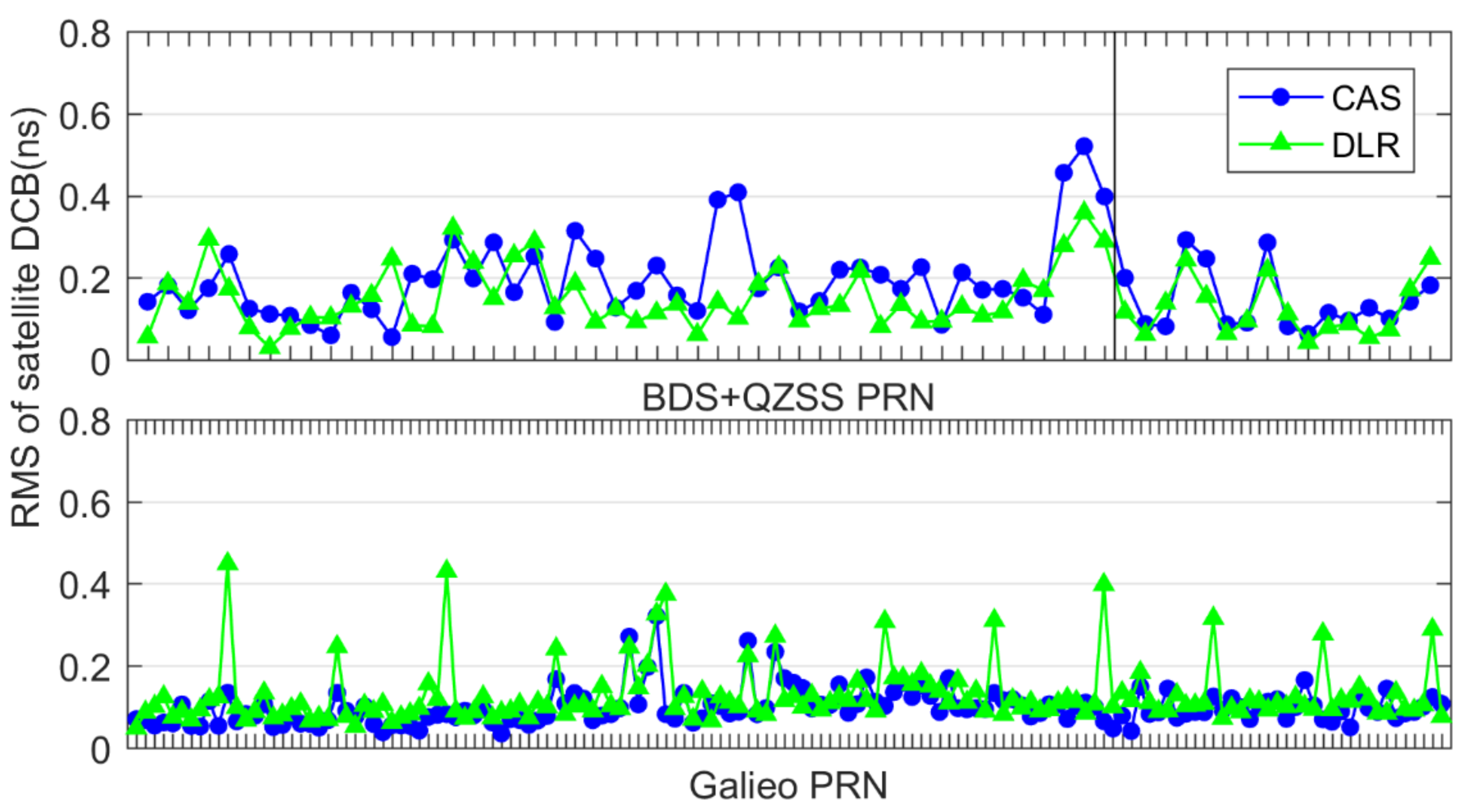
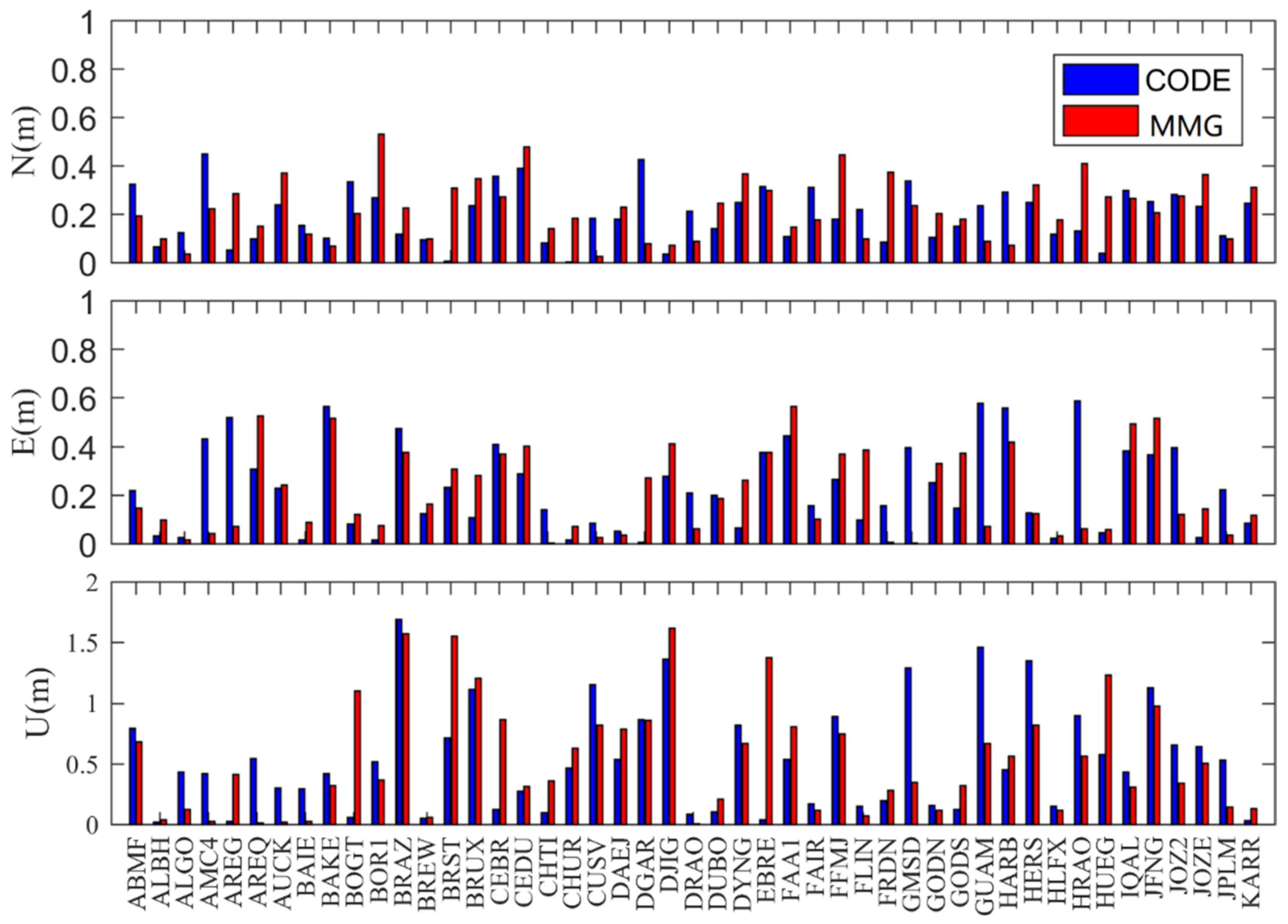
3.2. Satellite and Receiver DCB Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Aragón-Àngel, À.; García-Rigo, A.; Salazar, D.; Escudero, M. The ionosphere: Effects, GPS modeling and the benefits for space geodetic techniques. J. Geod. 2011, 85, 887–907. [Google Scholar] [CrossRef]
- Jin, S.; Occhipinti, G.; Jin, R. GNSS ionospheric seismology: Recent observation evidences and characteristics. Earth-Sci. Rev. 2015, 147, 54–64. [Google Scholar] [CrossRef]
- Yuan, Y.; Tscherning, C.C.; Knudsen, P.; Xu, G.; Ou, J. The ionospheric eclipse factor method (IEFM) and its application to determining the ionospheric delay for GPS. J. Geod. 2008, 82, 1–8. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Prieto-Cerdeira, R.; Orús-Pérez, R.; Breeuwer, E.; Lucas-Rodriguez, R.; Falcone, M. Performance of the Galileo Single-Frequency Ionospheric Correction During In-Orbit Validation. GPS World 2014, 6, 53–58. [Google Scholar]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Analytical performance and validations of the Galileo five-frequency precise point positioning models. Measurement 2021, 172, 108890. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Ibáñez-Segura, D.; Orús-Perez, R.; Juan, J.M.; Sanz, J.; González-Casado, G. Assessing the quality of ionospheric models through GNSS positioning error: Methodology and results. GPS Solut. 2019, 24, 4. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, Y.; Li, W.; Han, B.; Zhao, Z.; Zhang, T.; Huang, R. Analysis of ionospheric TEC response to solar and geomagnetic activities at different solar activity stages. Adv. Space Res. 2023, 71, 2225–2239. [Google Scholar] [CrossRef]
- Li, W.; Yue, J.; Yang, Y.; Li, Z.; Guo, J.; Pan, Y.; Zhang, K. Analysis of ionospheric disturbances associated with powerful cyclones in East Asia and North America. J. Atmos. Sol.-Terr. Phys. 2017, 161, 43–54. [Google Scholar] [CrossRef]
- Tariq, M.A.; Shah, M.; Inyurt, S.; Shah, M.A.; Liu, L. Comparison of TEC from IRI-2016 and GPS during the low solar activity over Turkey. Astrophys. Space Sci. 2020, 365, 179. [Google Scholar] [CrossRef]
- Li, W.; Yue, J.; Wu, S.; Yang, Y.; Li, Z.; Bi, J.; Zhang, K. Ionospheric responses to typhoons in Australia during 2005–2014 using GNSS and FORMOSAT-3/COSMIC measurements. GPS Solut. 2018, 22, 61. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, S.; Ye, X. A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map. Remote Sens. 2022, 14, 2002. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z.; Duan, B.; Hugentobler, U.; Wang, L. GPS and GLONASS observable-specific code bias estimation: Comparison of solutions from the IGS and MGEX networks. J. Geod. 2020, 94, 74. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Astronomical Institute, University of Berne: Bern, Switzerland, 1999. [Google Scholar]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef]
- Rizos, C.; Montenbruck, O.; Weber, R.; Weber, G.; Neilan, R.; Hugentobler, U. The IGS MGEX experiment as a milestone for a comprehensive multi-GNSS service. In Proceedings of the ION PNT, Honolulu, HI, USA, 23–25 April 2013; pp. 289–295. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside Gnss 2014, 9, 42–49. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Yuan, L.; Jin, S.; Hoque, M. Estimation of LEO-GPS receiver differential code bias based on inequality constrained least square and multi-layer mapping function. GPS Solut. 2020, 24, 57. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, S.; Hu, Y. Estimation of QZSS differential code biases using QZSS/GPS combined observations from MGEX. Adv. Space Res. 2020, 67, 1049–1057. [Google Scholar] [CrossRef]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Schaer, S.; Steigenberger, P. Determination and Use of GPS Differential Code Bias Values. pp. 8–11. Available online: https://files.igs.org/pub/resource/pubs/06_darmstadt/IGS%20Presentations%20PDF/2_2_Schaer.pdf (accessed on 1 September 2023).
- Jin, R.; Jin, S.G.; Feng, G.P. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. Gps Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, P.; Han, W.; Ge, M.; Shi, C. Eliminating negative VTEC in global ionosphere maps using inequality-constrained least squares. Adv. Space Res. 2013, 51, 988–1000. [Google Scholar] [CrossRef]
- Wang, C.; Shi, C.; Fan, L.; Zhang, H. Improved Modeling of Global Ionospheric Total Electron Content Using Prior Information. Remote Sens. 2018, 10, 63. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X. Multi-GNSS contributions to differential code biases determination and regional ionospheric modeling in China. Adv. Space Res. 2020, 65, 221–234. [Google Scholar] [CrossRef]



| No. | System | Bias Type | No. | System | Bias Type |
|---|---|---|---|---|---|
| 1 | GPS | C1C-C2W | 10 | Galileo | C1X-C5X |
| 2 | C1W-C2W | 11 | C1X-C7X | ||
| 3 | C1C-C5X | 12 | C1X-C8X | ||
| 4 | C1C-C5Q | 13 | C1C-C5Q | ||
| 5 | GLONASS | C1C-C2P | 14 | C1C-C7Q | |
| 6 | C1P-C2P | 15 | C1C-C8Q | ||
| 7 | C1C-C2C | 16 | QZSS | C1X-C2X | |
| 8 | BDS | C2I-C7I | 17 | C1X-C5X | |
| 9 | C2I-C6I | 18 | C1C-C2L | ||
| 19 | C1C-C5Q |
| System | DCB | CAS | DLR | CODE | System | DCB | CAS | DLR |
|---|---|---|---|---|---|---|---|---|
| GPS | C1C-C2W | 0.06 | 0.09 | GAL | C1X-C5X | 0.06 | 0.11 | |
| C1W-C2W | 0.06 | 0.16 | 0.07 | C1X-C7X | 0.07 | 0.11 | ||
| C1C-C5X | 0.07 | 0.08 | C1X-C8X | 0.08 | 0.12 | |||
| C1C-C5Q | 0.10 | 0.13 | C1C-C5Q | 0.10 | 0.11 | |||
| GLO | C1C-C2P | 0.12 | 0.12 | C1C-C7Q | 0.07 | 0.10 | ||
| C1P-C2P | 0.14 | 0.22 | 0.15 | C1C-C8Q | 0.08 | 0.10 | ||
| C1C-C2C | 0.17 | 0.13 | QZSS | C1X-C2X | 0.07 | 0.16 | ||
| BDS | C2I-C7I | 0.15 | 0.14 | C1X-C5X | 0.07 | 0.10 | ||
| C2I-C6I | 0.19 | 0.13 | C1C-C2L | 0.11 | 0.12 | |||
| C1C-C5Q | 0.09 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhu, J.; Hu, F. Ionosphere Total Electron Content Modeling and Multi-Type Differential Code Bias Estimation Using Multi-Mode and Multi-Frequency Global Navigation Satellite System Observations. Remote Sens. 2023, 15, 4607. https://doi.org/10.3390/rs15184607
Wang Q, Zhu J, Hu F. Ionosphere Total Electron Content Modeling and Multi-Type Differential Code Bias Estimation Using Multi-Mode and Multi-Frequency Global Navigation Satellite System Observations. Remote Sensing. 2023; 15(18):4607. https://doi.org/10.3390/rs15184607
Chicago/Turabian StyleWang, Qisheng, Jiaru Zhu, and Feng Hu. 2023. "Ionosphere Total Electron Content Modeling and Multi-Type Differential Code Bias Estimation Using Multi-Mode and Multi-Frequency Global Navigation Satellite System Observations" Remote Sensing 15, no. 18: 4607. https://doi.org/10.3390/rs15184607
APA StyleWang, Q., Zhu, J., & Hu, F. (2023). Ionosphere Total Electron Content Modeling and Multi-Type Differential Code Bias Estimation Using Multi-Mode and Multi-Frequency Global Navigation Satellite System Observations. Remote Sensing, 15(18), 4607. https://doi.org/10.3390/rs15184607





