Hyperspectral Prediction Model of Nitrogen Content in Citrus Leaves Based on the CEEMDAN–SR Algorithm
Abstract
:1. Introduction
- 1.
- A CEEMDAN–SR algorithm is proposed that can denoise the raw hyperspectral data of CL in the preprocessing stage. The algorithm improves the signal-to-noise ratio of spectral data by removing high-frequency noise, while retaining most of the effective information. The CEEMDAN–SR, SURE–LET, and SR algorithms are experimentally demonstrated for use as denoising algorithms for CL hyperspectral data in the preprocessing stage;
- 2.
- Based on the characteristics of CL hyperspectral data, a quantitative analysis was carried out to establish a model for predicting the nitrogen content of CL. The CEEMDAN–SR+PCA+GPR prediction model has a strong fitting effect and accuracy, with low error, and can be used for rapid nondestructive detection of nitrogen content in CL.
2. Materials and Methods
2.1. Study Area
2.2. Hyperspectral Data Acquisition and Nitrogen Content Determination
2.3. Spectra Pretreatment
2.3.1. Traditional Methods
2.3.2. SURE–LET
2.3.3. CEEMDAN
- 1.
- A new signal is obtained by adding positive and negative paired Gaussian white noise to the original signal , where q = 1 or 2. The EMD decomposition of the new signal yields the first-order IMF component , as shown in Formula (2):
- 2.
- 3.
- 4.
- A new signal is obtained by adding positive and negative pairwise Gaussian self-noise to , and this new signal is used as a carrier for EMD decomposition, to obtain the 1st IMF component , from which the 2nd IMF component can be obtained, as shown in Formula (5):
- 5.
- The residuals are calculated with the second IMF component removed, as shown in Formula (6):
- 6.
- The above steps are repeated until the residual signal obtained is a monotonic function and cannot be further decomposed. At this point, the number of IMF components obtained is K, and the original signal is then decomposed into K IMF and one residual, as shown in Formula (7).
2.3.4. SR
2.3.5. CEEMDAN–SR
- 1.
- Input the original spectral signal X. CEEMDAN decomposition of X is performed to obtain a set of eigenmode functions containing n IMFS and a residual ;
- 2.
- Solve for the correlation coefficient r with the input signal X for each IMF in the set , as shown in Formula (10):where represents the t-th element in , represents the mean value of the , represents the mean value of the original spectral signal X, and m represents the number of bands of the spectrum, where in this paper ;
- 3.
- Referring to the EMD improvement algorithm proposed by Lin et al. [36], this paper selects 0.1 as the correlation coefficient threshold. For IMFs with a correlation coefficient less than 0.1, they are regarded as pseudo-IMF components and are not involved in signal reconstruction. The IMFs with correlation coefficients less than 0.1 in are discarded, to obtain the set ;
- 4.
- 5.
- The elements of whose threshold are less than 0.3 are denoised using the SR algorithm to obtain set ;
- 6.
- The CEEMDAN reconstruction of and the residual is performed to obtain the reconstructed signal Y;
- 7.
- Output the denoised spectral signal Y.
2.4. Feature Extraction Methods
2.5. Model Building and Evaluation Methods
3. Results
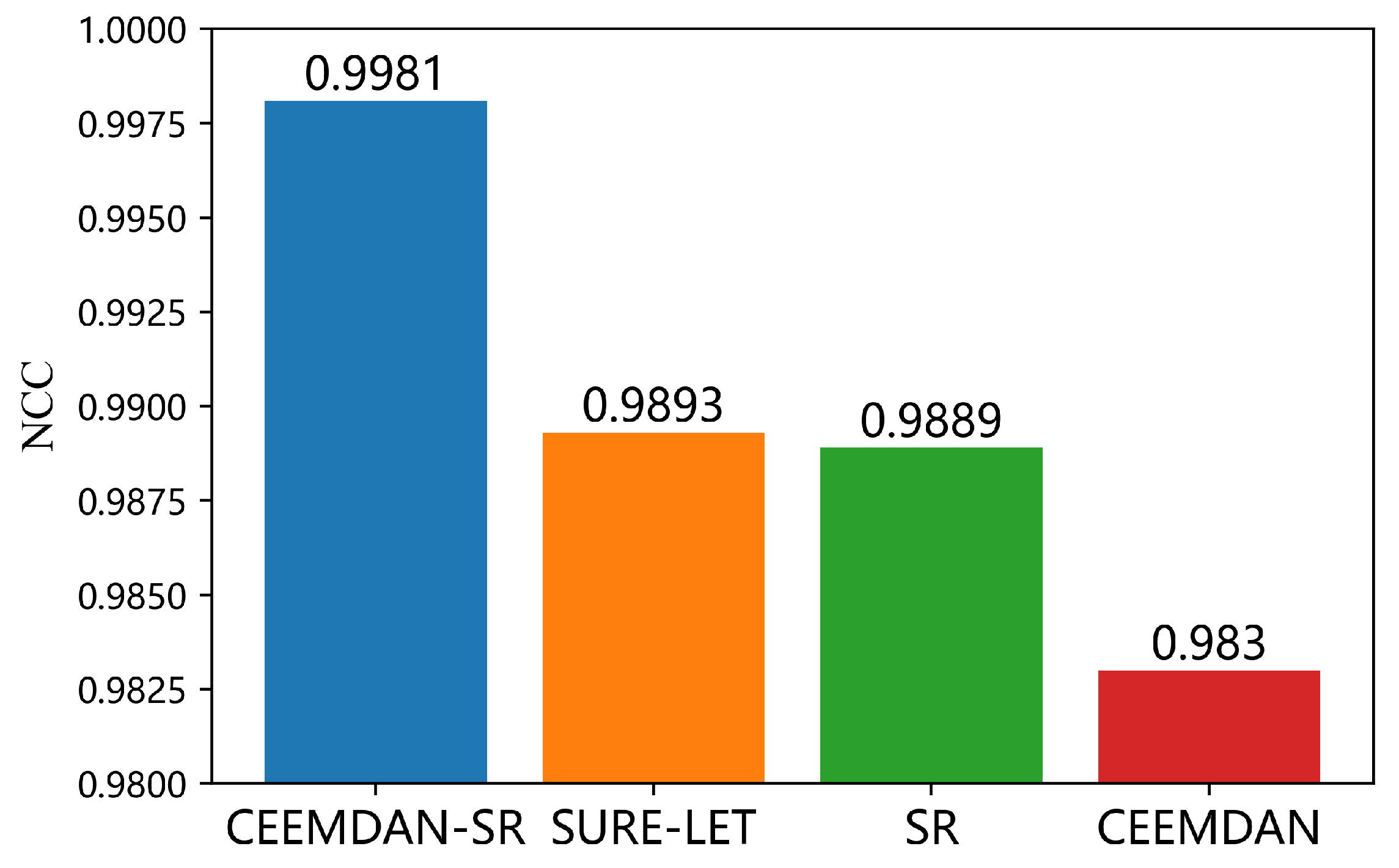
3.1. Comparison of the Denoising Effect of Different Preprocessing Methods
3.2. Construction of Prediction Models for CL Nitrogen Content
4. Discussion
4.1. Analysis of the Denoising Ability of the Preprocessing Algorithms
4.2. Performance of Prediction Models
4.3. Limitations and Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prado Osco, L.; Marques Ramos, A.P.; Roberto Pereira, D.; Akemi Saito Moriya, É.; Nobuhiro Imai, N.; Takashi Matsubara, E.; Estrabis, N.; de Souza, M.; Marcato Junior, J.; Gonçalves, W.N.; et al. Predicting canopy nitrogen content in citrus-trees using random forest algorithm associated to spectral vegetation indices from UAV-imagery. Remote Sens. 2019, 11, 2925. [Google Scholar] [CrossRef]
- Sorgonà, A.; Abenavoli, M.R.; Gringeri, P.G.; Cacco, G. A comparison of nitrogen use efficiency definitions in Citrus rootstocks. Sci. Hortic. 2006, 109, 389–393. [Google Scholar] [CrossRef]
- Quiñones, A.; Bañuls, J.; Primo-Millo, E.; Legaz, F. Recovery of the 15 N-labelled fertiliser in citrus trees in relation with timing of application and irrigation system. Plant Soil 2005, 268, 367–376. [Google Scholar] [CrossRef]
- Dian-Ming, W.; Yuan-Chun, Y.; Li-Zhong, X.; Shi-Xue, Y.; Lin-Zhang, Y. Soil fertility indices of citrus orchard land along topographic gradients in the three gorges area of China. Pedosphere 2011, 21, 782–792. [Google Scholar]
- Cui, Y.; Tian, Z.; Wang, G.; Ma, X.; Chen, W. Citrus extract improves the absorption and utilization of nitrogen and gut health of piglets. Animals 2020, 10, 112. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Dong, T.; Qiu, X.; Rong, Y.; Sun, G.; Wang, Z.; Zhu, J. Antioxidant enzyme activity and growth responses of Huangguogan citrus cultivar to nitrogen supplementation. Biosci. Biotechnol. Biochem. 2019, 83, 1924–1936. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Hu, W.; Wang, Y.; Zhang, P.; Zhou, Y.; Yang, L.T.; Li, Y.; Chen, L.S.; Guo, J. Declined photosynthetic nitrogen use efficiency under ammonium nutrition is related to photosynthetic electron transport chain disruption in citrus plants. Sci. Hortic. 2023, 308, 111594. [Google Scholar] [CrossRef]
- Esposti, M.D.D.; de Siqueira, D.L.; Pereira, P.R.G.; Venegas, V.H.A.; Salomão, L.C.C.; Filho, J.A.M. Assessment of nitrogenized nutrition of citrus rootstocks using chlorophyll concentrations in the leaf. J. Plant Nutr. 2003, 26, 1287–1299. [Google Scholar] [CrossRef]
- Yang, X.; Lei, S.; Zhao, Y.; Cheng, W. Use of hyperspectral imagery to detect affected vegetation and heavy metal polluted areas: A coal mining area, China. Geocarto Int. 2022, 37, 2893–2912. [Google Scholar] [CrossRef]
- Luo, X.; Liao, J.; Zang, Y.; Ou, Y.; Wang, P. Developing from Mechanized to Smart Agricultural Production in China. Strateg. Study CAE 2022, 24, 46–54. [Google Scholar] [CrossRef]
- Liu, H.; Yu, T.; Hu, B.; Hou, X.; Zhang, Z.; Liu, X.; Liu, J.; Wang, X.; Zhong, J.; Tan, Z. Uav-borne hyperspectral imaging remote sensing system based on acousto-optic tunable filter for water quality monitoring. Remote Sens. 2021, 13, 4069. [Google Scholar] [CrossRef]
- Miraglio, T.; Adeline, K.; Huesca, M.; Ustin, S.; Briottet, X. Monitoring LAI, chlorophylls, and carotenoids content of a woodland savanna using hyperspectral imagery and 3D radiative transfer modeling. Remote Sens. 2019, 12, 28. [Google Scholar] [CrossRef]
- Costa, L.; Kunwar, S.; Ampatzidis, Y.; Albrecht, U. Determining leaf nutrient concentrations in citrus trees using UAV imagery and machine learning. Precis. Agric. 2022, 23, 854–875. [Google Scholar] [CrossRef]
- Osco, L.P.; Ramos, A.P.M.; Faita Pinheiro, M.M.; Moriya, É.A.S.; Imai, N.N.; Estrabis, N.; Ianczyk, F.; Araújo, F.F.d.; Liesenberg, V.; Jorge, L.A.d.C.; et al. A machine learning framework to predict nutrient content in valencia-orange leaf hyperspectral measurements. Remote Sens. 2020, 12, 906. [Google Scholar] [CrossRef]
- Wu, W.; Li, J.; Zhang, Z.; Ling, C.; Lin, X.; Chang, X. Estimation model of LAI and nitrogen content in tea tree based on hyperspectral image. Trans. Chin. Soc. Agric. Eng. 2018, 34, 195–201. [Google Scholar]
- Zhu, Y.; Abdalla, A.; Tang, Z.; Cen, H. Improving rice nitrogen stress diagnosis by denoising strips in hyperspectral images via deep learning. Biosyst. Eng. 2022, 219, 165–176. [Google Scholar] [CrossRef]
- Sharan, T.; Sharma, S.; Sharma, N. Denoising and spike removal from Raman spectra using double density dual-tree complex wavelet transform. J. Appl. Spectrosc. 2021, 88, 117–124. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Estimating the distribution of chlorophyll content in CYVCV infected lemon leaf using hyperspectral imaging. Comput. Electron. Agric. 2022, 198, 107036. [Google Scholar] [CrossRef]
- Tang, T.; Chen, C.; Wu, W.; Zhang, Y.; Han, C.; Li, J.; Gao, T.; Li, J. Hyperspectral Inversion Model of Relative Heavy Metal Content in Pennisetum sinese Roxb via EEMD-db3 Algorithm. Remote Sens. 2023, 15, 251. [Google Scholar] [CrossRef]
- Zhao, X.; He, Y.; Zhai, Z.; Tong, L.; Cai, L.; Shang, T. LCEEMD Adaptive Denosing Method for Raman Spectra with Low SNR. Spectrosc. Spectr. Anal. 2018, 38, 3124–3128. [Google Scholar]
- Lu, T.; Li, S.; Fang, L.; Ma, Y.; Benediktsson, J.A. Spectral–spatial adaptive sparse representation for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2015, 54, 373–385. [Google Scholar] [CrossRef]
- Fang, Z.; Tao, Y.; Wang, W.; Zhang, W.; Duan, L.; Liu, Y.; Yan, C.; Qu, L.; Han, C. Joint sparse representation and denoising method for Raman spectrum. J. Raman Spectrosc. 2018, 49, 1972–1977. [Google Scholar] [CrossRef]
- Guo, Y.; Bi, Q.; Li, Y.; Du, C.; Huang, J.; Chen, W.; Shi, L.; Ji, G. Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing. Appl. Sci. 2022, 12, 7501. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, R.; Chen, J.; Liu, L.; Matsushita, B. A practical approach to reconstruct high-quality Landsat NDVI time-series data by gap filling and the Savitzky-Golay filter. ISPRS J. Photogramm. Remote Sens. 2021, 180, 174–190. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Huang, T.; Wang, J.; Lin, L.; Wang, L.; Yang, M. Estimation of Leaf Nitrogen Content in Wheat Using New Hyperspectral Indices and a Random Forest Regression Algorithm. Remote Sens. 2018, 10, 1940. [Google Scholar] [CrossRef]
- Luisier, F.; Blu, T.; Unser, M. A new SURE approach to image denoising: Interscale orthonormal wavelet thresholding. IEEE Trans. Image Process. 2007, 16, 593–606. [Google Scholar] [CrossRef]
- Zhang, X. The SURE-LET approach using hybrid thresholding function for image denoising. Comput. Electr. Eng. 2018, 70, 334–348. [Google Scholar] [CrossRef]
- Blu, T.; Luisier, F. The SURE-LET approach to image denoising. IEEE Trans. Image Process. 2007, 16, 2778–2786. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Manhattan, NY, USA, 2011; pp. 4144–4147. [Google Scholar]
- Fu, P.; Zhang, W.; Yang, K.; Meng, F. A novel spectral analysis method for distinguishing heavy metal stress of maize due to copper and lead: RDA and EMD-PSD. Ecotoxicol. Environ. Saf. 2020, 206, 111211. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Zhao, Y.; Zhu, S.; Liu, F.; He, Y. Noise reduction in the spectral domain of hyperspectral images using denoising autoencoder methods. Chemom. Intell. Lab. Syst. 2020, 203, 104063. [Google Scholar] [CrossRef]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Sandoval-Flórez, R.; Paredes, J.L.; Vivas, F.A.; Cabrera, F. Interpolation and denoising of seismic signals using orthogonal matching pursuit algorithm: An aplication in VSP and refraction data. CT&F-Cienc. Tecnol. Y Futuro 2018, 8, 57–63. [Google Scholar]
- Zhang, T. Sparse recovery with orthogonal matching pursuit under RIP. IEEE Trans. Inf. Theory 2011, 57, 6215–6221. [Google Scholar] [CrossRef]
- Lin, L.; Yu, L. Improvement on empirical mode decomposition based on correlation coefficient. Comput. Digit. Eng. 2008, 36, 28–29. [Google Scholar]
- Keshavarzi, Z.; Barzegari Banadkoki, S.; Faizi, M.; Zolghadri, Y.; Shirazi, F.H. Comparison of transmission FTIR and ATR spectra for discrimination between beef and chicken meat and quantification of chicken in beef meat mixture using ATR-FTIR combined with chemometrics. J. Food Sci. Technol. 2020, 57, 1430–1438. [Google Scholar] [CrossRef]
- Wu, D.; He, Y.; Nie, P.; Cao, F.; Bao, Y. Hybrid variable selection in visible and near-infrared spectral analysis for non-invasive quality determination of grape juice. Anal. Chim. Acta 2010, 659, 229–237. [Google Scholar] [CrossRef]
- Yun, L.; Qing-Wei, P.; Jian-Cheng, Y.; Yan-Lin, T. Identification of tea based on CARS-SWR variable optimization of visible/near-infrared spectrum. J. Sci. Food Agric. 2020, 100, 371–375. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. Adv. Neural Inf. Process. Syst. 1996, 9, 281–287. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Advanced Lectures on Machine Learning: ML Summer Schools 2003; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar]
- Wang, R.; Peng, F.; Xing, Y. A Denoising Algorithm for Ultraviolet-Visible Spectrum Based onCEEMDAN and Dua-Tree Complex Wavelet Transform. Spectrosc. Spectr. Anal. 2023, 43, 976–983. [Google Scholar]
- Cui, L.; Wang, Z.; Cen, Y.; Li, X.; Sun, J. An extension of the interscale SURE-LET approach for image denoising. Int. J. Adv. Robot. Syst. 2014, 11, 9. [Google Scholar] [CrossRef]
- Luisier, F.; Blu, T.; Unser, M. Image denoising in mixed Poisson–Gaussian noise. IEEE Trans. Image Process. 2010, 20, 696–708. [Google Scholar] [CrossRef]
- Zhang, X. Image denoising using local Wiener filter and its method noise. Optik 2016, 127, 6821–6828. [Google Scholar] [CrossRef]
- Song, X.; Wu, L.; Hao, H.; Xu, W. Hyperspectral image denoising based on spectral dictionary learning and sparse coding. Electronics 2019, 8, 86. [Google Scholar] [CrossRef]
- Kande, N.A.; Dakhane, R.; Dukkipati, A.; Yalavarthy, P.K. SiameseGAN: A generative model for denoising of spectral domain optical coherence tomography images. IEEE Trans. Med Imaging 2020, 40, 180–192. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Zhang, M.; Xu, Z.; Yang, T.; Su, Y.; Zhou, T.; Wang, H.; Wang, Y.; Lin, Y. Estimation of leaf nutrition status in degraded vegetation based on field survey and hyperspectral data. Sci. Rep. 2020, 10, 4361. [Google Scholar] [CrossRef]
- Feurer, M.; Eggensperger, K.; Falkner, S.; Lindauer, M.; Hutter, F. Auto-sklearn 2.0: Hands-free automl via meta-learning. J. Mach. Learn. Res. 2022, 23, 11936–11996. [Google Scholar]
- Liu, Y.; Lyu, Q.; He, S.; Yi, S.; Liu, X.; Xie, R.; Zheng, Y.; Deng, L. Prediction of nitrogen and phosphorus contents in citrus leaves based on hyperspectral imaging. Int. J. Agric. Biol. Eng. 2015, 8, 80–88. [Google Scholar]
- Zhongzhi, H.; Limiao, D. Application driven key wavelengths mining method for aflatoxin detection using hyperspectral data. Comput. Electron. Agric. 2018, 153, 248–255. [Google Scholar] [CrossRef]
- Vaysse, K.; Lagacherie, P. Using quantile regression forest to estimate uncertainty of digital soil mapping products. Geoderma 2017, 291, 55–64. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhao, X.; Su, X.; Wu, W. Lightweight detection networks for tea bud on complex agricultural environment via improved YOLO v4. Comput. Electron. Agric. 2023, 211, 107955. [Google Scholar] [CrossRef]









| Count | Mean/% | Standard Deviation/% | Min/% | Max/% | |
|---|---|---|---|---|---|
| N | 215 | 2.499 | 0.596 | 0.966 | 3.920 |
| Methods | Description | Reference |
| Partial least squares regression (PLSR) | PLSR is a linear model that aims to find latent variables that capture the maximum covariance between the predictor variables and the response variable, allowing for efficient modeling of complex relationships and handling of multicollinearity. | [40] |
| Support vector regression (SVR) | SVR is a supervised learning algorithm that utilizes support vector machines to perform regression tasks by finding an optimal hyperplane that maximizes the margin, while minimizing the error between the predicted and actual values. | [41] |
| Random forest (RF) | RF is an ensemble learning method that combines multiple decision trees to predict the response variable by averaging the predictions of individual trees. | [42] |
| Gaussian processes regression (GPR) | GPR is a probabilistic regression model that uses a collection of data points to estimate an underlying function by assuming a Gaussian distribution over possible functions, enabling flexible predictions and uncertainty quantification. | [43] |
| Models | Average Memory Space Required/Mib | Average Time Spent/s |
|---|---|---|
| CEEMDAN–SR+PCA+GPR | 180.023 | 2.046 |
| SURE–LET+PCA+GPR | 176.484 | 1.238 |
| SR+PCA+GPR | 179.539 | 1.207 |
| SG+UVE+GPR | 176.847 | 1.256 |
| FD+UVE+GPR | 176.882 | 1.247 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Tang, T.; Wu, W.; Zhang, F.; Luo, Y.; Wu, W.; Yao, B.; Li, J. Hyperspectral Prediction Model of Nitrogen Content in Citrus Leaves Based on the CEEMDAN–SR Algorithm. Remote Sens. 2023, 15, 5013. https://doi.org/10.3390/rs15205013
Gao C, Tang T, Wu W, Zhang F, Luo Y, Wu W, Yao B, Li J. Hyperspectral Prediction Model of Nitrogen Content in Citrus Leaves Based on the CEEMDAN–SR Algorithm. Remote Sensing. 2023; 15(20):5013. https://doi.org/10.3390/rs15205013
Chicago/Turabian StyleGao, Changlun, Ting Tang, Weibin Wu, Fangren Zhang, Yuanqiang Luo, Weihao Wu, Beihuo Yao, and Jiehao Li. 2023. "Hyperspectral Prediction Model of Nitrogen Content in Citrus Leaves Based on the CEEMDAN–SR Algorithm" Remote Sensing 15, no. 20: 5013. https://doi.org/10.3390/rs15205013
APA StyleGao, C., Tang, T., Wu, W., Zhang, F., Luo, Y., Wu, W., Yao, B., & Li, J. (2023). Hyperspectral Prediction Model of Nitrogen Content in Citrus Leaves Based on the CEEMDAN–SR Algorithm. Remote Sensing, 15(20), 5013. https://doi.org/10.3390/rs15205013









