Evaluation of the Accuracy of the Aerosol Optical and Microphysical Retrievals by the GRASP Algorithm from Combined Measurements of a Polarized Sun-Sky-Lunar Photometer and a Three-Wavelength Elastic Lidar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characterization of the Measurement Site
2.2. UPC Remote Sensing Instruments
2.2.1. Polarized Sun-Sky-Lunar Multispectral Photometer
2.2.2. UPC/EARLINET Lidar System
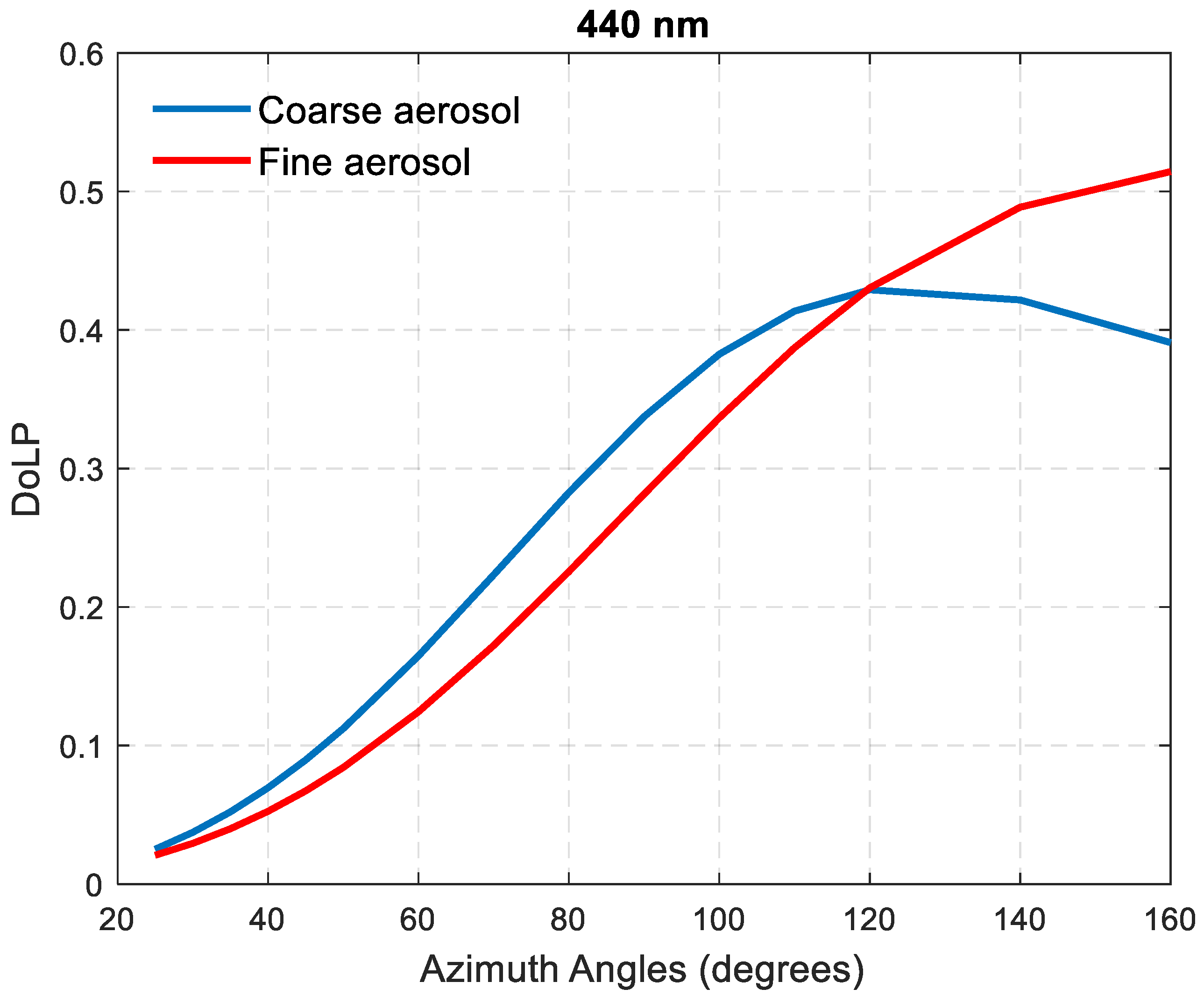
2.3. Degree of Linear Polarization
2.4. GRASP Algorithm
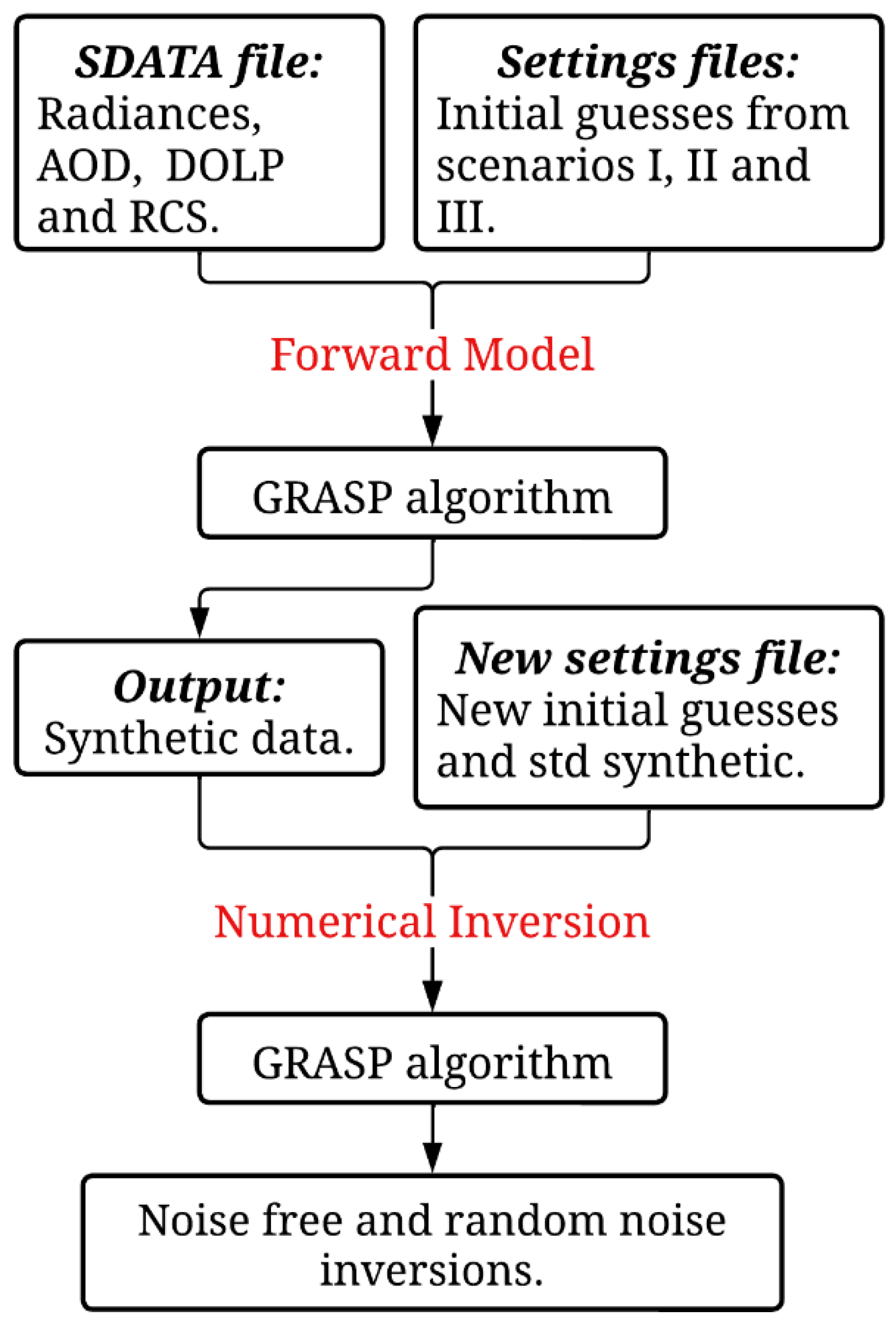
2.5. Data Simulations of UPC Remote Sensing Instruments
- Scenario I: dominant coarse mode with high aerosol load ( = 0.64),
- Scenario II: dominant coarse mode with low aerosol load ( = 0.26),
- Scenario III: dominant fine mode with high aerosol load ( = 0.33).
2.6. Initial Guesses
3. Results and Discussion
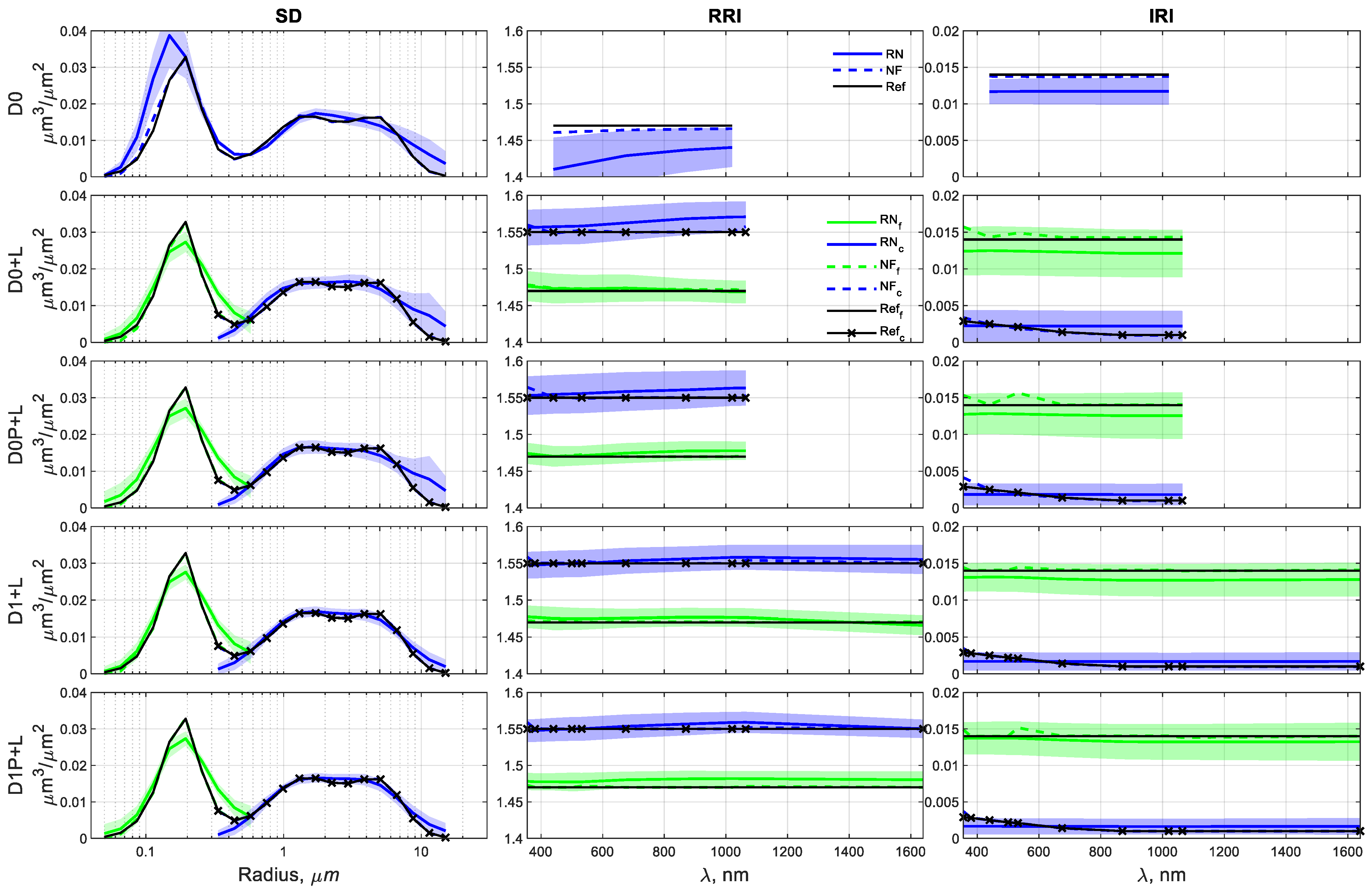
3.1. Inversions of the Noise-Free Data
3.2. Inversions with Random Noise Values
3.2.1. Scenario I
3.2.2. Scenario II
3.2.3. Scenario III
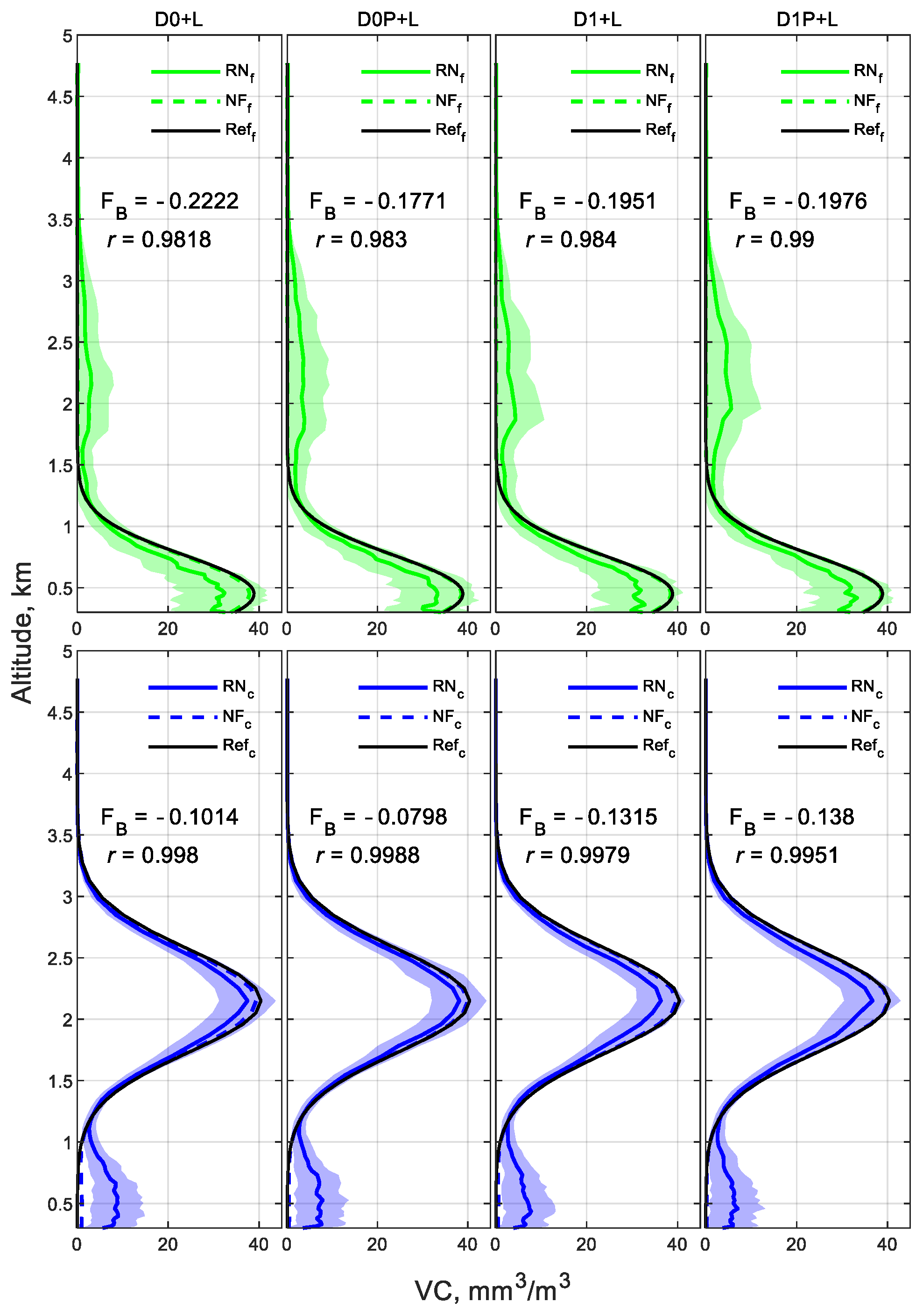
3.2.4. Root Mean Square Error and SF
4. Conclusions
- i.
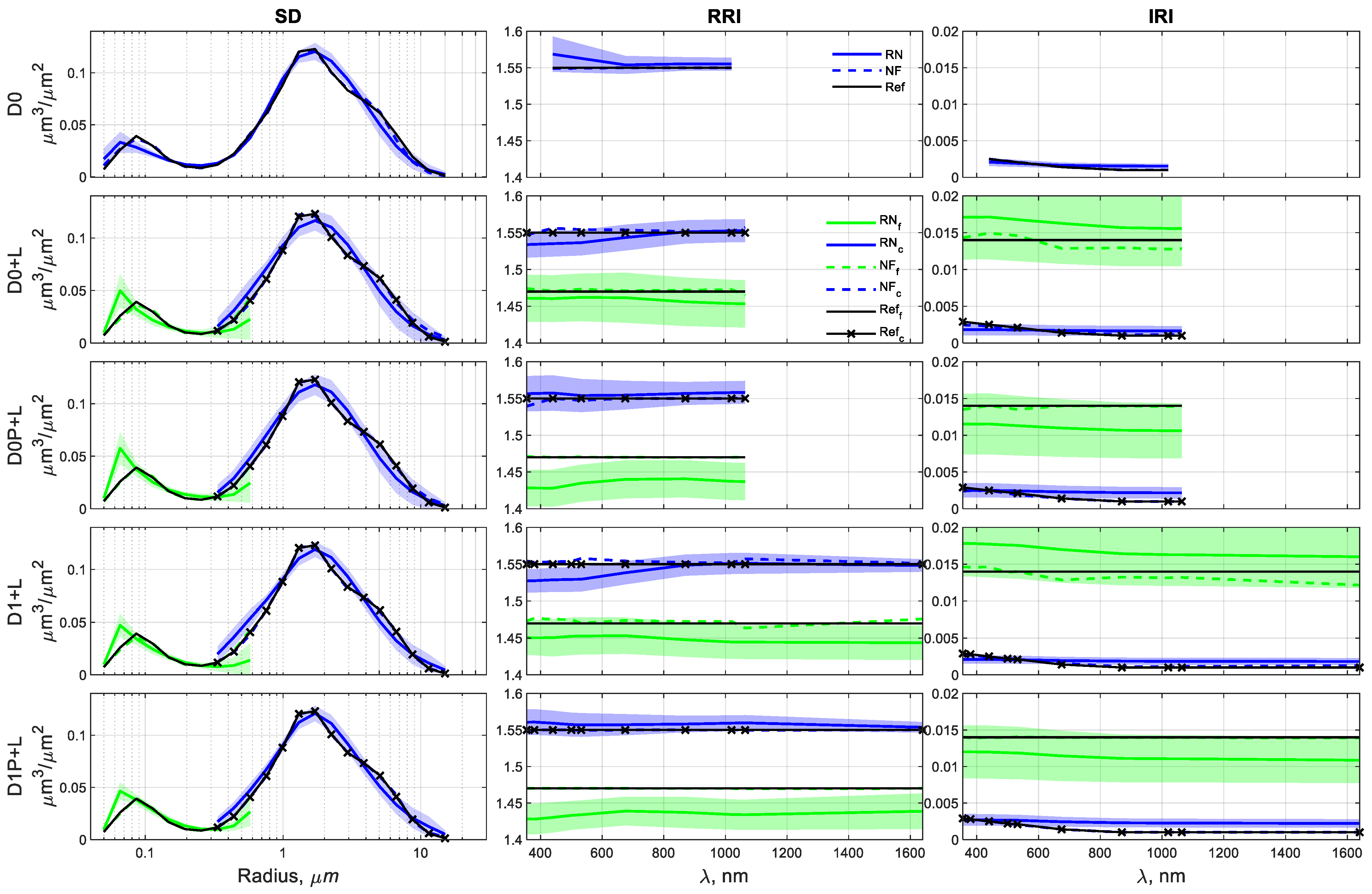
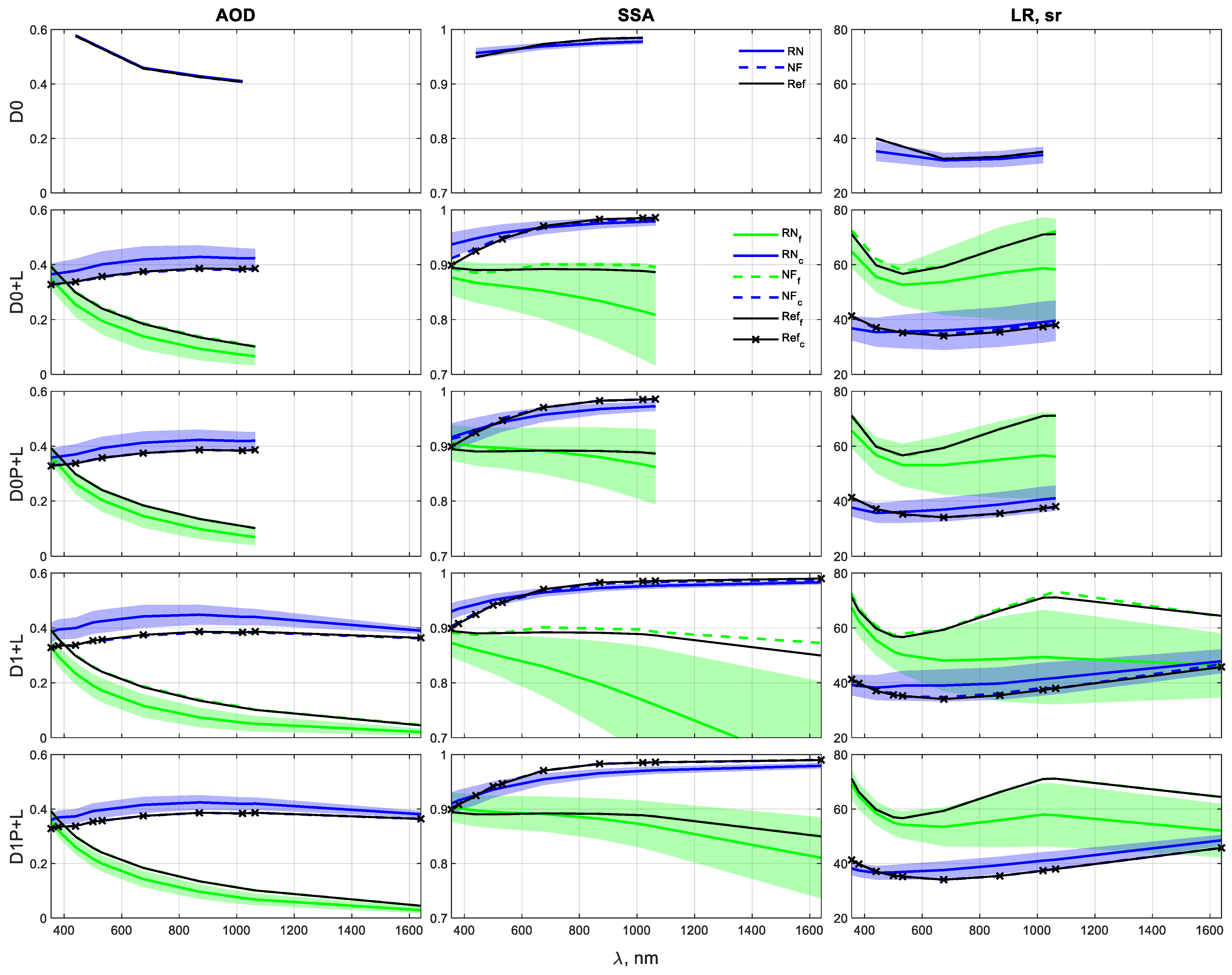
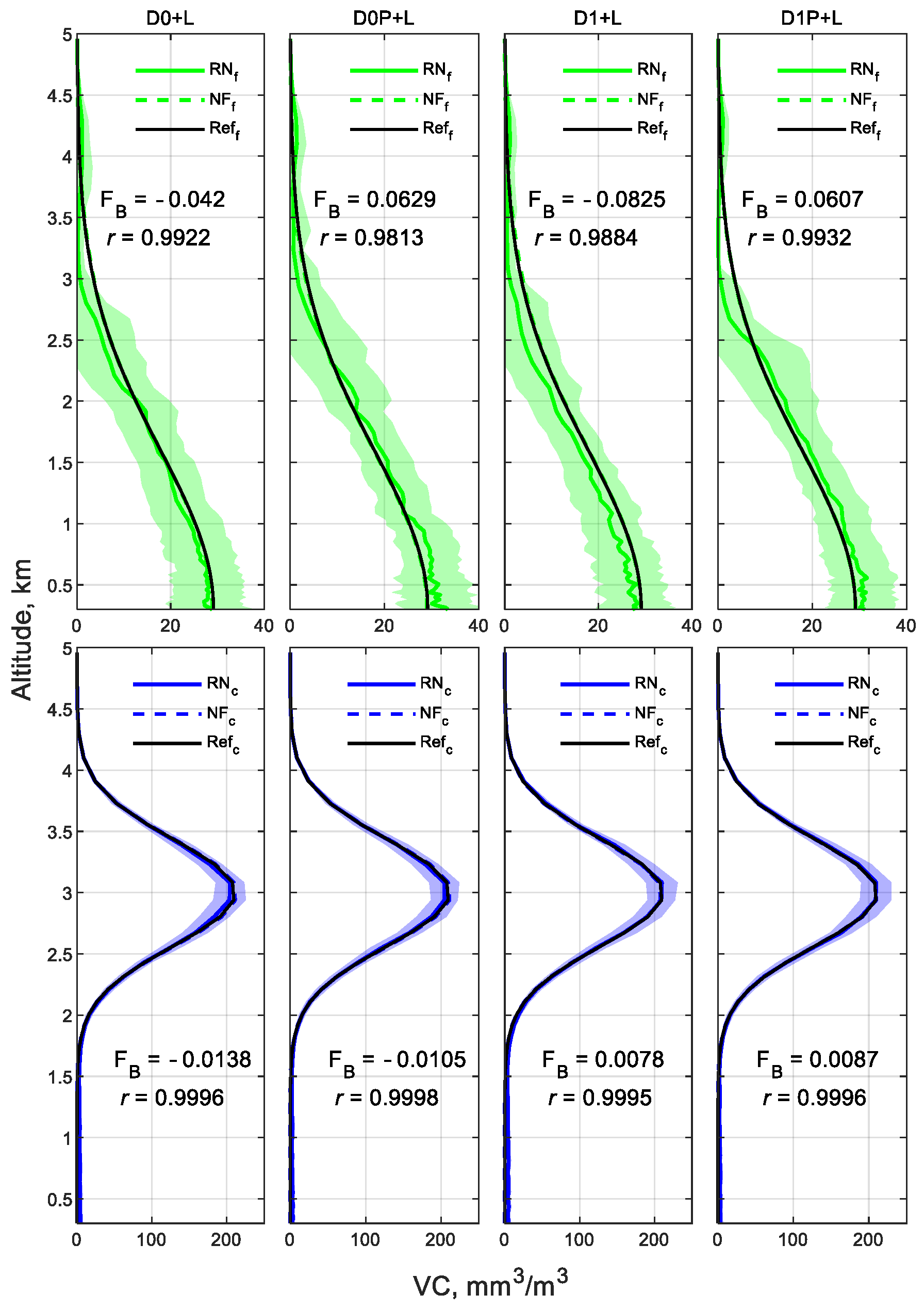
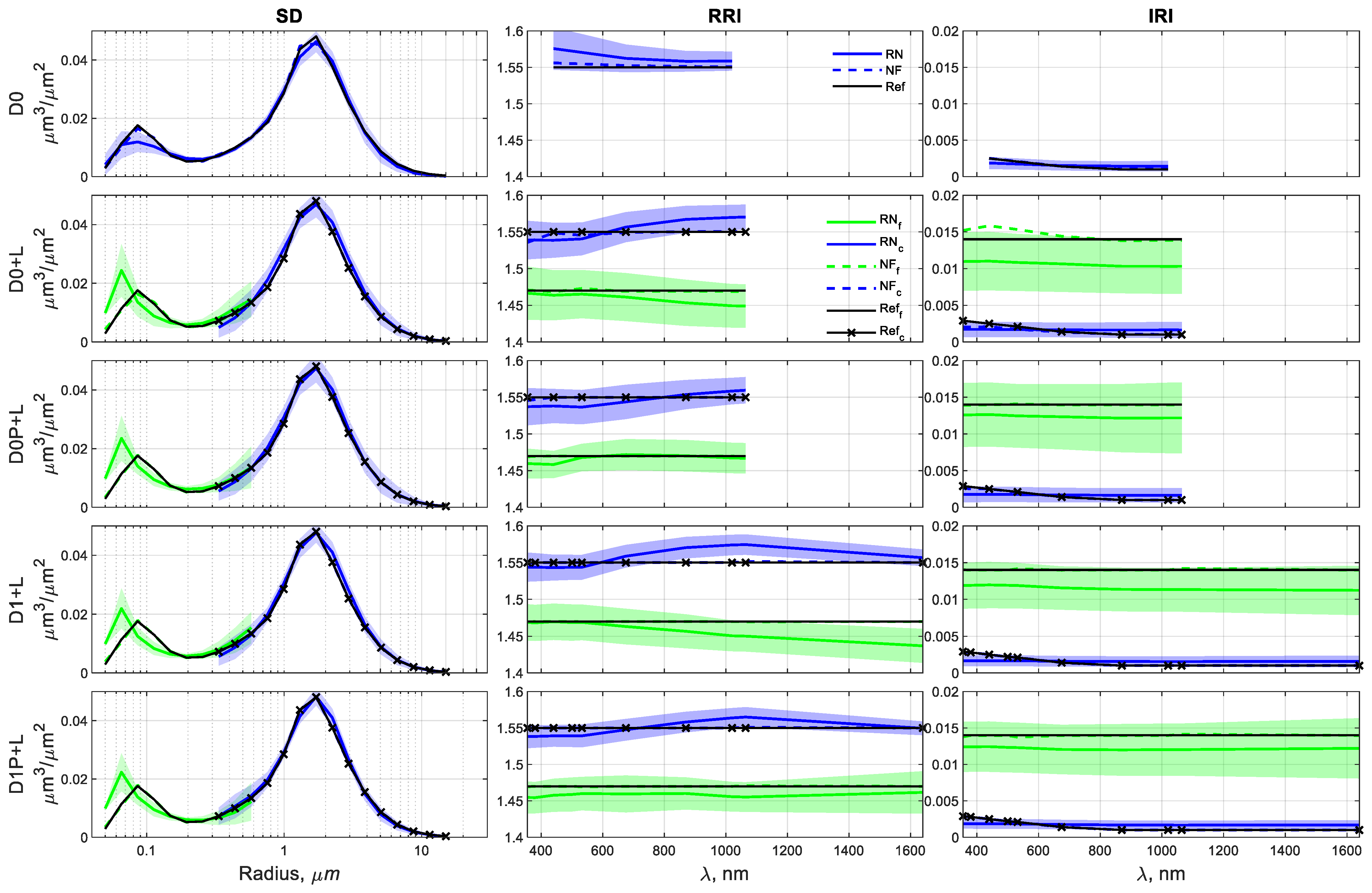
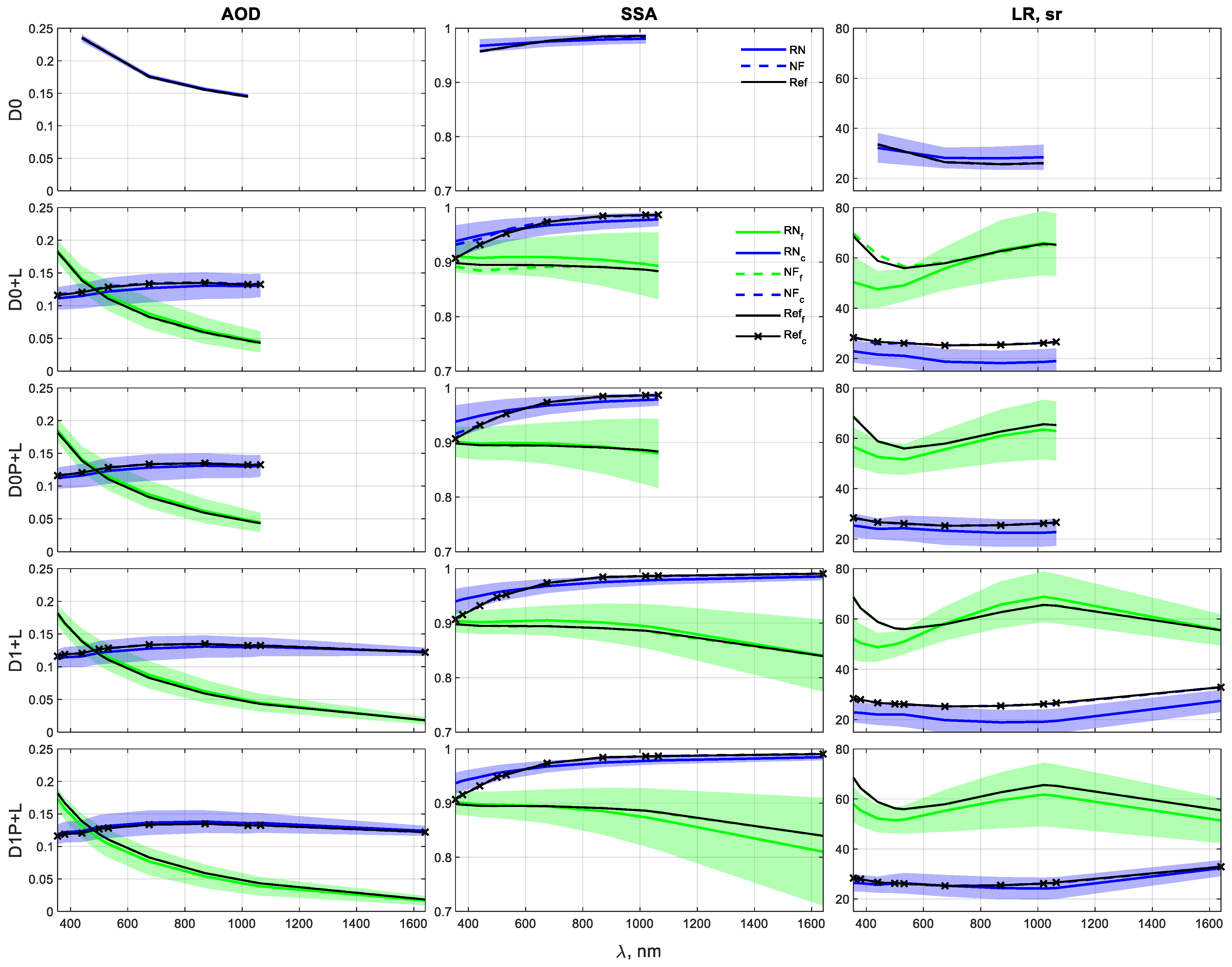
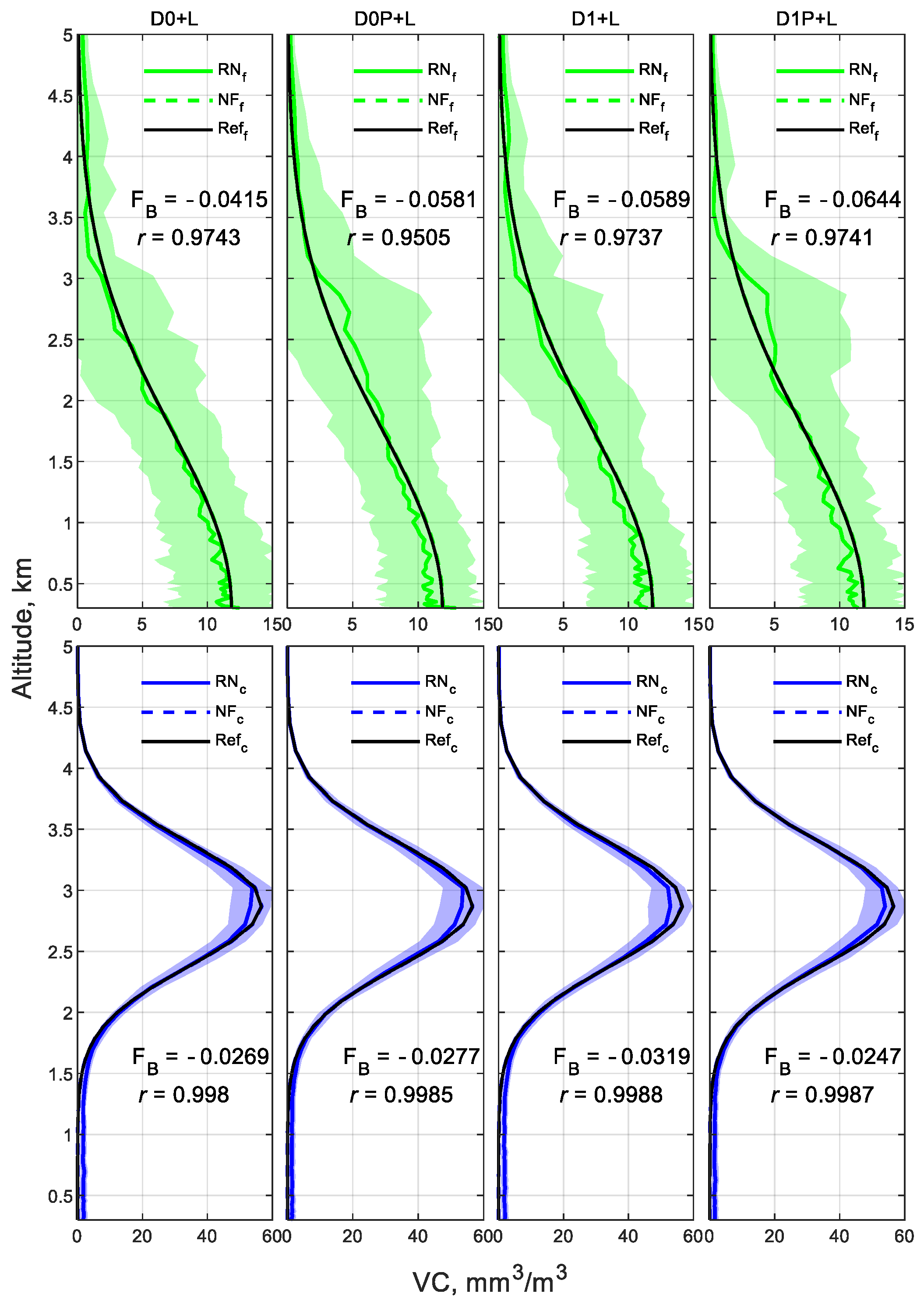
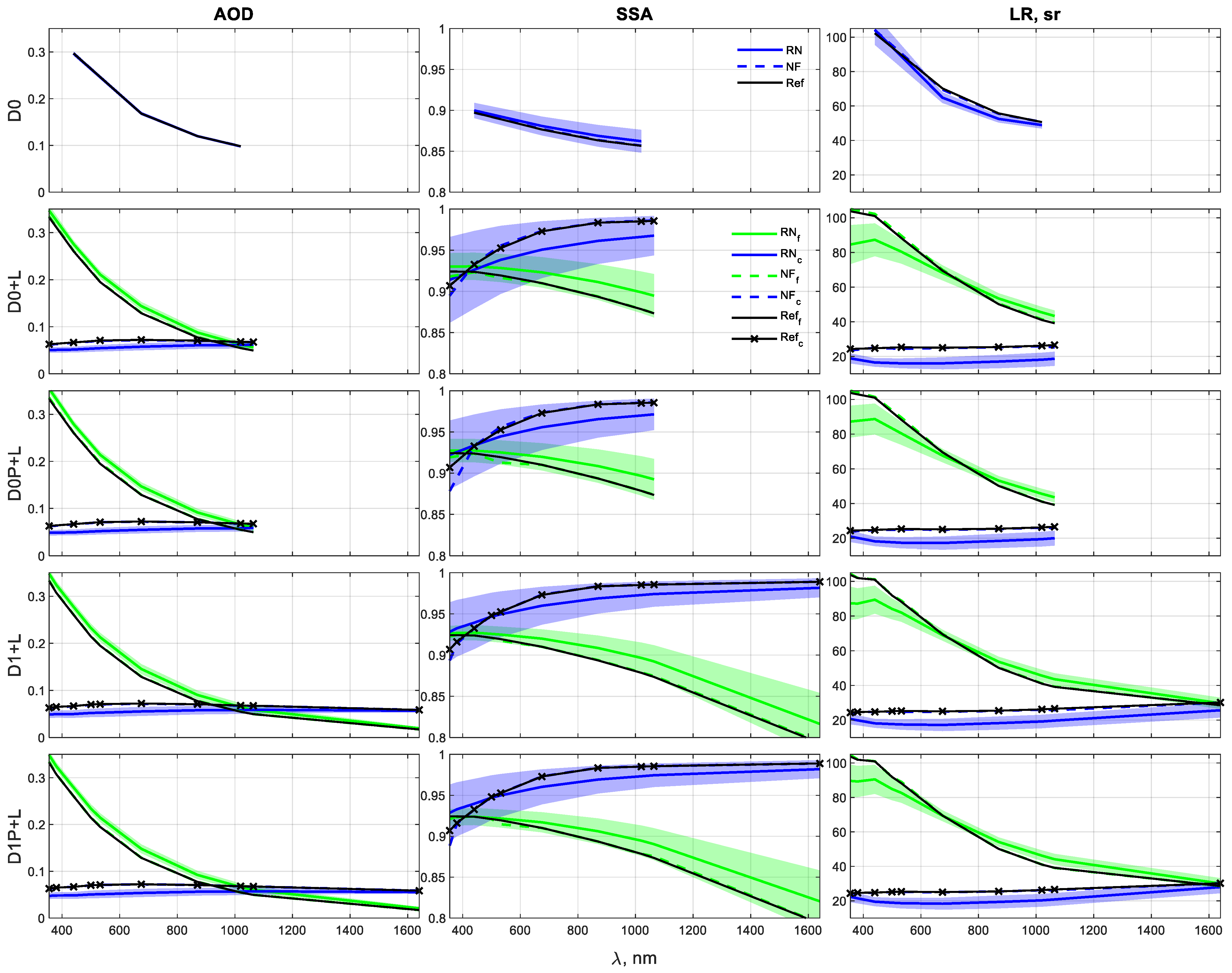
- Even when the fine mode is the non-dominant one (Scenarios I and II), GRASP retrievals with DoLP contributions can significantly improve some of the microphysical and optical properties of that mode. For instance, maximum reductions are observed in the uncertainties of 29% (IRI from D0P+L in Scenario I), 8% (AOD from D0P+L in Scenario II), 56% (SSA from D1P+L in Scenario I), 36% (LR from D1P+L in Scenario I), 46% (RRI from D0P+L in Scenario II), and better adjustments of the averaged RN inversions to the reference. So, in coarse mode-dominated regimes, the inclusion in GRASP of the DoLP parameter helps to improve the retrieval of aerosol properties in the non-dominant, fine mode.
- ii.
- The coarse mode of all scenarios presents gains with DoLP, mainly for D1P+L combination at longer wavelengths, which are expected because of the sensitivity of large particles to the polarized light when those particles are closer to their respective longer wavelengths (the opposite is also observed). The maximum reductions in the uncertainties are observed at 1020 and 1640 nm: 26% at 1020 nm and 15% at 1640 nm (RRI in Scenario I), 16% at 1640 nm (RRI in Scenario II), 28% at 1640 nm (LR in Scenario II), 36% at 1640 nm (RRI in Scenario III), and 16% at 1640 nm (LR in Scenario III). Thus, independently of the dominance or not of the coarse mode, the inclusion in GRASP of the DoLP parameter helps to retrieve the coarse mode of RRI and LR.
- iii.
- The DoLP contributes to the accuracy of GRASP retrievals in Scenario II, dominant coarse mode with low aerosol loading ( = 0.26), decreasing the overestimation and underestimation of the reference and reducing the uncertainties of the RN retrievals, with a maximum reduction of 46% (fine-mode RRI), 20% (coarse-mode RRI), 8% (fine-mode AOD), 7% (coarse-mode AOD), 2.5% (fine-mode SSA), 18% (coarse-mode SSA), 22% (fine-mode LR), and 28% (coarse-mode LR). This advantage can enhance the retrievals for low aerosol loading, in which better GRASP retrievals are expected for high aerosol loading [15,24,28,63].
- iv.
- The use of DoLP in the retrieval of a dominant fine aerosol (Scenario III) displays an evident impact on the refractive indexes. The uncertainties reduce up to 30% and 23% for RRI (D0P+L and D1P+L, respectively) and 16% for IRI (D0P+L) at shorter wavelengths of the fine mode. Furthermore, the coarse-mode IRI has uncertainty reductions of 30% (D0P+L) and 10% (D1P+L), which is in opposition to the coarse-mode IRI in Scenarios I and II (no enhancements), confirming that the linear polarization is more sensitive to RRI than IRI for small particles [6]. In addition to the improvements in Scenario III, there are good fittings of the RN inversions to the reference for the properties in the coarse mode. Once again, DoLP contributes to improving the fine-mode estimations of the GRASP inversions.
- v.
- For all scenarios, the addition of DoLP to the inversions has a minor contribution in the fine-mode SD and the coarse-mode VC.
- vi.
- The SF accuracy is more notable for Scenarios I and II (dominant coarse aerosols), where the sensitivity of the non-spherical particles is more evident [7], decreasing the SF by 71% (D0P+L) and 83% (D1P+L) for Scenario I and 21% (D0P+L) and 27% (D1P+L) for Scenario II;
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carslaw, K.S. Introduction. In Aerosols and Climate; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1–8. ISBN 978-0-12-819766-0. [Google Scholar]
- Sekera, Z. Introduction. In Polarization of Skylight; Springer: Berlin/Heidelberg, Germany, 1957; Volume 10/48, pp. 288–328. ISBN 978-3-642-45881-1. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D. Satellite Retrieval of Aerosol Properties over the Ocean Using Polarization as Well as Intensity of Reflected Sunlight. J. Geophys. Res. 1997, 102, 16989–17013. [Google Scholar] [CrossRef]
- Li, Z.; Goloub, P.; Devaux, C.; Gu, X.; Deuzé, J.-L.; Qiao, Y.; Zhao, F. Retrieval of Aerosol Optical and Physical Properties from Ground-Based Spectral, Multi-Angular, and Polarized Sun-Photometer Measurements. Remote Sens. Environ. 2006, 101, 519–533. [Google Scholar] [CrossRef]
- Dubovik, O.; Sinyuk, A.; Lapyonok, T.; Holben, B.N.; Mishchenko, M.; Yang, P.; Eck, T.F.; Volten, H.; Muñoz, O.; Veihelmann, B.; et al. Application of Spheroid Models to Account for Aerosol Particle Nonsphericity in Remote Sensing of Desert Dust. J. Geophys. Res. 2006, 111, D11208. [Google Scholar] [CrossRef]
- Li, Z.; Goloub, P.; Dubovik, O.; Blarel, L.; Zhang, W.; Podvin, T.; Sinyuk, A.; Sorokin, M.; Chen, H.; Holben, B.; et al. Improvements for Ground-Based Remote Sensing of Atmospheric Aerosol Properties by Additional Polarimetric Measurements. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1954–1961. [Google Scholar] [CrossRef]
- Fedarenka, A.; Dubovik, O.; Goloub, P.; Li, Z.; Lapyonok, T.; Litvinov, P.; Barel, L.; Gonzalez, L.; Podvin, T.; Crozel, D. Utilization of AERONET Polarimetric Measurements for Improving Retrieval of Aerosol Microphysics: GSFC, Beijing and Dakar Data Analysis. J. Quant. Spectrosc. Radiat. Transf. 2016, 179, 72–97. [Google Scholar] [CrossRef]
- Chaikovsky, A.P.; Dubovik, O.; Holben, B.N.; Bril, A.I. Bril Methodology to Retrieve Atmospheric Aerosol Parameters by Combining Ground-Based Measurements of Multiwavelength Lidar and Sun Sky-Scanning Radiometer; SPIE: Bellingham, WA, USA, 2002; Volume 4678, pp. 257–268. [Google Scholar]
- Chaikovsky, A.P.; Bril, A.I.; Barun, V.V.; Dubovik, O.; Holben, B.N.; Goloub, P.; Sobolewski, P. Sobolewski Methodology and Sample Results of Retrieving Aerosol Parameters by Combined Multiwavelength Lidar and Sun-Sky Scanning Measurements; SPIE: Bellingham, WA, USA, 2004; Volume 5397, pp. 146–157. [Google Scholar]
- Chaikovsky, A.; Dubovik, O.; Holben, B.; Bril, A.; Goloub, P.; Tanré, D.; Pappalardo, G.; Wandinger, U.; Chaikovskaya, L.; Denisov, S.; et al. Lidar-Radiometer Inversion Code (LIRIC) for the Retrieval of Vertical Aerosol Properties from Combined Lidar/Radiometer Data: Development and Distribution in EARLINET. Atmos. Meas. Tech. 2016, 9, 1181–1205. [Google Scholar] [CrossRef]
- Cuesta, J.; Flamant, P.H.; Flamant, C. Synergetic Technique Combining Elastic Backscatter Lidar Data and Sunphotometer AERONET Inversion for Retrieval by Layer of Aerosol Optical and Microphysical Properties. Appl. Opt. 2008, 47, 4598. [Google Scholar] [CrossRef]
- Ganguly, D.; Ginoux, P.; Ramaswamy, V.; Dubovik, O.; Welton, J.; Reid, E.A.; Holben, B.N. Inferring the Composition and Concentration of Aerosols by Combining AERONET and MPLNET Data: Comparison with Other Measurements and Utilization to Evaluate GCM Output. J. Geophys. Res. 2009, 114, D16203. [Google Scholar] [CrossRef]
- Ansmann, A.; Seifert, P.; Tesche, M.; Wandinger, U. Profiling of Fine and Coarse Particle Mass: Case Studies of Saharan Dust and Eyjafjallajökull/Grimsvötn Volcanic Plumes. Atmos. Chem. Phys. 2012, 12, 9399–9415. [Google Scholar] [CrossRef]
- Tesche, M.; Ansmann, A.; Müller, D.; Althausen, D.; Engelmann, R.; Freudenthaler, V.; Groß, S. Vertically Resolved Separation of Dust and Smoke over Cape Verde Using Multiwavelength Raman and Polarization Lidars during Saharan Mineral Dust Experiment 2008. J. Geophys. Res. 2009, 114, D13202. [Google Scholar] [CrossRef]
- Lopatin, A.; Dubovik, O.; Chaikovsky, A.; Goloub, P.; Lapyonok, T.; Tanré, D.; Litvinov, P. Enhancement of Aerosol Characterization Using Synergy of Lidar and Sun-Photometer Coincident Observations: The GARRLiC Algorithm. Atmos. Meas. Tech. 2013, 6, 2065–2088. [Google Scholar] [CrossRef]
- Dubovik, O.; Lapyonok, T.; Litvinov, P.; Herman, M.; Fuertes, D.; Ducos, F.; Torres, B.; Derimian, Y.; Huang, X.; Lopatin, A.; et al. GRASP: A Versatile Algorithm for Characterizing the Atmosphere. SPIE Newsroom 2014, 25, 2-1201408. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A Flexible Inversion Algorithm for Retrieval of Aerosol Optical Properties from Sun and Sky Radiance Measurements. J. Geophys. Res. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.N.; Lapyonok, T.; Sinyuk, A.; Mishchenko, M.I.; Yang, P.; Slutsker, I. Non-Spherical Aerosol Retrieval Method Employing Light Scattering by Spheroids. Geophys. Res. Lett. 2002, 29, 54-1–54-4. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of Absorption and Optical Properties of Key Aerosol Types Observed in Worldwide Locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Sinyuk, A.; Dubovik, O.; Holben, B.; Eck, T.F.; Breon, F.-M.; Martonchik, J.; Kahn, R.; Diner, D.J.; Vermote, E.F.; Roger, J.-C.; et al. Simultaneous Retrieval of Aerosol and Surface Properties from a Combination of AERONET and Satellite Data. Remote Sens. Environ. 2007, 107, 90–108. [Google Scholar] [CrossRef]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanré, D.; Deuzé, J.L.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically Optimized Inversion Algorithm for Enhanced Retrieval of Aerosol Properties from Spectral Multi-Angle Polarimetric Satellite Observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef]
- Dubovik, O.; Fuertes, D.; Litvinov, P.; Lopatin, A.; Lapyonok, T.; Doubovik, I.; Xu, F.; Ducos, F.; Chen, C.; Torres, B.; et al. A Comprehensive Description of Multi-Term LSM for Applying Multiple a Priori Constraints in Problems of Atmospheric Remote Sensing: GRASP Algorithm, Concept, and Applications. Front. Remote Sens. 2021, 2, 706851. [Google Scholar] [CrossRef]
- Lopatin, A.; Dubovik, O.; Fuertes, D.; Stenchikov, G.; Lapyonok, T.; Veselovskii, I.; Wienhold, F.G.; Shevchenko, I.; Hu, Q.; Parajuli, S. Synergy Processing of Diverse Ground-Based Remote Sensing and in Situ Data Using the GRASP Algorithm: Applications to Radiometer, Lidar and Radiosonde Observations. Atmos. Meas. Tech. 2021, 14, 2575–2614. [Google Scholar] [CrossRef]
- Torres, B.; Dubovik, O.; Toledano, C.; Berjon, A.; Cachorro, V.E.; Lapyonok, T.; Litvinov, P.; Goloub, P. Sensitivity of Aerosol Retrieval to Geometrical Configuration of Ground-Based Sun/Sky Radiometer Observations. Atmos. Chem. Phys. 2014, 14, 847–875. [Google Scholar] [CrossRef]
- Derimian, Y.; Dubovik, O.; Huang, X.; Lapyonok, T.; Litvinov, P.; Kostinski, A.B.; Dubuisson, P.; Ducos, F. Comprehensive Tool for Calculation of Radiative Fluxes: Illustration of Shortwave Aerosol Radiative Effect Sensitivities to the Details in Aerosol and Underlying Surface Characteristics. Atmos. Chem. Phys. 2016, 16, 5763–5780. [Google Scholar] [CrossRef]
- Torres, B.; Dubovik, O.; Fuertes, D.; Schuster, G.; Cachorro, V.E.; Lapyonok, T.; Goloub, P.; Blarel, L.; Barreto, A.; Mallet, M.; et al. Advanced Characterisation of Aerosol Size Properties from Measurements of Spectral Optical Depth Using the GRASP Algorithm. Atmos. Meas. Tech. 2017, 10, 3743–3781. [Google Scholar] [CrossRef] [PubMed]
- Román, R.; Benavent-Oltra, J.A.; Casquero-Vera, J.A.; Lopatin, A.; Cazorla, A.; Lyamani, H.; Denjean, C.; Fuertes, D.; Pérez-Ramírez, D.; Torres, B.; et al. Retrieval of Aerosol Profiles Combining Sunphotometer and Ceilometer Measurements in GRASP Code. Atmos. Res. 2018, 204, 161–177. [Google Scholar] [CrossRef]
- Herrera, M.E.; Dubovik, O.; Torres, B.; Lapyonok, T.; Fuertes, D.; Lopatin, A.; Litvinov, P.; Chen, C.; Benavent-Oltra, J.A.; Bali, J.L.; et al. Estimates of Remote Sensing Retrieval Errors by the GRASP Algorithm: Application to Ground-Based Observations, Concept and Validation. Atmos. Meas. Tech. 2022, 15, 6075–6126. [Google Scholar] [CrossRef]
- Herreras-Giralda, M.; Litvinov, P.; Dubovik, O.; Derimian, Y.; Lapyonok, T.; Fuertes, D.; Sourdeval, O.; Preusker, R.; Fischer, J. Thermal Emission in the Successive Orders of Scattering (SOS) Radiative Transfer Approach. J. Quant. Spectrosc. Radiat. Transf. 2022, 291, 108327. [Google Scholar] [CrossRef]
- Landi, T.; Bonasoni, P.; Brunetti, M.; Campbell, J.; Marquis, J.; Di Girolamo, P.; Lolli, S. Aerosol Direct Radiative Effects under Cloud-Free Conditions over Highly-Polluted Areas in Europe and Mediterranean: A Ten-Years Analysis (2007–2016). Remote Sens. 2021, 13, 2933. [Google Scholar] [CrossRef]
- Sicard, M.; Rocadenbosch, F.; Reba, M.N.M.; Comerón, A.; Tomás, S.; García-Vízcaino, D.; Batet, O.; Barrios, R.; Kumar, D.; Baldasano, J.M. Seasonal Variability of Aerosol Optical Properties Observed by Means of a Raman Lidar at an EARLINET Site over Northeastern Spain. Atmos. Chem. Phys. 2011, 11, 175–190. [Google Scholar] [CrossRef]
- Sicard, M.; Barragan, R.; Dulac, F.; Alados-Arboledas, L.; Mallet, M. Aerosol Optical, Microphysical and Radiative Properties at Regionalbackground Insular Sites in the Western Mediterranean. Atmos. Chem. Phys. 2016, 16, 12177–12203. [Google Scholar] [CrossRef]
- Sicard, M.; Izquierdo, R.; Alarcón, M.; Belmonte, J.; Comerón, A.; Baldasano, J.M. Near-Surface and Columnar Measurements with a Micro Pulse Lidar of Atmospheric Pollen in Barcelona, Spain. Atmos. Chem. Phys. 2016, 16, 6805–6821. [Google Scholar] [CrossRef]
- Sicard, M.; Jorba, O.; Ho, J.J.; Izquierdo, R.; De Linares, C.; Alarcón, M.; Comerón, A.; Belmonte, J. Measurement Report: Characterization of the Vertical Distribution of Airborne Pinus Pollen in the Atmosphere with Lidar-Derived Profiles–a Modeling Case Study in the Region of Barcelona, NE Spain. Atmos. Chem. Phys. 2021, 21, 17807–17832. [Google Scholar] [CrossRef]
- Smirnov, A.; Holben, B.N.; Eck, T.F.; Dubovik, O.; Slutsker, I. Cloud-Screening and Quality Control Algorithms for the AERONET Database. Remote Sens. Environ. 2000, 73, 337–349. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Smirnov, A.; Sinyuk, A.; Schafer, J.; Giles, D.; Dubovik, O. Aeronet’s Version 2.0 Quality Assurance Criteria. Tsay, S.-C., Nakajima, T., Singh, R.P., Sridharan, R., Eds.; SPIE: Bellingham, WA, USA, 2006; p. 64080Q. [Google Scholar] [CrossRef]
- Mallet, M.; Dubovik, O.; Nabat, P.; Dulac, F.; Kahn, R.; Sciare, J.; Paronis, D.; Léon, J.F. Absorption Properties of Mediterranean Aerosols Obtained from Multi-Year Ground-Based Remote Sensing Observations. Atmos. Chem. Phys. 2013, 13, 9195–9210. [Google Scholar] [CrossRef]
- Pappalardo, G.; Amodeo, A.; Apituley, A.; Comeron, A.; Freudenthaler, V.; Linné, H.; Ansmann, A.; Bösenberg, J.; D’Amico, G.; Mattis, I.; et al. EARLINET: Towards an Advanced Sustainable European Aerosol Lidar Network. Atmos. Meas. Tech. 2014, 7, 2389–2409. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Barreto, Á.; Cuevas, E.; Granados-Muñoz, M.-J.; Alados-Arboledas, L.; Romero, P.M.; Gröbner, J.; Kouremeti, N.; Almansa, A.F.; Stone, T.; Toledano, C.; et al. The New Sun-Sky-Lunar Cimel CE318-T Multiband Photometer—A Comprehensive Performance Evaluation. Atmos. Meas. Tech. 2016, 9, 631–654. [Google Scholar] [CrossRef]
- Li, Z.; Goloub, P.; Devaux, C.; Gu, X.; Qiao, Y.; Zhao, F.; Chen, H. Aerosol Polarized Phase Function and Single-Scattering Albedo Retrieved from Ground-Based Measurements. Atmos. Res. 2004, 71, 233–241. [Google Scholar] [CrossRef]
- Barreto, A.; Cuevas, E.; Damiri, B.; Guirado, C.; Berkoff, T.; Berjón, A.J.; Hernández, Y.; Almansa, F.; Gil, M. A New Method for Nocturnal Aerosol Measurements with a Lunar Photometer Prototype. Atmos. Meas. Tech. 2013, 6, 585–598. [Google Scholar] [CrossRef]
- Barreto, A.; Cuevas, E.; Damiri, B.; Romero, P.M.; Almansa, F. Column Water Vapor Determination in Night Period with a Lunar Photometer Prototype. Atmos. Meas. Tech. 2013, 6, 2159–2167. [Google Scholar] [CrossRef]
- Barreto, Á.; Román, R.; Cuevas, E.; Berjón, A.J.; Almansa, A.F.; Toledano, C.; González, R.; Hernández, Y.; Blarel, L.; Goloub, P.; et al. Assessment of Nocturnal Aerosol Optical Depth from Lunar Photometry at the Izaña High Mountain Observatory. Atmos. Meas. Tech. 2017, 10, 3007–3019. [Google Scholar] [CrossRef]
- Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 Database–Automated near-Real-Time Quality Control Algorithm with Improved Cloud Screening for Sun Photometer Aerosol Optical Depth (AOD) Measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef]
- Sinyuk, A.; Holben, B.N.; Eck, T.F.; Giles, D.M.; Slutsker, I.; Korkin, S.; Schafer, J.S.; Smirnov, A.; Sorokin, M.; Lyapustin, A. The AERONET Version 3 Aerosol Retrieval Algorithm, Associated Uncertainties and Comparisons to Version 2. Atmos. Meas. Tech. 2020, 13, 3375–3411. [Google Scholar] [CrossRef]
- Torres, B.; Fuertes, D. Characterization of Aerosol Size Properties from Measurements of Spectral Optical Depth: A Global Validation of the GRASP-AOD Code Using Long-Term AERONET Data. Atmos. Meas. Tech. 2021, 14, 4471–4506. [Google Scholar] [CrossRef]
- Rocadenbosch, F.; Sicard, M.; Comerón, A.; Baldasano, J.M.; Agishev, R.; Muñoz, C.; López, M.A.; García-Vizcaino, D. The UPC Scanning Raman Lidar: An Engineering Overview. In Proceedings of the 21st International Laser Radar Conference (ILRC), Quebec, QC, Canada, 8–12 July 2002; Volume 1, pp. 19–70. [Google Scholar]
- Kumar, D.; Rocadenbosch, F.; Sicard, M.; Comeron, A.; Muñoz, C.; Lange, D.; Tomás, S.; Gregorio, E. Six-Channel Polychromator Design and Implementation for the UPC Elastic/Raman Lidar; Singh, U.N., Pappalardo, G., Eds.; SPIE: Bellingham, WA, USA; p. 81820W. [CrossRef]
- Rodríguez-Gómez, A.; Sicard, M.; Granados-Muñoz, M.-J.; Chahed, E.B.; Muñoz-Porcar, C.; Barragán, R.; Comerón, A.; Rocadenbosch, F.; Vidal, E. An Architecture Providing Depolarization Ratio Capability for a Multi-Wavelength Raman Lidar: Implementation and First Measurements. Sensors 2017, 17, 2957. [Google Scholar] [CrossRef]
- Comerón, A.; Rodríguez-Gómez, A.; Sicard, M.; Barragán, R.; Muñoz-Porcar, C.; Rocadenbosch, F.; Granados-Muñoz, M. Considerations about the Determination of the Depolarization Calibration Profile of a Two-Telescope Lidar and Its Implications for Volume Depolarization Ratio Retrieval. Sensors 2018, 18, 1807. [Google Scholar] [CrossRef] [PubMed]
- Zenteno-Hernández, J.A.; Comerón, A.; Rodríguez-Gómez, A.; Muñoz-Porcar, C.; D’Amico, G.; Sicard, M. A Comparative Analysis of Aerosol Optical Coefficients and Their Associated Errors Retrieved from Pure-Rotational and Vibro-Rotational Raman Lidar Signals. Sensors 2021, 21, 1277. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Gómez, A.; Muñoz-Porcar, C.; Zenteno-Hernández, J.-A.; Comerón, A.; Dios, F.; Sicard, M.; Gil-Díaz, C.; Oliveira, D.C.F.S.; Mandal, C. Use of Pure Rotational Raman Channels for Lidar Measurement of Aerosol Extinction Coefficient: The EARLINET/ACTRIS Barcelona Station Experience. In Remote Sensing of Clouds and the Atmosphere XXVII; Comerón, A., Kassianov, E.I., Schäfer, K., Picard, R.H., Weber, K., Singh, U.N., Eds.; SPIE: Berlin, Germany, 2022; p. 13. [Google Scholar]
- Knobelspiesse, K.; van Diedenhoven, B.; Marshak, A.; Dunagan, S.; Holben, B.; Slutsker, I. Cloud Thermodynamic Phase Detection with Polarimetrically Sensitive Passive Sky Radiometers. Atmos. Meas. Tech. 2015, 8, 1537–1554. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Polarization of Light in the Atmosphere and Ocean; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-662-46761-9. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; Dover Publications: New York, NY, USA, 1960; ISBN 978-0-486-60590-6. [Google Scholar]
- Gassó, S.; Knobelspiesse, K.D. Circular Polarization in Atmospheric Aerosols. Atmos. Chem. Phys. 2022, 22, 13581–13605. [Google Scholar] [CrossRef]
- Dubovik, O. Optimization of Numerical Inversion in Photopolarimetric Remote Sensing; Springer: Dordrecht, The Netherlands, 2004; Volume 161. [Google Scholar]
- Gatebe, C.K.; Dubovik, O.; King, M.D.; Sinyuk, A. Simultaneous Retrieval of Aerosol and Surface Optical Properties from Combined Airborne- and Ground-Based Direct and Diffuse Radiometric Measurements. Atmos. Chem. Phys. 2010, 10, 2777–2794. [Google Scholar] [CrossRef]
- D’Amico, G.; Amodeo, A.; Baars, H.; Binietoglou, I.; Freudenthaler, V.; Mattis, I.; Wandinger, U.; Pappalardo, G. EARLINET Single Calculus Chain–Overview on Methodology and Strategy. Atmos. Meas. Tech. 2015, 8, 4891–4916. [Google Scholar] [CrossRef]
- D’Amico, G.; Amodeo, A.; Mattis, I.; Freudenthaler, V.; Pappalardo, G. EARLINET Single Calculus Chain–Technical–Part 1: Pre-Processing of Raw Lidar Data. Atmos. Meas. Tech. 2016, 9, 491–507. [Google Scholar] [CrossRef]
- Mattis, I.; D’Amico, G.; Baars, H.; Amodeo, A.; Madonna, F.; Iarlori, M. EARLINET Single Calculus Chain–Technical–Part 2: Calculation of Optical Products. Atmos. Meas. Tech. 2016, 9, 3009–3029. [Google Scholar] [CrossRef]
- Dubovik, O.; Smirnov, A.; Holben, B.N.; King, M.D.; Kaufman, Y.J.; Eck, T.F.; Slutsker, I. Accuracy Assessments of Aerosol Optical Properties Retrieved from Aerosol Robotic Network (AERONET) Sun and Sky Radiance Measurements. J. Geophys. Res. 2000, 105, 9791–9806. [Google Scholar] [CrossRef]
- O’Neill, N.T.; Eck, T.F.; Smirnov, A.; Holben, B.N.; Thulasiraman, S. Spectral Discrimination of Coarse and Fine Mode Optical Depth. J. Geophys. Res. 2003, 108, 4559. [Google Scholar] [CrossRef]
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Tasks for Vegetation Science; Springer Dordrecht: Dordrecht, The Netherlands, 1981; ISBN 978-90-6193-607-7. [Google Scholar]
- Li, X.; Strahler, A.H. Geometric-Optical Bidirectional Reflectance Modeling of the Discrete Crown Vegetation Canopy: Effect of Crown Shape and Mutual Shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A.H. On the Derivation of Kernels for Kernel-Driven Models of Bidirectional Reflectance. J. Geophys. Res. 1995, 100, 21077. [Google Scholar] [CrossRef]
- Nadal, F.; Breon, F.-M. Parameterization of Surface Polarized Reflectance Derived from POLDER Spaceborne Measurements. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1709–1718. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.-M.; Fédèle, E.; Bouvier, M. Polarized Reflectances of Natural Surfaces: Spaceborne Measurements and Analytical Modeling. Remote Sens. Environ. 2009, 113, 2642–2650. [Google Scholar] [CrossRef]
- Eck, T.F.; Holben, B.N.; Reid, J.S.; Dubovik, O.; Smirnov, A.; O’Neill, N.T.; Slutsker, I.; Kinne, S. Wavelength Dependence of the Optical Depth of Biomass Burning, Urban, and Desert Dust Aerosols. J. Geophys. Res. 1999, 104, 31333–31349. [Google Scholar] [CrossRef]
- Sicard, M.; D’Amico, G.; Comerón, A.; Mona, L.; Alados-Arboledas, L.; Amodeo, A.; Baars, H.; Baldasano, J.M.; Belegante, L.; Binietoglou, I.; et al. EARLINET: Potential Operationality of a Research Network. Atmos. Meas. Tech. 2015, 8, 4587–4613. [Google Scholar] [CrossRef]
- Emery, C.; Liu, Z.; Russell, A.G.; Odman, M.T.; Yarwood, G.; Kumar, N. Recommendations on Statistics and Benchmarks to Assess Photochemical Model Performance. J. Air Waste Manag. Assoc. 2017, 67, 582–598. [Google Scholar] [CrossRef]
- Benavent-Oltra, J.A.; Román, R.; Granados-Muñoz, M.J.; Pérez-Ramírez, D.; Ortiz-Amezcua, P.; Denjean, C.; Lopatin, A.; Lyamani, H.; Torres, B.; Guerrero-Rascado, J.L.; et al. Comparative Assessment of GRASP Algorithm for a Dust Event over Granada (Spain) during ChArMEx-ADRIMED 2013 Campaign. Atmos. Meas. Tech. 2017, 10, 4439–4457. [Google Scholar] [CrossRef]
| Property | Winter | Spring | Summer | Autumn | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| December | January | February | March | April | May | June | July | August | September | October | November | |
| (std) | 0.10 (0.07) | 0.11 (0.08) | 0.16 (0.12) | 0.16 (0.12) | 0.20 (0.12) | 0.18 (0.09) | 0.23 (0.11) | 0.25 (0.11) | 0.23 (0.11) | 0.21 (0.12) | 0.16 (0.11) | 0.11 (0.08) |
| (std) | 1.37 (0.34) | 1.35 (0.38) | 1.36 (0.36) | 1.27 (0.34) | 1.25 (0.38) | 1.28 (0.34) | 1.34 (0.39) | 1.30 (0.37) | 1.32 (0.36) | 1.34 (0.32) | 1.23 (0.35) | 1.33 (0.31) |
| Technical Specifications | |
|---|---|
| Tracking precision | 0.003° |
| Sun-moon tracking accuracy | 0.01° |
| Field of view | 1.29° |
| Digital count precision | <0.1% |
| Detectors | Silicon photodiodes and InGaAs |
| Spectral range | 340–1020 nm (Silicon detector) 1020–1640 nm (InGaAs detector) |
| Environmental temperature range | −20 °C to 50 °C |
| Power supply | 110–240 V |
| Technical Specifications | |
|---|---|
| Laser | Innolas Spitlight 400 |
| Zenith angle | 0° |
| Elastic wavelengths | 355, 532, and 1064 nm |
| Energy per pulse | 103, 154, and 97 mJ |
| Divergence | 28 mrad |
| Repetition rate | 20 Hz |
| Pulse duration | 3.6 ns |
| System configuration | Mono-static, vertical, biaxial |
| Spatial resolution | 3.75 m |
| Telescope model | Celestron CGE 1400 |
| Telephoto lens for depolarization measurements | TAIR-3S for 355 nm and 532 nm |
| Focal length of the telescope | 3.91 m |
| Telescope aperture Ø | 0.35 m |
| Detector | APD and PMT |
| Voltage Responsivity | 1.9 × 106 (355 nm), 1.5 × 106 (532 nm), and 3.7 × 105 (1064 nm) [V W−1] |
| Spectral bandwidth | 1 nm for all wavelengths |
| Acquisition | Licel transient recorder TR40-80—mixed 250 MHz PC + ADC 40 Msps/12 bit |
| Outputs | Aerosol-Related Products | Acronym |
|---|---|---|
| Direct | Vertical distribution of the aerosol concentration | AVP (h) |
| Size distribution | SD | |
| Real refractive index spectral | RRI (λ) | |
| Imaginary refractive index spectral distribution | IRI (λ) | |
| Ångström exponent spectral distribution | AE (λ) | |
| Aerosol optical depth spectral distribution | AOD (λ) | |
| Single scattering albedo spectral distribution | SSA (λ) | |
| Absorption AOD | AAOD (λ) | |
| Lidar ratio spectral distribution | LR (λ) | |
| Sphere fraction | SF | |
| Effective radii total | EffR | |
| Column-integrated volume concentration | VC | |
| Volume mean radius total | VMR | |
| Net forcing | NF | |
| Derived | Ångström exponent profile | AEP (λ, h) |
| Backscatter profile | β (λ, h) | |
| Extinction profile | α (λ, h) | |
| Single scattering albedo profile | SSAP (λ, h) | |
| Lidar ratio Profile | LRP (λ, h) | |
| Aerosol absorption profile | AAP (λ, h) |
| Notation | Inputs |
|---|---|
| D0 (AERONET-like) | AOD + R (4λ) |
| D0P | AOD + R + DoLP (4λ) |
| D0+L | AOD + R (4λ) + 3 RCS |
| D0P+L | AOD + R + DoLP (4λ) + 3 RCS |
| D1 | AOD + R (7λ) |
| D1P | AOD + R + DoLP (7λ) |
| D1+L | AOD + R (7λ) + 3 RCS |
| D1P+L | R + DoLP (7λ) + 3 RCS |
| Scenario | Comb. | R (rel) | AOD (abs) | DoLP (abs) | LS (rel) | Residual |
|---|---|---|---|---|---|---|
| I (High AOD and dominant coarse mode) | D0 | 3% | 0.01 | - | 20% | 0.04520 |
| D0+L | - | 0.00435 | ||||
| D0P+L | 0.01 | 0.00183 | ||||
| D1+L | - | 0.00593 | ||||
| D1P+L | 0.01 | 0.00080 | ||||
| II (Low AOD and dominant coarse mode) | D0 | 5% | 0.01 | - | 20% | 0.05149 |
| D0+L | - | 0.00753 | ||||
| D0P+L | 0.01 | 0.00055 | ||||
| D1+L | - | 0.00043 | ||||
| D1P+L | 0.01 | 0.00055 | ||||
| III (High AOD and dominant fine mode) | D0 | 3% | 0.01 | - | 25% | 0.02581 |
| D0+L | - | 0.00213 | ||||
| D0P+L | 0.05 | 0.00111 | ||||
| D1+L | - | 0.00148 | ||||
| D1P+L | 0.05 | 0.00121 |
| Sc. | Comb. | SD | RRI | IRI | AOD | SSA | LR | SF * | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fine | Coarse | Fine | Coarse | Fine | Coarse | Fine | Coarse | Fine | Coarse | Fine | Coarse | Mean (Std) | Total | ||
| I | D0+L | 0.011 | 0.008 | 0.012 | 0.010 | 0.0024 | 0.0007 | 0.042 | 0.041 | 0.051 | 0.018 | 8.55 | 2.26 | 0.035 (0.055) | 0.023 |
| D0P+L | 0.012 | 0.008 | 0.035 | 0.007 | 0.0030 | 0.0009 | 0.035 | 0.035 | 0.014 | 0.012 | 9.61 | 2.80 | 0.010 (0.022) | 0.001 | |
| D1+L | 0.012 | 0.009 | 0.021 | 0.016 | 0.0031 | 0.0007 | 0.060 | 0.059 | 0.096 | 0.016 | 13.54 | 3.28 | 0.024 (0.042) | 0.013 | |
| D1P+L | 0.009 | 0.007 | 0.037 | 0.009 | 0.0025 | 0.0009 | 0.036 | 0.035 | 0.016 | 0.012 | 8.13 | 2.85 | 0.004 (0.010) | 0.008 | |
| II | D0+L | 0.005 | 0.002 | 0.014 | 0.015 | 0.0034 | 0.0007 | 0.003 | 0.005 | 0.013 | 0.015 | 8.55 | 6.42 | 0.360 (0.093) | 0.164 |
| D0P+L | 0.005 | 0.001 | 0.006 | 0.010 | 0.0016 | 0.0007 | 0.003 | 0.004 | 0.003 | 0.015 | 5.60 | 2.96 | 0.285 (0.068) | 0.089 | |
| D1+L | 0.005 | 0.002 | 0.015 | 0.014 | 0.0024 | 0.0007 | 0.003 | 0.004 | 0.008 | 0.016 | 8.12 | 5.62 | 0.319 (0.076) | 0.123 | |
| D1P+L | 0.005 | 0.001 | 0.013 | 0.011 | 0.0018 | 0.0007 | 0.007 | 0.003 | 0.011 | 0.015 | 5.85 | 1.34 | 0.232 (0.036) | 0.036 | |
| III | D0+L | 0.003 | 0.003 | 0.003 | 0.015 | 0.0017 | 0.0009 | 0.013 | 0.012 | 0.015 | 0.017 | 9.75 | 8.12 | 0.470 (0.176) | 0.183 |
| D0P+L | 0.003 | 0.003 | 0.006 | 0.009 | 0.0013 | 0.0007 | 0.017 | 0.015 | 0.012 | 0.014 | 8.77 | 6.75 | 0.400 (0.106) | 0.113 | |
| D1+L | 0.003 | 0.002 | 0.006 | 0.005 | 0.0011 | 0.0008 | 0.014 | 0.014 | 0.013 | 0.012 | 8.78 | 6.53 | 0.427 (0.104) | 0.140 | |
| D1P+L | 0.003 | 0.002 | 0.010 | 0.005 | 0.0006 | 0.0008 | 0.016 | 0.016 | 0.012 | 0.012 | 7.86 | 5.33 | 0.366 (0.083) | 0.079 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos Oliveira, D.C.F.; Sicard, M.; Rodríguez-Gómez, A.; Comerón, A.; Muñoz-Porcar, C.; Gil-Díaz, C.; Lolli, S.; Dubovik, O.; Lopatin, A.; Herrera, M.E.; et al. Evaluation of the Accuracy of the Aerosol Optical and Microphysical Retrievals by the GRASP Algorithm from Combined Measurements of a Polarized Sun-Sky-Lunar Photometer and a Three-Wavelength Elastic Lidar. Remote Sens. 2023, 15, 5010. https://doi.org/10.3390/rs15205010
dos Santos Oliveira DCF, Sicard M, Rodríguez-Gómez A, Comerón A, Muñoz-Porcar C, Gil-Díaz C, Lolli S, Dubovik O, Lopatin A, Herrera ME, et al. Evaluation of the Accuracy of the Aerosol Optical and Microphysical Retrievals by the GRASP Algorithm from Combined Measurements of a Polarized Sun-Sky-Lunar Photometer and a Three-Wavelength Elastic Lidar. Remote Sensing. 2023; 15(20):5010. https://doi.org/10.3390/rs15205010
Chicago/Turabian Styledos Santos Oliveira, Daniel Camilo Fortunato, Michaël Sicard, Alejandro Rodríguez-Gómez, Adolfo Comerón, Constantino Muñoz-Porcar, Cristina Gil-Díaz, Simone Lolli, Oleg Dubovik, Anton Lopatin, Milagros Estefanía Herrera, and et al. 2023. "Evaluation of the Accuracy of the Aerosol Optical and Microphysical Retrievals by the GRASP Algorithm from Combined Measurements of a Polarized Sun-Sky-Lunar Photometer and a Three-Wavelength Elastic Lidar" Remote Sensing 15, no. 20: 5010. https://doi.org/10.3390/rs15205010
APA Styledos Santos Oliveira, D. C. F., Sicard, M., Rodríguez-Gómez, A., Comerón, A., Muñoz-Porcar, C., Gil-Díaz, C., Lolli, S., Dubovik, O., Lopatin, A., Herrera, M. E., & Herreras-Giralda, M. (2023). Evaluation of the Accuracy of the Aerosol Optical and Microphysical Retrievals by the GRASP Algorithm from Combined Measurements of a Polarized Sun-Sky-Lunar Photometer and a Three-Wavelength Elastic Lidar. Remote Sensing, 15(20), 5010. https://doi.org/10.3390/rs15205010












