Visual Navigation and Obstacle Avoidance Control for Agricultural Robots via LiDAR and Camera

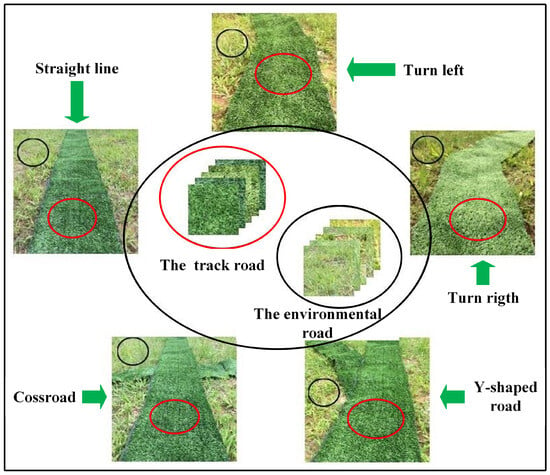
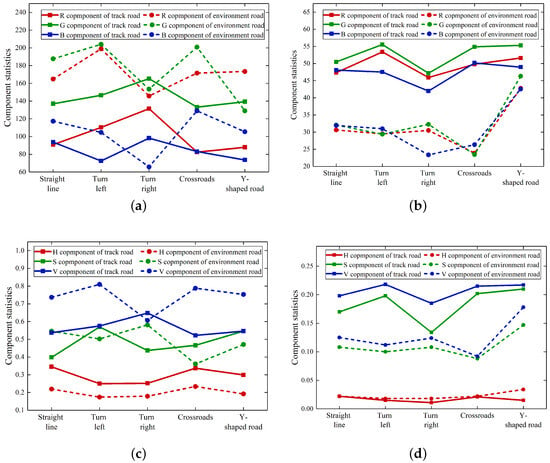
Abstract

Obstacle avoidance control and navigation in unstructured agricultural environments are key to the safe operation of autonomous robots, especially for agricultural machinery, where cost and stability should be taken into account. In this paper, we designed a navigation and obstacle avoidance system for agricultural robots based on LiDAR and a vision camera. The improved clustering algorithm is used to quickly and accurately analyze the obstacle information collected by LiDAR in real time. Also, the convex hull algorithm is combined with the rotating calipers algorithm to obtain the maximum diameter of the convex polygon of the clustered data. Obstacle avoidance paths and course control methods are developed based on the danger zones of obstacles. Moreover, by performing color space analysis and feature analysis on the complex orchard environment images, the optimal H-component of HSV color space is selected to obtain the ideal vision-guided trajectory images based on mean filtering and corrosion treatment. Finally, the proposed algorithm is integrated into the Three-Wheeled Mobile Differential Robot (TWMDR) platform to carry out obstacle avoidance experiments, and the results show the effectiveness and robustness of the proposed algorithm. The research conclusion can achieve satisfactory results in precise obstacle avoidance and intelligent navigation control of agricultural robots.

1. Introduction

Agricultural robots have been acknowledged as a highly promising frontier technology in agriculture. With the rapid development of modern electronic computers, sensors, the Internet of Things and other technologies, the application of agricultural robots is the best way to improve the efficiency and quality of agricultural production [1,2,3]. As a new type of intelligent agricultural equipment, agricultural robots integrate various advanced technologies such as artificial intelligence, automatic control and algorithmic development, and are widely used in the fields of agricultural harvesting, picking, transportation, and sorting, especially in the field of farm mobile inspection [4]. The key to the safe and efficient operation of agricultural mobile robots is to have obstacle avoidance and navigation capabilities, which require practicality and stability and, more importantly, simple and low-cost implementation [5]. However, other industrial mobile robots are not fully applicable in agricultural settings owing to technical limitations and differences in application scenarios. Similarly, unstructured agricultural scenarios and random and changeable environments pose huge challenges for agricultural robots. Therefore, the navigation and obstacle avoidance systems of agricultural robots must adopt stable and low-cost algorithms and control methods [6,7,8].

In order to develop agricultural robots, obstacle avoidance technology is the most important functional module of robots, which can improve the working efficiency of robots, reduce working errors, ensure that robots complete tasks and produce greater benefits. The obstacle avoidance process of agricultural robot integrates agricultural information perception, intelligent control and communication technology. The robot obtains the surrounding environment information through relevant sensors, including the status, size, and position of obstacles, and then makes a series of obstacle avoidance strategies. Therefore, LiDAR [9], ultrasonic sensors, and vision sensors have been widely used in navigation and obstacle avoidance technology because of their high precision and fast speed. Rouveure et al. described in detail millimeter-wave radar for mobile robots, including obstacle detection, mapping, and general situational awareness. The selection of Frequency Modulated Continuous Wave (FMCW) radar is explained and the theoretical elements of the solution are described in detail in [10]. Ball et al. described a vision-based obstacle detection and navigation system that uses an expensive combination of Global Positioning System (GPS) and inertial navigation systems for obstacle detection and visual guidance [11]. Santos et al. proposed a real-time obstacle avoidance method for steep slope farmland based on local observation, which has been successfully tested in vineyards. The LiDAR combined with depth cameras will be considered in the future to improve the perception of the elevation map [12]. However, high sensor costs have impeded researchers. To address this, Monaca et al. explored the “SMARTGRID” initiative. This project utilizes an integrated wireless safety network infrastructure, incorporating Bluetooth Low Energy (BLE) devices and passive Radio Frequency Identification (RFID) tags, designed for identifying obstacles, workers, and nearby vehicles, among other things [13]. Advanced sensors enable potential obstacle avoidance in intricate agricultural surroundings, although their high-cost ratio to accuracy persists and they necessitate the integration of well-developed and stable navigation and algorithmic technologies.

Similarly, robot navigation in obstacle environments remains a challenging problem, especially in the field of agriculture, where accurate navigation of robots in complex agricultural environments is a prerequisite for completing various tasks [14]. Gao et al. discussed the solution to the navigation problem of Mobile Wheeled Robots (WMRs) in agricultural engineering and analyzed the navigation mechanism of WMRs in detail, but do not delve into their cost [15]. Wangt et al. reviewed the advantages, disadvantages, and roles of different vision sensors and Machine Vision (MV) algorithms in agricultural robot navigation [16]. Durand et al. built a vision-based navigation system for autonomous robots, which they noted is low-cost because trees in an orchard can be quickly and accurately identified using four stereo cameras to provide point cloud maps of the environment [17]. Higuti et al. described an autonomous field navigation system based on LiDAR that uses only two-dimensional LiDAR sensors as a single sensing source, reducing costs while enabling robots to travel in a straight line without damaging plantation plants [18]. Gutonneau et al. proposed an autonomous agricultural robot navigation method based on LiDAR data, including a line-finding algorithm and a control algorithm, and performed well in tests with the ROS middleware and the Gazebo simulator. They focused on the sophistication of the algorithm at the expense of the complexity of the algorithm and the stability of the simulation results [19]. LiDAR has become prevalent in agricultural navigation, including vineyards [20] and cornfields [21]. Nevertheless, the equilibrium between cost and practical outcomes is an aspect frequently disregarded by numerous scholars.

Currently, low cost is vital for the development of agricultural robots. Cheap robotic hardware systems and software systems are always welcome as the users are farmers working in the agricultural industry. Global Navigation Satellite System (GNSS) technology provides autonomous navigation solutions for today’s commercial robotic platforms with centimeter-level accuracy. Researchers are trying to make agricultural navigation systems more reliable by using a fusion of GNSS, GPS technology, and other sensor technologies [22]. Winterhalter et al. proposed a GNSS reference map based approach for field localization and autonomous navigation via crop rows [23]. However, GNSS-based solutions are expensive and require a long preparation phase, while on the other hand, GNSS signals can fail or be interrupted in complex agricultural environments, which is hard for farmers to accept.

In this paper, we have developed a low-cost agricultural mobile robot platform based on LiDAR and vision-assisted navigation. The LiDAR is used to acquire information about obstacles in the surrounding environment. An improved density-based fast clustering algorithm is used to find the clustering centers of obstacles, and the maximum diameters of convex polygons in the clustering data are obtained by combining the convex shell algorithm and the rotating jamming algorithm. In addition, an effective orchard path tracking and control method is proposed in this paper, and effective and obvious feature components are selected as the color space components used by the robot in real-time tracking, which initially solves the orchard path feature recognition task and realizes the robot’s visual aided navigation. Finally, the feasibility of the proposed method in obstacle avoidance and navigation of agricultural robots is verified by experiments.

The main contributions of this paper are summarized in the following folds.

• An improved density-based fast clustering algorithm is proposed, combined with a convex hull algorithm and rotating jamming algorithm to analyze obstacle information, and an obstacle avoidance path and heading control method based on the dangerous area of obstacles is developed. The feasibility of low-cost obstacle avoidance using LiDAR in agricultural robots is realized.
• By analyzing the color space information of the orchard environment road and track road images, a robot track navigation route and control method based on image features were proposed. A vision camera was used to assist agricultural robots in navigation, and the orchard path feature recognition task was preliminarily solved.
• An agricultural robot navigation and obstacle avoidance system based on a vision camera and LiDAR is designed, which makes up for the shortcomings of poor robustness and easy to be disturbed by the environment of a single sensor, and realizes the stable work of agricultural robots working in the environment rejected by GNSS.

The rest of this article is organized as follows. Section 2 introduces the calibration work of LiDAR and visual camera. Section 3 provides the development and proposed method of robot obstacle avoidance system. Section 4 presents the research of robot vision system. In Section 5, the obstacle avoidance and navigation experiments of the robot are carried out. Finally, we make conclusions work of the whole manuscript.

2. Preliminaries

2.1. LiDAR Calibration and Filtering Processing

Since the process of collecting environmental data by LiDAR is relative to the form of LiDAR polar coordinate system [24], if LiDAR is installed on the robot platform, the coordinate system will be based on the robot. Therefore, it is necessary to re-calibrate the coordinate system relationship between LiDAR and the robot. There are three coordinate definitions in the robot positioning system, which are global coordinate system $X_w{O}_w{Y}_w$, robot coordinate system $X_v{O}_v{Y}_v$ and LiDAR coordinate system $X_s{O}_s{Y}_s$. The relationship between the robot and LiDAR coordinates is determined by the LiDAR’s relative position to the robot. Therefore, the global coordinate system and the robot coordinate system are the main research coordinate systems, in which the LiDAR coordinate system is $X_s{O}_s{Y}_s$, and the typical robot coordinate system relationship is shown in Figure 1. The pose of the robot in the global coordinate system is denoted as $(x,y,\theta )$, with $(x,y)$ representing the robot position, and $\theta$ representing the heading angle [25]. The relationship between any P point in the robot coordinate system and the global coordinate system can be obtained by Equation (1).

$$\begin{array}{c}\left(\begin{array}{c}{x}_w\hfill \\ y_w\hfill \end{array}\right)=\left[\begin{array}{cc}cos\left(\theta -\frac{\pi }{2}\right)& -sin\left(\frac{\pi }{2}\right)\\ sin\left(\theta -\frac{\pi }{2}\right)& cos\left(\theta -\frac{\pi }{2}\right)\end{array}\right]\times \left(\begin{array}{c}{x}_v\hfill \\ y_v\hfill \end{array}\right)+\left(\begin{array}{c}{X}_v\hfill \\ Y_v\hfill \end{array}\right)\hfill \end{array}$$

(1)

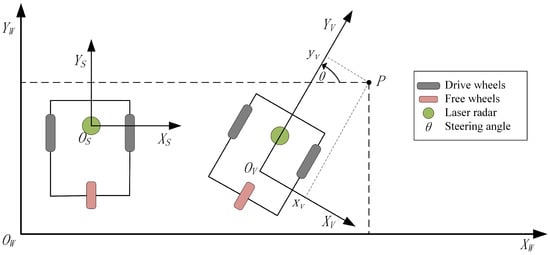
Figure 1. The relationship between robot, LiDAR, and global coordinate system.

The polar coordinate system is the working mode of LiDAR. Firstly, the LiDAR installed on the robot needs to be calibrated to obtain the relationship between LiDAR and robot [26,27]. As shown in Figure 1, the LiDAR coordinate system is $X_s{O}_s{Y}_s$, so the Cartesian coordinate of LiDAR is $(x_s,y_s)$, the polar coordinate form is $(L,\beta )$. The conversion relationship between Cartesian coordinates and polar coordinates of LiDAR is shown in Equation (2).

$$x_s=Lcos\beta ,y_s=Lsin\beta$$

(2)

The pose coordinate of the LiDAR is $(x_s,y_s,\varphi )$, where $\varphi$ is the angle from axis $O_v{X}_v$ to axis $O_s{X}_s$ of the robot coordinate system. Suppose the coordinate of LiDAR coordinate point s under robot is $(x_{vs},y_{vs})$, then the rotation translation of the coordinate system is as shown in Equation (3) [28].

$$\begin{array}{c}\left(\begin{array}{c}{x}_{vs}\hfill \\ y_{vs}\hfill \end{array}\right)=\left[\begin{array}{cc}cos\varphi & -sin\varphi \\ sin\varphi & cos\varphi )\end{array}\right]\times \left(\begin{array}{c}{x}_s\hfill \\ y_s\hfill \end{array}\right)+\left(\begin{array}{c}{X}_s\hfill \\ Y_s\hfill \end{array}\right)\hfill \end{array}$$

(3)

According to the above calibration method, a calibration test is carried out. Firstly, the pose of the robot in global coordinates is determined as $(X_s,Y_s,\varphi )$. The coordinate of the auxiliary calibration object placed in the global coordinate system is $(X_{wi},Y_{wi})$. According to the coordinate system relations in Figure 1, the relational data of the global coordinate system and the LiDAR coordinate system can be calculated.

The center of the auxiliary calibration object in the LiDAR coordinate system is calculated as $(X_{si},Y_{si})$ by the least square method. Further, the LiDAR pose coordinate is obtained by the m-estimation method in Equation (4).

$$\begin{array}{c}\hfill \begin{array}{c}\left(\begin{array}{c}{x}_w\hfill \\ y_w\hfill \end{array}\right)=\left[\begin{array}{cc}cos\left(\theta -\frac{\pi }{2}\right)& -sin\left(\frac{\pi }{2}\right)\\ sin\left(\theta -\frac{\pi }{2}\right)& cos\left(\theta -\frac{\pi }{2}\right)\end{array}\right]\times \left\{\left[\begin{array}{cc}cos\varphi & -sin\varphi \\ sin\varphi & cos\varphi \end{array}\right]\times \left(\begin{array}{c}{x}_s\hfill \\ y_s\hfill \end{array}\right)+\left(\begin{array}{c}{X}_s\hfill \\ Y_s\hfill \end{array}\right)\right\}+\left(\begin{array}{c}{X}_v\hfill \\ Y_v\hfill \end{array}\right)\hfill \end{array}\end{array}$$

(4)

Due to the data collected by LiDAR producing interference cloud signal, such interference noise will have an unstable influence on the detection effect of obstacles [29]. The laser radar data with median filtering effect depends on the filter window options, therefore, this paper adopts an improved median filtering method, which can first determine whether the data point is in the extreme value within the filtering window range. If yes, the point can be filtered; otherwise, the operation will be canceled [30]. Figure 2b shows the effect of the improved median filtering algorithm, the filtering algorithm is shown in Equation (5).

$$\begin{array}{c}{x}_i=\left\{\begin{array}{cc}med\left\{x_{i-s},\dots ,x_i,\dots ,x_{i+s}\right\}& x_i>x_{max}\mathrm{or}{x}_i\le x_{min}\\ \cdots x_i& x_{min}\le x\le x_{max}\end{array}\right.\hfill \\ x_{min}=min\left\{x_{i-s},\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_{i+s}\right\}\hfill \\ x_{max}=max\left\{x_{i-s},\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_{i+s}\right\}\hfill \end{array}$$

(5)

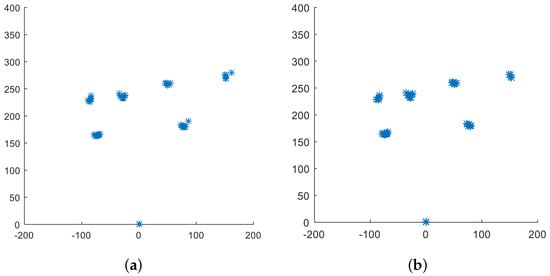
Figure 2. Comparison of median filtering effect before (a) and after (b).

2.2. Camera Visualization and Parameter Calibration

The camera is calibrated using the checkerboard method, with key points acquired. The MATLAB camera calibration function is called, and the camera parameters are calculated by the Zhang Zhengyou calibration algorithm. External parameters of the camera can be visually checked by visualizing 3D images to check the position of the checkerboard calibration board and camera [31,32]. Figure 3a,b are visualized 3D views based on the checkerboard calibration board reference frame and camera reference frame, respectively.

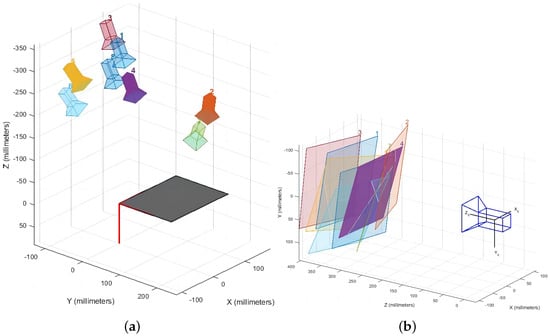
Figure 3. Visual 3D view of different reference frame modes. (a) Reference frame based on checkerboard calibration board; (b) camera reference system.

Finally, the values of internal parameters and external parameters in the camera are calculated by the MATLAB camera calibration algorithm. The matrix A in the camera is as follows:

$$A=\left[\begin{array}{ccc}2.8075\times {10}^3& 0& 0\\ 8.8390& 2.8217\times {10}^3& 0\\ 802.8544& 650.4047& 1\end{array}\right]$$

(6)

The radial distortion coefficient K of the camera lens is as follows:

$$k=\left[-0.0418\cdots -0.01981\cdots 0.7706\right]$$

(7)

The tangential distortion coefficient P of the camera lens is as follows:

$$p=\left[0.0024\cdots 0.0023\right]$$

(8)

3. Obstacle Avoidance System and Algorithm Implementation

In this section, for the obstacle avoidance system designed for autonomous robots, LiDAR is used to collect static obstacles in the moving direction in real-time; in addition, the obstacle information is analyzed by an improved clustering algorithm combined with the convex hull algorithm and the rotating jamming algorithm. Finally, an obstacle avoidance path and heading control method based on the dangerous area of obstacles is developed.

3.1. Improved Clustering Algorithm of Obstacle Point Cloud Information

The present research utilizes an improved algorithm to rapidly and accurately cluster obstacle cloud data, followed by determining the clustering center, which helps locate the obstacle cloud data center [33]. Compared with the traditional K-means algorithm, the clustering algorithm can obtain non-spherical clustering results, describe the data distribution well, and has lower algorithm complexity than the K-means algorithm. This paper first gives a conceptual definition of the algorithm. Two quantities need to be calculated for each data point i, including the local density and the minimum distance above the density of point i.

Local density is defined as follows:

$${\rho }_i=\sum jk(d_{ij}-d_c)$$

(9)

where

$$k\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}x<0\hfill \\ 0\hfill & \mathrm{if}x\ge 0\hfill \end{array}\right.$$

(10)

In this paper, the $d_c$ is a truncation distance which refers to the distance between all points from smallest to largest, accounting for two percent of the total. Distance is defined as

$$\begin{array}{c}j:{\rho }_j>{\rho }_i\\ {\delta }_i=min\left(d_{ij}\right)\end{array}$$

(11)

The ${\delta }_i$ denotes the smallest distance of point i among points whose density surpasses that of point i. A higher value indicates that point i is at a further distance from the high-density point, making it more likely to become the cluster center. For point i with the highest global density, ${\delta }_i$ is equal to the distance between point i and the maximum value of all points [34]. The obstacle point distribution, generated by the enhanced clustering algorithm, is presented in Figure 4.

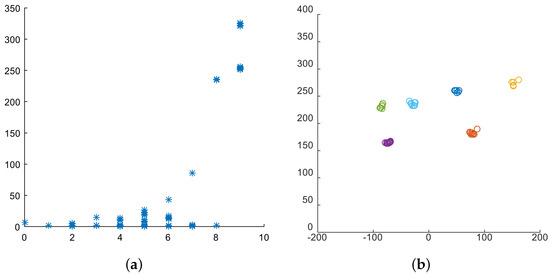
Figure 4. (a) The diagram of data decision; (b) the result of clustering algorithm.

3.2. The Fusion of Convex Hull Algorithm and Rotary Jamming Algorithm

Convex hull is a concept in computer geometry. In a real vector space V, for a given set X, the intersection S of all convex sets containing X is called the convex hull of X. The convex hull of X can be constructed from a linear combination of all points $X_1,X_2,\dots ,X_n$ in X. We use the Graham’s Scan algorithm to find the convex polygon corresponding to the obstacle clustering data collected by LiDAR.

The basic idea of Graham’s Scan algorithm is as follows: the convex hull problem is solved by setting a stack S of candidate points. Each point in the input set X is pushed once, and points that are not vertices in CH(X) (representing the convex hull of X) are eventually popped off the stack. At the end of the calculation, there are only vertices in CH(X) in stack S in the order in which the vertices appear counterclockwise on the boundary. Graham’s Scan algorithm is shown in Table 1. If there is more than one such point, the leftmost point is taken as $P_0$, meanwhile $\left|X\right|\ge 3$. Call the function TOP(S) TO return the point at the TOP of the stack S, and call the function next-to-top (S) TO return the point below the TOP of the stack without changing the structure of the stack [35]. The layout of obstacle cloud points processed by Graham’s Scan algorithm is shown in Figure 5a.

Table 1. Graham’s Scan (X) algorithm.

Steps	Content
Input	The remaining points in X($P_1,P_2,\dots ,P_n$);
Output	Convex hull results
1	Sort ($P_1,P_2,\dots ,P_n$) by its polar angle counterclockwise to $P_0$;
2	If several points have the same polar angle;
3	Then, remove the rest of the points;
4	Then, leaving only the point farthest from $P_0$;
5	PUSH($P_0$, S);
6	PUSH($P_1$, S);
7	PUSH($P_2$, S);
8	for i←3 to m;
10	Call the function: TOP(S) and $P_i$ form a non-left-turn do;
11	Call function NEXT-TOP(S) and return the following point;
12	POP(S);
13	PUSH($P_i$, S);
14	end for
15	return S

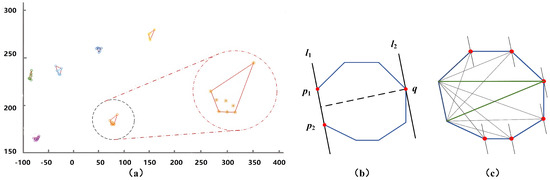
Figure 5. (a) The layout of obstacle cloud points processed by Graham’s Scan algorithm; (b) diagram of “point–edge” to heel point; (c) the distance between convex envelope and corresponding edge.

To determine the maximum diameter of the obstacle point cloud’s convex hull, some scholars have utilized the enumeration technique. However, this method, although easy to implement, sacrifices efficiency due to its time complexity of O($n^3$). Consequently, this paper introduces an alternative algorithm, the rotating caliper algorithm, which provides a time complexity of O(n) for computing convex hull diameter. Before introducing the Rotating Calipers Algorithm, we defined the term “heel point pair”: if two points P and Q (a convex polygon Q) lie on two parallel tangent lines, they form a heel point pair. What appears in this paper is the “point–edge” heel point pair, as shown in Figure 5b, which occurs when the intersection of one tangent line and polygon is one edge, and the other tangent line is unique to the tangent point of the polygon. The existence of tangents must contain the existence of two different “point–point” pairs of heel points. Therefore, $p_1$ and q, $p_2$, and q are two pairs of “heel point pairs” of convex polygon q, respectively. The Rotating Calipers Algorithm is shown in Table 2.

Table 2. Rotating Calipers algorithm.

Steps	Content
Input	Point coordinates of the polygon ($x_i,y_i$);
Output	Maximum diameter ($d_{max}$) and the “heel point pair”
1	$y_{min}$← min($y_i$);
2	$y_{max}$← max($y_i$), calculate the endpoints $y_{min}$ and $y_{max}$;
3	n← 1;
4	While n < N do;
5	$n++$;
6	$d_{max}$← ($d_1$), calculate the distance $d_1$ between $y_{min}$ and $y_{max}$;
7	Design two horizontal tangents $l_1$ and $l_2$ through $y_{min}$ and $y_{max}$;
8	Rotate $l_1$ and $l_2$ until they coincide with the other side of the polygon;
9	$d_{max}$← max($d_{max},d_2$), Create new heel points;
10	Calculate the new distance $d_2$ and compare the sizes;
11	End

There are the two furthest points on the convex hull through which a pair of parallel lines can be drawn. By rotating the pair of parallel lines to coincide with an edge on the convex hull, such as the $l_1$ line in Figure 5b, notice that q is the point farthest from the $l_1$ line on the convex hull. Points on the convex hull in turn form a single-peak function with the distance generated by the corresponding edge, as shown in Figure 5c. According to the characteristics of the convex hull, enumerating edges counterclockwise can avoid the repeated calculation of the farthest point and obtain the maximum pair of points of the convex hull diameter. The maximum diameter $d_{max}$ of the convex polygon in Figure 5a is 5.65 cm, 15.55 cm, 12.65 cm, 9.43 cm, 8.94 cm, and 12.04 cm, respectively, processed by the rotating jamming algorithm. Finally, the circle with the maximum diameter of the convex polygon $d_{max}$ is taken as the danger range.

3.3. Path Planning and Heading Control of the Robot

3.3.1. Obstacle Avoidance Path Planning

This paper improved the VFH+ path planning method to meet the basic obstacle avoidance requirements of the robot [36]. According to the distribution of obstacles in the surrounding environment on the guiding track of the robot, the passage direction interval is determined according to a certain angle threshold, and then the passage direction and speed are determined through calculation. Then, the robot is taken as the center to establish the coordinate system, as shown in Figure 6a. The steps are as follows.

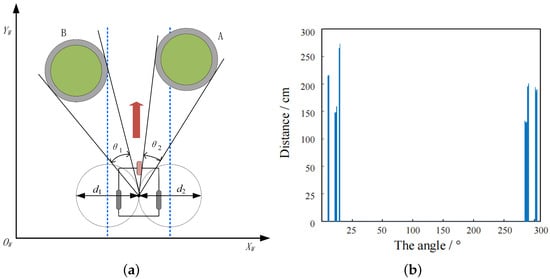
Figure 6. (a) Schematic diagram of obstacle angle determination; (b) the result diagram of obstacle angle determination.

(1) The path design of this paper adopts the particle filter theory considering the size of the robot, based on the obstacle identification and positioning in the previous section, the radius is expanded by expanding the cluster center circle to half the width of the robot. Through dynamic constraints, the robot will be limited in the turning process by setting a restricted area of $d_1$ and $d_2$ on both sides of the robot [37,38]; meanwhile, the dynamic constraint angle is set at ${30}^{\circ }$. As shown in Figure 6a, both A and B are obstacles, and the expansion part is the gray part on the edge of the obstacle. The LiDAR distance from the obstacle to the robot can be known from polar coordinates. Assuming the LiDAR scanning range [0, 360], angle $\alpha$ and distance l are expressed as a bar graph, as shown in Figure 6b.

(2) Determine the threshold and obtain the passage interval. According to the threshold $H\left(i\right)$, it is defined as follows:

$$H\left(i\right)=\left\{\begin{array}{cccc}1& l\left(i\right)\le T& and& l\left(i\right)\ne 0\\ 0& l\left(i\right)>T& or& l\left(i\right)=0\end{array}\right.$$

(12)

When $H\left(i\right)$ = 0, it indicates that i direction is passable and vice versa. In combination with the robot specifications and safe distance, the threshold is set at 20 cm, and the angle $\alpha$ and distance l are expressed as bar charts, as shown in Figure 6b.

3.3.2. Heading Control of the Robot

The movement of the robot is described by the motion process and motion model through state vectors in different time periods. The input control of the robot is shown in Equation (13) [39].

$$u={\left[\begin{array}{cccc}{v}_A& {\theta }_A& {\tau }_{rows}& {\alpha }_{rows}\end{array}\right]}^T$$

(13)

$v_A$ (m/s) is the linear velocity obtained from the wheel radius, ${\theta }_A$ (rad/s) is the speed measured by the rotational yaw rate, ${\tau }_{rows}$ (m) is the offset of the previous frame tracked by the trajectory, and ${\alpha }_{rows}$ (m) is a tracking mark.

The movement of the robot can be approximated by a small range of movement through a suitable rotation fine-tuning in each cycle. The forward motion of a robot is determined by speed $v_A$. The robot deflection is determined by a combination of visual guidance and LiDAR. The robot will prioritize visual tracking when the obstacle distance reaches a safe threshold, which triggers the LiDAR obstacle avoidance program [40,41], ${\alpha }_{rows}$ = 0, the steering angle of the robot is Equation (14).

$${\theta }_{v,k+1}={\theta }_{v,k}+{\widehat{\theta }}_{vk}△t$$

(14)

The tracker refreshes output through the robot’s heading, which is defined as the lateral offset of a navigation point (point C in Figure 7) that is perpendicular to the track and heading ${\beta }_{rows}$. On each refresh, navigation point C is perpendicular to the robot heading of the track distance, and then output. It can be seen from Figure 7 that the robot heading changes at frame k + 1 as follows [42,43]:

$${\theta }_{v,k+1}={\beta }_{rows}+\alpha$$

(15)

$\alpha$: the angle of the robot with respect to the track angle ${\beta }_{rows}$, which can be seen in Figure 7.

$$\begin{array}{c}\alpha =\alpha sin\left(\frac{\gamma +{\tau }_{rows}}{l_{AC}}\right)\end{array}$$

(16)

where $\gamma$ is described as follows:

$$\begin{array}{c}\gamma =(l_{AC}-v_{A,k}△t)sin({\beta }_{rows}-{\theta }_{v,k})\end{array}$$

(17)

$l_{AC}$ is the distance from point A to point C.

By combining the above equations, the angle of robot can be obtained as shown in Equation (18).

$${\theta }_{v,k+1}=\left\{\begin{array}{cc}{\beta }_{rows}+\alpha sin\left(\frac{\left(l_{AC}-v_{A,k}\Delta t\right)sin\left({\beta }_{rows}-{\theta }_{v,k}\right)+{\tau }_{rows}}{{\mathrm{l}}_{\mathrm{AC}}}\right)& {\alpha }_{rows=1}\\ {\theta }_{v,k}+{\theta }_{v,k}△t& others\end{array}\right.$$

(18)

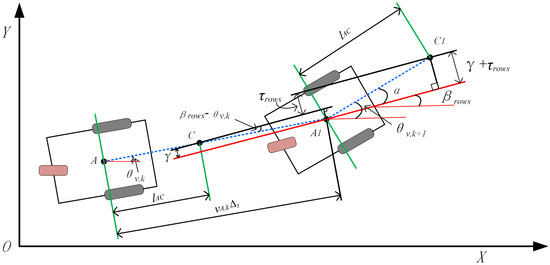
Figure 7. The course change chart of avoidance on robot.

4. Visual Navigation System

In order to achieve the visual guidance of the autonomous robot, in this section, statistical analysis of color space was carried out on the track-guiding road images and the surrounding environment road images collected by the vision system. The working conditions were selected as follows (straight line, left turn, right turn, intersection, and Y-shaped intersection). Through the comparative analysis results of color space, HSV color space was adopted as the preferred color space. On the H component of the track guide road image, the rectangular mean value is filtered, and the threshold value is obtained by Otsu’s algorithm for binarization processing. Finally, the ideal track guide image is obtained by corrosion processing.

4.1. Color Space of Track Road and Environment Road

In this section, trajectory road and environmental road images collected by robots are researched, the driving conditions of the robot are as follows: straight line driving, left turn, right turn, intersection and Y-shaped intersection, as shown in Figure 8. The red circle represents the robot’s walking track road image, and the black circle represents the surrounding environment road image. We analyzed the color system of the track road image and the environment road image, respectively, including the first-order moment (mean value) and second-order moment (variance) of the RGB component and HSV component [44]. The mean, which is the first moment, establishes the average intensity of every color component. The second moment, known as variance, indicates the variation in colors within the area under observation, commonly referred to as non-uniformity.

Figure 8. The image information acquisition of autonomous robot.

The statistical results for the mean value of the RGB component in both the trajectory road and environmental road images are displayed in Figure 9a below. The threshold values of the RGB components of the trajectory road images are all lower than those of the ambient road images, and only the G and B component thresholds of the trajectory road images are higher than those of the ambient road images in the right turn condition. The statistical results of the second moment (variance) are shown in Figure 9b below. The threshold values of the RGB components of the trajectory road images are all higher than those of the ambient road images, which also reflects the large difference between the trajectory road images and the ambient road images. The statistical results of the first moment (mean) of the HSV component of the track road image and the environmental road image are shown in Figure 9c below. The H-component threshold is the lowest for the track and environmental road images, and the H-component threshold is higher for the track image than for the environmental road image, which is consistent across the five operating conditions. The statistical results for the second moment (variance) are displayed in Figure 9d, indicating the lowest H-component threshold which presents some degree of stability.

Figure 9. The mean and variance analysis results of RGB and HSV components of trajectory road image and environment road image. (a) The mean value of the RGB component; (b) the variance of the RGB component; (c) the mean value of the HSV component; (d) the variance of the HSV component.

4.2. The Processing of Road Image of Guiding Trajectory

The distinction between the trajectory road image and the environment road image is key to the visual navigation of the robot. Analyzing the color information of trajectory road images can help robots judge and autonomously navigate based on the image information. The processing of track road images includes statistical analysis of image RGB, rgb, L*a*b*, HSV, and HIS color space, as shown in Figure 10. RGB is the basic color system of an image and is one of the most widely used color systems. HSV represents hue, saturation, and value, respectively, [45]. This color system more realistically reflects human reasoning and color observations than the RGB system. HSI, which stands for color, saturation, and intensity, is a framework that separates the intensity factor from the color knowledge presented by a color image [46].

Figure 10. The color space diagram of environmental road and track road, where (a–d) the images of RGB; (e–h) the images of rgb; (i–l) the images of L*a*b*; (m–p) the images of HSV; (q–t) the images of HSI.

Switching between RGB and HIS is accomplished by

$$H=\left\{\begin{array}{cc}\theta & B\le G\\ 360-\theta & B>G\end{array}\right.$$

(19)

then

$$\theta ={cos}^{-1}\left\{\frac{0.5\left[\right(\mathrm{R}-\mathrm{G})+(\mathrm{R}-\mathrm{B}\left)\right]}{{\left[{(\mathrm{R}-\mathrm{G})}^2+(\mathrm{R}-\mathrm{G})(\mathrm{G}-\mathrm{B})\right]}^{1/2}}\right\}$$

(20)

Saturation S:

$$S=1-\frac{3}{(R+G+B)}[min(R,G,B)]$$

(21)

Brightness I:

$$I=\frac{1}{3}(R+G+B)$$

(22)

The comparison and analysis results of color space between the trajectory road image and the environment road image show that the H-component segmentation effect is the best in HSV color space. First, we filter the guide trajectory of the H-component map of the road by using the rectangular mean filter, which has a faster calculation speed. The filtering method is shown in Equation (23).

$$g(x,y)=\frac{1}{M}\sum _{f\in S}f(x,y)$$

(23)

Otsu’s algorithm is used to calculate the optimal threshold of the image [47]. Let the gray level of the gray image of the trajectory be L, then the gray range is $[0,L-1]$. The threshold is calculated as shown in Equation (24).

$$T=Max\left[w_0\left(t\right)·{\left(u_0\left(t\right)-u\right)}^2+w_1\left(t\right)·{\left(u_1\left(t\right)-u\right)}^2\right]$$

(24)

where T represents the threshold, $w_0$ is the background proportion, $u_0$ is the background mean, $w_1$ is the foreground proportion, $u_1$ is the foreground mean, and u is the average of the entire image. Otsu’s algorithm was used to calculate the gray image thresholds of the guide track straight lines as $T_1=0.2706$ and $T_2=0.2667$, respectively. In the end, by constructing positive diamond structure elements with equal diagonal lines, the distance from the origin of the structure element to the furthest point of the positive diamond was defined as 25 pixels. Corrosion is defined in Equation (25).

$$A\ominus B=\left\{z\mid {\left(B\right)}_z\cap A^c=\varnothing \right\}$$

(25)

where $A\ominus B$ denotes that A is corroded by B, and z is the set of all points z where B in A is translated by z. $A^c$ is the complement of A. The linear trajectory driving effect of the robot after corrosion treatment is shown in Figure 11.

Figure 11. Comparison of image processing effect of guide track road. (a) The HSV diagram of linear trajectory after mean filtering; (b) the filtered H component of HSV color space; (c) the trajectory diagram after threshold segmentation; (d) the track image after corrosion treatment.

4.3. Fuzzy Logic Vision Control System Based on Visual Pixels

In this section, to improve the robustness of the control system, a visual pixel-based fuzzy logic vision system is designed based on fuzzy control theory for the final visual trajectory images obtained by the autonomous robot. The principle is as follows: 11 seed points are selected on the vertical centerline of the trajectory image, a horizontal line is made from the above seed points, and the left and right sides are scanned to determine the path widths of the left and right sides, respectively. If the number of pixels on the left and right sides is the same, it is determined to be in the middle of the path. If the number of pixels on the left side is greater than the number of pixels on the right side, the right side of the deviation path is determined, and then the fuzzy control system makes a shift to the left centerline. If the number of pixels on the right is greater than the number of pixels on the left, the left side of the deviation path is determined, and then the fuzzy control system will make an offset motion to the right center line [48]. In this paper, the fuzzy logic vision control system is designed with two inputs and two outputs. The inputs are PCLeft and PCRight and the outputs are speed instruction v and angle instruction $\theta$, as shown in Equation (26).

$$\begin{array}{cc}\hfill \mathrm{PCLeft}& =\frac{1}{11}\sum _{i=1}^{11}pc{l}_i\hfill \\ \hfill \mathrm{PCRight}& =\frac{1}{11}\sum _{i=1}^{11}pc{r}_i\hfill \end{array}$$

(26)

where $pc{l}_i$ and $pc{r}_i$ are the number of pixel points on the left and right side of the scan line, respectively.

Fuzzy membership functions of input variables are obtained in Equations (27) and (28), where each input variable is fuzzy with three membership functions: Small (S), Medium (M) and Large (L). Membership functions of PCLeft and PCRight are shown in Figure 12.

$$\begin{array}{c}\hfill \begin{array}{c}{\mu }_s\left(\mathrm{PCLeft}\right)=\left\{\begin{array}{cc}\left(\frac{S_{c1}-\mathrm{PCLeft}}{S_{c1}-S_{b1}}\right)& S_{b1}<\mathrm{PCLeft}<S_{c1}\\ 1& 0\le \mathrm{PCLeft}\le S_{b1}\\ 0& \mathrm{other}\end{array}\right.\\ {\mu }_M\left(\mathrm{PCLeft}\right)=\left\{\begin{array}{cc}\left(\frac{\mathrm{PCLeft}-m_{a1}}{m_{b1}-m_{a1}}\right)& m_{a1}<\mathrm{PCLeft}<m_{b1}\\ \left(\frac{m_{c1}-\mathrm{PCLeft}}{m_{c1}-m_{b1}}\right)& m_{b1}\le \mathrm{PCLeft}\le m_{c1}\\ 0& \mathrm{other}\end{array}\right.\\ {\mu }_L\left(\mathrm{PCLeft}\right)=\left\{\begin{array}{cc}\left(\frac{\mathrm{PCLeft}-l_{a1}}{l_{b1}-l_{a1}}\right)& l_{a1}<\mathrm{PCLeft}<l_{b1}\\ 1& \mathrm{PCLeft}\ge l_{b1}\\ 0& \mathrm{other}\end{array}\right.\end{array}\end{array}$$

(27)

$$\begin{array}{c}\hfill \begin{array}{c}{\mu }_s\left(\mathrm{PCRight}\right)=\left\{\begin{array}{cc}\left(\frac{S_{cr}-\mathrm{PCRight}}{S_{cr}-S_{br}}\right)& S_{br}<\mathrm{PCRight}<S_{cr}\\ 1& 0\le \mathrm{PCRight}\le S_{br}\\ 0& \mathrm{other}\end{array}\right.\\ {\mu }_M\left(\mathrm{PCRight}\right)=\left\{\begin{array}{cc}\left(\frac{\mathrm{PCRight}-m_{ar}}{m_{br}-m_{ar}}\right)& m_{ar}<\mathrm{PCRight}<m_{br}\\ \left(\frac{m_{cr}-\mathrm{PCRight}}{m_{cr}-m_{br}}\right)& m_{br}\le \mathrm{PCRight}\le m_{cr}\\ 0& \mathrm{other}\end{array}\right.\\ {\mu }_L\left(\mathrm{PCRight}\right)=\left\{\begin{array}{cc}\left(\frac{\mathrm{PCRight}-l_{ar}}{l_{br}-l_{ar}}\right)& l_{ar}<\mathrm{PCRight}<l_{br}\\ 1& \mathrm{PCRight}\ge l_{br}\\ 0& \mathrm{other}\end{array}\right.\end{array}\end{array}$$

(28)

Figure 12. (a) PCLeft membership function; (b) PCRight membership function.

The fuzzy output of linear velocity is a standard value, which is multiplied by a suitable gain K. After fuzzy processing by the weighted average method, the output linear velocity instruction $v_{vis}$ and the output steering angle instruction ${\theta }_{vis}$ can be calculated as below:

$$\begin{array}{c}\hfill {\mathit{v}}_{vis}=K\ast \left(\frac{{\sum }_{i=1}^N{\mathit{v}}_{visi}\ast {\mathit{\alpha }}_i\left(x\right)}{{\sum }_{i=1}^N{\mathit{\alpha }}_i\left(x\right)}\right)\end{array}$$

(29)

$$\begin{array}{c}\hfill {\mathit{\theta }}_{vis}=\frac{{\sum }_{i=1}^N{\mathit{\theta }}_{visi}\ast {\mathit{\alpha }}_i\left(x\right)}{{\sum }_{i=1}^N{\mathit{\alpha }}_i\left(x\right)}\end{array}$$

(30)

where ${\alpha }_i\left(x\right)$ represents the trigger strength.

It must be emphasized that the use of fuzzy logic control depends on the number of rules that must be evaluated. Moreover, large systems with many rules require very powerful and fast processors for real-time computation. The smaller the rule base, the less computing power is required [49]. Therefore, unlike pure fuzzy logic controllers encountered in rule expansion problems, the visual pixel-based fuzzy logic control system designed in this paper has only nine if/then rules, and it uses trigonometric membership functions to make their structure simpler. The constructed fuzzy rule basis is shown in Table 3.

Table 3. The constructed fuzzy rule.

Number	PCLeft	PCRight	${\mathit{v}}_{\mathit{vis}}$	${\mathit{\theta }}_{\mathit{vis}}{/}^{\circ }$
1	Small	Small	$0.9$	90
2	Small	Medium	$0.5$	67
3	Small	Large	$0.1$	45
4	Medium	Small	$0.5$	112
5	Medium	Medium	$0.9$	90
6	Medium	Large	$0.5$	67
7	Large	Small	$0.1$	135
8	Large	Medium	$0.5$	112
9	Large	Large	$0.9$	60

5. Experimental Test Results of Autonomous Robot

5.1. System Composition

To verify the performance of the robot visual navigation and obstacle avoidance control system described in Section 3 and Section 4, a Three-Wheeled Differential Mobile Robot (TWDMR) was used [50]. It is mainly composed of a vision camera, laser radar (RPLIDAR S2, measuring radius 30 m, frequency 32 K), a wheeled robot chassis, and ROS software control system. The visual camera is used for visual navigation, collecting environmental image information, data acquisition and environment modeling of obstacle avoidance systems with LiDAR. The wheeled robot chassis includes stepper motors on both sides, universal wheels, and uses differential control to change or maintain course. The ROS control system was used to verify the feasibility of the algorithm and integrated the visual navigation control algorithm based on image features and the obstacle avoidance control algorithm based on LiDAR data.

5.2. Test of Obstacle Avoidance System

Figure 13 shows the obstacle avoidance test scenario for an autonomous robot, which integrates the obstacle avoidance control algorithm developed in this paper to implement the obstacle avoidance function. To increase the complexity of the obstacle during the test, six plastic tubes with a diameter of 20 cm were placed at different positions and angles to act as obstacles. The autonomous robot was tested directly through six obstacles at different speeds of 0.25 m/s, 0.5 m/s, and 1 m/s. Following the theoretical analysis in Section 3, the central circle of the obstacle is enlarged using a modified clustering algorithm. The expanded part is shown in the gray part, and the theoretical obstacle avoidance trajectory of the robot when it passes the obstacle is shown in Figure 14a. Finally, real-time scanning of the surrounding environment information via LiDAR is used to locate and measure the robot’s trajectory using the slam-map modeling method on top of the computer’s Ubuntu system to obtain the robot’s moving position and pose in real time. The results show that the robot can successfully pass through obstacles at three different speeds: 0.25 m/s, 0.5 m/s, and 1 m/s, and achieve obstacle avoidance function at different speeds. The actual obstacle avoidance trajectory of the robot when passing obstacles is shown in Figure 14b. This test preliminarily proves that the autonomous robot (TWDMR) designed in this paper is equipped with LiDAR and vision camera only (detailed parameters are introduced in Section 5.1), and the obstacle avoidance function is realized by using the developed algorithm. It does not require sophisticated GPS navigation and RTK localization modules, reflecting its convenience and low-cost advantages.

Figure 13. A diagram of the field test of the Three-Wheeled Mobile Differential Robot (TWMDR).

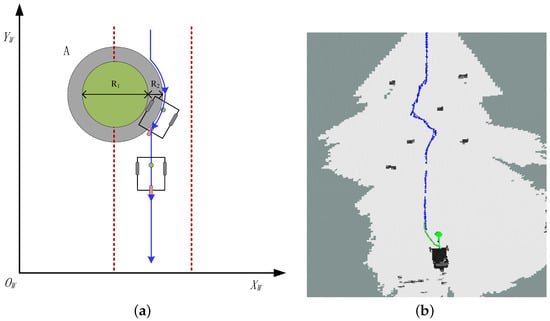
Figure 14. (a) The theoretical obstacle avoidance analysis diagram of robot; (b) the SLAM obstacle avoidance trajectory diagram of robot.

5.3. Test of Visual Guidance System

The experimental test is carried out in the robot (TWDMR), which uses a vision system to control the steering. The visual guidance trajectory and the operational specifications of the robot platform are shown in Table 4. The experimental testing procedure is based on a guided trajectory of first running straight, then turning, and finally running straight again. Figure 15 depicts the real-time variation in the left and right wheel speeds of the robot. Specifically, when the sampling number is 100, the robot starts to turn in the right corner; when the sampling number reaches 150, the right turn ends; when the sampling number reaches 250, the robot starts to turn left; when the sampling number reaches 290, the left turn ends. In the case of linear guidance trajectory, the deviation between the rotation speed of the left and right wheels of the robot platform is within $2.3$ r/min.

Table 4. The operating parameters of the robot platform.

Sampling Rate (S·s${}^{-1}$)	The Length of Robot (/cm)	The Width of Robot (/cm)	The Width of Trajectory (/cm)	The Average Rotational Speed of Robot (/r·min${}^{-1}$)
10	30	45	35	20

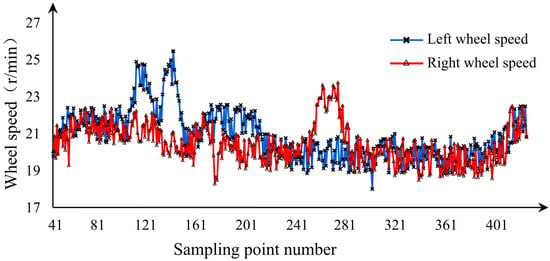
Figure 15. Real-time change in robot left and right wheel speed.

Figure 16 shows the test results of the robot trajectory tracking, including the transverse center deviation $\Delta S$ and angular deviation $\Delta \psi$, where the negative value represents the left deviation and the positive value is the right deviation. The test results show that the center deviation of the navigation track is within the range of −2.5 cm to 2 cm, the maximum deviation to the left of the track center is shown at point A in Figure 16, and the maximum deviation to the right is shown at point B in Figure 16. Meanwhile, the angle deviation is within the range of $-0.5^{\circ }$ to $0.4^{\circ }$, the maximum deviation to the left is shown at point D in Figure 17, and the maximum deviation to the right is shown at point C in Figure 17.

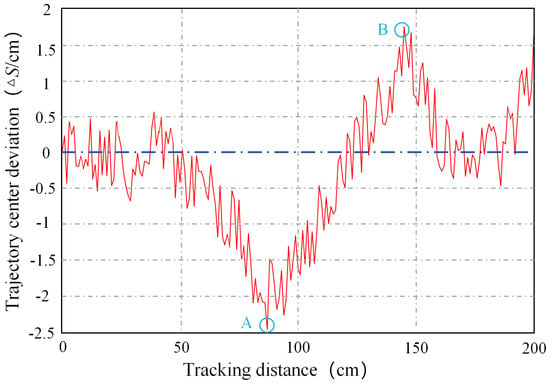
Figure 16. The deviation of the lateral center of the trajectory.

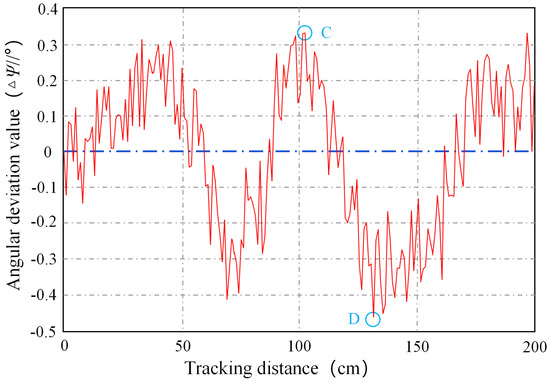
Figure 17. The deviation of trajectory angle.

6. Conclusions and Future Works

In this paper, we develop and design an agricultural mobile robot platform with visual navigation and obstacle avoidance capabilities to address the problem of low-cost obstacle detection for agricultural unmanned mobility platforms. As an obstacle detection sensor, LiDAR suffers from several drawbacks, such as a small amount of data, incomplete information about the detection environment, and redundant obstacle information during clustering. In this paper, we propose an improved clustering algorithm for obstacle avoidance systems to extract dynamic and static obstacle information and obtain the centers of obstacle scan points. Then, the maximum diameter of the convex polygon of the cluster data are obtained by fusion of the rotating jamming algorithm and the convex hull algorithm, and the obstacle danger zone is established with the cluster center as the center, and the VFH+ obstacle avoidance path planning and heading control method is proposed. Compared to the field linear navigation system built by Higuti et al. [18] in the same context using LiDAR only, our autonomous mobile robot is capable of turning and avoiding obstacles. On the other hand, the color-space analysis and feature analysis of complex orchard environment images were performed to obtain the H component of the HSV color space, which was used to obtain the ideal visual guidance trajectory images by means of mean-filtering and corrosion treatment. Finally, the effectiveness and robustness of the proposed algorithm are verified through the three-wheeled mobile differential robot platform. Compared with the proposed LiDAR–vision–inertial odometer fusion navigation method for agricultural vehicles by Zhao et al. [51], we can achieve obstacle avoidance and navigation functions for agricultural robots by using only LiDAR and camera. It embodies the advantages of simplicity, low cost, and efficiency, and is easier to meet the operational needs of the agricultural environment and farmers.

In this paper, the visual navigation and obstacle avoidance functions of agricultural mobile robots are realized based on the three-wheeled mobile differential robot platform. In contrast to the methods proposed by Ball and Winterhalter et al. [11,23], for agricultural navigation based on GNSS and GPS technology, the stable operation of agricultural robots working in environments rejected by GNSS is achieved. It is expected to shorten the development cycle of agricultural robot navigation systems when GNSS is not working, and has the advantages of low cost, simple operation, and good stability. In our future research work, we will transfer the proposed algorithm and hardware platform to agricultural driverless tractors for field trials and increase the construction of environmental maps for agricultural tractors.