Signal Occlusion-Resistant Satellite Selection for Global Navigation Applications Using Large-Scale LEO Constellations
Abstract
:1. Introduction
2. The Geometric Dilution of Precision and Genetic Algorithm
2.1. GDOP Criterion
2.2. Recursive Algorithm
- 1.
- Calculate the current satellites’ positions through ephemeris data.
- 2.
- Calculate all visible satellites’ contribution values .
- 3.
- Rank the visible satellites in the order of .
- 4.
- If the of each visible satellite is larger than or equal to a threshold, the selection result is all visible satellites. Otherwise, proceed to the next step.
- 5.
- Remove the satellites whose value is smaller than the threshold, and the rest of the satellites are selected [3].
2.3. Genetic Algorithm
- 1.
- Encoding and generating the initial populationDepending on the nature of the problem, we select the appropriate coding method and generate an initial population of N chromosomes with a defined length randomly:
- 2.
- Calculate the fitness value for each chromosomeCalculate the fitness of each chromosome in the population :
- 3.
- Determine whether the algorithm has converged. If so, output the search results; otherwise, continue with the following steps;
- 4.
- Perform selectionThe fitness value of each individual determines the likelihood of selection:Using the probability distribution given by Equation (21), we randomly sample some chromosomes from the current generation population and pass them on to the next generation population, forming a novel population.
- 5.
- Perform crossoverWe mate the chromosomes with probability and obtain a population of N chromosomes .
- 6.
- Perform mutation
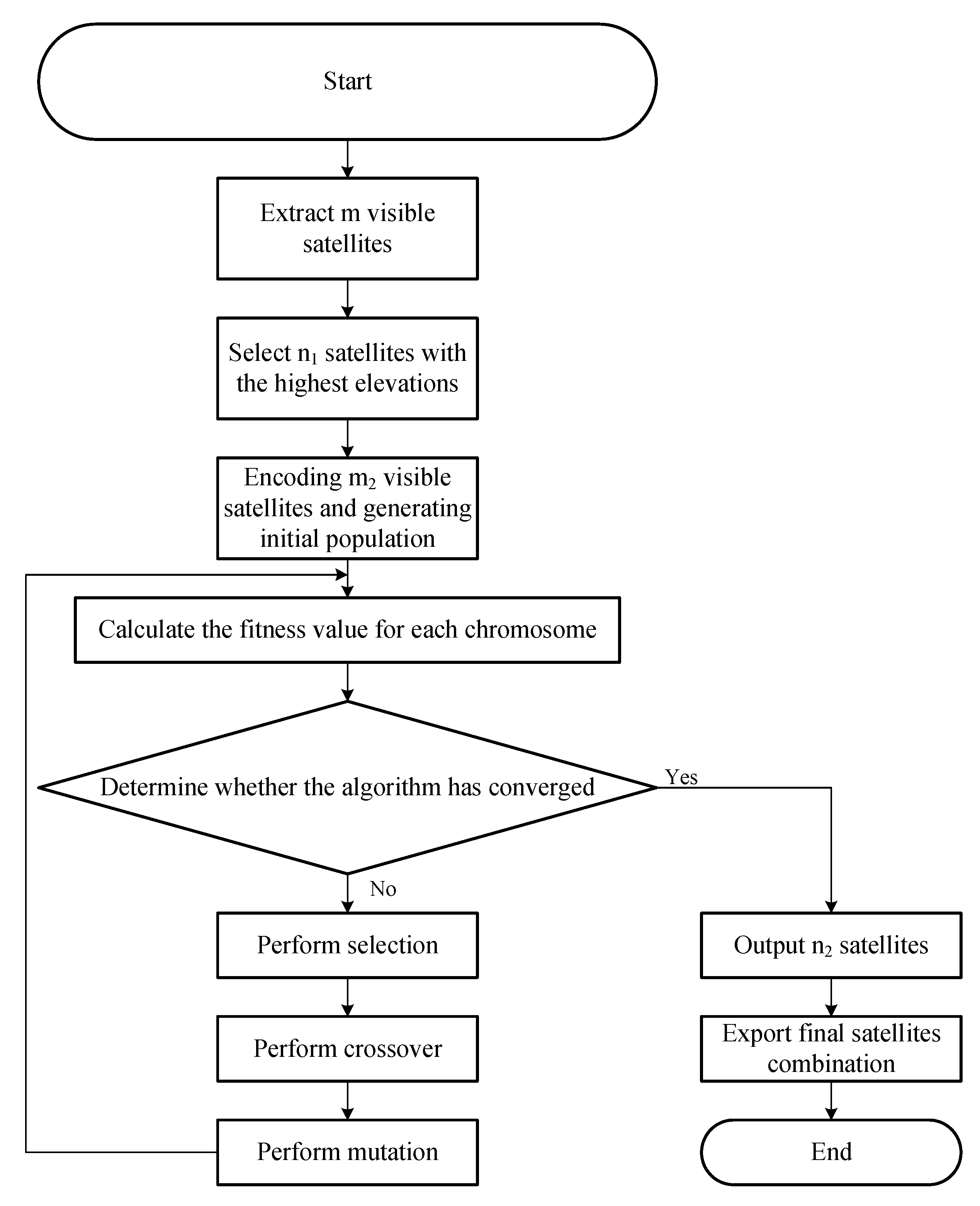
3. Methodology
3.1. Configurations with the Lowest GDOP
- (1)
- Since the matrix Equation (23) is a nonlinear equation, it may have a finite number of solutions, no solutions, or infinite solutions.
- (2)
- GDOP is a continuous function; that is, in the vicinity of the “ideal extreme point”, its GDOP will increase continuously without any sudden change.
- (3)
3.2. A Satellite Selection Algorithm Incorporating a Genetic Algorithm to Overcome the Effect of Obstruction
- Step 1: Calculate the overall visible m satellites’ elevation and azimuth by dividing all the satellites in view into two regions: : (–) and (–), known as the low elevation area and the high elevation area.
- Step 2: Selecting satellites with elevation angles ranked from high to low from the high elevation area according to the ratio .
- Step 3: Encoding visible satellites and generating an initial population
- Step 4: Calculate the fitness value for each chromosome.
- Step 5: If the algorithm has converged, the algorithm will select a final satellite combination, stop searching, and proceed to Step 7.
- Step 6: Apply selection, crossover, and mutation, and repeat Step 5.
- Step 7: Export the result from the satellite selection process.
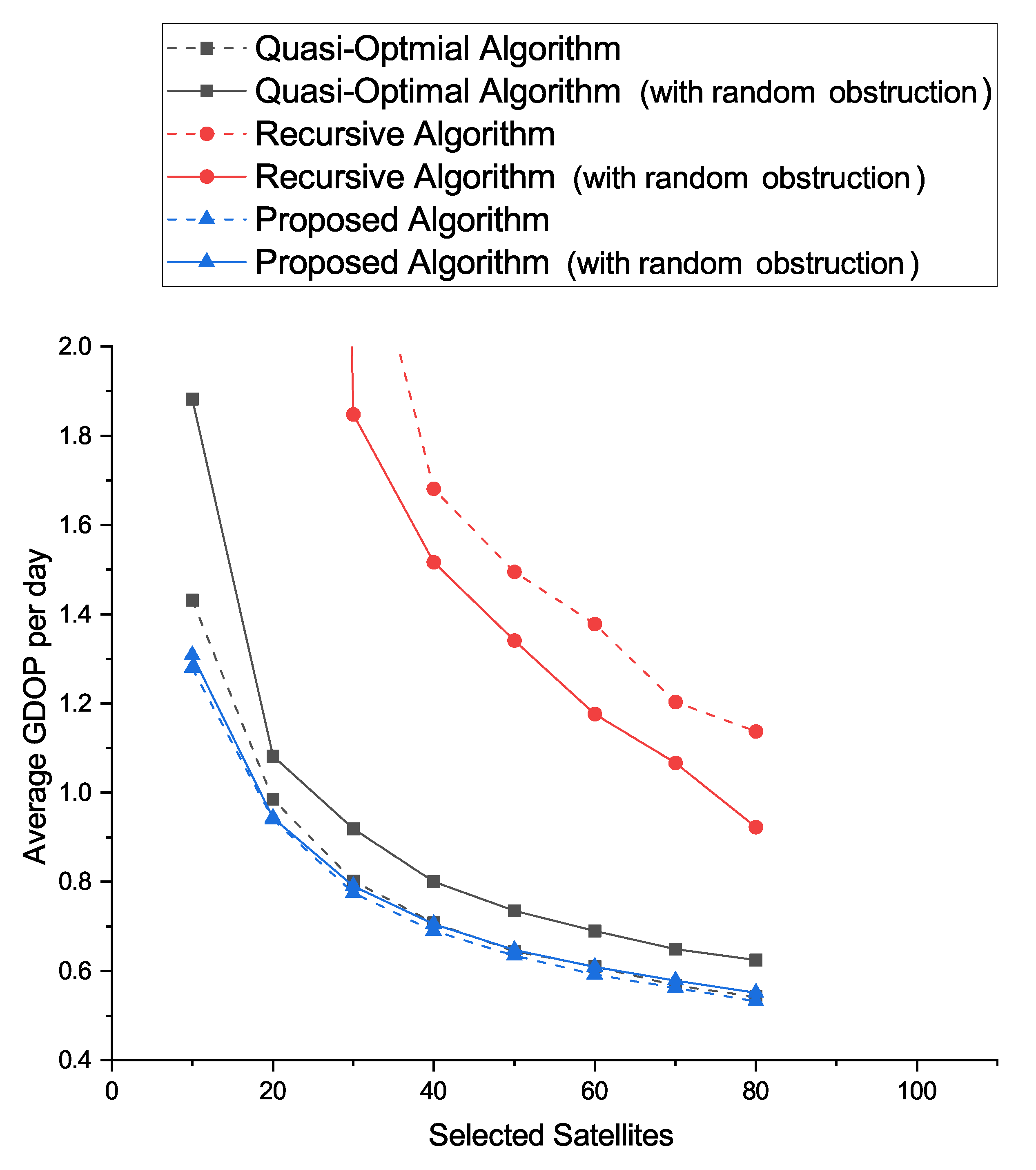
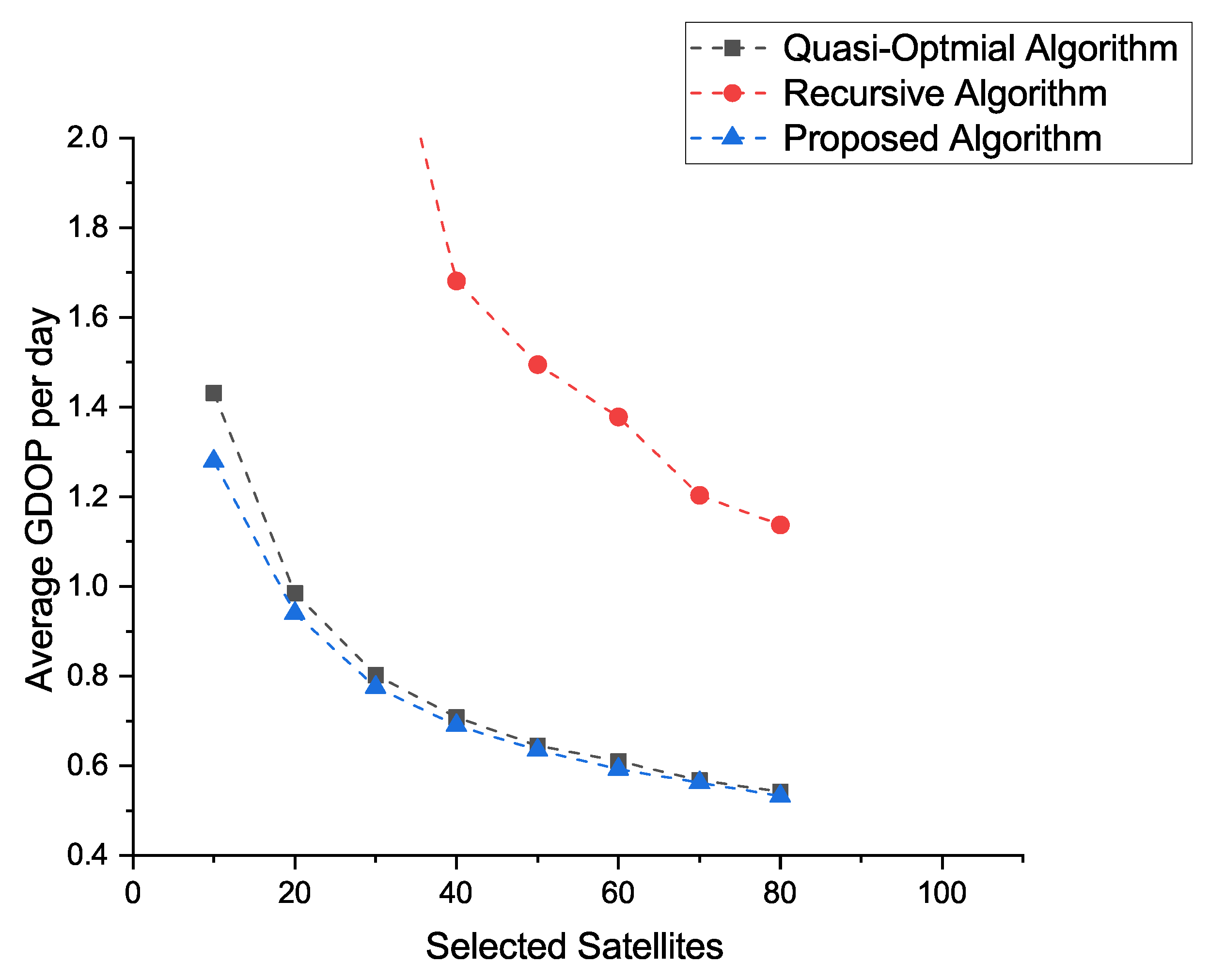
4. Result Analysis and Discussion
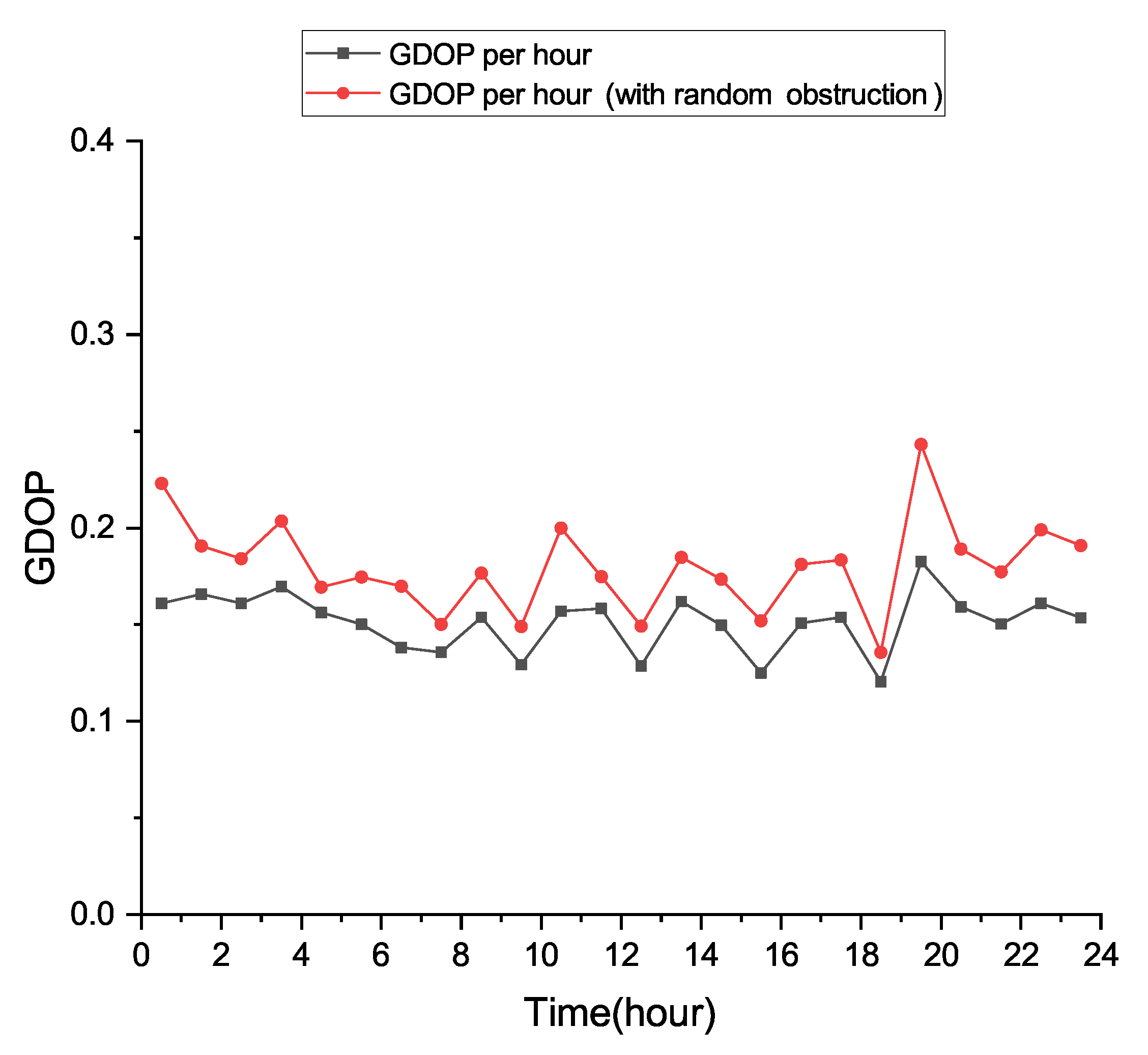
4.1. Random 60° Obstruction Simulations-One Single Large-Angle Obstruction
4.2. Random 240° Obstruction Simulations-Multiple Small-Angle Obstructions
5. Conclusions
- (a)
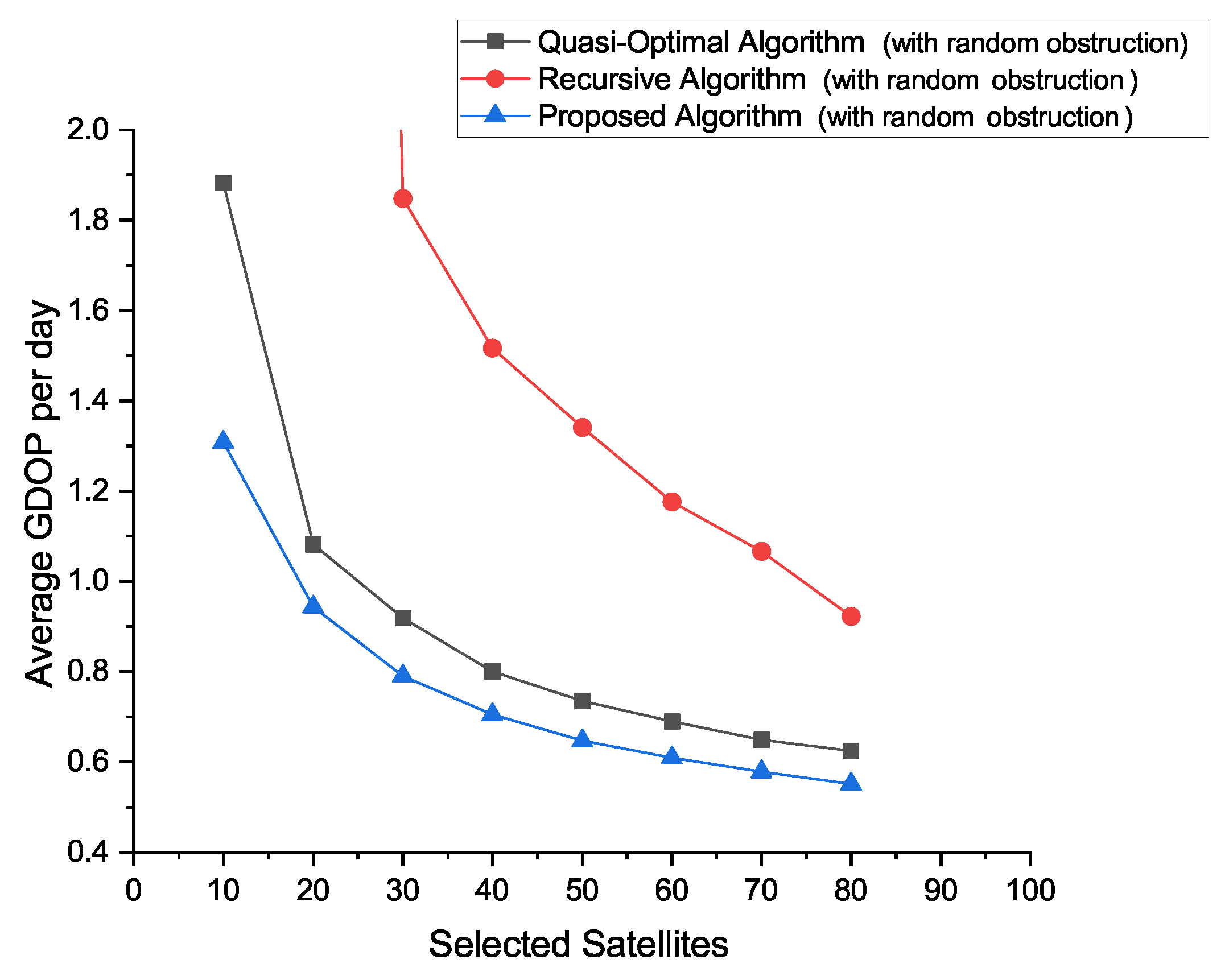
- The recursive algorithm cannot be well applied when selecting a small number of satellites out of a large number for localization. Therefore, its application is more appropriate in scenarios where the number of observable satellites is close to that of the number to be selected.
- (b)
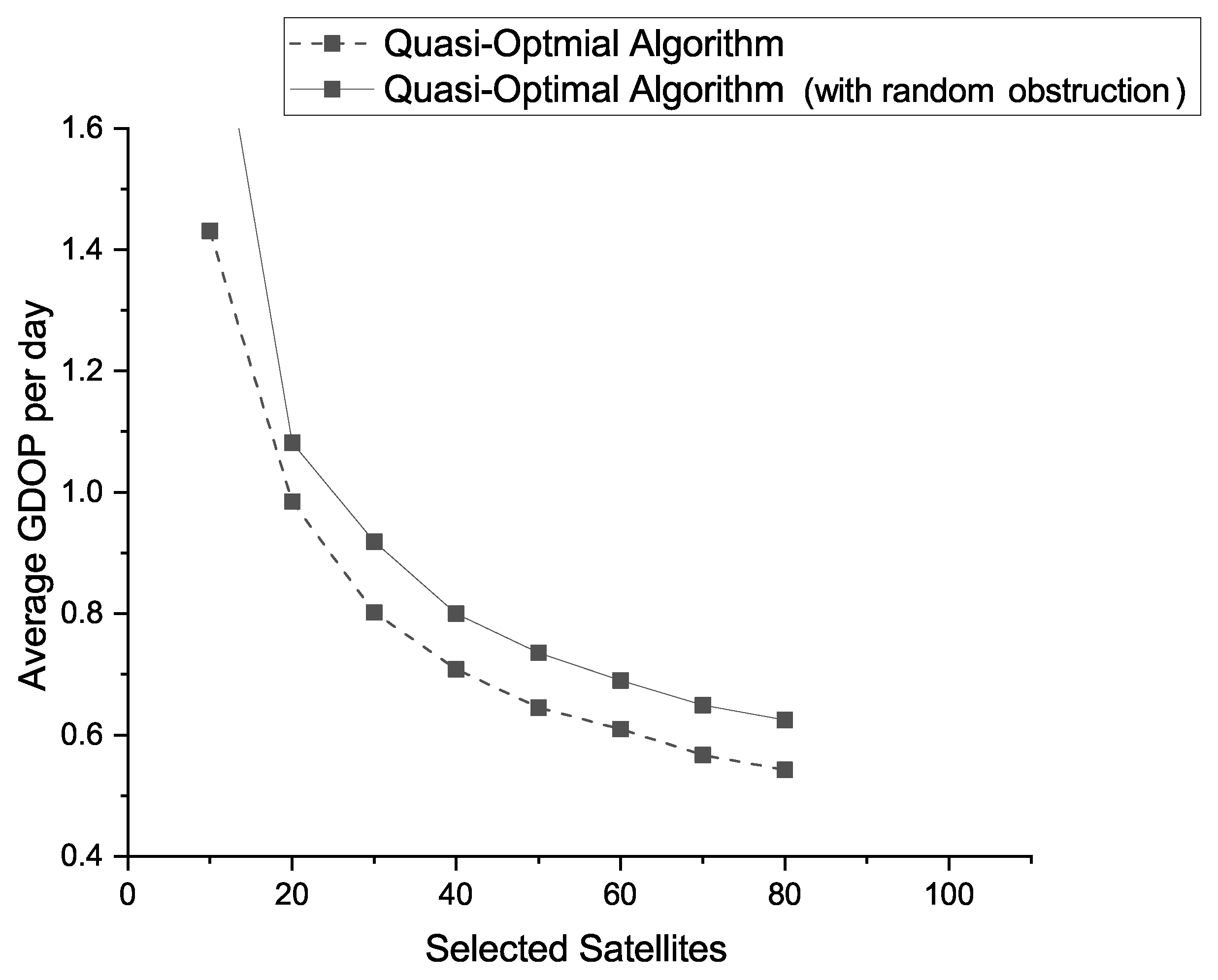
- Obstruction has a significant impact on the performance of current classical geometric satellite selection algorithms, such as the Quasi-Optimal algorithm, which limits engineering applications.
- (c)
- The proposed algorithm can overcome the limitation that some of the satellites cannot be observed due to obstructions.
- (d)
- It is easier to obtain a uniform distribution for multiple small-angle obstructions compared with a single large-angle obstruction, which makes the performance difference between the Quasi-Optimal algorithm and the proposed algorithm smaller than when there is a single large-angle obstruction, but the proposed algorithm still has a higher stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Phatak, M. Recursive method for optimum GPS satellite selection. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 751–754. [Google Scholar] [CrossRef]
- Liu, M.; Fortin, M.A.; Landry, R., Jr. A Recursive Quasi-optimal Fast Satellite Selection Method for GNSS Receivers. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (Ion Gnss 2009), Savannah, GA, USA, 22–25 September 2009; pp. 2061–2071. [Google Scholar]
- Li, G.; Xu, C.; Zhang, P.; Hu, C. A Modified Satellite Selection Algorithm Based on Satellite Contribution for GDOP in GNSS. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 176, pp. 415–421. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, J. New Characteristics of Geometric Dilution of Precision (GDOP) for Multi-GNSS Constellations. J. Navig. 2014, 67, 1018–1028. [Google Scholar] [CrossRef]
- Ou, G.; Li, G.; Peng, A. Fast satellite selection method for multi-constellation Global Navigation Satellite System under obstacle environments. IET Radar Sonar Navig. 2014, 8, 1051–1058. [Google Scholar] [CrossRef]
- Nie, Z.; Gao, Y.; Wang, Z.; Ji, S. A new method for satellite selection with controllable weighted PDOP threshold. Surv. Rev. 2017, 49, 285–293. [Google Scholar] [CrossRef]
- Zhang, P. Research on satellite selection algorithm in ship positioning based on both geometry and geometric dilution of precision contribution. Int. J. Adv. Robot. Syst. 2019, 16, 172988141983024. [Google Scholar] [CrossRef]
- Abedi, A.A.; Mosavi, M.R.; Mohammadi, K. A new recursive satellite selection method for multi-constellation GNSS. Surv. Rev. 2020, 52, 330–340. [Google Scholar] [CrossRef]
- Shi, J.; Li, K.; Chai, L.; Liang, L.; Tian, C.; Xu, K. Fast satellite selection algorithm for GNSS multi-system based on Sherman–Morrison formula. GPS Solut. 2023, 27, 44. [Google Scholar] [CrossRef]
- Park, C.W.; How, J.P. Quasi-Optimal Satellite Selection Algorithm for Real-Time Applications. In Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001; pp. 3018–3028. [Google Scholar]
- Zheng, Z.-y.; Huang, C.; Feng, C.-g.; Zhang, F.-p. Selection of GPS satellites for the optimum geometry. Chin. Astron. Astrophys. 2004, 28, 80–87. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J. A Fast Satellite Selection Algorithm: Beyond Four Satellites. IEEE J. Sel. Top. Signal Process. 2009, 3, 740–747. [Google Scholar] [CrossRef]
- Li, F.; Li, Z.; Gao, J.; Yao, Y. A Fast Rotating Partition Satellite Selection Algorithm Based on Equal Distribution of Sky. J. Navig. 2019, 72, 1053–1069. [Google Scholar] [CrossRef]
- Yang, L.; Gao, J.; Li, Z.; Li, F.; Chen, C.; Wang, Y. New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning. Appl. Sci. 2019, 9, 5280. [Google Scholar] [CrossRef]
- Jang, J.; Park, D.; Sung, S.; Lee, Y.J. HDOP and VDOP Analysis in an Ideal Placement Environment for Dual GNSSs. Sensors 2022, 22, 3475. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, J. A closed-form formula to calculate geometric dilution of precision (GDOP) for multi-GNSS constellations. GPS Solut. 2016, 20, 331–339. [Google Scholar] [CrossRef]
- Meng, F.; Wang, S.; Zhu, B. Research of Fast Satellite Selection Algorithm for Multi-constellation. Chin. J. Electron. 2016, 25, 1172–1178. [Google Scholar] [CrossRef]
- Blanco-Delgado, N.; Duarte Nunes, F.; Seco-Granados, G. On the relation between GDOP and the volume described by the user-to-satellite unit vectors for GNSS positioning. GPS Solut. 2017, 21, 1139–1147. [Google Scholar] [CrossRef]
- Verma, P.; Hajra, K.; Banerjee, P.; Bose, A. Evaluating PDOP in Multi-GNSS Environment. IETE J. Res. 2019, 68, 1705–1712. [Google Scholar] [CrossRef]
- Xue, S.; Yang, Y. Positioning configurations with the lowest GDOP and their classification. J. Geod. 2015, 89, 49–71. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, J.; Huang, Q. Mathematical minimum of Geometric Dilution of Precision (GDOP) for dual-GNSS constellations. Adv. Space Res. 2016, 57, 183–188. [Google Scholar] [CrossRef]
- Xue, S.; Yang, Y. Understanding GDOP minimization in GNSS positioning: Infinite solutions, finite solutions and no solution. Adv. Space Res. 2017, 59, 775–785. [Google Scholar] [CrossRef]
- Song, J.; Xue, G.; Kang, Y. A Novel Method for Optimum Global Positioning System Satellite Selection Based on a Modified Genetic Algorithm. PLoS ONE 2016, 11, e0150005. [Google Scholar] [CrossRef]
- Huang, P.; Rizos, C.; Roberts, C. Satellite selection with an end-to-end deep learning network. GPS Solut. 2018, 22, 108. [Google Scholar] [CrossRef]
- Singh, P.; Joshi, J.; Dey, A.; Sharma, N. GNSS Satellite Selection-based on Per-satellite Parameters Using Deep Learning. IETE J. Res. 2022, 1–12. [Google Scholar] [CrossRef]
- Wang, E.; Sun, C.; Wang, C.; Qu, P.; Huang, Y.; Pang, T. A satellite selection algorithm based on adaptive simulated annealing particle swarm optimization for the BeiDou Navigation Satellite System/Global Positioning System receiver. Int. J. Distrib. Sens. Netw. 2021, 17, 155014772110317. [Google Scholar] [CrossRef]
- Guan, X.; Chai, H.; Xiao, G.; Han, J.; Han, S.; Shufeng, M. A fast satellite selection algorithm for multi-GNSS marine positioning based on improved particle swarm optimisation. Surv. Rev. 2021, 54, 554–565. [Google Scholar] [CrossRef]
- Zhao, D.; Cai, C.; Li, L. A binary discrete particle swarm optimization satellite selection algorithm with a queen informant for Multi-GNSS continuous positioning. Adv. Space Res. 2021, 68, 3521–3530. [Google Scholar] [CrossRef]
- Biswas, S.K. Unsupervised learning-based satellite selection algorithm for GPS–NavIC multi-constellation receivers. GPS Solut. 2022, 26, 61. [Google Scholar] [CrossRef]
- Luo, S.; Wang, L.; Tu, R.; Zhang, W.; Wei, J.; Chen, C. Satellite selection methods for multi-constellation advanced RAIM. Adv. Space Res. 2020, 65, 1503–1517. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, Y.; Cheng, C.; Li, S.; Li, Z. Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications. Remote Sens. 2021, 13, 1725. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, L.; Jian, X. A Satellite Selection Strategy of SURF IA in Airport Intelligent Monitoring. Math. Probl. Eng. 2022, 2022, 8966814. [Google Scholar] [CrossRef]
- Rajasekhar, C.; Srilatha Indira Dutt, V.; Sasibhushana Rao, G. Weighted GDoP for improved position accuracy using NavIC and GPS hybrid constellation over Indian sub-continent. Int. J. Intell. Netw. 2021, 2, 42–45. [Google Scholar] [CrossRef]
- Du, H.; Hong, Y.; Xia, N.; Zhang, G.; Yu, Y.; Zhang, J. A Navigation Satellites Selection Method Based on ACO with Polarized Feedback. IEEE Access 2020, 8, 168246–168261. [Google Scholar] [CrossRef]
- Xia, N.; Zhi, Q.; He, M.; Hong, Y.; Du, H. A navigation satellite selection algorithm for optimized positioning based on Gibbs sampler. Int. J. Distrib. Sens. Netw. 2020, 16, 155014772092962. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, S.; Zhang, Q.; Zheng, N.; Zhang, W.; Ding, N. A novel partial ambiguity resolution based on ambiguity dilution of precision- and convex-hull-based satellite selection for instantaneous multiple global navigation satellite systems positioning. J. Navig. 2022, 75, 832–848. [Google Scholar] [CrossRef]
- Yoshida, S. Study on Cloud-Based GNSS Positioning Architecture with Satellite Selection Algorithm and Report of Field Experiments. IEICE Trans. Commun. 2022, 105, 388–398. [Google Scholar] [CrossRef]
- Niu, X.; Dai, Y.; Liu, T.; Chen, Q.; Zhang, Q. Feature-based GNSS positioning error consistency optimization for GNSS/INS integrated system. GPS Solut. 2023, 27, 89. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2012; pp. 199–232. [Google Scholar]
- Wei, M.; Liu, Z.; Li, C.; Yang, R.; Li, B.; Xu, Q. A Combined Satellite Selection Algorithm. In Proceedings of the 2018 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Jinan, China, 14–17 December 2018; pp. 477–480. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Population size | Number of bottom satellites to be selected |
| Max Generations | 100 |
| Function Tolerance | |
| Crossover probability | 0.8 |
| Mutation probability | 0.01 |
| perturbation function | Gaussian perturbation function . |
| Time (hour) | Maximum Number of Satellites Observed per Hour | Maximum Number of Satellites Observed per Hour (with Random Obstruction) |
|---|---|---|
| 1 | 239 | 195 |
| 2 | 232 | 201 |
| 3 | 251 | 208 |
| 4 | 232 | 187 |
| 5 | 252 | 218 |
| 6 | 250 | 213 |
| 7 | 220 | 190 |
| 8 | 270 | 227 |
| 9 | 263 | 212 |
| 10 | 214 | 183 |
| 11 | 263 | 218 |
| 12 | 268 | 234 |
| 13 | 214 | 181 |
| 14 | 253 | 217 |
| 15 | 260 | 215 |
| 16 | 216 | 183 |
| 17 | 259 | 219 |
| 18 | 253 | 216 |
| 19 | 210 | 177 |
| 20 | 253 | 215 |
| 21 | 248 | 210 |
| 22 | 217 | 183 |
| 23 | 246 | 208 |
| 24 | 252 | 201 |
| Algorithm | Consumed Time (s) |
|---|---|
| Quasi_Optimal Algorithm | |
| Recursive Algorithm | 10.326 (form 200 to 10) |
| Proposed Algorithm | 0.132 |
| Satellites | Quasi_Optimal Algorithm | Recursive Algorithm | Proposed Algorithm | Quasi_Optimal Algorithm (with Random Obstruction) | Recursive Algorithm (with Random Obstruction) | Proposed Algorithm (with Random Obstruction) |
|---|---|---|---|---|---|---|
| 10 | 1.431 | 1855.158 | 1.279 | 1.882 | 782.354 | 1.308 |
| 20 | 0.985 | 32.339 | 0.940 | 1.082 | 9.481 | 0.943 |
| 30 | 0.802 | 2.398 | 0.775 | 0.919 | 1.848 | 0.790 |
| 40 | 0.708 | 1.682 | 0.690 | 0.800 | 1.516 | 0.705 |
| 50 | 0.645 | 1.495 | 0.634 | 0.735 | 1.340 | 0.647 |
| 60 | 0.610 | 1.378 | 0.592 | 0.690 | 1.176 | 0.609 |
| 70 | 0.567 | 1.203 | 0.562 | 0.649 | 1.066 | 0.578 |
| 80 | 0.542 | 1.137 | 0.532 | 0.625 | 0.923 | 0.551 |
| Time (hour) | Maximum Visible Satellites per Hour | 10 Satellites GDOP (Proposed Algorithnm) | 10 Satellites GDOP (Quasi-Optimal Algorithm) |
|---|---|---|---|
| 1 | 98 | 1.249 | 1.432 |
| 2 | 80 | 1.252 | 1.423 |
| 3 | 74 | 1.293 | 2.422 |
| 4 | 63 | 1.373 | 2.625 |
| 5 | 86 | 1.252 | 1.522 |
| 6 | 93 | 1.321 | 1.351 |
| 7 | 74 | 1.242 | 1.660 |
| 8 | 88 | 1.224 | 1.720 |
| 9 | 91 | 1.231 | 1.485 |
| 10 | 72 | 1.274 | 1.523 |
| 11 | 85 | 1.165 | 1.432 |
| 12 | 95 | 1.329 | 1.829 |
| 13 | 77 | 1.351 | 1.774 |
| 14 | 89 | 1.293 | 1.388 |
| 15 | 96 | 1.353 | 1.531 |
| 16 | 64 | 1.340 | 1.461 |
| 17 | 86 | 1.285 | 2.044 |
| 18 | 77 | 1.306 | 1.555 |
| 19 | 71 | 1.274 | 1.389 |
| 20 | 74 | 1.435 | 1.539 |
| 21 | 79 | 1.417 | 2.243 |
| 22 | 72 | 1.262 | 1.884 |
| 23 | 80 | 1.323 | 1.782 |
| 24 | 92 | 1.177 | 1.279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Wang, Y.; Sun, C. Signal Occlusion-Resistant Satellite Selection for Global Navigation Applications Using Large-Scale LEO Constellations. Remote Sens. 2023, 15, 4978. https://doi.org/10.3390/rs15204978
Guo J, Wang Y, Sun C. Signal Occlusion-Resistant Satellite Selection for Global Navigation Applications Using Large-Scale LEO Constellations. Remote Sensing. 2023; 15(20):4978. https://doi.org/10.3390/rs15204978
Chicago/Turabian StyleGuo, Junqi, Yang Wang, and Chenyang Sun. 2023. "Signal Occlusion-Resistant Satellite Selection for Global Navigation Applications Using Large-Scale LEO Constellations" Remote Sensing 15, no. 20: 4978. https://doi.org/10.3390/rs15204978
APA StyleGuo, J., Wang, Y., & Sun, C. (2023). Signal Occlusion-Resistant Satellite Selection for Global Navigation Applications Using Large-Scale LEO Constellations. Remote Sensing, 15(20), 4978. https://doi.org/10.3390/rs15204978






