Adaptive Beamforming with Sidelobe Level Control for Multiband Sparse Linear Array
Abstract
:1. Introduction
2. Signal Model
3. Proposed Multiband Sparse Array Design
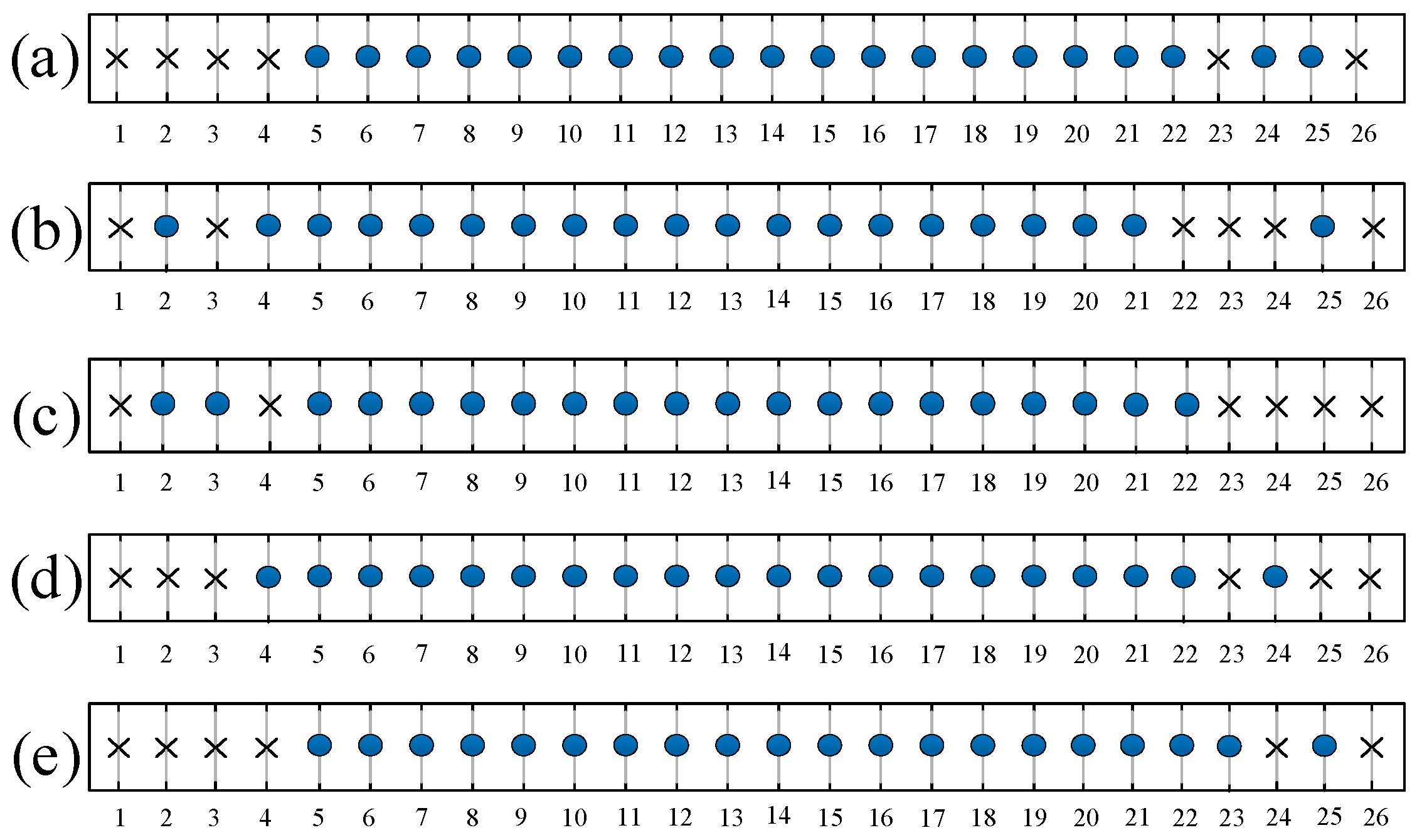
3.1. Problem Formulation
3.2. Proposed SDR-Based Iterative Reweighted Algorithm
| Algorithm 1 Multiband Sparse Array Design with Sidelobe Level Control |
Input: N,K,, , , . Initialization: Set , is an all-one matrix. 1: whiledo 2: Obtain using (22); 3: Obtain using (24); 4: Obtain using (23); 5: Update the value of by the binary search approach; 6: ; 7: end while Output: Multiband beamforming weights . |
4. Analysis of Computational Complexity
5. Numerical Results
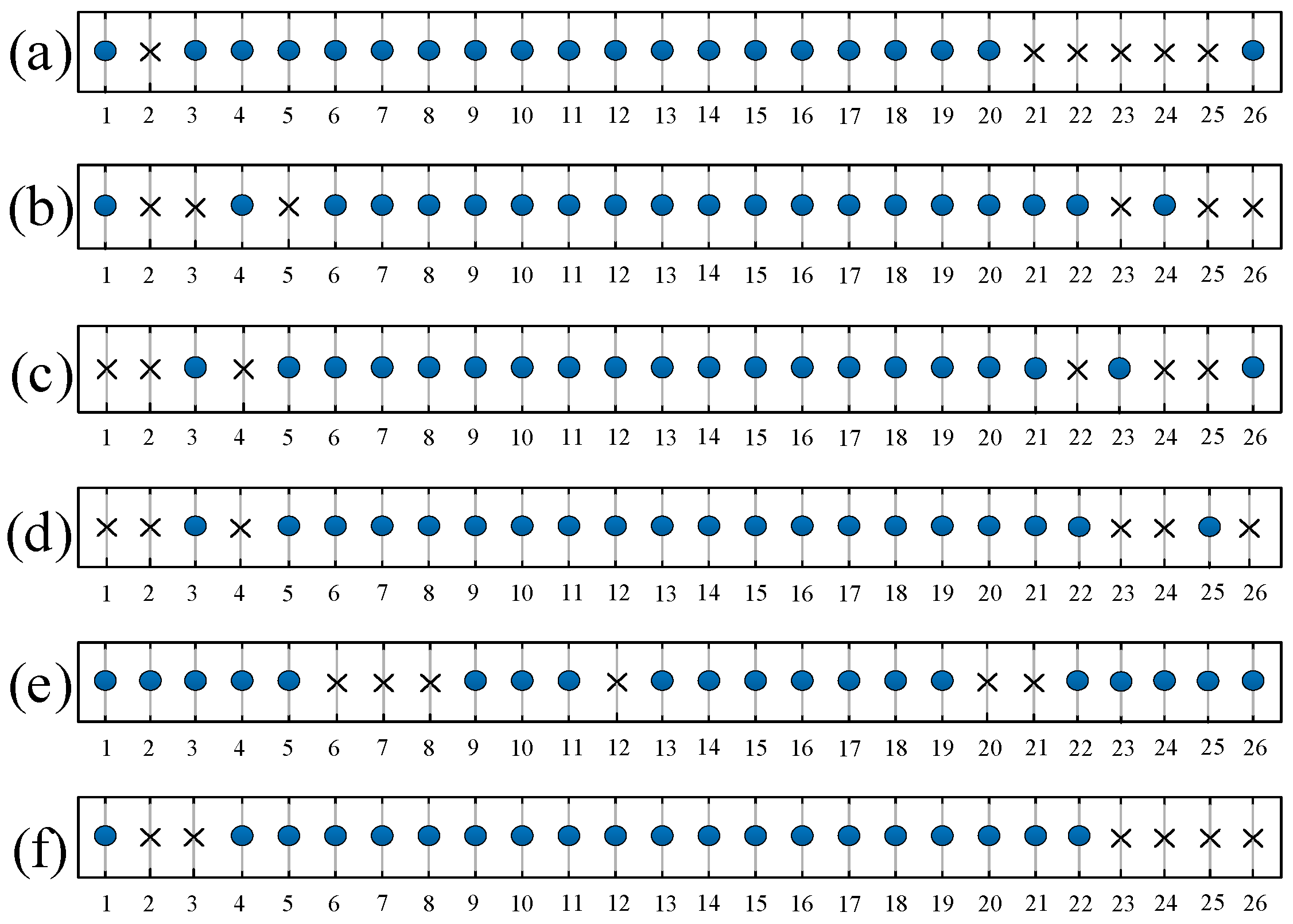
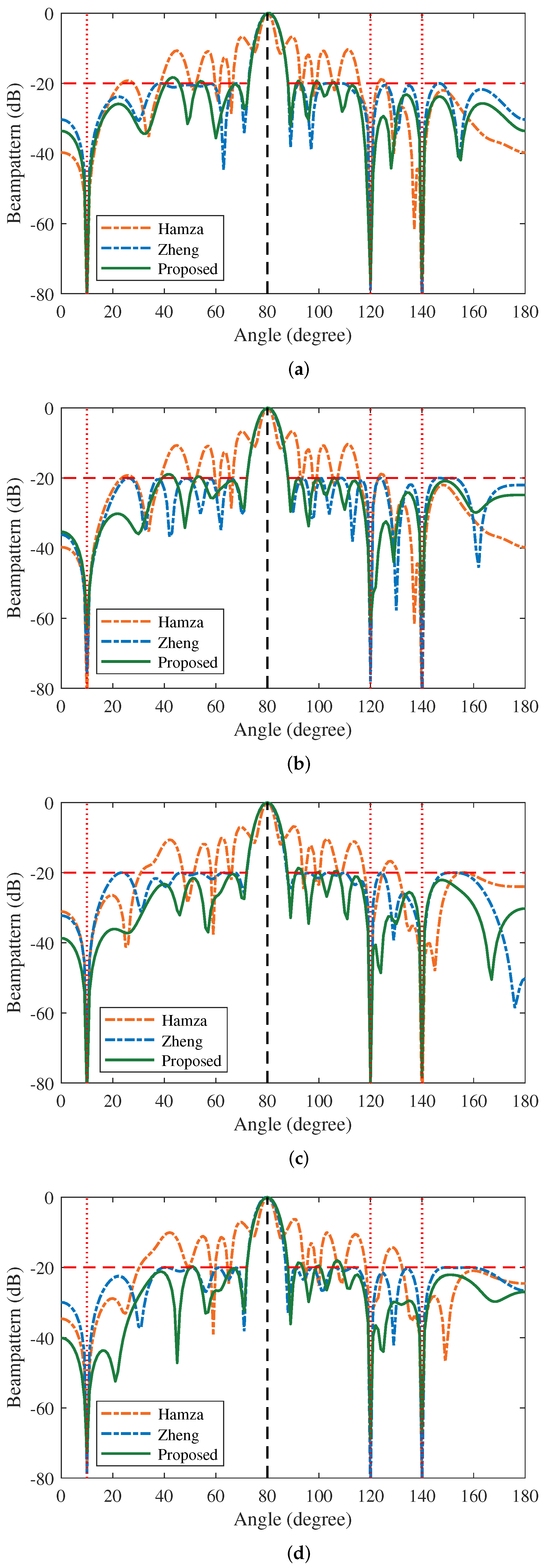
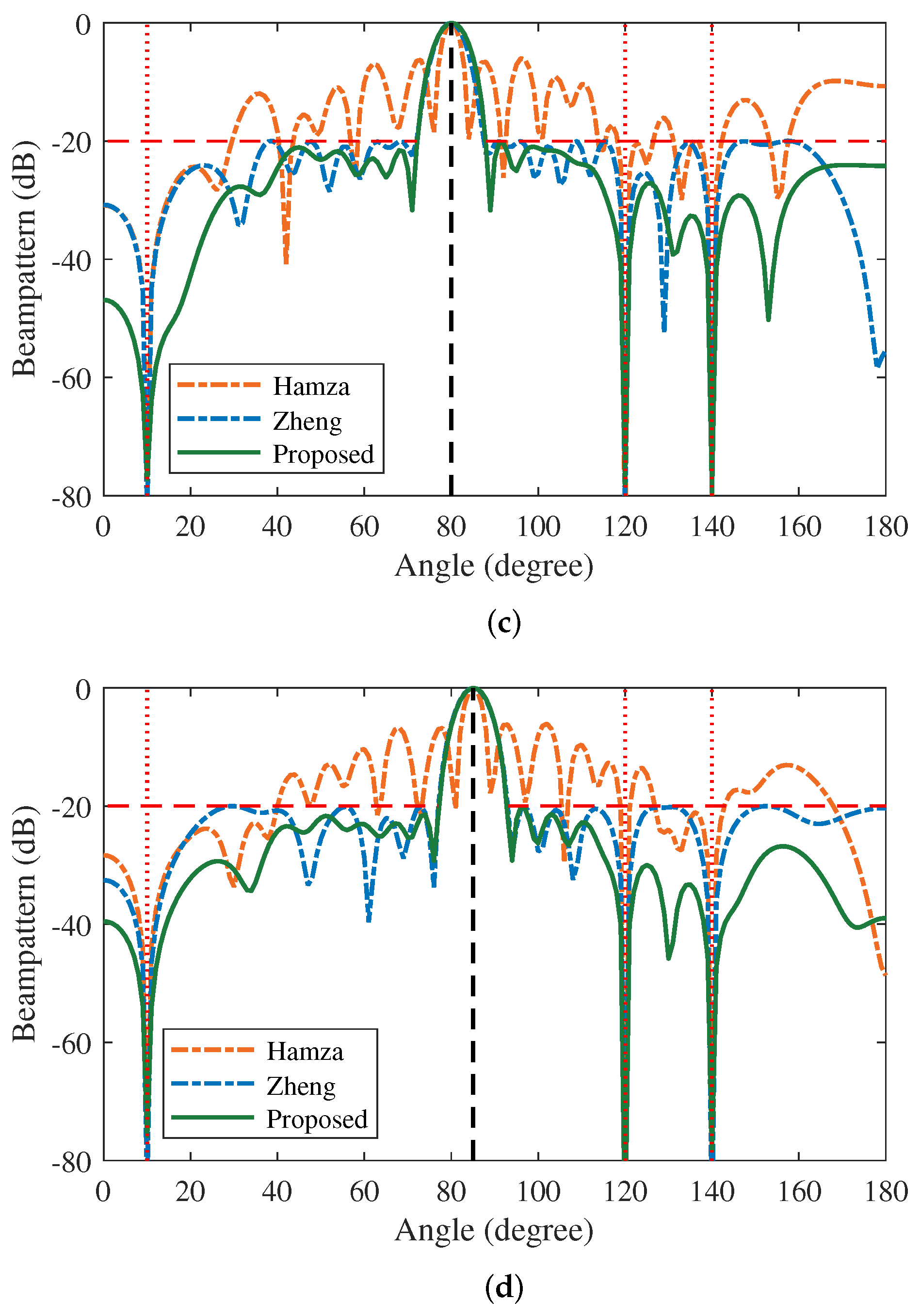
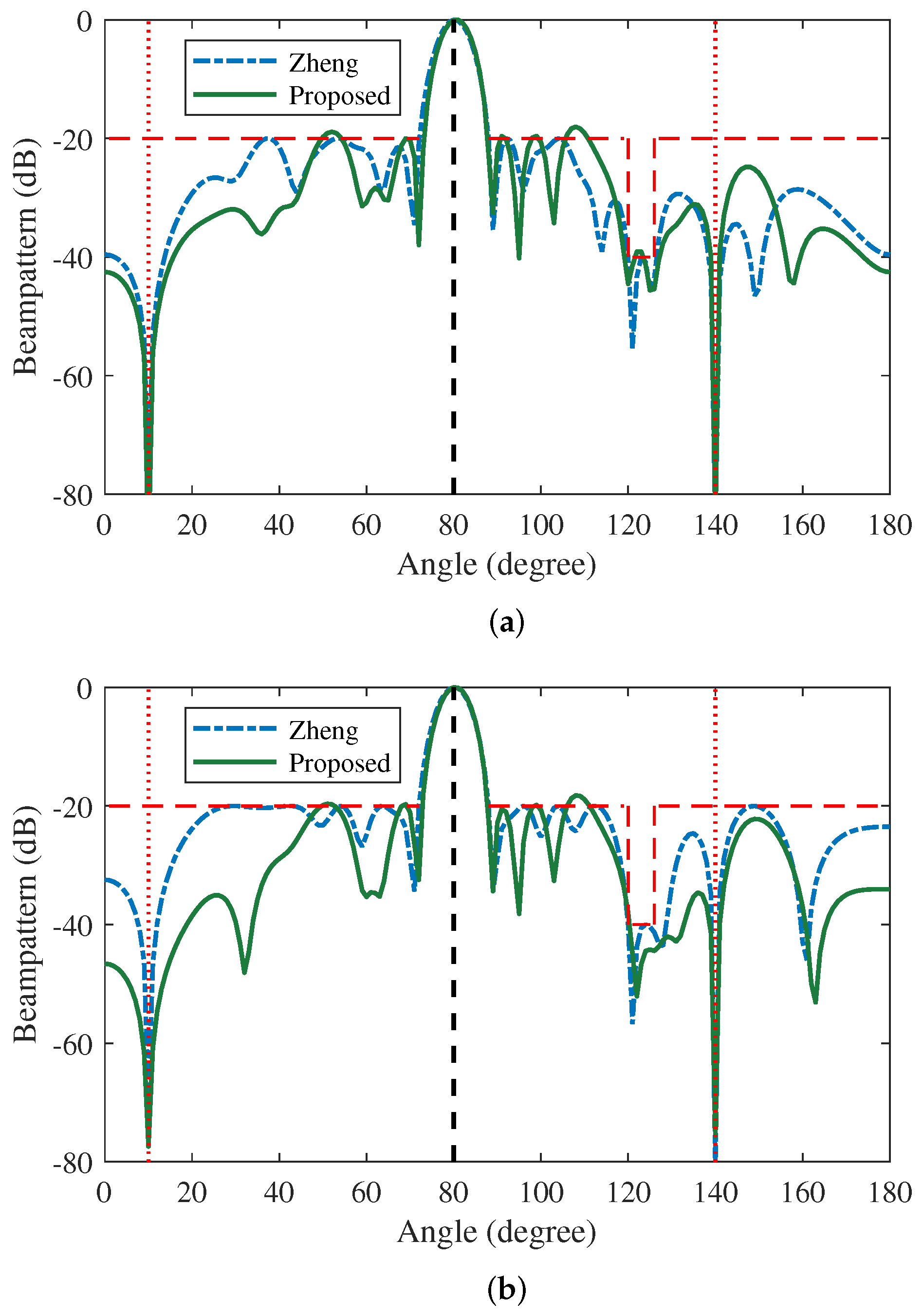
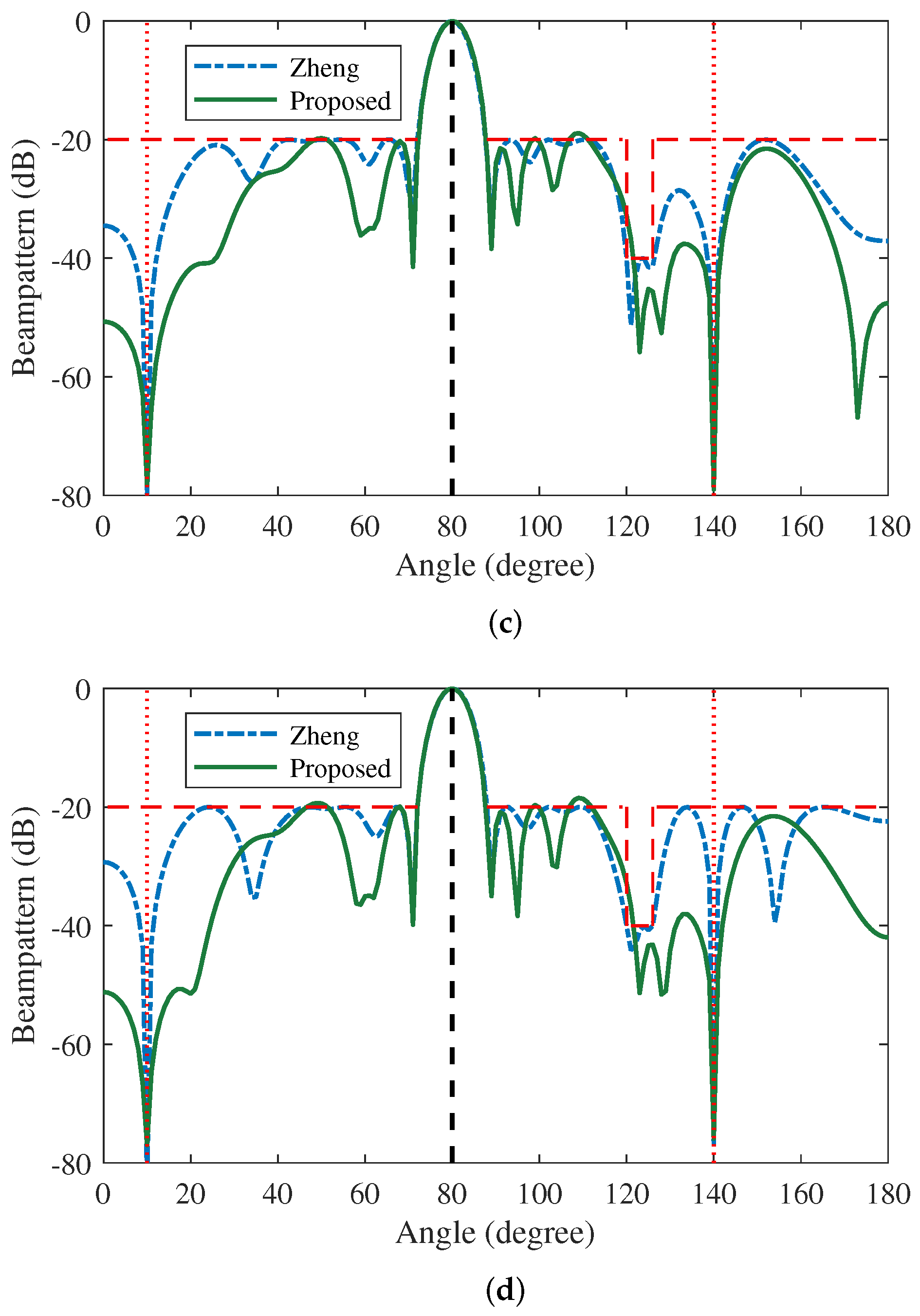
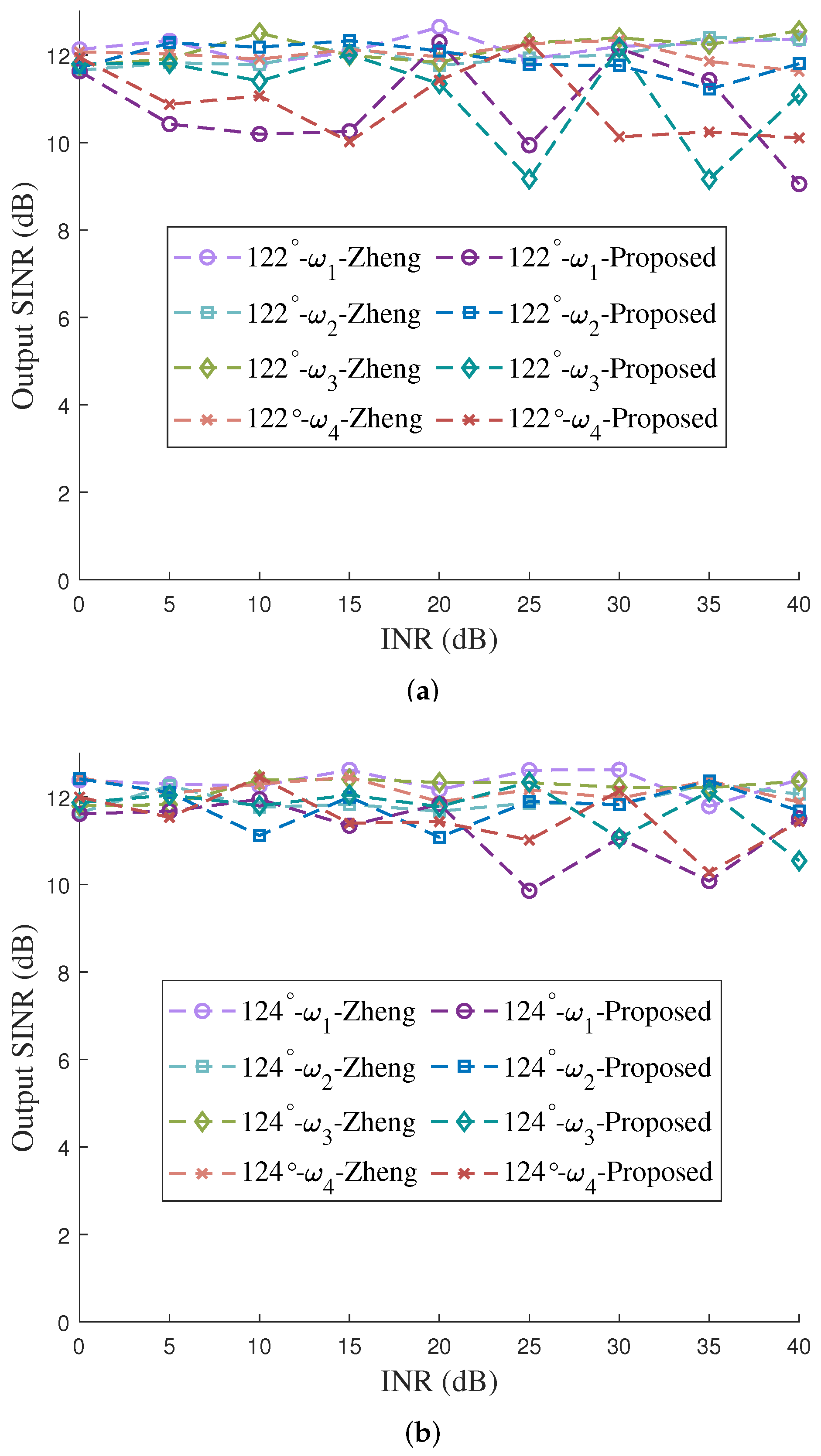
5.1. Beamforming with Multiple Interferences at the Same Desired DOA
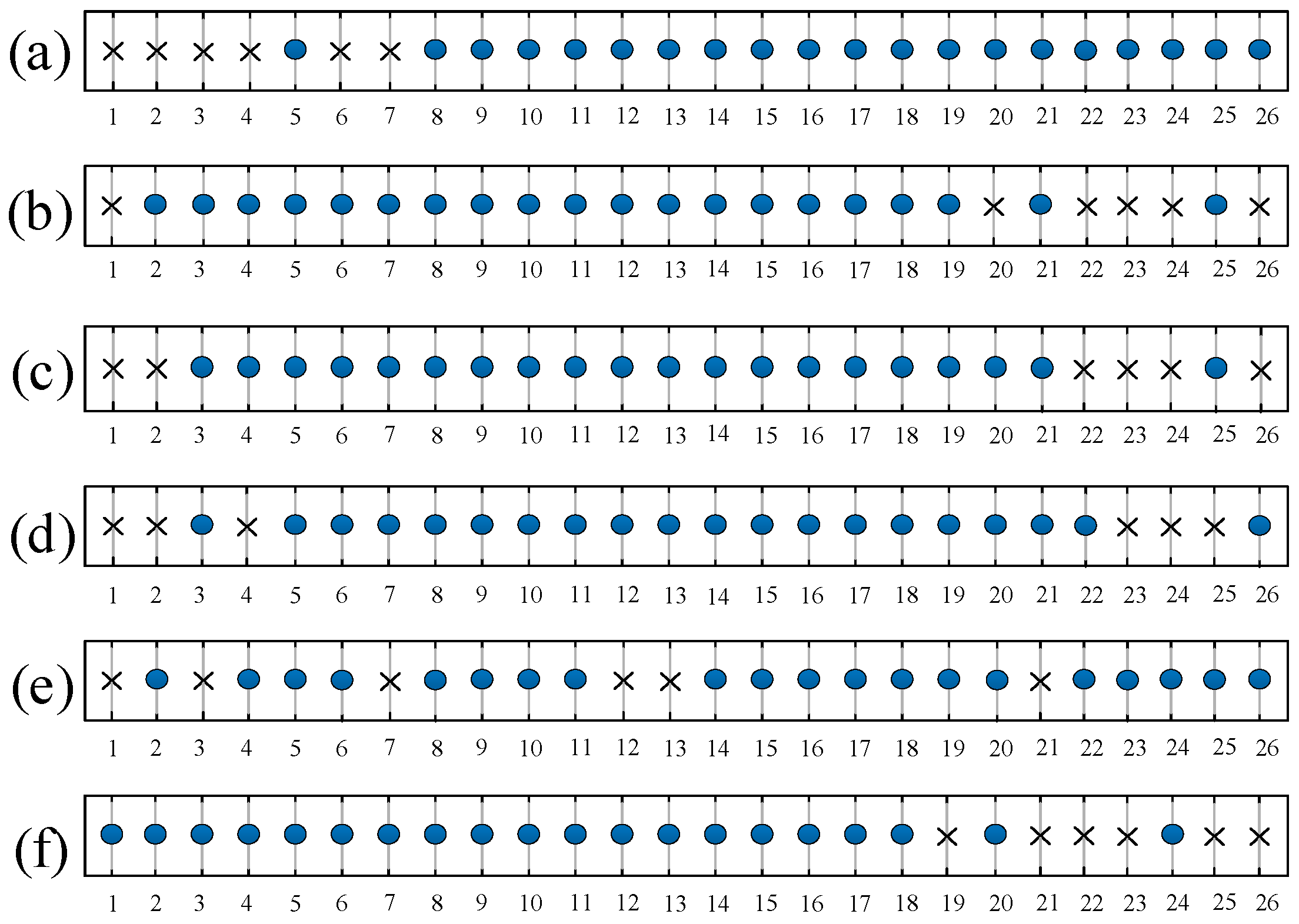
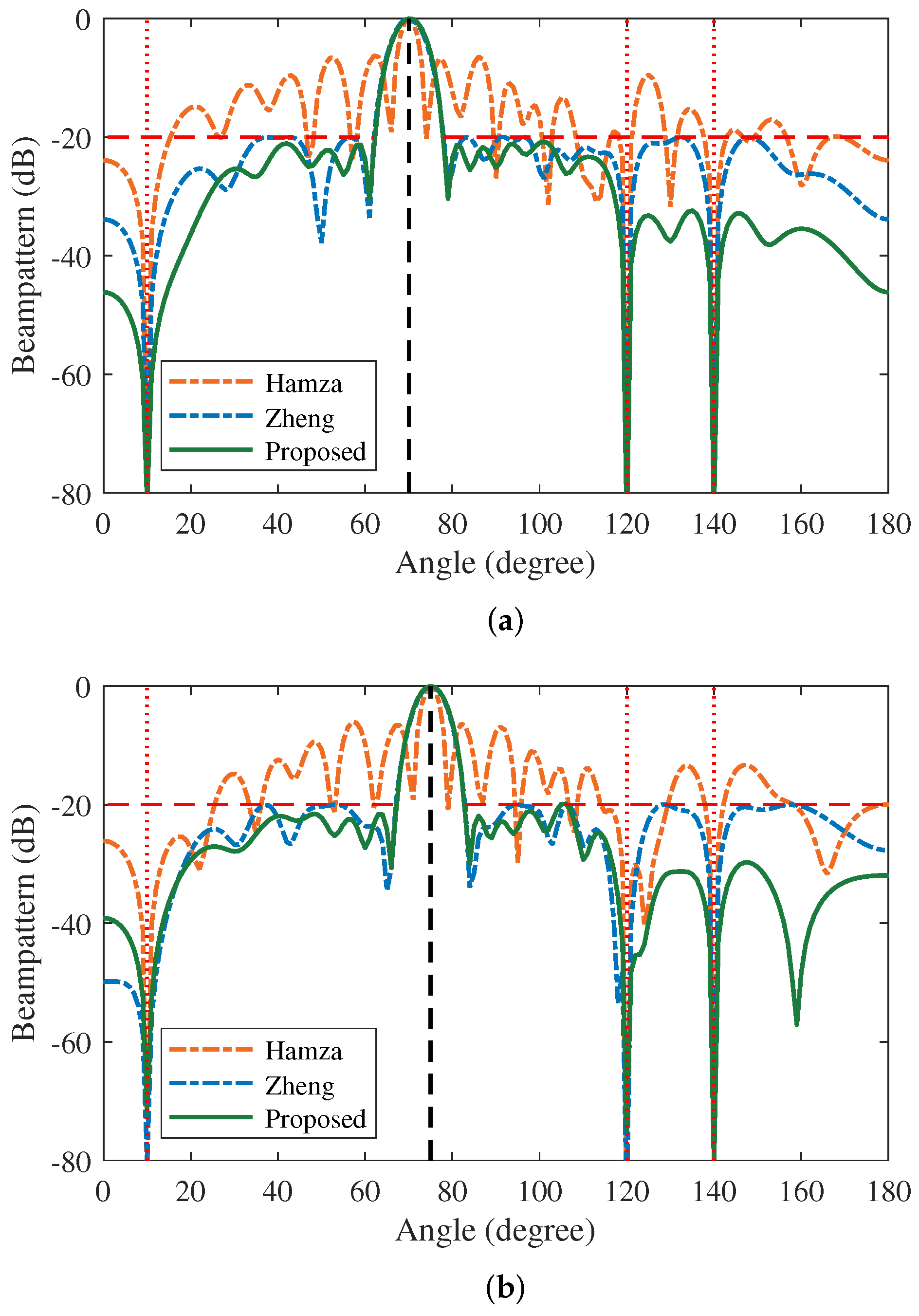
5.2. Beamforming with Multiple Interferences at the Distinct Desired DOAs
5.3. Nulling Forming at the Same Desired DOA
5.4. Nulling Anti-Interference Performance
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
- The following abbreviations are used in this manuscript:
| SINR | Signal-to-interference-and-noise ratio |
| DOA | Direction-of-arrival |
| DoF | Degree-of-freedom |
| SDR | Semi-definite relaxation |
| SCA | Sequential convex approximation |
| ADMM | Alternating direction method of multipliers |
| DNN | Deep neural network |
| TDL | Tapped delay line |
| DFT | Discrete Fourier transform |
| FI | Frequency-invariant |
| SOCP | Second-order cone programming |
| SLL | Sidelobe level |
References
- He, X.Y.; Chang, L.; Chen, L.L. A multifunction broad-beam antenna with dual bands and dual circular-polarizations. In Proceedings of the 2016 IEEE MTT-S International Wireless Symposium (IWS), Shanghai, China, 14–16 March 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Sanad, M.; Antennas, A.; Hassan, N. A Multi-band Antenna Configuration for MIMO WiMax in Multi-standard Multifunction Handsets. In Proceedings of the 2009 IEEE Mobile WiMAX Symposium, Napa Valley, CA, USA, 9–10 July 2009; pp. 195–200. [Google Scholar] [CrossRef]
- Haider, N.; Caratelli, D.; Yarovoy, A.G. Recent Developments in Reconfigurable and Multiband Antenna Technology. Int. J. Antennas Propag. 2013, 2013, 869170. [Google Scholar] [CrossRef]
- Li, Y.; Sim, C.Y.D.; Luo, Y.; Yang, G. Multiband 10-Antenna Array for Sub-6 GHz MIMO Applications in 5-G Smartphones. IEEE Access 2018, 6, 28041–28053. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2010, 59, 573–586. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; He, S.; Shi, Z. A Robust and Efficient Algorithm for Coprime Array Adaptive Beamforming. IEEE Trans. Veh. Technol. 2018, 67, 1099–1112. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, T.; Wang, W.Q.; Zhang, S. Robust adaptive beamforming via coprime coarray interpolation. Signal Process. 2020, 169, 107382. [Google Scholar] [CrossRef]
- Nai, S.E.; Ser, W.; Yu, Z.L.; Chen, H. Beampattern Synthesis for Linear and Planar Arrays with Antenna Selection by Convex Optimization. IEEE Trans. Antennas Propag. 2010, 58, 3923–3930. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Zhang, X.; Wang, X.; Amin, M.G. Enhanced Automotive Sensing Assisted by Joint Communication and Cognitive Sparse MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4782–4799. [Google Scholar] [CrossRef]
- Fuchs, B. Synthesis of Sparse Arrays with Focused or Shaped Beampattern via Sequential Convex Optimizations. IEEE Trans. Antennas Propag. 2012, 60, 3499–3503. [Google Scholar] [CrossRef]
- Nongpiur, R.C.; Shpak, D.J. Synthesis of Linear and Planar Arrays with Minimum Element Selection. IEEE Trans. Signal Process. 2014, 62, 5398–5410. [Google Scholar] [CrossRef]
- Fuchs, B.; Rondineau, S. Array Pattern Synthesis with Excitation Control via Norm Minimization. IEEE Trans. Antennas Propag. 2016, 64, 4228–4234. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, X.; So, H.C.; Zhou, D. Sparse Array Beampattern Synthesis via Alternating Direction Method of Multipliers. IEEE Trans. Antennas Propag. 2018, 66, 2333–2345. [Google Scholar] [CrossRef]
- Wang, X.; Aboutanios, E.; Amin, M.G. Thinned Array Beampattern Synthesis by Iterative Soft-Thresholding-Based Optimization Algorithms. IEEE Trans. Antennas Propag. 2014, 62, 6102–6113. [Google Scholar] [CrossRef]
- Oliveri, G.; Massa, A. Bayesian Compressive Sampling for Pattern Synthesis with Maximally Sparse Non-Uniform Linear Arrays. IEEE Trans. Antennas Propag. 2011, 59, 467–481. [Google Scholar] [CrossRef]
- Hamza, S.A.; Amin, M.G. Hybrid Sparse Array Beamforming Design for General Rank Signal Models. IEEE Trans. Signal Process. 2019, 67, 6215–6226. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, Y.; Wang, W.Q. Sparse Array Beamforming Design for Coherently Distributed Sources. IEEE Trans. Antennas Propag. 2021, 69, 2628–2636. [Google Scholar] [CrossRef]
- Huang, H.; So, H.C.; Zoubir, A.M. Sparse Array Beamformer Design via ADMM. In Proceedings of the 2022 IEEE 12th Sensor Array and Multichannel Signal Processing Workshop (SAM), Trondheim, Norway, 20–23 June 2022; pp. 336–340. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, Y.; Wang, W.Q.; So, H.C. Sparse Array Design for Adaptive Beamforming via Semidefinite Relaxation. IEEE Signal Process. Lett. 2020, 27, 925–929. [Google Scholar] [CrossRef]
- Wang, X.; Greco, M.S.; Gini, F. Adaptive Sparse Array Beamformer Design by Regularized Complementary Antenna Switching. IEEE Trans. Signal Process. 2021, 69, 2302–2315. [Google Scholar] [CrossRef]
- Hamza, S.A.; Amin, M.G. Learning Sparse Array Capon Beamformer Design Using Deep Learning Approach. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020. [Google Scholar] [CrossRef]
- Hamza, S.A.; Amin, M.G.; Chalise, B.K. Phase-Only Reconfigurable Sparse Array Beamforming Using Deep Learning. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022. [Google Scholar] [CrossRef]
- Crocco, M.; Trucco, A. Stochastic and Analytic Optimization of Sparse Aperiodic Arrays and Broadband Beamformers with Robust Superdirective Patterns. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2433–2447. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Ye, L.; Nie, Z.; Liu, Q.H. Synthesis of Sparse Arrays with Frequency-Invariant-Focused Beam Patterns Under Accurate Sidelobe Control by Iterative Second-Order Cone Programming. IEEE Trans. Antennas Propag. 2015, 63, 5826–5832. [Google Scholar] [CrossRef]
- Hawes, M.B.; Liu, W. Sparse array design for wideband beamforming with reduced complexity in tapped delay-lines. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1236–1247. [Google Scholar] [CrossRef]
- Trucco, A. Synthesizing wide-band sparse arrays by simulated annealing. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 2, pp. 989–994. [Google Scholar] [CrossRef]
- Doblinger, G. Optimized design of interpolated array and sparse array wideband beamformers. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Hawes, M.B.; Liu, W. Location Optimization of Robust Sparse Antenna Arrays with Physical Size Constraint. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1303–1306. [Google Scholar] [CrossRef]
- Hamza, S.A.; Amin, M.G. Sparse Array Beamforming Design for Wideband Signal Models. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1211–1226. [Google Scholar] [CrossRef]
- Hamza, S.A.; Amin, M.G. Sparse Array DFT Beamformers for Wideband Sources. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wei Liu, S.W. Wideband Beamforming: Concepts and Techniques; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Liu, Y.; Zhang, L.; Zhu, C.; Liu, Q.H. Synthesis of Nonuniformly Spaced Linear Arrays with Frequency-Invariant Patterns by the Generalized Matrix Pencil Methods. IEEE Trans. Antennas Propag. 2015, 63, 1614–1625. [Google Scholar] [CrossRef]
- El-Khamy, S.E.; El-Sayed, H.F.; Eltrass, A.S. A new adaptive beamforming of multiband fractal antenna array in strong-jamming environment. Wirel. Pers. Commun. 2022, 126, 285–304. [Google Scholar] [CrossRef]
- Monzingo, R.A.; Miller, T.W. Introduction to Adaptive Arrays; Scitech Publishing: Tamil Nadu, India, 2004. [Google Scholar]
- Mehanna, O.; Sidiropoulos, N.D.; Giannakis, G.B. Joint Multicast Beamforming and Antenna Selection. IEEE Trans. Signal Process. 2013, 61, 2660–2674. [Google Scholar] [CrossRef]
- Joshi, S.; Boyd, S. Sensor selection via convex optimization. IEEE Trans. Signal Process. 2008, 57, 451–462. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Ma, W.K.; So, A.M.C.; Ye, Y.; Zhang, S. Semidefinite Relaxation of Quadratic Optimization Problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Karipidis, E.; Sidiropoulos, N.D.; Luo, Z.Q. Quality of Service and Max-Min Fair Transmit Beamforming to Multiple Cochannel Multicast Groups. IEEE Trans. Signal Process. 2008, 56, 1268–1279. [Google Scholar] [CrossRef]
| Hamza’s method | |||||
| Frequency | |||||
| Interference | |||||
| −83.60 | −83.60 | −83.22 | −77.56 | ||
| −74.35 | −74.35 | −75.84 | −74.58 | ||
| −87.38 | −87.38 | −88.64 | −82.39 | ||
| Zheng’s method | |||||
| Frequency | |||||
| Interference | |||||
| −80.88 | −75.81 | −74.66 | −78.79 | ||
| −79.05 | −78.02 | −81.36 | −84.77 | ||
| −82.02 | −82.50 | −77.95 | −82.41 | ||
| Proposed method | |||||
| Frequency | |||||
| Interference | |||||
| −79.33 | −62.62 | −84.10 | −72.68 | ||
| −76.67 | −61.02 | −79.84 | −68.79 | ||
| −75.59 | −59.63 | −78.29 | −66.52 | ||
| Frequency | ||||
|---|---|---|---|---|
| Hamza’s method | 11.22 | 11.74 | 11.55 | 11.20 |
| Zheng’s method | 11.93 | 13.07 | 12.59 | 12.17 |
| Proposed | 11.78 | 10.34 | 12.07 | 11.77 |
| Hamza’s method | |||||
| Frequency | |||||
| Interference | |||||
| −74.14 | −84.16 | −77.44 | −77.22 | ||
| −79.17 | −90.14 | −87.49 | −89.83 | ||
| −77.55 | −77.62 | −79.92 | −80.79 | ||
| Zheng’s method | |||||
| Frequency | |||||
| Interference | |||||
| −76.50 | −80.15 | −83.78 | −85.28 | ||
| −74.86 | −87.93 | −82.38 | −77.31 | ||
| −77.27 | −76.28 | −76.92 | −90.73 | ||
| Proposed method | |||||
| Frequency | |||||
| Interference | |||||
| −81.45 | −71.98 | −77.27 | −75.81 | ||
| −86.18 | −74.81 | −78.34 | −93.93 | ||
| −82.68 | −80.69 | −79.41 | −78.29 | ||
| Frequency | ||||
|---|---|---|---|---|
| Hamza’s method | 11.21 | 11.28 | 11.01 | 11.15 |
| Zheng’s method | 12.54 | 12.33 | 12.53 | 11.97 |
| Proposed | 12.09 | 12.11 | 12.22 | 11.59 |
| Zheng’s method | |||||
| Frequency | |||||
| Interference | |||||
| −78.00 | −70.18 | −79.79 | −83.28 | ||
| −85.39 | −80.60 | −70.88 | −76.77 | ||
| Proposed method | |||||
| Frequency | |||||
| Interference | |||||
| −89.98 | −77.42 | −78.29 | −77.00 | ||
| −85.42 | −75.73 | −78.98 | −75.90 | ||
| Frequency | ||||
|---|---|---|---|---|
| Zheng’s method | 12.43 | 12.35 | 11.97 | 12.11 |
| Proposed | 12.31 | 11.78 | 11.71 | 12.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Ran, L.; He, C.; Ding, Z.; Chen, S. Adaptive Beamforming with Sidelobe Level Control for Multiband Sparse Linear Array. Remote Sens. 2023, 15, 4929. https://doi.org/10.3390/rs15204929
Li H, Ran L, He C, Ding Z, Chen S. Adaptive Beamforming with Sidelobe Level Control for Multiband Sparse Linear Array. Remote Sensing. 2023; 15(20):4929. https://doi.org/10.3390/rs15204929
Chicago/Turabian StyleLi, Hongtao, Longyao Ran, Cheng He, Zhoupeng Ding, and Shengyao Chen. 2023. "Adaptive Beamforming with Sidelobe Level Control for Multiband Sparse Linear Array" Remote Sensing 15, no. 20: 4929. https://doi.org/10.3390/rs15204929
APA StyleLi, H., Ran, L., He, C., Ding, Z., & Chen, S. (2023). Adaptive Beamforming with Sidelobe Level Control for Multiband Sparse Linear Array. Remote Sensing, 15(20), 4929. https://doi.org/10.3390/rs15204929






