A Seabed Terrain Feature Extraction Transformer for the Super-Resolution of the Digital Bathymetric Model
Abstract
:1. Introduction
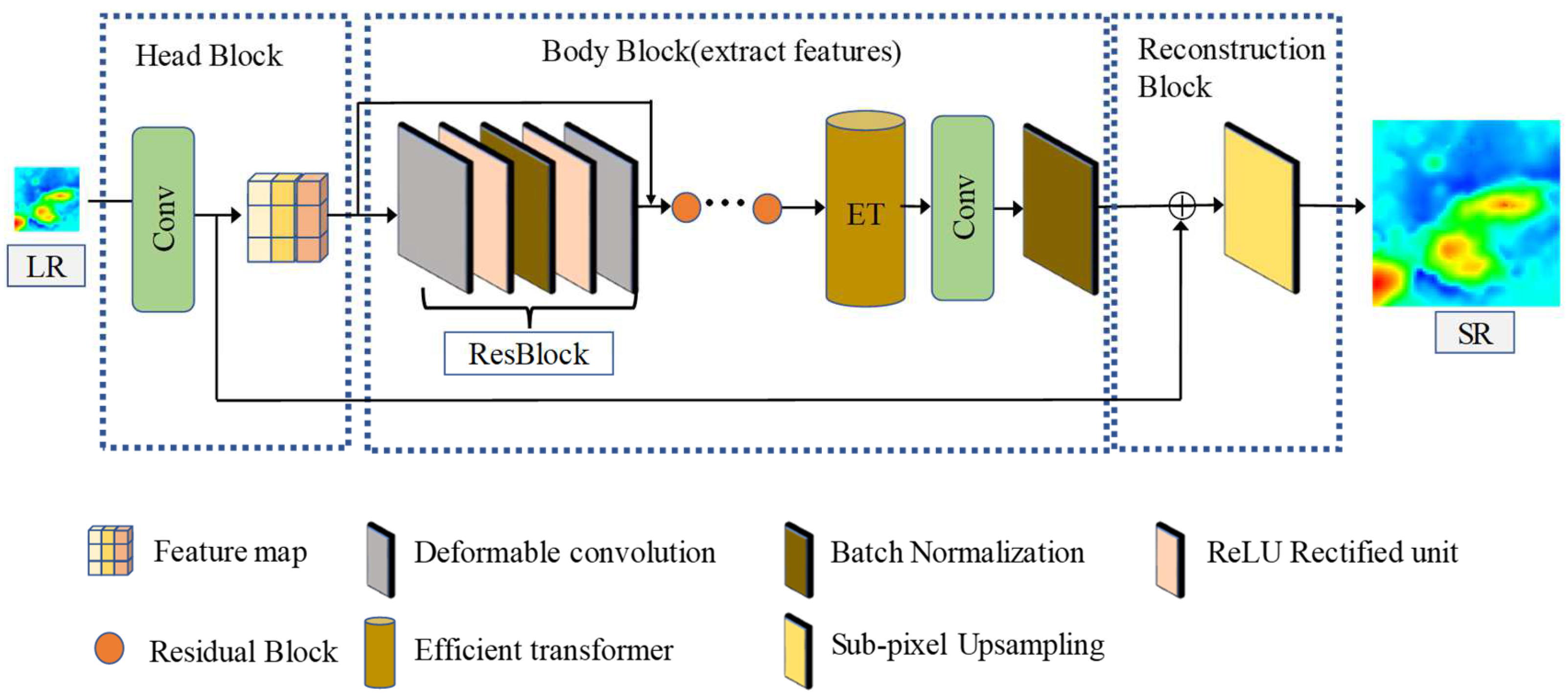
- This study is an early attempt to restore HR DBMs from LR DBMs using a transformer. In addition, we utilize the proposed transformer-based model, combined with ResNet and deformable convolutional layers, which ensures that STFET can capture both local and global seafloor topographic features.
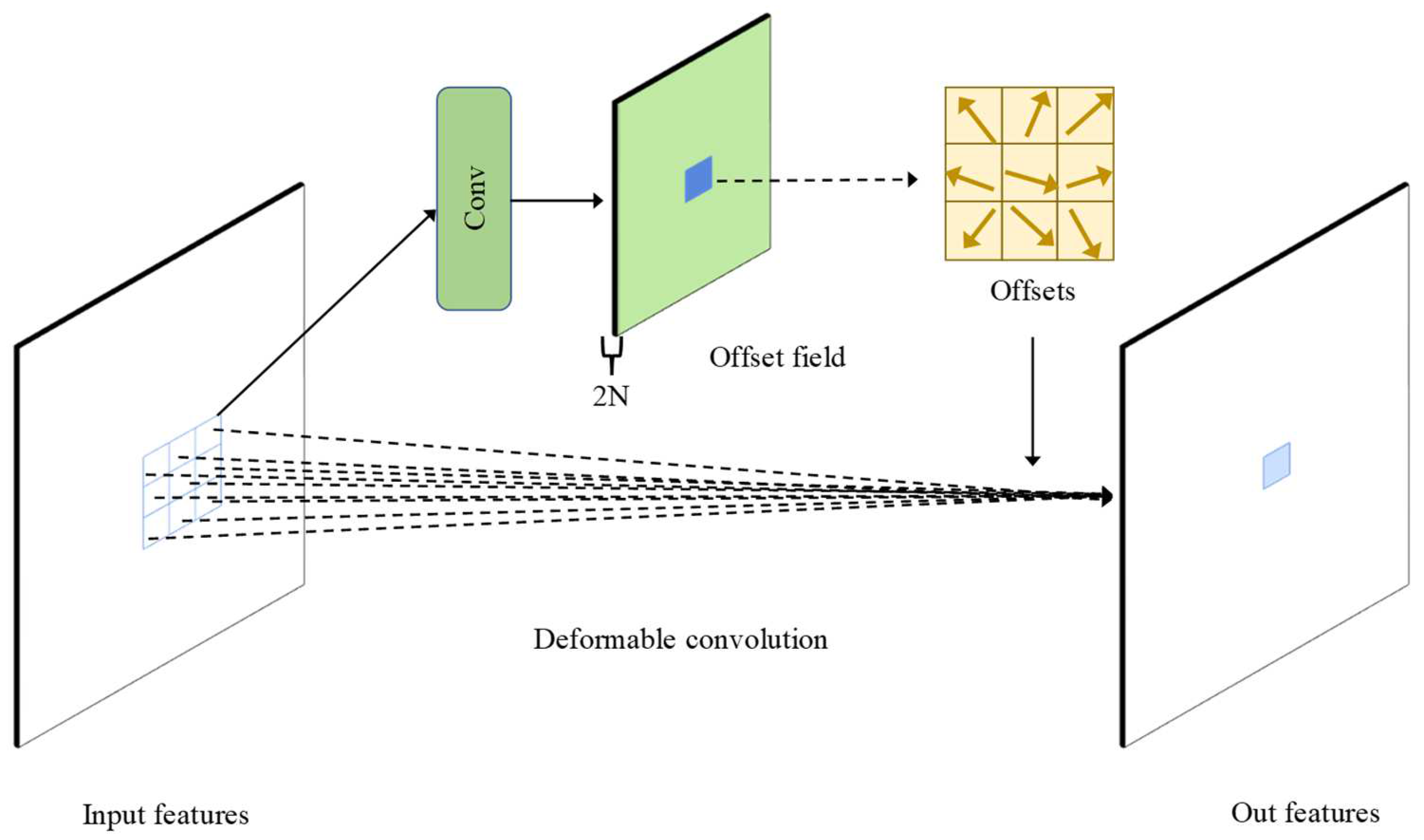
- Given the characteristics of large changes and rapid fluctuations in the DBM terrain, the traditional convolutional layers in ResNet are replaced by deformable convolutional layers, which have the ability to flexibly modify the sampling position of the convolution kernel to align with irregular features, improving the extraction of local seabed terrain features.
- The transformer’s self-attention mechanism allows long-term dependencies to be established between similar regions in the DBM, improving global terrain feature reconstruction. In addition, the matrix is broken down into smaller matrices for parameter manipulation, increasing the speed of model operations.
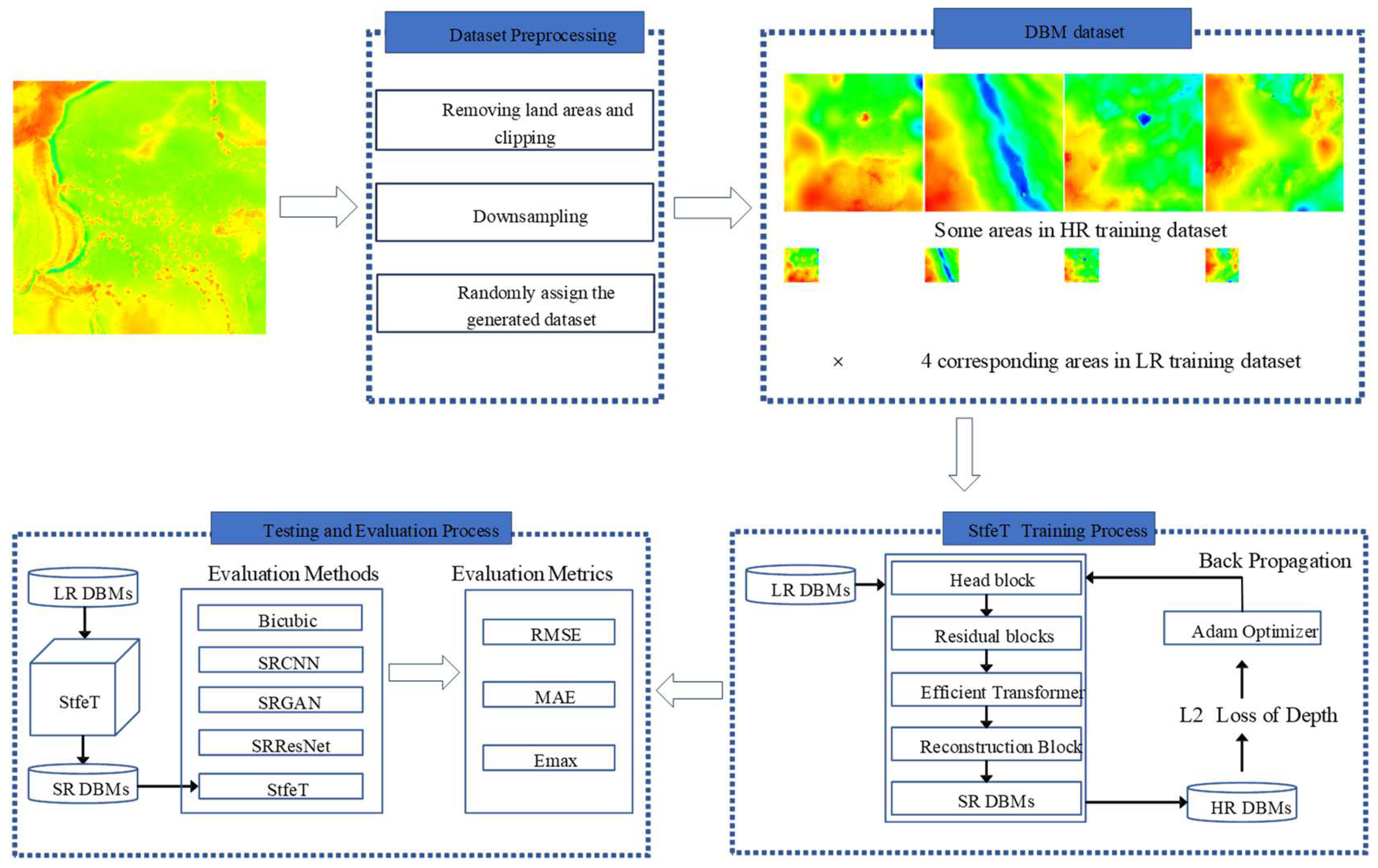
2. Methodology
2.1. Network Architecture
2.2. Seabed Terrain Feature Extraction Module
2.3. Efficient Transformer Module
3. Experimental Setup
3.1. Network Hyperparameters
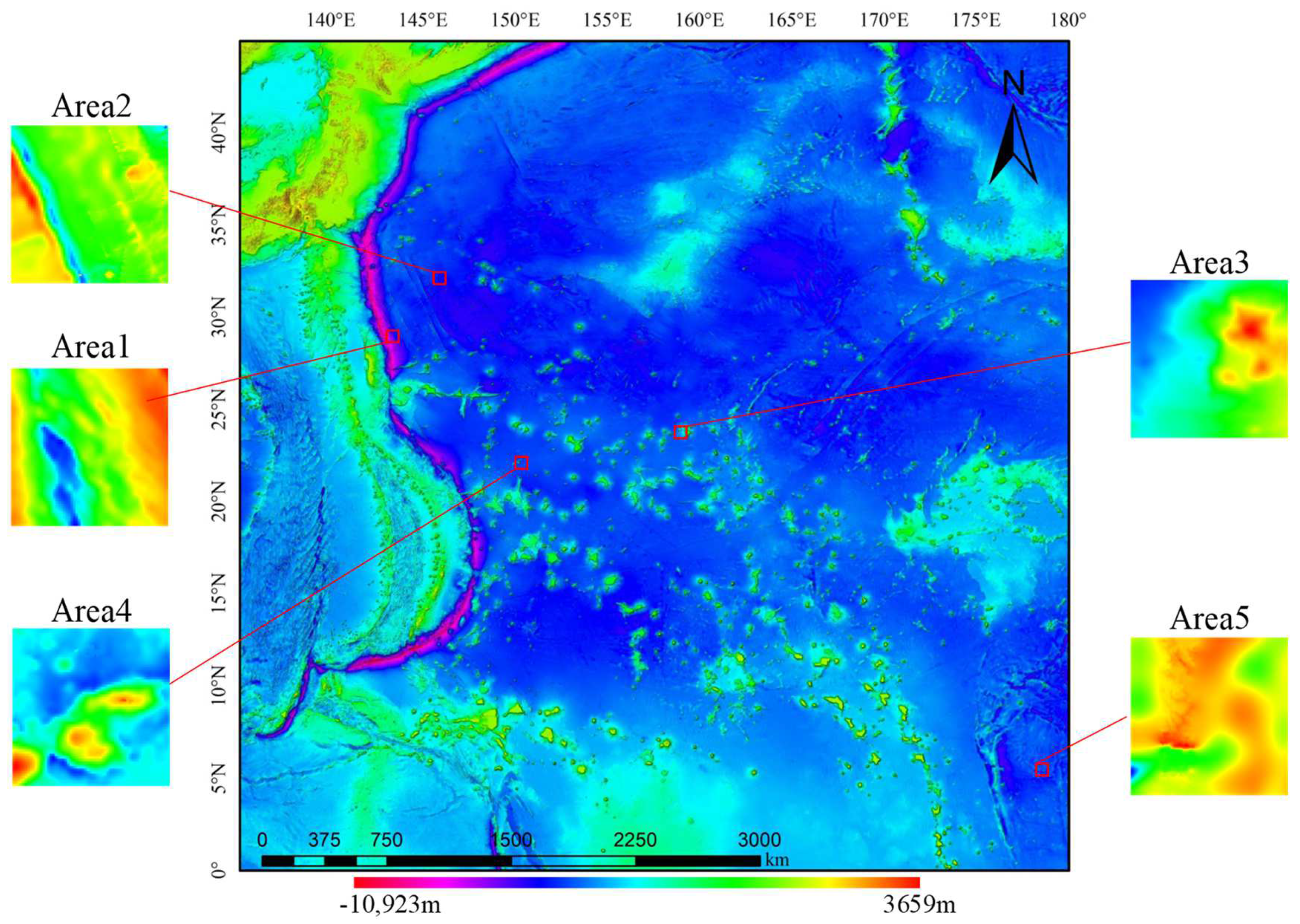
3.2. Study Area and Data
3.3. Evaluation Methods
4. Results and Discussions
4.1. Results on DBMs
4.2. Quantitative Evaluation Results on Complex Regions
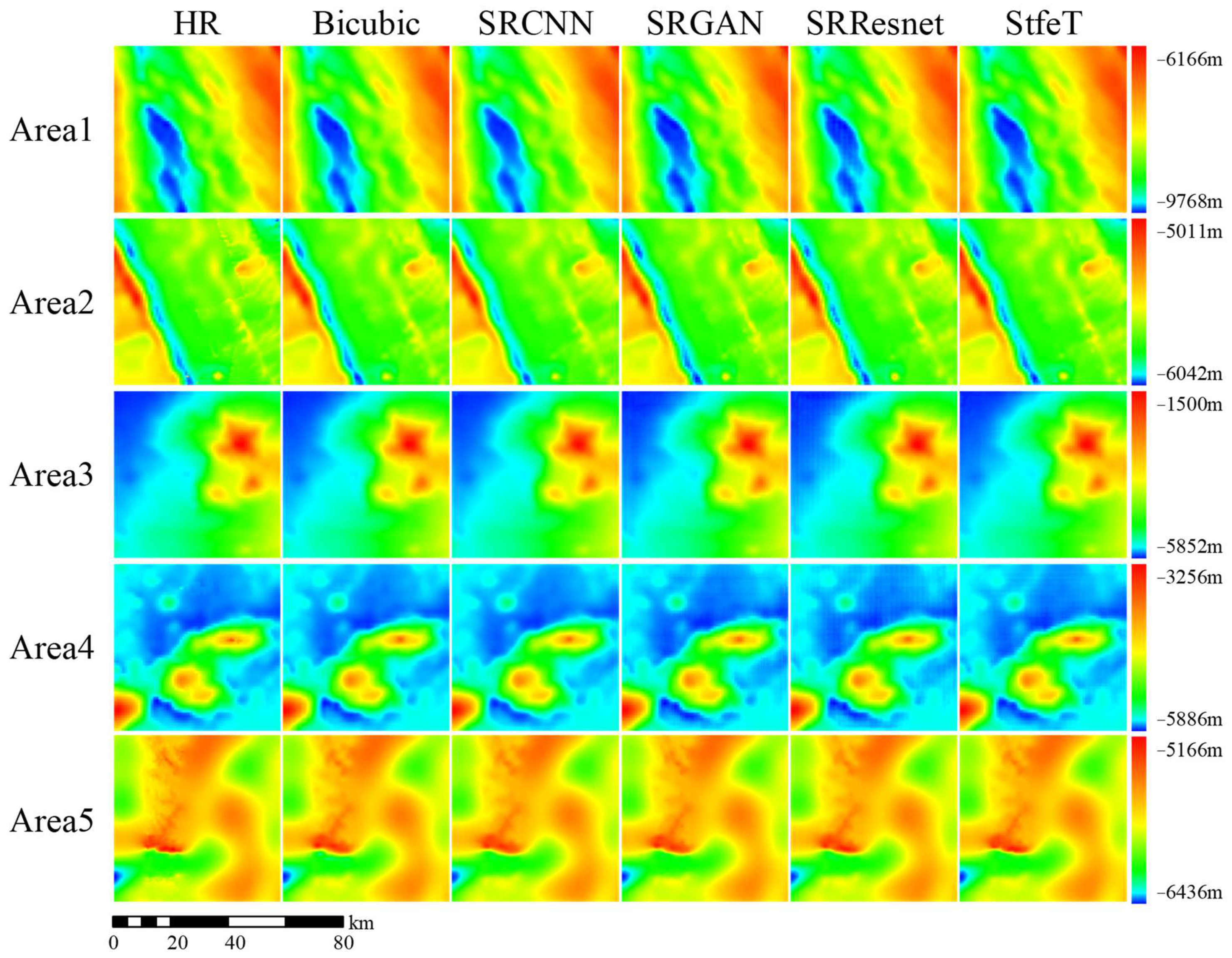
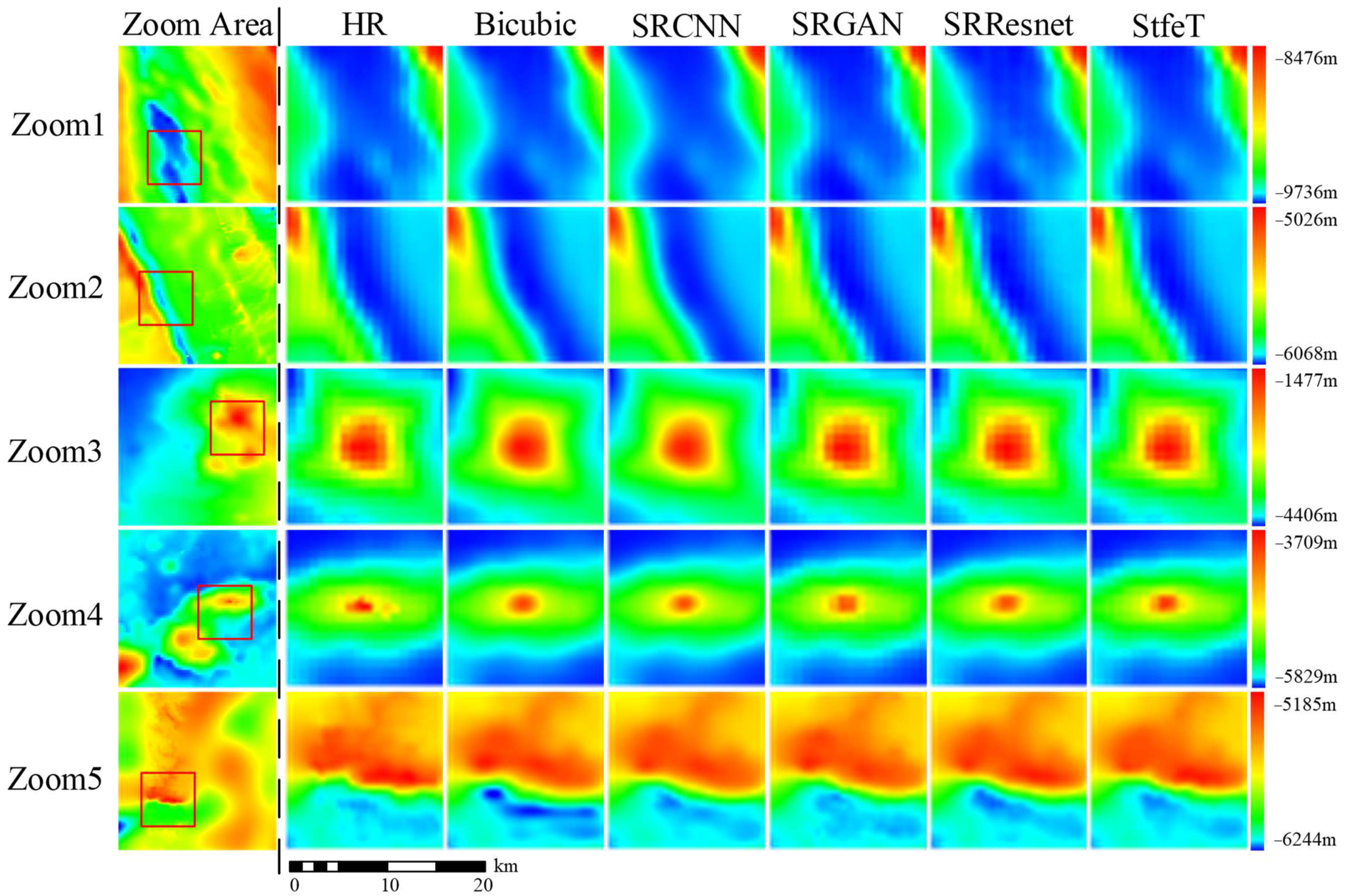
4.3. Visual Evaluation of Different Methods
4.4. Residual Evaluation of Different Methods
4.5. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Z.; Li, J.; Jin, X.; Shang, J.; Li, S.; Jin, X. Distribution, features, and influence factors of the submarine topographic boundaries of the Okinawa Trough. Sci. China Earth Sci. 2014, 57, 1885–1896. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. Solid Earth 1997, 102, 10039–10054. [Google Scholar] [CrossRef]
- Wang, M.; Wu, Z.; Yang, F.; Ma, Y.; Wang, X.H.; Zhao, D. Multifeature extraction and seafloor classification combining LiDAR and MBES data around Yuanzhi Island in the South China Sea. Sensors 2018, 18, 3828. [Google Scholar] [CrossRef]
- Picard, K.; Brooke, B.P.; Harris, P.T.; Siwabessy, P.J.; Coffin, M.F.; Tran, M.; Spinoccia, M.; Weales, J.; Macmillan-Lawler, M.; Sullivan, J. Malaysia Airlines flight MH370 search data reveal geomorphology and seafloor processes in the remote southeast Indian Ocean. Mar. Geol. 2018, 395, 301–319. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation—GEBCO seabed 2030 project: The quest to see the world’s oceans completely mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef]
- Schaffer, J.; Timmermann, R.; Arndt, J.E.; Kristensen, S.S.; Mayer, C.; Morlighem, M.; Steinhage, D. A global, high-resolution data set of ice sheet topography, cavity geometry, and ocean bathymetry. Earth Syst. Sci. Data 2016, 8, 543–557. [Google Scholar] [CrossRef]
- Ramillien, G.; Cazenave, A. Global bathymetry derived from altimeter data of the ERS-1 geodetic mission. J. Geodyn. 1997, 23, 129–149. [Google Scholar] [CrossRef]
- Briggs, I.C. Machine contouring using minimum curvature. Geophysics 1974, 39, 39–48. [Google Scholar] [CrossRef]
- Smith, W.H.; Wessel, P. Gridding with continuous curvature splines in tension. Geophysics 1990, 55, 293–305. [Google Scholar] [CrossRef]
- Glenn, J.; Tonina, D.; Morehead, M.D.; Fiedler, F.; Benjankar, R. Effect of transect location, transect spacing and interpolation methods on river bathymetry accuracy. Earth Surf. Process. Landforms 2016, 41, 1185–1198. [Google Scholar] [CrossRef]
- Merwade, V. Effect of spatial trends on interpolation of river bathymetry. J. Hydrol. 2009, 371, 169–181. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Y.; Wilson, J.P.; Zhou, A.; Chen, Y.; Su, H. An Enhanced Residual Feature Fusion Network Integrated with a Terrain Weight Module for Digital Elevation Model Super-Resolution. Remote Sens. 2023, 15, 1038. [Google Scholar] [CrossRef]
- Habib, M. Evaluation of DEM interpolation techniques for characterizing terrain roughness. Catena 2021, 198, 105072. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the ECCV: 13th European Conference, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.H.; Liao, Q. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Xu, Z.; Hou, W. Convolutional neural network based dem super resolution. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2016, 41, 247–250. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, C.; Van Den Hengel, A. Wider or deeper: Revisiting the resnet model for visual recognition. Pattern Recognit. 2019, 90, 119–133. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Z.; Yi, W.; Gui, Q.; Hou, W.; Ding, M. Deep gradient prior network for DEM super-resolution: Transfer learning from image to DEM. ISPRS J. Photogramm. Remote Sens. 2019, 150, 80–90. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Husz’ar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, W. Comparison of DEM Super-Resolution Methods Based on Interpolation and Neural Networks. Sensors 2022, 22, 745. [Google Scholar] [CrossRef]
- Zhou, A.; Chen, Y.; Wilson, J.P.; Su, H.; Xiong, Z.; Cheng, Q. An Enhanced double-filter deep residual neural network for generating super resolution DEMs. Remote Sens. 2021, 13, 3089. [Google Scholar] [CrossRef]
- Zhang, B.; Xiong, W.; Ma, M.; Wang, M.; Wang, D.; Huang, X.; Yu, L.; Zhang, Q.; Lu, H.; Hong, D. Super-resolution reconstruction of a 3 arc-second global DEM dataset. Sci. Bull. 2022, 67, 2526–2530. [Google Scholar] [CrossRef]
- Zhou, A.; Chen, Y.; Wilson, J.P.; Chen, G.; Min, W.; Xu, R. A multi-terrain feature-based deep convolutional neural network for constructing super-resolution DEMs. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103338. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiong, L.; Huang, X.; Li, S.; Shen, W. Super-resolution for terrain modeling using deep learning in high mountain Asia. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103296. [Google Scholar] [CrossRef]
- Yutani, T.; Yono, O.; Kuwatani, T.; Matsuoka, D.; Kaneko, J.; Hidaka, M.; Kasaya, T.; Kido, Y.; Ishikawa, Y.; Ueki, T. Super-Resolution and Feature Extraction for Ocean Bathymetric Maps Using Sparse Coding. Sensors 2022, 22, 3198. [Google Scholar] [CrossRef] [PubMed]
- Hidaka, M.; Matsuoka, D.; Kuwatani, T.; Kaneko, J.; Kasaya, T.; Kido, Y.; Ishikawa, Y.; Kikawa, E. Super-resolution for Ocean Bathymetric Maps Using Deep Learning Approaches: A Comparison and Validation. Geoinformatics 2021, 32, 3–13. (In Japanese) [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, W.; Zhu, D. Terrain feature-aware deep learning network for digital elevation model superresolution. ISPRS J. Photogramm. Remote Sens. 2022, 189, 143–162. [Google Scholar] [CrossRef]
- Lu, Z.; Li, J.; Liu, H.; Huang, C.; Zhang, L.; Zeng, T. Transformer for single image super-resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2022; pp. 457–466. [Google Scholar] [CrossRef]
- Zheng, X.; Bao, Z.; Yin, Q. Terrain Self-Similarity-Based Transformer for Generating Super Resolution DEMs. Remote Sens. 2023, 15, 1954. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very DeeConvolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and PatternRecognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar] [CrossRef]
- Zhu, X.; Hu, H.; Lin, S.; Dai, J. Deformable convnets v2: More deformable, better results. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9308–9316. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Han, D. Comparison of Commonly Used Image Interpolation Methods. In Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering (ICCSEE 2013), Hangzhou, China, 22–23 March 2013; pp. 1556–1559. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018; pp. 63–79. [Google Scholar]
- Zhang, W.; Liu, Y.; Dong, C.; Qiao, Y. Ranksrgan: Generative adversarial networks with ranker for image super-resolution. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3096–3105. [Google Scholar] [CrossRef]


| Method | RMSE (m) | MAE (m) | Emax (m) |
|---|---|---|---|
| Bicubic | 15.85 | 8.08 | 295.80 |
| SRCNN | 14.78 | 7.26 | 293.48 |
| SRGAN | 15.27 | 7.87 | 306.98 |
| SRResNet | 15.13 | 7.89 | 300.07 |
| STFET | 13.30 | 6.88 | 262.05 |
| Area | Method | RMSE (m) | MAE (m) | Emax (m) |
|---|---|---|---|---|
| 1 | Bicubic | 32.26 | 24.90 | 157.34 |
| SRCNN | 31.69 | 24.72 | 201.30 | |
| SRGAN | 15.11 | 11.03 | 175.39 | |
| SRResNet | 21.40 | 16.25 | 140.28 | |
| STFET | 11.98 | 8.41 | 198.65 | |
| 2 | Bicubic | 17.58 | 9.78 | 494.95 |
| SRCNN | 17.26 | 9.73 | 483.92 | |
| SRGAN | 14.49 | 7.44 | 484.46 | |
| SRResNet | 14.69 | 7.87 | 492.02 | |
| STFET | 12.57 | 6.12 | 491.90 | |
| 3 | Bicubic | 30.08 | 17.66 | 189.57 |
| SRCNN | 29.77 | 18.04 | 196.98 | |
| SRGAN | 12.44 | 9.27 | 136.85 | |
| SRResNet | 15.22 | 10.97 | 126.56 | |
| STFET | 10.92 | 8.18 | 125.52 | |
| 4 | Bicubic | 27.10 | 14.30 | 314.91 |
| SRCNN | 26.42 | 14.63 | 295.98 | |
| SRGAN | 13.99 | 7.94 | 357.04 | |
| SRResNet | 16.69 | 9.50 | 310.11 | |
| STFET | 12.84 | 6.99 | 360.42 | |
| 5 | Bicubic | 16.63 | 6.42 | 268.70 |
| SRCNN | 15.63 | 5.05 | 279.80 | |
| SRGAN | 14.16 | 5.45 | 259.50 | |
| SRResNet | 12.93 | 5.27 | 207.15 | |
| STFET | 11.29 | 4.58 | 194.97 |
| Method | Number (Error < 25 m) | Number (25 m < Error < 100 m) | Number (100 m < Error < 200 m | Number (Error > 200 m |
|---|---|---|---|---|
| Bicubic | 61,711 | 19,390 | 793 | 26 |
| SRCNN | 61,378 | 19,876 | 642 | 24 |
| SRGAN | 77,494 | 4344 | 60 | 22 |
| SRResNet | 71,029 | 10,704 | 163 | 24 |
| StfeT | 78,893 | 2949 | 56 | 22 |
| Method | RMSE (m) | MAE (m) | Emax (m) |
|---|---|---|---|
| SRResNet | 15.13 | 7.89 | 300.07 |
| SRResNet-dconv | 15.10 | 7.70 | 322.98 |
| SRResNet-ET | 15.01 | 7.70 | 319.30 |
| STFET | 13.30 | 6.88 | 262.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, W.; Liu, Y.; Chen, Y.; Dong, Z.; Yuan, H.; Li, N. A Seabed Terrain Feature Extraction Transformer for the Super-Resolution of the Digital Bathymetric Model. Remote Sens. 2023, 15, 4906. https://doi.org/10.3390/rs15204906
Cai W, Liu Y, Chen Y, Dong Z, Yuan H, Li N. A Seabed Terrain Feature Extraction Transformer for the Super-Resolution of the Digital Bathymetric Model. Remote Sensing. 2023; 15(20):4906. https://doi.org/10.3390/rs15204906
Chicago/Turabian StyleCai, Wuxu, Yanxiong Liu, Yilan Chen, Zhipeng Dong, Hanxiao Yuan, and Ningning Li. 2023. "A Seabed Terrain Feature Extraction Transformer for the Super-Resolution of the Digital Bathymetric Model" Remote Sensing 15, no. 20: 4906. https://doi.org/10.3390/rs15204906
APA StyleCai, W., Liu, Y., Chen, Y., Dong, Z., Yuan, H., & Li, N. (2023). A Seabed Terrain Feature Extraction Transformer for the Super-Resolution of the Digital Bathymetric Model. Remote Sensing, 15(20), 4906. https://doi.org/10.3390/rs15204906






