PM2.5 Estimation in Day/Night-Time from Himawari-8 Infrared Bands via a Deep Learning Neural Network
Abstract
:1. Introduction
1.1. Satellite Data
1.2. Ground-Based PM2.5 Concentration Measurements
- Missing values in a site record lasting three hours or less are infilled by linear interpolation to help reduce the noise;
- Repeated values that last for more than four consecutive hours and implausible zeros are removed;
- Values beyond the concurrent PM10 measurements in a site are removed;
- Regional consistency checks are performed by comparing sites with their neighboring sites to remove outliers.
1.3. Meteorological Variables
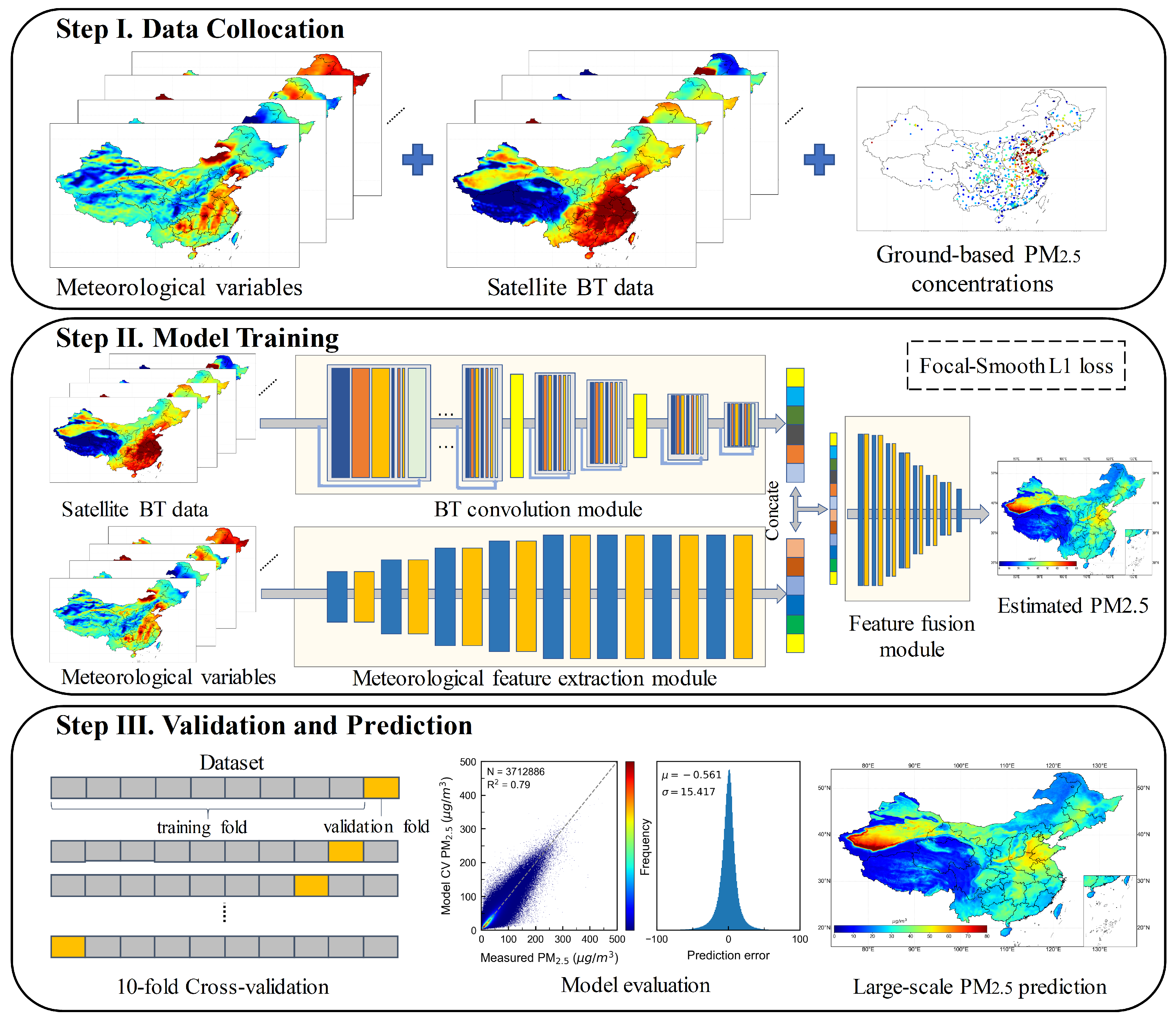
2. Methodology
2.1. Network Architecture
2.2. Loss Function
2.3. Model Training and Evaluation
3. Results
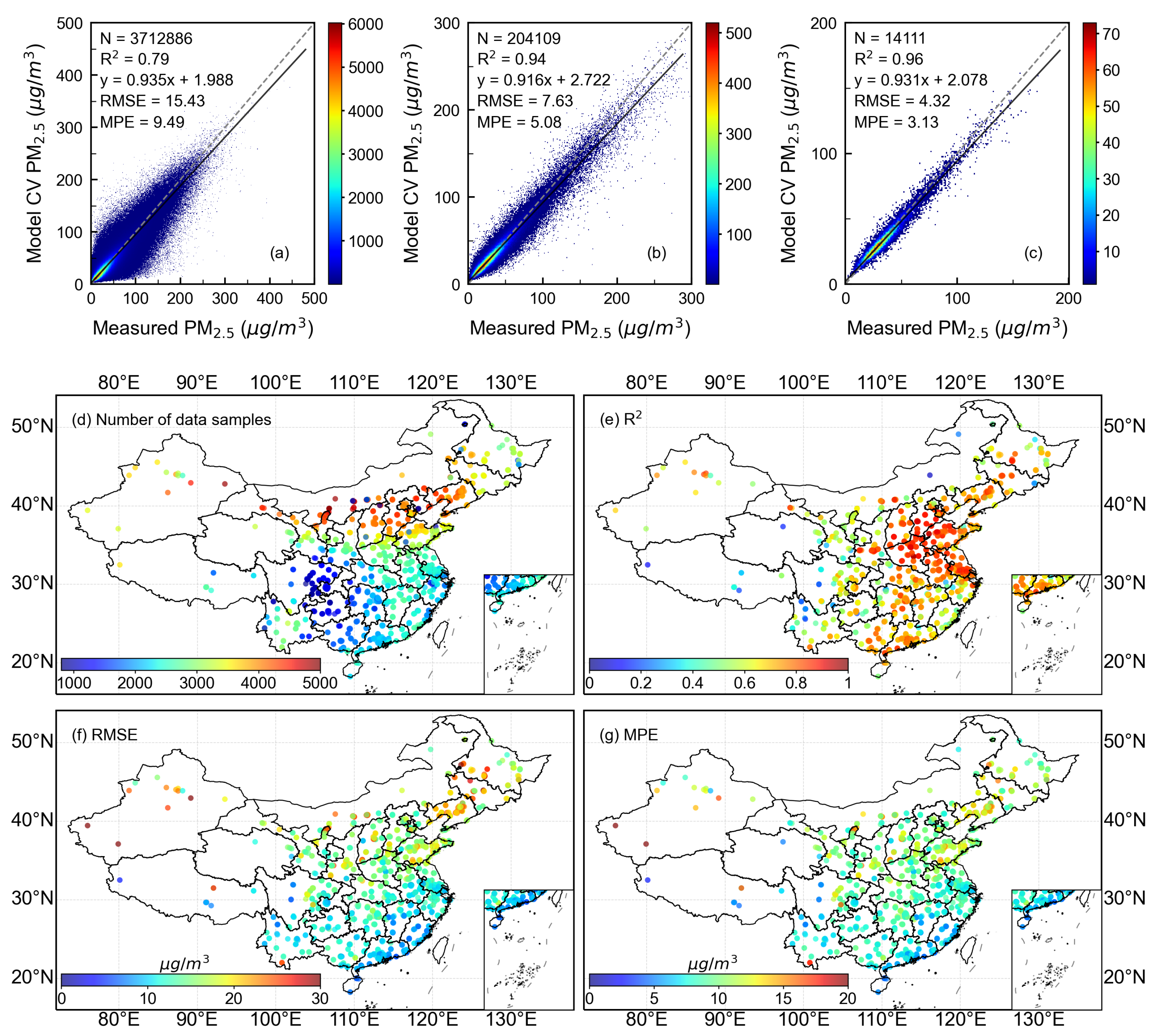
3.1. Cross-Validation Results
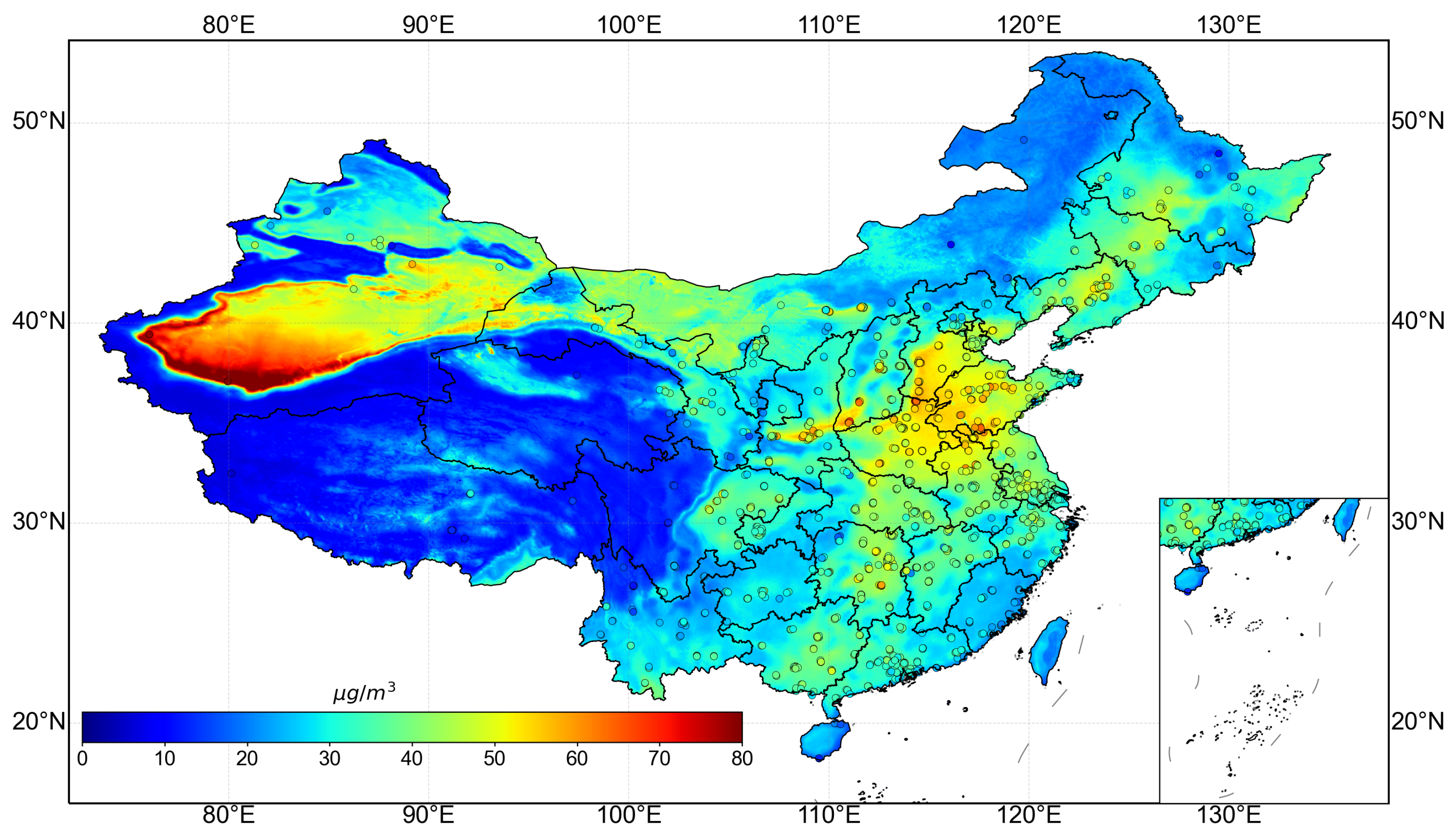
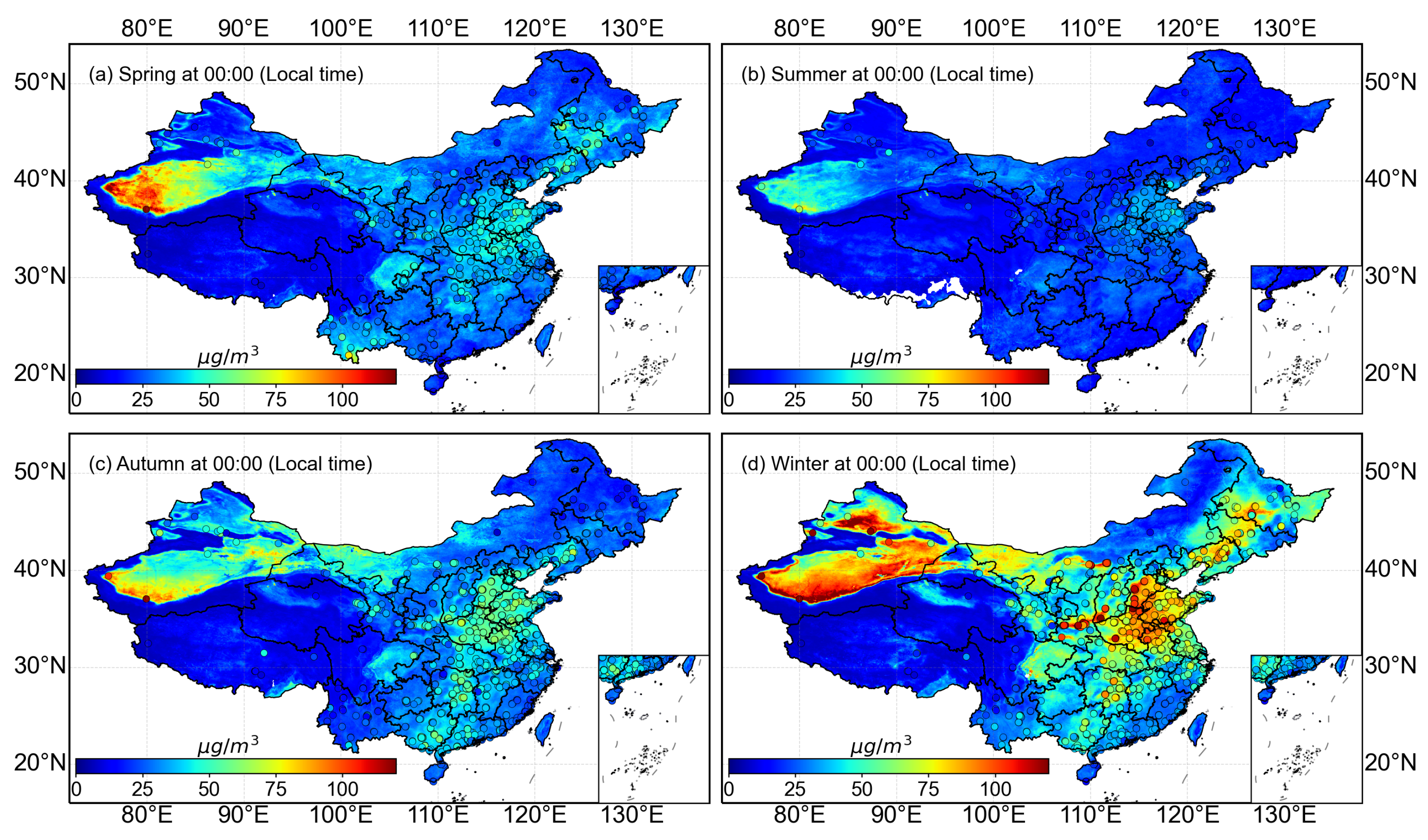
3.2. Spatiotemporal Distribution of Model-Estimated Results in China
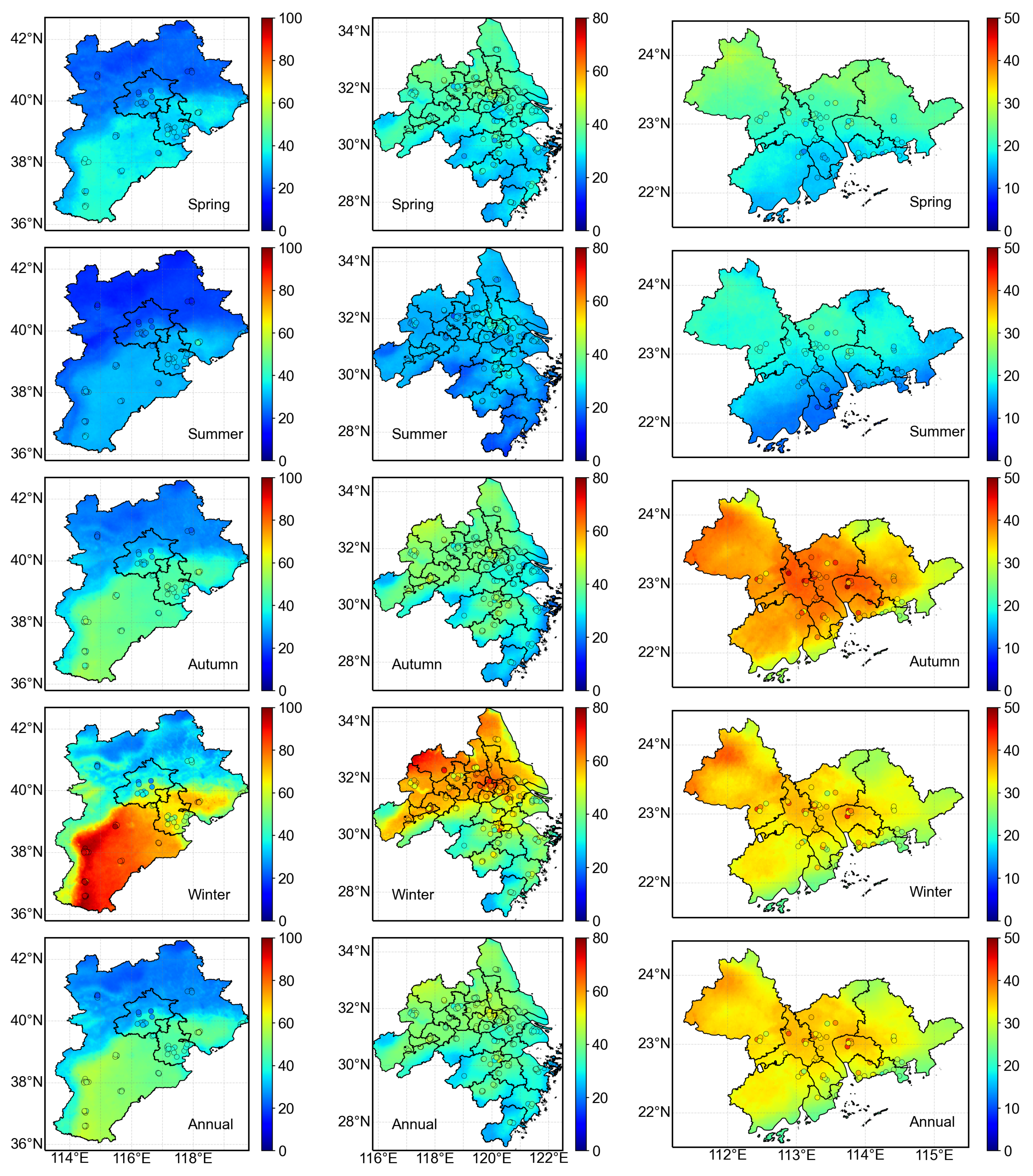
3.3. Results of Typical Regions in China
3.4. Nighttime Results across China
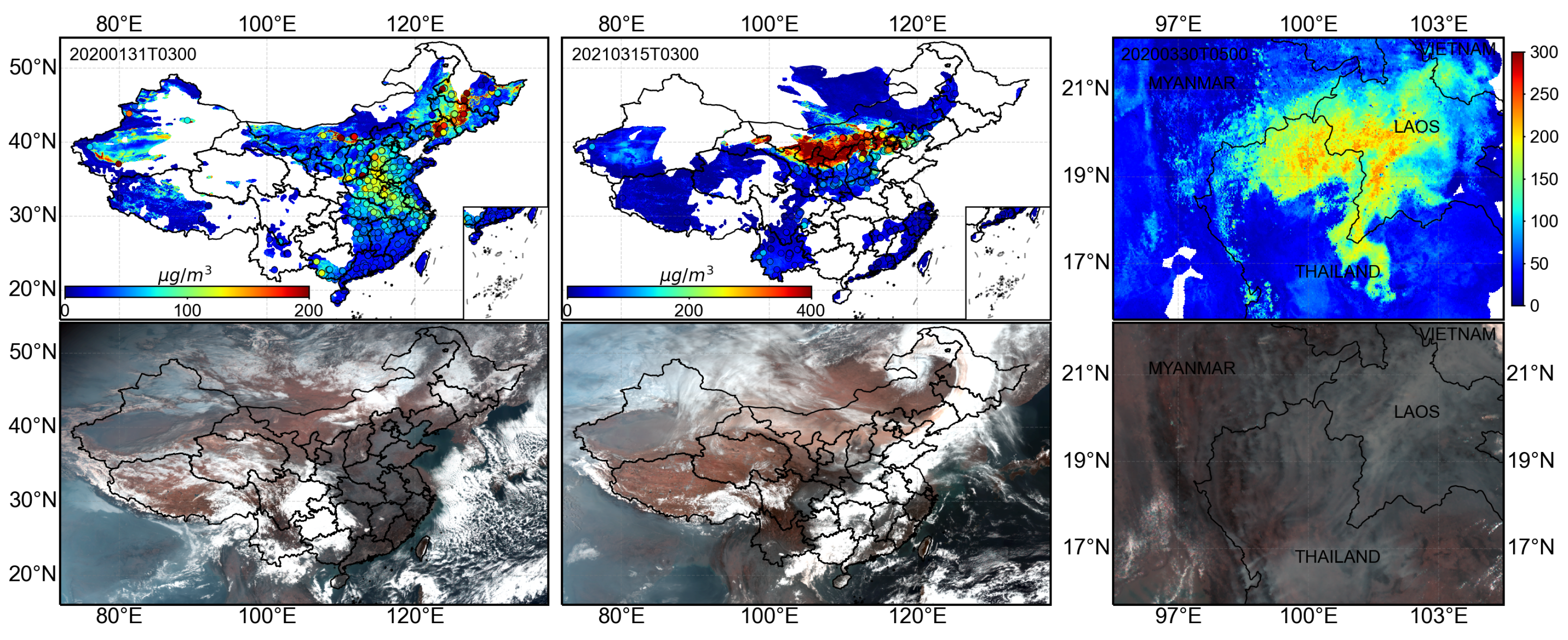
3.5. Typical Test Cases
3.6. Comparison with Other Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-based spatiotemporal trends in PM2.5 concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Dey, S.; Purohit, B.; Balyan, P.; Dixit, K.; Bali, K.; Kumar, A.; Imam, F.; Chowdhury, S.; Ganguly, D.; Gargava, P.; et al. A satellite-based high-resolution (1-km) ambient PM2.5 database for India over two decades (2000–2019): Applications for air quality management. Remote Sens. 2020, 12, 3872. [Google Scholar] [CrossRef]
- Semlali, B.E.B.; El Amrani, C.; Ortiz, G.; Boubeta-Puig, J.; Garcia-de Prado, A. SAT-CEP-monitor: An air quality monitoring software architecture combining complex event processing with satellite remote sensing. Comput. Electr. Eng. 2021, 93, 107257. [Google Scholar] [CrossRef]
- Wang, J.; Christopher, S.A. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30, 2095. [Google Scholar] [CrossRef]
- Koelemeijer, R.; Homan, C.; Matthijsen, J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe. Atmos. Environ. 2006, 40, 5304–5315. [Google Scholar] [CrossRef]
- Lin, C.; Li, Y.; Yuan, Z.; Lau, A.K.; Li, C.; Fung, J.C. Using satellite remote sensing data to estimate the high-resolution distribution of ground-level PM2.5. Remote Sens. Environ. 2015, 156, 117–128. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Liu, Y.; Park, R.J.; Jacob, D.J.; Li, Q.; Kilaru, V.; Sarnat, J.A. Mapping annual mean ground-level PM2.5 concentrations using Multiangle Imaging Spectroradiometer aerosol optical thickness over the contiguous United States. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar]
- van Donkelaar, A.; Martin, R.V.; Spurr, R.J.; Drury, E.; Remer, L.A.; Levy, R.C.; Wang, J. Optimal estimation for global ground-level fine particulate matter concentrations. J. Geophys. Res. Atmos. 2013, 118, 5621–5636. [Google Scholar] [CrossRef]
- Geng, G.; Zhang, Q.; Martin, R.V.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Liu, Y.; Franklin, M.; Kahn, R.; Koutrakis, P. Using aerosol optical thickness to predict ground-level PM2.5 concentrations in the St. Louis area: A comparison between MISR and MODIS. Remote Sens. Environ. 2007, 107, 33–44. [Google Scholar] [CrossRef]
- Sorek-Hamer, M.; Strawa, A.; Chatfield, R.; Esswein, R.; Cohen, A.; Broday, D. Improved retrieval of PM2.5 from satellite data products using non-linear methods. Environ. Pollut. 2013, 182, 417–423. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G., Jr.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern US using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in China using satellite remote sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
- Song, W.; Jia, H.; Huang, J.; Zhang, Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Lee, H.; Liu, Y.; Coull, B.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Zhao, Q.; Liu, M.; Zhou, Y.; Bi, J. Satellite-derived high resolution PM2.5 concentrations in Yangtze River Delta Region of China using improved linear mixed effects model. Atmos. Environ. 2016, 133, 156–164. [Google Scholar] [CrossRef]
- Guo, Y.; Tang, Q.; Gong, D.Y.; Zhang, Z. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model. Remote Sens. Environ. 2017, 198, 140–149. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.; Lyapustin, A.; Wang, Y.; Liu, Y. 10-year spatial and temporal trends of PM2.5 concentrations in the southeastern US estimated using high-resolution satellite data. Atmos. Chem. Phys. 2014, 14, 6301–6314. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Chang, H.H.; Geng, G.; Liu, Y. An ensemble machine-learning model to predict historical PM2.5 concentrations in China from satellite data. Environ. Sci. Technol. 2018, 52, 13260–13269. [Google Scholar] [CrossRef] [PubMed]
- Xue, T.; Zheng, Y.; Tong, D.; Zheng, B.; Li, X.; Zhu, T.; Zhang, Q. Spatiotemporal continuous estimates of PM2.5 concentrations in China, 2000–2016: A machine learning method with inputs from satellites, chemical transport model, and ground observations. Environ. Int. 2019, 123, 345–357. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, R.; Liu, Y.; Bi, J. Effects of air pollution control policies on PM2.5 pollution improvement in China from 2005 to 2017: A satellite-based perspective. Atmos. Chem. Phys. 2019, 19, 6861–6877. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Lei, C.; Xu, X.; Ma, Y.; Jin, S.; Liu, B.; Gong, W. Full Coverage Estimation of the PM Concentration Across China Based on an Adaptive Spatiotemporal Approach. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating ground-level PM2.5 by fusing satellite and station observations: A geo-intelligent deep learning approach. Geophys. Res. Lett. 2017, 44, 11–985. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: 2. A neural network approach. J. Geophys. Res. Atmos. 2009, 114, D011497. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Wang, Y.; Zhang, L.; Yi, Z.; Zhang, H.; Mathiopoulos, P.T. A Spatiotemporal Interpolation Graph Convolutional Network for Estimating PM2.5 Concentrations Based on Urban Functional Zones. IEEE Trans. Geosci. Remote. Sens. 2022, 61, 1–14. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Sun, L.; Peng, Y.; Zhang, Z.; Li, Z.; Su, T.; Feng, L.; Cai, Z.; Wu, H. Evaluation and uncertainty estimate of next-generation geostationary meteorological Himawari-8/AHI aerosol products. Sci. Total Environ. 2019, 692, 879–891. [Google Scholar] [CrossRef]
- Liu, J.; Weng, F.; Li, Z. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]
- Xie, Y.; Zhao, B.; Zhang, L.; Luo, R. Spatiotemporal variations of PM2.5 and PM10 concentrations between 31 Chinese cities and their relationships with SO2, NO2, CO and O3. Particuology 2015, 20, 141–149. [Google Scholar] [CrossRef]
- Mao, F.; Hong, J.; Min, Q.; Gong, W.; Zang, L.; Yin, J. Estimating hourly full-coverage PM2.5 over China based on TOA reflectance data from the Fengyun-4A satellite. Environ. Pollut. 2021, 270, 116119. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Liu, D.; Tang, Y.; Seyler, B.C.; Deng, X.; Zhan, Y. Comparison of GOCI and Himawari-8 aerosol optical depth for deriving full-coverage hourly PM2.5 across the Yangtze River Delta. Atmos. Environ. 2019, 217, 116973. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Liu, D.; Tang, Y.; Seyler, B.C.; Zhou, Z.; Hu, X.; Yang, F.; Zhan, Y. Deriving hourly full-coverage PM2.5 concentrations across China’s Sichuan Basin by fusing multisource satellite retrievals: A machine-learning approach. Atmos. Environ. 2022, 271, 118930. [Google Scholar] [CrossRef]
- Wang, J.; Aegerter, C.; Xu, X.; Szykman, J.J. Potential application of VIIRS Day/Night Band for monitoring nighttime surface PM2.5 air quality from space. Atmos. Environ. 2016, 124, 55–63. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, H.; Yu, H.; Yang, P. Inversion of nighttime PM2.5 mass concentration in Beijing based on the VIIRS day-night band. Atmosphere 2016, 7, 136. [Google Scholar] [CrossRef]
- Fu, D.; Xia, X.; Duan, M.; Zhang, X.; Li, X.; Wang, J.; Liu, J. Mapping nighttime PM2.5 from VIIRS DNB using a linear mixed-effect model. Atmos. Environ. 2018, 178, 214–222. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Li, W.; Liu, K. Evaluating the use of DMSP/OLS nighttime light imagery in predicting PM2.5 concentrations in the northeastern United States. Remote Sens. 2017, 9, 620. [Google Scholar] [CrossRef]
- Ji, G.; Tian, L.; Zhao, J.; Yue, Y.; Wang, Z. Detecting spatiotemporal dynamics of PM2.5 emission data in China using DMSP-OLS nighttime stable light data. J. Clean. Prod. 2019, 209, 363–370. [Google Scholar] [CrossRef]
- Zhang, G.; Shi, Y.; Xu, M. Evaluation of LJ1-01 nighttime light imagery for estimating monthly PM2.5 concentration: A comparison with NPP-VIIRS nighttime light data. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 3618–3632. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.; Huang, B.; Li, S.; Lin, Y. Estimation and analysis of the nighttime PM2.5 concentration based on lj1-01 images: A case study in the pearl river delta urban agglomeration of china. Remote Sens. 2021, 13, 3405. [Google Scholar] [CrossRef]
- Johnson, T.J.; Sams, R.L.; Sharpe, S.W. The PNNL Quantitative Infrared Database for Gas-Phase Sensing: A Spectral Library for Environmental, Hazmat, and Public Safety Standoff Detection. In Proceedings of the Chemical and Biological Point Sensors for Homeland Defense, International Society for Optics and Photonics, 8 March 2004; Volume 5269, pp. 159–167. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/5269/1/The-PNNL-quantitative-infrared-database-for-gas-phase-sensing/10.1117/12.515604.short (accessed on 4 October 2023).
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.; Skinner, F.; Conway, E.; Hill, C.; Kochanov, R.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Ishikawa, H.; Oku, Y.; Hu, Z. An algorithm for land surface temperature retrieval using three thermal infrared bands of Himawari-8. J. Meteorol. Soc. Jpn. Ser. II 2018, 96B, 59–76. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. Atmos. 2009, 114, D011496. [Google Scholar] [CrossRef]
- Liu, Y. New Directions: Satellite driven PM2.5 exposure models to support targeted particle pollution health effects research. Atmos. Environ. 2013, 68, 52–53. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.bd0915c6 (accessed on 4 October 2023).
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-based ground PM2.5 estimation using timely structure adaptive modeling. Remote Sens. Environ. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Wang, W. Estimating national-scale ground-level PM25 concentration in China using geographically weighted regression based on MODIS and MISR AOD. Environ. Sci. Pollut. Res. 2016, 23, 8327–8338. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Mao, F.; Zang, L.; Chen, J.; Lu, X.; Hong, J. Retrieving PM2.5 with high spatio-temporal coverage by TOA reflectance of Himawari-8. Atmos. Pollut. Res. 2021, 12, 14–20. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, f. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]

| No. | Layer | Arguments | |
|---|---|---|---|
| 1 | TemporalBlock | in: 10, out: 32 | |
| 1: weight_norm(Conv1d) | k3s1n32 | ||
| 2: BatchNorm1d | 32 | ||
| 3: PReLU | / | ||
| 4: weight_norm(Conv1d) | k3s1n32 | ||
| 5: BatchNorm1d | 32 | ||
| 6: PReLU | / | ||
| Elementwise Sum to (1) | |||
| 7: PReLU | / | ||
| 2 | TemporalBlock | in: 32, out: 32 | |
| 3 | TemporalBlock | in: 32, out: 64 | |
| 4 | TemporalBlock | in: 64, out: 64 | |
| 5 | TemporalBlock | in: 64, out: 128 | |
| 6 | TemporalBlock | in: 128, out: 128 | |
| 7 | TemporalBlock | in: 128, out: 256 | |
| 8 | MaxPool1d | k2s1 | |
| 9 | TemporalBlock | in: 256, out: 128 | |
| 10 | TemporalBlock | in: 128, out: 128 | |
| 8 | MaxPool1d | k2s1 | |
| 9 | TemporalBlock | in: 128, out: 128 | |
| 10 | TemporalBlock | in: 128, out: 128 | |
| No. | Layer | Arguments |
|---|---|---|
| 1 | Linear | in: 10, out: 32 |
| 2 | PReLU | / |
| 3 | Linear | in: 32, out: 32 |
| 4 | PReLU | / |
| 5 | Linear | in: 32, out: 64 |
| 6 | PReLU | / |
| 7 | Linear | in: 64, out: 128 |
| 8 | PReLU | / |
| 9 | Linear | in: 128, out: 256 |
| 10 | PReLU | / |
| No. | Layer | Arguments |
|---|---|---|
| 1 | Linear | in: 512, out: 512 |
| 2 | PReLU | / |
| 3 | Linear | in: 512, out: 512 |
| 4 | PReLU | / |
| 5 | Linear | in: 512, out: 256 |
| 6 | PReLU | / |
| 7 | Linear | in: 256, out: 128 |
| 8 | PReLU | / |
| 9 | Linear | in: 128, out: 64 |
| 10 | PReLU | / |
| 11 | Linear | in: 64, out: 32 |
| 12 | PReLU | / |
| 13 | Linear | in: 32, out: 16 |
| 14 | PReLU | / |
| 15 | Linear | in: 16, out: 1 |
| Time Scale | N | R2 | RMSE | MPE | Estimated PM2.5 (Mean ± Std) | Observed PM2.5 (Mean ± Std) |
|---|---|---|---|---|---|---|
| hourly | 3,712,886 | 0.79 | 15.43 | 9.49 | 38.71 ± 31.68 | 39.27 ± 33.63 |
| daily | 204,109 | 0.94 | 7.63 | 5.08 | 38.44 ± 27.48 | 38.99 ± 29.91 |
| monthly | 14,111 | 0.96 | 4.32 | 3.13 | 37.41 ± 18.76 | 37.94 ± 20.11 |
| spring | 1347 | 0.86 | 3.40 | 2.53 | 31.28 ± 7.57 | 31.87 ± 8.87 |
| summer | 1344 | 0.84 | 2.88 | 2.20 | 23.09 ± 5.56 | 23.11 ± 6.90 |
| autumn | 1363 | 0.90 | 3.60 | 2.71 | 36.54 ± 9.93 | 36.88 ± 11.13 |
| winter | 1364 | 0.94 | 5.06 | 3.70 | 53.32 ± 18.69 | 54.30 ± 20.37 |
| Time (Local) | Daily | Monthly | Time (Local) | Daily | Monthly | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | R2 | RMSE | MPE | N | R2 | RMSE | MPE | N | R2 | RMSE | MPE | N | R2 | RMSE | MPE | ||
| 0:00 | 166,377 | 0.81 | 15.47 | 9.53 | 12,368 | 0.92 | 6.55 | 4.63 | 12:00 | 152,564 | 0.80 | 14.54 | 8.91 | 11,728 | 0.91 | 6.20 | 4.30 |
| 1:00 | 166,577 | 0.82 | 15.08 | 9.38 | 12,330 | 0.93 | 6.36 | 4.53 | 13:00 | 141,850 | 0.82 | 13.17 | 8.16 | 11,249 | 0.92 | 5.67 | 3.97 |
| 2:00 | 166,300 | 0.82 | 14.81 | 9.22 | 12,313 | 0.93 | 6.17 | 4.46 | 14:00 | 140,156 | 0.83 | 12.35 | 7.69 | 10,994 | 0.92 | 5.04 | 3.64 |
| 3:00 | 163,446 | 0.82 | 15.06 | 9.28 | 12,194 | 0.93 | 6.22 | 4.50 | 15:00 | 140,360 | 0.81 | 12.43 | 7.61 | 10,768 | 0.92 | 5.00 | 3.60 |
| 4:00 | 158,182 | 0.81 | 15.02 | 9.31 | 11,843 | 0.93 | 6.11 | 4.45 | 16:00 | 140,209 | 0.79 | 13.41 | 8.00 | 10,647 | 0.91 | 5.24 | 3.71 |
| 5:00 | 155,585 | 0.80 | 15.43 | 9.61 | 11,907 | 0.92 | 6.36 | 4.67 | 17:00 | 143,018 | 0.75 | 15.04 | 8.84 | 10,893 | 0.89 | 6.24 | 4.21 |
| 6:00 | 150,552 | 0.77 | 16.24 | 10.09 | 11,414 | 0.90 | 6.91 | 5.00 | 18:00 | 145,908 | 0.76 | 15.34 | 9.38 | 11,157 | 0.90 | 6.30 | 4.46 |
| 7:00 | 147,568 | 0.75 | 16.67 | 10.59 | 11,223 | 0.89 | 7.11 | 5.17 | 19:00 | 153,659 | 0.78 | 15.54 | 9.67 | 11,848 | 0.90 | 6.63 | 4.71 |
| 8:00 | 155,714 | 0.73 | 17.48 | 10.96 | 11,755 | 0.88 | 7.44 | 5.37 | 20:00 | 155,622 | 0.79 | 15.96 | 9.92 | 12,031 | 0.91 | 7.00 | 4.93 |
| 9:00 | 159,155 | 0.74 | 17.68 | 11.03 | 11,938 | 0.89 | 7.53 | 5.34 | 21:00 | 159,746 | 0.79 | 16.36 | 10.07 | 12,195 | 0.91 | 7.07 | 4.96 |
| 10:00 | 161,732 | 0.76 | 16.87 | 10.41 | 12,105 | 0.90 | 7.22 | 5.07 | 22:00 | 164,020 | 0.79 | 16.50 | 10.09 | 12,381 | 0.91 | 7.14 | 5.00 |
| 11:00 | 158,642 | 0.79 | 15.46 | 9.49 | 11,916 | 0.91 | 6.61 | 4.61 | 23:00 | 165,944 | 0.80 | 15.87 | 9.73 | 12,454 | 0.92 | 6.73 | 4.76 |
| Model | R2 | MSE | Data | Temporal Resolution | Spatial Resolution | Study Period |
|---|---|---|---|---|---|---|
| Geographically weighted regression [16] | 0.64 | 32.98 | AOD | daytime, daily | 10 km | 2000–2013 |
| Timely structure adaptive modeling [57] | 0.80 | 22.75 | AOD | daytime, daily | 10 km | 2013–2014 |
| Generalized regression neural network [58] | 0.67 | 20.93 | AOD | daytime, daily | 3 km | 2013–2014 |
| Geographically weighted regression [59] | 0.79 | 18.6 | AOD | daytime, daily | 3 km | 2014 |
| Deep belief network [29] | 0.88 | 13.03 | AOD | daytime, daily | 3 km | 2015 |
| Space-time random forest [27] | 0.85 | 15.57 | AOD | daytime, daily | 1 km | 2016 |
| Random forest [34] | 0.86 | 16.8 | TOAR | daytime, hourly | 5 km | 2016 |
| Efficient gradient boosting decision tree [60] | 0.86 | 16.9 | TOAR | daytime, hourly | 5 km | 2016 |
| Deep neural network(ours) | 0.79 | 15.43 | BT | full-time, hourly | 2 km | 2019–2020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Gao, K.; Hu, X.; Zhang, X.; Wang, H.; Hu, Z.; Yang, Z.; Zhang, P. PM2.5 Estimation in Day/Night-Time from Himawari-8 Infrared Bands via a Deep Learning Neural Network. Remote Sens. 2023, 15, 4905. https://doi.org/10.3390/rs15204905
Wang J, Gao K, Hu X, Zhang X, Wang H, Hu Z, Yang Z, Zhang P. PM2.5 Estimation in Day/Night-Time from Himawari-8 Infrared Bands via a Deep Learning Neural Network. Remote Sensing. 2023; 15(20):4905. https://doi.org/10.3390/rs15204905
Chicago/Turabian StyleWang, Junwei, Kun Gao, Xiuqing Hu, Xiaodian Zhang, Hong Wang, Zibo Hu, Zhijia Yang, and Peng Zhang. 2023. "PM2.5 Estimation in Day/Night-Time from Himawari-8 Infrared Bands via a Deep Learning Neural Network" Remote Sensing 15, no. 20: 4905. https://doi.org/10.3390/rs15204905
APA StyleWang, J., Gao, K., Hu, X., Zhang, X., Wang, H., Hu, Z., Yang, Z., & Zhang, P. (2023). PM2.5 Estimation in Day/Night-Time from Himawari-8 Infrared Bands via a Deep Learning Neural Network. Remote Sensing, 15(20), 4905. https://doi.org/10.3390/rs15204905






