Monitoring Shoreline Changes along the Southwestern Coast of South Africa from 1937 to 2020 Using Varied Remote Sensing Data and Approaches
Abstract
1. Introduction
2. Materials and Methods
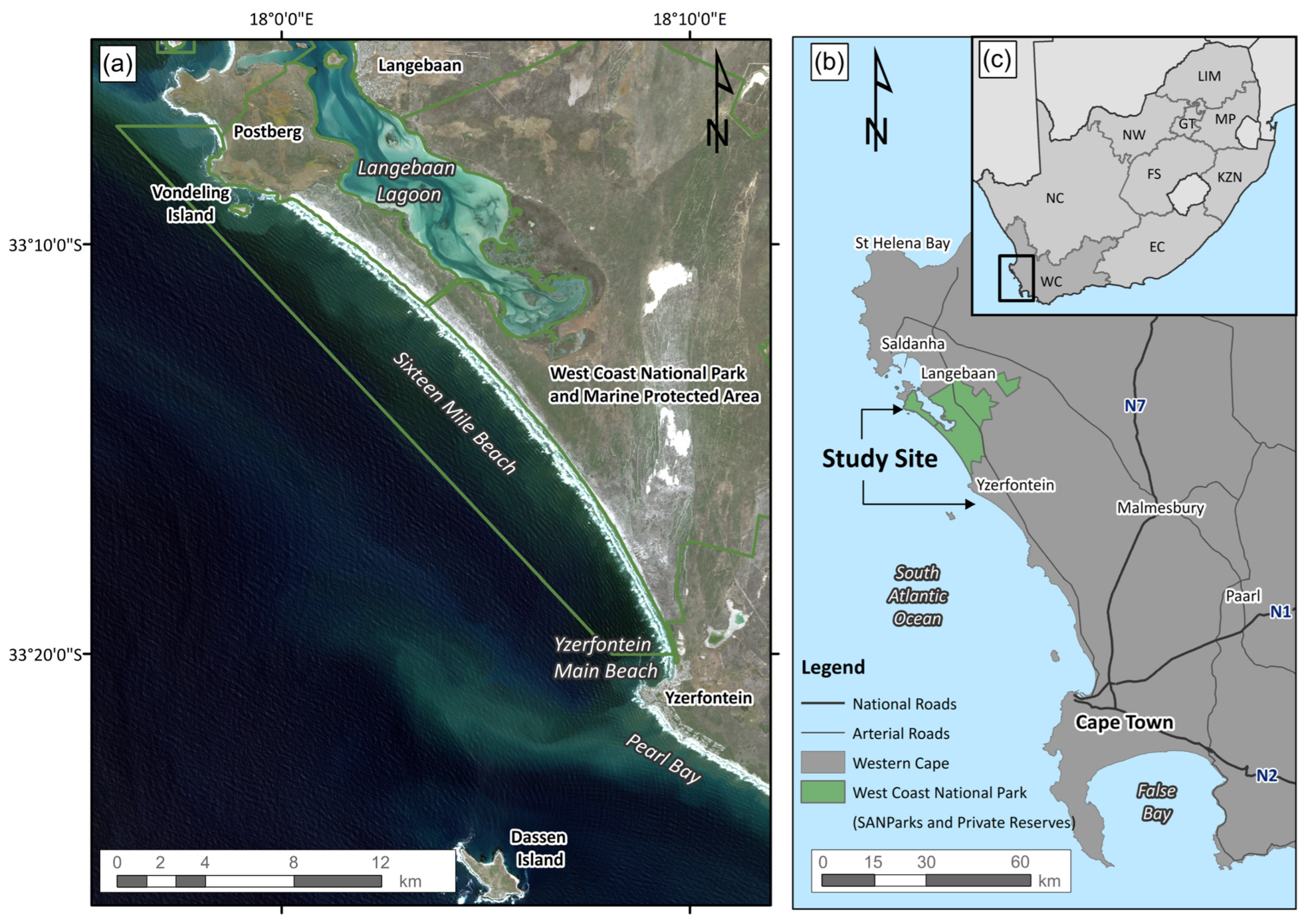
2.1. Description of the Study Site
2.1.1. Yzerfontein Main Beach
2.1.2. Pearl Bay
2.1.3. Sixteen Mile Beach
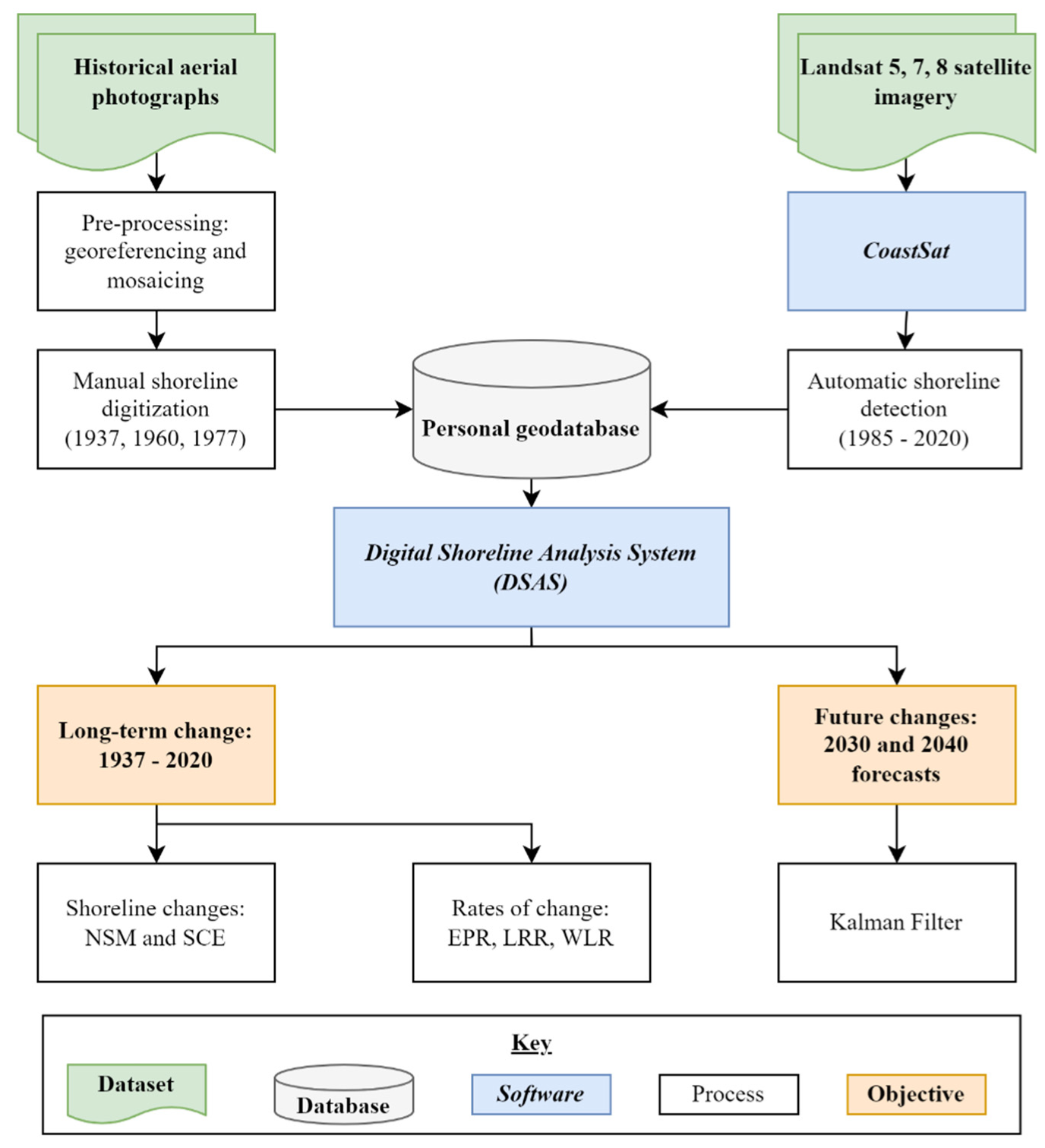
2.2. Remote Sensing Data
2.2.1. Aerial Photography
2.2.2. Landsat Imagery
2.3. Shoreline Change Detection
2.3.1. Shoreline Extraction from Aerial Photographs
2.3.2. CoastSat Shoreline Extraction
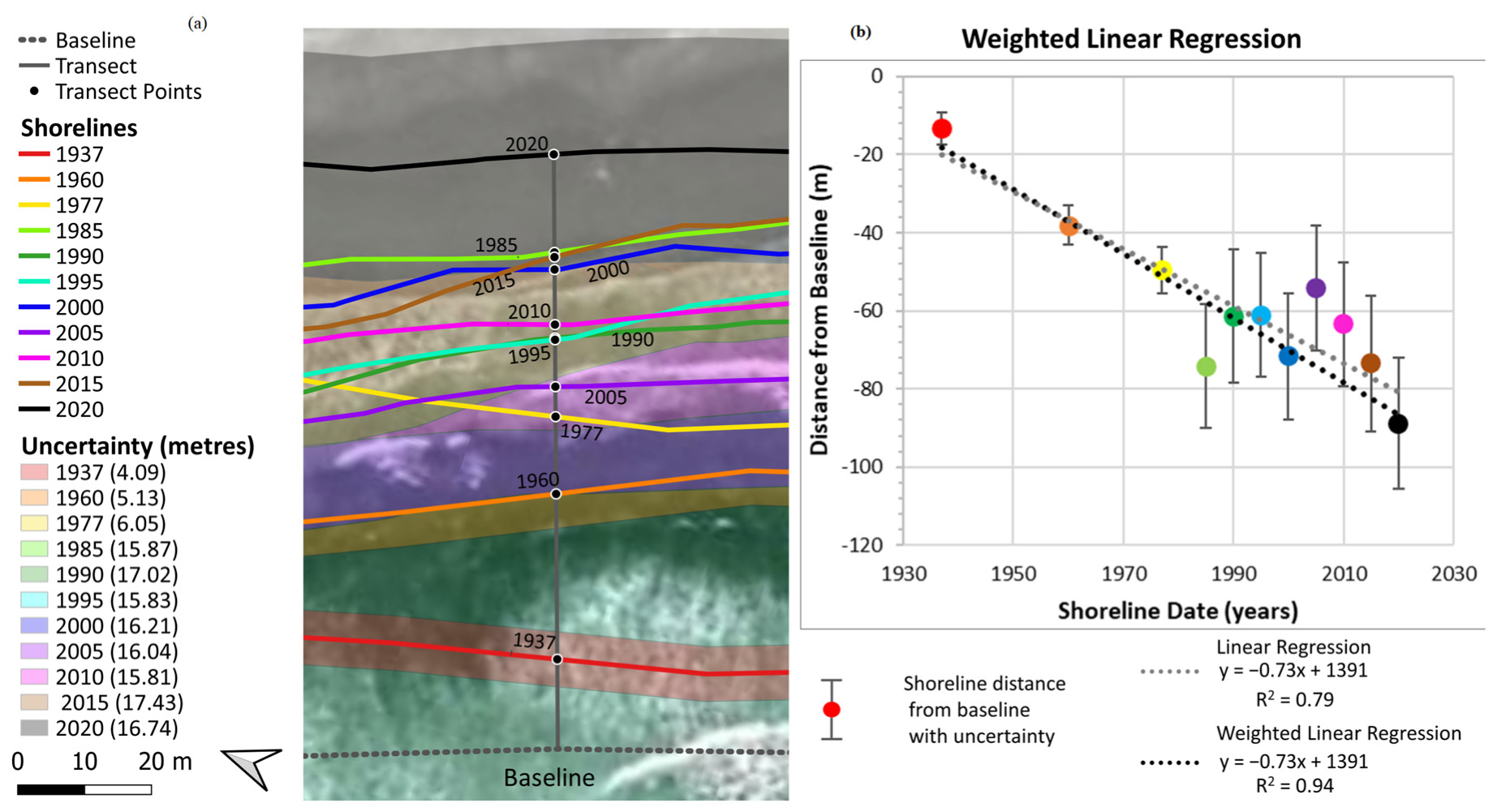
2.4. Long-Term Shoreline Change Analysis
- (a)
- Net Shoreline Movement (NSM): the horizontal distance between the oldest and the youngest shorelines;
- (b)
- Shoreline Change Envelope (SCE): a measure of the greatest horizontal change in shoreline movement irrespective of the dates;
- (c)
- End Point Rate (EPR): the distance of shoreline movement between the oldest and the youngest shoreline positions divided by the time elapsed;
- (d)
- Linear Regression Rate (LRR): an ordinary least square regression of shoreline change over time;
- (e)
- Weighted linear regression (WLR): a least square regression of the transects which considers the uncertainty of the shoreline position, with the weight equal to the inverse squared of the uncertainty [42].
2.5. Future Shoreline Forecasting
3. Results
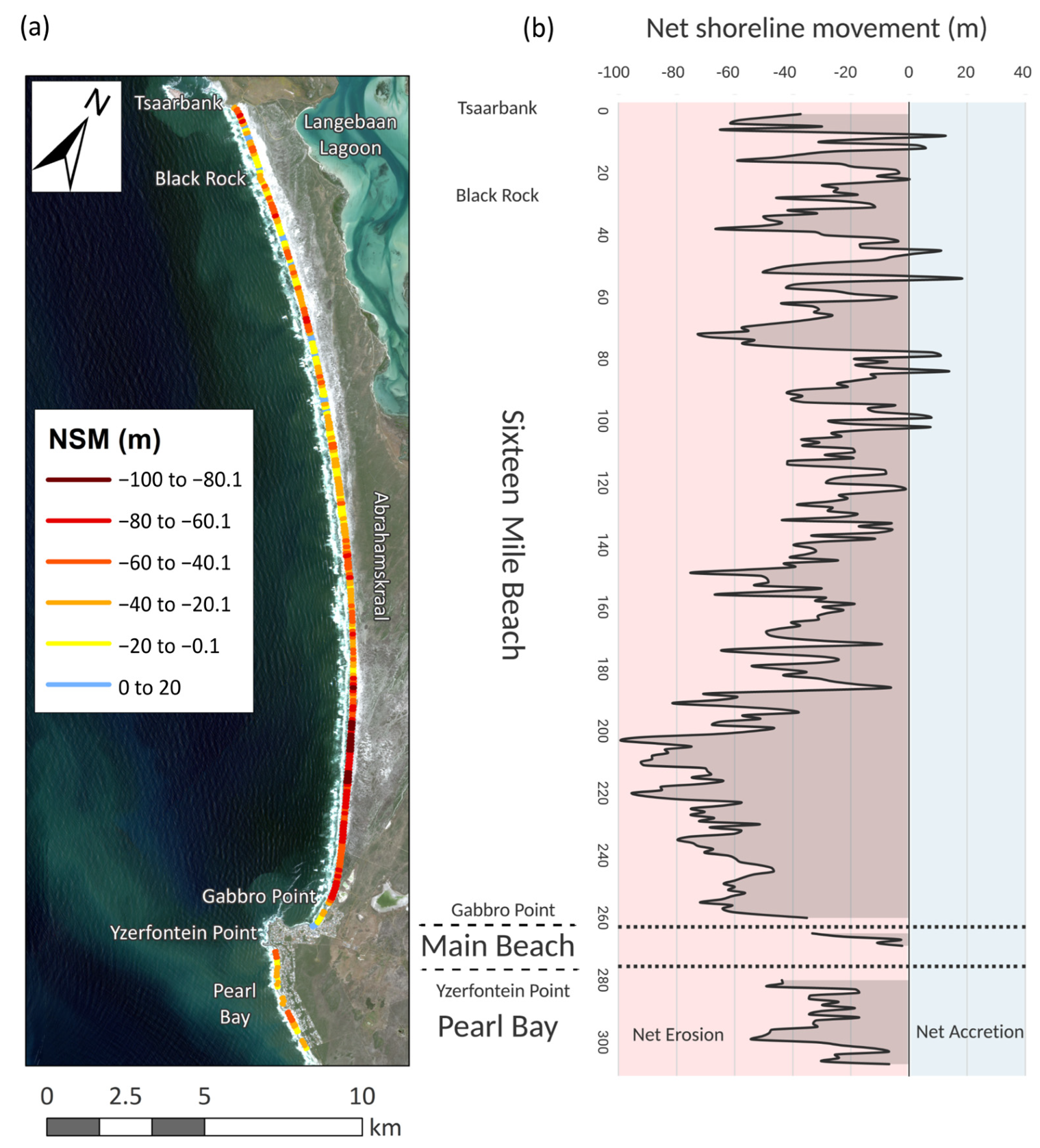
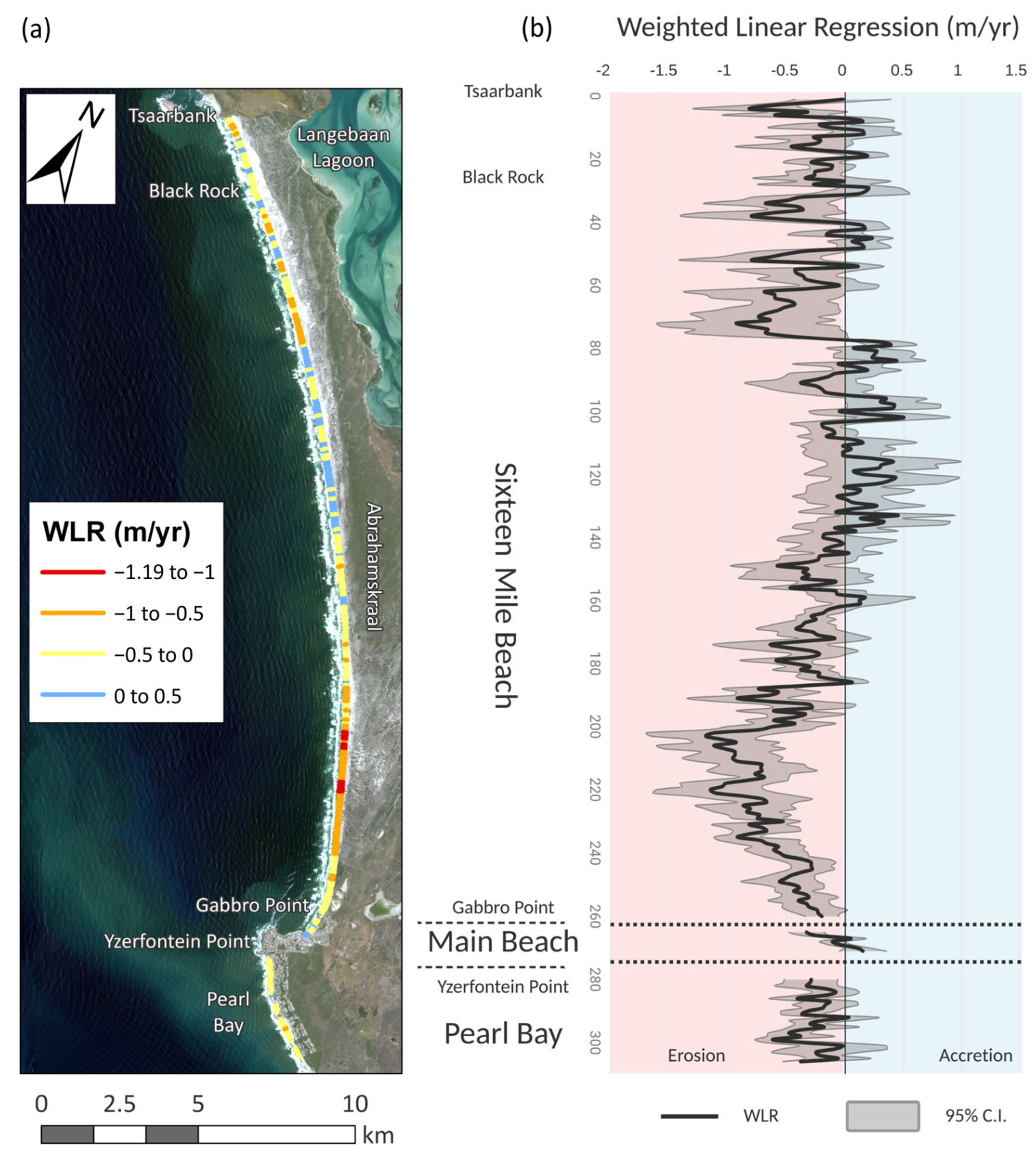
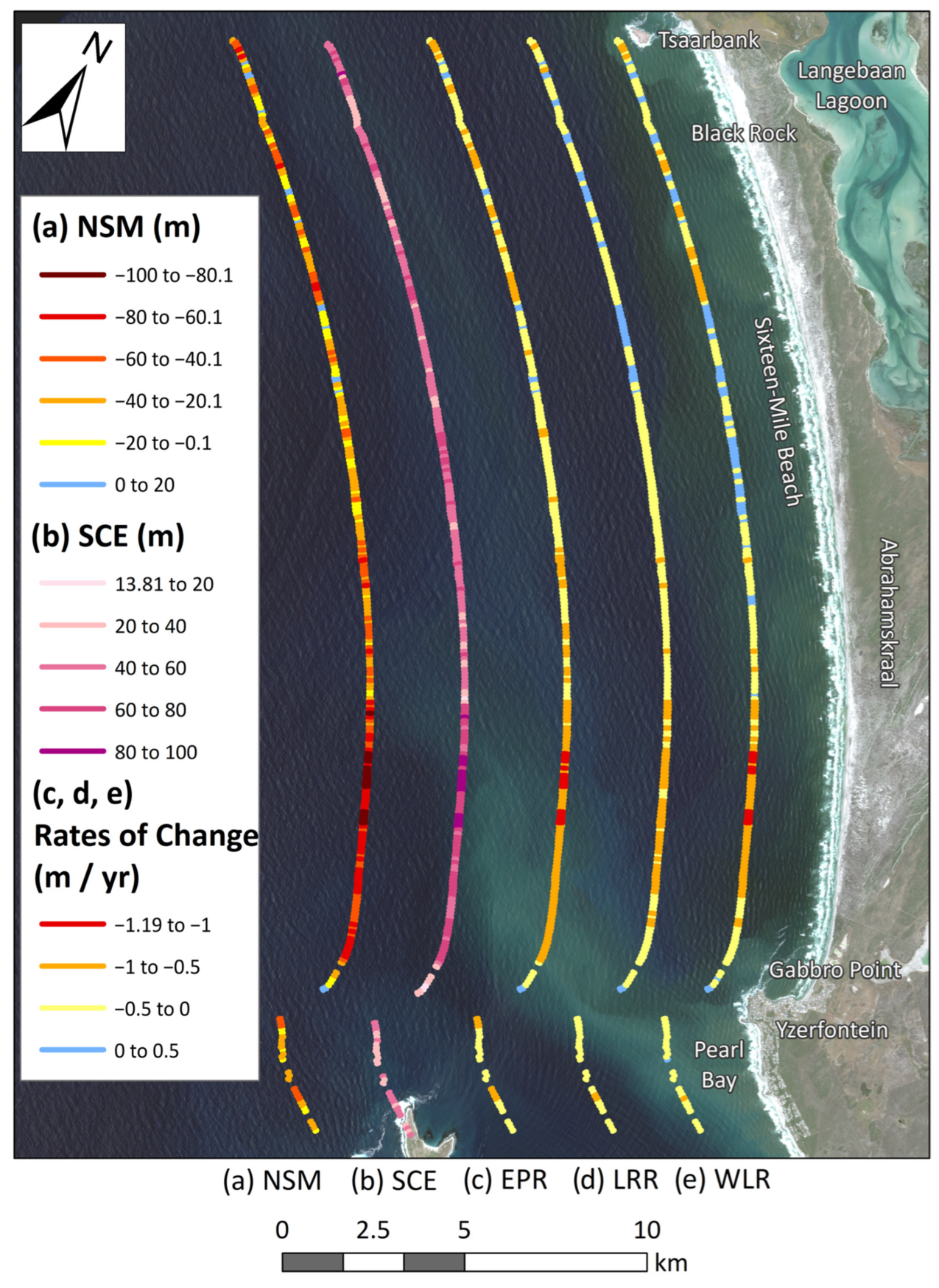
3.1. Long-Term Shoreline Change Analysis
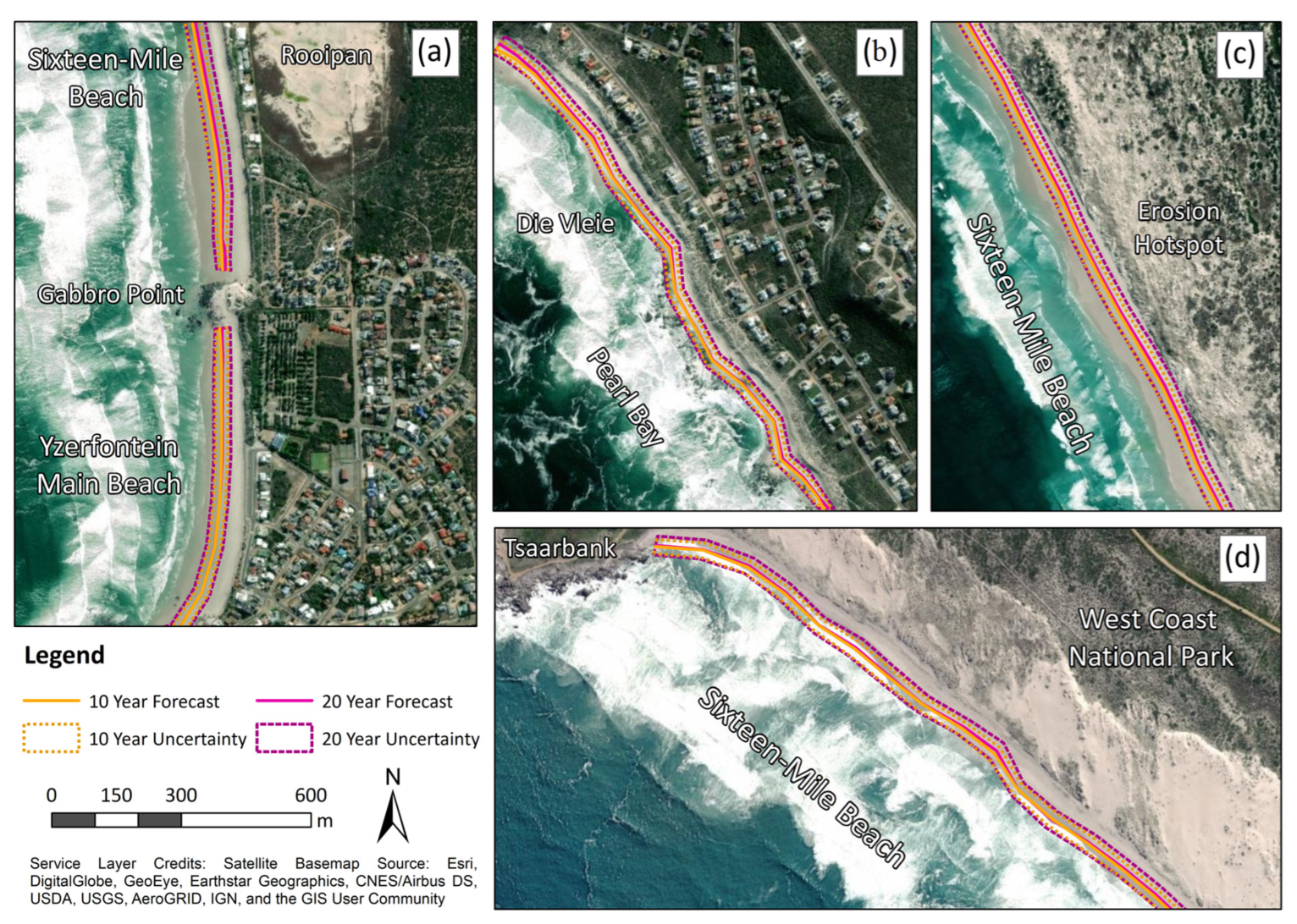
3.2. Future Shoreline Changes
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shetty, A.; Jayappa, K.S.; Mitra, D. Shoreline Change Analysis of Mangalore Coast and Morphometric Analysis of Netravathi-Gurupur and Mulky-Pavanje Spits. Aquat. Procedia 2015, 4, 182–189. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.-F.; Voukouvalas, E.; Feyen, L. Global Long-Term Observations of Coastal Erosion and Accretion. Sci. Rep. 2018, 8, 12876. [Google Scholar] [CrossRef]
- Syvitski, J.; Ángel, J.R.; Saito, Y.; Overeem, I.; Vörösmarty, C.J.; Wang, H.; Olago, D. Earth’s Sediment Cycle during the Anthropocene. Nat. Rev. Earth Environ. 2022, 3, 179–196. [Google Scholar] [CrossRef]
- Ghazali, N.H.M.; Awang, N.A.; Mahmud, M.; Mokhtar, A. Impact of Sea Level Rise and Tsunami on Coastal Areas of North-West Peninsular Malaysia. Irrig. Drain. 2018, 67, 119–129. [Google Scholar] [CrossRef]
- Tian, H.; Xu, K.; Goes, J.I.; Liu, Q.; do Gomes, H.R.; Yang, M. Shoreline Changes along the Coast of Mainland China—Time to Pause and Reflect? ISPRS Int. J. Geo-Inf. 2020, 9, 572. [Google Scholar] [CrossRef]
- Hinkel, J.; Nicholls, R.J.; Tol, R.S.; Wang, Z.B.; Hamilton, J.M.; Boot, G.; Vafeidis, A.T.; McFadden, L.; Ganopolski, A.; Klein, R.J. A Global Analysis of Erosion of Sandy Beaches and Sea-Level Rise: An Application of DIVA. Glob. Planet. Change 2013, 111, 150–158. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy Coastlines under Threat of Erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Cooper, J.A.G.; Masselink, G.; Coco, G.; Short, A.D.; Castelle, B.; Rogers, K.; Anthony, E.; Green, A.N.; Kelley, J.T.; Pilkey, O.H. Sandy Beaches Can Survive Sea-Level Rise. Nat. Clim. Chang. 2020, 10, 993–995. [Google Scholar] [CrossRef]
- Theron, A.K. Analysis of Potential Coastal Zone Climate Change Impacts and Possible Response Options in the Southern African Region. In Proceedings of the IPCC TGICA Conference: Integrating Analysis of Regional Climate Change and Response Options, Nadi, Fiji, 20–22 June 2007; pp. 205–216. Available online: https://www.ipcc.ch/site/assets/uploads/2018/08/tgica_reg-meet-fiji-2007.pdf (accessed on 10 August 2022).
- Wigley, R. Geohazards in Coastal Areas; Council for Geoscience: Bellville, South Africa, 2011; pp. 1–12. [Google Scholar]
- RSA South Africa’s Ocean Economy. Available online: https://www.gov.za/sites/default/files/gcis_document/201706/saoceaneconomya.pdf (accessed on 15 September 2022).
- Fourie, J.-P.; Ansorge, I.; Backeberg, B.; Cawthra, H.C.; MacHutchon, M.R.; van Zyl, F.W. The Influence of Wave Action on Coastal Erosion along Monwabisi Beach, Cape Town. S. Afr. J. Geomat. 2015, 4, 96–109. [Google Scholar] [CrossRef]
- Rautenbach, C.; Daniels, T.; de Vos, M.; Barnes, M.A. A Coupled Wave, Tide and Storm Surge Operational Forecasting System for South Africa: Validation and Physical Description. Nat. Hazards 2020, 103, 1407–1439. [Google Scholar] [CrossRef]
- Barnes, M.A.; Turner, K.; Ndarana, T.; Landman, W.A. Cape Storm: A Dynamical Study of a Cut-off Low and Its Impact on South Africa. Atmos. Res. 2021, 249, 105290. [Google Scholar] [CrossRef]
- Noujas, V.; Thomas, K.V.; Ajeesh, N.R. Shoreline Management Plan for a Protected but Eroding Coast along the Southwest Coast of India. Int. J. Sediment Res. 2017, 32, 495–505. [Google Scholar] [CrossRef]
- Narayana, A.C. Shoreline Changes. In Encyclopedia of Estuaries; Kennish, M.J., Ed.; Springer: Dordrecht, The Netherlands, 2016; pp. 590–602. [Google Scholar]
- Szuster, B.W.; Chen, Q.; Borger, M. A Comparison of Classification Techniques to Support Land Cover and Land Use Analysis in Tropical Coastal Zones. Appl. Geogr. 2011, 31, 525–532. [Google Scholar] [CrossRef]
- Choung, Y.; Li, R.; Jo, M.-H. Development of a Vector-Based Method for Coastal Bluffline Mapping Using LiDAR Data and a Comparison Study in the Area of Lake Erie. Mar. Geod. 2013, 36, 285–302. [Google Scholar] [CrossRef]
- Cabezas-Rabadán, C.; Pardo-Pascual, J.E.; Palomar-Vázquez, J.; Fernández-Sarría, A. Characterizing Beach Changes Using High-Frequency Sentinel-2 Derived Shorelines on the Valencian Coast (Spanish Mediterranean). Sci. Total Environ. 2019, 691, 216–231. [Google Scholar] [CrossRef] [PubMed]
- Maglione, P.; Parente, C.; Vallario, A. Coastline Extraction Using High Resolution WorldView-2 Satellite Imagery. Eur. J. Remote Sens. 2014, 47, 685–699. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Ling, F.; Liu, Y.; Fang, F. Spatio-Temporal Change Detection of Ningbo Coastline Using Landsat Time-Series Images during 1976–2015. ISPRS Int. J. Geo-Inf. 2017, 6, 68. [Google Scholar] [CrossRef]
- Xu, N. Detecting Coastline Change with All Available Landsat Data over 1986–2015: A Case Study for the State of Texas, USA. Atmosphere 2018, 9, 107. [Google Scholar] [CrossRef]
- Specht, M.; Specht, C.; Lewicka, O.; Makar, A.; Burdziakowski, P.; Dąbrowski, P. Study on the Coastline Evolution in Sopot (2008–2018) Based on Landsat Satellite Imagery. J. Mar. Sci. Eng. 2020, 8, 464. [Google Scholar] [CrossRef]
- Mao, Y.; Harris, D.L.; Xie, Z.; Phinn, S. Efficient Measurement of Large-Scale Decadal Shoreline Change with Increased Accuracy in Tide-Dominated Coastal Environments with Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2021, 181, 385–399. [Google Scholar] [CrossRef]
- Liu, X.; Hu, G.; Chen, Y.; Li, X.; Xu, X.; Li, S.; Pei, F.; Wang, S. High-Resolution Multi-Temporal Mapping of Global Urban Land Using Landsat Images Based on the Google Earth Engine Platform. Remote Sens. Environ. 2018, 209, 227–239. [Google Scholar] [CrossRef]
- Amani, M.; Brisco, B.; Afshar, M.; Mirmazloumi, S.M.; Mahdavi, S.; Mirzadeh, S.M.J.; Huang, W.; Granger, J. A Generalized Supervised Classification Scheme to Produce Provincial Wetland Inventory Maps: An Application of Google Earth Engine for Big Geo Data Processing. Big Earth Data 2019, 3, 378–394. [Google Scholar] [CrossRef]
- Mauger, C.L.; Compton, J.S. Formation of Modern Dolomite in Hypersaline Pans of the Western Cape, South Africa. Sedimentology 2011, 58, 1678–1692. [Google Scholar] [CrossRef]
- About Yzerfontein—Yzerfontein Tourism. Available online: https://www.yzerfonteintourism.co.za/about-yzerfontein/ (accessed on 25 September 2022).
- Lemmen, A.C. Second Home Development in South Africa. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2011. [Google Scholar]
- Hanekom, N.; Randall, R.M.; Nel, P.; Kruger, N. West Coast National Park, State of Knowledge; South African National Parks Scientific Services: Sedgefield, South Africa, 2009; pp. 1–65.
- About NGI. Available online: https://ngi.dalrrd.gov.za/index.php/home/about-ngi (accessed on 25 September 2022).
- Fundamentals of Georeferencing a Raster Dataset—Help|ArcGIS for Desktop. Available online: https://desktop.arcgis.com/en/arcmap/10.3/manage-data/raster-and-images/fundamentals-for-georeferencing-a-raster-dataset.htm (accessed on 20 September 2020).
- Moore, L.J.; Ruggiero, P.; List, J.H. Comparing Mean High Water and High Water Line Shorelines: Should Proxy-Datum Offsets Be Incorporated into Shoreline Change Analysis? J. Coast. Res. 2006, 22, 894–905. [Google Scholar] [CrossRef]
- Pollard, J.A.; Brooks, S.M.; Spencer, T. Harmonising Topographic & Remotely Sensed Datasets, a Reference Dataset for Shoreline and Beach Change Analysis. Sci. Data 2019, 6, 42. [Google Scholar]
- Hapke, C.; Schwab, W.; Gayes, P.; McCoy, C.; Viso, R.; Lentz, E. Inner Shelf Morphologic Controls on the Dynamics of the Beach and Bar System, Fire Island, New York. In Coastal Sediments 2011; Rosati, J.D., Wang, P., Roberts, T.M., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1034–1047. [Google Scholar]
- Burningham, H.; Fernandez-Nunez, M. Shoreline Change Analysis. In Sandy Beach Morphodynamics; Jackson, D.W.T., Short, A.D., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 439–460. [Google Scholar]
- Niang, A.J. Monitoring Long-Term Shoreline Changes along Yanbu, Kingdom of Saudi Arabia Using Remote Sensing and GIS Techniques. J. Taibah Univ. Sci. 2020, 14, 762–776. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A Google Earth Engine-Enabled Python Toolkit to Extract Shorelines from Publicly Available Satellite Imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-Annual to Multi-Decadal Shoreline Variability from Publicly Available Satellite Imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide; Open-File Report 2018–1179; US Geological Survey: Reston, VA, USA, 2018.
- Burningham, H.; French, J. Understanding Coastal Change Using Shoreline Trend Analysis Supported by Cluster-Based Segmentation. Geomorphology 2017, 282, 131–149. [Google Scholar] [CrossRef]
- Sarkar, D.; Andrews, F.; Wright, K.; Klepeis, N.; Murrell, P. Lattice: Trellis Graphics for R 2021. Available online: https://cran.r-project.org/web/packages/lattice/index.html (accessed on 21 August 2022).
- Franceschini, G. Geology of Aeolian and Marine Deposits in the Saldanha Bay Region, Western Cape, South Africa. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 2003. [Google Scholar]
- Franceschini, G.; Compton, J.S. Holocene Evolution of the Sixteen Mile Beach Complex, Western Cape, South Africa. J. Coast. Res. 2006, 22, 1158–1166. [Google Scholar] [CrossRef]
- Compton, J. The Rocks and Mountains of Cape Town; Earthspun Books: Cape Town, South Africa, 2019; pp. 73–105. [Google Scholar]
- Kandel, A.W.; Conard, N.J. Stone Age Economics and Land Use in the Geelbek Dunes. In The Archaeology of the West Coast of South Africa; Archaeopress: Oxford, UK, 2013; pp. 24–49. [Google Scholar]
- Henrico, I.; Bezuidenhout, J. Determining the Change in the Bathymetry of Saldanha Bay Due to the Harbour Construction in the Seventies. S. Afr. J. Geomat. 2020, 9, 236–249. [Google Scholar] [CrossRef]


| Year | Month | Scale | Number of Photographs |
|---|---|---|---|
| 1937 | April | 1:22,000 | 11 |
| 1960 | December | 1:36,000 | 6 |
| 1977 | March | 1:60,000 | 3 |
| Year | Acquisition Date | Satellite Mission |
|---|---|---|
| 1985 | 9 April | Landsat 5 |
| 1990 | 19 December | Landsat 5 |
| 1995 | 30 October | Landsat 5 |
| 2000 | 20 November | Landsat 7 |
| 2005 | 9 October | Landsat 5 |
| 2010 | 29 March | Landsat 5 |
| 2015 | 22 November | Landsat 8 |
| 2020 | 9 October | Landsat 8 |
| Measurement Uncertainty (m) | 1937 | 1960 | 1977 |
|---|---|---|---|
| Georeferencing error (Eg) (Average Total RMSE) | 2.35 | 2.52 | 2.32 |
| Pixel error (Ep) | 3.00 | 4.00 | 5.00 |
| Digitization error (Ed) | 1.50 | 2.00 | 2.50 |
| Total shoreline uncertainty (U) | 4.09 | 5.13 | 6.05 |
| Measurement Uncertainty (m) | 1985 | 1990 | 1995 | 2000 | 2005 | 2010 | 2015 | 2020 |
|---|---|---|---|---|---|---|---|---|
| Georeferencing error (Eg) (RMSE) | 5.18 | 8.06 | 5.07 | 6.15 | 5.68 | 4.99 | 8.88 | 7.43 |
| Pixel error (Ep) | 15.0 | 15.0 | 15.0 | 15.0 | 15.0 | 15.0 | 15.0 | 15.0 |
| Total shoreline uncertainty (U) | 15.87 | 17.02 | 15.83 | 16.21 | 16.04 | 15.81 | 17.43 | 16.74 |
| Net Shoreline Movement (m) | |||||
|---|---|---|---|---|---|
| Shoreline | Average | Net Erosion (%) | Maximum Erosion | Net Accretion (%) | Maximum Accretion |
| Sixteen Mile Beach | −39.36 | 95 | −99.29 | 5 | +18.3 |
| Yzerfontein Main | −08.58 | 71 | −32.29 | 29 | +6.72 |
| Pearl Bay | −30.44 | 100 | −54.86 | - | - |
| Total study site | −37.79 | 95 | −99.29 | 5 | +18.3 |
| Shoreline Change Envelope (m) | |||
|---|---|---|---|
| Shoreline | Average | Maximum | Minimum |
| Sixteen Mile Beach | 54.21 | 99.29 | 18.69 |
| Yzerfontein Main Beach | 22.73 | 38.52 | 13.81 |
| Pearl Bay | 40.23 | 25.12 | 57.25 |
| Total study site | 52.13 | 99.29 | 13.81 |
| End Point Rate (m/yr) | |||||||
|---|---|---|---|---|---|---|---|
| Shoreline | Overall Rate | Average Erosion Rate | Percent of Negative Rates (Statistically Significant) (%) | Maximum Rate of Erosion | Average Accretion Rate | Percent of Positive Rates (Statistically Significant) (%) | Maximum Rate of Accretion |
| Sixteen Mile Beach | −0.47 ± 0.21 | −0.50 ± 0.21 | 95 (85) | −1.19 ± 0.21 | +0.09 ± 0.21 | 5 (0.4) | +0.22 ± 0.21 |
| Yzerfontein Main Beach | −0.10 ± 0.21 | −0.17 ± 0.21 | 71 (29) | −0.40 ± 0.21 | +0.07 ± 0.21 | 29 (0) | +0.08 ± 0.21 |
| Pearl Bay | −0.36 ± 0.21 | −0.36 ± 0.21 | 100 (82) | −0.65 ± 0.21 | - | - | - |
| Study Site | −0.45 ± 0.21 | −0.48 ± 0.21 | 95 (82) | −1.19 ± 0.21 | +0.09 ± 0.21 | 5 (0.3) | +0.22 ± 0.21 |
| Linear Regression Rate (m/yr) | |||||||
|---|---|---|---|---|---|---|---|
| Shoreline | Overall Rate | Average Erosion Rate | Percent of Negative Rates (Statistically Significant) (%) | Maximum Rate of Erosion | Average Accretion Rate | Percent of Positive Rates (Statistically Significant) (%) | Maximum Rate of Accretion |
| Sixteen Mile Beach | −0.28 ± 0.40 | −0.35 ± 0.40 | 85 (32) | −0.89 ± 0.50 | +0.10 ± 0.40 | 15 (0) | +0.30 ± 0.43 |
| Yzerfontein Main Beach | −0.05 ± 0.19 | −0.11 ± 0.18 | 71 (14) | −0.24 ± 0.23 | +0.08 ± 0.23 | 29 (0) | +0.10 ± 0.23 |
| Pearl Bay | −0.27 ± 0.30 | −0.27 ± 0.30 | 100 (43) | −0.58 ± 0.29 | - | - | - |
| Study Site | −0.28 ± 0.39 | −0.34 ± 0.39 | 86 (34) | −0.89 ± 0.50 | +0.10 ± 0.39 | 13 (0) | +0.30 ± 0.43 |
| Weighted Linear Regression (m/yr) | |||||||
|---|---|---|---|---|---|---|---|
| Shoreline | Overall Rate | Average Erosion Rate | Percent of Negative Rates (Statistically Significant) (%) | Maximum Rate of Erosion | Average Accretion Rate | Percent of Positive Rates (Statistically Significant) (%) | Maximum Rate of Accretion |
| Sixteen Mile Beach | −0.29 ± 0.35 | −0.44 ± 0.35 | 77 (46) | −1.19 ± 0.47 | +0.20 ± 0.35 | 23 (3) | +0.50 ± 0.40 |
| Yzerfontein Main Beach | −0.06 ± 0.13 | −0.19 ± 0.12 | 57 (29) | −0.33 ± 0.15 | +0.10 ± 0.15 | 43 (0) | +0.15 ± 0.20 |
| Pearl Bay | −0.25 ± 0.24 | −0.26 ± 0.24 | 96 (56) | −0.62 ± 0.15 | +0.03 ± 0.26 | 4 (0) | +0.03 ± 0.26 |
| Study Site | −0.28 ± 0.33 | −0.41 ± 0.33 | 78 (47) | −1.19 ± 0.47 | +0.19 ± 0.34 | 22 (3) | +0.50 ± 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murray, J.; Adam, E.; Woodborne, S.; Miller, D.; Xulu, S.; Evans, M. Monitoring Shoreline Changes along the Southwestern Coast of South Africa from 1937 to 2020 Using Varied Remote Sensing Data and Approaches. Remote Sens. 2023, 15, 317. https://doi.org/10.3390/rs15020317
Murray J, Adam E, Woodborne S, Miller D, Xulu S, Evans M. Monitoring Shoreline Changes along the Southwestern Coast of South Africa from 1937 to 2020 Using Varied Remote Sensing Data and Approaches. Remote Sensing. 2023; 15(2):317. https://doi.org/10.3390/rs15020317
Chicago/Turabian StyleMurray, Jennifer, Elhadi Adam, Stephan Woodborne, Duncan Miller, Sifiso Xulu, and Mary Evans. 2023. "Monitoring Shoreline Changes along the Southwestern Coast of South Africa from 1937 to 2020 Using Varied Remote Sensing Data and Approaches" Remote Sensing 15, no. 2: 317. https://doi.org/10.3390/rs15020317
APA StyleMurray, J., Adam, E., Woodborne, S., Miller, D., Xulu, S., & Evans, M. (2023). Monitoring Shoreline Changes along the Southwestern Coast of South Africa from 1937 to 2020 Using Varied Remote Sensing Data and Approaches. Remote Sensing, 15(2), 317. https://doi.org/10.3390/rs15020317








