Abstract
River deltaic estuaries are dynamic ecosystems characterised by linkages between tidal currents, river water discharge, and sediment from the basin. The present study is based on the application of remote data: multispectral satellite images, DEM, LULC (Land use and land cover), lithology, and hydroclimatic factors. The standardised methodology was based on the adoption of a coupled modelling approach for this work, involving the semi-distributed catchment scale hydrological Soil and Water Assessment Tool (SWAT) model and the statistical Digital Shoreline Analysis System (DSAS) for (1) identifying environmental drivers of sediment transport changes of the estuarine reach; (2) analysis of retrospective changes in shoreline configuration; (3) assessing discharge and sediment dynamics of the estuarine section, and (4) generating future projection scenarios for the estuary’s state to take action for its long-term ecological stability. Our study employs a coupled modelling framework to fill the research gap for Subarnarekha deltaic estuary. Integrating outputs derived from DSAS and SWAT, a comprehensive understanding of the changes in watershed hydrology, water diversions, and damming of rivers have altered the magnitude and temporal patterns of freshwater flow and sediment, which potentially contributed to the receding of the Digha Coast shoreline.
1. Introduction
The coastal areas include river deltas, estuaries, and coastal wetlands and floodplains at the downstream sections of large rivers forming deltaic river estuaries (RDE). RDE are dynamic ecosystems characterised by linkages between physical indicators, e.g., tidal currents, river discharge, and groundwater [1,2]. There are sensitive to landscape anthropogenic changes due to increased land use, human impact, and climate changes. At the global scale, river systems are altered by drastically increased or decreased sediment and nutrient loads leading to worsening ecosystem services for humanity, especially in terms of water regulation, supply, and wastewater treatment [3]. Many river systems are modified by dam construction [4], which has become a significant driver of sediment delivery to the oceans on a global scale [5,6], leading to shifts in hydrological connectivity in the RDE [7]. Coastal zones are very dynamic and vulnerable, and with storm surges and rising sea levels, the impact of global climate change on coastal hazards and risks is growing [8,9,10,11,12]. In RDE, coastal erosion constitutes severe risk and calamity [9,13,14]. Coastal erosion affects more than 80% of the world’s coasts, with erosion rates ranging from 1 cm/year to 30 m/year, posing a significant coastal hazard across several coastal zones [15]. As a result, coastal erosion occurs worldwide along estuaries inducing huge sediment outflows [16]. Thus, the bulk of sediment in estuaries is generated by freshwater inflow, regulated mainly by runoff from precipitation and groundwater discharges across the watershed [17,18]. The RDE is also heavily populated. It has been estimated that 61% of the world’s population lives along the coastal margin [2,19]. Thus, they are highly vulnerable to anthropogenic disruptions, such as rapid urbanisation, tourism, dam construction, industrial development, pollution, etc. [18,20,21].
Knowledge and assessment of the changes in shoreline position are crucial in the overall understanding of dynamics in RDE and the watershed processes driving the change. Evaluating environmental effects at the watershed scale is possible by applying the Soil and Water Assessment Tool (SWAT) hydrological modelling system [22], which is simple to operate for data input and is excellent at simulating the mechanism of climate change [1]. Several variables are included throughout the modelling process, including the climate, land use, topography, soil, and geological changes [23]. SWAT can model hydrological parameters, including water discharge, streamflow, soil erosion, and sediment yields at the watershed scale under present and projected environmental scenarios [24,25,26,27,28,29]. Aside from that, SWAT has been utilised to assess the extent of disintegration within the watershed and the level of sediment transport and soil loss across different HRUs in the sub-basin, from which critical zones can be identified [30].
Regarding modelling of the RDE hydrodynamics, SWAT is applied by Li et al. [1] to simulate climate change’s influence on hydrological systems and nutrient influx in Yamen Estuary, South China. Kim et al. [31] used SWAT to assess the effects of prospective climate and land-use changes on sediment input to assess shoreline changes in Korea’s Hoeya River estuary. Olaoye et al. [32] applied SWAT to evaluate the impacts of predicted 21st-century climate change over water quality metrics (nitrogen, phosphorus, chlorophyll, and dissolved oxygen) in the Old Woman Creek estuary watershed. As far as coastal hydrological modelling works on monsoon regions are concerned, Yaduvanshi et al. [33] estimated discharge (1982-2005) using two models: SWAT and the probability distribution model. Rao et al. [34] simulated the monthly streamflow using SW and calibration and uncertainty assessment using the SUFI-2 algorithm. In order to estimate surface runoff and evaluate the effects of land use changes, Dandapat [35] applied SWAT and calibrated it with the SUFI-2 algorithm. Murmu et al. [36] conducted a SWAT simulation of daily precipitation to evaluate the yearly and monthly runoff for their corresponding rainfall.
Evaluating the dynamics of shoreline movements and changes at both shorter and longer time scales is possible by applying the Digital Shoreline Analysis System (DSAS). DSAS is used in historical trend analysis to examine the past, present, and future shoreline positions or geometry within computing the rate of change statistics for a time series of shoreline positions [37,38,39,40]. The Digital Shoreline Analysis System (DSAS) is an ArcGIS tool that can assess coastal behaviour and shoreline dynamics. The DSAS has been developed by the United States Geological Survey (USGS) and the TPMC Environmental Services [41,42] as a freely available extension to ArcGIS by ESRI. The DSAS model could be applied to calculate rate-of-change statistics using multiple significant shoreline positions extracted from multispectral satellite images by performing radiometric on each band of satellite images by converting DN values to radiance and radiance values to reflectance values [43]. The use of advanced statistical methods, such as end point rate (EPR), shoreline change envelope (SCE), linear regression rate (LRR), and net shoreline movement (NSM), allows for an assessment of erosion/accretion scenarios for water body shoreline [44,45]. In the case of coastal modelling, Nath et al. [15,29] used the DSAS techniques to identify the pattern of coastal erosion deposition over 43 years (1975–2018) over a 72 km coastal length of the Subarnarekha estuary.
As part of this study, coupled modelling of SWAT and DSAS is the main operation. The SWAT is applied to assess the flow and sediment dynamics (growth and loss of sediments) across the study area. Then DSAS is applied primarily to define the impact of flow-induced sediment dynamics on the shoreline section of the study area and to generate an estimated scenario for the future. Hence, coupled modelling will better understand the operating hydrodynamics in the study area and its impact on its physical condition. The current study has been undertaken on the estuarine section of the lower sub-basin (Delta) of the Subarnarekha river basin, situated over the western Bay of Bengal. This research is attractive because the area in question has been subject to intense pressure from having endured severe forest devastation over nearly 40 years [29], which most likely impacted coastal degradation and shoreline recession. The climate of the Bay of Bengal reflects the instability and variability of the monsoon in the tropical regions of the country. The variability and instability of the monsoon, alongside human activities, can significantly influence the hydrological parameters of a river basin. Based on a review of the literature on the SWAT model’s application on estuarine watersheds, it is applied to the study area to estimate selected operating hydrological processes like discharge, soil loss, inflow, and outflow of sediment, as well as the influence of the monsoon upon them. Aside from that, as previously stated [29], differences in sediment fluxes and runoff across the watershed have potentially resulted in significant erosion and accretion on the estuary section and occurring shoreline changes. This study aims to test the coupling of SWAT and DSAS models and select the best input source combination obtained from the watersheds for the optimal assessment of retrospective and prospective river deltaic estuaries development. This work demonstrates how to contribute to new research avenues on data-scarce regions. Like our study case, we also aimed to explore the applicability of remote sensing for insufficiently monitored river basins.
Section 2 provides the study’s methodology and gives a short setup for the research. Section 3 provides a detailed analysis of the results and discusses them in other sub-chapters. Finally, we present the overall study conclusions. The current study employs a coupled modelling framework to fill the research gap for Subarnarekha deltaic estuary. Integrating outputs derived from DSAS and SWAT, a comprehensive understanding of the current estuarine hydrodynamics of the Subarnarekha basin’s estuary on the lower sub-basin (Delta) and the causes and implications caused by the dynamics could be attained.
2. Materials and Methods
2.1. Study Area
The area under the current study is the Subarnarekha river basin’s estuary, which consists of the riverbed and the coastal strip on the left and right side of the funnel-shaped mouth of the river to the Bay of Bengal. The mouth includes a fragment of Digha Coast, the most popular sea beach in West Bengal. It is located 187 km south-west of Kolkata. (Figure 1). The Subarnarekha River is the smallest river basin (area 18,951 km2) among India’s fourteen major river basins. It starts near Nagri village (in the Chota Nagpur Plateau) of Jharkhand and outfalls into the Bay of Bengal after flowing over 395 km. The mean discharge of the river is around 250 m3/s. According to Das [46], yearly sediment yield in the upper and middle Subarnarekha basin varies between 200 and 260 t km2 year−1. Several areas in the lower reaches of the Subarnarekha, particularly the coastal states of Odisha and West Bengal, are within the flood hazard zone, with the highest flood level over 12 m (e.g., in 1997, 2007). In the upper reach are reservoirs and hydroelectric power stations: Getalsud reservoir (commissioned in 1971), Chandil and Galudih barrages (1982–1983). About 62% of the basin area is classified as cultivable (sown 40%, 22% fallow land), and nearly 31% is devoted to forests. The study area falls under India’s humid subtropical belt, defined by a lengthy, dry, hot season, a brief duration of relatively cold weather, and a long spell of low to modest rainfall [47].
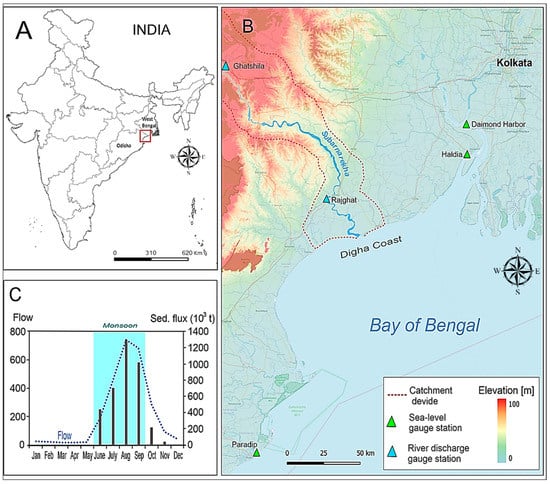
Figure 1.
Location of the study area on the map of the Indian states (West Bengal, Odisha) (A), on the physical map with the location of measurement stations (B) and monthly mean water discharge and sediment fluxes for station Ghatshila in the period 1970–2015 (C).
During the monsoon period (South-west Monsoon), longshore currents dominate the middle-lower part of the basin, moving from south-west to northeast. However, due to changes in the wind direction, a low impact current blows from north-east to south-west [40]. A long-shore current of 1.22 m/s was recorded in the Subarnarekha estuary, and a current of 1.23 m/s was recorded on the adjacent Digha Coast. This south-west monsoon-dominated region under the current study is affected by micro-tidal waves with a range of 4.5–5.0 m [48]. The mean monthly temperature across the study area ranges between 22 and 34 °C [40]. As a result of regional sea level rise, riverbank erosion, and diversity in sediment availability in this study area under Subarnarekha river’s middle-lower stream, fluvio-marine erosion and accretion mechanisms, as well as ongoing paedogenesis events, modify landforms and can result in the formation of contemporary landforms [49].
Calculations for the models were carried out on a fragment of the catchment called Delta sub-basin (Figure A1 in Appendix A), separated on the basis of the approach proposed by Acharyya et al. [29]. The Delta sub-basin covers spanning the Indian states of Jharkhand, Odisha, and West Bengal. The Delta sub-basin spans the medial and lower course of the Subarnarekha river and its adjacent deltaic region, located between 86°29′0.90′′ and 87°22′13.05′′E Longitude and 21°33′2.16′′ and 22°42′12.42′′N Latitude.
2.2. Data
This chapter focuses on the datasets and steps required for data processing for the current study based on the coupled modelling framework involving DSAS and SWAT. Table 1 shows the input datasets used to execute the simulation procedures of the SWAT and DSAS models, which are the primary applications of this coupled modelling framework employed to conduct the evaluations for this current study.

Table 1.
Data sources for simulation of the SWAT model.
This section’s main emphasis is on the particular input parameters necessary for running the SWAT model to carry out the analytical simulation of the distinct hydrological processes (discharge, soil loss, sediment loss, and gain)—according to Arnold et al. [22]. These parameters required for efficiently executing the simulation are listed as follows: (1) 30 m grid resolution DEM Shuttle Radar Topography Mission (SRTM 2011), (2) sub-basin, (3) land use and land cover (LULC), (4) Slope from DEM, (5) soil map, and (6) meteorological data.
Sea Level Data
In support of the statistical analysis of shoreline change mentioned above, the Seal-level dataset of PSMSL (Permanent Service of the Mean Sea Level), a world repository of the tide-gauge statistics built-in 1933, headquartered in Liverpool at ‘The National Sea Level Oceanography Centre’, UK, was used [50]. PSMSL is presented in Figure 2 in the revised local reference (RLR). The RLR dataset has a uniform database of benchmark measurements for each gauge, implying that the SL is evaluated against documented land-based data. The datasets of RLR are published after year-to-year analyses are carried out based on a standard date and are ideal for assessing long-term changes in the sea level [51]. The RLR time series data were gathered from measurements made at RLR gauge stations nearer the Subarnarekha river estuary, including Paradip, followed by Haldia and Diamond Harbour. In conjunction with the continuous increase in global sea level, they show changes in relative sea level and probable regional and local causes at a sampling point, which might affect vertical land modifications [52]. Since it is proximate to the study area, the RLR data of the Indian gauge station Haldia were included in the current investigation.
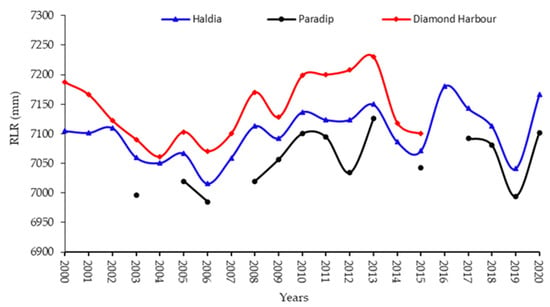
Figure 2.
Temporal variations in yearly sea level at the Haldia, Paradip, and Diamond Harbour RLR gauge stations on the Bay of Bengal nearby the Subarnarekha river estuary (https://www.psmsl.org/data/obtaining/rlr.diagrams/1270.php (accessed on 7 May 2022)).
2.3. Model Setup of SWAT and DSAS
2.3.1. SWAT Model’s Setup
The SWAT model’s efficacy has improved due to its compatibility with software packages such as ArcGIS 10.3 [53]. As shown in Figure 3, the Arc SWAT interface within the ArcGIS environment has been used for setting up the SWAT model, which was designed using all of the parameters stated above. Then the sub-basin was identified in the first step using hydrologically corrected DEM data. The datasets mentioned above of soil, LULC, slope, and climatic factors were considered while defining hydrological response units (HRU). Flügel [54] defined an HRU as a homogeneous structured element with similar climate, land use, and soil properties, hence a homogeneous hydrological response under equivalent meteorological forcing. Each HRU produces a quantity of runoff directed to calculate the total runoff [55].
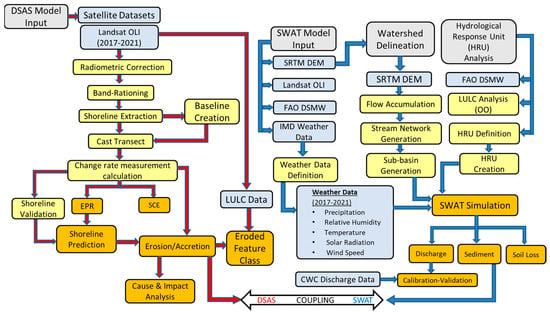
Figure 3.
Flowchart illustrating the coupling SWAT and DSAS to assess the erosion-accretion scenario through the Delta sub-basins estuarine section of Subarnarekha River.
The hydrological calculations of the SWAT are based on the water balance Equation (1) [22,56].
where SWt is the final soil water contents on a particular day, and SWo is the initial soil water content. The equation subtracts all forms of water loss on day i from precipitation on day i (Rday), including surface runoff (Qsurf), evapotranspiration (Ea), percolation (Wperc), and return flow (Qgw). All are given in millimetres, and time (t) is in days (Arnold et al. 1998).
SWAT uses the MUSLE (modified universal soil loss equation) (Equation (2)) to simulate the soil and sediment dynamics operating across a watershed [57], which in turn has been applied to the area under the current study. This model was successfully implemented earlier by the authors in the study area [29], which allowed for a more thorough analysis in this study.
where SED is the sediment yield on a given day (tons); Qsurf is the surface runoff rate (mmH2O/ha); Qpeak is the peak runoff rate (m3/s); areahru is the area of the HRU (ha); Kusle is the USLE soil edibility factor; Cusle is the USLE cover and management factor; Pusle is the USLE support practice factor; LSusle is the USLE topographic factor; CRFG is the coarse fragment factor (CRFG = exp (−0.053 × %)).
SWAT model-based simulations run on the Delta Sub-Basin has been calibrated and validated using the field-based discharge data [50] gathered from Rajghat (Odisha) CWC hydrological gauge station (Figure 1). The calibration through the SUFI-2 method was performed over a two-year period in SWAT CUP (SWAT Calibration and Uncertainty Program) [58] by comparing the simulated daily discharge with the observed daily discharge data from the aforementioned hydrological gauge station. Since this gauge station is the closest to the estuarine section, the shoreline along the estuary was also considered in analysing sediment transport and erosion–accretion scenarios. Thus, the closest gauge station data were used for the calibration-validation procedure. Therefore, the period of validation and calibration was determined to be 2017–2018 and 2019–2021 based on the location of the gauge stations, the availability of observed data, and the research period. Tests of the coefficient of determination (R2) using Equation (3) and the Nash–Sutcliffe efficiency [59] were carried out (Equation (4)). Root mean square error (RMSE), as shown in Equation (5), and percentage of deviation from observed data (PBIAS, Equation (6)) were estimated for both model calibration and validation purposes for the current study. In addition, the P-factor and d-factor were used to determine the capability of calibration as well as uncertainty measures [58].
MUSLE is used in hydrology and environmental engineering to compute the potential soil erosion and sediment yield according to Mishra et al. [60] and it is the best model to estimate the sediment yield of the watershed, based on the runoff characteristics as the best indicator for sediment yield prediction [57], from the amount of soil erosion in different HRUs of the sub-basin where vulnerable regions can be recognised [30].
2.3.2. DSAS Model’s Setup
The DSAS tool as well as further information on its installation and use can be accessed at http://woodshole.er.usgs.gov/projectpages/dsas/ (accessed on 2 March 2022). One of the primary benefits of employing the DSAS in coastal alteration study is its capability to calculate rate change statistics over a time series across shoreline sites [38]. Statistics enable measuring and investigating the process of coastal dynamics and changing patterns Oyedotun [37]. It uses five statistical approaches to calculate the rate of changes along the coastline over the short and long term, including EPR (endpoint rate), SCE (shoreline change envelope), NSM (net shoreline movement), LRR (linear regression rate), and LMS (least median of squares) [37,38]. Among these three techniques, EPR and SCE (Equations (7) and (8)) were the best for efficiently executing the current investigation.
Endpoint rate (EPR) is determined using Equation (7), which is as follows:
where Sr is per year rate of shoreline change/distance among the average and the shoreline at the oldest point at the transect (m/year); fo is the distance between baseline and shoreline at the oldest date at a particular transect (xn); fy is the distance between baseline and shoreline in recent date at the same above transect (xn); n is the total number of years from the oldest date to most recent date [38].
Equation (8) depicts the shore change envelope (SCE), which is expressed as:
where Sd is a shoreline change distance (m); df is the distance between the baseline and farthest shoreline (m) at a particular transect (xn); dc is the distance between the baseline and closest shoreline (m) at the same above transect (xn) [38].
Then, analysis involving statistical modules within DSAS was conducted using the multi-temporal and multi-resolution satellite imageries of Landsat technology covering the study area under Path/Row-138/45 of Landsat OLI/TRS. The images were then geometrically rectified, and the satellite images were radiometrically corrected for each band. Transforming the digital number (DN) values into radiance values and, subsequently, the radiance values into reflectance values are the two vital steps required for shoreline analysis using DSAS [61].
- Shoreline Delineation
Due to the prevalence of water-saturated regions along the land-water borderline, automated delineation of shorelines is challenging [44]. The current study was based on the band rationing approach [62], which used a ratio of bands 2 and 4 between bands 2 and 5 on the shoreline in coastal regions to filter vegetation for accurate shoreline delineation. Since the band-2/band-5 means of water are higher than 1 and those for land are less than 1, part of the vegetative regions should be assigned water [62,63]. Consequently, the persistent coastline locations were recorded in two distinct years, 2017 and 2021, but for ascertaining the accuracy of the DSAS model, a preceding year (2012) was also considered. Then, the binary raster data were transformed into vector data, and the shoreline boundary was delineated.
- Transect Casting Method from Baseline
As part of this method, a single baseline from the shoreline must be established before the transect is created; two primary baseline delineation techniques are the buffering technique and the baseline formation technique from a certain coastline distance [63]. The buffer technique is the most precise and exact since it adopts a similar sinuosity structure as the neighbouring shoreline [39]
In order to start the baseline computation in the DSAS application, the following attribute fields must be filled in: ID, OBJECTID, SHAPE, Length, Group, OFFshore, and CastDir. These attributes give the DSAS the necessary information regarding the baseline placement in relation to the shoreline and the sequence of the transects (onshore or offshore).
In order to forecast the coastline, this study has solely utilised the shorelines from the years 2012 and 2017, using Equation (9) by Pramanick et al. [61].
2.3.3. Coupling of SWAT with DSAS
As per the current methodology of this study, after accurately setting up and running both models of SWAT and DSAS over the Delta sub-basin, the main focus is pioneering to make fit specific outputs of them within a coupling framework, which is depicted below in Figure 3. One of the objectives of the current study is to assess the erosion-accretion scenario induced by the adjoining hydrological processes (discharge, soil loss, sediment loss, and gain) operating within this estuarine sub-basin. Thus, to accomplish the objectives mentioned above, the SWAT simulation of sediment loss and gain taking place across the Delta sub-basins estuarine section of Subarnarekha River has been coupled with the trend of shoreline change scenario generated by the statistical module EPR of the DSAS model. Since the erosion-accretion scenario is very much evident on the shoreline, thus, the SWAT outputs of both sediment loss and sediment gain are coded as SED_IN and SED_OUT. Then, the EPR module of DSAS has been considered as optimum for accurately highlighting the evident scenario of erosion-accretion and its dynamics taking place across the study area from 2017 to 2021. This coupled modelling framework will provide a comprehensive understanding of estuarine hydrodynamics and the causes and implications induced by the dynamics.
3. Results and Discussion
3.1. SWAT Model Outputs
Based on the delineation of the watershed, Arc SWAT’s HRU analysis was applied to assess land use, slope, and soil parameters, which enabled the parameters for analysing the dispersion of the HRUs to be determined. In the next section, we summarise the simulations of SWAT’s hydrological processes, such as discharge, soil loss, and sediment dynamics, using the above Equations (1) and (2).
3.1.1. Discharge
The amount of water moving through the river or channel per time unit is called discharge, commonly stated in cubic ft./s, cubic m/s, or gallon/day. It is often calculated using the conventional current meter technique, which divides the channel’s cross-section into various subsections, followed by measurements of the exact dimensions of the stream to calculate the total discharge [64]. Whereas the current methodology of this study calculates the discharge (Q) of various time steps (daily, monthly, and yearly) by combining DEM, LULC, Soil, and weather datasets, as well as the water balance Equation (1). Furthermore, the whole Subarnarekha river basin has been divided into five distinct sub-basins (Muri, Ghatshila, Jamshedpur, Adityapur, and Delta) [29], and the daily discharges of the Delta sub-basin have been generated by the model (Figure 4). On a daily time step, the volume of the total discharge rate between 1 January 2017 and 30 December 2021 is divided into characteristic seasons: Pre-monsoon (March–May), Monsoon (June–September), and Post-monsoon (October–November) [65] (Figure 4). During the study period, the annual discharge was 48.77 m3 s−1, and the mean value of the pre-monsoon period was 34.67 m3 s−1 and three times increased to 97.19 m3 s−1 in monsoon and 41.36 m3 s−1 in post-monsoon. As a result of the simulation, it was found that the daily discharges are most profound during the monsoon time. There were a few solitary events of peak flows (Q > 1000 m3 s−1) during pre-monsoon and post-monsoon periods, particularly between 2019 and 2021 (Figure 4). This can be attributed to the monsoonal and post-monsoonal tropical cyclonic events named Fani (26 April 2019), Bulbul (5 November 2019), Amphaan (20 May 2020), and Yaas (26 May 2021) that hit this region along the Indian East coast [66].
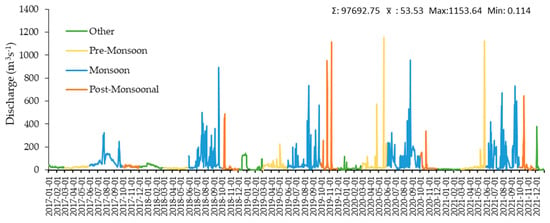
Figure 4.
The simulated hydrograph of daily discharges variations on Subarnarekha river on the Delta Sub-Basin.
Figure 5 depicts the simulated monthly discharge pattern within the Delta sub-basin from the research period, which, like the daily discharge (Figure 5), has been subdivided into pre-monsoonal, monsoonal, and post-monsoonal periods. The average discharge rate during these months is higher than in other sub-basins of the Subarnarekha basin, such as Ghatshila, Jamshedpur, and Muri [29]. Generally, the discharge corresponds to the rainfall throughout the research period. During the pre-monsoon months, the total outflow was 18.5%; during monsoonal months it was 57%, and for the post-monsoon 12.7%. Flows in the river correlated with precipitation (Figure 5) and amounted accordingly: 70.82 mm, 241.01 mm, and 51.7 mm of overall rainfall.
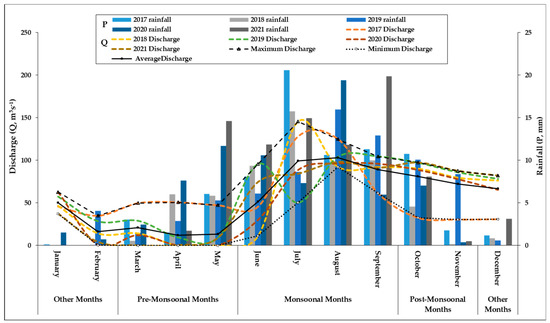
Figure 5.
The simulated hydrographs of monthly discharges (lines) against the background of the observed monthly amount of rainfall (a bar chart) along with the minimum, maximum, and average discharge in 2017–2021 on the Delta Sub-Basin of Subarnarekha River Basin.
During the research period, the Subarnarekha river on the Delta Sub-Basin average discharge ranged from 12.1 m3 s−1 to 103.2 m3 s−1, with maximum flows ranging from 35.1 m3 s−1 to 145.6 m3 s−1 and lowest flows ranging from <0.5 to 92.2 m3 s−1 (Table 2, Figure 5). The circumstances of inundation, droughts, or normal circumstances may be determined by measuring the maximal, minimum, and average discharge of water flow in the sub-basin.

Table 2.
Simulated characteristic monthly discharges in 2017–2021 on the Subarnarekha river.
3.1.2. Soil Loss
On the basis of the SWAT model, it was possible to calculate the total monthly values of soil loss in the area of the studied catchment from the research period (Figure 6). Aside from that, the maximal soil loss periods between 2017 and 2021 are depicted in Figure 7. Figure 6 indicates that the rate of soil loss during January is approximately 686.13 t ha−1 then drops to 88.93 t ha−1 in March, and finally hits a trough of 10.03 t ha−1 in April. The graph begins to rise in April (35.21 t ha−1), signifying a rise in the soil loss rate; it steadily rises during the monsoon by 1247.13 t ha−1 by July and peaks in August with a figure of 1323.99 t ha−1. The graph then slopes downward, and the loss rate falls slightly to 1288.64 t ha−1 in October. Then it declines more, reaching 1020.31 t ha−1 by December. According to earlier research [29], for the pre-monsoon period in the area of the entire catchment, the soil loss ranged from 0 to 0.0059 t ha−1, which indicates an extremely low risk of soil loss. Previous research also confirms that the Delta sub-basin area is under a very high-risk zone of soil erosion due to higher rainfall than any other sub-basin and due to the underlying Ferric Luvisols, which covers 67% of the Delta sub-basin [29]. As these are soils with a highly saturated base, the horizon has a moderate, unstable structure and a weak physical structure in the topsoil, enabling a higher soil loss [67].
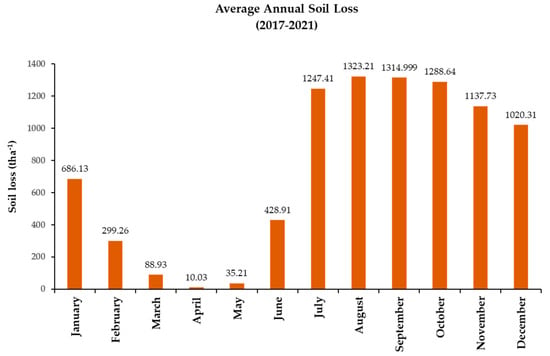
Figure 6.
Average total monthly soil loss from 2017 to 2021.
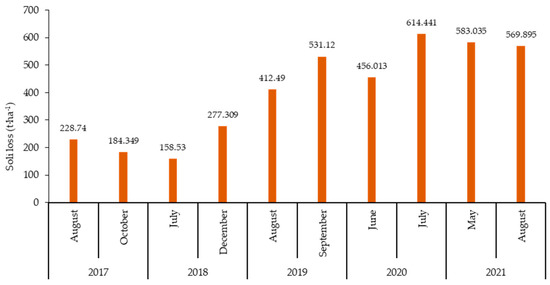
Figure 7.
Months of maximum soil loss from 2017 to 2021.
On the basis of the SWAT model, it became feasible to quantify the fraction of average soil loss between June and October, when the maximum amount of soil was eroded. Figure 7 demonstrates that, in 2017, the highest soil loss occurred in the monsoon months of August (228.74 t ha−1) and October (184.35 t ha−1), as the erosion rate is significantly lower than in the years 2019, 2020, and 2021. The data mentioned above may be used to deduce that June, July, August, and September are the most often occurring months when the rate of soil erosion is at its highest. The soil loss peaks in these months were also confirmed by earlier research conducted for the entire Subarnarekha basin for the period 2000–2013 [29].
3.1.3. Sediment Transport
The current section emphasises on employing the SWAT watershed model to model the sediment transported with water into and out of the main reach of the Subernarekha river basin’s lower segment comprising the Delta sub-basin. In light of the monsoonal uncertainty surrounding the study area, we aimed to examine the coastal hydrodynamic character of the Subarnarekha river basin and its estuarine section. Thus, to achieve this goal, it is necessary to examine sediment transport dynamics across the research region and the estuary section since sediment movement is one of the primary coastal processes that govern shoreline dynamics [40]. Hence, based on SWAT outputs (Figure 8 and Figure 9), the analysis of sediment transport scenarios in the study region can be conducted. The effects on the estuarine shorelines can be further assessed.
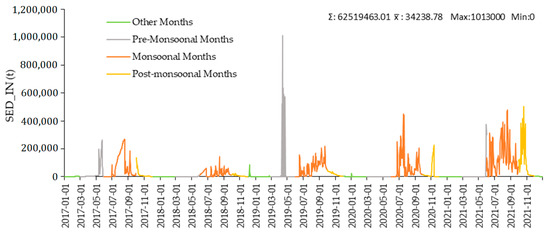
Figure 8.
Simulated hydrographs displaying daily sediment influx (SED_IN) and its variations during pre-monsoon, monsoon, and post-monsoon.
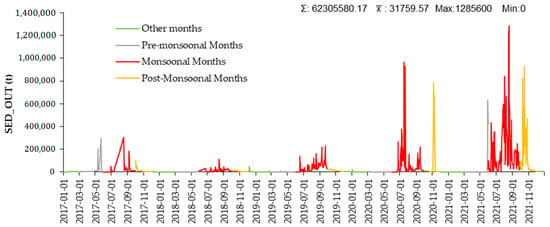
Figure 9.
Simulated hydrographs displaying daily sediment outflux (SED_OUT) and its variations during pre-monsoon, monsoon, and post-monsoon.
Figure 8 shows the quantity of sediments that water generated by tidal action brought into the reach per day from the research period throughout the research region. This is known as sediment inflow, coded as SED_IN by SWAT. It has been calculated using SWAT, and the daily SED_IN data were subdivided into discrete pre-monsoon, monsoon, and post-monsoon periods to investigate the effect of monsoonal variability on sediment influx. According to Figure 8, the average inflow of sediment transport during pre-monsoon was 16,750.21 tons from the research period, increasing to 71,539.59 tons during monsoon, and decreasing to 35,323.77 tons by post-monsoon.
In contrast to SED_IN, the amount of sediment supplied by the tidal flow of water out the reach daily from 2017 to 2021, referred to as sediment outflow, is coded as SED_OUT by SWAT. In order to explore the influence of monsoonal variability on sediment outflux, the daily SED OUT data were segmented into distinct pre-monsoon, monsoon, and post-monsoon periods to investigate the effect of monsoonal variability on sediment influx. Figure 9 shows that from 2017 to 2021, the average outflow of pre-monsoon sediment transport was 80,014.12 tonnes, which is over half of the sediment influx during the pre-monsoon period.
While the average sediment outflux increases during the monsoon to 72,602.09 metric tonnes, which is higher than the influx volume during the same period, it decreases to 44,852.17 metric tonnes during the post-monsoon period, despite being higher than the mean influx volume during the post-monsoon from 2017 to 2021. Thus, it can be observed that during monsoonal and post-monsoonal months from 2017 to 2021, sediment outflux is greater than the influx, which induces the scenario of coastal deterioration and shoreline recession. The results of our study, modelling sediment transport (SWAT) and showing clear coastal erosion trends align with the statistically proven trend of decreasing sediment delivery from the catchment [46]. For the last four decades, sediment load on the Subarnarekha river has shown a decreasing trend where the change is significant in downstream regions. According to Das [46], abrupt changes in the sediment load were found downstream from 1998 after the period of construction of dams on the upper part.
Therefore, from the above-mentioned outputs, it is evident that throughout 2017–2021, monsoonal variability and its repercussions dominate water discharge and sediment transport, resulting in the alteration of the study area’s riparian and coastal environment. The following section focuses on the coastal process induced by the hydrological processes operating within the study area, which have been modelled using DSAS.
3.2. Regression and Correlation Analysis
An analysis of bivariate linear regression between the observed and simulated datasets (rainfall, discharge, and soil loss) has been made to determine the impact of each on the persisting hydrological process within the study area. Considering the research period of the current study, linear regression calculations were made based on the observed mean rainfall and simulated mean discharge in the study area. As shown in Figure 10, the observed mean rainfall is the independent variable (x), while the SWAT simulated mean discharge is the dependent variable (y). The scatter plot in Figure 10 shows the value of the coefficient of determination is 0.93, between observed mean rainfall and simulated mean discharge, which depicts that rainfall plays a perfectly positive role in influencing the rate of discharge within the study area of Delta Sub-basin.
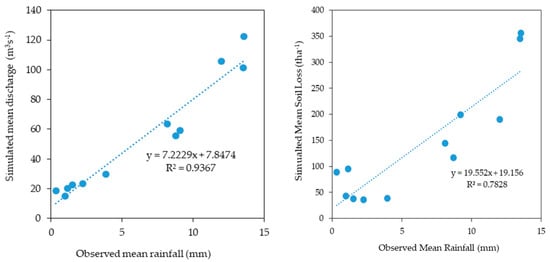
Figure 10.
A bivariate scatterplot demonstrates the linear correlation between observed and simulated parameters for 2017–2021.
In Figure 10, another scatter plot compares expected total soil loss with observed mean discharge in the Delta sub-basin between 2017 and 2021. The observed mean discharge data from the CWC’s Rajghat station is referred to as the independent variable (x), whereas the SWAT simulated soil loss values are referred to as the dependent variable (x) (y). The variables were investigated using a bivariate scatter plot and the linear regression method. The fact that the coefficient of determination is 0.84 indicates that the rate of discharge is actively impacting soil loss and that the two are tightly related.
3.3. DSAS Outputs
In the results of this study, the shoreline changes along the coast near the Subarnarekha River mouth reach in the elapsed period from 2017 to 2021 are easily detected and computed using geospatial techniques and automatic calculations by DSAS. In this study, two prominent statistical models, the EPR and SCE, depicted in Equations (7) and (8), were used to calculate the rate of changes in the shoreline. As mentioned above, the EPR is calculated by splitting the length of shoreline displacement by the time disparity between the dataset’s oldest (2017) and newest (2021) shorelines [68] regarding the current study. Thanks to the SCE method and a similar approach to Pramanick et al. [61], evaluation of the total variation in shoreline movements became possible taking into consideration all accessible shoreline positions and noting their lengths without respect to their specific daily dates from 2017 to 2021.
3.3.1. Changes along the Coastline as a Result of the End Point Rate Analysis
As per the end point rate (EPR) output, it depicts the transect-wise shoreline alteration rate that was recorded and plotted (Figure 11) and is determined using Equation (7). The presented graph emphasises the EPR depicting positive and negative values corresponding to shoreline change, indicating that the study region’s shoreline segment was dominated by erosion (bank retreat) in the period examined for the current study.
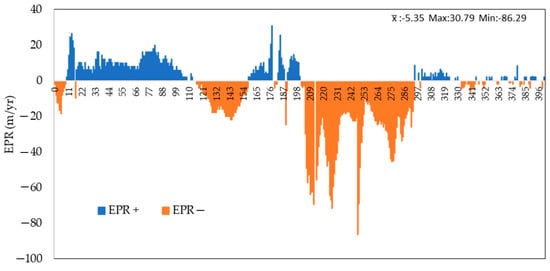
Figure 11.
Calculation curve of Subarnarekha’s estuarine section for shoreline change of Digha Coast. Axis x shows the transect number. The numbering of the transects increases towards the East.
The mean EPR value of the erosion rate is −5.35 m per year, and the highest and minimum EPR values are −86.29 and 30.79, respectively. The findings of the plot in Figure 11 show that this eroding rate has been significant, reaching −86.29 in the estimated plot’s medial section (transects no. 205-292). The erosion rate subsequently varies in the midpoint of the estimated plot, and the erosion rate is much greater in the plot’s middle than in the plot’s initial area. As observed in the extreme end segment of the graph, the amount of erosion-accretion is significantly balanced in this sector among the entire EPR curve.
In Figure 12, the shoreline position of the research area is shown along with the extent of shoreline erosion at the maximal, moderate, and minimal scales. Figure 12 depicts the geographical and temporal deterioration in the estuarine section from 2017 to 2021. The highest amount of shoreline erosion has been concentrated on the estuary’s eastern margin, as indicated by the red and orange transect lines in Figure 12. Figure 12 depicts moderate to lesser erosion along the western shores, represented by deep to light green-coloured transect lines.
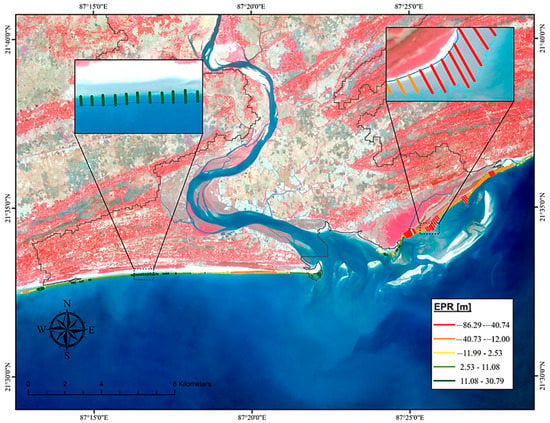
Figure 12.
Transect-wise EPR on the Landsat 8 OLI/TIRS image of the Subarnarekha’s estuarine section (Digha Coast).
3.3.2. Shoreline Change Envelope
The statistical technique of shoreline change envelope (SCE) is determined using Equation (8) and is used in this research for monitoring the distance among the shorelines closest to the baseline at every transect. The overall change in coastline movements was observed for all identifiable shoreline sites, and the rate of shift of shoreline was taken into account in relation to the baseline position. Figure 13 depicts the distance across the two farthest shorelines and the closest shoreline near the baseline along each transect. From 2017 to 2021, this depicts the total change in shoreline movement for all accessible coastline sites in the Subarnarekha’s estuary region under the Delta sub-basin. Figure 13 depicts how the shift in the coastline has spread throughout the research region. The variation in uniform was substantial in the Eastern sector’s medial region of the research area’s estuary section, extending from 239.4 to 431.4 m, as represented by deep red-coloured transact lines (Figure 13).
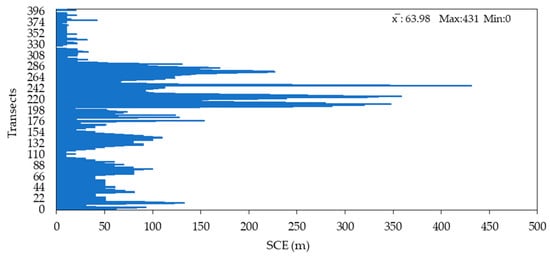
Figure 13.
SCE calculation curve of Subarnarekha’s estuarine section under Delta Sub-basin. The numbering of the transects increases towards the East.
The shift of the shoreline has been moderate to extreme across the estuarine section’s 115.3–431.4 m change, as indicated by orange and red transect lines. The shift was greatest on the estuary section’s western beaches, with 110–156 m of change represented by deep blue, green, and light blue transect lines in the DSAS-based scenario illustrated in Figure 14.
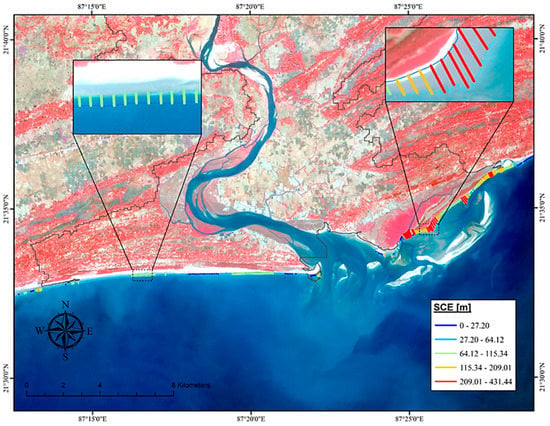
Figure 14.
Transect-wise SCE of the Subarnarekha’s estuarine section (Digha Coast).
3.3.3. Erosion-Accretion Scenario
The above-mentioned spatial analyses employing statistical methods (EPR and SCE) incorporating DSAS are carried out in a GIS environment to determine the degree of erosion and accretion along the shore of the estuarine part of the research region between 2017 and 2021. In the GIS platform, a polygon is formed alongside the land–water border of a shoreline segment for a particular year, yielding the area that has undergone erosion and accretion. As a result of using the aforementioned procedures, the year-by-year areal change that occurred in the study region was calculated. Table 3 depicts the magnitude of erosion and accretion and the persisting land cover classes that underwent erosion-accretion.

Table 3.
Erosion-Accretion scenario across the estuarine section of Subarnarekha River.
Table 3 shows that all three types of land cover, i.e., cropland, mangroves, and sand deposits, have experienced erosion, with sand deposits suffering the most (1.02 km2), mangroves experiencing 0.37 km2, and croplands incurring 0.14 km2. Regarding the situation of accumulation, sand deposits [49,69] of 0.67 sq. km have accumulated among the aforementioned land cover groups. This demonstrates the validity of the SWAT-simulated sediment transport scenario and the fact that, between 2017 and 2021, the sediment outflux was much more than the sediment inflow. Figure 15 provides a geographical illustration of the erosion-accretion scenario, demonstrating how the land-cover classes in the eastern portion of the shoreline have experienced erosion while sand deposits have accumulated in the western section. The analysis reflects the changes in the dynamics of the coastline position. It has been shown that over five years, the entire zone Subarnarekha River near the estuary faced several changes. Still, most of the shorelines are characterized by moderate accretion and a high erosional zone. The length of 15 km of shoreline falls under the erosional area, and 11.00 km of shoreline is dominated by an accretional pattern (most potent on the western coast). Maximum erosion has been identified in the eastern part of the study area. In the case of over 72 km coastal length of Digha Coast modelling by the DSAS techniques, Nath et al. [15,40] identified the same pattern of coastal development. Over 43 years (1975–2018), the shoreline shifting erosional activities were observed, with a maximum during 2000–2018 (the highest erosion −78.54 m year−1).
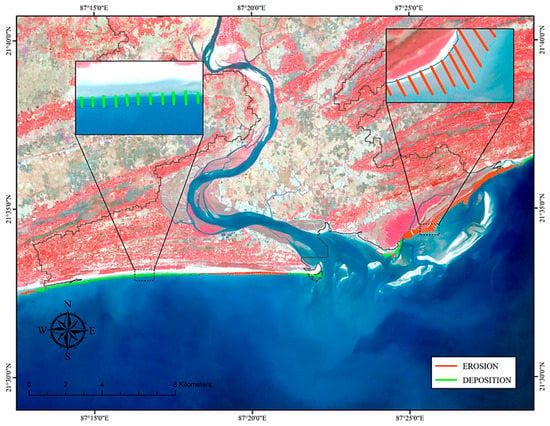
Figure 15.
Geospatial output illustration of the Erosion-Accretion scenario (2017–2021) of the Subarnarekha’s estuarine section (Digha Coast).
3.3.4. Shoreline Change Prediction
According to the change rate over time, the EPR model is a crucial technique employed in the present study to forecast changes in the coastal section [61], which has been applied to the study region. In order to forecast the coastline for the year 2027, this study has solely utilised the shorelines from the years 2012 and 2017, using Equation (9).
As a result, shorelines from 2012, 2017, and 2021 were used to anticipate the position of the study region’s estuarine sector in 2027. Coastal erosion caused the beach to retreat by 68 m between 2017 and 2021. Furthermore, the shoreline is projected to retreat by 36 m by 2027, compared to its current position in 2021 (Figure 16). This erosional pattern of Subarnarekha’s estuarine section development may result from a long-term change in sediment supply. It is believed that the present rate of continental erosion is being intensified by human activity [70], but at the same time, a decrease in the loads of transported sediment in the estuary sections of most large rivers in the world is being observed [71]. A report by Panda et al. [72] indicates that there is a negative change in the sediment load of the tropical rivers in India, while in a few rivers, the change is significant. Panda et al. [72] indicate the recent climate change and its intensification of human activities. Thus, the effects of ever higher discharge events during monsoon, which result in shortened backwater lengths on the estuary section and increased transport capacities, lead to increased erosion. Similar relationships were observed by Dong et al. [73] in the Selenga delta. In the case of the Subarnarekha River, the Delta is distinguished by a lower number of small channels. In the structure of the Delta, almost no channels lose their connection with the main riverbed network during the year, so the sediment is not retained.
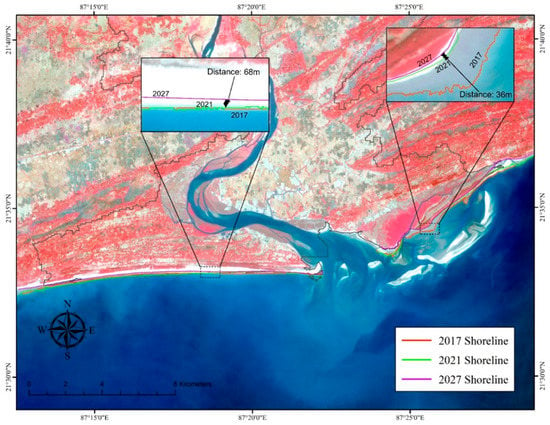
Figure 16.
The predicted shoreline position in 2027 of the Subarnarekha’s estuarine section (Digha Coast).
The aforementioned results generated using the methodology applied in the current study can be replicated and applied to other river deltaic estuaries worldwide since all steps of hydrological modelling and DSAS statistical analysis were performed using open-access software and remote sensing data. In India, monitoring abilities still need to be improved, and this approach possesses the potential to enhance the capacities for managing and conserving coastal zones and river estuaries.
The Subarnarekha river estuary and Digha Coast receive a vast population, mainly from the Kolkata metropolitan region, due to the tourism influx during the summer and winter vacations doubling the local ecosystem services demand. Moreover, the Subarnarekha Delta sub-catchment is experiencing a land-use intensification trend which, along with climate change (monsoon power intensity), can heighten the current problems associated with coastal erosion. Further research in this area should involve developed studies considering response scenarios to climate change to anticipate and respond to their potential impact.
4. Conclusions
RDE is usually classified as depositional zones where large amounts of sediments are stored due to the loss of stream power and the existence of abundant wetlands. Our study benefits from applying remote sensing data and coupling SWAT and DSAS models. The accurate simulation of water discharges and sediment fluxes helped us understand the influence of monsoon variability on the hydrological processes in the Subarnarekha basin. In particular, we conclude:
- The SWAT model efficiently assessed the influence and extent of climatic instability (monsoonal variability) across the Subarnarekha River basin and its sub-basins.
- Simulating hydrological processes, e.g., discharge, soil loss, and sediment loss, with SWAT and combining it with a statistical model of DSAS enabled the assessment of sediment dynamics in the basin’s estuarine region (study area).
- The SWAT model’s result indicates that sediment loss along the Delta sub-basin dramatically increased recently (28,737 tons in 2017 to 83,749 tons in 2021).
- In addition, the prediction-based geospatial output of the study area produced by the DSAS model supports the simulation of SWAT mentioned above.
- Accretion along the shoreline, as per DSAS output, is also supported by the tidal action-induced sediment inflow simulated by SWAT.
- The coupled model framework indicates that the right bank of the Subarnarekha estuary experienced coastal erosion due to sediment loss. In contrast, the left bank of the estuary experienced deposition due to sediment intake.
As previously mentioned, since all steps of the hydrological modelling and DSAS statistical analysis were carried out using open-source software and remote sensing datasets, this study, which uses a remote sensing-based, coupled hydrological and coastal modelling approach, can be replicated and adapted to other river deltaic estuarine environments in the world.
Author Contributions
Conceptualisation, R.A.; methodology, R.A., M.H. and A.M.; software, R.A.; validation, R.A., M.H. and A.M.; formal analysis, R.A., M.H. and A.M.; investigation, R.A. and A.M.; resources, R.A., M.H. and A.M.; writing—original draft preparation, R.A., M.H. and A.M.; writing—review and editing, R.A., M.H. and A.M.; visualisation, R.A., M.H. and A.M.; supervision, A.M. and M.H.; funding acquisition: R.A. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Kazimierz Wielki University with regular financial support from the Polish Ministry of Science and Education.
Data Availability Statement
Publicly available data sets were analysed in this study. These data can be found here: Indian Metrological Department (www.mausam.imd.gov.in), accessed on 20 April 2022.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| CRFG | Coarse Fragment Factor |
| CWC | Central Water Commission |
| DEM | Digital Elevation Model |
| DN | Digital Number |
| DSAS | Digital Shoreline Analysis System |
| EPR | End Point Rate |
| HRU | Hydrological Response Unit |
| IMD | Indian Metrological Department |
| LMS | Least Median of Squares |
| LULC | Land use and land cover |
| LRR | Linear Regression Rate |
| MUSLE | Modified Universal Soil Loss Equation |
| NSM | Net Shoreline Movement |
| NSE | Nash–Sutcliffe Efficiency |
| PBIAS | Per cent Bias |
| PSMSL | Permanent Service of the Mean Sea Level |
| RDE | River Deltaic Estuaries |
| R2 | Coefficient Of Determination |
| RMSE | Root mean square error |
| RLR | Revised Local Reference |
| SCE | Shoreline Change Envelope |
| SUFI-2 | Sequential Uncertainty Fitting Version-2 |
| SWAT | Soil and Water Assessment Tool |
| SWAT CUP | SWAT Calibration and Uncertainty Program |
| SRTM | Shuttle Radar Topography Mission |
| TPMC | Terranear Project Management Consultancy |
| USGS | United States Geological Survey |
Appendix A
The Delta sub-basin owes its name to its deltaic geomorphology, composed of lateritic uplands, older, younger, and recent deltaic plains [48,74]. The land use is dominated by forested areas (36.3%), followed by vegetated lands (49.31%), water bodies (3.5%), rivers (2.93%), and sand deposits across the river course (1.8%) (Figure A2). The settlement has a minuscule percentage of the total area, accounting for 0.79%. Lateritic uplands are composed of iron- and aluminium-rich gravelly minerals dominated by Ferric Luvisols (Figure A3) overlying Archean and Gondwana rocks, collectively forming the basin margin zone [48]. Other than that, the distinctive formations of the deltaic plain (Older, Younger, and Recent) developed during the Late Pleistocene to Early Holocene period mainly due to concurrent sea level changes [49,75]. The old deltaic plain over the lower course consists of valley-cut with valley-filled terraces generated by fluvial, aquatic, and estuarine processes during the aggradation phase of grey clayey soil (Eurtric Luvisols) with concretionary nodules [76,77]. The Subarnarekha and associated river systems have separated the old deltaic plain from the lateritic uplands, and the elevation difference between the latter and the former (Figure A1) is mostly owing to neo-tectonic activity and pressure release caused by a coastal retreat into the sea [49]. The Younger Deltaic Plain stretches nearly to the coast of the study area from the Old Deltaic Plain’s margin. It is narrower (around 20 km) in the south and more comprehensive (around 45 km) in the north. It is covered by Eutric Luvisols (Figure A3), made up of fine sand, silt, cover, dark grey clay, and mudflats formed during flooding events by marine and estuarine processes [77]. During the Late Pleistocene period, the Subarnarekha River and its tributaries (Raru, Kanchi, Karkari, Kharkai, Garra, Sankh, Jumar, and Dulung) deposited the aforementioned materials from the Upper Laterite uplands [69,78]. Then, the Recent Deltaic Plains developed by open marine, external, and interior estuarine processes throughout the Holocene phase of landform evolution. The depositional surfaces of the Older, Younger, and Recent deltaic plains are now entirely covered by Holocene alluvium carried by the same river since sea levels changed concurrently with the relative elevation and subsidence of basin zones in past geological times [69]. Aside from the deltaic plains, other geomorphic features, such as beaches, mud flats, and dunes, have evolved in the study area during the preceding 6000 years [79].
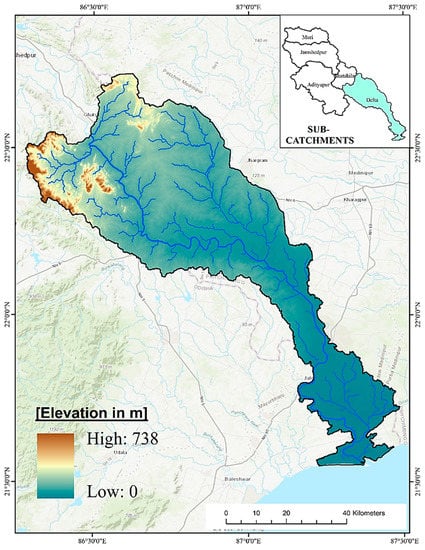
Figure A1.
The elevation map of the Delta Sub-basin of the Subarnarekha River (Based on: srtm.csi.cgiar.org (accessed on 2 May 2022)).
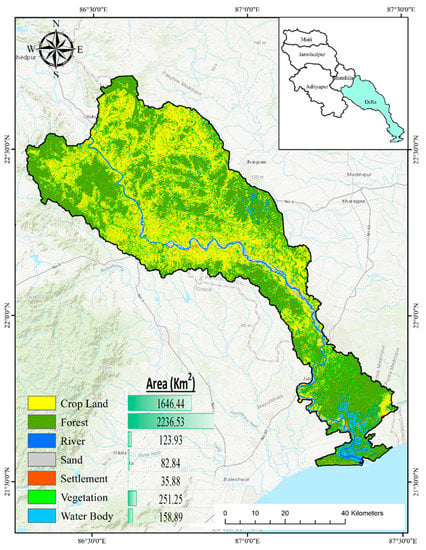
Figure A2.
LULC (Land use and Land cover) map of Delta sub-basin (Based on: earthexplorer.usgs.gov (accessed on 2 May 2022)).
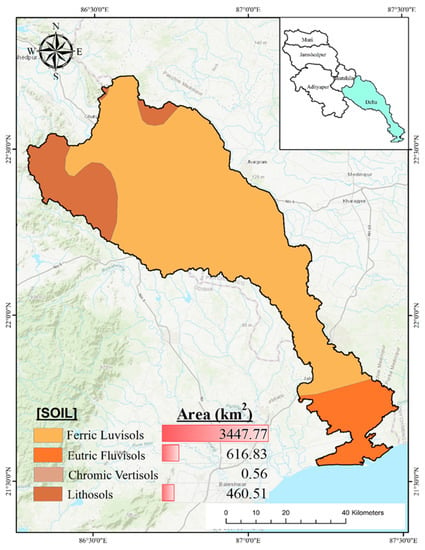
Figure A3.
Soil map of Delta sub-Basin (Based on: fao.org (accessed on 2 May 2022)).
The Subarnarekha Basin’s sub-basins were identified in the study’s 90 m grid resolution DEM SRTM 2011 [80]. This dataset is the most critical parameter for delineating the five sub-basins: Muri, Jamshedpur, Adityapur, Ghatshila, and Delta (Figure A1). Figure A1 demonstrates that the basin’s highest elevation is 945 m, mainly across the northwestern section. Approximately 62% of the height is below 283 m, according to the hypsometric curve illustrated in Figure A1. In addition, the lower section of the Subarnarekha basin, under the states of West Bengal and Odisha, constitutes the area (Delta sub-basin) under the current study (Figure A1). Using the DEM dataset, it has been determined that the study area consists of four physiographic subdivisions (plateau, transition zone, alluvial reaches, deltaic plain) with a maximum elevation of 738 m. In the north-west and in the south-east, the elevation is nil or equal to sea level since the Subarnarekha river meets sea level in this estuarine section.
One of the most crucial components of the hydrological mechanism is land use and land cover (LULC). Here, a series of seven different LULC classes was assigned to the study area (Figure A2) using the Arc-SWAT interface, including WATR (River, Water Body), WETN (Sand Deposits), BARR (Barren or Fallow Land), FRST (Forest and Vegetation), and URML (Settlement).
The complexity of the various soil classes was considered when compiling the soil data. The necessary soil information for the Delta sub-basin of Subarnarekha Basin is taken from the DSMW (Digital Soil Map of the World) [81]. In the sub-basin, there are four textural classes of soil: clay, clay loam, sandy clay loam, and sandy loam. When taking into account textural classifications, the soil groups were separated for the sub-basin: ferric luvisols (76.18%), eutric fluvisols (13.63%), lithosols (10.18%), chromic vertisols (0.012%) (Figure A3).
Meteorological inputs drive all of the processes modelled in the Delta sub-basin. SWAT considers climatic variables, such as rainfall, ambient temperature, wind speed, relative humidity, and solar radiation. Daily gridded precipitation and temperature data from IMD (India Metrological Department) stations over the research region from 2017 to 2021 were used for the current study. Each station’s surroundings have comparable climate characteristics. Thus, monthly temperature and rainfall data are shown in Table A1 and Figure A4.

Table A1.
Monthly temperature and precipitation statistics of Delta Sub-basin (2017–2021). Data Source: IMD.
Table A1.
Monthly temperature and precipitation statistics of Delta Sub-basin (2017–2021). Data Source: IMD.
| Months | Maximum Temperature (°C) | Minimum Temperature (°C) | Average Temperature (°C) | Average Rainfall (mm) |
|---|---|---|---|---|
| January | 20.9 | 19.1 | 19.9 | 9.5 |
| February | 23.5 | 21.2 | 22.7 | 25.3 |
| March | 28.1 | 26 | 26.8 | 41.1 |
| April | 29.3 | 28.3 | 28.8 | 110.7 |
| May | 30.05 | 29.1 | 29.6 | 262.5 |
| June | 30 | 29.3 | 29.7 | 273.6 |
| July | 29.4 | 29 | 29.2 | 415.3 |
| August | 29.2 | 29 | 29 | 422.4 |
| September | 29.15 | 28.58 | 28.85 | 355.48 |
| October | 28.36 | 27.65 | 28.042 | 247.388 |
| November | 25.13 | 24.25 | 24.634 | 64.268 |
| December | 21.13 | 20.38 | 20.84 | 35.224 |
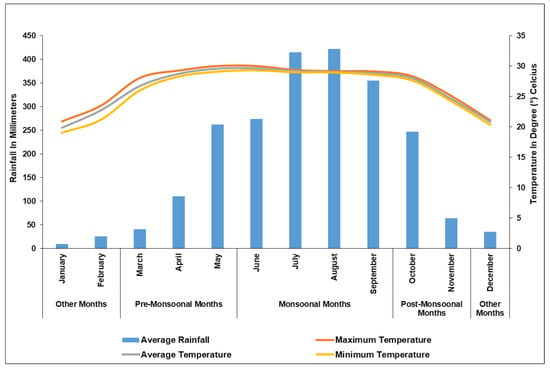
Figure A4.
Monthly temperature and precipitation graph for the Subarnarekha River, area of Delta Sub-basin (2017–2021). Data Source: IMD.
Appendix B
Appendix B.1. Calibration and Validation of SWAT
One of the results of the work carried out is the successful calibration and validation of our SWAT model. Calibration entails altering model parameters to reconcile sample output and findings with standard observed data in order to decrease prediction inadequacies for a particular model setup. Validation, on the other hand, verifies the model’s ability to render accurate simulations. The calibration result is as shown in Figure A5. A combination of goodness-of-fit measures (Table A2), including R2, NSE (Nash–Sutcliffe efficiency), RMSE (root mean square error), and PBIAS, are used to evaluate the model’s ability to deal with discharge data acquired from gauge stations, as a percentage of deviation from observed data.

Table A2.
Statistical results of the model’s effectiveness premised on the model’s validation and calibration.
Table A2.
Statistical results of the model’s effectiveness premised on the model’s validation and calibration.
| Statistical Index | Range | Calibration | Validation |
|---|---|---|---|
| R2 | 0, 1 | 0.66 | 0.83 |
| NSE | ∞, 1 | 0.34 | 0.67 |
| RMSE | 0, 1 | 0.68 | 0.92 |
| PBIAS | −∞, ∞ | −32.1 | −6.2 |
R2 is a measure of how much of the overall variance shown by the conditions is present. As a result, R2 has calibration-validation values of 0.76 and 0.83 (Table A2). R2 runs from 0.0 to 1.0, with higher values indicating better outcomes and 0.5 being deemed sufficient [82].
The present study’s calibration and validation values are 0.66 and 0.83, respectively. According to Nash and Sutcliffe [59], NSE ranges between −∞ to 1, with values ranging from 0.0 to 1.0 indicating adequate levels of model performance. While 0.5 is regarded as decent, 0.65 is considered efficient, and 0.75–1.0 is considered excellent model competence in particular.
The validation and calibration values for the RMSE test are 0.64 and 0.92, respectively. However, it is widely accepted that the lower the RMSE value, the finer the model performance [83].
According to the current analysis, the validation and calibration values for PBIAS are −25 and −6.2, respectively. In PBIAS, a value less than 20% is regarded as acceptable, a value between 20% and 40% is considered good, and a value greater than 40% is deemed inadequate [83], as determined by Equation (8).
Other than that, p and d factors were employed to estimate calibration capacity and uncertainty estimates [58]. The p-factor was calculated by dividing the proportion of expected outcomes by 95PPU (“95% prediction uncertainty”). The value of 95PPU is estimated using the Latin hypercube sampling method, with 5% of the bad simulations disabled at an average sample level of 2% and 97.5%. The proportion of the standard deviation of observed data to the average 95 PPU bandwidth represents the calibration’s capability [84]. The p and d factors exhibit values of 0.26 and 0.65, correspondingly. When the model’s uncertainties are taken into account, these numbers indicate that the calibration was adequate, and the graph can be traced in Figure A5.
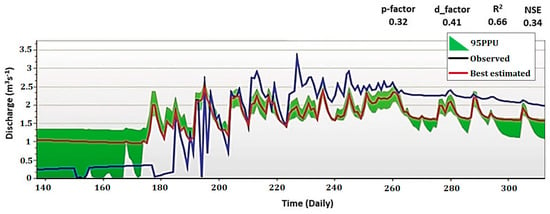
Figure A5.
Observed and estimated discharge, 95% model uncertainty, and best approximation derived from SWAT after the calibration—original chart generated from SWAT Calibration and Uncertainty Program.
For the SWAT model, validation of simulated discharge with daily-observed flows makes use of a data collection of the observed daily discharge dataset from 2017 to 2018. The R2, NSE, RMSE, and PBIAS were used to test validation output (Figure A6). Despite the SWAT model effectively replicating the persisting discharge scenario, daily and observed discharge discrepancies were detected. The model overestimated discharge on the sub-basin during the pre-monsoon months, particularly under zero-flow circumstances. Analysis of the daily discharge scenario found that observed discharge conditions in the study area were not as constant as those estimated by SWAT during dry periods (Figure A6). During the monsoon months of 2017, the model underestimated flows while overestimating flows during the monsoon months of 2018 (Figure A6). The observed discharge rose and dropped quickly, and it did not last as long as the simulated discharge.
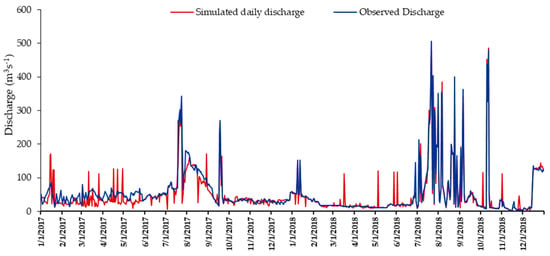
Figure A6.
Validation of SWAT simulated discharge with daily observed discharge from Rajghat hydrological station from 2017 to 2018.
Appendix B.2. Validation of DSAS
As illustrated above, the DSAS outputs show shorelines for 2017 and 2021. However, using Landsat data for 2013, 2017, and 2021, the study area shorelines were extracted mainly to validate the DSAS model results. Firstly, the shorelines of 2013 and 2017 were used to generate a predicted shoreline for 2021. An error was generated when the predicted shoreline of 2021 was cross-validated with the actual shoreline of 2021 extracted from satellite data, which was corrected. Then, using 2017 and 2021 shorelines, the projected shoreline of 2027 was estimated.
Furthermore, for validating the current investigation using DSAS, which is illustrated above, the Sea-Level (SL) dataset was collected from the PSMSL international archive. Thanks to this research, we can depict the yearly change in seal level computed from the RLR time-series data (2000–2020) in Haldia, Paradip, and Diamond Harbour gauge stations (Figure 2). Time series statistics demonstrate that negative development was severe in SL, but there was also a sequential rise in SL via fluctuations over the past few years. The SL was lowest in 2003 (6985 mm) at Paradip and highest in 2013 (7230 mm) at Diamond Harbour, with a difference of 245 mm. The change in SL from 2017 had a significant effect on the area of the estuary and coastline sector of the research area, according to RLR statistics of these three RLR gauge stations, with a mean SL of 7098.2 mm. It can be supposed by estimating from the statistics mentioned above and figures that if the rate of change of shoreline and SL rise persists in the same manner, the extent and position of the shoreline in the immediate future may conform to the projected shoreline (2027) shown in Figure 16.
References
- Li, Y.; Chen, B.M.; Wang, Z.G.; Peng, S.L. Effects of temperature change on water discharge, and sediment and nutrient loading in the lower Pearl River basin based on SWAT modelling. Hydrol. Sci. J. 2011, 56, 68–83. [Google Scholar] [CrossRef]
- Bianchi, T.S. Biogeochemistry of Estuaries; Oxford University Press on Demand: Oxford, UK, 2007. [Google Scholar]
- Costanza, R.; de Groot, R.; Sutton, P.; van der Ploeg, S.; Anderson, S.J.; Kubiszewski, I.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Glob. Environ. Chang. 2014, 26, 152–158. [Google Scholar]
- Habel, M.; Mechkin, K.; Podgorska, K.; Saunes, M.; Babiński, Z.; Chalov, S.; Absalon, D.; Podgórski, Z.; Obolewski, K. Dam and reservoir removal projects: A mix of social-ecological trends and cost-cutting attitudes. Sci. Rep. 2020, 10, 1–16. [Google Scholar]
- Walling, D.E.; Fang, D. Recent trends in the suspended sediment loads of the world’s rivers. Glob. Planet Chang. 2003, 39, 111–126. [Google Scholar]
- Cohen, S.; Kettner, A.J.; Syvitski, J.P.M. Global suspended sediment and water discharge dynamics between 1960 and 2010: Continental trends and intra-basin sensitivity. Glob. Planet Chang. 2014, 115, 44–58. [Google Scholar] [CrossRef]
- Chalov, S.; Prokopeva, K.; Habel, M. North to South Variations in the Suspended Sediment Transport Budget within Large Siberian River Deltas Revealed by Remote Sensing Data. Remote Sens. 2021, 13, 4549. [Google Scholar] [CrossRef]
- Arkema, K.K.; Guannel, G.; Verutes, G.; Wood, S.A.; Guerry, A.; Ruckelshaus, M.; Kareiva, P.; Lacayo, M.; Silver, J.M. Coastal habitats shield people and property from sea-level rise and storms. Nat. Clim. Chang. 2013, 3, 913–918. [Google Scholar] [CrossRef]
- Masselink, G.; Russell, P. Impacts of climate change on coastal erosion. MCCIP Sci. Rev. 2013, 2013, 71–86. [Google Scholar]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; van de Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar]
- Lins-de-Barros, F.M. Integrated coastal vulnerability assessment: A methodology for coastal cities management integrating socioeconomic, physical and environmental dimensions-Case study of Região dos Lagos, Rio de Janeiro, Brazil. Ocean Coast Manag. 2017, 149, 1–11. [Google Scholar]
- Kantamaneni, K.; Phillips, M.; Thomas, T.; Jenkins, R. Assessing coastal vulnerability: Development of a combined physical and economic index. Ocean Coast Manag. 2018, 158, 164–175. [Google Scholar]
- Leatherman, S.P.; Zhang, K.; Douglas, B.C. Sea level rise shown to drive coastal erosion. Eos Trans. Am. Geophys. Union 2000, 81, 55–57. [Google Scholar]
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Global warming and coastal erosion. Clim. Chang. 2004, 64, 41–58. [Google Scholar] [CrossRef]
- Nath, A.; Koley, B.; Saraswati, S.; Choudhury, T.; Um, J.S.; Ray, B.C. Geospatial analysis of short term shoreline change behavior between Subarnarekha and Rasulpur estuary, east coast of India using intelligent techniques (DSAS). GeoJournal 2022, 1–21. [Google Scholar] [CrossRef]
- Ghosh, T.; Hajra, R.; Mukhopadhyay, A. Island erosion and afflicted population: Crisis and policies to handle climate change. In Climate Change Management; Springer: Berlin/Heidelberg, Germany, 2014; pp. 217–225. [Google Scholar]
- Khojasteh, D.; Glamore, W.; Heimhuber, V.; Felder, S. Sea level rise impacts on estuarine dynamics: A review. Sci. Total Environ. 2021, 780, 146470. [Google Scholar]
- Sondi, I.; Lojen, S.; Juračić, M.; Prohić, E. Mechanisms of land–sea interactions–the distribution of metals and sedimentary organic matter in sediments of a river-dominated Mediterranean karstic estuary. Estuar. Coast Shelf. Sci. 2008, 80, 12–20. [Google Scholar] [CrossRef]
- Alongi, D.M. Coastal Ecosystems Processes; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Nayak, S. Use of satellite data in coastal mapping. Indian Cartogr. 2002, 22, 1. [Google Scholar]
- Thia-Eng, C. Essential elements of integrated coastal zone management. Ocean Coast Manag. 1993, 21, 81–108. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling And Assessment Part I: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT 2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. Int. J. 2005, 19, 563–572. [Google Scholar]
- Dadhwal, V.K.; Mishra, N.; Aggarwal, S.P. Hydrological Simulation of Mahanadi River Basin and Impact of Land Use/Land Cover Change on Surface Runoff Using a Macro Scale Hydrological Model. ISPRS TC VII Symp. –100 Years ISPRS Vienna Austria 2010, XXXVIII, 165–170. [Google Scholar]
- Srinivasan, R.; Santhi, C.; Harmel, R.D.; Griensven, A. v SWAT: Model Use, Calibration, and Validation. Am. Soc. Agric. Biol. Eng. 2012, 55, 1491–1508. [Google Scholar]
- Chanapathi, T.; Thatikonda, S.; Raghavan, S. Analysis of Rainfall Extremes and Water Yield of Krishna River Basin Under Future Climate Scenarios. J. Hydrol. Reg. Stud. 2018, 19, 287–306. [Google Scholar] [CrossRef]
- Rathjens, H.; Oppelt, N.; Bosch, D.D.; Arnold, J.G.; Volk, M. Development of a grid-based version of the SWAT landscape model. Hydrol. Process 2015, 29, 900–914. [Google Scholar] [CrossRef]
- Hallouz, F.; Meddi, M.; Mahé, G.; Alirahmani, S.; Keddar, A. Modeling of Discharge and sediment transport through the SWAT Model in the basin of Harraza (Northwest of Algeria). Water Sci. 2018, 32, 79–88. [Google Scholar] [CrossRef]
- Acharyya, R.; Pramanick, N.; Mukherjee, S.; Ghosh, S.; Chanda, A.; Pal, I.; Mitra, D.; Mukhopadhyay, A. Evaluation of catchment hydrology and soil loss in non-perennial river system: A case study of Subarnarekha Basin, India. Model Earth Syst. Env. 2021, 8, 2401–2429. [Google Scholar] [CrossRef]
- Nguyen, B.N.; Nguyen, H.K.L. Basin resources management: Simulating soil erosion risk by soil and water assessment tool (SWAT) in Ta Trach river watershed, central Vietnam. J. Vietnam. Environ. 2014, 6, 165–170. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.; Choi, C.; Hwang, C. Forecasting the Potential Effects of Climatic and Land-Use Changes on Shoreline Variation in Relation to Watershed Sediment Supply and Transport. J. Coast Res. 2017, 33, 874–888. [Google Scholar]
- Olaoye, I.A.; Confesor, R.B.; Ortiz, J.D. Impact of seasonal variation in climate on water quality of old woman creek watershed ohio using swat. Climate 2021, 9, 50. [Google Scholar]
- Yaduvanshi, A.; Srivastava, P.; Worqlul, A.W.; Sinha, A.K. Uncertainty in a Lumped and a Semi-Distributed Model for Discharge Prediction in Ghatshila Catchment. Water 2018, 10, 381. [Google Scholar]
- Madhusudana Rao, C.; Bardhan, A.; Patra, J.P. Assessment of hydrological response in Subarnarekha river basin under anticipated climate change scenarios. Glob. Nest J. 2020, 22, 207–219. [Google Scholar]
- Dandapat, A.K. Evaluation of loss models and effect of LULC changes on surface runoff in Subarnarekha River Basin in India. ISH J. Hydraul. Eng. 2018, 27, 542–555. [Google Scholar]
- Murmu, R.S. Murmu, R.S. Murmu Simulation of Runoff for Subarnarekha Catchment Using SWAT Model. In Water Security and Sustainability: Proceedings of Down To Earth 2019; Bhuiyan, C., Ed.; Springer: Singapore, 2021; Volume 115, pp. 157–168. [Google Scholar]
- Oyedotun, T.D.T. Shoreline Geometry: DSAS as a Tool for Historical Trend Analysis. Geomorphol. Tech. 2014, 2, 1–12. [Google Scholar]
- Bheeroo, R.A.; Chandrasekar, N.; Kaliraj, S.; Magesh, N.S. Shoreline change rate and erosion risk assessment along the Trou Aux Biches–Mont Choisy beach on the northwest coast of Mauritius using GIS-DSAS technique. Environ. Earth Sci. 2016, 75, 444. [Google Scholar] [CrossRef]
- Nassar, K.; Mahmod, W.E.; Fath, H.; Masria, A.; Nadaoka, K.; Negm, A. Shoreline change detection using DSAS technique: Case of North Sinai coast, Egypt. Mar. Georesources Geotechnol. 2018, 37, 81–95. [Google Scholar]
- Nath, A.; Koley, B.; Saraswati, S.; Ray, B.C. Identification of the coastal hazard zone between the areas of Rasulpur and Subarnarekha estuary, east coast of India using multi-criteria evaluation method. Model Earth Syst. Environ. 2021, 7, 2251–2265. [Google Scholar]
- Thieler, E.R.; Himmelstoss, E.A.; Zichichi, J.L.; Ergul, A. The Digital Shoreline Analysis System (DSAS) Version 4.0-an ArcGIS Extension for Calculating Shoreline Change; US Geological Survey: Asheville, NC, USA, 2009. [Google Scholar]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide; US Geological Survey: Reston, Virginia, USA, 2018. [Google Scholar]
- Huang, C.; Wylie, B.; Yang, L.; Homer, C. Derivation of a tasselled cap transformation based on Landsat 7 at-satellite reflectance. Int. J. Remote Sens. 2002, 23, 1741–1748. [Google Scholar]
- Maiti, S.; Bhattacharya, A.K. Shoreline change analysis and its application to prediction: A remote sensing and statistics based approach. Mar. Geol. 2009, 257, 11–23. [Google Scholar]
- Mukhopadhyay, A.; Mukherjee, S.; Mukherjee, S.; Ghosh, S.; Hazra, S.; Mitra, D. Automatic shoreline detection and future prediction: A case study on Puri Coast, Bay of Bengal, India. Eur. J. Remote Sens. 2012, 45, 201–213. [Google Scholar]
- Das, S. Four decades of water and sediment discharge records in Subarnarekha and Burhabalang basins: An approach towards trend analysis and abrupt change detection. Sustain. Water Resour. Manag. 2019, 5, 1665–1676. [Google Scholar] [CrossRef]
- Negi, S.S. Biodiversity and Its Conservation in India; Indus Publishing: New Delhi, India, 1993. [Google Scholar]
- Paul, A.K. Coastal Geomorphology and Environment: Sundarban Coastal Plain, Kanthi Coastal Plain, Subarnarekha Delta Plain; ACB Publications: Washington, DC, USA, 2002. [Google Scholar]
- Jana, S.; Paul, A.K. Assessment of morphogenetic sedimentary depositional environments of different morphological surfaces of middle-lower and deltaic courses of Subarnarekha River. J. Coast. Sci. 2018, 6, 1–11. [Google Scholar]
- National Oceanography Centre Permanent Service for Mean Sea Level, Tide Gauge Data. Available online: https://www.psmsl.org/ (accessed on 7 May 2022).
- Nandy, S.; Bandyopadhyay, S. Trend of Sea Level Change in the Hugli Estuary, India; NISCAIR-CSIR: New Delhi, India, 2011. [Google Scholar]
- Kumar Mandal, U.; Bikas Nayak, D.; Samui, A.; Kumar Jana, A.; Mullick, S.; Lama, T.D.; Bhardwaj, A.K.; Mahanta, K.K.; Mandal, S.; Raut, S.; et al. Trend of Sea-level-rise in West Bengal Coast. Indian J. Coast. Agric. Res. 2018, 36, 64–73. [Google Scholar]
- Hosseini, S.H.; Khaleghi, M.R. Application of SWAT model and SWAT-CUP software in simulation and analysis of sediment uncertainty in arid and semi-arid watersheds (case study: The Zoshk–Abardeh watershed). Model Earth Syst. Environ. 2020, 6, 2003–2013. [Google Scholar] [CrossRef]
- Flügel, W. Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany. Hydrol. Process 1995, 9, 423–436. [Google Scholar] [CrossRef]
- Aznarez, C.; Jimeno-Sáez, P.; López-Ballesteros, A.; Pacheco, J.P.; Senent-Aparicio, J. Analysing the impact of climate change on hydrological ecosystem services in Laguna del Sauce (Uruguay) using the SWAT model and remote sensing data. Remote Sens. 2021, 13, 2014. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Technical Report no. 406; Texas Water Resources Institute: College Station, TX, USA, 2011; pp. 641–647. [Google Scholar]
- Williams, J.R. Predicting Sediment Yield Frequency for Rural Basins to Determine Man’s Effect on Long-Term Sedimentation; IAHS Publication: Wallingford, UK, 1975; pp. 105–108. [Google Scholar]
- Abbaspour, K.C. SWAT CUP: SWAT Calibration and Uncertainity Program—A User Manual; Eawag: Dübendorf, Switzerland, 2015; pp. 16–70. [Google Scholar]
- Nash, J.E.; Stutcliffe, J. v River Flow Forecasting through Conceptual Models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Mishra, S.K.; Tyagi, J.; Singh, V.P.; Singh, R. SCS-CN-based modeling of sediment yield. J. Hydrol. 2006, 324, 301–322. [Google Scholar]
- Pramanick, N.; Islam, E.; Banerjee, S.; Mukherjee, R.; Maity, A.; Acharyya, R.; Chanda, A.; Pal, I.; Mukhopadhyay, A. Threats from Sea Level Rise and Erosion. Urban Ecol. Glob. Clim. Chang. 2022, 16, 321–345. [Google Scholar]
- Ryu, J.-H.; Won, J.-S.; Min, K.D. Waterline extraction from Landsat TM data in a tidal flat: A case study in Gomso Bay, Korea. Remote Sens. Environ. 2002, 83, 442–456. [Google Scholar] [CrossRef]
- Nandi, S.; Ghosh, M.; Kundu, A.; Dutta, D.; Baksi, M. Shoreline shifting and its prediction using remote sensing and GIS techniques: A case study of Sagar Island, West Bengal (India). J. Coast Conserv. 2016, 20, 61–80. [Google Scholar]
- Buchanan, T.J.; Somers, W.P. Discharge measurements at gaging stations. In Techniques of Water-Resources Investigation; Turnipseed, D.P., Sauer, V.B., Eds.; U.S. Geological Survey: Reston, Virginia, USA, 2010; p. 106. [Google Scholar]
- Yuan, Y.; Xiong, D.; Han, W.; Liu, L.; Li, W.; Chidi, C.; Dahal, N.M.; Neupane, N. Using 137Cs and 210Pbex to trace soil erosion rates for a small catchment in the mid-hills of Nepal. J. Soils Sediments 2021, 21, 403–418. [Google Scholar]
- Worlddata.info Cyclones in India. Available online: https://www.worlddata.info/asia/india/cyclones.php (accessed on 15 November 2022).
- Bouwman, A.F. The role of soils and land use in the greenhouse effect. Neth. J. Agric. Sci. 1989, 37, 13–19. [Google Scholar] [CrossRef]
- Fenster, M.S.; Dolan, R.; Elder, J.F. A new method for predicting shoreline positions from historical data. J. Coast Res. 1993, 9, 147–171. [Google Scholar]
- Jana, S.; Paul, A.K. Genetical Classification of Deltaic and Non Deltaic Sequences of Landforms of Subarnarekha Middle Course and Lower Course Sections in Odisha and Parts of West Bengal with Application of Geospatial Technology. J. Coast. Sci. 2018, 5, 16–26. [Google Scholar]
- Wilkinson, B.H.; McElroy, B.J. The impact of humans on continental erosion and sedimentation. GSA Bulletin. 2007, 119, 140–156. [Google Scholar] [CrossRef]
- Syvitski, J.P.; Kettner, A.J.; Overeem, I.; Hutton, E.W.; Hannon, M.T.; Brakenridge, G.R.; Nicholls, R.J. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar]
- Panda, D.K.; Kumar, A.; Mohanty, A. Recent trends in sediment load of the tropical (Peninsular) river basins of India. Glob. Planet Chang. 2011, 75, 108–111. [Google Scholar] [CrossRef]
- Dong, T.Y.; Nittrouer, J.A.; Il’icheva, E.; Pavlov, M.; McElroy, B.; Czapiga, M.J.; Ma, H.; Parker, G. Controls on gravel termination in seven distributary channels of the Selenga River Delta, Baikal Rift basin, Russia. Geol. Soc. Am. Bull. 2016, 128, 1297–1312. [Google Scholar] [CrossRef]
- Biswas, A. Laterites and lateritoids of Rarh Bengal. Explorations in the Tropics. Prof. KD Dikshit Felicitation Vol. Comm. 1987, 6, 48–54. [Google Scholar]
- Niyogi, D. Quaternary mapping in plains of West Bengal. In Program of the Seminar on Geomorphology, Geohydrology and Geotechnics of the Lower Ganga Basin; Indian Institute of Technology: Khargpurs, India, 1972; Volume 86, Available online: https://www.automationjournal.org/download/indian-geomorphology/ (accessed on 20 May 2022).
- Niyogi, D.; Mallick, S. Morphology of the Midnapore district, West Bengal. In Proc. Seminar Geomorphology, Geohydrology and Geotectonic of the Lower Ganga Basin; Indian Institute of Technology: Kharagpurs, India, 1972; Volume 86, Available online: https://www.automationjournal.org/download/indian-geomorphology/ (accessed on 20 May 2022).
- Mallick, S.; Bhattacharya, A.; Niyogi, D. A comparative study of the Quaternary formations in the Baitarani valley, Orissa with those of the Damodar-Ajoy delta area, Lower Ganga Basin. In Proc. Seminar Geomorphology, Geohydrology and Geotectonic of the Lower Ganga Basin; Indian Institute of Technology: Kharagpurs, India, 1972; Volume 86, pp. 91–104. Available online: https://www.automationjournal.org/download/indian-geomorphology/ (accessed on 20 May 2022).
- Singh, A.K.; Giri, S. Subarnarekha River: The Gold Streak of India. In The Indian Rivers: Scientific and Socio-Economic Aspects; Singh, D., Ed.; Springer Singapore: Singapore, 2018; pp. 273–285. [Google Scholar]
- Dey, S.; Ghosh, P.; Nayak, A. The influences of natural environment upon the evolution of sands dunes in tropical environment along Medinipur Coastalarea, India. Indones. J. Geogr. 2005, 37, 1. [Google Scholar]
- Jarvis, A.; Reuter, H.; Nelson, A.; Guevara, E. SRTM 90m DEM Digital Elevation Database. Available online: http://srtm.csi.cgiar.org (accessed on 2 January 2020).
- FAO-UN-Land and Water Division (CBL). Digital Soil Map of the World. Available online: www.fao.org (accessed on 5 December 2019).
- Dodge, Y. Coefficient of Determination. In The Concise Encyclopedia of Statistics; Springer New York: New York, NY, USA, 2008; pp. 88–91. [Google Scholar]
- AgriMetSoft Online Calculators. 2019. Available online: https://agrimetsoft.com/ (accessed on 6 February 2023).
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R. Assessment of Future Climate Change Impacts on Water Resources of Upper Sind River Basin, India Using SWAT Model. Water Resour. Manag. 2013, 27, 3647–3662. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).