Drone Photogrammetry for Accurate and Efficient Rock Joint Roughness Assessment on Steep and Inaccessible Slopes
Abstract
:1. Introduction
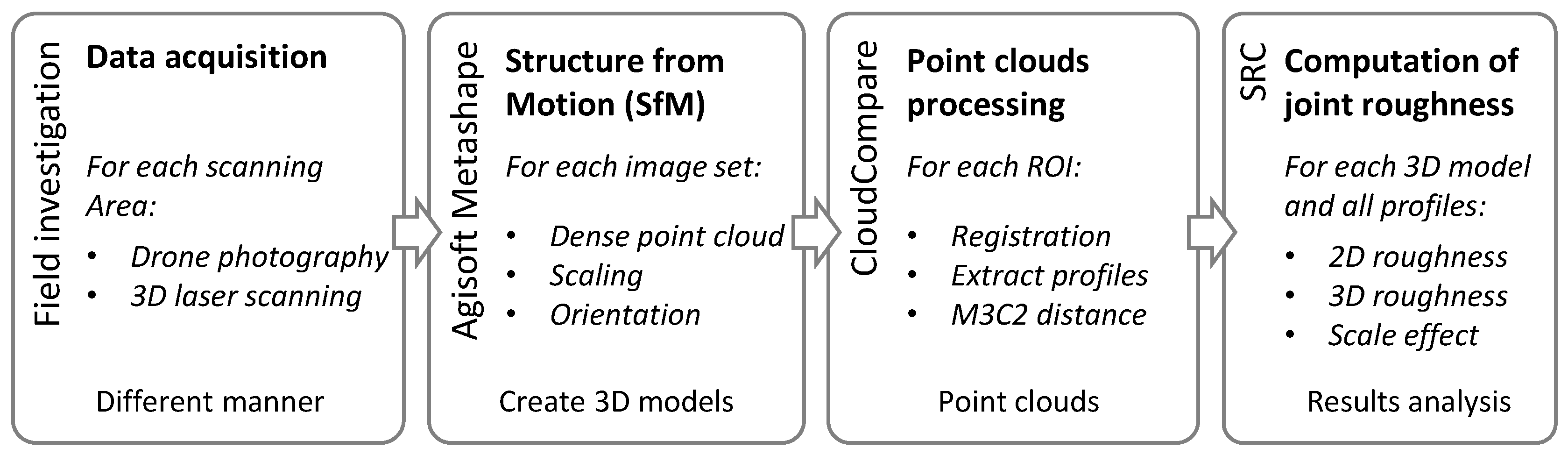
2. Materials and Methods
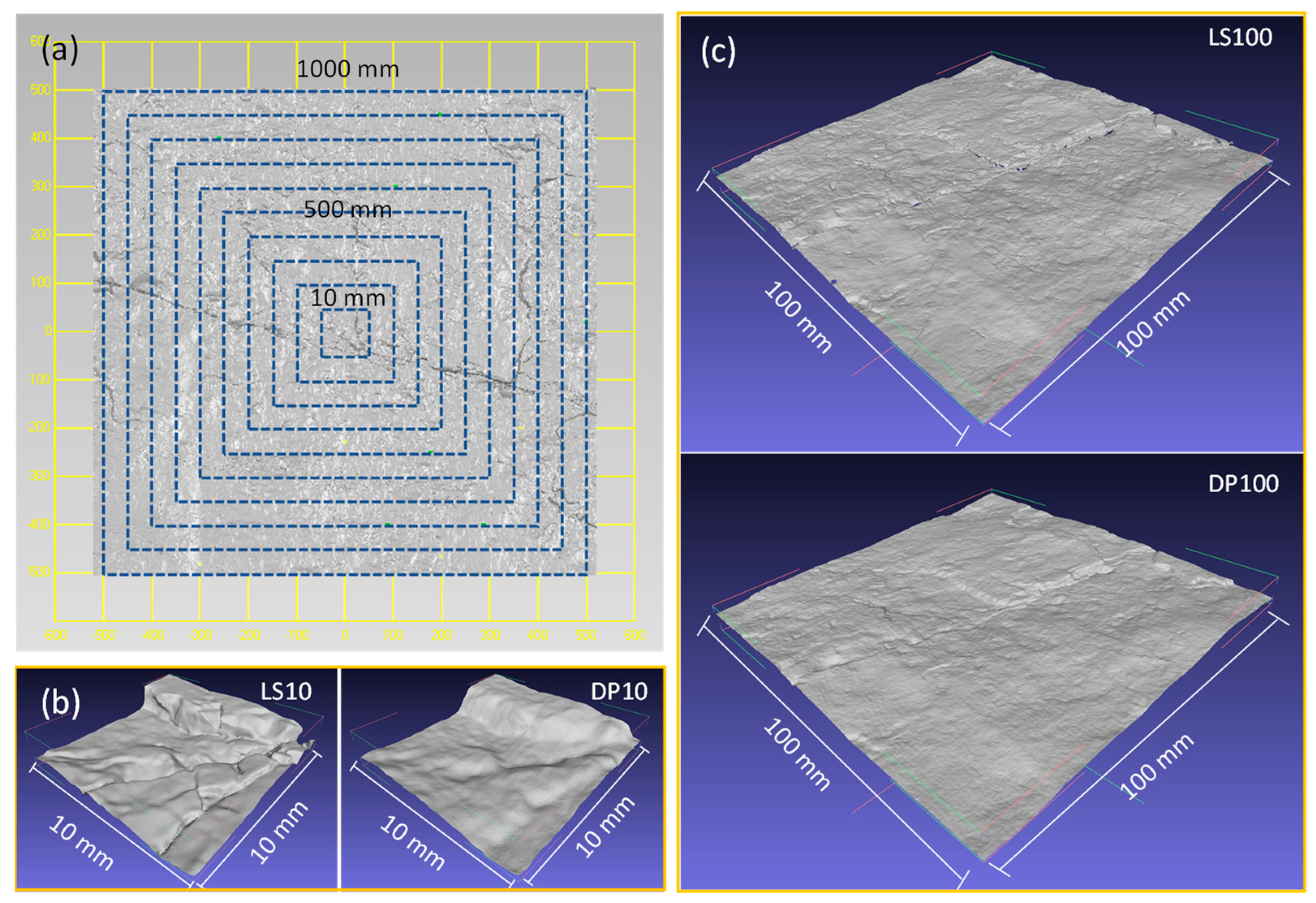
2.1. Description of the Joint Surface
2.2. Point Clouds Generated with Drone Photogrammetry
2.2.1. Image Capture
2.2.2. Point Cloud Reconstruction
2.3. Point Clouds Acquired with Laser Scanning
2.4. Comparison between Laser Scanning and Drone Photogrammetry
2.4.1. Point Cloud Processing and 2D Profile Extraction
2.4.2. Point Cloud Comparison
2.4.3. Joint Roughness Estimation
3. Results
3.1. Point Clouds Generated with Drone Photogrammetry
3.2. Cloud-to-Cloud Distance
3.3. Measurement Error of Drone Photogrammetry
3.3.1. Measurement Error in 2D Profiles
3.3.2. Measurement Error in 3D Surfaces
4. Discussion
4.1. How Accurate Is Accurate Enough in Joint Roughness Measurement?
4.2. Challenges and Considerations in Drone Photogrammetry
4.3. Point Cloud Postprocessing and Roughness Estimation
5. Conclusions
- The M3C2 distances between models generated using drone photogrammetry and laser scanning show that the shooting distance is the primary factor influencing the accuracy of drone photogrammetry. Under a 3 m image capture distance using drone photogrammetry, the root mean square error of M3C2 distance is less than 0.5 mm. The processing quality in Agisoft Metashape, rather than the surface morphology, primarily impacts the level of detail in the resulting model.
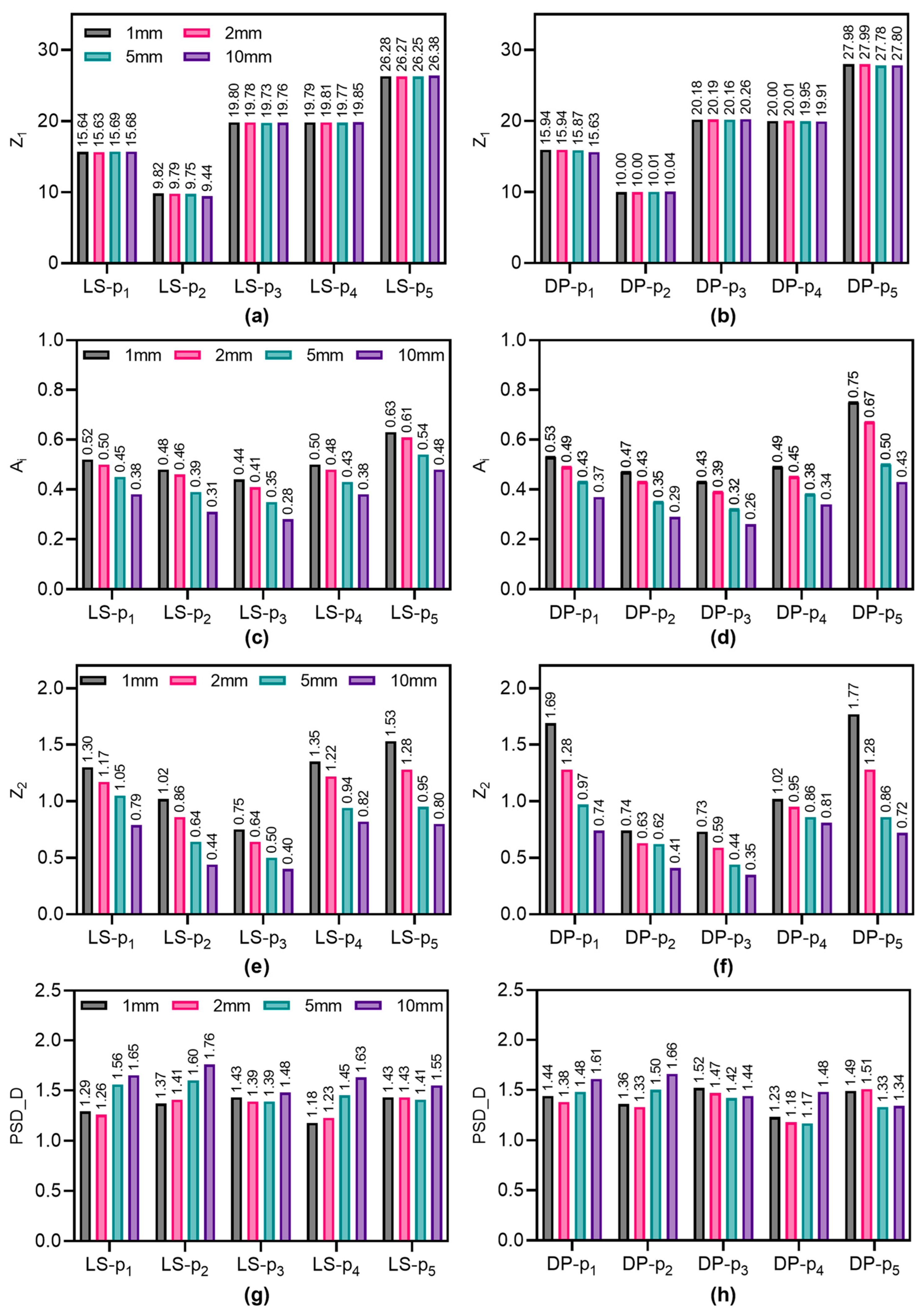
- The measurement error of drone photogrammetry for most roughness parameters does not exceed 10%. For the 2D roughness parameters Z1, Ai, and PSD-D were 3.4%, 7.8%, and 7.6%, respectively. The measurement error of parameter Z2 is negatively correlated with the point spacing, with an error of 22.5% at a point spacing of 1.0 mm, and an error of 8.1% at a point spacing of 10.0 mm.
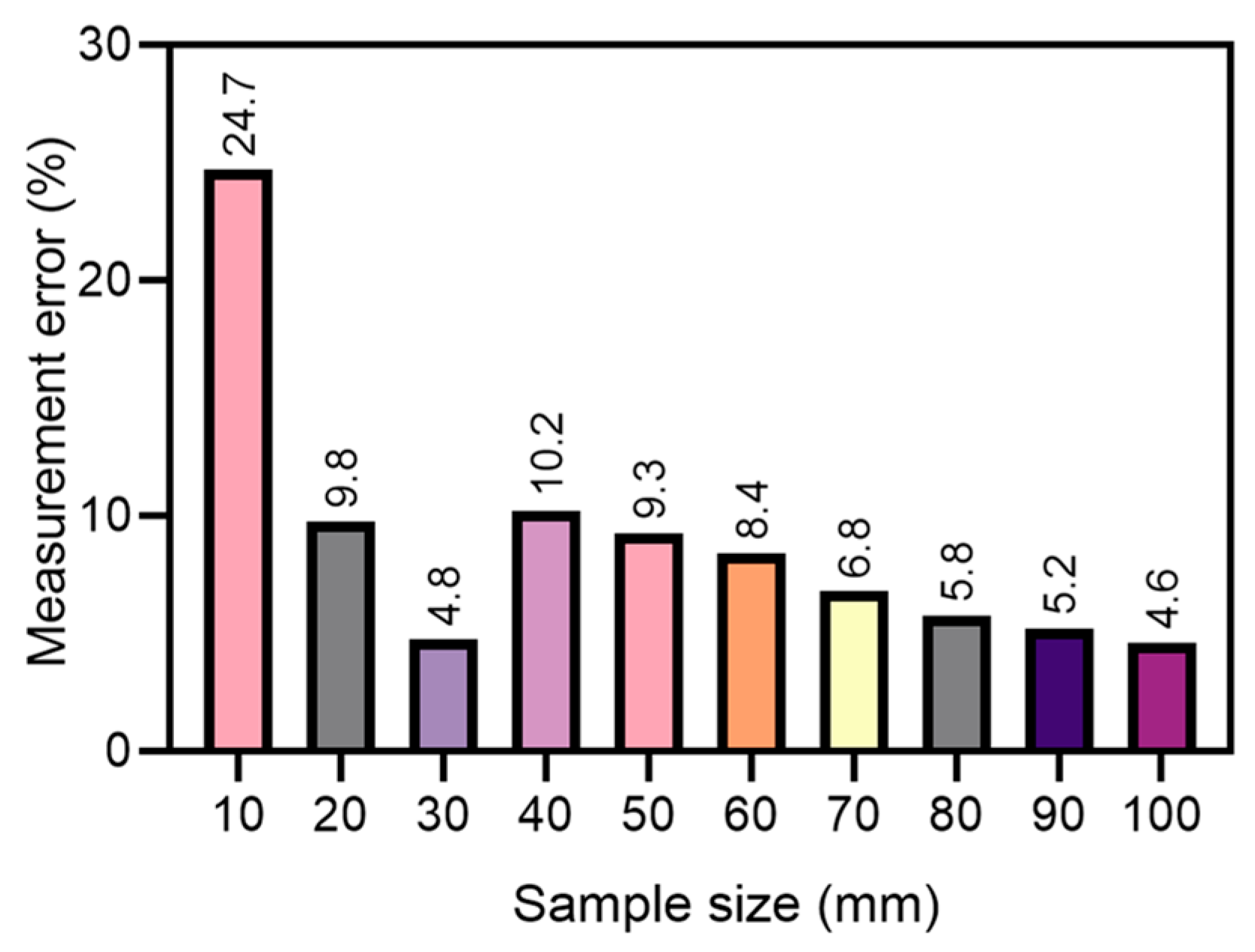
- The measurement error of drone photogrammetry for 3D roughness () decreases exponentially with increasing joint scale. For small joint surfaces measuring 10 cm × 10 cm, the error is 24.7%. However, for larger joint surfaces measuring 100 cm × 100 cm, the error decreases to around 4.6%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kwasniewski, M.A.; Wang, J.-A. Surface Roughness Evolution and Mechanical Behavior of Rock Joints under Shear. Int. J. Rock Mech. Min. Sci. 1997, 34, 709. [Google Scholar]
- Belem, T.; Souley, M.; Homand, F. Modeling Surface Roughness Degradation of Rock Joint Wall during Monotonic and Cyclic Shearing. Acta Geotech. 2007, 2, 227–248. [Google Scholar]
- Barton, N.; Wang, C.; Yong, R. Advances in Joint Roughness Coefficient (JRC) and Its Engineering Applications. J. Rock Mech. Geotech. Eng. 2023. [Google Scholar] [CrossRef]
- Wu, Q.; Kulatilake, P.H.S.W. REV and Its Properties on Fracture System and Mechanical Properties, and an Orthotropic Constitutive Model for a Jointed Rock Mass in a Dam Site in China. Comput. Geotech. 2012, 43, 124–142. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, Y.; Tang, H.; Kang, J.; Wang, L.; Li, C.; Wang, D.; Liu, Z. Experimental Study of the Influence of Wetting and Drying Cycles on the Strength of Intact Rock Samples from a Red Stratum in the Three Gorges Reservoir Area. Eng. Geol. 2023, 314, 107013. [Google Scholar] [CrossRef]
- Guo, S.; Qi, S. Numerical Study on Progressive Failure of Hard Rock Samples with an Unfilled Undulate Joint. Eng. Geol. 2015, 193, 173–182. [Google Scholar] [CrossRef]
- Park, J.-W.; Song, J.-J. Numerical Method for the Determination of Contact Areas of a Rock Joint under Normal and Shear Loads. Int. J. Rock Mech. Min. Sci. 2013, 58, 8–22. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.; Qin, W.; Wei, S.; Tian, H.; Fang, K. Behaviour of Pile-Anchor Reinforced Landslides under Varying Water Level, Rainfall, and Thrust Load: Insight from Physical Modelling. Eng. Geol. 2023, 325, 107293. [Google Scholar] [CrossRef]
- Tatone, B.S. Quantitative Characterization of Natural Rock Discontinuity Roughness In-Situ and in the Laboratory; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Morelli, G.L. On Joint Roughness: Measurements and Use in Rock Mass Characterization. Geotech. Geol. Eng. 2014, 32, 345–362. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Ankah, M.L.Y. Rock Joint Roughness Measurement and Quantification—A Review of the Current Status. Geotechnics 2023, 3, 116–141. [Google Scholar] [CrossRef]
- Stimpson, B. A Rapid Field Method for Recording Joint Roughness Profiles. In Proceedings of the International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Pergamon: Oxford, UK, 1982; Volume 19, pp. 345–346. Available online: https://www.sciencedirect.com/science/article/abs/pii/0148906282913699?via%3Dihub (accessed on 18 September 2023).
- Weissbach, G. A New Method for the Determination of the Roughness of Rock Joints in the Laboratory. Int. J. Rock Mech. Min. Sci. 1978, 15. [Google Scholar] [CrossRef]
- Maerz, N.H.; Franklin, J.A.; Bennett, C.P. Joint Roughness Measurement Using Shadow Profilometry. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 329–343. [Google Scholar] [CrossRef]
- Wang, C.; Yong, R.; Luo, Z.; Du, S.; Karakus, M.; Huang, C. A Novel Method for Determining the Three-Dimensional Roughness of Rock Joints Based on Profile Slices. Rock Mech. Rock Eng. 2023. [Google Scholar] [CrossRef]
- Du, S. Simple profile instrument and its application on studying joint roughness coefficient of rock. Geol. Sci. Technol. Inf. 1992, 11, 91–95. [Google Scholar]
- Mah, J.; Samson, C.; McKinnon, S.D.; Thibodeau, D. 3D Laser Imaging for Surface Roughness Analysis. Int. J. Rock Mech. Min. Sci. 2013, 58, 111–117. [Google Scholar] [CrossRef]
- Marsch, K.; Wujanz, D.; Fernandez-Steeger, T.M. On the Usability of Different Optical Measuring Techniques for Joint Roughness Evaluation. Bull. Eng. Geol. Environ. 2020, 79, 811–830. [Google Scholar] [CrossRef]
- Li, B.; Mo, Y.; Zou, L.; Wu, F. An Extended Hyperbolic Closure Model for Unmated Granite Fractures Subject to Normal Loading. Rock Mech. Rock Eng. 2022, 55, 4139–4158. [Google Scholar] [CrossRef]
- Khoshelham, K.; Altundag, D.; Ngan-Tillard, D.; Menenti, M. Influence of Range Measurement Noise on Roughness Characterization of Rock Surfaces Using Terrestrial Laser Scanning. Int. J. Rock Mech. Min. Sci. 2011, 48, 1215–1223. [Google Scholar] [CrossRef]
- Jiang, Q.; Feng, X.; Gong, Y.; Song, L.; Ran, S.; Cui, J. Reverse Modelling of Natural Rock Joints Using 3D Scanning and 3D Printing. Comput. Geotech. 2016, 73, 210–220. [Google Scholar] [CrossRef]
- García-Luna, R. Characterization of Joint Roughness Using Spectral Frequencies and Photogrammetric Techniques. BGM 2020, 131, 445–458. [Google Scholar] [CrossRef]
- García-Luna, R.; Senent, S.; Jimenez, R. Using Telephoto Lens to Characterize Rock Surface Roughness in SfM Models. Rock Mech. Rock Eng. 2021, 54, 2369–2382. [Google Scholar] [CrossRef]
- Paixão, A.; Muralha, J.; Resende, R.; Fortunato, E. Close-Range Photogrammetry for 3D Rock Joint Roughness Evaluation. Rock Mech. Rock Eng. 2022, 55, 3213–3233. [Google Scholar] [CrossRef]
- Kim, D.H.; Poropat, G.; Gratchev, I.; Balasubramaniam, A. Assessment of the Accuracy of Close Distance Photogrammetric JRC Data. Rock Mech. Rock Eng. 2016, 49, 4285–4301. [Google Scholar]
- Zhao, L.; Huang, D.; Chen, J.; Wang, X.; Luo, W.; Zhu, Z.; Li, D.; Zuo, S. A Practical Photogrammetric Workflow in the Field for the Construction of a 3D Rock Joint Surface Database. Eng. Geol. 2020, 279, 105878. [Google Scholar] [CrossRef]
- An, P.; Fang, K.; Jiang, Q.; Zhang, H.; Zhang, Y. Measurement of Rock Joint Surfaces by Using Smartphone Structure from Motion (SfM) Photogrammetry. Sensors 2021, 21, 922. [Google Scholar] [CrossRef]
- An, P.; Fang, K.; Zhang, Y.; Jiang, Y.; Yang, Y. Assessment of the Trueness and Precision of Smartphone Photogrammetry for Rock Joint Roughness Measurement. Measurement 2022, 188, 110598. [Google Scholar] [CrossRef]
- Zhang, F.; Hassanzadeh, A.; Kikkert, J.; Pethybridge, S.J.; van Aardt, J. Comparison of UAS-Based Structure-from-Motion and LiDAR for Structural Characterization of Short Broadacre Crops. Remote Sens. 2021, 13, 3975. [Google Scholar] [CrossRef]
- Battulwar, R.; Winkelmaier, G.; Valencia, J.; Naghadehi, M.Z.; Peik, B.; Abbasi, B.; Parvin, B.; Sattarvand, J. A Practical Methodology for Generating High-Resolution 3D Models of Open-Pit Slopes Using UAVs: Flight Path Planning and Optimization. Remote Sens. 2020, 12, 2283. [Google Scholar] [CrossRef]
- Cheng, Z.; Gong, W.; Tang, H.; Juang, C.H.; Deng, Q.; Chen, J.; Ye, X. UAV Photogrammetry-Based Remote Sensing and Preliminary Assessment of the Behavior of a Landslide in Guizhou, China. Eng. Geol. 2021, 289, 106172. [Google Scholar] [CrossRef]
- Salvini, R.; Vanneschi, C.; Coggan, J.S.; Mastrorocco, G. Evaluation of the Use of UAV Photogrammetry for Rock Discontinuity Roughness Characterization. Rock Mech. Rock Eng. 2020, 53, 3699–3720. [Google Scholar] [CrossRef]
- García-Luna, R.; Senent, S.; Jimenez, R. Characterization of Joint Roughness Using Close-Range UAV-SfM Photogrammetry. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012064. [Google Scholar] [CrossRef]
- Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; Marcial-Pablo, M.d.J.; Enciso, J. Digital Terrain Models Generated with Low-Cost UAV Photogrammetry: Methodology and Accuracy. ISPRS Int. J. Geo-Inf. 2021, 10, 285. [Google Scholar] [CrossRef]
- Bruno, N.; Giacomini, A.; Roncella, R.; Thoeni, K. Influence of illumination changes on image-based 3D surface reconstruction. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 701–708. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; Walter de Gruyter: Berlin, Germany, 2013; ISBN 3-11-030278-0. [Google Scholar]
- Taddia, Y.; González-García, L.; Zambello, E.; Pellegrinelli, A. Quality Assessment of Photogrammetric Models for Façade and Building Reconstruction Using DJI Phantom 4 RTK. Remote Sens. 2020, 12, 3144. [Google Scholar] [CrossRef]
- Fang, K.; An, P.; Tang, H.; Tu, J.; Jia, S.; Miao, M.; Dong, A. Application of a Multi-Smartphone Measurement System in Slope Model Tests. Eng. Geol. 2021, 295, 106424. [Google Scholar] [CrossRef]
- An, P.; Tang, H.; Li, C.; Fang, K.; Lu, S.; Zhang, J. A Fast and Practical Method for Determining Particle Size and Shape by Using Smartphone Photogrammetry. Measurement 2022, 193, 110943. [Google Scholar] [CrossRef]
- Fang, K.; Zhang, J.; Tang, H.; Hu, X.; Yuan, H.; Wang, X.; An, P.; Ding, B. A Quick and Low-Cost Smartphone Photogrammetry Method for Obtaining 3D Particle Size and Shape. Eng. Geol. 2023, 322, 107170. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar]
- Belem, T.; Homand-Etienne, F.; Souley, M. Quantitative Parameters for Rock Joint Surface Roughness. Rock Mech. Rock Eng. 2000, 33, 217–242. [Google Scholar] [CrossRef]
- Magsipoc, E.; Zhao, Q.; Grasselli, G. 2D and 3D Roughness Characterization. Rock Mech. Rock Eng. 2020, 53, 1495–1519. [Google Scholar] [CrossRef]
- Tatone, B.S.A.; Grasselli, G. A Method to Evaluate the Three-Dimensional Roughness of Fracture Surfaces in Brittle Geomaterials. Rev. Sci. Instrum. 2009, 80, 125110. [Google Scholar] [CrossRef] [PubMed]
- American Society for Photogrammetry. Remote Sensing ASPRS Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, 1–26. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The Shear Strength of Rock Joints in Theory and Practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Muralha, J.; Grasselli, G.; Tatone, B.; Blümel, M.; Chryssanthakis, P.; Yujing, J. ISRM Suggested Method for Laboratory Determination of the Shear Strength of Rock Joints: Revised Version. In The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Ulusay, R., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 131–142. ISBN 978-3-319-07713-0. [Google Scholar]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-Based Surface Reconstruction in Geomorphometry-Merits, Limits and Developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar]
- Hosseininaveh Ahmadabadian, A.; Karami, A.; Yazdan, R. An Automatic 3D Reconstruction System for Texture-Less Objects. Robot. Auton. Syst. 2019, 117, 29–39. [Google Scholar] [CrossRef]
- Dai, W.; Zheng, G.; Antoniazza, G.; Zhao, F.; Chen, K.; Lu, W.; Lane, S.N. Improving UAV-SfM Photogrammetry for Modelling High-Relief Terrain: Image Collection Strategies and Ground Control Quantity. Earth Surf. Process. Landf. 2023. [Google Scholar] [CrossRef]
- James, M.R.; Chandler, J.H.; Eltner, A.; Fraser, C.; Miller, P.E.; Mills, J.P.; Noble, T.; Robson, S.; Lane, S.N. Guidelines on the Use of Structure-from-motion Photogrammetry in Geomorphic Research. Earth Surf. Process. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Barbero-García, I.; Lerma, J.L.; Mora-Navarro, G. Fully Automatic Smartphone-Based Photogrammetric 3D Modelling of Infant’s Heads for Cranial Deformation Analysis. ISPRS J. Photogramm. Remote Sens. 2020, 166, 268–277. [Google Scholar] [CrossRef]







| Equipment | Shooting | Processing | Shooting | Model No. |
|---|---|---|---|---|
| Distance (m) | Accuracy | Direction | ||
| Phantom 4 RTK | 3 | Lowest | Oblique | DP-3-lowest |
| Phantom 4 RTK | 3 | Low | Oblique | DP-3-low |
| Phantom 4 RTK | 3 | Medium | Oblique | DP-3-medium |
| Phantom 4 RTK | 3 | High | Oblique | DP-3-high |
| Phantom 4 RTK | 3 | Ultrahigh | Oblique | DP-3-ultrahigh |
| Phantom 4 RTK | 6 | Ultrahigh | Vertical | DP-5-ultrahigh |
| Phantom 4 RTK | 15 | Ultrahigh | Horizontal | DP-15-ultrahigh |
| Model No. | Number of Images | Average Ground Sample Distance (mm/pixel) | Processing Quality | Tie Point | Dense Point Cloud | PT * (seconds) | NPS ** (mm) |
|---|---|---|---|---|---|---|---|
| LS | - | - | - | - | 5,373,602 | - | 0.43 |
| DP-3-lowest | 53 | 1.1 | lowest | 6126 | 492,329 | 39 | 15.26 |
| DP-3-low | 53 | 1.1 | low | 30,298 | 2,023,343 | 82 | 7.52 |
| DP-3-medium | 53 | 1.1 | medium | 136,851 | 8,421,748 | 319 | 3.74 |
| DP-3-high | 53 | 1.1 | high | 220,947 | 33,241,996 | 1736 | 1.86 |
| DP-3-ultrahigh | 53 | 1.1 | ultrahigh | 198,687 | 131,175,924 | 2285 | 0.92 |
| DP-6-ultrahigh | 11 | 2.1 | ultrahigh | 9844 | 60,255,510 | 204 | 2.47 |
| DP-15-ultrahigh | 9 | 4.8 | ultrahigh | 11,713 | 63,331,233 | 155 | 3.90 |
| Model No. | M3C2 | RMSE (mm) | ||
|---|---|---|---|---|
| Frequency | Mean (mm) | Standard Deviation (mm) | ||
| DP-3-lowest | 4292 | −0.08 | 1.09 | 1.16 |
| DP-3-low | 17,685 | −0.01 | 0.32 | 0.46 |
| DP-3-medium | 71,440 | −0.003 | 0.288 | 0.44 |
| DP-3-high | 288,987 | 0.005 | 0.27 | 0.42 |
| DP-3-ultrahigh | 1,169,755 | −0.086 | 0.301 | 0.52 |
| DP-6-ultrahigh | 163,848 | −0.096 | 2.047 | 1.9 |
| DP-15-ultrahigh | 65,615 | −0.082 | 1.563 | 2.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Du, S.; Yong, R.; Wang, C.; An, P. Drone Photogrammetry for Accurate and Efficient Rock Joint Roughness Assessment on Steep and Inaccessible Slopes. Remote Sens. 2023, 15, 4880. https://doi.org/10.3390/rs15194880
Song J, Du S, Yong R, Wang C, An P. Drone Photogrammetry for Accurate and Efficient Rock Joint Roughness Assessment on Steep and Inaccessible Slopes. Remote Sensing. 2023; 15(19):4880. https://doi.org/10.3390/rs15194880
Chicago/Turabian StyleSong, Jiamin, Shigui Du, Rui Yong, Changshuo Wang, and Pengju An. 2023. "Drone Photogrammetry for Accurate and Efficient Rock Joint Roughness Assessment on Steep and Inaccessible Slopes" Remote Sensing 15, no. 19: 4880. https://doi.org/10.3390/rs15194880
APA StyleSong, J., Du, S., Yong, R., Wang, C., & An, P. (2023). Drone Photogrammetry for Accurate and Efficient Rock Joint Roughness Assessment on Steep and Inaccessible Slopes. Remote Sensing, 15(19), 4880. https://doi.org/10.3390/rs15194880









