Abstract
A long-wavelength geoidal geometry characterizes the most pronounced features of the Indian Ocean geoid low and the West Pacific and North Atlantic geoid highs. These large geoid undulations (globally roughly within ±100 m) are mainly attributed to a deep mantle structure and large lithospheric density and geometry variations (such as the African superswell), while maximum geoid modifications by a topographic relief of Himalaya and Tibet are up to ~30 m. To enhance the mantle signature in a long-wavelength geoidal geometry, gravimetric, isostatic, and spectral decomposition methods can be applied. In this study, we demonstrate that isostatic schemes yield isostatic geoid models that closely resemble a long-wavelength geoidal geometry. The gravimetric method, on the other hand, modifies the mantle geoid significantly. Further modifications of the mantle geoid by removing gravitational contributions of lithospheric mantle density and lithospheric thickness variations should (optimally) enhance the signature of the deep mantle in the sub-lithospheric mantle geoid. Our results confirm this assumption by revealing (large-scale) positive anomalies in the Central Pacific and along the Atlantic Ocean that are coupled by two negative anomalies in the East Pacific and South Eurasia. A gravimetric method thus better enhances the mantle signature in the geoidal geometry than isostatic and spatial decomposition methods. Nonetheless, our results also indicate the presence of possibly large errors in geoid modelling results that limit their full implementation in gravimetric studies of the Earth’s mantle density structure without using tomographic images of the mantle and additional geophysical, geothermal, and geochemical constraints.
1. Introduction
Over the last few decades, remote sensing data acquired from interferometric synthetic aperture radars, satellite altimetry, gravity-dedicated satellite missions, and other space geodetic techniques have been used to develop global topographic, bathymetric, ice thickness, and gravitational models. These models have been facilitated in numerous Earth science applications. Since seismic data coverage is still sparse and uneven in many parts of the world, these models have also been used in studies of the Earth’s interior. In global and large-scale regional studies, for instance, the Earth’s external gravitational field derived from orbital perturbations of satellites and (more recently) directly from gravity-dedicated satellite missions helped scientists to better understand the mantle structure that mainly propagates into a long-wavelength geoidal geometry (e.g., [1,2,3,4,5,6,7,8,9,10,11]). These satellite missions involved the Challenging Mini-satellite Payload (CHAMP) [12], the Gravity Recovery and Climate Experiment (GRACE) [13], the Gravity field and steady-state Ocean Circulation Explorer (GOCE) [14,15], and the GRACE Follow-On (GRACE-FO) [16]. The GOCE provides information about the external gravitational field with a spatial resolution ~80 km (in terms of a half-wavelength) that has further been refined by incorporating available ground-based, air-borne, and sea-borne gravity measurements as well as marine gravity data derived from processing satellite altimetry observables (e.g., [17]).
In gravimetric studies of the Earth’s interior, gravitational, topographic, bathymetric, and ice thickness models together with additional geophysical and geological information are typically used to investigate the lithospheric structure (e.g., [18,19,20,21,22,23,24,25,26]). To study structures deeper in the mantle, long-wavelength geoidal undulations are more suitable for this purpose [27]. The reason is that a geoidal geometry mainly comprises a long-wavelength signature of the mantle density structure, while a medium-to-higher-frequency part of the gravity spectrum (largely attributed to lithospheric density and geometry) is to some extent filtered out in the geoidal geometry. In contrast, the lithospheric signature (including topographic and ocean floor relief) is better pronounced in the gravity field. This is evident from the global geoid and free-air gravity maps shown in Figure 1.
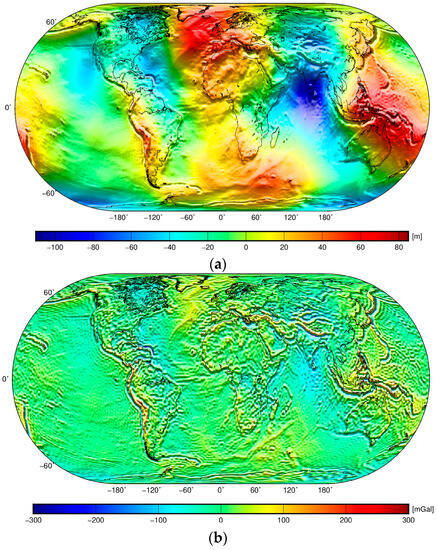
Figure 1.
Global maps of (a) the geoid heights [m] and (b) the free-air gravity disturbances [mGal = 10−5 m·s−2] computed with a spectral resolution complete to a spherical harmonic degree of 180 by using the EIGEN-6C4 global gravitational model [28].
As already stated, more detailed features in the geoidal geometry attributed to lithospheric density and geometry variations are to some extent filtered out. Nevertheless, the gravimetric interpretation of the Earth’s mantle density structure (controlled mainly by mantle convection flow) might be improved by applying forward modelling and the subsequent removing of the gravitational signature of lithospheric density and geometry variations in the geoidal geometry. This procedure is applicable only if lithospheric thickness and density models are sufficiently accurate. Alternatively, an approximate method might be used that is based on applying a particular isostatic theory. In addition, methods based on spectral decomposition and filtering techniques have been used to enhance the long-wavelength signature of deeper sources and to suppress random noise in order to enhance real signals (or systematic trends) in gravity field quantities (i.e., potential, gravity, and gravity gradient data).
In global and large-scale regional studies, the CRUST1.0 [29] and LITHO1.0 [30] models can be used to compute and remove the gravitational contribution of lithospheric structures. These models were derived from tomographic surveys based on the conversion of seismic wave velocities to rock density values [31]. Both models, however, have limited accuracy and resolution because a direct relation between seismic velocities and rock densities does not exist (e.g., [31,32]). Moreover, global seismic data coverage is very irregular, with large parts of the world not yet surveyed by passive and active seismic methods. In regions with sparse and irregular seismic data coverage, the CRUST1.0 and LITHO1.0 density models then rely heavily on the Rayleigh wave group velocities that are not very suitable to recover density information. In addition, globally averaged datasets from active seismic methods and deep drilling profiles were used to predict sediment and underlying crustal structures where no seismic measurements were available (most of Africa, South America, Greenland, and large parts of the oceanic lithosphere) by a generalization to similar geological and tectonic settings.
To partially mitigate expected large uncertainties in available global lithospheric models, additional density information could be used (but only with a very limited impact on accuracy improvement in global lithospheric models). The UNB_TopoDens global lateral topographic density model, prepared by Sheng et al. [33], provides information about the upper continental crustal density. This model was prepared from the Global Lithology Model (GLiM) by assigning probable surface density values and error estimates to GLiM lithologies. The GLiM was produced by Hartmann and Moosdorf [34] by merging various regional data sources from across the globe. Sheng et al. [33] assigned the density and associated standard deviations to the GLiM lithologies according to results published by Carmichael [35] and Tenzer et al. [36]. In addition, numerous studies of the lithospheric density structure conducted in many parts of the world could be used (e.g., [37,38,39,40,41]) in regional gravity modelling and gravity interpretations.
Different isostatic principles have been proposed to explain a compensation mechanism within the crust. Airy [42] suggested that differences between observed and predicted values of the deflection of the plumbline found during astro-geodetic observations at the Himalayan foothills in the 19th century are due to a compensation mechanism based on an increasing depth of compensation (see also Heiskanen and Vening Meinesz [43]). Pratt [44] proposed a different hypothesis. He suggested that this compensation is attributed to crustal density variations (see also Hayford [45] and Hayford and Bowie [46]). Seismic studies generally affirmed that Airy’s hypothesis better explains an isostatic mechanism under orogens and large parts of the stable continental crust (such as Archean cratons). Small variations in the oceanic crustal thickness (5–15 km) [47], on the other hand, suggest that Pratt’s theory probably better describes an isostatic mechanism of the oceanic lithosphere that is mainly controlled by conductive cooling and a subsequent isostatic rebalance of the oceanic lithosphere, both manifested by an ocean floor (and consequently Moho) deepening with the increasing age of the oceanic lithosphere. Since the viscoelastic response of the lithosphere on a load is regional rather than local, Vening Meinesz [48] proposed a regional flexural isostatic model to explain how large topographic loads, such as seamounts (e.g., the Hawaiian Islands), could be compensated by a regional displacement of the lithosphere. Moritz [49] generalized Vening Meinesz’s theory by adopting a global isostatic compensation mechanism and by applying a spherical approximation to the problem. Sjöberg [50] reformulated the Moritz problem, called the Vening Meinesz–Moritz (VMM) inverse problem of isostasy, as that of solving a nonlinear Fredholm integral equation of the first kind in order to estimate compensation depth from gravity data (see also Bagherbandi and Sjöberg [51]).
The applicability of the aforementioned isostatic models alone without using seismic and other geophysical measurements and geological evidences is obviously restricted to regions where the isostatic state of the crust is largely governed by a particular compensation mechanism. This is typically not the case along active divergent continental tectonic margins (i.e., rift systems) as well as oceanic divergent tectonic margins (i.e., mid-oceanic ridges). In both examples, mantle upwelling is responsible for extensional tectonism. Consequently, the elevated topography (of a non-orogenic origin) on both sides of continental rift zones and the elevated ocean floor relief (i.e., abyssal hills) on both sides of mid-oceanic ridges are better explained by lateral tectonic forces and mantle buoyancy. Rathnayake et al. [52], for instance, demonstrated the limitations of modelling oceanic crustal thickness based on applying the Airy, combined Airy–Pratt, and Vening Meinesz–Moritz isostatic models. The other problem associated with the application of isostatic models is the fact that they (usually) assume that isostatic balance occurs within the crust. In reality, however, isostatic balance more likely takes place deeper in the lithospheric mantle [53,54,55,56]. Several authors have argued that isostatic balance is also influenced by the changing rigidity of crustal plates [18,57], plate flexure [58], plate tectonics, and other geophysical processes occurring within the lithosphere and deeper mantle.
As discussed above, the insufficient accuracy of global lithospheric density models is a major disadvantage of using gravimetric forward modelling to recover the gravitational signature of mantle density structure. The use of isostatic methods is, on the other hand, limited mainly by the fact that these theoretical models could not fully describe a real compensation mechanism within large parts of the lithosphere. An alternative choice of using commonly applied spectral decomposition and filtering techniques for this purpose is also somewhat questionable. The reason is that the unique separation of different gravitational sources by these (purely mathematical) procedures is not feasible because any gravitational signal theoretically occupies the entire spectrum of the gravitational field. To critically examine these aspects, we compared various methods for a possible enhancement of the mantle signature in the geoidal geometry, particularly by using gravimetric, isostatic, and spectral decomposition methods. It is worth noting that according to our results (not presented herein in detail), the application of filtering techniques, particularly by using the Gauss filter, does not significantly enhance the long-wavelength pattern in the geoidal geometry. Error analysis of available crustal models and their possible improvement are out of the scope of this study. Instead, we focused here only on identifying the most feasible method of enhancing the mantle signature in the long-wavelength geoidal geometry. We also checked the possibility of further enhancing a mantle convection pattern by incorporating available lithospheric mantle density and lithospheric thickness models in gravimetric forward modelling. The methods applied in this study used existing lithospheric density models (in a gravimetric method) and utilized isostatic theories. Direct gravimetric modelling of the mantle density structure based on converting seismic velocity anomalies to mass density anomalies under the assumption that the mantle structure is mainly controlled by its thermal state (rather than its composition) was not applied here.
In the gravimetric approach, we used forward modelling to isolate and subsequently remove gravitational contributions of crustal (and lithospheric) density and geometry variations in order to reveal the signature of the mantle (and sub-lithospheric mantle) structure in the geoidal geometry. In isostatic methods, we compared results obtained by applying the Airy–Heiskanen, Pratt–Hayford, and Vening Meinesz–Moritz isostatic schemes. In the spectral decomposition technique, we inspected different spectral resolutions of the long-wavelength geoidal geometry. All computations were realized globally. The methods are briefly reviewed in Section 2. Data acquisition is explained in Section 3. The results are presented and discussed in Section 4 and Section 5, respectively. The major findings are summarized and the study is concluded in Section 6.
2. Theory
We applied and compared three methods for a possible augmenting of a mantle signature in the long-wavelength geoidal geometry. The basic principles of these numerical methods are summarized below.
2.1. Geoid
The geoid height is defined by (e.g., [59])
where the disturbing potential ([m2·s−2]) is stipulated at the geoid surface, and the normal gravity ([m·s−2]) is computed at the ellipsoid surface according to Somigliana–Pizzetti’s theory of a normal gravity field [60,61].
2.2. Isostatic Geoid
The isostatic geoid is computed as follows:
The isostatic compensation correction in Equation (2) to the geoid is defined as a function of the Bouguer disturbing potential and the isostatic compensation potential in the following form:
The Bouguer disturbing potential reads
where is the gravitational potential of topographic masses (i.e., the topographic potential), is the gravitational potential of ocean density contrast (i.e., the bathymetric potential), is the gravitational potential of polar glaciers (i.e., the ice potential), and is the gravitational potential of inland bathymetry (i.e., the lake potential).
The gravitational potentials in Equation (4) were computed by applying methods for a spherical harmonic analysis and synthesis according to expressions derived by Tenzer et al. [55,62] and Tenzer et al. [22]. The topographic, ice, and lake potentials were computed with respect to the reference topographic density . The bathymetric potential was computed with respect to the reference crustal density . In other words, the gravitational potentials of crustal density structures distributed above the geoid were computed for the reference topographic density, while the reference crustal density was used to compute the gravitational potentials of crustal density structures below the geoid surface. We, therefore, computed the bathymetric potential for the ocean density contrast defined as a function of the seawater density and the reference crustal density. Moreover, we computed the ice and lake potentials individually for masses above and below the geoid surface because large parts of the glacial bedrock relief in Antarctica are below the geoid surface. Similarly, the floor of Baikal Lake reaches depths below the geoid surface. We note that the atmospheric correction to geoidal geometry is completely negligible [63,64]. More details on the definitions of particular density models are given in Section 3.
Expressions for computing the isostatic compensation potentials according to the Airy–Heiskanen, Pratt–Hayford, and Vening Meinesz–Moritz isostatic schemes are summarized in Appendix A, Appendix B and Appendix C.
2.3. Sub-Lithospheric Mantle Geoid
In the gravimetric forward modelling scheme, the gravitational contribution of lithospheric density heterogeneities is subtracted from the geoid in order to enhance the gravitational signature of the sub-lithospheric mantle density structure. This procedure yields the sub-lithospheric mantle geoid. Hence, we write
The computation of the sub-lithospheric mantle disturbing potential in Equation (5) is realized in the numerical steps explained next.
2.3.1. Crust-Stripped Disturbing Potential
The gravitational potentials of sediments and consolidated crust are computed and subsequently subtracted from the Bouguer disturbing potential . This procedure yields the crust-stripped disturbing potential [54]
where the density contrasts of sediments and consolidated crust are defined with respect to the reference crustal density.
2.3.2. Mantle Disturbing Potential
When disregarding errors due to crustal density model uncertainties, the crust-stripped disturbing potential should comprise a gravitational signature of Moho geometry, lithospheric mantle, and deeper mantle structures within the asthenosphere (e.g., [65]), mantle transition zone (e.g., [66]), and lower mantle (e.g., [67]) including the (Gutenberg) core–mantle boundary zone (e.g., [68,69,70,71,72]). To reveal a gravitational signal that is attributed to a mantle density structure, the Moho signature has to be subtracted from the crust-stripped disturbing potential. This procedure yields the mantle disturbing potential. In this study, the mantle disturbing potential was computed according to a method proposed by Tenzer et al. [22]. They applied this method to compile the global mantle gravity map. The computation of the mantle disturbing potential is then realized by subtracting the gravitational potential of Moho geometry from the crust-stripped disturbing potential . We then write
2.3.3. Lithosphere-Stripped Disturbing Potential
The mantle disturbing potential optimally comprises a gravitational signal of the whole mantle. Depending on available mantle density models, additional corrections could be applied to reveal the gravitational signature of a particular mantle structure. Following this principle, the lithospheric mantle gravitational potential is computed and subtracted from the mantle disturbing potential in order to remove the gravitational signature of density heterogeneities within the lithospheric mantle. This procedure yields the lithosphere-stripped disturbing potential, so
2.3.4. Sub-Lithospheric Mantle Disturbing Potential
The computation of the lithosphere-stripped disturbing potential should theoretically enhance the signature of the lithosphere–asthenosphere boundary (LAB). To enhance the gravitational signature of the sub-lithospheric mantle, the gravitational signal of the LAB geometry has to be removed. By analogy with the computation of the mantle disturbing potential (in Section 2.3.2), this numerical procedure is realized by stripping the whole lithosphere with respect to the density contrast between the reference lithospheric density and the asthenosphere density in order to obtain the sub-lithospheric mantle disturbing potential. The sub-lithospheric mantle disturbing potential is then computed as
2.4. Spectral Decomposition
We investigated different degrees of geoidal spherical harmonics to enhance a mantle signature in the geoidal geometry.
3. Data Acquisition
We first computed the geoid from the EIGEN-6C4 [28] gravitational coefficients corrected for the GRS80 [73] normal gravity component. We then computed the Bouguer disturbing potential (Equation (4)) by subtracting (from the disturbing potential) the gravitational potentials of topography, bathymetry, ice, and lakes. The topographic potential was computed individually for a uniform and variable anomalous topographic density. The gravitational potential of uniform topographic density was computed for the average topographic density 2670 kg·m−3 [74,75]. The gravitational potential of variable anomalous topographic density was computed by using the UNB_TopoDens topographic density model [33]. The anomalous topographic density was taken with respect to the average topographic density 2670 kg·m−3. The same density was adopted to define the density contrasts of lakes and ice above the geoid surface. A freshwater density of 997 kg·m−3 was used to define the density contrast of lakes. A glacial density of 917 kg·m−3 [76] was used to define the ice density contrast. For glacier and lake masses below the geoid surface, the ice and freshwater density contrasts were defined with respect to the reference crustal density of 2900 kg·m−3. The bathymetric potential was computed (with respect to the reference crustal density of 2900 kg·m−3) by using the depth-dependent seawater density model developed by Gladkikh and Tenzer [77]; see also Tenzer et al. [78]. These gravitational potentials were computed by using the Earth2014 [71] datasets of topographic heights, bathymetric depths, inland bathymetry, and glacial bedrock relief.
The gravitational potentials of sediments and consolidated crust were computed from the CRUST1.0 model that was updated for the sediment and crustal layers of the Antarctic lithosphere according to Baranov et al. [79]. In addition to the CRUST1.0 sediment data, we used a density model of marine sediments [80,81,82] in combination with 5 × 5 arc-min data of the total sediment thickness for the world’s oceans and marginal seas [72] to improve the accuracy of the gravitational potential of marine sediments. The sediment and consolidated crust density contrasts were defined with respect to the reference crustal density of 2900 kg m−3. The gravitational potentials of sediments and consolidated crust were subtracted from the Bouguer disturbing potential in order to obtain the crust-stripped disturbing potential (Equation (6)). We then computed the mantle disturbing potential by subtracting the gravitational potential of Moho geometry from the crust-stripped disturbing potential (Equation (7)). This gravitational potential was computed by using the CRUST1.0 Moho depth data. The variable Moho density contrast was computed from the LITHO1.0 uppermost mantle density data with respect to the reference crustal density of 2900 kg·m−3. For this reference crustal density, the Moho density contrast varies from 110 to 560 kg·m−3. We clarify here that the Moho density contrast could not be computed as the difference between the LITHO1.0 uppermost mantle and the CRUST1.0/LITHO1.0 lower crustal layer because crustal density heterogeneities with respect to the reference crust density of 2900 kg·m−3 were already considered in the computation of the crust-stripped disturbing potential. The use of the same density value of 2900 kg·m−3 for the continental and oceanic crust (below the geoid surface) does not have any impact on qualitative interpretations of geoidal maps [23], provided that the average densities of the lower continental and oceanic crust are quite similar (see estimates by Carlson and Raskin [83]; Christensen and Mooney [32]; Tenzer and Gladkikh [80]; or Chen and Tenzer [84]). We further computed the lithosphere-stripped disturbing potential (Equation (8)) by subtracting the lithospheric mantle gravitational potential from the mantle disturbing potential. The LITHO1.0 uppermost mantle density and LAB geometry datasets were used in this numerical step. The Moho depth was again considered from the CRUST1.0 model. Finally, we removed the gravitational signature of the LAB geometry from the lithosphere-stripped disturbing potential (Equation (9)). The sub-lithospheric mantle disturbing potential was then used to compute the corresponding sub-lithospheric mantle geoid model (Equation (5)). In the absence of reliable information about a lateral density distribution within the asthenosphere, this computation was realized based on the principle of minimizing the spatial correlation between the sub-lithospheric mantle disturbing potential and the LAB geometry. The LAB density contrast was defined with respect to the lithospheric mantle density of 3200 kg·m−3 that is typically used. It is worth noting that Griffin et al. [85] reported values of 3300–3400 kg·m−3 based on petrological evidence.
The Airy–Heiskanen and Pratt–Hayford isostatic compensation potentials were computed according to the parameters given in Appendix A and Appendix B. The Vening Meinesz–Moritz compensation potential was computed according to the expressions given in Appendix C by using the CRUST1.0 Moho data and adopting a constant value of the Moho density contrast of 480 kg·m−3 [31]. The isostatic disturbing potentials were scaled by the normal gravity values computed on the ellipsoid surface in order to obtain the corresponding isostatic geoid models (Equation (3)). Finally, we applied spectral decomposition to compute long-wavelength geoid models for the maximum degrees 5, 10, 15, 20, and 25 of spherical harmonics [86].
4. Results
The gravitational potentials computed and applied to obtain the sub-lithospheric mantle gravity disturbances are plotted in Figure 2, with the statistical summary of individual results given in Table 1. The isostatic compensation potentials are shown in Figure 3, with their statistics in Table 2. The statistics of the sub-lithospheric mantle disturbing potential values and intermediate results are summarized in Table 3. The sub-lithospheric mantle geoid together with intermediate results are presented in Figure 4, and their statistical summary is given in Table 4. Since the spatial patterns of disturbing potential values and corresponding geoid models are basically the same, only geoid models are visualized. In addition, the corresponding gravity maps are plotted in Figure 5 (with statistics in Table 5) for a comparative interpretation of geoidal and gravity maps. The isostatic geoid models are shown in Figure 6, with the statistics given in Table 6. For comparison, the corresponding isostatic gravity maps are also plotted in Figure 7, and their statistics are summarized in Table 7. The long-wavelength geoid models computed by using different degrees of the EIGEN-6C4 spherical harmonics are presented in Figure 8, with their statistics in Table 8.

Table 1.
Statistics of the gravitational potentials of lithospheric structure. For the notation used, see the legend in Figure 2.
Table 1.
Statistics of the gravitational potentials of lithospheric structure. For the notation used, see the legend in Figure 2.
| Gravitational Potential | Min [m2·s−2] | Max [m2·s−2] | Mean [m2·s−2] | STD [m2·s−2] |
|---|---|---|---|---|
| 2226 | 8494 | 3589 | 1114 | |
| −3472 | −312 | −731 | 729 | |
| −6 | 0 | −0.2 | 0.2 | |
| −28,533 | −16,402 | −22,386 | 3185 | |
| −3862 | −1937 | −2719 | 444 | |
| 11,529 | 25,075 | 15,661 | 2741 | |
| −69,885 | −46,423 | −55,734 | 5832 | |
| 174,276 | 262,661 | 213,366 | 17,795 | |
| −244,558 | −168,987 | −203,311 | 16,194 |
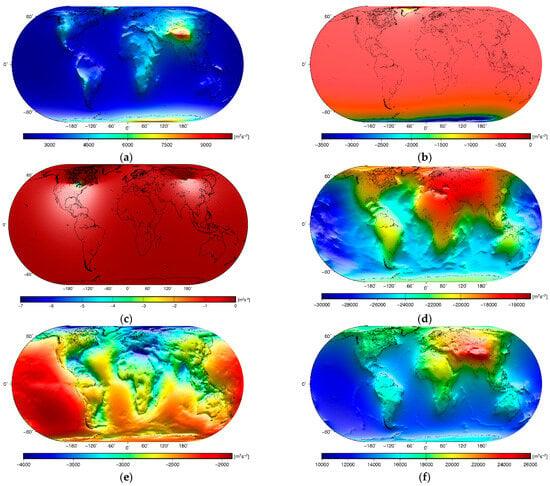
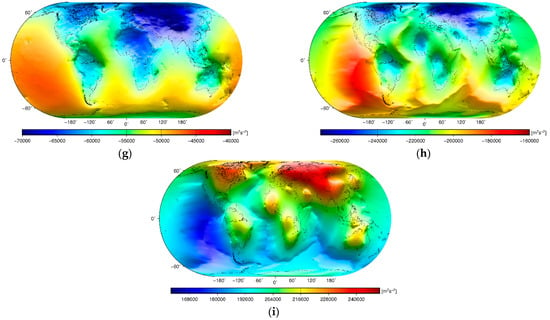
Figure 2.
Global maps of the gravitational potentials of: (a) topography , (b) ice , (c) lakes , (d) bathymetry , (e) sediments , (f) consolidated crust , (g) Moho geometry, (h) lithospheric mantle , and (i) LAB geometry.

Table 2.
Statistics of the isostatic compensation potentials. For the notation used, see the legend in Figure 3.
Table 2.
Statistics of the isostatic compensation potentials. For the notation used, see the legend in Figure 3.
| Isostatic Potential | Min [m2·s−2] | Max [m2·s−2] | Mean [m2·s−2] | STD [m2·s−2] |
|---|---|---|---|---|
| −26,859 | −9411 | −19,264 | 3905 | |
| −26,347 | −9529 | −18,977 | 3791 | |
| −26,860 | −9406 | −19,264 | 3910 |
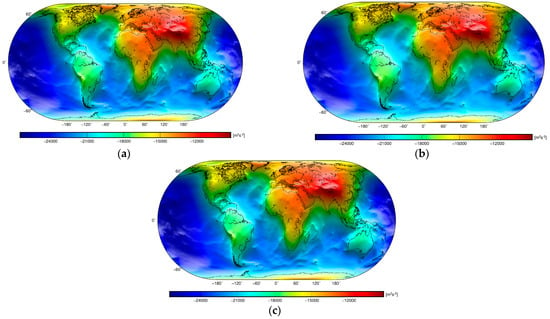
Figure 3.
Global maps of the isostatic compensation potentials: (a) Airy–Heiskanen , (b) Pratt–Hayford , and (c) Vening Meinesz–Moritz .

Table 3.
Statistics of the topography-corrected , the topography- and bathymetry-corrected , Bouguer , crust-stripped , mantle , lithosphere-stripped , and sub-lithospheric mantle disturbing potential values. The statistics of the disturbing potential values used to compute the geoid in Figure 1a are also given.
Table 3.
Statistics of the topography-corrected , the topography- and bathymetry-corrected , Bouguer , crust-stripped , mantle , lithosphere-stripped , and sub-lithospheric mantle disturbing potential values. The statistics of the disturbing potential values used to compute the geoid in Figure 1a are also given.
| Disturbing Potential | Min [m2·s−2] | Max [m2·s−2] | Mean [m2·s−2] | STD [m2·s−2] |
|---|---|---|---|---|
| −1036 | 833 | −8 | 284 | |
| −8824 | −1701 | −3595 | 1215 | |
| 8589 | 26,406 | 18,793 | 3873 | |
| 11,746 | 28,869 | 22,245 | 3491 | |
| −13,311 | 17,086 | 6584 | 6177 | |
| 56,568 | 64,854 | 62,316 | 1262 | |
| 235,290 | 325,580 | 275,670 | 17,985 | |
| 63,164 | 82,212 | 72,370 | 3652 |

Table 4.
Statistics of the geoid models. For the notation used, see the legend in Figure 4.
Table 4.
Statistics of the geoid models. For the notation used, see the legend in Figure 4.
| Refined Geoid | Min [m] | Max [m] | Mean [m] | STD [m] |
|---|---|---|---|---|
| −106 | 85 | −1 | 29 | |
| 1198 | 2946 | 2269 | 356 | |
| −1358 | 1743 | 671 | 630 | |
| 5772 | 6617 | 6358 | 128 | |
| 24,009 | 33,222 | 28,130 | 1835 | |
| 6445 | 8388 | 7384 | 372 |
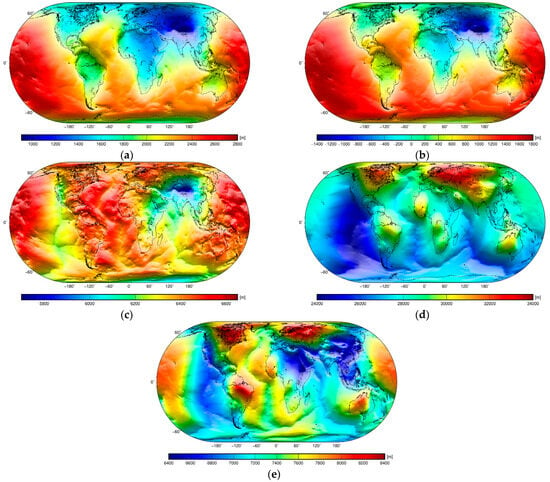
Figure 4.
Global models of: (a) the Bouguer geoid , (b) the crust-stripped geoid , (c) the mantle geoid , (d) the lithosphere-stripped geoid , and (e) the sub-lithospheric mantle geoid .

Table 5.
Statistics of the gravity disturbances. For the notation used, see the legend in Figure 5.
Table 5.
Statistics of the gravity disturbances. For the notation used, see the legend in Figure 5.
| Gravity Disturbances | Min [mGal] | Max [mGal] | Mean [mGal] | STD [mGal] |
|---|---|---|---|---|
| −310 | 287 | −1 | 30 | |
| −492 | 743 | 329 | 225 | |
| −994 | 712 | 189 | 316 | |
| 393 | 1521 | 1011 | 125 | |
| −7024 | −949 | −3216 | 1262 | |
| 754 | 4611 | 1548 | 196 |
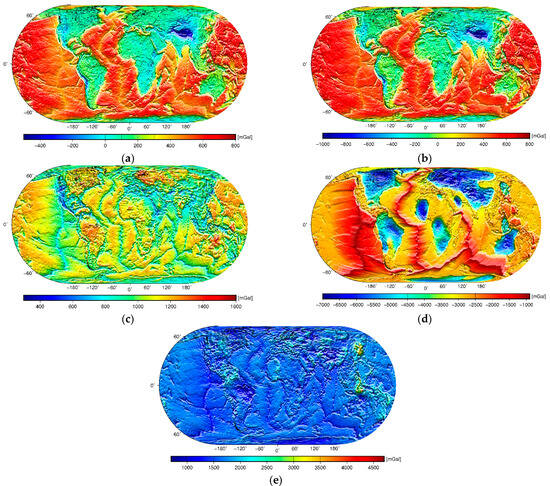
Figure 5.
Global gravity maps of: (a) the Bouguer gravity disturbances , (b) the crust-stripped gravity disturbances , (c) the mantle gravity disturbances , (d) the lithosphere-stripped gravity disturbances , and (e) the sub-lithospheric mantle gravity disturbances according to results presented by Tenzer and Chen [23].

Table 6.
Statistics of the isostatic geoid models. For the notation used, see the legend in Figure 6.
Table 6.
Statistics of the isostatic geoid models. For the notation used, see the legend in Figure 6.
| Isostatic Geoid | Min [m] | Max [m] | Mean [m] | STD [m] |
|---|---|---|---|---|
| −108 | 74 | −8 | 30 | |
| −76 | 113 | 27 | 33 | |
| −108 | 75 | −8 | 30 |
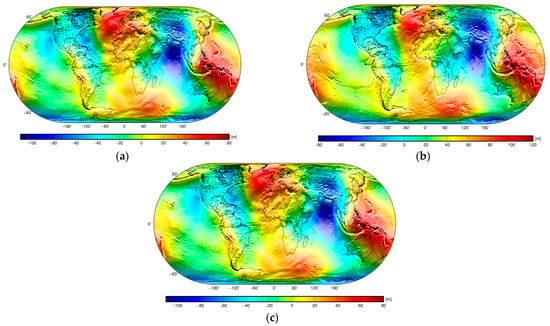
Figure 6.
Global maps of the isostatic geoid models: (a) Airy–Heiskanen , (b) Pratt–Hayford , and (c) Vening Meinesz–Moritz .

Table 7.
Statistics of the isostatic gravity disturbances. For the notation used, see the legend in Figure 7.
Table 7.
Statistics of the isostatic gravity disturbances. For the notation used, see the legend in Figure 7.
| Isostatic Gravity Data | Min [mGal] | Max [mGal] | Mean [mGal] | STD [mGal] |
|---|---|---|---|---|
| −267 | 227 | −2 | 28 | |
| −232 | 190 | 2 | 32 | |
| −260 | 221 | −2 | 28 |
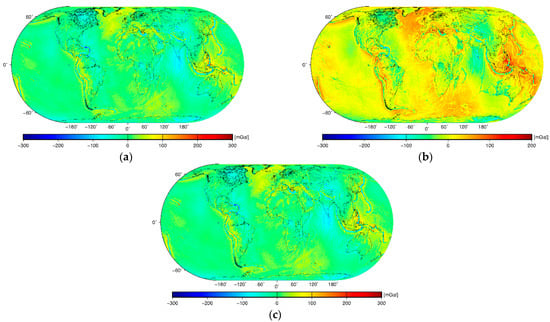
Figure 7.
Global maps of the isostatic gravity disturbances: (a) Airy–Heiskanen , (b) Pratt–Hayford , and (c) Vening Meinesz–Moritz .

Table 8.
Long-wavelength geoid models computed up to a maximum degree (5, 10, 15, 20, and 25) of spherical harmonics.
Table 8.
Long-wavelength geoid models computed up to a maximum degree (5, 10, 15, 20, and 25) of spherical harmonics.
| Maximum Degree of Geoid | Min [m] | Max [m] | Mean [m] | STD [m] |
|---|---|---|---|---|
| 5 | −78 | 74 | −1 | 27 |
| 10 | −102 | 75 | −1 | 29 |
| 15 | −103 | 76 | −1 | 29 |
| 20 | −105 | 77 | −1 | 29 |
| 25 | −103 | 78 | −1 | 29 |
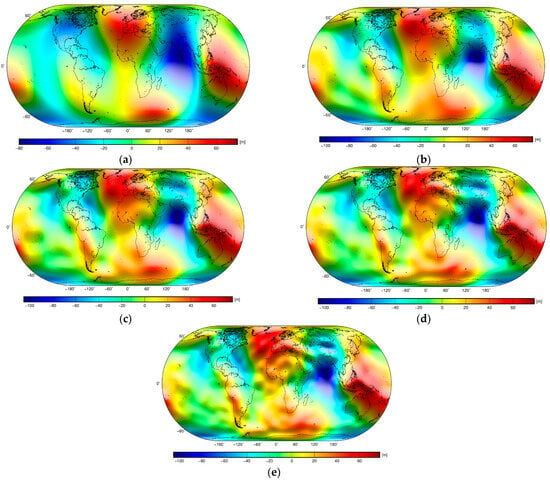
Figure 8.
Long-wavelength geoid models computed up to a maximum degree of spherical harmonics: (a) 5, (b) 10, (c) 15, (d) 20, and (e) 25.
The global geoidal geometry (Figure 1a) is characterized by relatively small fluctuations, mostly within ±100 m. The largest variations have a long-wavelength spatial pattern that is attributed to large-scale structures within the mantle and the crust (such as the African superswell). More localized geoidal undulations attributed mainly to topographic and ocean floor relief are, on the other hand, less pronounced. Nevertheless, we could recognize a signature of large orogens and partially also the ocean floor relief (such as some oceanic subductions, mid-oceanic ridges, and major volcanic islands). The topographic signature of the Andes is particularly well pronounced. The topographic signature of the Himalayas and Tibet is also clearly manifested, with relatively large geoidal modifications up to ~30 m along the Himalayan foothills. The spatial pattern in the free-air gravity map (Figure 1b) is characterized by relatively small gravity fluctuations, mostly within the interval ±100 mGal. A long-wavelength pattern due to (large-scale) mantle and crustal density structures is still recognized, but this signature is much less pronounced in the gravity map than in the geoidal geometry. In contrast, the lithospheric density and geometry signature are more clearly exhibited in the free-air gravity map. Nevertheless, since most of the major topographic features and large lithospheric density structures are in an isostatic equilibrium, the largest gravity variations (roughly within ±300 mGal) mark mainly uncompensated or overcompensated structures along active convergent tectonic margins.
The most pronounced feature over continents in the Bouguer gravity map (Figure 5a) is the isostatic signature of major orogens, while the offshore gravity pattern is dominated by a gravitational signature of the ocean floor relief. In the corresponding Bouguer geoid (Figure 4a), this pattern is almost absent. Instead, we see a prevailing long-wavelength pattern with maxima in the Central Pacific and minima in Central Eurasia.
The crust-stripped gravity map (Figure 5b) largely mimics a Moho geometry. The contrast between a thin oceanic crust and a much thicker continental crust is manifested by mostly positive gravity disturbances over oceans that are coupled by negative gravity disturbances over continents. The largest negative values correspond to a maximum Moho deepening under orogens of the Himalayas, Tibet, and the Andes (e.g., [54]). A relatively vague manifestation of the isostatic signature in the Rocky Mountains was explained by their formation attributed to a flat-slab subduction of the Pacific Ocean plate underneath the North American plate (e.g., [87]). The crust-stripped geoidal geometry (Figure 4b) to a large extent resembles the Bouguer geoid (Figure 4a).
The mantle gravity pattern (Figure 5c) reflects significant lateral density variations within the lithospheric mantle that are mainly attributed to its thermal state (especially under oceans). Mantle gravity lows mark volcanically and seismically active convergent tectonic margins (in the Pacific, Mediterranean, and Caribbean). Mantle gravity lows along mid-oceanic spreading ridges increase with the ocean floor’s age. This prevailing trend was explained by an increasing density due to a conductive cooling of the oceanic lithosphere. Tenzer et al. [55] demonstrated that the mantle gravity disturbances increase nonlinearly with the ocean floor’s age. They also identified an additional systematic trend between the mantle gravity disturbances and the ocean floor depth that was explained by thermal lithospheric contraction (due to conductive cooling) that is isostatically compensated by ocean floor deepening. For more information about the oceanic lithospheric structure and its relation with ocean floor depth and age as well as gravity changes, we refer readers to theoretical and numerical studies by Davis and Lister [88], Sclater et al. [89], Parsons and Sclater [90], Parsons and McKenzie [91], Richter and McKenzie [92], Houseman and McKenzie [93], Robinson and Parsons [94], Phipps and Smith [95], Stein and Stein [96], Shoberg et al. [97], DeLaughter et al. [98], Huang and Zhong [99], Hillier and Watts [100], Doin and Fleitout [101], Crosby et al. [102], Tenzer et al. [22], and references therein. The mantle gravity pattern over continents is more complex, reflecting the lithospheric mantle composition governed by a tectonic province configuration and its age (e.g., [103,104,105,106]). Gravity lows mark active continental divergent margins [23], while a thermal signature along transform faults is mostly missing. Old, cold, tectonically stable cratonic formations are typically characterized by mantle gravity highs [107].
Whereas a spatial pattern in the mantle gravity map reflects mainly the lithospheric mantle structure and its thermal state, the mantle geoidal geometry (Figure 4c) exhibits both lithospheric mantle as well as deep mantle signatures. This is evident, for instance, in the Pacific, where we see not only the signature of a large low-shear-velocity province (LLSVP) in the Central Pacific, but also the lithospheric mantle signature of mid-oceanic ridges in the Southeast Pacific. We could recognize the thermal signature of the oceanic lithospheric mantle in the mantle geoid, even if it is much less consistent than in the corresponding mantle gravity map. The thermal signature of the continental lithospheric mantle is much less pronounced in the mantle geoidal geometry. We could partially recognize a contrast between younger orogenic lithospheric structures under the Rocky Mountains compared to the older cratonic formations of the North American Craton. Similarly, smaller mantle geoid heights along the East African Rift System and along the Red Sea Rift are coupled by larger values over cratonic formations that form most of West Africa. Moreover, mantle geoid lows along the Alpine-Himalayan orogenic belt are coupled to the north by larger values over cratonic formations in North Eurasia. These findings indicate that the thermal signature of the lithospheric mantle is still more or less superimposed over the mantle convection signature in the mantle geoid pattern.
The lithospheric thickness variations are the most pronounced features in the lithosphere-stripped gravity (Figure 5d) and geoid (Figure 4d) maps. Similarities in both spatial patterns are explained by the relatively deep location of the LAB. Nevertheless, the LAB geometry is obviously still slightly more pronounced in the lithosphere-stripped gravity map. As stated above, the lithosphere-stripped gravity and geoid maps exhibit a very similar spatial pattern attributed to the lithosphere–asthenosphere boundary. Contrary to this finding, the spatial patterns in the sub-lithospheric mantle gravity (Figure 5e) and geoid (Figure 4e) maps completely differ. In the former, gravity lows to some extent mark mantle upwelling currents under mid-oceanic spreading ridges. Tenzer and Chen [23] explained this finding by the existence of a molten asthenosphere, particularly below mid-oceanic spreading ridges, although the asthenosphere is mostly almost solid. Nonetheless, the sub-lithospheric mantle gravity map in fact does not exhibit any particular density structure anomaly, except for a more pronounced signature of subducted slabs in the West Pacific. The thermal signature of the asthenosphere under the continental lithospheric mantle is slightly more pronounced under some cratonic formations (Laurentian, Baltic and Amazonian Shields, and São Francisco and East Antarctic Cratons). This finding agrees with the hypothesis that in the thickest cratonic portions of very fast seismic velocity (e.g., [108,109]), the cold and dense layers within the cratonic crust or the lithospheric mantle are isostatically compensated and neutrally buoyant due to the positive buoyancy of depleted cratonic mantle peridotites [110].
The sub-lithospheric mantle geoid pattern (Figure 4e) differs significantly from the long-wavelength geoidal geometry (Figure 1a). The West Pacific geoid high is mostly absent, while the sub-lithospheric mantle geoid high spreads over most of the Central Pacific. The North Atlantic geoid high is also absent in the sub-lithospheric mantle geoid map. Instead, we see two geoid highs in the Hudson Bay region and Northeast Eurasia. The Indian Ocean geoid low coincides with the sub-lithospheric mantle geoid low, but this anomaly is distributed much more broadly over most of South Eurasia while further spreading over Northeast Africa and the North Indian Ocean. The sub-lithospheric mantle geoid high in the Central Pacific is apparently delineated by oceanic subductions in the North Pacific and by mid-oceanic ridges in the East Pacific, but the exact location of their margins could not clearly be ascertained (due to a prevailing long-wavelength geoidal pattern). A more detailed discussion of these findings is postponed until Section 5.
The Airy–Heiskanen, Pratt–Hayford, and Vening Meinesz–Moritz isostatic geoids (Figure 6) very closely resemble the long-wavelength geoidal geometry (Figure 1a). Interestingly, even more detailed features in all three isostatic geoid models are very similar to the geoid pattern. We could still depict, for instance, the topographic signature of Tibet and the Himalayas, especially along the Himalayan foothills, even after applying isostatic correction. The largest localized differences between the geoid and isostatic geoids are seen along the Andes, where the topographic signature is almost completely removed. The Airy–Heiskanen and Vening Meinesz–Moritz isostatic gravity maps (Figure 7a,c) are very similar, with both having a smooth pattern. The application of isostatic correction thus removed the signature of isostatically uncompensated or overcompensated lithospheric structures to a large extent, especially along active convergent tectonic margins. As a result, the long-wavelength pattern is more pronounced in both isostatic geoid models. Interestingly, this long-wavelength pattern is more clearly manifested in the Pratt–Hayford isostatic geoid (Figure 7b).
As seen in Figure 8, the spatial decomposition gradually filters out more detailed features in the geoidal geometry when decreasing the maximum degree of spherical harmonics used to compute the geoid models. Nevertheless, the topographic signature of Tibet and the Himalayas is still partially displayed in the long-wavelength geoidal geometry computed up to a degree of 10 and higher. This topographic signature becomes almost completely absent only in the geoidal geometry computed up to a maximum degree of 5. These results confirm that the separation of gravitational signatures from different depth structures inside the Earth is not unique. Thus, this method works only under the assumption that anomalous density structures increase with depth. In reality, however, this trend is typically the opposite (i.e., the largest density variations are within the upper crust).
5. Discussion
The results presented in Section 4 are discussed next. We first briefly summarize findings from isostatic results and then focus more on the interpretation of the gravimetric forward modelling results.
5.1. Isostatic Results
The global isostatic geoid models (Figure 6) demonstrated that the Airy–Heiskanen, Pratt–Hayford, and Vening Meinesz–Moritz isostatic compensation schemes generally enhance long-wavelength geoidal geometries, while removing the signature of isostatically overcompensated and undercompensated lithospheric structures, particularly along active convergent tectonic margins. The results also revealed that there was no significant difference between adopting the Airy local compensation principle or the Vening-Meinesz regional (or global) compensation principle. Both isostatic schemes provided a smooth isostatic gravity field, while exhibiting mostly its long-wavelength pattern.
5.2. Gravimetric Forward Modelling Results
The long-wavelength geoidal geometry (see Figure 1a) was characterized by the Indian Ocean geoid low and the West Pacific and North Atlantic geoid highs. Additional geoid lows were detected in North America and the Southwest Pacific and a geoid high was seen also in the Southwest Indian Ocean. Hager and Richards [2] argued that most large-scale geoidal undulations can be explained by mantle density anomalies (inferred from seismic tomography) and subducted slab models. To inspect this aspect more thoughtfully, we first calibrated the mantle and sub-lithospheric mantle geoid models so their mean values equaled zero and then computed these models by using different maximum degrees of spherical harmonics. Both results are plotted in Figure 9 and Figure 10, and the summary statistics are given in Table 9 and Table 10.

Table 9.
The (rectified) long-wavelength mantle geoid models computed up to a maximum degree of 5, 10, 15, 20, and 25 of spherical harmonics.
Table 9.
The (rectified) long-wavelength mantle geoid models computed up to a maximum degree of 5, 10, 15, 20, and 25 of spherical harmonics.
| Degree | Min [m] | Max [m] | Mean [m] | STD [m] |
|---|---|---|---|---|
| 5 | −372 | 276 | 0 | 116 |
| 10 | −503 | 253 | 0 | 126 |
| 15 | −542 | 262 | 0 | 127 |
| 20 | −579 | 251 | 0 | 128 |
| 25 | −591 | 256 | 0 | 128 |
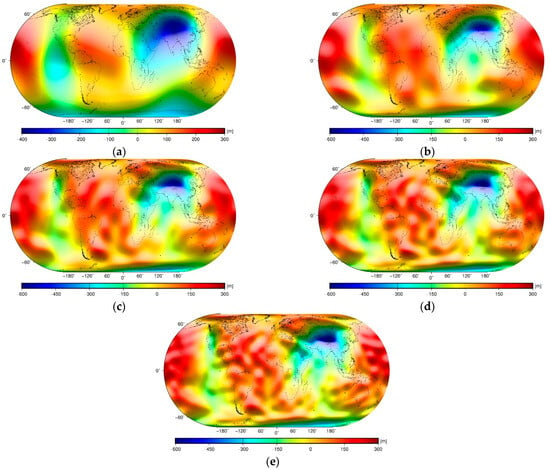
Figure 9.
The (rectified) long-wavelength mantle geoid models computed up to a maximum degree: (a) 5, (b) 10, (c) 15, (d) 20, and (e) 25 of spherical harmonics.

Table 10.
The (rectified) long-wavelength sub-lithospheric mantle geoid models computed up to a maximum degree of 5, 10, 15, 20, and 25 of spherical harmonics.
Table 10.
The (rectified) long-wavelength sub-lithospheric mantle geoid models computed up to a maximum degree of 5, 10, 15, 20, and 25 of spherical harmonics.
| Degree | Min [m] | Max [m] | Mean [m] | STD [m] |
|---|---|---|---|---|
| 5 | −911 | 796 | 0 | 344 |
| 10 | −884 | 1000 | 0 | 366 |
| 15 | −929 | 950 | 0 | 370 |
| 20 | −903 | 956 | 0 | 370 |
| 25 | −901 | 981 | 0 | 371 |
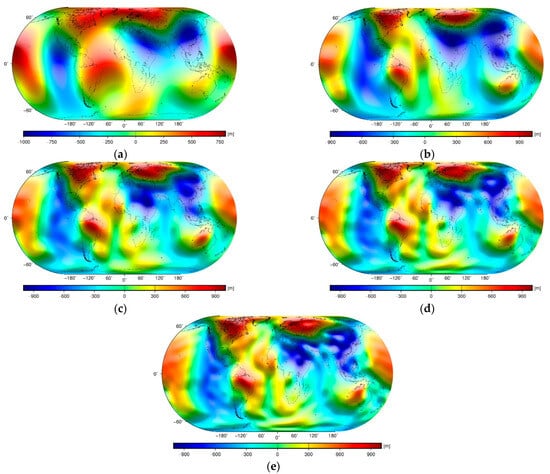
Figure 10.
The (rectified) long-wavelength sub-lithospheric mantle geoid models computed up to a maximum degree of spherical harmonics: (a) 5, (b) 10, (c) 15, (d) 20, and (e) 25.
5.2.1. Comparison of Long-Wavelength Geoid and Mantle Geoid Models
As seen from the comparison of long-wavelength geoid and mantle geoid models (Figure 8 and Figure 9), the mantle geoidal geometry enhanced the mantle signature. The most significant changes were related to modifications of the Indian Ocean geoid low and the West Pacific and North Atlantic geoid highs that were much less pronounced or even absent in the mantle geoid pattern. Instead, the long-wavelength geoidal geometry resembled more a spatial pattern in the sub-lithospheric geoidal geometry (Figure 10) dominated by large positive anomalies in the Central Pacific and Atlantic regions coupled by negative anomalies in Central Eurasia and in the Southeast Pacific. Obviously, the same general findings apply for the comparison of mantle and isostatic geoid models, because long-wavelength geoid and isostatic geoid patterns are very similar. If we assume that the CRUST1.0 density structure model is reasonably accurate, we could conclude that the application of isostatic compensation corrections does not enhance the mantle density structure in the geoidal geometry. Instead, isostatic models only smooth the geoidal geometry.
5.2.2. Comparison of Long-Wavelength Geoid and Sub-lithospheric Mantle Geoid Models
As seen in Figure 8 and Figure 10, the long-wavelength patterns in the geoid and sub-lithospheric mantle geoid models generally disagreed. The most prominent feature in the sub-lithospheric mantle geoidal geometry was a large-scale positive anomaly in the Central Pacific. A less pronounced positive anomaly was detected over the Atlantic Ocean with extension towards the Southwest Indian Ocean. These two sub-lithospheric mantle geoid highs were coupled by two lows in the East Pacific and South Eurasia (with an extension towards Northeast Africa). To further examine how closely the spatial pattern in the sub-lithospheric mantle geoid exhibited a mantle convection pattern, we visually compared it with selected global dynamic topography models.
5.2.3. Comparison of Long-Wavelength Sub-lithospheric Mantle Geoid and Dynamic Topography Models
Despite methods of modelling dynamic topography being generally not consistent [111], their concept is theoretically rather simple. Dynamic topography represents surface deformations caused by vertical stresses generated by mantle convection flow. The isostatic component of surface deformations that depends on the composition and thickness of the lithosphere is, therefore, not taken into consideration. Following this idea, we corrected the geoidal geometry for the gravitational contribution of lithospheric density and geometry variations. With respect to this, we speculate that a spatial pattern in the sub-lithospheric mantle geoid could partially mimic the main spatial features in the dynamic topography. It is important to emphasize, however, that the geoid and dynamic topography are not equivalent quantities. The former is an equipotential surface (modified by removing the gravitational contributions of lithospheric density and geometry variations), while the latter represents the topographic manifestations of vertical stresses due to mantle convection flow.
The long-wavelength sub-lithospheric mantle geoid (in Figure 10a) was compared with the dynamic topography models compiled by Müller et al. [112] and Barnett-Moore et al. [113] (Figure 11). A visual inspection of dynamic topography models prepared by Richards et al. [114], Steinberger [115], Conrad and Husson [116], Spasojevic and Gurnis [117], Flament et al. [118], and others confirmed overall similarities in their spatial patterns with models compiled by Müller et al. [112] and Barnett-Moore et al. [113]. We, therefore, selected only these two models for a comparison of the major features, instead of providing an extensive analysis of differences between numerous models.
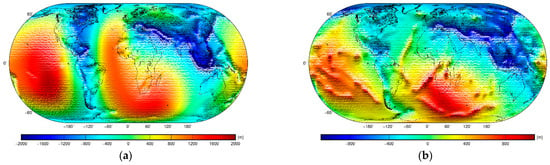
Figure 11.
Global dynamic topography models prepared by (a) Müller et al. [112] and (b) Barnett-Moore et al. [113].
As seen in Figure 11, the most pronounced features in the dynamic topography models are positive anomalies in the Pacific and Africa (including the Central and South Indian Ocean and the East Atlantic). These two positive anomalies are coupled by two negative anomalies. One expands along the West Atlantic and North and South America. The other one spreads over Asia, the North Indian Ocean, the Western Pacific, and Australia. The major differences between these two models are related to more detailed features seen in the Barnett-Moore et al. [113] solution.
The spatial pattern in the dynamic topography models (Figure 11) generally disagrees with the long-wavelength geoid undulations. Steinberger et al. [119] explained this by the fact that the long-wavelength topography is largely dynamically supported from the sub-lithospheric mantle dominated by the signature of the LLSVPs. Second-degree geoidal spherical harmonics (when corrected for the Earth’s flattening by considering the Earth’s hydrostatic model [120]) are also mostly dominated by the LLSVP signature, but the gravitational contribution of the sub-lithospheric mantle prevails at higher degrees of geoidal spherical harmonics. The long-wavelength geoidal geometry thus reflects thermal and compositional density anomalies within the whole mantle, while the dynamic topography is controlled mostly by the density structure within the lowermost mantle. This suggests that the sub-lithospheric mantle geoid geometry (corrected for the gravitational contribution of the whole lithosphere) might better agree with the dynamic topography pattern. This is evident from the comparison of spatial patterns of the sub-lithospheric geoid and dynamic topography models plotted in Figure 10 and Figure 11. In this case, we could recognize more similarities between the long-wavelength sub-lithospheric mantle geoid and the dynamic topography than between the long-wavelength geoid (as well as isostatic geoid and mantle geoid) models and the dynamic topography. Nonetheless, significant inconsistencies between the sub-lithospheric mantle geoidal geometry and the dynamic topography pattern are also clearly recognized.
As seen, the positive anomaly of the sub-lithospheric mantle geoid in the Central Pacific coincides with a broader positive anomaly of the dynamic topography that spreads over most of the Pacific. The positive anomaly in the Atlantic Ocean partially overlaps the positive anomaly of the dynamic topography in the East Atlantic and the South Indian Ocean. The negative sub-lithospheric mantle geoid anomaly in the East Pacific is shifted when compared to the negative anomaly of the dynamic topography along North and South America, including the West Atlantic. The negative sub-lithospheric mantle geoid anomaly in South Eurasia to some extent mimics the negative anomaly in the dynamic topography. It is worth noting that both dynamic topography models (in Figure 11) were prepared from subducted slab models. Both dynamic topography models thus mainly reflect the lower mantle structure. Apparent overall similarities between the dynamic topography and sub-lithospheric mantle geoid models indicate that the geoid model corrected for the gravitational contributions of lithospheric density and geometry variations exhibits mainly low-density upwelling (marked by the sub-lithospheric mantle geoid highs) and high-density downwelling (marked by the sub-lithospheric mantle geoid lows). Despite these overall similarities, significant inconsistencies between the sublithosphere mantle geoid and dynamic topography patterns also exist, particularly marking locations with a maximum lithospheric thickness.
6. Summary and Concluding Remarks
We investigated the possibility of enhancing a mantle signature in the long-wavelength geoidal geometry by applying gravimetric, isostatic, and spectral decomposition methods. In the gravimetric method, we applied gravimetric forward modelling to isolate and subsequently remove the gravitational contributions of crustal density and geometry variations from the geoidal geometry in order to enhance the mantle signature. In the isostatic method, we applied the Airy–Heiskanen, Pratt–Hayford, and Vening Meinesz–Moritz isostatic compensation schemes for this purpose. In the spectral decomposition method, we computed the long-wavelength geoidal geometry with a limited spectral resolution. In addition, we also inspected the possibility of using a filtering technique, but our results (not presented in this study) showed that the Gauss filter did not sufficiently smooth the geoidal geometry.
According to our numerical results, the gravimetric forward modelling better enhanced the mantle signature in the geoidal geometry than the isostatic and spectral decomposition methods. Whereas the former modified the geoidal geometry substantially, the latter mostly only smoothed the long-wavelength geoidal geometry. A similar finding was related to mantle and isostatic gravity maps. Whereas the mantle gravity map relatively realistically manifested a thermal signature of the lithospheric mantle, the isostatic gravity maps mostly enhanced the long-wavelength gravity pattern that very closely agreed with the corresponding long-wavelength geoidal geometry. Evidently, the concerning question is how realistic modifications of the geoidal geometry by subtracting the gravitational contribution of crust are, because available global models of the crustal density structure and geometry (such as the CRUST1.0 and LITHO1.0 models) have a limited accuracy and resolution.
We further used lithospheric models to subtract the gravitational contributions of lithospheric mantle density and lithospheric thickness variations from the mantle geoid. This procedure yielded the sub-lithospheric mantle geoid that should better exhibit the signature of the mantle convection pattern than the mantle geoid. The result revealed the existence of two positive sub-lithospheric mantle geoid anomalies in the Central Pacific and along the Atlantic Ocean and two negative anomalies in the East Pacific and South Eurasia.
Despite the overall similarities between the major features in the sub-lithospheric mantle geoid and dynamic topography models, large differences between their spatial patterns were also found. This finding confirmed that the spatial pattern of the sub-lithospheric mantle geoid is not compatible (despite overall similarities) with the spatial pattern of dynamic topography. The main reason is that the former reflects lateral mantle density anomalies below the lithosphere–asthenosphere boundary, while the latter represents topographic manifestations of vertical stresses due to convection flow. Moreover, large positive anomalies in the sub-lithospheric mantle geoid at locations with a maximum lithospheric thickness suggest large inaccuracies in the CRUST1.0 and LITHO1.0 models. A detailed inspection of these errors will be the subject of a forthcoming study.
Author Contributions
Conceptualization, R.T. and W.C.; methodology, R.T.; software, W.C.; validation, R.T. and W.C.; formal analysis, R.T. and W.C.; investigation, R.T. and W.C.; resources, R.T. and W.C.; data curation, R.T. and W.C.; writing—original draft preparation, R.T. and W.C.; writing—review and editing, R.T. and W.C.; visualization, R.T. and W.C.; supervision, R.T. and W.C.; project administration, R.T. and W.C.; funding acquisition, R.T. and W.C. All authors have read and agreed to the published version of the manuscript.
Funding
Tenzer R conducted this research during his sabbatical leave at the German Research Centre for Geosciences—GFZ Potsdam in Germany. Chen W was funded by the National Natural Science Foundation of China (NSFC Grant Number: 42264001), Jiangxi University of Science and Technology High-level Talent Research Startup Project (205200100588).
Data Availability Statement
The global mantle and sub-lithospheric mantle geoid models compiled up to degree 5 of spherical harmonics are available at: https://github.com/wjchennjtech/mantle-and-sub-lithospherical-geoid (accessed on 25 August 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Airy–Heiskanen Compensation Potential
According to the Airy–Heiskanen isostatic model, the compensation potential is defined by [121,122]
The parameter is defined based on a hydrostatic equilibrium of continents (roots) and oceans (anti-roots) by assuming the planar approximation to the problem. With reference to Lambeck [123], we write (see also Rummel et al. [124] and Tsoulis [125])
Expressing the fundamental harmonic function for the external convergence domain (and ) and applying the binomial theorem, we arrive at
From Equations (A2) and (A3), the coefficients of the Airy–Heiskanen compensation potential are given by [123]
Appendix B. Pratt–Hayford Compensation Potential
In the Pratt–Hayford isostatic model, isostatic mass balance is achieved with a variable compensation density , which is typically smaller than the adopted value of reference crust density in mountains, while it is larger for the oceanic crust. Sjöberg [121] defined the residual compensation density for continents as follows (see also Heiskanen and Moritz [59] and Heiskanen and Vening-Meinesz [43]):
The Pratt–Hayford isostatic compensation potential then becomes [122]
The corresponding spectral representation of reads (ibid.)
The coefficients of the Pratt–Hayford compensation potential are defined as
Appendix C. Vening Meinesz–Moritz Compensation Potential
In the Vening Meinesz–Moritz model, the isostatic compensation potential is defined by (Sjöberg [50])
The spectral representation of in Equation (A11) is given in the following form:
The coefficients of the compensation potential (up to the third order) read
References
- Hager, B.H.; Clayton, R.W.; Richards, M.A.; Comer, R.P.; Dziewonski, A.M. Lower mantle heterogeneity, dynamic topography and the geoid. Nature 1985, 313, 541–545. [Google Scholar] [CrossRef]
- Hager, B.; Richards, M. Long-wavelength variations in Earth’s geoid: Physical models and dynamical implications. Philos. Trans. R. Soc. Math. Phys. Sci. 1989, 328, 309–327. [Google Scholar]
- Wen, L.; Anderson, D.L. Layered mantle convection: A model for geoid and topography. Earth Plane Sci. Lett. 1997, 146, 367–377. [Google Scholar] [CrossRef]
- Zhong, S.; Davies, G. Effects of plate and slab viscosities on the geoid. Earth Planet. Sci. Lett. 1999, 170, 487–496. [Google Scholar] [CrossRef]
- Steinberger, B. Slabs in the lower mantle—Results of dynamic modelling compared with tomographic images and the geoid. Phys. Earth Planet. Inter. 2000, 118, 241–257. [Google Scholar] [CrossRef]
- Zhong, S. Role of ocean-continent contrast and continental keels on plate motion, net rotation of lithosphere and the geoid. J. Geophys. Res. 2001, 106, 703–712. [Google Scholar] [CrossRef]
- Čadek, O.; Fleitout, L. Effect of lateral viscosity variations in the top 300 km on the geoid and dynamic topography. Geophys. J. Int. 2003, 152, 566–580. [Google Scholar] [CrossRef]
- Moucha, R.; Forte, A.; Mitrovica, J.; Daradich, A.D. Lateral variations in mantle rheology: Implications for convection related surface observables and inferred viscosity models. Geophys. J. Int. 2007, 169, 113–135. [Google Scholar] [CrossRef]
- Yoshida, M.; Nakakuki, T. Effects on the long-wavelength geoid anomaly of lateral viscosity variations caused by stiff subducting slabs, weak plate margins and lower mantle rheology. Phys. Earth Planet. Inter. 2009, 172, 278–288. [Google Scholar] [CrossRef]
- Ghosh, A.; Becker, T.W.; Zhong, S.J. Effect of lateral viscosity variations on the geoid. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Coblentz, D.; van Wijk, J.; Richardson, R.M.; Sandiford, M. The upper mantle geoid: Implications for continental structure and the intraplate stress field. Geol. Soc. Am. Spec. Pap. 2015, 514, 197–214. [Google Scholar]
- Reigber, C.; Lühr, H.; Schwintzer, P. CHAMP mission status. Adv. Space Res. 2002, 30, 129–134. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Drinkwater, M.; Floberghagen, R.; Haagmass, R.; Muzi, D.; Papescu, A. GOCE: ESA’s first Earth explorer core mission. Space Sci. Rev. 2003, 17, 419–432. [Google Scholar] [CrossRef]
- Floberghagen, R.; Fehringer, M.; Lamarre, D.; Muzi, D.; Frommknecht, B.; Steiger, C.; Piñeiro, J.; Costa, A. Mission design, operation and exploitation of the Gravity field and steady-state Ocean Circulation Explorer mission. J. Geod. 2011, 85, 749–758. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The gravity recovery and climate experiment follow-on mission. J. Spacecr. Rocket. 2019, 56, 3. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Braitenberg, C.; Wienecke, S.; Wang, Y. Basement structures from satellite-derived gravity field: South China Sea ridge. J. Geophys. Res. Solid Earth 2006, 111, B05407. [Google Scholar] [CrossRef]
- Xu, S.H.; Braitenberg, C.; Fang, J.; Wang, Y. Moho undulations beneath Tibet from GRACE-integrated gravity data. Geophys. J. Int. 2007, 170, 971–985. [Google Scholar]
- Braitenberg, C.; Ebbing, J. New insights into the basement structure of the West Siberian Basin from forward and inverse modelling of Grace satellite gravity data. J. Geophys. Res. 2009, 114, B06402. [Google Scholar]
- Alvarez, O.; Gimenez, M.; Braitenberg, C.; Folguera, A. GOCE Satellite derived Gravity and Gravity gradient corrected for topographic effect in the South Central Andes Region. Geophys. J. Int. 2012, 190, 941–959. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W.; Tsoulis, D.; Bagherbandi, M.; Sjöberg, L.E.; Novák, P.; Jin, S. Analysis of the refined CRUST1.0 crustal model and its gravity field. Surv. Geophys. 2015, 36, 139–165. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W. Mantle and sub-lithosphere mantle gravity maps from the LITHO1.0 global lithospheric model. Earth-Sci. Rev. 2019, 194, 38–56. [Google Scholar] [CrossRef]
- Mahatsente, R.; Önal, G.; Çemen, I. Lithospheric structure and the isostatic state of Eastern Anatolia: Insight from gravity data modelling. Lithosphere 2018, 10, 279–290. [Google Scholar] [CrossRef]
- Chisenga, C.; Yan, J. A new crustal thickness model for mainland China derived from EIGEN-6C4 gravity data. J. Asian Earth Sci. 2019, 179, 430–442. [Google Scholar] [CrossRef]
- Rathnayake, S.; Tenzer, R.; Eshagh, M.; Pitoňák, M. Gravity maps of the lithospheric structure beneath the Indian Ocean. Surv. Geophys. 2019, 40, 1055–1093. [Google Scholar] [CrossRef]
- Tenzer, R.; Bagherbandi, M.; Chen, W.; Sjöberg, L.E. Global isostatic gravity maps from satellite missions and their applications in the lithospheric structure studies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 549–561. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.L.; Abrikosov, O.; Lemoine, J.M.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Serv. 2014, 10. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M.E. Update on CRUST1.0—A 1-degree global model of Earth’s crust. Geophys. Res. Abstr. 2013, 15, 2658. [Google Scholar]
- Pasyanos, M.E.; Masters, T.G.; Laske, G.; Ma, Z. LITHO1.0: An updated crust and lithospheric model of the Earth. J. Geophys. Res. 2014, 119, 2153–2173. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Christensen, N.I.; Mooney, W.D. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Sheng, M.B.; Shaw, C.; Vaníček, P.; Kingdon, R.W.; Santos, M.; Foroughi, I. Formulation and validation of a global laterally varying topographical density model. Tectonophysics 2019, 762, 45–60. [Google Scholar] [CrossRef]
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth’s surface. Geochem. Geophys. Geosystems 2012, 13, Q12004. [Google Scholar] [CrossRef]
- Carmichael, R.S. Practical Handbook of Physical Properties of Rocks and Minerals; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Tenzer, R.; Sirguey, P.; Rattenbury, M.; Nicolson, J. A digital bedrock density map of New Zealand. Comput. Geosci. 2011, 37, 1181–1191. [Google Scholar] [CrossRef]
- Kaban, M.K.; Walter, D. Mooney Density structure of the lithosphere in the southwestern United States and its tectonic significance. J. Geophys. Res. 2001, 106, 721–739. [Google Scholar] [CrossRef]
- Djomani, Y.; O’Reilly, S.; Griffin, W.; Morgan, P. The density structure of subcontinental lithosphere through time. Earth Planet. Sci. Lett. 2001, 184, 605–621. [Google Scholar] [CrossRef]
- Ebbing, J.; Braitenberg, C.; Götze, H.-J. The lithospheric density structure of the Eastern Alps. Tectonophysics 2006, 414, 145–155. [Google Scholar] [CrossRef]
- Maurya, S.; Montagner, J.P.; Kumar, M.R.; Stutzmann, E.; Kiselev, S.; Burgos, G.; Rao, N.P.; Srinagesh, D. Imaging the lithospheric structure beneath the Indian continent. J. Geophys. Res. Solid Earth 2016, 121, 7450–7468. [Google Scholar] [CrossRef]
- Ravikumar, M.; Singh, B.; Pavan Kumar, V.; Satyakumar, A.V.; Ramesh, D.S.; Tiwari, V.M. Lithospheric density structure and effective elastic thickness beneath Himalaya and Tibetan plateau: Inference from the integrated analysis of gravity, geoid, and topographic data incorporating seismic constraints. Tectonics 2020, 39, e2020TC006219. [Google Scholar] [CrossRef]
- Airy, G.B. On the computations of the effect of the attraction of the mountain masses as disturbing the apparent astronomical latitude of stations in geodetic surveys. Philos. Trans. R. Soc. Lond. 1855, 145, 101–104. [Google Scholar] [CrossRef][Green Version]
- Heiskanen, W.A.; Vening Meinesz, F.A. The Earth and its Gravity Field; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1958. [Google Scholar]
- Pratt, J.H. On the attraction of the Himalaya Mountains and of the elevated regions beyond upon the plumb-line in India. Philos. Trans. R. Soc. Lond. 1855, 145, 53–100. [Google Scholar]
- Hayford, J.F. The Figure of the Earth and Isostasy from measurements in the United States; US Government Printing Office: Washington, DC, USA, 1909. [Google Scholar]
- Hayford, J.F.; Bowie, W. The Effect of Topography and Isostatic Compensation upon the Intensity of Gravity; US Coast and Geodetic Survey Publication Special Publication: Washington, DC, USA, 1912; Volume 10. [Google Scholar]
- Bassin, C.; Laske, G.; Masters, T.G. The current limits of resolution for surface wave tomography in North America. EOS Trans. Am. Geophys. Union 2000, 81, F897. [Google Scholar]
- Vening Meinesz, F.A. Une nouvelle méthode pour la réduction isostatique régionale de l’intensité de la pesanteur. Bull. Géodésique 1931, 931, 33–51. [Google Scholar] [CrossRef]
- Moritz, H. The Figure of the Earth; Wichmann: Karlsruhe, Germany, 1990. [Google Scholar]
- Sjöberg, L.E. Solving Vening Meinesz-Moritz inverse problem in isostasy. Geophys. J. Int. 2009, 179, 1527–1536. [Google Scholar] [CrossRef]
- Bagherbandi, M.; Sjöberg, L.E. Non-isostatic effects on crustal thickness: A study using CRUST2.0 in Fennoscandia. Phys. Earth Planet. Inter. 2012, 200, 37–44. [Google Scholar] [CrossRef]
- Rathnayake, S.; Tenzer, R.; Chen, W.; Eshagh, M.; Pitoňák, M. Comparison of different methods for a Moho modeling under oceans and marginal Seas: A case study for the Indian Ocean. Surv. Geophys. 2021, 42, 839–897. [Google Scholar] [CrossRef]
- Kaban, M.K.; Schwintzer, P.; Tikhotsky, S.A. Global isostatic gravity model of the Earth. Geophys. J. Int. 1999, 136, 519–536. [Google Scholar] [CrossRef]
- Tenzer, R.; Hamayun, K.; Vajda, P. Global maps of the CRUST2.0 crustal components stripped gravity disturbances. J. Geophys. Res. 2009, 114, B05408. [Google Scholar]
- Tenzer, R.; Gladkikh, V.; Vajda, P.; Novák, P. Spatial and spectral analysis of refined gravity data for modelling the crust-mantle interface and mantle-lithosphere structure. Surv. Geophys. 2012, 33, 817–839. [Google Scholar] [CrossRef]
- Forte, A.M.; Rowley, D.B. Earth’s isostatic and dynamic topography—A critical perspective. Geochem. Geophys. Geosystems 2022, 23, e2021GC009740. [Google Scholar] [CrossRef]
- Wienecke, S.; Braitenberg, C.; Götze, H.-J. A new analytical solution estimating the flexural rigidity in the Central Andes. Geophys. J. Int. 2007, 169, 789–794. [Google Scholar] [CrossRef]
- Watts, A.B. Isostasy and Flexure of the Lithosphere; Cambridge University Press: Cambridge, UK, 2001; p. 458. [Google Scholar]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W. H. Freeman: New York, NY, USA, 1967. [Google Scholar]
- Pizzetti, P. Sopra il calcolo teorico delle deviazioni del geoide dall’ellissoide. Atti Della R. Accad. Delle Sci. Di Torino 1911, 46, 331–350. [Google Scholar]
- Somigliana, C. Teoria Generale del Campo Gravitazionale dell’Ellisoide di Rotazione. Mem. Della Soc. Astron. Ital. IV 1929, 4, 425. [Google Scholar]
- Tenzer, R.; Novák, P.; Vajda, P.; Gladkikh, V.; Hamayun. Spectral harmonic analysis and synthesis of Earth’s crust gravity field. Comput. Geosci. 2012, 16, 193–207. [Google Scholar] [CrossRef][Green Version]
- Tenzer, R.; Novák, P.; Moore, P.; Vajda, P. Atmospheric effects in the derivation of geoid-generated gravity anomalies. Stud. Geophys. Geod. 2006, 50, 583–593. [Google Scholar] [CrossRef]
- Tenzer, R.; Vajda, P.; Hamayun. Global atmospheric corrections to the gravity field quantities. Contrib. Geophys. Geod. 2009, 39, 221–236. [Google Scholar] [CrossRef]
- Barrel, J. The strength of the crust, Part VI. Relations of isostatic movements to a sphere of weakness—The asthenosphere. J. Geol. 1914, 22, 655–683. [Google Scholar]
- Flanagan, M.P.; Shearer, P.M. Global mapping of topography on transition zone velocity discontinuities by stacking SS precursors. J. Geophys. Res. 1998, 103, 2673–2692. [Google Scholar] [CrossRef]
- Fiquet, G.; Guyot, F.; Badro, J. The Earth’s lower mantle and core. Elements 2008, 4, 177–182. [Google Scholar] [CrossRef]
- Schmerr, N. The Gutenberg discontinuity: Melt at the lithosphere-asthenosphere boundary. Science 2012, 335, 1480–1483. [Google Scholar] [CrossRef]
- Lekic, V.; Cottaar, S.; Dziewonski, A.; Romanowicz, B. Cluster analysis of global lower mantle. Earth Planet. Sci. Lett. 2012, 357–358, 68–77. [Google Scholar] [CrossRef]
- Lay, T.; Hernlund, J.; Buffett, B.A. Core-mantle boundary heat flow. Nat. Geosci. 2008, 1, 25–32. [Google Scholar] [CrossRef]
- Hirt, C.; Rexer, M. Earth2014: 1 arc-min shape, topography, bedrock and ice-sheet models—Available as gridded data and degree-10,800 spherical harmonics. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 103–112. [Google Scholar] [CrossRef]
- Divins, D. Total Sediment Thickness of the World’s Oceans and Marginal Seas; NOAA National Geophysical Data Center: Boulder, CO, USA, 2003. [Google Scholar]
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–162. [Google Scholar] [CrossRef]
- Hinze, W.J. Bouguer reduction density, why 2.67? Geophysics 2003, 68, 1559–1560. [Google Scholar] [CrossRef]
- Artemjev, M.E.; Kaban, M.K.; Kucherinenko, V.A.; Demjanov, G.V.; Taranov, V.A. Subcrustal density inhomogeneities of Northern Eurasia as derived from the gravity data and isostatic models of the lithosphere. Tectonophysics 1994, 240, 248–280. [Google Scholar] [CrossRef]
- Cutnell, J.D.; Kenneth, W.J. Physics, 3rd ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Gladkikh, V.; Tenzer, R. A mathematical model of the global ocean saltwater density distribution. Pure Appl. Geophys. 2011, 169, 249–257. [Google Scholar] [CrossRef]
- Tenzer, R.; Novák, P.; Gladkikh, V. The bathymetric stripping corrections to gravity field quantities for a depth-dependent model of the seawater density. Mar. Geod. 2012, 35, 198–220. [Google Scholar] [CrossRef]
- Baranov, A.; Tenzer, R.; Bagherbandi, M. Combined gravimetric-seismic crustal model for Antarctica. Surv. Geophys. 2018, 39, 23–56. [Google Scholar] [CrossRef]
- Tenzer, R.; Gladkikh, V. Assessment of density variations of marine sediments with ocean and sediment depths. Sci. World J. 2014, 2014, 823296. [Google Scholar] [CrossRef]
- Gu, X.; Tenzer, R.; Gladkikh, V. Empirical models of the ocean-sediment and marine sediment-bedrock density contrasts. Geosci. J. 2014, 18, 439–447. [Google Scholar] [CrossRef]
- Chen, W.; Tenzer, R.; Gu, X. Sediment stripping correction to marine gravity data. Mar. Geod. 2014, 37, 419–439. [Google Scholar] [CrossRef]
- Carlson, R.L.; Raskin, G.S. Density of the ocean crust. Nature 1984, 311, 555–558. [Google Scholar] [CrossRef]
- Chen, W.; Tenzer, R. Harmonic coefficients of the Earth’s Spectral Crustal Model 180—ESCM180. Earth Sci. Inform. 2015, 8, 147–159. [Google Scholar] [CrossRef]
- Griffin, W.L.; O’Reilly, S.Y.; Afonso, J.C.; Begg, G.C. The Composition and Evolution of Lithospheric Mantle: A Re-evaluation and its Tectonic Implications. J. Petrol. 2009, 50, 1185–1204. [Google Scholar] [CrossRef]
- Bowin, C. Mass anomaly structure of the Earth. Rev. Geophys. 2000, 38, 355–387. [Google Scholar] [CrossRef]
- Humphreys, E.D.; Coblentz, D.D. North American dynamics and western U. S. tectonics. Rev. Geophys. 2003, 45, RG3001. [Google Scholar] [CrossRef]
- Davis, E.E.; Lister, C.R.B. Fundamentals of ridge crest topography. Earth Planet. Sci. Lett. 1974, 21, 405–413. [Google Scholar] [CrossRef]
- Sclater, J.G.; Lawver, L.A.; Parsons, B. Comparison of long-wavelength residual elevation and free-air gravity anomalies in the North Atlantic and possible implications for the thickness of the lithospheric plate. J. Geophys. Res. 1975, 80, 1031–1052. [Google Scholar] [CrossRef]
- Parsons, B.; Sclater, J.G. An analysis of the variation of ocean floor bathymetry and heat flow with age. J. Geophys. Res. 1977, 82, 803–827. [Google Scholar] [CrossRef]
- Parsons, B.; McKenzie, D. Mantle convection and the thermal structure of the plates. J. Geophys. Res. 1978, 83, 4485–4496. [Google Scholar] [CrossRef]
- Richter, F.M.; McKenzie, D.P. Parameterizations for the horizontally-averaged temperature of infinite Prandtl Number convection. J. Geophys. Res. 1981, 86, 1738–1744. [Google Scholar] [CrossRef]
- Houseman, G.; McKenzie, D.P. Numerical experiments on the onset of convective instability in the Earth’s mantle. Geophys. J. R. Astron. Soc. 1982, 68, 133–164. [Google Scholar] [CrossRef]
- Robinson, E.M.; Parsons, B. Effect of a shallow, low viscosity zone on small-scale instabilities under the cooling oceanic plates. J. Geophys. Res. 1988, 93, 3468–3479. [Google Scholar] [CrossRef]
- Phipps Morgan, J.; Smith, W.H.F. Flattening of the sea floor depth-age curve as a response to asthenospheric flow. Nature 1992, 359, 524–527. [Google Scholar] [CrossRef]
- Stein, C.A.; Stein, S. A model for the global variation in oceanic depth and heat flow with age. Nature 1992, 359, 123–129. [Google Scholar] [CrossRef]
- Shoberg, T.; Stein, C.; Stein, S. Constraints on lithospheric thermal structure for the Indian ocean basin from depth and heat flow data. Geophys. Res. Lett. 1993, 20, 1095–1098. [Google Scholar] [CrossRef]
- DeLaughter, J.; Stein, S.; Stein, C.A. Extraction of a lithospheric cooling signal from oceanwide geoid data. Earth Planet. Sci. Lett. 1999, 174, 173–181. [Google Scholar] [CrossRef]
- Huang, J.; Zhong, S. Sub-lithospheric small-scale convection and its implications for the residual topography at old ocean basins and the plate model. J. Geophys. Res. 2005, 110, B05404. [Google Scholar]
- Hillier, J.K.; Watts, A.B. The relationship between depth and age in the North Pacific Ocean. J. Geophys. Res. 2005, 110, B02405. [Google Scholar] [CrossRef]
- Doin, M.P.; Fleitout, L. Flattening of the oceanic topography and geoid: Thermal versus dynamic origin. Geophys. J. Int. 2000, 143, 582–594. [Google Scholar] [CrossRef]
- Crosby, A.G.; McKenzie, D.; Sclater, J.G. The relationship between depth, age and gravity in the oceans. Geophys. J. Int. 2006, 166, 553–573. [Google Scholar] [CrossRef]
- Rudnick, R.L.; McDonough, W.F.; Connell, R.J. Thermal structure, thickness and composition of continental lithosphere. Chem. Geol. 1998, 145, 395–411. [Google Scholar] [CrossRef]
- Artemieva, I.M.; Mooney, W.D. Thermal thickness and evolution of Precambrian lithosphere: A global study. J. Geophys. Res. 2001, 106, 16387–16414. [Google Scholar] [CrossRef]
- Kaban, M.K.; Schwintzer, P.; Artemieva, I.M.; Mooney, W.D. Density of the continental roots: Compositional and thermal contributions. Earth Planet. Sci. Lett. 2003, 209, 53–69. [Google Scholar] [CrossRef]
- Artemieva, I.M. Global 1° × 1° thermal model TC1 for the continental lithosphere: Implications for lithosphere secular evolution. Tectonophysics 2006, 416, 245–277. [Google Scholar] [CrossRef]
- Mooney, W.D.; Kaban, M.K. The North American upper mantle: Density, composition, and evolution. J. Geophys. Res. Solid Earth 2010, 115, 24. [Google Scholar] [CrossRef]
- Jordan, T.H. The continental tectosphere. Rev. Geophys. 1975, 13, 1–12. [Google Scholar] [CrossRef]
- Gung, Y.C.; Panning, M.; Romanowicz, B. Global anisotropy and the thickness of continents. Nature 2003, 422, 707–711. [Google Scholar] [CrossRef]
- Kelly, R.K.; Kelemen, P.B.; Jull, M. Buoyancy of the continental upper mantle. Geochem. Geophys. Geosystems 2003, 4, 1017. [Google Scholar] [CrossRef]
- Steinberger, B. Topography caused by mantle density variations: Observation-based estimates and models derived from tomography and lithosphere thickness. Geophys. J. Int. 2016, 205, 604–621. [Google Scholar] [CrossRef]
- Müller, R.D.; Flament, N.; Matthews, K.J.; Williams, S.E.; Gurnis, M. Formation of Australian continental margin highlands driven by plate-mantle interaction. Earth Planet. Sci. Lett. 2016, 441, 60–70. [Google Scholar] [CrossRef]
- Barnett-Moore, N.; Hassan, R.; Müller, R.D.; Williams, S.E.; Flament, N. Dynamic topography and eustasy controlled the paleogeographic evolution of northern Africa since the mid-Cretaceous. Tectonics 2017, 36, 929–944. [Google Scholar] [CrossRef]
- Ricard, Y.; Richards, M.; Lithgow-Bertelloni, C.; Le Stunff, Y. A geodynamic model of mantle density heterogeneity. J. Geophys. Res. Solid. Earth 1993, 98, 21895–21909. [Google Scholar] [CrossRef]
- Steinberger, B. Effects of latent heat release at phase boundaries on flow in the Earth’s mantle, phase boundary topography and dynamic topography at the Earth’s surface. Phys. Earth Planet. Inter. 2007, 164, 2–20. [Google Scholar] [CrossRef]
- Conrad, C.P.; Husson, L. Influence of dynamic topography on sea level and its rate of change. Lithosphere 2009, 1, 110–120. [Google Scholar] [CrossRef]
- Spasojevic, S.; Gurnis, M. Sea level and vertical motion of continents from dynamic earth models. AAPG Bull. 2012, 96, 2037–2064. [Google Scholar] [CrossRef]
- Flament, N.; Gurnis, M.; Muller, R.D. A review of observations and models of dynamic topography. Lithosphere 2013, 5, 189–210. [Google Scholar] [CrossRef]
- Steinberger, B.; Werner, S.C.; Torsvik, T.H. Deep versus shallow origin of gravity anomalies, topography and volcanism on Earth, Venus and Mars. Icarus 2004, 207, 564–577. [Google Scholar] [CrossRef]
- Chambat, F.; Ricard, Y.; Valette, B. Flattening of the Earth: Further from hydrostaticity than previously estimated. Geophys. J. Int. 2010, 183, 727–732. [Google Scholar] [CrossRef]
- Sjöberg, L.E. On the Pratt and Airy models of isostatic geoid undulations. J. Geodyn. 1998, 26, 137–147. [Google Scholar] [CrossRef]
- Sjöberg, L.E. The exterior Airy/Heiskanen topographic-isostatic gravity potential, anomaly and the effect of analytical continuation in Stokes’s formula. J. Geod. 1998, 72, 654–662. [Google Scholar]
- Lambeck, K. Geophysical geodesy. In The Slow Deformations of the Earth; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Rummel, R.; Rapp, R.H.; Sünkel, H.; Tscherning, C.C. Comparison of Global Topographic/Isostatic Models to the Earth’s Observed Gravitational Field; The Ohio State University: Columbus, OH, USA, 1988. [Google Scholar]
- Tsoulis, D.A. Comparison between the Airy-Heiskanen and the Pratt-Hayford isostatic models for the computation of potential harmonic coefficients. J. Geod. 2001, 74, 637–643. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).