Abstract
Aeromagnetic measurement plays an important role in mineral exploration, but unmanned aerial vehicles generate maneuvering noise during aerial flight, which negatively impacts the accuracy of aeromagnetic measurement data. Therefore, aeromagnetic compensation is an indispensable step in aeromagnetic data processing. The multicollinearity of variables in the aeromagnetic compensation model based on linear regression affects its accuracy, resulting in a large difference in the compensation effect of the same group of compensation coefficients in different directions. In order to obtain high-quality aeromagnetic data, this study proposes an adaptive model-based method for suppressing aeromagnetic maneuvering noise. First, due to the fact that the variables that cause multiple collinearity in the compensation model are related to the flight heading, the model variables are adaptively assigned to each heading based on the characteristics of the variable data for different headings. The compensation model is optimized and improved, and the impact of multiple collinearity is thus suppressed. In adaptive modeling, variables with greater significance and smaller multicollinearity are automatically allocated to build the optimal heading model, and then high-precision compensation coefficients are obtained. This algorithm was applied to the data collected by a certain unmanned aerial vehicle aeromagnetic measurement platform in Ma’anshan and compared with traditional methods. The experimental results show that the adaptive modeling-based aeromagnetic compensation algorithm is superior to traditional algorithms, with fewer errors and a higher improvement ratio. Hence, the method can effectively solve the ill-conditioned problem of a model affected by multicollinearity and further improve its compensation accuracy and robustness. Moreover, the feasibility and value of this algorithm were verified in actual mineral resource detection.
1. Introduction
Aeromagnetic detection is an effective method for finding metal deposits. In recent years, many scholars [1,2,3] have conducted research using aeromagnetic data for robust and low-cost identification of polymetallic minerals. Therefore, improving the quality of aeromagnetic data can lead to more effective mineral resource exploration. The process of processing and interpreting aeromagnetic data is mainly divided into two aspects: one is aeromagnetic compensation, and the other is aeromagnetic data interpretation [4]. This study mainly focuses on the research of aeromagnetic compensation; the interpretation of aeromagnetic data will be carried out in subsequent research. During aircraft flight, magnetic sensors record the required aeromagnetic data and the magnetic interference generated by the aircraft. In order to obtain high-quality aeromagnetic data, it is necessary to carry out aeromagnetic compensation research [5].
The earliest research was the mathematical model (T-L model) established by Tolles and Lawson for magnetic interference and aircraft attitude [6]. Based on this research, Leliak designed a compensation model to solve for the compensation coefficient in order to eliminate magnetic interference [7]. Bickel proposed an effective method to solve for the compensation coefficient using a small signal approximation [8] with strict requirements for compensation actions. Leach proposed a ridge regression (RR) algorithm to solve the multicollinearity problem in the T-L compensation model [9], overcoming the poor robustness possible from the least squares (LS) method. Wu used principal component analysis (PCA) to eliminate multicollinearity to some extent through linear dimensionality reduction [10]. Ren [11] proposed a truncated singular value decomposition (TSVD) algorithm to further remove redundancy in the data and improve compensation accuracy on the basis of PCA. Inaba designed a compensation coefficient solution method based on FIR filtering [12]. Zhao [13] proposed a multimodel aeromagnetic compensation method, which removed model variables that contribute significantly to multicollinearity. Although this method somewhat limits the influence of multicollinearity, the only factor it considers when constructing multiple models is the VIF value of the variable, ignoring the impact of variable significance on the model. Zhao [14] proposed a fast processing method for aeromagnetic compensation based on fluxgate estimation, and its effectiveness was verified through simulation. Zhang [15] used fuzzy adaptive Kalman filtering to estimate compensation coefficients, which is relatively lenient and easy to implement. Pan [16] derived parameter estimation and compensation formulas for the unsteady geomagnetic field and modified the T-L model. Through simulation, it has been proven that the improved model has a good compensatory effect on magnetic interference. Xu [17] established a binary classification network for magnetic anomaly detection and a regression network for geomagnetic noise suppression and applied deep learning to magnetic anomaly detection and noise elimination. Zhang [18] analyzed the sway interference of aircraft not considered in the T-L model and used a one-dimensional convolutional neural network to eliminate the influence of tail beam sway. Zhou [19] conducted numerical simulation experiments on magnetic interference in aeromagnetic data based on unmanned aerial vehicles and, for the first time, proposed the radial basis function (RBF) artificial neural network (ANN) algorithm to compensate for aeromagnetic data. Feng [20] proposed an improved geomagnetic gradient compensation method, which improves the compensation accuracy by modeling the geomagnetic gradient and subtracting the estimated geomagnetic gradient from the measured data. Chen [21] designed a compensation method that combines an inertial navigation system and fluxgate magnetometer based on the errors existing in the fluxgate magnetometer and then verified the effectiveness of the algorithm through experiments.
Most methods consider a figure-of-merit (FOM) flight as a whole to solve for compensation coefficients, with little consideration for the impact of the scale of flight heading and attitude changes. Meanwhile, due to the fact that the T-L model consists of cosine functions and their derivatives, the variables between the models are not independent, which inevitably leads to multicollinearity [22]. Due to the ill-conditioned nature of the model, the accuracy of the solved compensation coefficient is not high, thus affecting the quality of the aeromagnetic data. Therefore, this study is based on the principle that the variables that cause multicollinearity in the compensation model are different in different directions. It introduces an adaptive strategy idea that reduces the correlation between coefficient matrix variables and increases the significance of variables on magnetic interference to model the four directions of FOM flight separately in order to weaken the multicollinearity of the model and improve the compensation accuracy. This will be verified through compensation flight and line flight experiments. Interpretation of the aeromagnetic data will be carried out in subsequent research.
This study first analyzes the causes and properties of aeromagnetic maneuvering noise and establishes a magnetic compensation model using mathematical modeling. Subsequently, the compensation method for adaptive modeling and the method for evaluating compensation results proposed in this article are described in detail. Through compensating flight experiments, the effectiveness of the adaptive modeling compensation method was verified by comparing it with the traditional T-L model compensation method. Finally, a line flight experiment was conducted to obtain clearer magnetic anomalies, providing support for subsequent inversion and interpretation research.
In the flight test of the survey line, a 1:10,000 aeromagnetic method was carried out in a certain survey area in Ma’anshan to delineate the range of aeromagnetic anomalies, providing further research data and a basis for the peripheral and deep exploration of old mines in this area. The experimental measurement area is located in the middle section of the Ningwu Mesozoic fault basin, and the geological overview of the area is shown in the inner circle of Figure 1. The area mainly develops a set of sedimentary facies and a set of volcanic rock facies strata, and the folding structures in the area can be divided into basement folds and volcanic rock series folds [23]. The regional fault structure is very developed and is mainly a series of vertical, horizontal, and oblique faults formed during the Yanshan period, dividing the region into several diamond-shaped fault blocks that restrict the distribution of volcanic intrusion activities and related minerals in the region. The geological conditions in the Ningwu Basin are favorable for mineralization, with iron ore as the main metal mineral, followed by copper and gold, which are very rich in mineral resources.
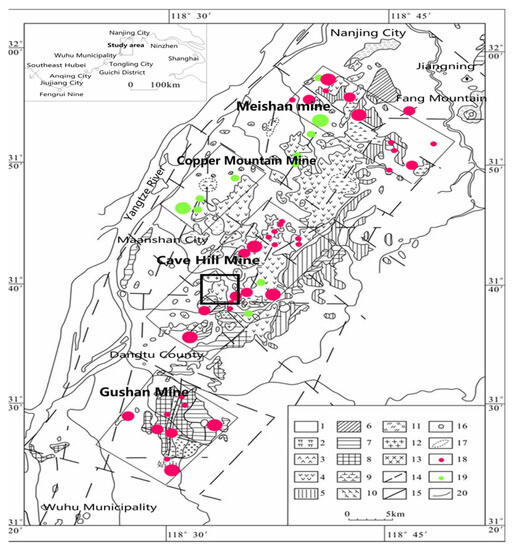
Figure 1.
Geological and mineral resources diagram of the Ningwu Basin (cited from [24]). 1. Quaternary; 2. Niangniangshan Formation volcanic rocks; 3. Gushan Formation volcanic rocks; 4. Dawangshan Formation volcanic rocks; 5. Longwangshan Formation volcanic rocks; 6. Upper Jurassic; 7. Middle and Lower Jurassic; 8. Triassic; 9. Gabbro-diorite porphyrite; 10. Andesitic porphyrite, crude porphyry, trachyte porphyry; 11. Monzonite and quartz diorite; 12. Granite; 13. Gabbro; 14. Inferred fault; 15. Measured fault; 16. Volcano; 17. Concealed speculation according to geological drilling; 18. Iron deposit; 19. Copper deposit; 20. Ore field boundary.
2. Compensation Model and Method
There are multiple steps in aeromagnetic data processing, as shown in Figure 2. After the aeromagnetic measurement is completed, the measured data are imported into the corresponding database for a series of calibration and aeromagnetic compensation processes. After leveling, magnetic data interpretation technology is used to locate the geometric locations of underground minerals [25]. This study mainly focuses on the aeromagnetic compensation process in aeromagnetic data processing. Aeromagnetic compensation technology is mainly divided into three parts: construction of the compensation model, calculation of compensation coefficients, and compensation flight. Firstly, a magnetic interference compensation model is established, and then magnetic interference and other aeromagnetic data are obtained through the compensation flight, which are incorporated into the compensation model. The compensation coefficients are calculated through the compensation algorithm, thereby achieving the purpose of aeromagnetic compensation.
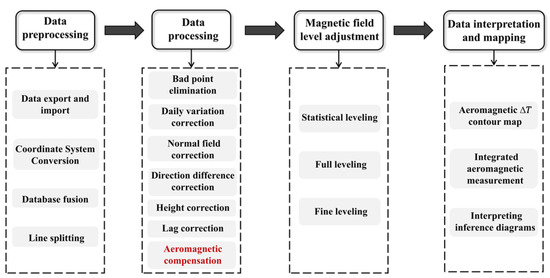
Figure 2.
Aeromagnetic data processing flowchart.
2.1. T-L Model
Aircraft maneuvering noise includes three primary parts [6]: the constant magnetic field () generated by the residual magnetization of ferromagnetic objects in the aircraft, the induced magnetic field () generated by the magnetization of ferromagnetic objects in the aircraft by the Earth’s magnetic field, and the eddy current magnetic field () generated by the cutting of the Earth’s magnetic field by soft magnetic objects in the aircraft, which can be expressed as follows:
where are compensation coefficients; are the derivatives of , respectively, and is the Earth’s magnetic field. are the directional cosines of the geomagnetic field in three directions in the aircraft coordinate system and can be calculated based on the aircraft attitude ().
As shown in Figure 3, is the coordinate axis of the aircraft coordinate system, is the coordinate axis of the local coordinate system, and the origin coincides. is the angle between and . Let represent the magnetic dip angle and heading angle. Let be the respective pitch, roll, and yaw angles.
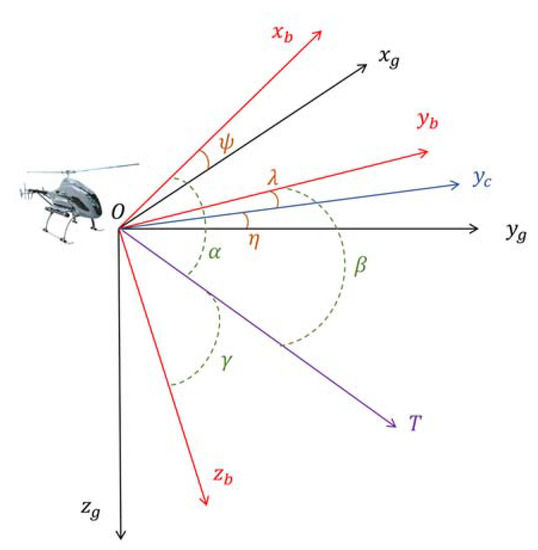
Figure 3.
Coordinate system and aircraft attitude.
Then, can be represented as follows:
For pitches:
For rolls:
For yaws:
For flat:
The total magnetic interference field can be expressed as follows:
The magnetic interference compensation model is simplified as follows:
where is composed of column vectors and is a column vector.
2.2. Adaptive Compensation Method
Zhao’s analysis [13] shows that the variables that lead to the multicollinearity of the T-L model are related to the flight heading. On this basis, we further consider the impact of variable significance on the model through adaptive methods.
Figure 4 shows the implementation process. First, two compensatory flights were performed. In the data processing stage, two flight data sets were preprocessed separately, the four headings were identified, and the heading data were obtained. Subsequently, in the calibration phase, the variables are adaptively assigned based on the characteristics of the calibration flight data (), an optimal heading model is constructed, and the compensation coefficients are calculated. As shown in the orange part of Figure 4, the standard of adaptive variable allocation is to repeatedly exclude the variable with the largest variance inflation factor (VIF) value until the multicollinearity of the remaining variable is small and then conduct a t-test to repeatedly eliminate the variable with less significance until the variable of the heading model is constructed with greater significance and less contribution to multicollinearity. Based on these variables, the heading model is constructed. The model was used to compensate for aeromagnetic interference and obtain the compensation coefficients . The compensation coefficient is calculated using the least squares method (LS) and the ridge regression method (RR):
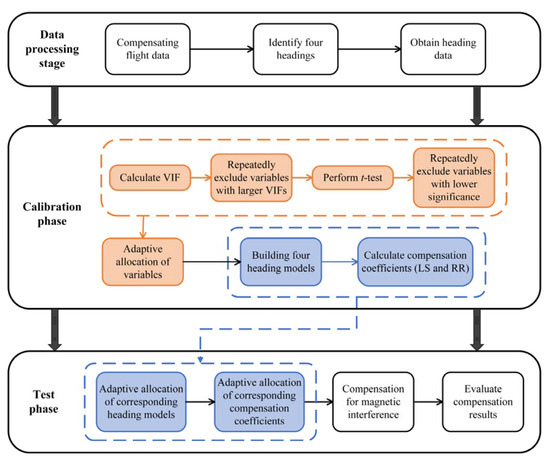
Figure 4.
Flowchart of the aeromagnetic compensation method based on adaptive modeling.
During the testing phase, by identifying the current heading of the test flight data (), as shown in the blue part of Figure 4, the corresponding heading models and compensation coefficients are automatically assigned, and the magnetic interference is compensated as follows:
The magnetic interference after compensation is Finally, the compensation results are evaluated.
The VIF quantifies the severity of multicollinearity in regression models, with larger values indicating a high degree of collinearity in the model. The VIF of the th regression coefficient is defined as follows: where is the value between an independent variable and the remaining independent variables in the linear regression model.
The t-test can be used to test the significance of the regression coefficient and whether the corresponding explanatory variable has a significant impact on the dependent variable, i.e., whether the T-L model variable has a significant impact on the magnetic interference .
The null hypothesis corresponds to, and the alternative corresponds to, where ; is the th regression coefficient, and is the number of variables in the compensation model.
The T-statistic is the following:
where is the degree of freedom, is the number of samples, and is the standard deviation of the th regression coefficient.
The rejection region is the following:
where is the significance level.
The variable of the T-statistic is its significance probability. If
, the original assumption is accepted, and the explanatory variable has no significant impact on the dependent variable; if , the null hypothesis is rejected and the alternative solution is accepted, indicating that the variable corresponding to the th regression coefficient has a significant impact.
The multicollinearity of the model directly leads to the ill condition of the regression equation, increasing the confidence interval of the solution, affecting its sensitivity to noise, and therefore reducing the quality of aeromagnetic compensation [26]. Effective variables are automatically allocated through adaptive modeling, and the multicollinearity of the T-L model can be effectively weakened by reducing the strong and insignificant variables of multicollinearity.
The compensation coefficient solution in this study mainly uses LS and RR. The LS solution of the T-L equation is the following:
When a strong correlation exists between variables, due to the singularity of , the LS solution variance will be large, leading to deviations, which in turn affect the compensation accuracy [27]. RR improves the stability and reliability of the compensation model by abandoning the unbiased nature of LS and obtaining regression coefficients at the cost of some information loss and reduced accuracy. It has good results in repairing and fitting ill-conditioned data. RR adds an identity matrix to the coefficient matrix to improve stability. The solution is expressed as follows:
where µ is a ridge parameter, and I is the identity matrix. Numerous scholars have conducted research on the optimal selection of µ, such as using a combination of nonlinear programming models and Kibria’s method to select µ, which can enable the estimator to achieve high performance [28].
Hardwick [29] suggested using the standard deviation (STD) and improvement ratio (IR) of the signal to evaluate data quality improvement. The STD can provide a good performance evaluation for the compensation system without being misunderstood and can better reflect the performance of the airborne magnetic measurement system. The larger the IR value, the higher the accuracy of compensation. The STD and IR are defined as follows:
where is the arithmetic mean of the variable, and and are the respective standard deviations of the uncompensated and compensated data.
3. Compensation Flight Experiment
3.1. Compensation Flight
To validate the method proposed in this research, the study refers to a FOM flight experiment designed by Leliak [7]. This experiment obtains the magnetic interference data generated during the flight process by flying in a specific way and brings it into the magnetic interference compensation model. The compensation parameters are solved through compensation algorithms. Compensation parameters are applied to another set of flight data for compensation processing. As shown in Figure 5a, the FOM flight includes maneuvers in four directions: north, east, south, and west. Each direction undergoes ±5° yaw, ±5° pitch, and ±10° roll attitude maneuvers, with a duration of 5–10 s for each attitude and a 5 s flat between each group of attitudes. The actual FOM flight paths for flights A and B are shown in Figure 5b; a square represents the beginning of the flight, and a diamond represents the end of the flight. The magnetic interference data measured by the optical pumping magnetometer installed on the aircraft during the flight are shown in Figure 6.
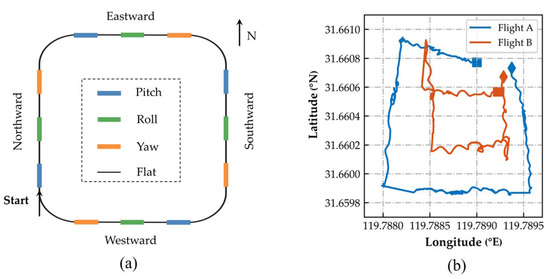
Figure 5.
(a) FOM flight schematic; (b) actual trajectory map of the FOM flight.
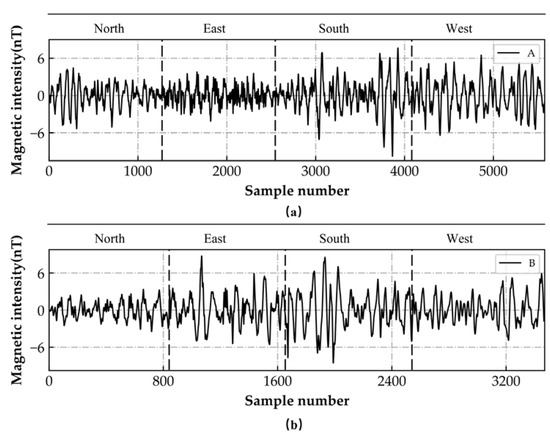
Figure 6.
Magnetic interference during flight. (a) Flight A; (b) Flight B.
3.2. Adaptive Modeling
Fight A is used as a calibration flight, and flight B is used as a test flight. Taking the north heading of flight A as an example, the method in Section 2.2 is used to establish a heading model adaptively.
Firstly, the correlations between variables are analyzed in the T-L model. Here, a thermodynamic diagram (Figure 7) is used to display the correlation between variables visually. The numbers on the graph represent the correlation coefficient matrix, and different colors represent varying degrees of correlation. The closer the correlation coefficient is to 0, the lighter the color is, and the more irrelevant the variables are. The closer the correlation coefficient is to 1 or −1, the darker the color and the higher the degree of linear relationship between variables. Therefore, it can be seen that there is a high correlation between the compensation model variables , indicating the existence of severe multicollinearity in the T-L model.
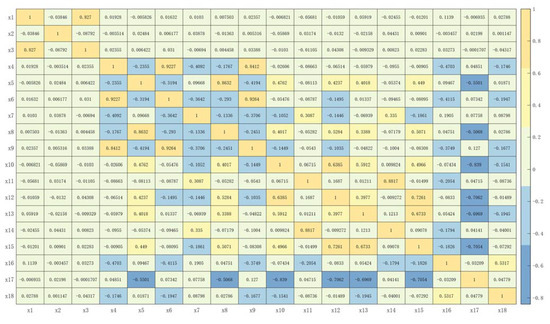
Figure 7.
Thermal diagram of the correlation coefficient matrix of the north heading variable for flight A.
Therefore, in order to eliminate multicollinearity in the model, it is necessary to adaptively allocate effective variables based on the VIF and t-test and then establish a heading model. Table 1 shows the process of adaptive allocation of variables in the north direction of flight A. In model 1, all the variables are input, and their VIFs are listed. The largest is for , which is . That means makes the largest contribution to the multicollinearity of the model and should be excluded. Subsequently, model 2 was established with 17 input variables, excluding , which has the largest VIF. This operation was performed in sequence until the VIF of all variables in the final model 4 decreased, and the multicollinearity was weak (green column, Table 1). Then, on this basis, the variables were allocated according to the-value of the t-test, similar to the VIF-based variable allocation process above. Using the remaining variables, model 5 excluded the variable with the highest -value, in sequence, until the -values of all variables approached 0. In model 7 (orange column, Table 1), the variables have small multicollinearity and high significance, which can suppress the impact of multicollinearity on magnetic interference compensation.

Table 1.
Process of adaptive allocation of variables for flight A north heading.
Finally, after obtaining the adaptively assigned heading model, fitting tests need to be conducted to verify its effectiveness and accuracy further. The residual histogram of the regression model and the normal probability diagram (P-P diagram) of the regression standardized residual are used to test whether the residual follows a normal distribution. If the residual histogram is concentrated near the centerline and presents a normal distribution, and the P-P diagram is approximately a straight line that conforms to a normal distribution, then the regression model meets the assumption of the residual distribution, and the fitting effect is good. On the contrary, the model may have systemic bias, homoscedasticity, or heteroscedasticity. As shown in Figure 8, the residual error of the model meets the normal distribution, indicating that the confidence interval is stable, the regression coefficient solution accuracy is higher, and a heading model with strong regression ability can be obtained.
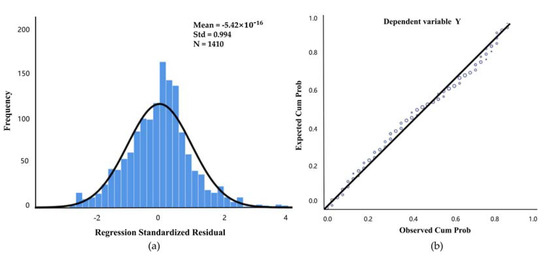
Figure 8.
(a) Residual histogram of the regression model; (b) normalized P-P plot of the regression normalization residuals.
3.3. Magnetic Interference Compensation
In the previous section, a heading model with strong regression ability was obtained, and then flight B was compensated after solving for the compensation coefficient. Figure 9 shows the compensation results of the T-L model using the LS and RR algorithms for flight B, and Figure 10 shows the results of the adaptive established heading model. Taking the north heading as an example, when compensated using the LS algorithm, the T-L model reduces the STD from 1.297 to 0.219, and the IR is 5.922. The heading model lowers the STD to 0.182, and the IR is 7.126. Using the RR algorithm for compensation, the T-L model reduces the STD from 1.297 to 0.166, and the IR is 7.813. The heading model lowers the STD to 0.126, and the IR is 10.294. It can be seen that the IR of the heading model is higher than that of the T-L model, which can effectively weaken the influence of multicollinearity and achieve high-precision aeromagnetic compensation. The fitting ability of RR is stronger than that of LS, with higher compensation accuracy and stronger stability.
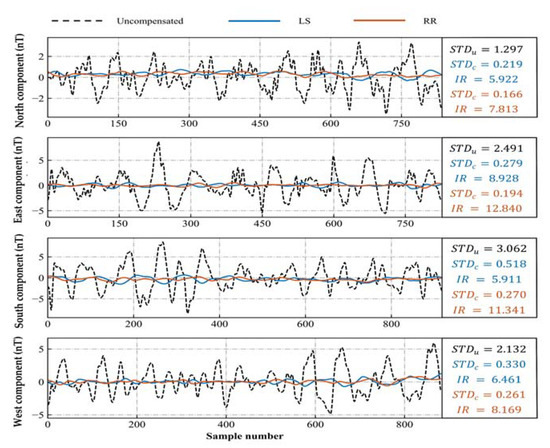
Figure 9.
Compensation results of the T-L model for four headings of flight B.
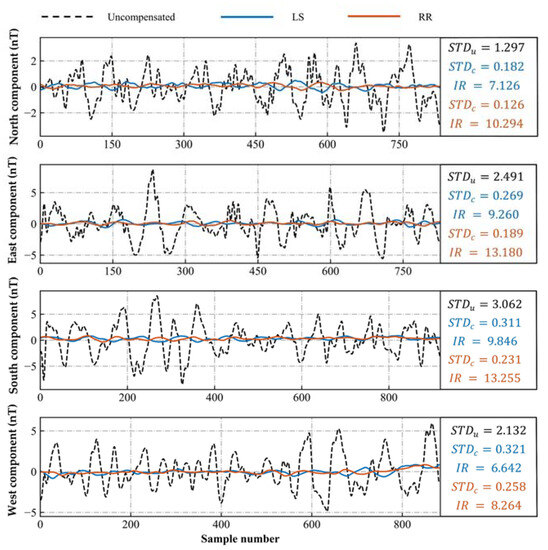
Figure 10.
Compensation results of the heading model for four headings of flight B.
Similarly, flight B is used as a calibration flight, flight A as a test flight, and magnetic compensation is performed using the adaptive modeling-based aeromagnetic compensation algorithm. Figure 11 and Figure 12 show the compensation results of flight A using the LS and RR algorithms for the T-L and heading models, respectively. Compared to LS, RR reduces the compensated STD and increases the IR. RR is different from LS unbiased estimation, as its estimated partial regression coefficients are often closer to the real situation and have better fitting ability. When using the RR algorithm for compensation, the heading model compensates for a smaller STD and a larger IR than the T-L model. This shows that the adaptive modeling algorithm reduces the multicollinearity between variables in the T-L model, improves the performance of the regression algorithm, and improves the accuracy of aeromagnetic compensation. Similarly, when using the LS algorithm, the compensation effect of the heading model is better than that of the T-L model. The above experiments show that the heading model obtained through adaptive variable allocation has a higher regression ability than the traditional T-L model, and the compensated magnetic interference has less error and a higher improvement ratio. This shows that the method effectively solves the ill-conditioned problem of the model caused by multicollinearity, thus improving the compensation accuracy and confirming the effectiveness of our proposed algorithm.
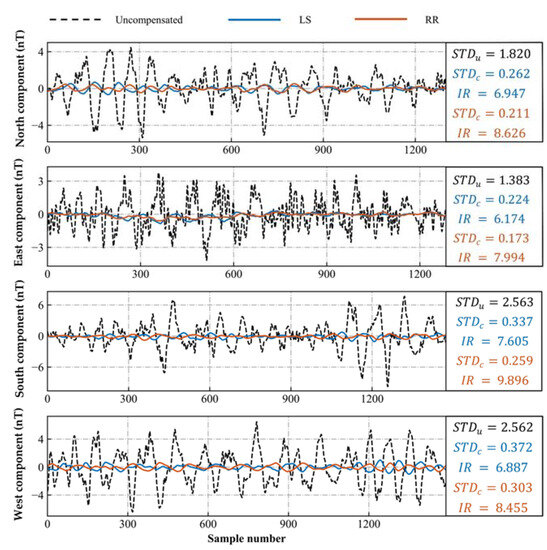
Figure 11.
Compensation results of the T-L model for four headings of flight A.
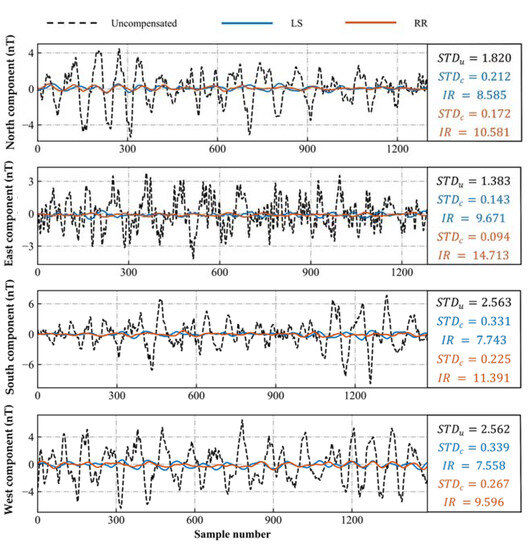
Figure 12.
Compensation results of the heading model for four headings of flight A.
4. Line Flight Experiment
According to existing data, the structure and stratigraphy in the study area include NEE-trending and NE-trending structures [23]. A total of 32 north-south survey lines are arranged at intervals of 100 m to consider two different geological bodies. The measurement area is 8.99 km2, the flight direction angles are 0° and 180°, and the average flight altitude is 164 m. Satellite remote sensing images of the survey area are shown in Figure 13a, while the plane section of the original total magnetic anomaly is shown in Figure 13b. Line 160 (north heading) and Line 170 (south heading) were selected as examples, and adaptive model methods were used as compensation algorithms.
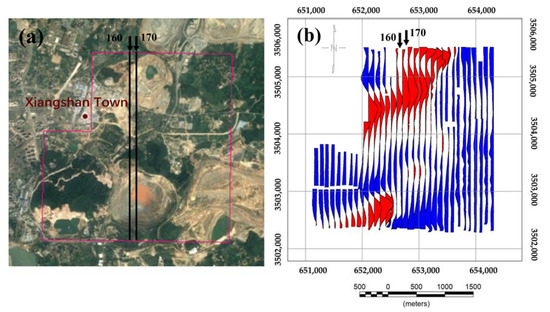
Figure 13.
(a) Satellite remote sensing images of the survey area; the 160 and 170 measuring lines are the two required lines for this experiment; (b) original magnetic anomaly plane section.
The compensation results of the measuring line are shown in Figure 14. It can be seen that the compensated signal is smoother than the original signal because the adaptive modeling compensation method eliminates the aeromagnetic maneuvering noise, so the obvious sawtooth interference in the measurement line is compensated. Applying this algorithm to all line data, according to the magnetic anomaly map of the original data (Figure 15a), it can be seen that there are some obvious magnetic anomaly areas. Some local anomalies correspond to known mineral deposits in the region. However, there are many serrations, ellipses, protrusions, and other forms of high-frequency anomalies distributed throughout the entire anomalous area. Part of these are caused by maneuvering noise during the aeromagnetic measurement process, which can affect the resolution of the magnetic anomaly map and increase the inaccuracy in subsequent inversions. As shown in the circular part of Figure 15b, the method proposed in this article was used for compensation processing to eliminate high-frequency anomalies in the region, especially in the southwestern region where the local anomaly shape is more pronounced. The range of magnetic anomalies is made clearer and smoother, providing better data for subsequent data inversion and interpretation combined with geological data.
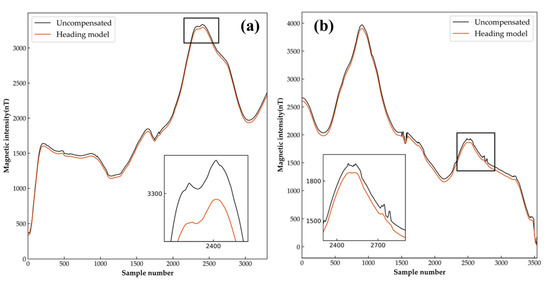
Figure 14.
(a) Flight compensation results of the north direction line; (b) flight compensation results of the south direction line.
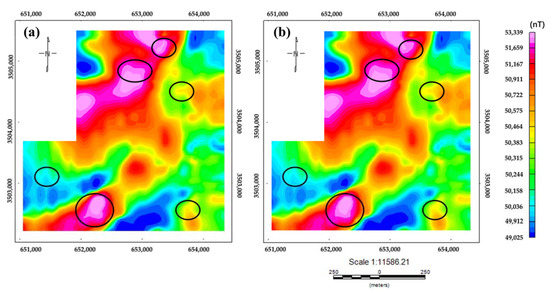
Figure 15.
(a) The original magnetic anomaly; (b) the compensated magnetic anomaly.
5. Discussion
There has been extensive research on high-precision solutions for aviation magnetic compensation models based on linear regression. However, few studies have considered the effects of flight heading and attitude changes on FOM flights. Due to differences in the variables that cause multicollinearity in the compensation model under different heading conditions, this research adaptively modeled FOM flight for different headings. When modeling, the correlation and significance of the variables were considered through the VIF value of variables and the p-value of the t-test to reduce the compensation model’s multicollinearity and improve the impact of variables on magnetic interference, thereby achieving higher compensation accuracy. Through experiments, it was proven that in using the same compensation algorithm, the compensation results through adaptive modeling are more accurate than those of traditional T-L models, verifying the effectiveness of this method.
However, this method cannot completely eliminate all magnetic interference, as the multicollinearity of the compensation model not only comes from model variables and aircraft headings but also from the dependence of the UAV flight on control and real-time meteorological factors, which can lead to unstable flight attitude and result in abnormal data noise and multicollinearity of the model. Therefore, in order to improve compensation accuracy, it is necessary to have a more accurate grasp of drone flight.
Due to the high computational resources involved in adaptive modeling and compensation coefficient calculation, its running time is 0.784 s, which is longer than the T-L model’s running time of 0.392 s. Therefore, further consideration must be given to computational complexity and real-time performance in practical applications.
6. Conclusions
The aeromagnetic compensation model has multicollinearity issues, which will lead to significant bias in the estimation of magnetic interference compensation, reducing interpretability and stability. This research decouples the magnetic interference of the aeromagnetic detection platform through independent modeling and numerical analysis of multiple directions and proposes a new adaptive modeling compensation method. By adaptively assigning variables with high significance and low multicollinearity, different heading models are established that effectively solve the problem of ill-conditioned models on multiple headings. Through FOM flight experiments, it was shown that the magnetic interference compensation effect (IR = 10.294) generated by the aircraft after directional adaptive modeling is better than the traditional T-L model method (IR = 7.813), which verifies the effectiveness of the method. In addition, clear and smooth magnetic anomalies were obtained in the line flight experiment, providing a better data basis for subsequent inversion and interpretation research.
Author Contributions
P.Y., J.J., F.B.: Conceptualization, Methodology, Software; J.J., L.Z.: Resources Data curation; F.B.: Writing—Original draft preparation; F.B., X.Z.: Visualization; J.J., F.B., S.Z.: Writing—Reviewing and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jilin, grant number 20220101147JC, and the National Natural Science Foundation of China, grant number 42274187.
Data Availability Statement
Data available on request due to restrictions eg privacy or ethical. The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the data is provided by a classified project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aali, A.A.; Shirazy, A.; Shirazi, A.; Pour, A.B.; Hezarkhani, A.; Maghsoudi, A.; Hashim, M.; Khakmardan, S. Fusion of Remote Sensing, Magnetometric, and Geological Data to Identify Polymetallic Mineral Potential Zones in Chakchak Region, Yazd, Iran. Remote Sens. 2022, 14, 6018. [Google Scholar] [CrossRef]
- Shabani, A.; Ziaii, M.; Monfared, M.S.; Shirazy, A.; Shirazi, A. Multi-Dimensional Data Fusion for Mineral Prospectivity Mapping (MPM) Using Fuzzy-AHP Decision-Making Method, Kodegan-Basiran Region, East Iran. Minerals 2022, 12, 1629. [Google Scholar] [CrossRef]
- Jiang, D.; Zeng, Z.; Zhou, S.; Guan, Y.; Lin, T. Integration of an Aeromagnetic Measurement System Based on an Unmanned Aerial Vehicle Platform and Its Application in the Exploration of the Ma’anshan Magnetite Deposit. IEEE Access 2020, 8, 189576–189586. [Google Scholar] [CrossRef]
- Noriega, G. Performance measures in aeromagnetic compensation. Leading Edge 2011, 30, 1122–1127. [Google Scholar] [CrossRef]
- Walter, C.; Braun, A.; Fotopoulos, G. Characterizing electromagnetic interference signals for unmanned aerial vehicle geophysical surveys UAV electromagnetic interference. Geophys. J. Soc. Explor. Geophys. 2021, 86, J21–J32. [Google Scholar]
- Tolles, W.E.; Lawson, J.D. Magnetic Compensation of MAD Equipped Aircraft; Airborne Instruments Lab. Inc.: Mineola, NY, USA, 1950; p. 201. [Google Scholar]
- Leliak, P. Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft. IRE Trans. Aerosp. Navig. Electr. 1961, 3, 95–105. [Google Scholar] [CrossRef]
- Bickel, S.H. Small Signal Compensation of Magnetic Fields Resulting from Aircraft Maneuvers. IEEE Trans. AES 1979, 15, 518–525. [Google Scholar] [CrossRef]
- Leach, B.W. Aeromagnetic compensation as a linear regression problem. In Information Linkage between Applied Mathematics and Industry II; Academic Press: London, UK, 1980; pp. 139–161. [Google Scholar]
- Wu, P.L.; Zhang, Q.Y. Aeromagnetic compensation algorithm based on principal component analysis. J. Sens. 2018, 2018, 7. [Google Scholar] [CrossRef]
- Ren, K.X. Research on Magnetic Interference Compensation and Simulation Technology for Aviation Platforms; Harbin Institute of Technology: Harbin, China, 2016. [Google Scholar]
- Inaba, T.; Shima, A.; Konishi, M. Magnetic noise compensation using FIR model parameter estimation method. Electron. Commun. Jpn. 2002, 85, 1–11. [Google Scholar] [CrossRef]
- Zhao, G.; Han, Q.; Peng, X. An Aeromagnetic Compensation Method Based on a Multimodel for Mitigating Multicollinearity. Sensors 2019, 19, 2931. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, X.C.; Jiao, J. Fast Processing Method of Aeromagnetic Compensation Basedon Fluxgate Estimation. J. Jilin Univ. 2019, 49, 857–864. [Google Scholar]
- Zhang, Y.; Zhao, Y.X.; Chang, S. An aeromagnetic compensation algorithm for aircraft based on fuzzy adaptive kalman filter. J. Appl. Math. 2014, 2014, 405671. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, Q. An aeromagnetic compensation method considering geomagnetic gradient changes. Sensors and Microsystems 2020, 39, 4. [Google Scholar]
- Xu, X.; Huang, L.; Liu, X. DeepMAD: Deep Learning for Magnetic Anomaly Detection and Denoising. IEEE Access 2020, 99, 121257–121266. [Google Scholar] [CrossRef]
- Zhang, D.K. Analysis of Aeromagnetic Swing Noise and Corresponding Compensation Method. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–10. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, C.; Su, Z. An Aeromagnetic Compensation Algorithm Based on Radial Basis Function Artificial Neural Network. Appl. Sci. 2022, 13, 136. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Q.; Zheng, Y.; Qu, X.; Wu, F.; Fang, G. An Improved Aeromagnetic Compensation Method Robust to Geomagnetic Gradient. Appl. Sci. 2022, 12, 1490. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, K.; Yan, B.; Zhu, W. The Conjunctive Compensation Method Based on Inertial Navigation System and Fluxgate Magnetometer. Appl. Sci. 2023, 13, 5138. [Google Scholar] [CrossRef]
- Yu, P.; Zhao, X.; Jiao, J. An improved neural network method for aeromagnetic compensation. Meas. Sci. Technol. 2021, 32, 045106. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Z.; Du, Y.; Luo, G.; Zhang, Y.; Zheng, Z.; Ren, C. Mineralogical characteristics and genetic significance of the Hemushan iron deposit in the southern section of Ningwu. Depos. Geol. 2015, 34, 163–178. [Google Scholar]
- Liu, Y.; Ma, M.; Shen, X. Analysis of the Tectonic Construction Characteristics and Metallogenic Control of Mineral Fields in the Ningwu Area. Adv. Geosci. 2018, 8, 640. [Google Scholar]
- Yu, P.; Zhao, X.; Jiao, J. An Aeromagnetic Compensation Algorithm Based on a Deep Autoencoder. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Gamey, T.J.; Doll, W.E.; Beard, L.P. Analysis of Correlated Noise in Airborne Magnetic Gradients for Unexploded Ordnance Detection. J. Environ. Eng. Geophys. 2004, 9, 115–125. [Google Scholar] [CrossRef]
- Zhang, N.; Lin, C. Modeling and Compensation of Aircraft Background Magnetic Interference Based on Improved Ridge Estimation. Syst. Eng. Electron. Technol. 2012, 34, 5. [Google Scholar]
- Hefnawy, A.E.; Farag, A. A combined nonlinear programming model and Kibria method for choosing ridge parameter regression. Commun. Stat.-Simul. Comput. 2014, 43, 1442–1470. [Google Scholar] [CrossRef]
- Hardwick, C.D. Important design considerations for inboard airborne magnetic gradiometers. Geophysics 1984, 49, 2004–2018. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).