Robust GNSS Positioning Using Unbiased Finite Impulse Response Filter
Abstract
:1. Introduction
- (1)
- The proposed method offers a novel approach to estimating position information that effectively eliminates the requirement for calculating error covariances during the iteration process.
- (2)
- Because the UFIR operates only with the adjacent points in a batch form, the accumulation of errors is ultimately suppressed.
- (3)
- Two field tests were conducted, and comparative analyses were performed with LS and KF methods. The results show that the UFIR solution can significantly improve GNSS positioning performance.
2. Problem Formulation
2.1. GNSS Position Calculation
2.2. Least Square Method
2.3. Kalman Filter
3. Optimization Framework
3.1. Extended Model
3.2. UFIR Estimator
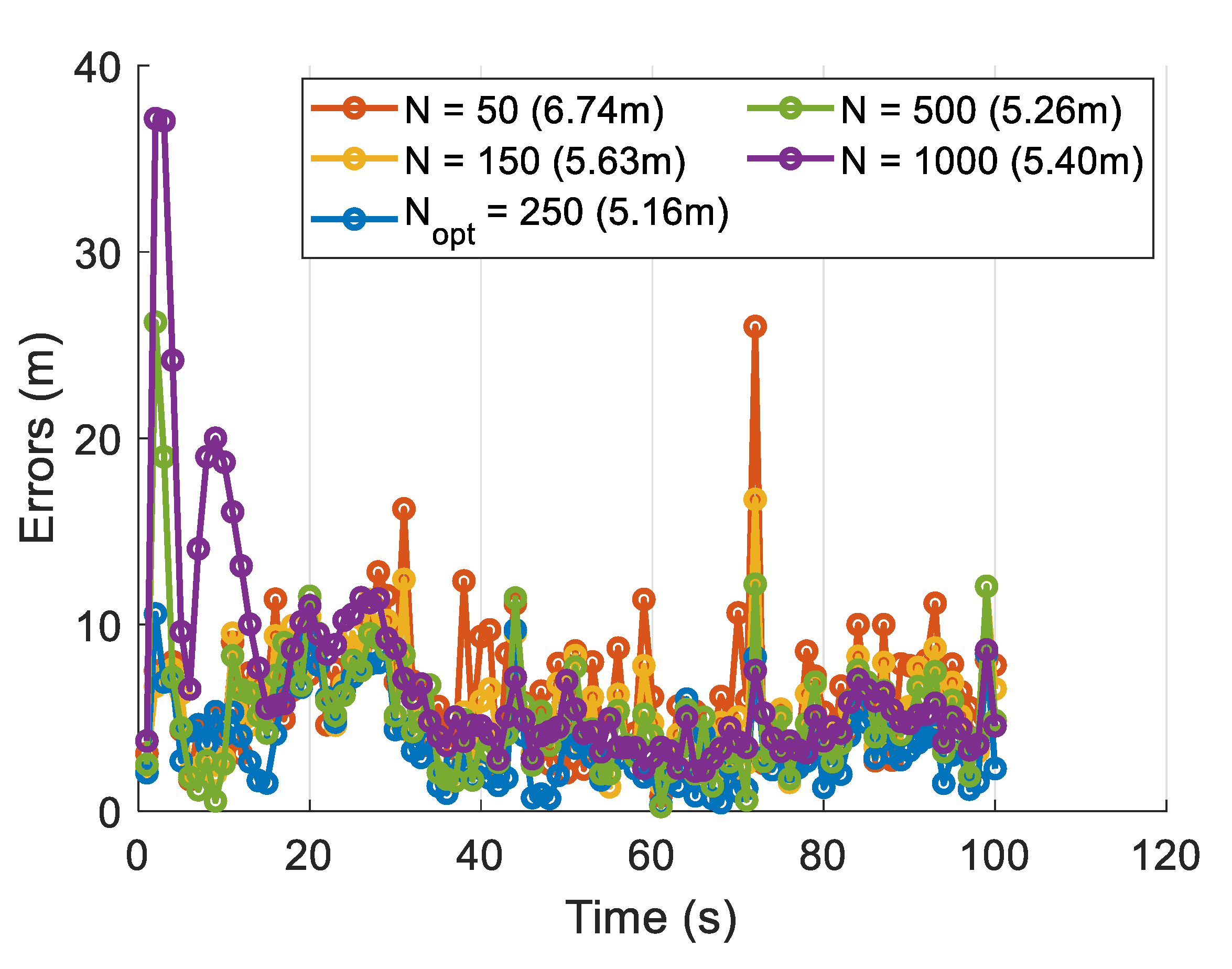
3.3. Turning of UFIR
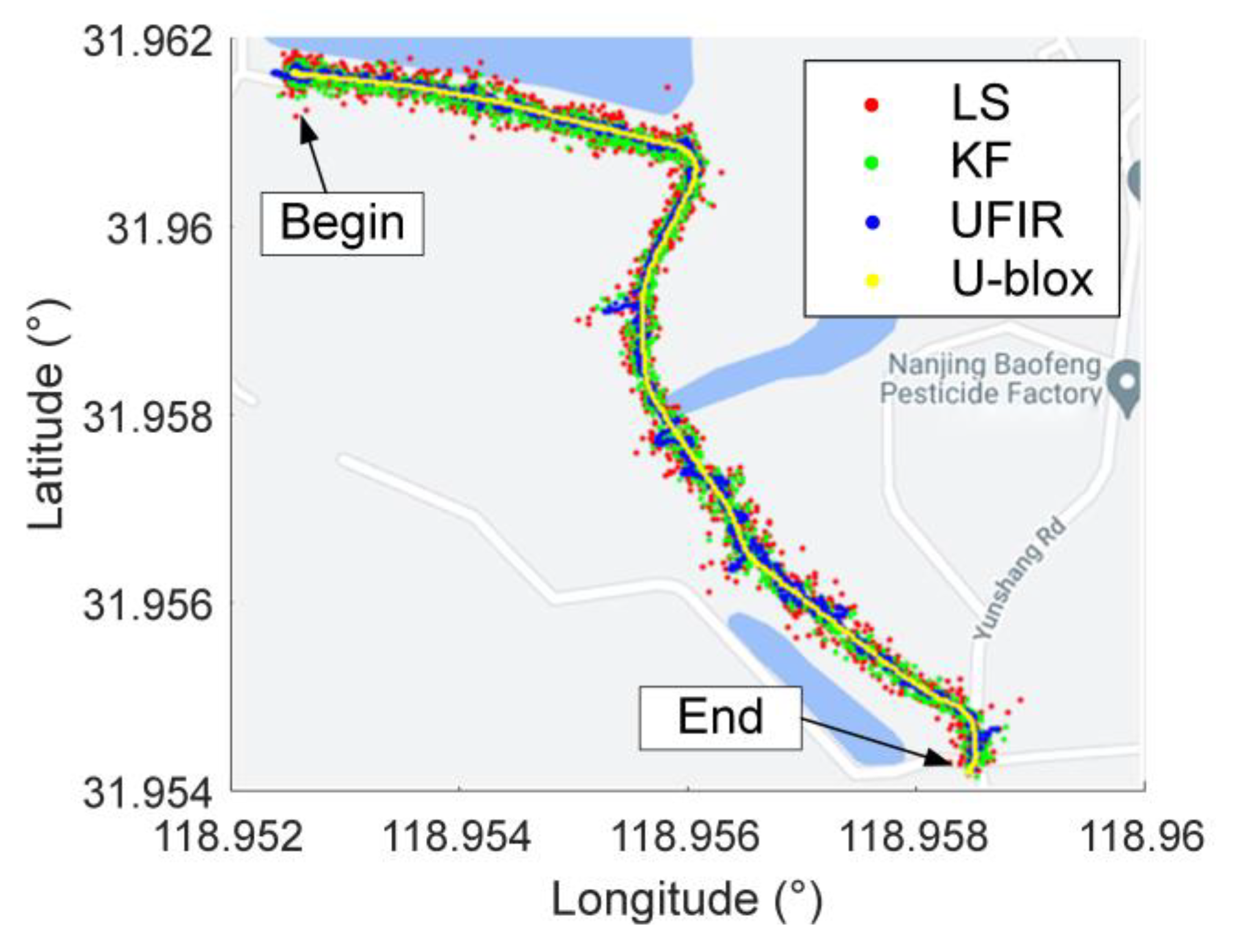
4. Experiments and Results
4.1. Data Description
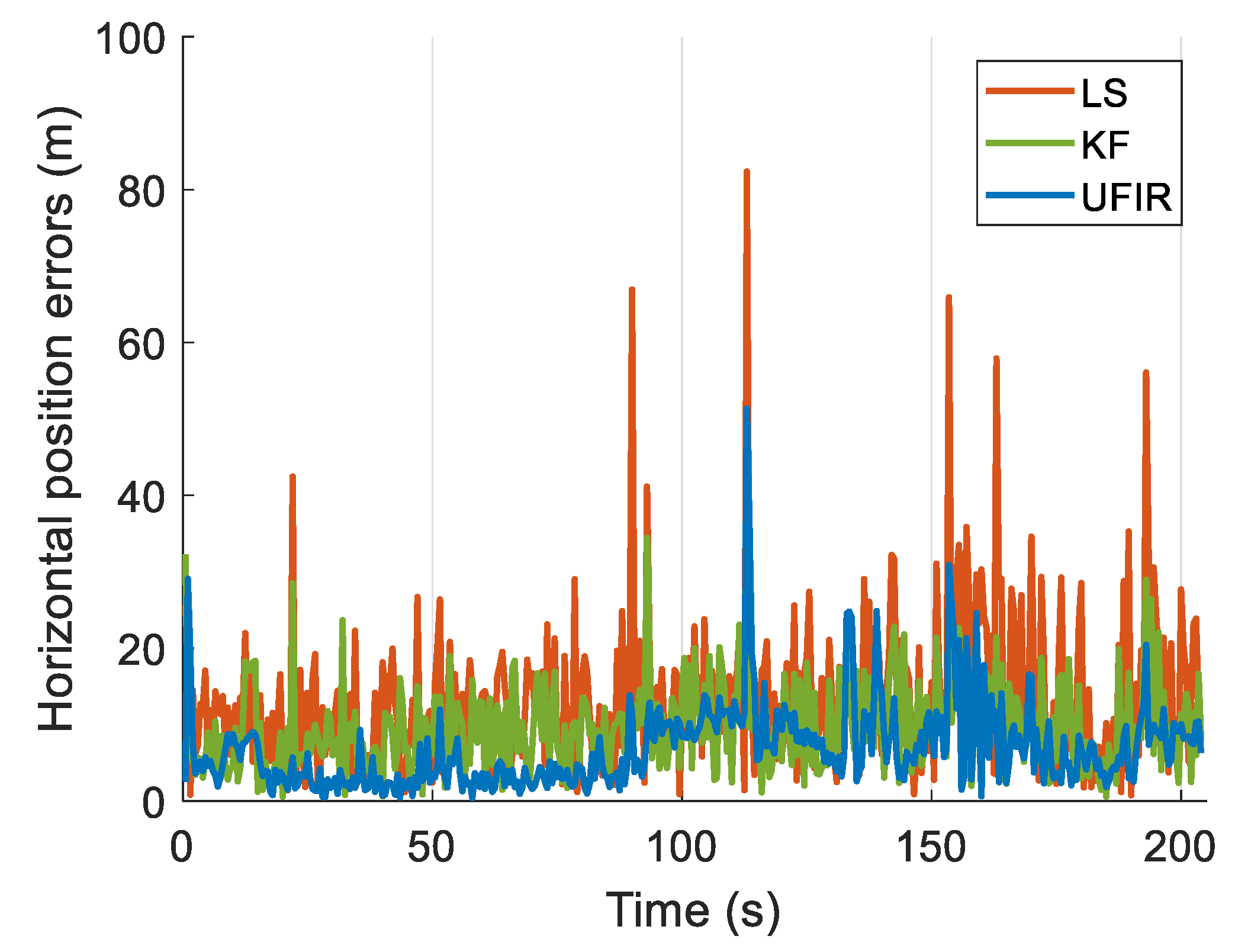
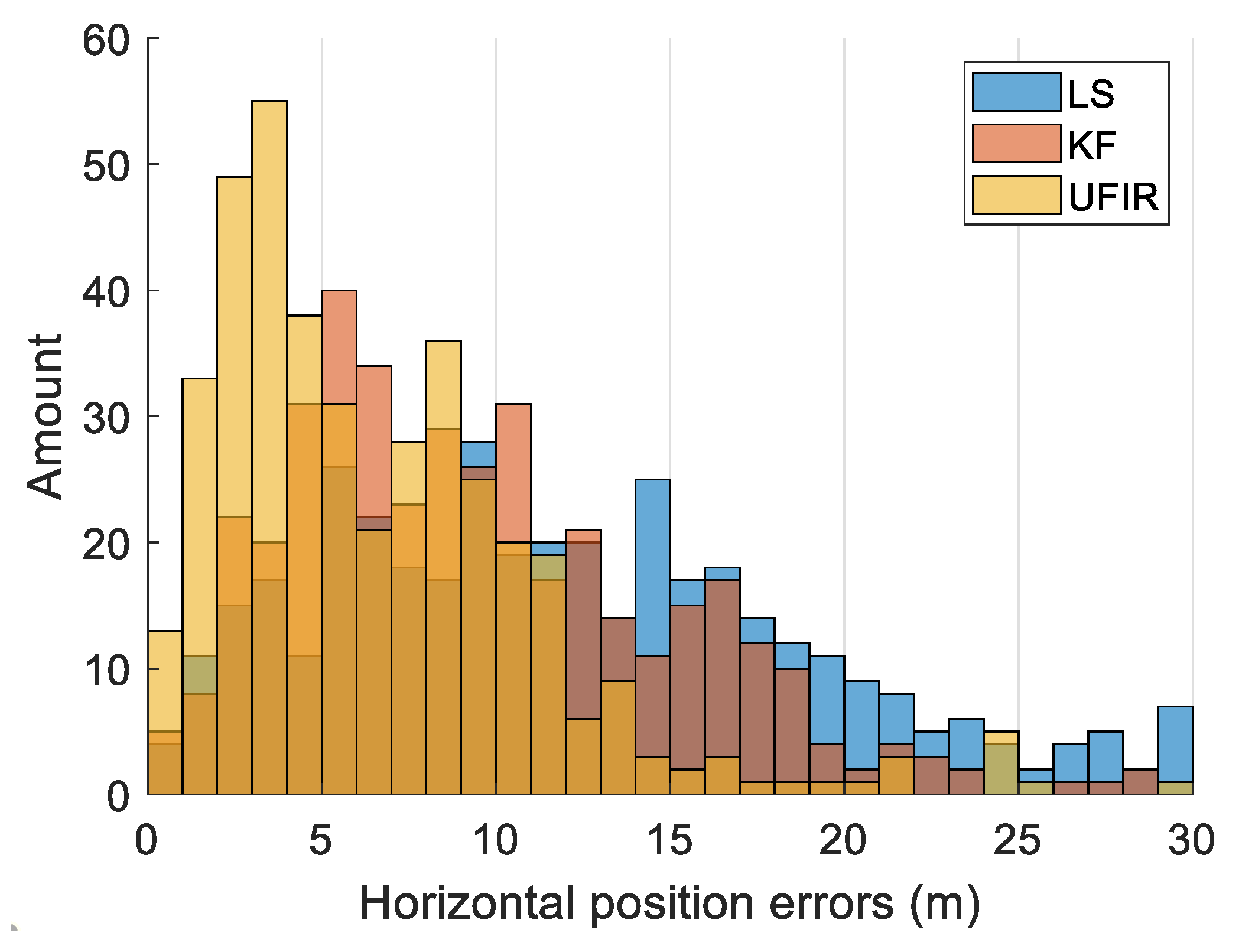
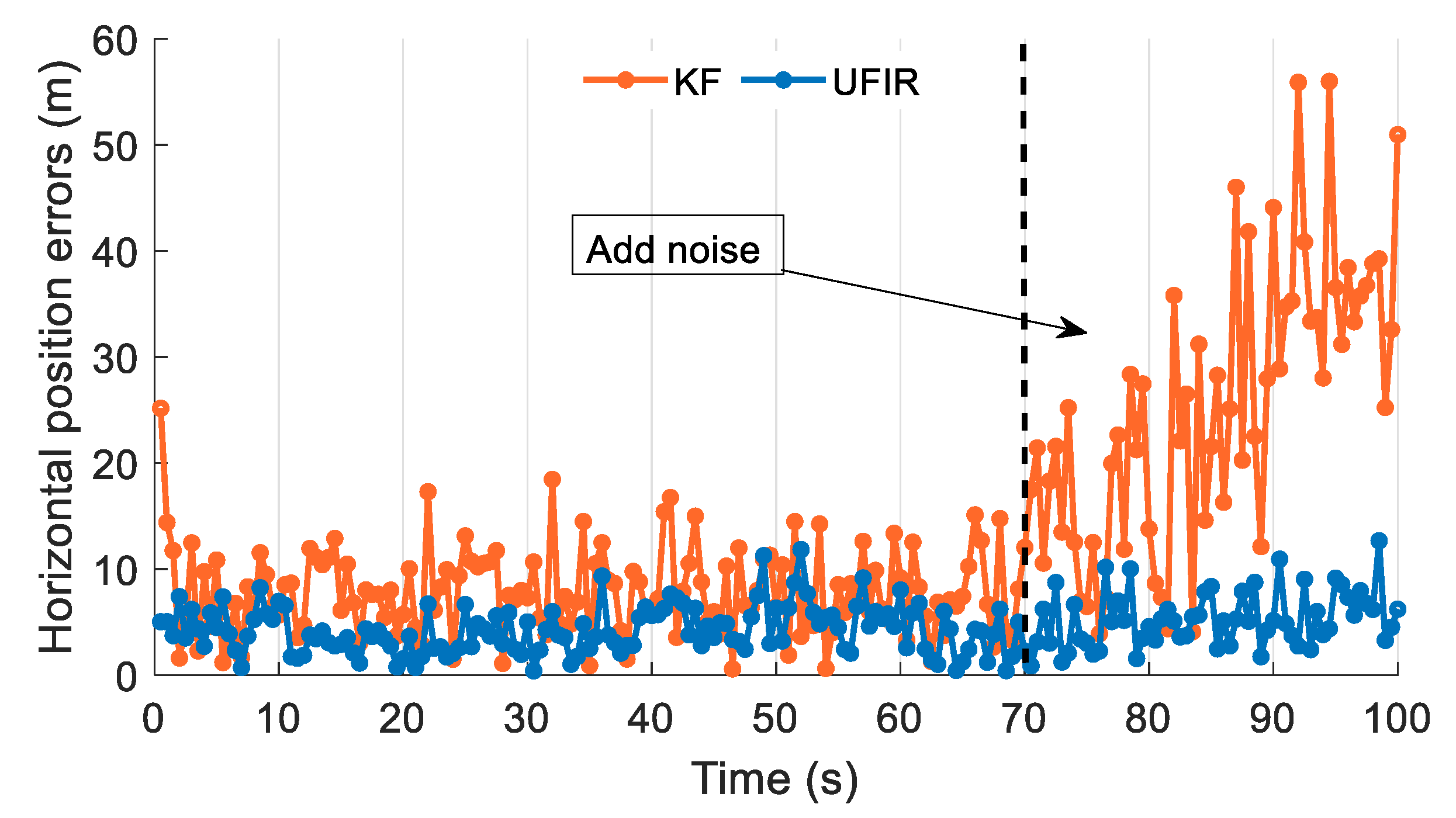
4.2. Positioning Performance Evaluation
4.2.1. Test I: Urban Area, Bumpy Road
4.2.2. Test II: Suburban Area, Smooth Road
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Janssen, T.; Koppert, A.; Berkvens, R.; Weyn, M. A Survey on IoT Positioning Leveraging LPWAN, GNSS and LEO-PNT. IEEE Internet Things J. 2023, 10, 11135–11159. [Google Scholar] [CrossRef]
- Hesselbarth, A.; Medina, D.; Ziebold, R.; Sandler, M.; Hoppe, M.; Uhlemann, M. Enabling Assistance Functions for the Safe Navigation of Inland Waterways. IEEE Intell. Transp. Syst. Mag. 2020, 12, 123–135. [Google Scholar] [CrossRef]
- Sanwale, J.; Chada, S.R.; Patel, A.; Rustagi, V.; Kothari, M. Roll Angle Estimation of Smart Projectiles Using GNSS Signal. IFAC-PapersOnLine 2022, 55, 211–216. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, J.; Bo, Y.; Chen, Y.; Jiang, C.; Jia, J.; Duan, Z.; Karjalainen, M.; Hyyppä, J. Pedestrian Smartphone Navigation Based on Weighted Graph Factor Optimization Utilizing GPS/BDS Multi-Constellation. Remote Sens. 2023, 15, 2506. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Srivastava, P.K. GPS and GNSS Technology in Geosciences; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128186176. [Google Scholar]
- Parkinson, B.W.; Telecom, S. Global Positioning System: Theory and Applications, Volume I; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 1996; Volume 2, ISBN 1563471078. [Google Scholar]
- Herrera, A.M.; Suhandri, H.F.; Realini, E.; Reguzzoni, M.; de Lacy, M.C. GoGPS: Open-Source MATLAB Software. GPS Solut. 2016, 20, 595–603. [Google Scholar] [CrossRef]
- Bernabeu, J.; Palafox, F. Peer reviewed A Collection of SDRs for Global Navigation Satellite Systems (GNSS). In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 25–27 January 2022; pp. 906–919. [Google Scholar]
- Filic, M.; Grubisic, L.; Filjar, R. Improvement of Standard Gps Position Estimation Algorithm through Utilization of Weighted Least-Square approach. In Proceedings of the 11th Annual Baška GNSS Conference, Baška, Croatia, 7–9 May 2017; pp. 7–19. [Google Scholar]
- Barbu, A.L.; Laurent-Varin, J.; Perosanz, F.; Mercier, F.; Marty, J.C. Efficient QR Sequential Least Square Algorithm for High Frequency GNSS Precise Point Positioning Seismic Application. Adv. Space Res. 2018, 61, 448–456. [Google Scholar] [CrossRef]
- Li, L.; Zhong, J.; Zhao, M. Doppler-Aided GNSS Position Estimation with Weighted Least Squares. IEEE Trans. Veh. Technol. 2011, 60, 3615–3624. [Google Scholar] [CrossRef]
- Jiménez-Martínez, M.J.; Farjas-abadia, M.; Quesada-olmo, N. An Approach to Improving Gnss Positioning Accuracy Using Several Gnss Devices. Remote Sens. 2021, 13, 1149. [Google Scholar] [CrossRef]
- Xu, P.; Liu, J.; Shi, Y. Almost Unbiased Weighted Least Squares Location Estimation. J. Geod. 2023, 97, 68. [Google Scholar] [CrossRef]
- Greiff, M.; Berntorp, K. Optimal Measurement Projections with Adaptive Mixture Kalman Filtering for GNSS Positioning. Proc. Am. Control Conf. 2020, 2020, 4435–4441. [Google Scholar] [CrossRef]
- Tao, X.; Zhang, X.; Zhu, F.; Liu, W.; Li, L. A Hybrid State Representation-Based GNSS Filtering Model to Improve Vehicular Positioning Performance. IEEE Sens. J. 2023, 23, 3924–3935. [Google Scholar] [CrossRef]
- Gao, X.; Luo, H.; Ning, B.; Zhao, F.; Bao, L.; Gong, Y.; Xiao, Y.; Jiang, J. RL-AKF: An Adaptive Kalman Filter Navigation Algorithm Based on Reinforcement Learning for Ground Vehicles. Remote Sens. 2020, 12, 1704. [Google Scholar] [CrossRef]
- Lotfy, A.; Abdelfatah, M.; El-Fiky, G. Improving the Performance of GNSS Precise Point Positioning by Developed Robust Adaptive Kalman Filter. Egypt. J. Remote Sens. Space Sci. 2022, 25, 919–928. [Google Scholar] [CrossRef]
- Bahadur, B.; Nohutcu, M. Integration of Variance Component Estimation with Robust Kalman Filter for Single-Frequency Multi-GNSS Positioning. Meas. J. Int. Meas. Confed. 2021, 173, 108596. [Google Scholar] [CrossRef]
- Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments. Sensors 2021, 21, 1250. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yang, Y.; Xiang, Q.; He, Q.; Zhou, Z.; Yao, Y. Noise Adaptive Kalman Filter for Joint Polarization Tracking and Channel Equalization Using Cascaded Covariance Matching. IEEE Photonics J. 2018, 10, 7900911. [Google Scholar] [CrossRef]
- Salcedo-Bosch, A.; Rocadenbosch, F.; Sospedra, J. A Robust Adaptive Unscented Kalman Filter for Floating Doppler Wind-LiDAR Motion Correction. Remote Sens. 2021, 13, 4167. [Google Scholar] [CrossRef]
- Xue, W.; Luan, X.; Zhao, S.; Liu, F. An Online Performance Index for the Kalman Filter. IEEE Trans. Instrum. Meas. 2022, 71, 1007912. [Google Scholar] [CrossRef]
- Shmaliy, Y.S.; Zhao, S.; Ahn, C.K. Unbiased Finite Impluse Response Filtering: An Iterative Alternative to Kalman Filtering Ignoring Noise and Initial Conditions. IEEE Control Syst. 2017, 37, 70–89. [Google Scholar] [CrossRef]
- Zhao, S.; Shmaliy, Y.S.; Andrade-Lucio, J.A.; Liu, F. Multipass Optimal FIR Filtering for Processes with Unknown Initial States and Temporary Mismatches. IEEE Trans. Ind. Inform. 2021, 17, 5360–5368. [Google Scholar] [CrossRef]
- Xu, Y.; Shmaliy, Y.S.; Shen, T.; Chen, D.; Sun, M.; Zhuang, Y. INS/UWB-Based Quadrotor Localization under Colored Measurement Noise. IEEE Sens. J. 2021, 21, 6384–6392. [Google Scholar] [CrossRef]
- Ramirez-Echeverria, F.; Sarr, A.; Shmaliy, Y.S. Optimal Memory for Discrete-Time FIR Filters in State-Space. IEEE Trans. Signal Process. 2014, 62, 557–561. [Google Scholar] [CrossRef]
- Xu, B.; Hsu, L.T. Open-Source MATLAB Code for GPS Vector Tracking on a Software-Defined Receiver. GPS Solut. 2019, 23, 46. [Google Scholar] [CrossRef]
- Xu, B.; Jia, Q.; Hsu, L.-T. Vector Tracking Loop-Based GNSS NLOS Detection and Correction: Algorithm Design and Performance Analysis. IEEE Trans. Instrum. Meas. 2019, 69, 4604–4619. [Google Scholar] [CrossRef]
- Xue, W.; Luan, X.; Zhao, S.; Liu, F. A Fusion Kalman Filter and UFIR Estimator Using the Influence Function Method. IEEE/CAA J. Autom. Sin. 2022, 9, 709–718. [Google Scholar] [CrossRef]
- Zhao, S.; Shmaliy, Y.S.; Ahn, C.K.; Liu, F. Self-Tuning Unbiased Finite Impulse Response Filtering Algorithm for Processes with Unknown Measurement Noise Covariance. IEEE Trans. Control Syst. Technol. 2021, 29, 1372–1379. [Google Scholar] [CrossRef]
- Contreras-Gonzalez, J.; Ibarra-Manzano, O.; Shmaliy, Y.S. Clock State Estimation with the Kalman-like UFIR Algorithm via TIE Measurement. Meas. J. Int. Meas. Confed. 2013, 46, 476–483. [Google Scholar] [CrossRef]
- Dey, A.; Iyer, K.; Xu, B.; Sharma, N.; Hsu, L.T. Performance Evaluation of Vectorized NavIC Receiver Using Improved Dual-Frequency NavIC Measurements. IEEE Trans. Instrum. Meas. 2023, 72, 8505213. [Google Scholar] [CrossRef]


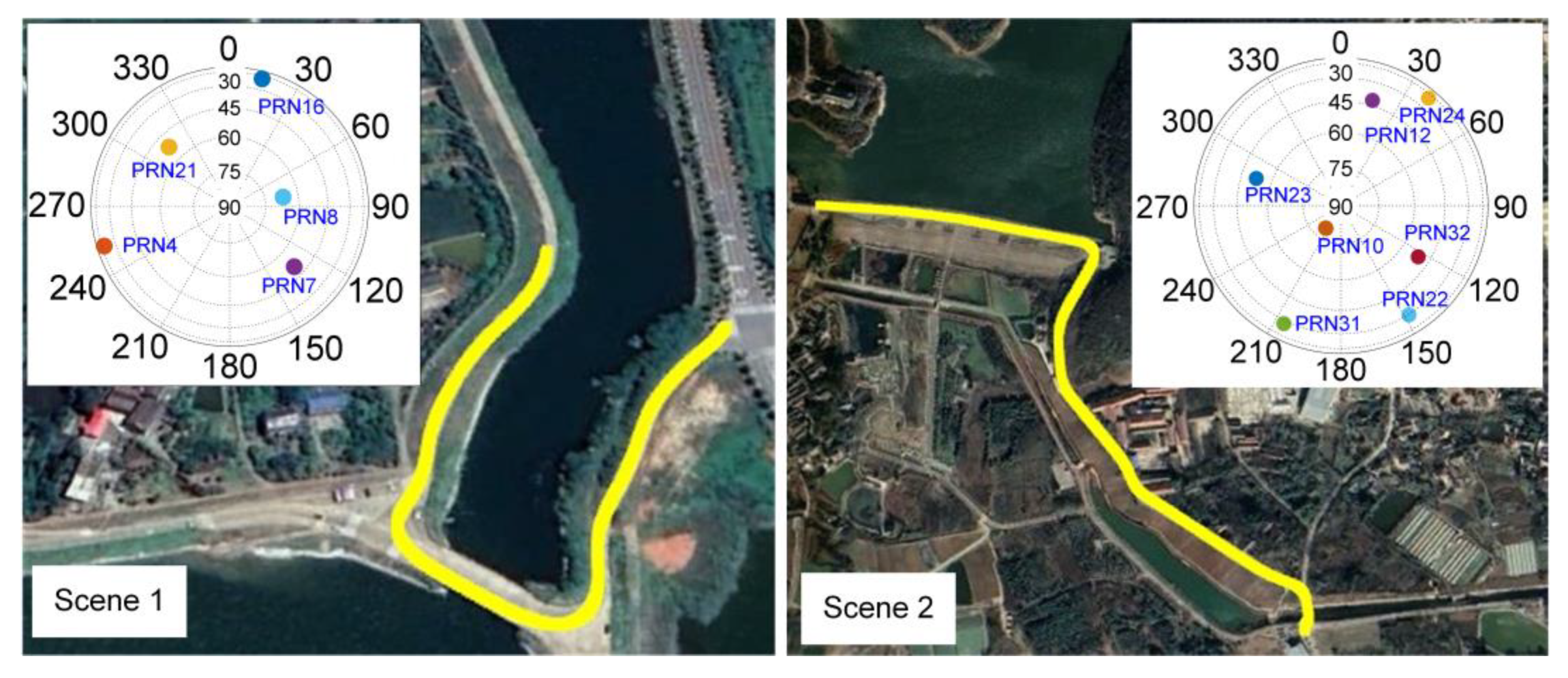
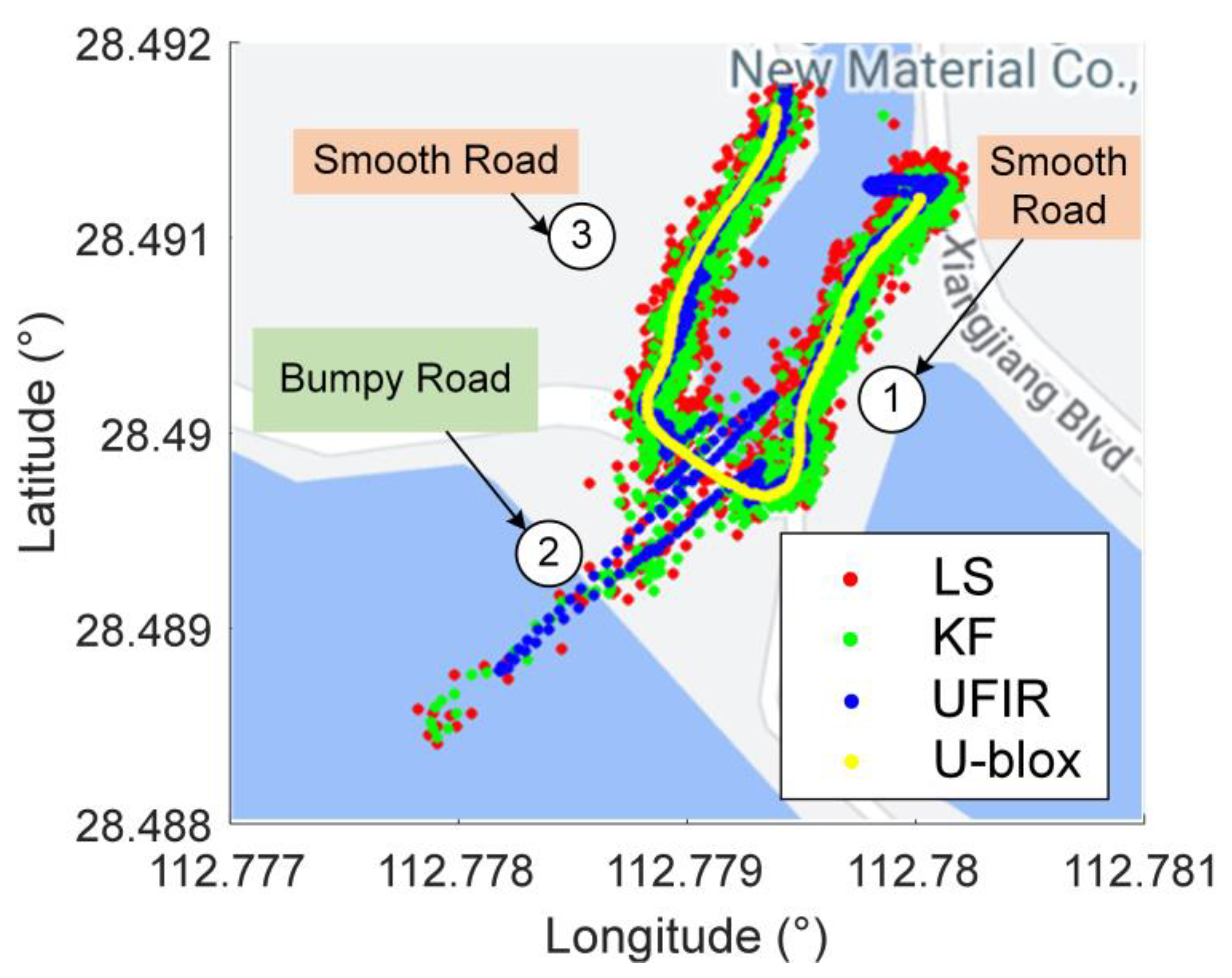

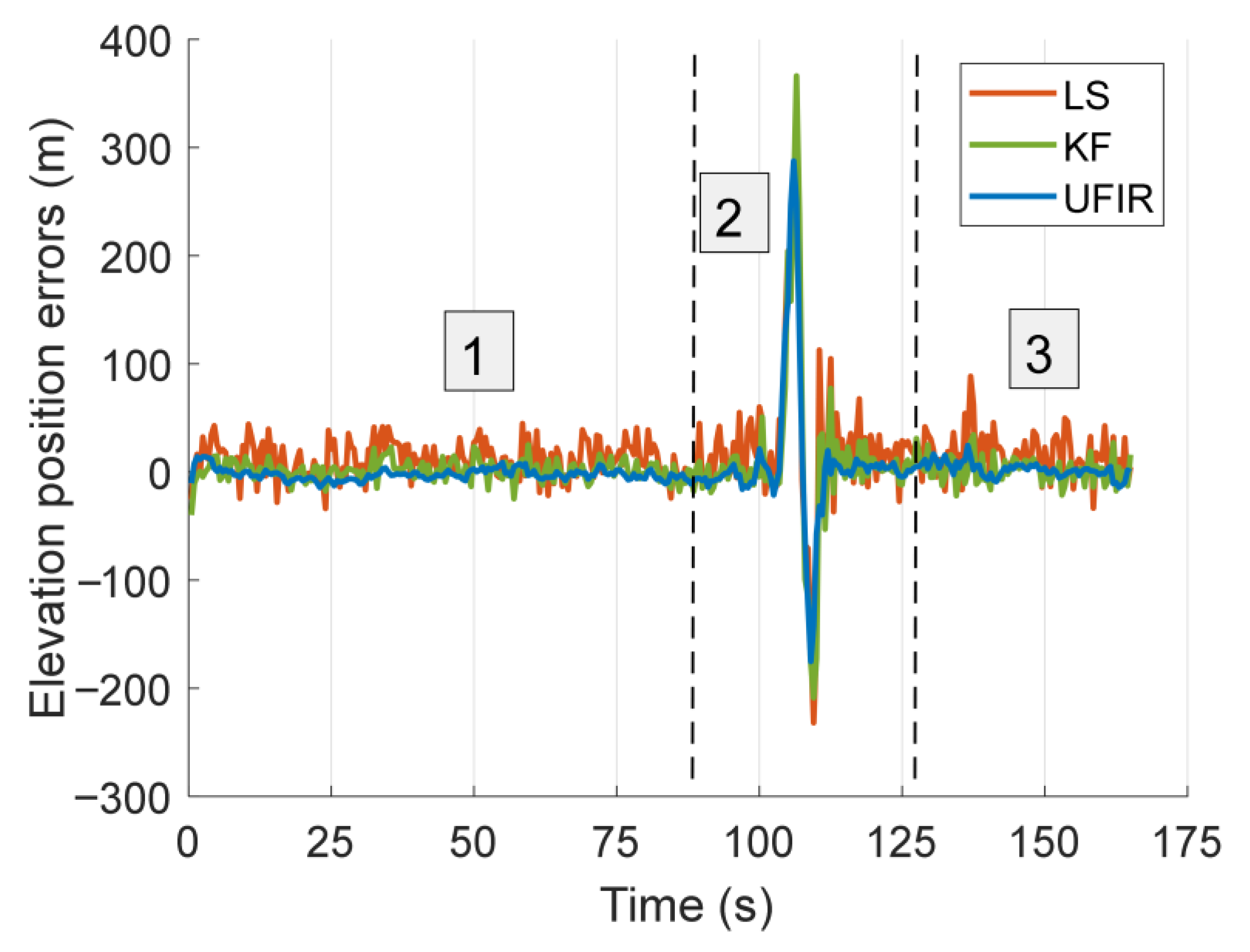
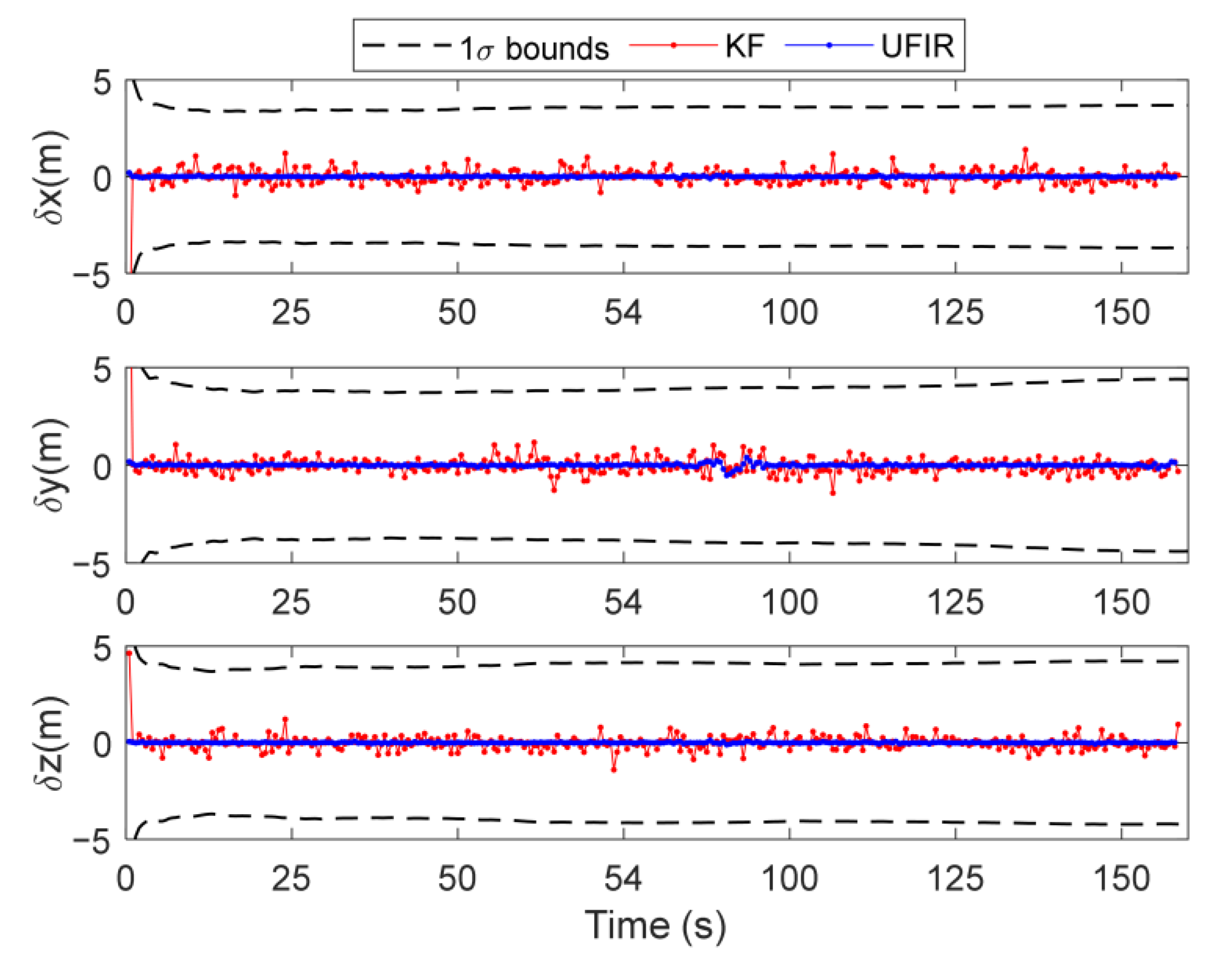
| Equipment | Parameter | Value | Unit |
|---|---|---|---|
| Antenna | Polarization | Right-hand circularly polarized (RHCP) | - |
| Low noise amplifier (LNA) gain | 32 ± 3.0 | dB | |
| Elevation coverage | 360° | - | |
| Noise figure | <2.0 | dB | |
| Front-end | GNSS signal | GPS L1 | - |
| Sampling rate | 16.368 | MHz | |
| IF | 4.092 | MHz | |
| IF bandwidth | 2.5 | MHz | |
| Quantization | IQ-2 | bit | |
| U-blox NEO-M8T | Channel | 72 | - |
| Horizontal position accuracy | 2.0 (Typical) 2.5 (SBAS) | m | |
| Position update rate | 10 (Max) | Hz | |
| Channel | 72 | - |
| Methods | Median | Mean | STD | Unit |
|---|---|---|---|---|
| LS | 12.33 | 10.86 | 6.57 | Meter |
| KF | 8.53 | 8.08 | 5.34 | Meter |
| UFIR | 5.93 | 5.79 | 4.16 | Meter |
| Horizon Length | N = 50 | N = 150 | N = 250 | N = 500 | N = 1000 |
|---|---|---|---|---|---|
| Time (s) | 1721.44 | 1745.98 | 1808.87 | 2050.98 | 2443.28 |
| Memory used (Mb) | 101.00 | 137.48 | 162.58 | 247.48 | 497.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, J.; Xu, B.; Dou, L. Robust GNSS Positioning Using Unbiased Finite Impulse Response Filter. Remote Sens. 2023, 15, 4528. https://doi.org/10.3390/rs15184528
Dou J, Xu B, Dou L. Robust GNSS Positioning Using Unbiased Finite Impulse Response Filter. Remote Sensing. 2023; 15(18):4528. https://doi.org/10.3390/rs15184528
Chicago/Turabian StyleDou, Jie, Bing Xu, and Lei Dou. 2023. "Robust GNSS Positioning Using Unbiased Finite Impulse Response Filter" Remote Sensing 15, no. 18: 4528. https://doi.org/10.3390/rs15184528
APA StyleDou, J., Xu, B., & Dou, L. (2023). Robust GNSS Positioning Using Unbiased Finite Impulse Response Filter. Remote Sensing, 15(18), 4528. https://doi.org/10.3390/rs15184528








