Abstract
Due to the scarcity of observational data and the intricate precipitation–runoff relationship, individually applying physically based hydrological models and machine learning (ML) techniques presents challenges in accurately predicting floods within data-scarce glacial river basins. To address this challenge, this study introduces an innovative hybrid model that synergistically harnesses the strengths of multi-source remote sensing data, a physically based hydrological model (i.e., Spatial Processes in Hydrology (SPHY)), and ML techniques. This novel approach employs MODIS snow cover data and remote sensing-derived glacier mass balance data to calibrate the SPHY model. The SPHY model primarily generates baseflow, rain runoff, snowmelt runoff, and glacier melt runoff. These outputs are then utilized as extra inputs for the ML models, which consist of Random Forest (RF), Gradient Boosting (GDBT), Long Short-Term Memory (LSTM), Deep Neural Network (DNN), Support Vector Machine (SVM) and Transformer (TF). These ML models reconstruct the intricate relationship between inputs and streamflow. The performance of these six hybrid models and SPHY model is comprehensively explored in the Manas River basin in Central Asia. The findings underscore that the SPHY-RF model performs better in simulating and predicting daily streamflow and flood events than the SPHY model and the other five hybrid models. Compared to the SPHY model, SPHY-RF significantly reduces RMSE (55.6%) and PBIAS (62.5%) for streamflow, as well as reduces RMSE (65.8%) and PBIAS (73.51%) for floods. By utilizing bootstrap sampling, the 95% uncertainty interval for SPHY-RF is established, effectively covering 87.65% of flood events. Significantly, the SPHY-RF model substantially improves the simulation of streamflow and flood events that the SPHY model struggles to capture, indicating its potential to enhance the accuracy of flood prediction within data-scarce glacial river basins. This study offers a framework for robust flood simulation and forecasting within glacial river basins, offering opportunities to explore extreme hydrological events in a warming climate.
1. Introduction
High mountainous regions (e.g., Himalayas, Alps, Tien) encompass a myriad of glaciers, snow cover, alpine lakes, and rivers, making them pivotal components of global ecosystems and water resources. These regions are particularly sensitive to climate change due to their unique interaction between climate forcing and complex terrain gradients. Recent decades have seen a notable acceleration in glacier ablation due to the warming climate [1]. Concurrently, shifts in snow accumulation and melt dynamics have been induced [2]. Moreover, the intensity of extreme rainfall events in high-elevation regions has exhibited a remarkable 15% amplification for every degree Celsius of warming, a pace roughly twice as rapid as previously documented [3]. These shifts have substantial implications for runoff patterns, overall water availability [4], and the occurrence of floods, such as the severe flood in Pakistan in 2022 [5]. Consequently, the imperative for dependable flood prediction in this context is paramount to support sustainable water resource planning and management strategies.
Flood or streamflow simulation models are generally categorized into three primary groups: physical-based models, statistical or machine learning-based models, and a hybrid of both. The physical-based hydrological models rely on climate forcings and represent various hydrological processes through mathematical formulations [6]. Notable examples include Spatial Processes in Hydrology (SPHY) [7], Variable Infiltration Capacity model (VIC) [8], and Soil Water Assessment Tool (SWAT) [9], which have found extensive use in simulating catchment dynamics and runoff processes in alpine regions [10]. However, acquiring high-quality climate data as inputs and streamflow records for model calibration is a noteworthy challenge. The limited density of meteorological observation networks often gives rise to significant uncertainties [11]. Additionally, physical-based hydrological models are constrained by their simplified representation of hydrological processes. Even with abundant climate forcings and deliberated calibration, the physical-based model cannot fully reproduce the observed streamflow [12]. Furthermore, physical-based models can only simulate hydrologic fluxes and state variables predefined during model configuration. They cannot leverage other observed land surface characteristics (e.g., land surface temperature) to improve model performance. These limitations ultimately impede the attainment of precise flood prediction.
The statistical or machine learning (ML) approach has been successfully applied to water environment research over two decades [13,14] by exacting the patterns from hydrologic observations. The ML-based hydrological models generally consist of meteorological variables and an expression accounting for the statistical relationship between these variables and streamflow [15]. Typically, ML-based hydrological models require less expertise and time for developing and calculating [16], and can solve highly nonlinear problems without considering the physical processes [17]. Furthermore, they usually perform better than physical-based hydrological models [11,18]. In recent years, the long short-term memory (LSTM) model, with its unique internal structure, has demonstrated unparalleled popularity and robustness in hydrologic modeling [19]. However, the main problem of ML-based hydrological models is that it has no physical process and can only find rules from the data. This requires the observation records used to train the ML model to cover a wide range of hydrologic variability, which is usually unavailable in data-scarce high mountainous regions. For example, ML-based hydrological models cannot describe the dynamic accumulation and melting process of glaciers, so it is difficult to capture their tipping points [20] under climate change in alpine regions, leading to inaccurate predictions in many situations. Therefore, the performance of the ML approaches may suffer from extrapolation, limiting their applications in prediction under changing climate.
To address the inability of ML-based hydrological models to account for complex physical processes, the hybrid model was proposed to combine the strengths of physical-based hydrological models and ML techniques. Currently, the commonly used hybridization approach is adding the outputs of physically informed models into ML models. The outputs of physically informed models could be simulated streamflow and intermediate variables (e.g., snowmelt runoff) [20]. Similarly, Xu et al. [21] used the outputs (i.e., snowmelt and rainfall) of physically informed models as inputs of Convolutional Long Short-Term Memory. Though hybrid models have made significant progress, most of the daily scale or flood studies focus on low-altitude areas, or the application of hybrid models in high mountainous regions is mainly applied to monthly scale runoff simulation. However, there is no report on applying the hybrid model to study streamflow or flood in high mountainous areas. This is due to data-scarce regions like high-altitude glacial river basins; obtaining reliable hydrological data can be challenging. Sparse and irregular data coverage, coupled with the complex interactions between glaciers, snow, and rain, poses significant hurdles to conventional modeling approaches. Since accurate streamflow prediction leads to effective water resources management and flood warning, it is valuable and necessary to enhance the performance of streamflow or flood simulation over alpine regions.
To this end, the primary aim of this study is to enhance flood event simulations in high-altitude glacial river basins with limited available data. By merging the strengths of multi-source remote sensing data to calibrate model parameters and integrating the physical insights of the widely used Spatial Processes in Hydrology (SPHY) model with the predictive capabilities of ML algorithms, we intend to elevate the accuracy and dependability of flood simulations. The study’s objectives are to address the following questions: (1) Can the proposed hybrid model enhance the capacity for flood event simulation? (2) Can the multi-objective parameter calibration method improve the ability of runoff simulation for the SPHY model? (3) Can better alignment of inputs to physical processes improve the hybrid’s flood simulation capabilities? This study diverges from its predecessors in three key aspects: (1) It attempts hybrid modeling in data-limited glacial river basins in high mountainous regions to amplify flood modeling capacity; (2) It employs multi-source remote sensing data and emphasizes the calibration of physical models to augment flood simulation performance; (3) The bootstrap sampling technique was used to provide uncertain intervals for flood prediction results of the hybrid model. This innovative hybrid model is tested to simulate daily streamflow in Central Asia’s typical alpine region, the Manas River basin.
In summary, this research aims to bridge the methodology and information gap between physical-based hydrological modeling and ML approaches to enhance the simulation of flood events in data-scarce high-altitude glacial river basins. By combining the strengths of these two methodologies, we aspire to contribute to advancing hydrological modeling techniques, ensuring more accurate predictions of flood patterns. Ultimately, this study has the potential to provide valuable insights for water resource management, disaster mitigation, and climate change adaptation strategies in regions highly vulnerable to the impacts of climate change.
2. Study Area and Data
2.1. Study Area
This study was conducted in the source region of the Manas River Basin (MRB). The Manas River originates on the northern slope of the Tianshan Mountains, situated in the heartland of Central Asia. It is China’s largest artificial oasis area and the fourth largest irrigation district [22]. Additionally, the river forms a crucial part of the Economic Belt on the Northern Slope of the Tianshan Mountains. The MRB encompasses the catchment between 84°30′~86°30′E and 43°~44°N, with an upstream contributing area of 5156 km2, extending to the Kensiwate station (Figure 1). Discharge at the Kensiwate station follows an uneven seasonal distribution, with approximately 80% occurring during the months from June to September. As Ji and Chen [23] reported the annual average precipitation in the MRB at around 550 mm. The genesis of floods within the Manas River is primarily attributed to its mountainous terrain. Floods in the lower mountain regions result from heavy rainfall, while in the middle mountain areas, snow melting and intense rainfall contribute to floods. In the high mountain regions, permanent snowmelt constitutes the predominant flood source. The basin features elevations exceeding 3100 m, characterized by perennial snow and glaciers, while the lower mountain and hilly areas experience thicker snow accumulation during autumn and winter.
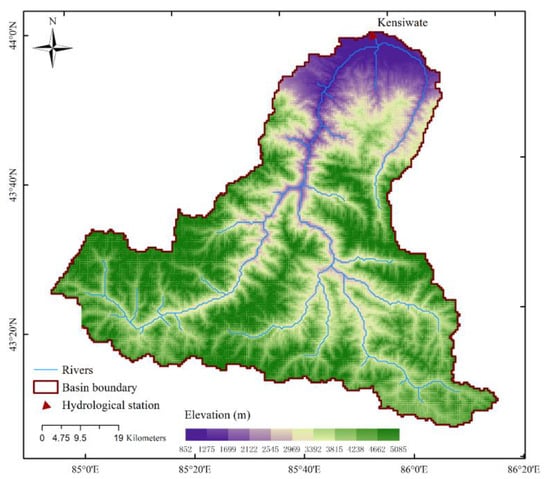
Figure 1.
Map of the headwater catchment of Manas River Basin.
With the gradual increase in temperatures during July and August, the annual peak floods typically manifest within this timeframe, occasionally extending to June. The principal flood type in the Manas River is associated with snowmelt, accompanied by rain-induced and mixed-type floods, the latter being more pronounced during significant flood events. The annual peak flow predominantly transpires between June and August, particularly from late July to early August. Floods primarily originate from the middle mountain areas, marked by substantial year-to-year fluctuations in peak flow. The steep topography pronounced longitudinal slopes of the mountainous regions and the watershed’s inherent limited storage capacity contribute to rapid flood escalation and decline, short-lived peak durations, and brief peak occurrences.
From hydrological records spanning 1955 to 2008 at the Kensiwate Hydrological Station, the highest recorded peak flow within the mountainous of the Manas River reached 1110 m3/s, while the lowest was measured at 192 m3/s [24]. Among the 53 years of recorded flood data from the Kensiwate Hydrological Station, the highest flow frequencies were observed in July, surpassing half of the total series. Moreover, within a 30-day interval from mid-July to early August, the highest flow frequencies accounted for 81.1% of the entire series.
2.2. Data
The observed daily streamflow data at the Kensiwate hydrological station were collected by the Xinjiang Hydrological Bureau during 2002–2012. IMERG-F (Integrated Multi-satellite Retrievals for Global Precipitation Measurement Final) is a remote-sensing precipitation product [25] with a spatial resolution of 0.1° × 0.1° used in this study. It utilizes microwave and infrared observational data from multiple satellites, including the GPM satellite and satellite-based precipitation estimators. It combines these data with ground-based precipitation measurement site information and employs advanced precipitation estimation algorithms to achieve global-scale estimation of precipitation distribution. The average, maximum, and minimum temperatures were collected from China’s meteorological forcing datasets (2002–2012) [26]. The MOD15A2H MODIS Leaf Area Index was used to calculate potential evapotranspiration [27].
The Digital Elevation Model (DEM) with a grid size of 90 m was obtained from the CGIAR Consortium for Spatial Information (CGIAR-CSI) (http://eros.usgs.gov/find-data, accessed on 1 September 2023). These data were resampled to 1 km × 1 km model resolution to calculate the slope, cell drainage direction, and for lapsing of temperature fields [28], to extract watersheds into sub-basins, generated river networks, and define water bodies and outlets. The glacier outlines defined in RGI6.0 for the RGI region 13 (Central Asia) were used in this study [29]. The initial ice thicknesses for individual glaciers were derived from modeled glacier ice depths [30]. MODIS snow cover data [31] and Geodetic glacier mass balance data [1] calibrate snow and glacier melt parameters over glaciers. Hydraulic soil properties used in this study were derived from HiHydroSoil (1 km × 1 km) and resampled to model resolution [32]. Land use data used in the model were derived from the European Space Agency Climate Change Initiative (ESA CCI) data set [33].
3. Methodology
3.1. SPHY Model
In this investigation, we employ the Spatial Processes in Hydrology (SPHY) v3 model, which is a spatially distributed (raster-based) “leaky-bucket”-type water balance model [34]. This model has been purposefully designed to facilitate large-scale cryospheric-hydrological research; it effectively integrates a range of hydrological processes, encompassing (a) rainfall–runoff, (b) cryospheric processes, (c) evapotranspiration, and (d) soil hydrological processes. Notably, SPHY exhibits remarkable versatility in its spatial scalability, accommodating various spatial scales such as sub-basin, basin, and regional levels. For this particular investigation, the model operates on a daily time step with a spatial resolution of 1 × 1 km. The total runoff () for each grid cell at any time step in the model is the sum of glacier melt runoff (), snowmelt runoff (), rainfall–runoff (), and baseflow ().
The model maintains dynamic snow storage, soil water storage, and groundwater storage for each grid cell. Snowmelt runoff is computed for snow-covered land surface grid cells, and the corresponding runoff over glacier surfaces is termed glacier runoff. Calculating snowmelt involves a degree-day approach with calibrated melt rates. Before melt calculation at each time step, sublimation is estimated and removed from snow storage. The model also considers meltwater refreezing within the snowpack. Snowmelt runoff is generated when snowmelt surpasses the storage threshold. Rainfall–runoff encompasses surface runoff from rainfall and lateral flow from soil water storage. Surface runoff is determined through saturation excess runoff. The model derives reference evapotranspiration using the Modified Hargreaves method [35]. Soil moisture, influenced by soil properties, land use, and capillary rise, is subjected to evapotranspiration, with any remaining water contributing to river discharge via lateral flow or surface runoff. Baseflow runoff arises from groundwater storage release, and each type of runoff is routed downstream through a simple recession coefficient method.
To address model equifinality concerns effectively, a three-step calibration strategy is implemented. Firstly, parameters associated with snow processes are calibrated utilizing MODIS snow cover data [31]. Following this, parameters linked to glacier melt are fine-tuned utilizing remote sensing-based geodetic glacier mass balance data [1]. Finally, rainfall–runoff and routing parameters are calibrated by leveraging observed streamflow data.
The parameter calibration of the physical process model typically involves three phases: model warm-up, calibration, and verification. To ensure an accurate comparison with the hybrid approach, our study designates 2002 as the warm-up period, although no direct comparison is drawn. The calibration and validation periods span from 2003 to 2007 and 2008 to 2012, respectively, and are collectively termed the training and testing periods in subsequent analysis.
3.2. Machine Learning Algorithms
ML is a branch of Artificial Intelligence that focuses on enabling computers to learn from data and improve performance automatically without explicit programming. The fundamental idea of ML is to allow computers identification of patterns, rules, and trends from extensive data, accomplishment of tasks like prediction, classification, and recognition. Currently, there exists a wide array of ML algorithms, making it challenging to enumerate them all. However, the primary objective of this study is to test whether hybrid models can enhance the accuracy of flood simulations in high mountainous regions. Thus, the following provides a brief introduction to six ML algorithms, including classical Support Vector Machine (SVM), ensemble learning algorithms like Random Forest (RF) and Gradient Boosting (GDBT), as well as the deep learning algorithms that have garnered significant attention recently, such as Deep Neural Networks (DNN), LSTM, and Transformer (TF).
All six ML models are implemented in Python, mainly using two Python modules, sklearn and torch. The GridSearchCV technique [36] was utilized in this study to optimize the hyperparameters. GridSearchCV meticulously navigates the ML model’s performance landscape by exhaustively scanning the designated hyperparameter combinations, leading to the identification of the optimal hyperparameter configuration. Consequently, the optimal hyperparameter combinations for the six selected ML models are obtained and presented in Table 1.

Table 1.
Hyperparameter settings for RF, GDBT, LSTM, TF, SVM and DNN.
In the context of the hybrid model, data are partitioned into two subsets: the training dataset and the testing dataset. Each subset encompasses 50% of the data, the proportional division chosen due to the SPHY model’s training period spanning from 2003 to 2007, with the subsequent testing period occurring between 2008 and 2012. To ensure a fair and balanced comparison, an equivalent-length testing dataset is selected. The training dataset primarily serves the purpose of determining model parameters, whereas the testing dataset is primarily employed to assess and compare the performance of different models.
3.2.1. Random Forest
RF is an ensemble method rooted in decision trees, random subspace, and Bootstrap aggregating, commonly used for regression tasks [37]. It averages predicted values from multiple decision trees to produce the final result [38]. In RF, each decision tree is built using a subset of training data and random features, curbing overfitting and enhancing generalization. Its strength is handling intricate variable relationships, capturing non-linear patterns, and mitigating noisy data. Prediction-wise, individual tree outputs are combined through techniques like averaging (for regression) or voting (for classification), yielding a dependable result. RF highlights feature importance, aiding in identifying pivotal variables. With its robustness, scalability, and applicability to diverse domains—finance, healthcare, language processing, and image analysis—RF effectively addresses bias and variance, making it a favored choice among data scientists and ML practitioners.
3.2.2. Gradient Boosting
GDBT is a robust ensemble learning algorithm for regression prediction tasks [39]. By iteratively constructing decision trees, GDBT gradually deepens and increases their number to capture intricate relationships among input and output variables. It effectively manages large-scale datasets and high-dimensional features [40]. GDBT sequentially combines weak learners to create a strong predictor to enhance model accuracy. Through iterative iterations, each new model rectifies the errors made by its predecessors, refining predictions. It accomplishes this by adjusting misclassified instance weights, ultimately delivering precise predictions. The optimization process involves gradient descent, progressively enhancing the model’s performance by minimizing a predefined loss function. The technique’s popularity is evident in notable implementations like XGBoost, LightGBM, and CatBoost, which efficiently handle diverse data types. Widely used in regression, classification, and ranking tasks, GDBT excels at managing complex relationships and generating robust predictions.
3.2.3. Long Short-Term Memory
LSTM is a specialized variant of the recurrent neural network (RNN), adept at predicting time series phenomena [41]. In contrast to conventional RNNs, LSTM replaces hidden units with memory cells encompassing memory cell state, input gate, forget gate, and output gate. This gate-controlled information and memory flow addresses gradient vanishing/exploding issues [42]. LSTM excels at capturing intricate patterns and long-term dependencies, adapting to various data distributions, and bolstering capacity through stacked layers. These attributes are suitable for complicated hydrological time series analysis [43]. For supervised learning, the time series dataset can be structured using past time steps to predict subsequent steps via the sliding window approach. This study adopts a window width of one, transforming the time series into a supervised learning problem. The LSTM model consists of an input layer, two LSTM layers, and an output layer. To combat overfitting, early stopping regularization is employed during training. This technique halts training when validation loss ceases to improve.
3.2.4. Transformer
TF is a groundbreaking deep learning architecture that revolutionized natural language processing and beyond. Introduced by Vaswani et al. [44] in 2017, it replaced traditional sequence-to-sequence models by introducing the “self-attention” mechanism, allowing it the capture of long-range dependencies in data. The TF’s core innovation is the attention mechanism, which assigns different weights to different words in a sequence based on their contextual relevance, enabling it to process inputs in parallel rather than sequentially. This boosts efficiency and parallelism in computation, making it highly scalable. The TF architecture is divided into an encoder and a decoder, allowing it the handling of tasks like machine translation, text generation, and time series forecasting and classification [45]. Its effectiveness and versatility have led to its adoption beyond NLP, finding applications in image generation, speech recognition, and even drug discovery. With its attention-based model and parallel processing capabilities, the TF has become the foundation for many state-of-the-art deep learning models, showcasing its enduring impact on many AI applications.
3.2.5. Support Vector Machine
SVM is a robust supervised ML algorithm for classification and regression tasks [46]. It works by finding the optimal hyperplane that best separates different classes of data points in a high-dimensional space. SVM aims to maximize the margin between classes, making it robust against overfitting. It can handle linear and nonlinear data using different kernels to transform the input space. SVM is effective for both small and large datasets and is widely used in image recognition, text categorization, and bioinformatics due to its ability to handle complex decision boundaries and high-dimensional data. Due to its good generalization ability and robustness, SVR is suitable for handling high-dimensional data and is particularly effective in dealing with nonlinear problems [47].
3.2.6. Deep Neural Network
A DNN is an advanced ML model inspired by the human brain’s neural structure. It consists of multiple layers of interconnected nodes called neurons which process and transform input data. DNNs excel in learning intricate patterns and features from complex data, making them highly effective for tasks like image and speech recognition, natural language processing, and even game playing. DNN depth enables them to automatically extract hierarchical representations of data, learning abstract features at each layer. DNNs adjust their internal weights during training through backpropagation to minimize prediction errors. This process allows them good generalization to new, unseen data. While their power lies in capturing intricate relationships, DNNs also require substantial data and computational resources for training, which might lead to overfitting without proper regularization techniques. Despite these challenges, DNNs have revolutionized various fields, advancing AI capabilities and driving innovation across industries [48].
3.3. Hybrid Model
Figure 2 illustrates the three-step process for constructing the proposed hybrid model. In Step 1, meteorological data (precipitation (P), average temperature (Tair), maximum temperature (Tmax), and minimum temperature (Tmin)), static data (DEM, soil data, land use data), and remote sensing data (glacier depth, glacier area, LAI data) are employed to establish the SPHY model. Additionally, MODIS snow cover fraction (SCF) data, remote-sensing-derived glacier mass balance (GMB) data, and observed data are used to calibrate the SPHY model, with the parameter calibration utilizing the NSGA-Ⅱ algorithm. Moving to Step 2, the SPHY model’s outputs (baseflow, glacier melt runoff, snowmelt runoff, and rain runoff), along with the meteorological data and SCF, are combined as inputs to create hybrid models. Subsequently, the simulated streamflow and flood of these hybrid models are compared. In Step 3, the optimal hybrid model is selected based on the comparisons from Step 2. To quantify uncertainty, the bootstrap resampling technique is applied to derive the uncertainty interval of the selected optimal hybrid model, and then the uncertainty is analyzed.
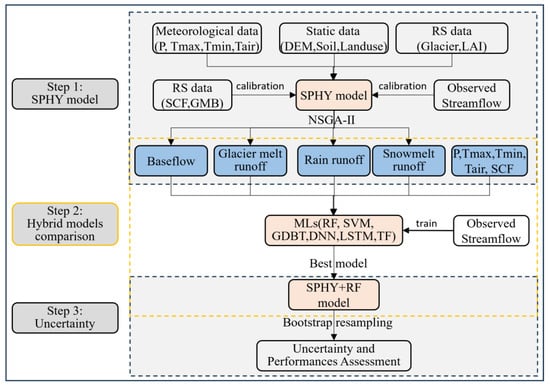
Figure 2.
Flowchart of constructing the proposed hybrid model.
3.4. Performance Measures
Given the versatility and ease of interpretation, the following four performance measures were comprehensively used to qualitatively evaluate the performance of the developed models: root mean squared error (RMSE), correlation coefficient (CC), Nash–Sutcliffe efficiency coefficient (NSE), and percent bias (PBIAS), which were expressed as follows:
where n is the number of observations; represents the simulated streamflow; is the observed flow; and , denote the average of observed and simulated streamflow, respectively. The CC, ranging from −1 to 1, quantifies the collinearity between simulations and observations. A value of CC = 0 indicates an absence of linear relationship, while CC = 1 or −1 signifies a perfect positive or negative linear relationship. The RMSE measures the standard deviation of the differences between predicted and observed streamflow values. A smaller RMSE signifies closer agreement between predictions and observations. The NSE is a normalized metric that gauges the relative residual variance against the variance of measured data. Meanwhile, the PBIAS, ranging from −∞ to ∞, captures the average tendency of simulated data to exceed or fall short of observed values, presenting over- and underestimation as a percentage, the best value of PBIAS is 0. The performance evaluation criteria of the hydrological models in regard to NSE and PBIAS is shown in Table 2.

Table 2.
The performance evaluation criteria of the hydrological models [49].
4. Results
4.1. Streamflow Simulated by SPHY Model
Effective model inputs are crucial for enhancing simulation capabilities, demanding thorough attention. Prior investigations underscore the significance of glacier runoff and snowmelt runoff within the hybrid model [20], substantiating their pivotal role in enhancing runoff simulation accuracy. In line with these insights, the present study employs a multi-objective calibration approach to meticulously calibrate model parameters across various components.
The snow module parameters are systematically optimized to minimize discrepancies between mean monthly simulated snow cover fractions within the SPHY model and those observed through MODIS snow cover data [31]. Figure 3a displays the time series of simulated snow cover fractions for the Manas basin, while Table 3 presents the corresponding performance metrics. Utilizing the parameter set calibrated via the NSGA-II algorithm, the SPHY model exhibits robust performance, closely aligning its simulated snow cover fractions with those derived from Muhammad, S. and Thapa, A. [31]. During the training period, the modeled and observed outcomes exhibit remarkable proximity, evidenced by an NSE value of 0.76, a CC value reaching 0.88, an RMSE value of merely 0.1, and a Bias value of 6.46%. The model’s performance showcases even greater consistency to some extent during the testing period, reflecting an RMSE value of approximately 0.07, an NSE value of 0.87, a CC value of 0.93, and a Bias value hovering around −3.47. The performance during the testing period exhibited improvement, potentially attributed to the SPHY model’s ability to capture a higher snow cover fraction within that timeframe, aided by the parameters calibrated based on the MODIS SCF data. Figure 2b displays the multi-year monthly mean of simulated and observed snow cover fractions for the Manas basin. SPHY underestimates snow cover fractions for the autumn, while the other months simulate very well. Given the influence of cloud shading on the MODIS snow area product, the snow simulation is considered as notably satisfactory.
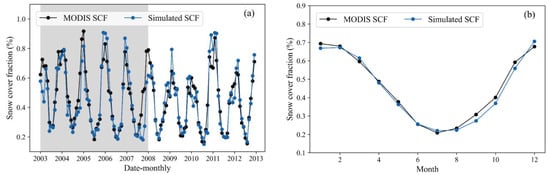
Figure 3.
(a) Monthly simulated snow cover fractions (SCF) by SPHY model and MODIS SCF; (b) multi-year monthly mean simulated SCF by SPHY model and MODIS SCF.

Table 3.
Statistical evaluations of annual glacier melt, monthly snow cover fraction and daily streamflow simulated by the SPHY model.
The time series of simulated glacier mass balance for the Manas basin is shown in Figure 4, and Table 3 shows corresponding performance metrics. With the calibrated optimal parameter, the SPHY model performs well and simulated glacier mass balances are consistent with observations [1]. Throughout the training period, the modeled and measured glacier mass balance for the Manas Basin Glacier exhibited remarkable proximity, reflected in an impressive correlation coefficient (CC) value of up to 0.94, a remarkably low root mean square error (RMSE) value of merely 0.04 km3, and a bias value of 4.05%. Although the model’s performance undergoes a slight decline during the testing period, it remains acceptable across the entirety of the study duration, as evidenced by relatively favorable performance metrics—approximately 0.13 km3 for RMSE, 0.51 for the CC value, and about 1.18% for Bias. The observed performance dip during the testing period is primarily attributed to the suboptimal accuracy displayed in 2009 and 2010, manifesting as substantial overestimations and underestimations. Despite NSE values of 0.21 during training and −12.9 during testing, indicating subpar performance, the simulation remains relatively satisfactory. This is primarily due to the inherent discontinuities in both the temporal and spatial dimensions of the glacier mass balance data sourced from Hugonnet et al. [1], necessitating interpolation. Consequently, the temporal alterations in glacier mass balance data are comparatively modest. In actuality, the melt of the Manas River glacier is significantly influenced by temperature and precipitation. A glance at Figure 3 reveals that in 2009 and 2010, there was a conspicuous reduction in snow cover area in contrast to other years, resulting in a significantly elevated glacier melt volume in 2010. Conversely, the diminished snow cover in 2009 contributed to a reduced glacier melt volume, primarily attributable to lower temperatures. This, in turn, resulted in noticeably diminished runoff for the same year, which can be found in Figure 5a. Furthermore, the multi-year average glacier melt volume from the simulation closely converges with observation at 0.329 km3 and 0.321 km3, respectively. Additionally, the trends of annual glacier melt volumes, −0.017 km3/year for simulation and −0.013 km3/year for observation, are remarkably consistent. These simulated values adeptly capture the glacier’s melting trend. Hence, the results of the glacier simulation presented in this study are deemed reasonable.
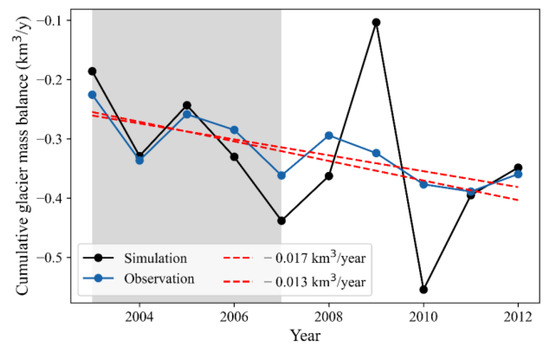
Figure 4.
Annual cumulative glacier balance simulated by SPHY model.
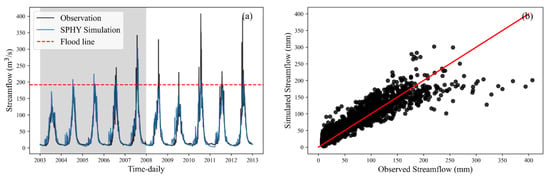
Figure 5.
Simulated streamflow using the SPHY model and observations presented as time series (a) and scatter (b). The red dotted line in (a) indicates the flood line. The solid red line in (b) indicates a 1:1 line.
The time series simulated daily streamflow within the Manas basin, which is presented in Figure 5, while Table 3 provides an exposition of the corresponding performance metrics. Notably, the SPHY model exhibits commendable performance, with the simulated daily streamflow closely aligned with observational data. Specifically, for the Manas basin, the concurrence between modeled and observed streamflow is particularly pronounced during the calibration period. With a notable NSE value of 0.85, an impressive correlation coefficient (CC) value of up to 0.93, an RMSE value of only 19.09 m3/s, and a Bias value of 7.10%, the model’s fidelity is evident. Evaluation indicators presented in Table 3 substantiate the model’s robustness during the testing period, with an RMSE value approximating 20.88 m3/s, an NSE value of 0.86, a CC value of 0.93, and a Bias value of around 1.6%. Comparing the NSE, CC, and RMSE values between the training and validation periods underscores their close alignment, affirming the model’s adeptness and strong generalization capabilities.
In this study, flood is defined as the minimum flood record value of the Kensiwate hydrological station which is 192 m3/s. From Figure 5a, it can be found that the uneven distribution of flood occurrences across various years is notable. Over the ten years from 2003 to 2012, 81 flood events were recorded. Remarkably, during the training period, merely 29 floods were observed, while the testing period accounted for 52 floods. The average magnitude of simulated flood events during the training interval registered at 189.67 m3/s. In contrast, the corresponding observed average flood magnitude was 228.60 m3/s, denoting an underestimation of 17.02%. A similar pattern was observed during the testing period, where the average observed flood magnitude reached 244.80 m3/s, in contrast to the simulated average flood magnitude of 172.11 m3/s, translating to an underestimation of 29.69%. As can be seen from Figure 5b, the SPHY model significantly underestimates flooding but is very good for other runoff simulations. These findings distinctly underscore the limitations of the SPHY hydrological model in encapsulating flood events.
In fact, it is common for runoff simulations to underestimate flood events in high mountain areas [50], in particular the physical-based hydrological model. The root of this limitation can be traced to the paucity of high-quality observed temperature and precipitation data within the Manas River basin. Moreover, the utilization of remote sensing precipitation products, characterized by the averaging of precipitation over a 0.1° × 0.1° grid, while the spatial resolution of the SPHY model is set as 1 km × 1 km, results in the attenuation of precipitation peaks. As an integral factor influencing flood simulations, temperature similarly contributes to this limitation. Despite downscaling through bilinear interpolation, the lower resolution of temperature products impedes accurate reconstruction of temperature peaks, subsequently hampering precise flood simulation. This issue resonates as a universal challenge across data-scarce regions.
4.2. Streamflow Simulated by Hybrid Models
Table 4 displays the statistical metrics of NSE, CC, RMSE and PBIAS for both the training and testing periods for six hybrid models (namely SPHY-RF, SPHY-GDBT, SPHY-SVM, SPHY-DNN, SPHY-LSTM, and SPHY-TF) utilized for simulating streamflow in the Manas River basin. The optimal outcomes among the six models are highlighted in bold. Notably, the NSEs indicate “very good” ratings (i.e., NSE > 0.70) for six hybrid models. Furthermore, compared with the results in Table 3, it becomes evident that the performance of all hybrid models notably surpasses that of the physical-based SPHY model. This aligns with the common observation that statistical models tend to outperform physical-based models in streamflow simulation [51]. This highlights the capacity enhancement of streamflow modeling by combining physical models with ML. Assessing CC, NSE, and RMSE among the six hybrid models, the SPHY-GDBT model excels during the training period, while SPHY-RF performs best during the testing period. In terms of generalization, SPHY-RF is better suited for streamflow simulation. Additionally, a comparison among the hybrid models reveals that ensemble-learning-based hybrid models (SPHY-GDBT and SPHY-RF) significantly outperform the simple Support-Vector-Machine (SPHY-SVM)- and deep-learning-based hybrid models (SPHY-DNN, SPHY-LSTM, and SPHY-TF). It is also noticeable that the performance of the simple SVM is comparatively poorer. Thirdly, deep-learning-based hybrid models (SPHY-DNN, SPHY-LSTM) demonstrate remarkable stability, exhibiting minimal deviation between the training and testing periods, consistent with prior research [21].

Table 4.
Statistical evaluations of daily streamflow simulated by hybrid models.
To evaluate the performance of hybrid models in streamflow simulation, the simulated streamflow of the hybrid models was compared against the physical-based model SPHY, as shown in Figure 6, since the training and testing datasets for hybrid models are divided based on the same distribution principle. In contrast, the physical model divides them based on chronological order; for a fair comparison, all simulated data were juxtaposed. From Figure 6, it is evident that all hybrid models outperform the SPHY model. Among them, SPHY-SVM performs the poorest (Figure 6c), with only partial simulated results outperforming the physical model. The advantage is insignificant for most points, and even some high flows are noticeably underestimated. Although SPHY-DNN beats SPHY-SVM regarding evaluation metrics in Table 4, the comparison between Figure 6c,d reveals a similar high-flow simulation performance that some high flows are noticeably underestimated. The SPHY-TF model (Figure 6f) exhibits a slight advantage over the physical model in a flood simulation. However, within 50~150 m3/s of streamflow, it tends to overestimate, and this phenomenon does not occur in other models. Moreover, all the other five hybrid models can significantly reduce the overestimations of the SPHY model around 200 m3/s. Comparing the well-performing models SPHY-RF, SPHY-GDBT, and SPHY-LSTM, it is observed that relative to SPHY-LSTM, both SPHY-RF and SPHY-GDBT can simulate high-flow effectively. Among them, SPHY-GDBT performs better, possibly due to better performance during the training period and some degree of overfitting, leading to its inferior performance compared to SPHY-RF during validation. Through the above results, it is found that the hybrid model, namely SPHY-RF, is more suitable for streamflow simulation and prediction.
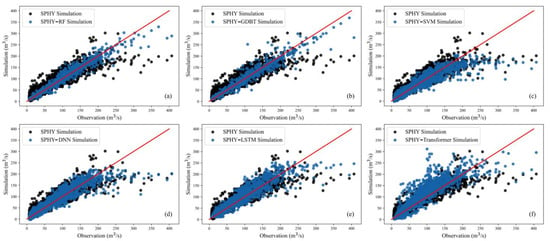
Figure 6.
Comparison of the streamflow simulated by the SPHY model and hybrid models presented as scatter The solid red line in (a–f) indicates a 1:1 line.
4.3. Flood Simulated by Hybrid Models
Accurate prediction of high flows is paramount for informed decision-making to prevent water resource wastage during flood events. This study defines the minimum flood value as the lowest recorded flood value of the Kensiwate hydrological station, amounting to 192 m3/s [24]. To evaluate the flood simulation performance of various hybrid models during the testing period, the results of each model are compared to observed values, as depicted in Figure 7. The graphical representation distinctly showcases the superior flood simulation performance of the SPHY-RF hybrid model over the other five counterparts. Specifically, SPHY-SVM (Figure 7c), SPHY-DNN (Figure 7d) and SPHY-LSTM (Figure 7e) exhibit substantial underestimation of flood values, with their scatter plots exhibiting high similarity. This suggests their unsuitability for flood prediction. Moreover, despite SPHY-TF’s comparatively lower performance when juxtaposed with SPHY-RF and SPHY-GDBT, it still demonstrates notable potential in flood prediction. Contrary to the prevalent belief in the pronounced advantages of deep learning algorithms in diverse studies, this research asserts that for straightforward, small-scale size problems, RF outperforms them. Deep learning algorithms such as LSTM and TF might require a larger quantity of samples to effectively train model parameters and attain a heightened level of model stability.
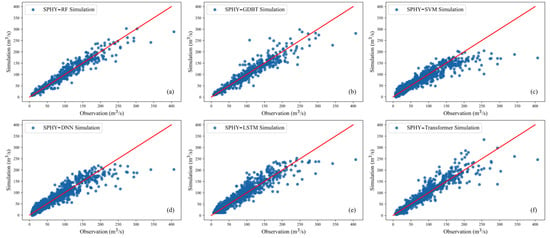
Figure 7.
Comparison of the streamflow simulated by the hybrid models presented as scatter for the testing period The solid red line in (a–f) indicates a 1:1 line.
Table 5 presents the evaluation metrics for flood simulations by hybrid models and the SPHY hydrological model to assess the flood modeling capability of hybrid models. Although the training and testing period divisions differ between the SPHY and the hybrid models, the simulation results of the SPHY model still hold certain reference values. From Table 5, it is evident that during the training period, almost all hybrid models outperform the SPHY model, except for SPHY-SVM, which performs better in terms of NSE but worse in other metrics than the SPHY model, suggesting that SPHY-SVM may not be suitable for flood simulation. Among the hybrid models, SPHY-GDBT exhibits the best performance during the training period, but its testing results deteriorate rapidly, possibly due to overfitting. Regarding the testing period, SPHY-RF achieves the best results, with the highest NSE, CC, and lowest RMSE, PBIAS. Although NSE and CC decreased more than the training period, the consistent performance of RMSE and PBIAS indicates the reliability of SPHY-RF’s training outcomes. The hybrid models based on deep learning demonstrate noticeable improvements over the physical SPHY model, yet they still lag behind SPHY-RF, suggesting that deep learning models still have room for enhancement in flood simulation. All models in Table 5 exhibit negative PBIAS values in both training and testing periods, indicating an underestimation of flood values. Like other ML streamflow forecasting models, discrepancies with observed peaks could be attributed to various factors: (1) IMERG remote sensing’s inability to capture extreme precipitation; (2) the absence of consideration for glacial lake bursts during summer; (3) inaccurate outputs generated by SPHY due to limited climate data, and (4) challenges inherent to ML in predicting extreme values. Typically, extreme values reside in the tail of the data distribution, while most training data cluster around the distribution’s center. Models might lack sufficient examples of extreme values to predict such scenarios accurately. In conclusion, all the analysis above highlights that the SPHY-RF model excels not only in curve fitting ability during the training period but also in its capacity for generalization.

Table 5.
Statistical evaluations of flood simulated by hybrid models and the SPHY model.
To enhance flood simulation and provide more informative flood forecasting, this study employed the Bootstrap resampling technique to sample the inputs of the SPHY-RF model 10,000 times. The resulting 95% confidence interval was utilized to quantify uncertainty. As depicted in Figure 8a, the uncertainty interval width for all data was 12.20 m3/s, with a Percentage of Coverage (POC) of 92.03%. Notably, the majority of observed values were encompassed within the 95% confidence interval, except for certain extreme flood events. Figure 8b displays the uncertainty intervals for 84 flood values from 2003 to 2012. The uncertainty interval width was 91.66 m3/s, with a POC of 87.65%. Although certain flood events lie outside the realm of the uncertainty interval, this interval still offers valuable insights. According to statistical analysis, the average value of points exceeding the upper boundary of the uncertainty interval is 30.51 m3/s. In contrast, the average value of these flood events is 263.4 m3/s. This indicates that the upper boundary of the uncertainty interval underestimates floods by 11.5%. However, in practical application, this discrepancy can be rectified through real-time corrections. Certainly, the hybrid model failed to capture certain flood events due to the absence of flood-related information among the inputs, such as exceptional heavy rainfall and abrupt events like glacier lake outbursts. Consequently, regardless of the sampling approach, consistently underestimated points will remain so. Furthermore, the figure indicates that flood predictions above approximately 220 m3/s generally tend to underestimate actual values. This discrepancy might arise from the scarcity of samples representing such extreme floods in the hybrid models dataset, leading to larger deviations and consequently increased uncertainty intervals in predictions.
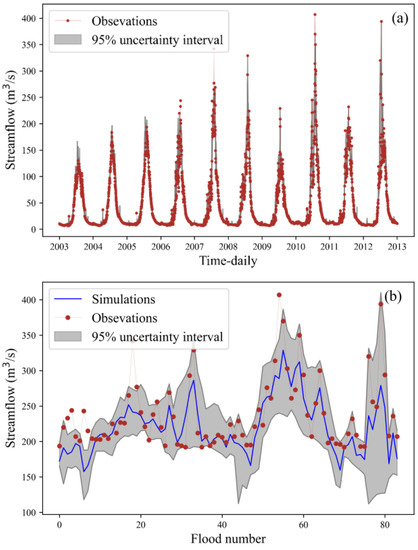
Figure 8.
Uncertainty estimation by SPHY-RF: (a) streamflow, (b) flood.
5. Discussion
5.1. Can the Multi-Objective Parameter Calibration Method Improve the Ability of SPHY Model Streamflow Simulation?
To answer the question of whether the combined use of MODIS snow cover data, remote sensing-derived glacier mass balance data, and streamflow for calibrating the SPHY model can enhance its runoff simulation capability, an experiment was conducted that calibrating the SPHY model parameters by streamflow alone. The results are presented in Table 6. A comparison between the evaluation metrics in Table 2 and Table 6 reveals that simulation through multi-objective calibration of parameters significantly outperforms those obtained through streamflow-only calibration. Notably, NSE improved by 4.9% during training and 13.1% during testing. A comparison of simulation results during both training and testing periods indicates that multi-objective calibration yields more consistent results, as evidenced by NSE, CC, and RMSE values closely aligning. In contrast, the streamflow-only calibration demonstrates noticeable disparities, possibly due to overfitting. Numerous studies have explored the advantages of multi-objective calibration. For instance, Chen et al. [52] employed the MODIS snow cover area (SCA) product, the snow water equivalent (SWE) product, and Gravity Recovery and Climate Experiment (GRACE) satellite-derived total water storage (TWS) to calibrate model parameters, highlighting superior outcomes compared to single-objective calibration. Similarly, in a study by Liu et al. [53], multi-objective calibration schemes employing ET and TWSC products exhibited enhanced accuracy in runoff simulation. Such investigations underline the complexity of hydrological issues in high-altitude regions, encompassing interwoven factors like snowmelt, rainfall, snowmelt runoff, and glacier runoff. Multi-objective calibration effectively captures this complexity, enhancing model accuracy by balancing various performance indicators and avoiding over-optimizing specific metrics, thereby enhancing the model’s predictive capacity for unforeseen future scenarios.

Table 6.
Statistical evaluations of daily streamflow simulated by the SPHY model calibrated by streamflow alone.
5.2. Can Better Alignment of Inputs to Physical Processes Improve the Hybrid Model’s Flood Simulation Capabilities?
The findings from Section 4.2 and Section 4.3 highlight SPHY-RF’s superiority over other models. Thus, we exclusively employed the RF algorithm to couple with the SPHY model, calibrated solely by streamflow (referred to as SPHY-RF2), to explore whether incorporating the ML algorithm inputs aligned with actual physical processes can enhance streamflow and flood simulation capabilities. The statistical assessments of daily streamflow simulated by SPHY-RF2 are presented in Table 7. Compared it to the results of the SPHY model calibrated by streamflow alone (referred to as single-objective calibrated) in Table 6, it can be seen that SPHY-RF2 exhibits improved runoff simulation capability. However, similar to the single-objective calibrated SPHY model, it performs better during the training than the testing period.

Table 7.
Statistical evaluations of daily streamflow and flood simulated by the SPHY-RF2 model while the SPHY model calibrated by streamflow alone.
In contrast to SPHY-RF, besides the closely matched PBIAS metric, SPHY-RF2 consistently outperforms all other indicators during training and testing periods, indicating that aligning input variables with actual processes enhances runoff simulation. Furthermore, distinct differences emerge in flood simulation between SPHY-RF and SPHY-RF2, with the latter demonstrating superior performance. This underscores that alignment with actual processes significantly enhances flood simulation. In ML, model performance heavily hinges on input samples. Floods, being extreme values with limited samples, could be improved for effective information representation. Inadequate capture of flood-related details by input factors results in simulation degradation. When comparing single-objective calibrated (Table 6) with multi-objective calibrated (Table 3) approaches, the latter consistently yields superior NSE performance. This metric’s sensitivity to extremes implies that fewer flood-related details are captured in the single-objective calibrated SPHY model. Consequently, capturing flood information becomes challenging even when employing RF fitting, leading to poorer performance.
5.3. The Potential of Hybrid Models for Flood Prediction in High Mountainous Regions
Combining physical models with ML methods holds immense potential for flood forecasting in high mountainous, usually data-scarce regions [54]. This synergistic approach leverages the strengths of both methods to address the complexity and uncertainty inherent in flood prediction within these intricate environments. Firstly, physical models provide a robust foundation by integrating fundamental physical laws that govern hydrological processes. Coupling these models with ML techniques allows for a deeper understanding of the intricate interactions among glacier melt, snowmelt, rainfall, and other runoff components. ML algorithms excel at capturing nonlinear relationships, capturing subtle nuances that traditional models might overlook. Secondly, ML methods adapt to real-time data, enabling dynamic adjustments in predictions based on rapidly changing meteorological conditions and evolving patterns of glaciers and snowmelt. This adaptability is crucial for capturing the rapid responses characteristic of high-altitude environments. Thirdly, uncertainty is inherent in hydrological modeling, especially in data-scarce regions. Employing ML techniques aids in quantifying uncertainty, providing more reliable probabilistic flood forecasts, which are vital for decision-makers and emergency responders. Fourthly, ML models trained in one region can be fine-tuned and generalized for other data-scarce mountainous areas, aiding regions lacking sufficient historical data to swiftly adopt predictive models. In conclusion, combining physical models and ML methods is pivotal in flood forecasting in high-altitude regions. This integrated approach enhances predictive accuracy and contributes to wiser decision-making, disaster preparedness, and sustainable water resource management, particularly in areas vulnerable to the impacts of climate change.
5.4. Limitations of the Current Study
The results of this study suggest that integrating physical models and ML methods to predict floods in high-altitude mountainous areas is a promising approach that comes with several limitations. Firstly, this hybrid model lacks model interpretability. ML methods often manifest as black-box models, making it challenging to interpret their decision-making processes. Although the hybrid model inputs in this study have physical properties, there are no physical constraints in the process of being used for ML, which makes it still hard to understand the contributing factors to a flood event. Secondly, the issue of data imbalance is noteworthy. Flood events are typically infrequent, resulting in datasets predominantly composed of non-flood events and a sparse representation of flood events. Extra measures may be necessary to balance the data to prevent the model from leaning excessively toward non-flood events. Thirdly, the risk of overfitting still exists. When integrating complex models with numerous parameters, there is a risk of overfitting, particularly when data are limited. For example, the best performing model in this study, SPHY-RF, performed better in the training period than in the testing period, so it is necessary to use more data to train the model in practical applications. Furthermore, there are concerns regarding the applicability of this approach under changing climate conditions. Predicting floods under changing climate conditions is challenging. Changes in precipitation and temperature can lead to fluctuations in the outputs of models like SPHY. When incorporated into hybrid models, these variations can compound, making it difficult to apply the model to predict floods under changing climate conditions. Despite these limitations, integration of physical models and machine learning methods still promises to improve flood prediction accuracy in high-altitude mountainous regions, especially when data are scarce. Overcoming these challenges requires further research and methodological enhancements to fully harness the potential of this approach.
6. Conclusions
To enhance flood simulation in data-scarce glacial river basins, we present a novel hybrid modeling approach that leverages multi-source remote sensing data, a physically based hydrological model (SPHY), and machine learning (ML) techniques. Within this hybrid model, remote sensing data, including MODIS snow cover data and glacier mass balance data, are effectively employed to calibrate the SPHY model. The SPHY model generates crucial components like baseflow, rain runoff, snowmelt runoff, and glacier melt runoff in the high mountainous regions, which act as new inputs for the subsequent ML components. This newly developed hybrid model undergoes rigorous training and validation assessments. Subsequently, the best performing hybrid model is selected through comprehensive comparisons, followed by an uncertainty analysis.
Through a case study within the Manas River basin in Central Asia, our study reveals several significant insights. First and foremost, the hybrid model (SPHY-RF) markedly enhances flood simulation accuracy compared to the standalone physical-based hydrological model (SPHY) which plays an important role in flood forecasting. Remarkably, SPHY-RF outperforms five other hybrid models (SPHY-GDBT, SPHY-LSTM, SPHY-DNN, SPHY-TF, SPHY-SVM) regarding both streamflow and flood simulation in the testing period. It may be due to the lack of training data that the performance of hybrid models based on deep learning algorithms is not as good as that of RF. Additionally, the integration of multi-objective optimization demonstrates its potential to improve streamflow simulation for the SPHY model, subsequently enhancing the streamflow and flood simulation performance of the SPHY-RF model. By utilizing bootstrap sampling, the 95% uncertainty interval for SPHY-RF is established, effectively covering 87.65% of flood events.
In conclusion, our findings highlight the substantial potential of the hybrid modeling approach for simulating floods in data-scarce glacial river basins. This approach not only establishes a robust framework for flood simulation and forecasting in complex environments, but also lays the groundwork for investigating extreme hydrological events under the influence of a warming climate in alpine regions worldwide.
Author Contributions
All authors contributed to the work. Conceptualization, X.L. and D.Z.; methodology, Y.W. and W.R.; software, T.M. and W.R.; validation, J.S., R.Z. and W.R.; formal analysis, W.R.; investigation, W.R.; resources, W.R.; data curation, W.R. and T.M.; writing—original draft preparation, W.R.; writing—review and editing, X.L., D.Z. and R.Z.; visualization, W.R. and T.M.; supervision, X.L. and D.Z.; project administration, X.L. and D.Z.; funding acquisition, W.R. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Nos. 42101406 and 42101397).
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the editors and the reviewers for their crucial. comments and suggestions, which improved the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hugonnet, R.; McNabb, R.; Berthier, E.; Menounos, B.; Nuth, C.; Girod, L.; Farinotti, D.; Huss, M.; Dussaillant, I.; Brun, F.; et al. Accelerated global glacier mass loss in the early twenty-first century. Nature 2021, 592, 726–731. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Stigter, E.E.; Yao, T.; Immerzeel, W.W. Climate change decisive for Asia’s snow meltwater supply. Nat. Clim. Chang. 2021, 11, 591–597. [Google Scholar] [CrossRef]
- Ombadi, M.; Risser, M.D.; Rhoades, A.M.; Varadharajan, C. A warming-induced reduction in snow fraction amplifies rainfall extremes. Nature 2023, 619, 305–310. [Google Scholar] [CrossRef]
- Cui, T.; Yang, T.; Xu, C.-Y.; Shao, Q.; Wang, X.; Li, Z. Assessment of the impact of climate change on flow regime at multiple temporal scales and potential ecological implications in an alpine river. Stoch. Environ. Res. Risk Assess 2018, 32, 1849–1866. [Google Scholar] [CrossRef]
- Nanditha, J.S.; Kushwaha, A.P.; Singh, R.; Malik, I.; Solanki, H.; Chuphal, D.S.; Dangar, S.; Mahto, S.S.; Vegad, U.; Mishra, V. The Pakistan flood of August 2022: Causes and implications. Earth’s Future 2023, 11, e2022EF003230. [Google Scholar] [CrossRef]
- Robertson, D.E.; Pokhrel, P.; Wang, Q.J. Improving statistical forecasts of seasonal streamflow using hydrological model output. Hydrol. Earth Syst. Sci. 2013, 17, 579–593. [Google Scholar] [CrossRef]
- Khanal, S.; Lutz, A.F.; Kraaijenbrink, P.D.A.; van den Hurk, B.; Yao, T. Variable 21st century climate change response for rivers in High Mountain Asia at seasonal to decadal time scales. Water Resour. Res. 2021, 57, e2020WR029266. [Google Scholar] [CrossRef]
- Wang, N.; Liu, W.; Wang, H.; Sun, F.; Duan, W.; Li, Z.; Li, Z.; Chen, Y. Improving streamflow and flood simulations in three headwater catchments of the Tarim River based on a coupled glacier-hydrological model. J. Hydrol. 2021, 603, 127048. [Google Scholar] [CrossRef]
- Duan, Y.; Meng, F.; Liu, T.; Huang, Y.; Luo, M.; Xing, W.; De Maeyer, P. Sub-daily simulation of mountain flood processes based on the modified soil water assessment tool (swat) model. Int. J. Environ. Res. Public Health 2019, 16, 3118. [Google Scholar] [CrossRef]
- Yang, T.; Cui, T.; Xu, C.-Y.; Ciais, P.; Shi, P. Development of a new IHA method for impact assessment of climate change on flow regime. Glob. Planet Chang. 2017, 156, 68–79. [Google Scholar] [CrossRef]
- Ren, W.; Yang, T.; Shi, P.; Xu, C.-Y.; Zhang, K.; Zhou, X.; Shao, Q.; Ciais, P. A probabilistic method for streamflow projection and associated uncertainty analysis in a data sparse alpine region. Glob. Planet Chang. 2018, 165, 100–113. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Bayesian neural network for rainfall-runoff modeling. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Adnan, R.M.; Heddam, S.; Liang, Z.; Zounemat-Kermani, M. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydrometeorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. WIREs Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- Wang, X.; Yang, T.; Wortmann, M.; Shi, P.; Hattermann, F.; Lobanova, A.; Aich, V. Analysis of multi-dimensional hydrological alterations under climate change for four major river basins in different climate zones. Clim. Chang. 2017, 141, 438. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Z.; Lin, J.; Huang, J. Machine learning-based estimation of riverine nutrient concentrations and associated uncertainties caused by sampling frequencies. PLoS ONE 2022, 17, e0271458. [Google Scholar] [CrossRef]
- Humphrey, G.B.; Gibbs, M.S.; Dandy, G.C.; Maier, H.R. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. J. Hydrol. 2016, 540, 623–640. [Google Scholar] [CrossRef]
- Feng, D.; Liu, J.; Lawson, K.; Shen, C. Differentiable, learnable, regionalized process-based models with multiphysical outputs can approach state-of-the-art hydrologic prediction accuracy. Water Resour. Res. 2022, 58, e2022WR032404. [Google Scholar] [CrossRef]
- Ren, W.W.; Yang, T.; Huang, C.S.; Xu, C.Y.; Shao, Q.X. Improving monthly streamflow prediction in alpine regions: Integrating HBV model with Bayesian neural network. Stoch. Environ. Res. Risk Assess 2018, 32, 3381–3396. [Google Scholar] [CrossRef]
- Xu, T.; Longyang, Q.; Tyson, C.; Zeng, R.; Neilson, B.T. Hybrid Physically Based and Deep Learning Modeling of a Snow Dominated, Mountainous, Karst Watershed. Water Resour. Res. 2022, 58, e2021WR030993. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; He, X. Progress in the research on glacial change and water resources in Manas river basin. Int. Soil. Water Conserv. Res. 2014, 25, 332–337. (In Chinese) [Google Scholar]
- Ji, X.; Chen, Y. Characterizing spatial patterns of precipitation based on corrected TRMM 3B43 data over the mid Tianshan Mountains of China. J. Mt. Sci. 2012, 9, 628–645. [Google Scholar] [CrossRef]
- Ye, J. Analysis on Ecological Environment Protection and Monitoring of Water Source Project in Manas River in Xinjiang. WCSTE 2021, 27, 41–44. (In Chinese) [Google Scholar]
- Huffman, G.J. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); NASA Algorithm Theoretical Basis Doc., Version 06; NASA: Washington, DC, USA, 2020; p. 39. Available online: https://gpm.nasa.gov/sites/default/files/2020-05/IMERG_ATBD_V06.3.pdf (accessed on 1 September 2023).
- Chen, Y.; Yang, K.; He, J.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod15a2h_v006/ (accessed on 1 September 2023).
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos Trans. AGU 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Wyatt, F. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Fürst, J.J.; Landmann, J.; Machguth, H.; Maussion, F.; Pandit, A. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 2019, 12, 168–173. [Google Scholar] [CrossRef]
- Muhammad, S.; Thapa, A. An improved Terra–Aqua MODIS snow cover and Randolph Glacier Inventory 6.0 combined product (MOYDGL06*) for high-mountain Asia between 2002 and 2018. Earth Syst. Sci. Data 2020, 12, 345–356. [Google Scholar] [CrossRef]
- Böer, F.D. HiHydroSoil: A high resolution soil map of hydraulic properties (Version 1.2), Report 984. Future Water 2016, 31, 1–32. [Google Scholar]
- Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lamarche, C. Land Cover cci-Product User Guide-Version 2, ESA Public Doc. CCI-LC-PUG(2.4). 2014. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-land-cover?tab=overview (accessed on 1 September 2023).
- Terink, W.; Lutz, A.F.; Simons, G.W.H.; Immerzeel, W.W.; Droogers, P. SPHY v2.0: Spatial Processes in HYdrology. Geosci. Model Dev. 2015, 8, 1687–1748. [Google Scholar] [CrossRef]
- Hargreaves, G.; Samani, Z. Reference crop evapotranspiration from temperature. Appl. Eng. Agric 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B. Scikit-learn: Machine learning in Python. J. Mach. Learn Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Schoppa, L.; Disse, M.; Bachmair, S. Evaluating the performance of random forest for large-scale flood discharge simulation. J. Hydrol. 2020, 590, 125531. [Google Scholar] [CrossRef]
- Bui, Q.T.; Chou, T.Y.; Hoang, T.V.; Fang, Y.M.; Mu, C.Y.; Huang, P.H.; Meadows, M.E. Gradient boosting machine and object-based CNN for land cover classification. Remote Sens. 2021, 13, 2709. [Google Scholar] [CrossRef]
- Rahman, A.; Hosono, T.; Quilty, J.M.; Das, J.; Basak, A. Multiscale groundwater level forecasting: Coupling new machine learning approaches with wavelet transforms. Adv. Water Resour. 2020, 141, 103595. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Huang, H.; Feng, G.; Cao, Y.; Feng, G.; Dai, Z.; Tian, P.; Wei, J.; Cai, X. Simulation and Driving Factor Analysis of Satellite-Observed Terrestrial Water Storage Anomaly in the Pearl River Basin Using Deep Learning. Remote Sens. 2023, 15, 3983. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, Y.; Liu, J. Application of a New Hybrid Deep Learning Model That Considers Temporal and Feature Dependencies in Rainfall–Runoff Simulation. Remote Sens. 2023, 15, 1395. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Adv. Neural Inf. Process. Syst 2019, 32, 5243–5253. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support vector method for function approximation, regression estimation, and signal processing. Adv. Neural Inf. Process. Syst. Denver 1996, 9, 281–287. [Google Scholar]
- Tongal, H.; Booij, M.J. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H.; Peng, L. Flood susceptibility mapping using convolutional neural network frameworks. J. Hydrol. 2020, 582, 124482. [Google Scholar] [CrossRef]
- Kalin, L.; Isik, S.; Schoonover, J.E.; Lockaby, B.G. Predicting Water Quality in Unmonitored Watersheds Using Artificial Neural Networks. J. Environ. Qual. 2010, 39, 1429–1440. [Google Scholar] [CrossRef]
- Wijngaard, R.R.; Lutz, A.F.; Nepal, S.; Khanal, S.; Pradhananga, S.; Shrestha, A.B.; Immerzeel, W.W. Future changes in hydro-climatic extremes in the Upper Indus, Ganges, and Brahmaputra River basins. PLoS ONE 2017, 12, e0190224. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. Product-Units neural networks for catchment runoff forecasting. Adv. Water Resour. 2012, 49, 97–113. [Google Scholar] [CrossRef]
- Chen, X.; Long, D.; Hong, Y.; Zeng, C.; Yan, D. Improved modeling of snow and glacier melting by a progressive two-stage calibration strategy with GRACE and multisource data: How snow and glacier meltwater contributes to the runoff of the Upper Brahmaputra River basin? Water Resour. Res. 2017, 53, 2431–2466. [Google Scholar] [CrossRef]
- Liu, X.; Yang, K.; Ferreira, V.G.; Bai, P. Hydrologic model calibration with remote sensing data products in global large basins. Water Resour. Res. 2022, 58, e2022WR032929. [Google Scholar] [CrossRef]
- Li, X.; Feng, M.; Ran, Y.; Su, Y.; Liu, F.; Huang, C.; Shen, H.; Xiao, Q.; Su, J.; Yuan, S.; et al. Big Data in Earth system science and progress towards a digital twin. Nat. Rev. Earth Environ. 2023, 4, 319–332. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).