Adaptive High Coherence Temporal Subsets SBAS-InSAR in Tropical Peatlands Degradation Monitoring
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Study Area
2.2. Dataset
2.2.1. Sentinel-1 Datasets
2.2.2. Landsat Datasets
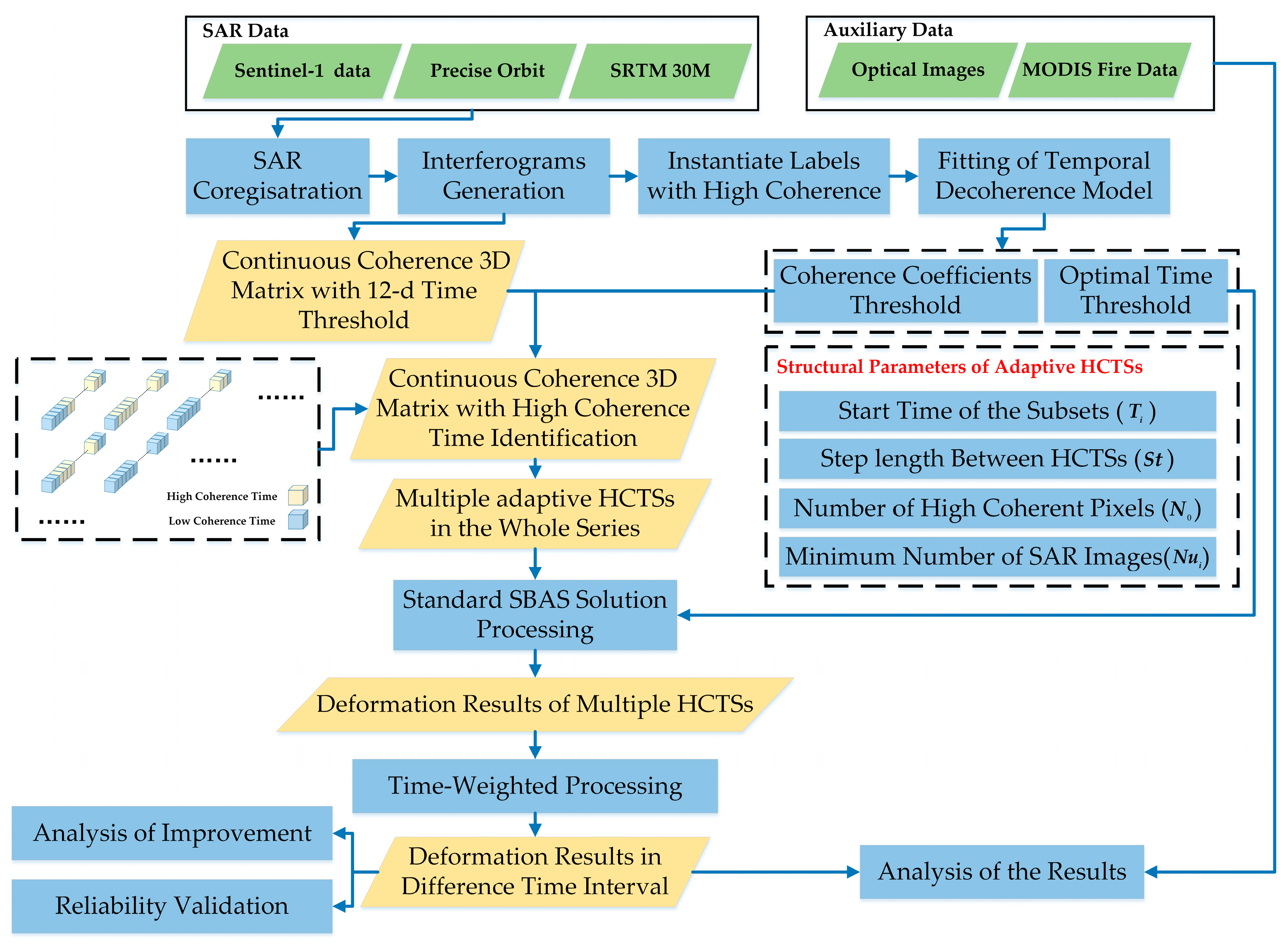
3. Methodology
3.1. Temporal Decorrelation Model in Peatlands
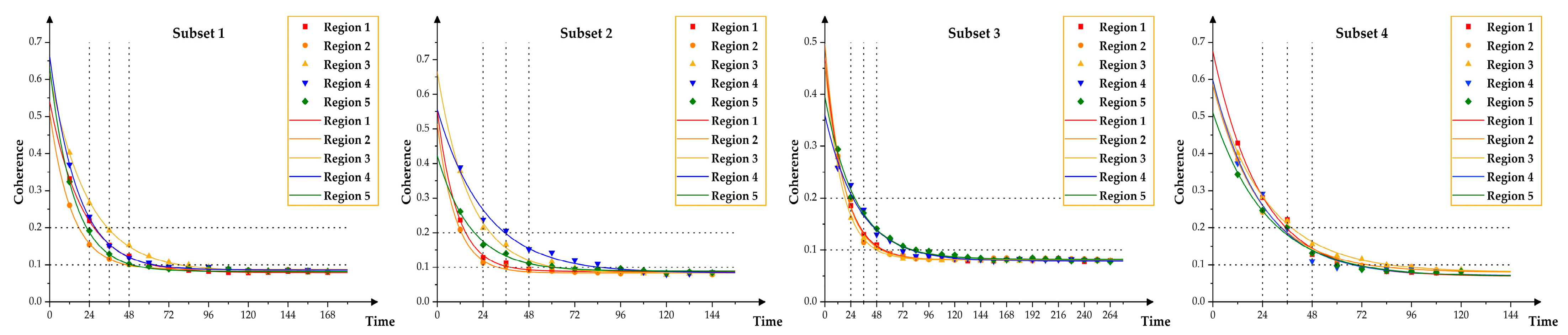
- The coherence coefficient of tropical peatlands exhibited a high value during the initial stages of dynamic changes (with approximately 0.54) and decreased with time, approaching incoherence scatterers (with approximately 0.08) finally. Besides, the coherence decreased slowly in the rainy seasons ( is about 18.5 days in Subset 1, 2, 3, and about 24.5 days in Subset 4).
- The coherence coefficient’s changes of labeled regions during the same period were also different. Such as in Subset 2, the coherence coefficient in regions 2 and 3 dropped to about 0.1 with 24-day time threshold, but region 4 still kept a high coherence, which had a similar initial coherence with regions 2, 3.
- Spatial distribution of regions with high coherence was different within different subsets, so it was hard for peatlands to keep a high coherence for a long time.
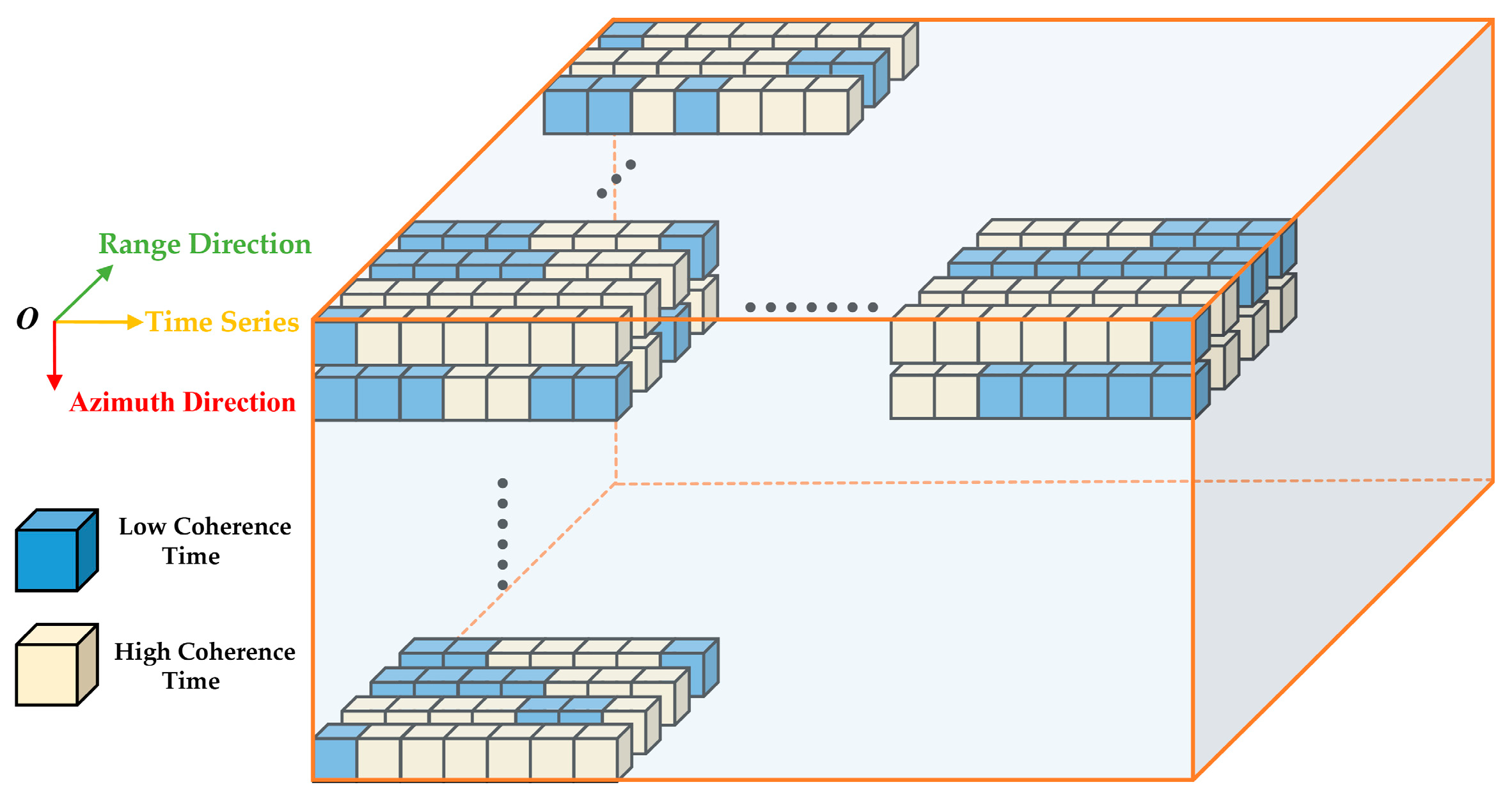
3.2. Continuous Coherence Three-Dimensional (3D) Model with 12-Day Time Threshold
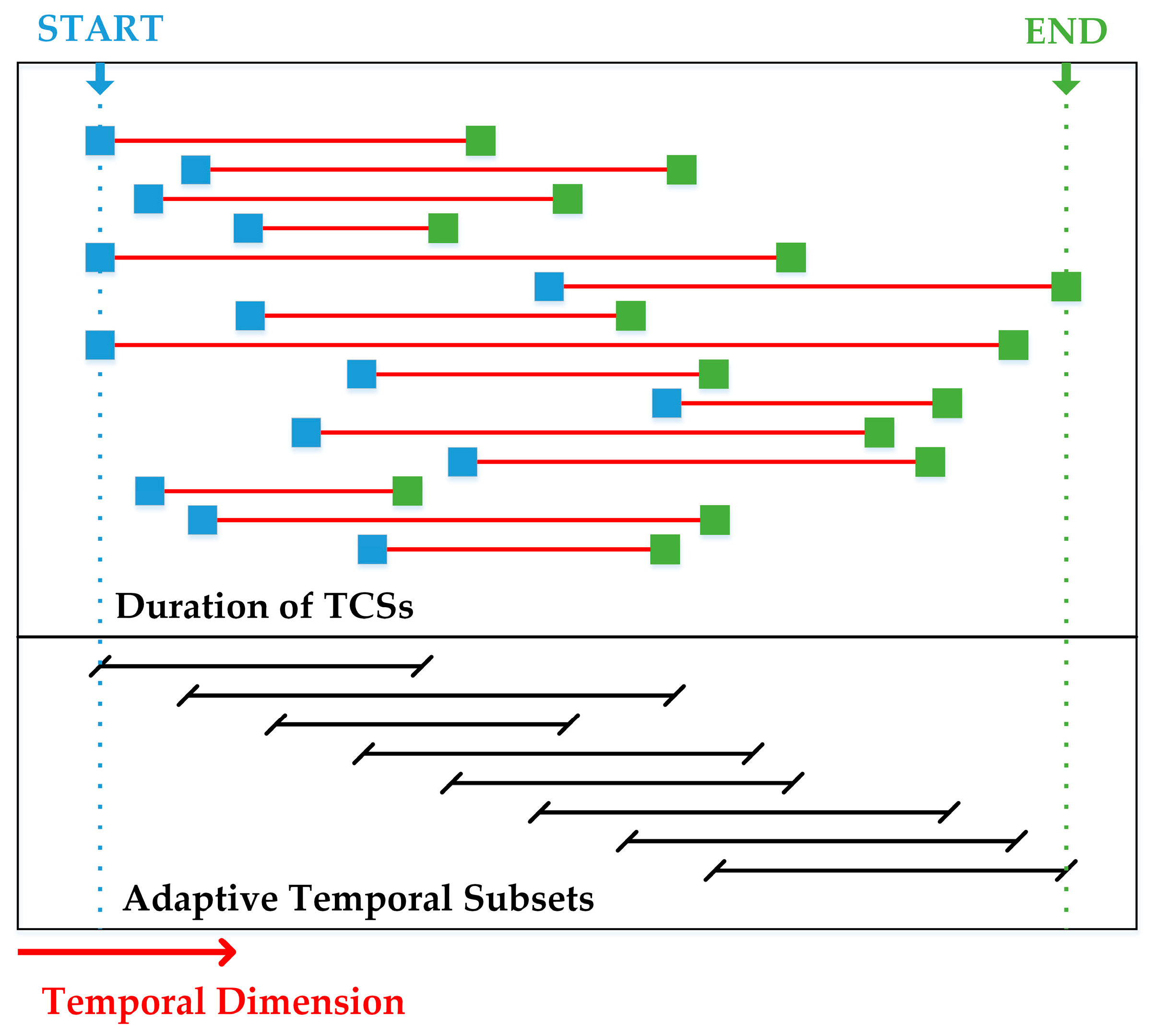
3.3. Construction of Adaptive HCTSs
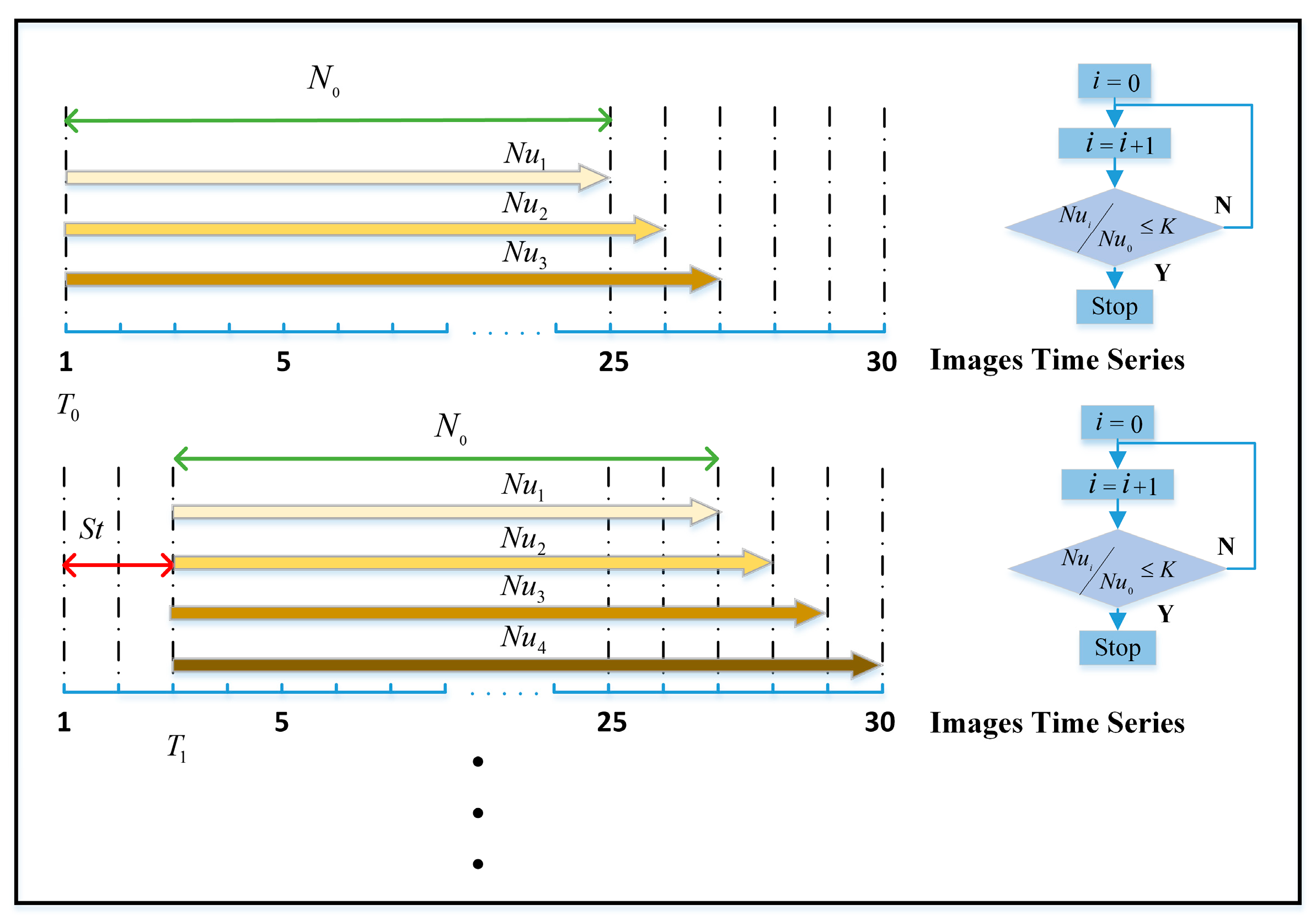
- Start time of HCTS: HCTS will start with the first SAR image in the whole time series.
- Time span of HCTSs: Cigna et al. [37] established the correlation between the velocity standard errors and the number of interference pairs, as shown in Equation (3). Based on the empirical correlation, the minimum number of interferograms () required for a temporal subset can be calculated by setting an acceptable maximum error.
- Stop time of HCTSs: An initial time subset has been established based on the aforementioned elements, but subsets require more SAR images because more interferograms (more observations) can reduce the error of the rate. However, it is necessary to realize that pixels’ coherence may be hard to keep high coherence for a longer time because there are more uncertainties. Therefore, taking into account the relationship between the length and number of TCSs in the temporal subset holistically, a method is proposed to create adaptive temporal subsets, which utilize the change of measurement points to optimize stop time. The detailed process is as follows:
- 4.
- Step length between temporal subsets: HCTS is established after completing the above steps. However, it is necessary to recognize that there are multiple temporal subsets rather than only one in the whole time series in most cases. Step length between temporal subsets needs to be considered because starting with each SAR image will produce many temporal subsets, which will slow down the efficiency of InSAR processing in large-scale and long-time series monitoring.
3.4. SBAS-InSAR Processing with Time-Weighted in HCTSs
3.5. Reliability Analysis of the Deformation Rate
4. Results and Analysis
4.1. Results of the Adaptive HCTSs
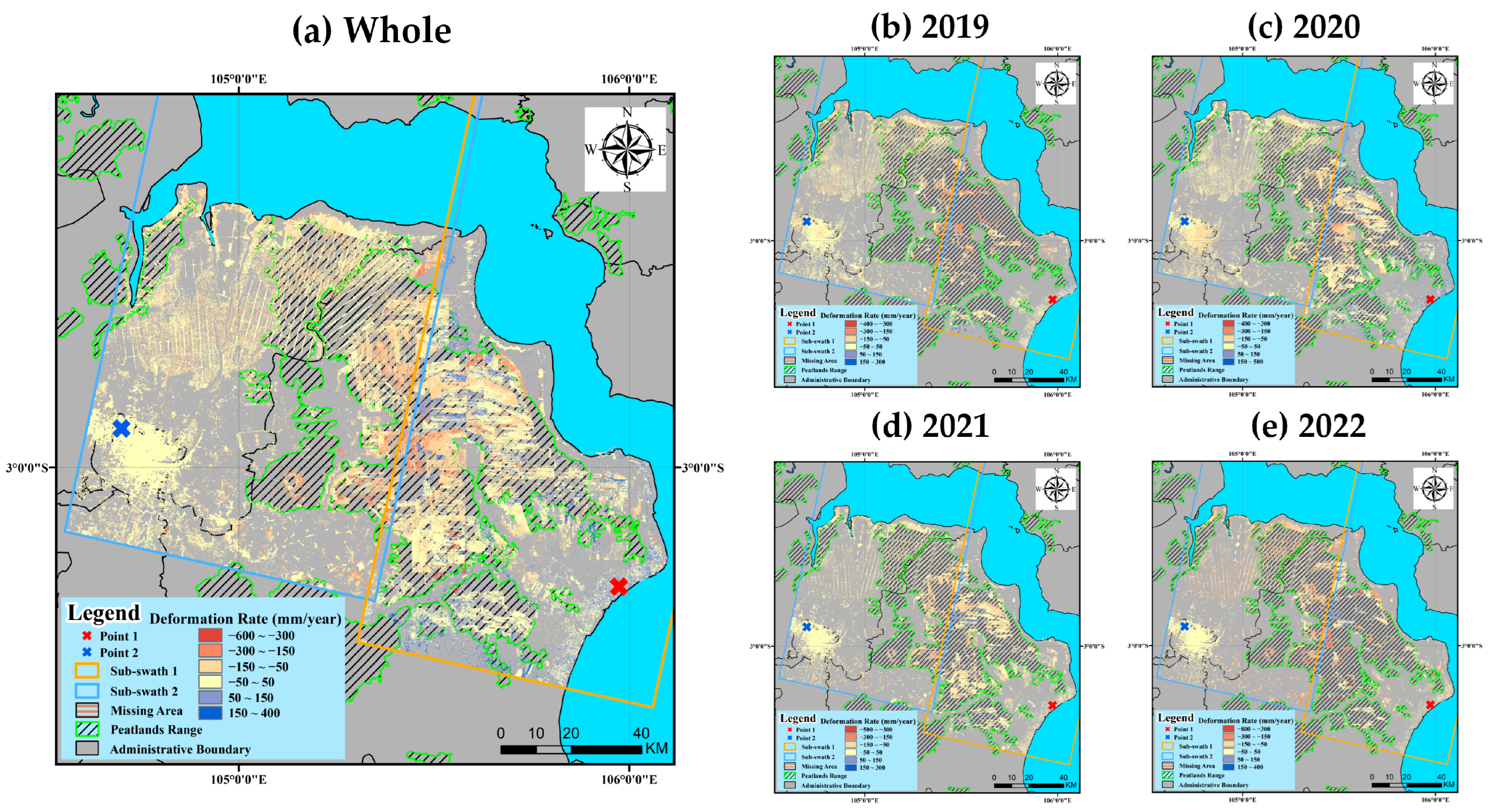
4.2. Deformation Results of Peatlands in South Sumatra Province from 2019 to 2022
4.3. Reliability Validation of the Peatlands’ Deformation Results
4.4. Comparison and Evaluation of Deformation Results of Adaptive HCTSs SBAS-InSAR
5. Discussion
6. Conclusions
- Based on the deformation results, the widespread and rapid degradation of peatlands in South Sumatra province between 2019 and 2022 was observed, with the deformation rate ranging from −567 to 347 mm/year. The spatial distribution of subsidence was closely related to the scope of peatlands.
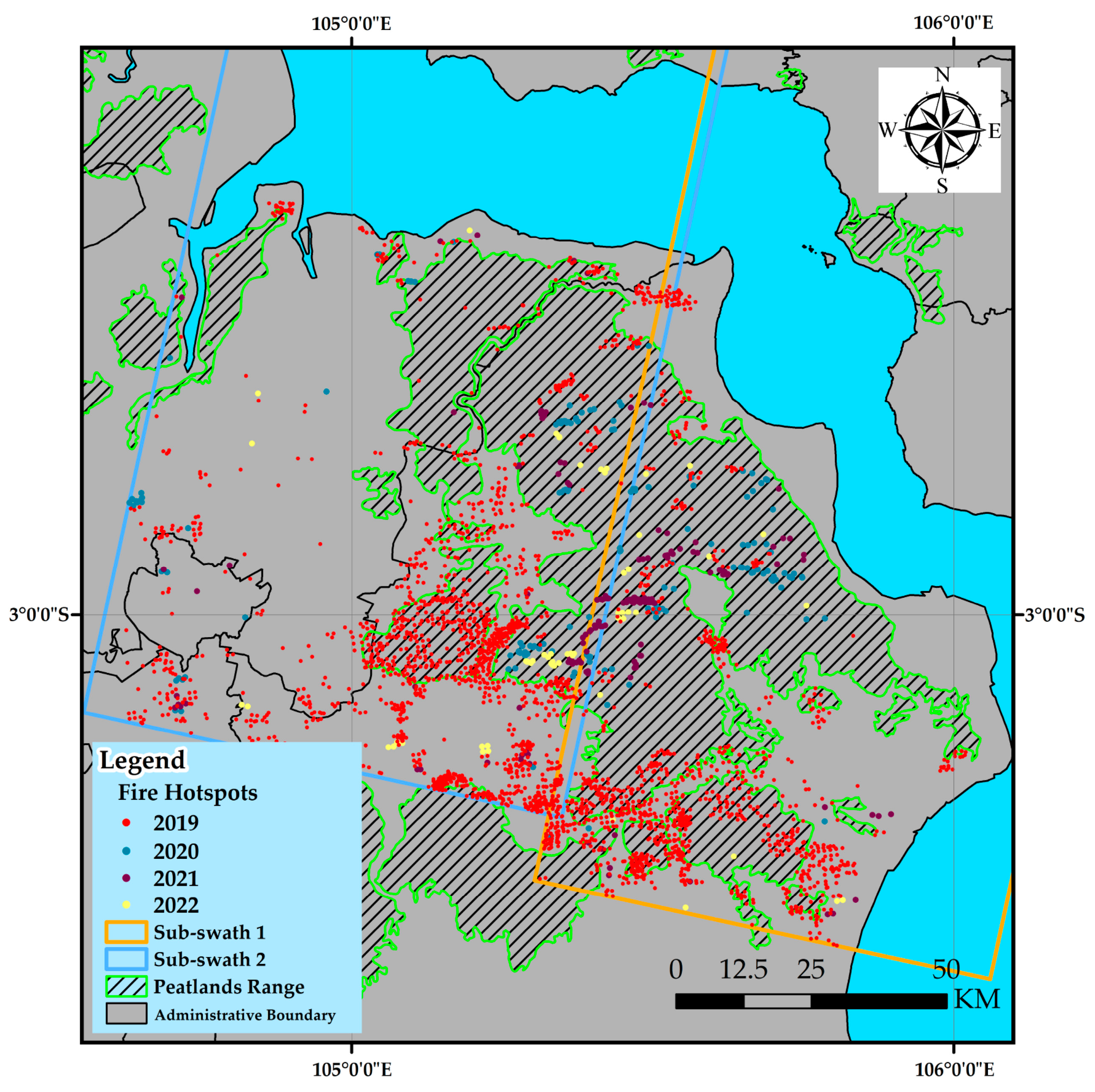
- The study found that peatlands’ deformation rate and the number of measurement points were affected by fires and the change in land cover. Fires caused higher rates of peatland deformation, after which the rate of deformation decreased slightly and then increased with time. At the same time, the change in land cover, such as the newly reclaimed industrial plantation, also contributed to the rapid deformation of peatlands. Besides, the number of measurement points increased after fires or deforestation because there is a lot of soil exposed and decreases with the restoration of vegetation.
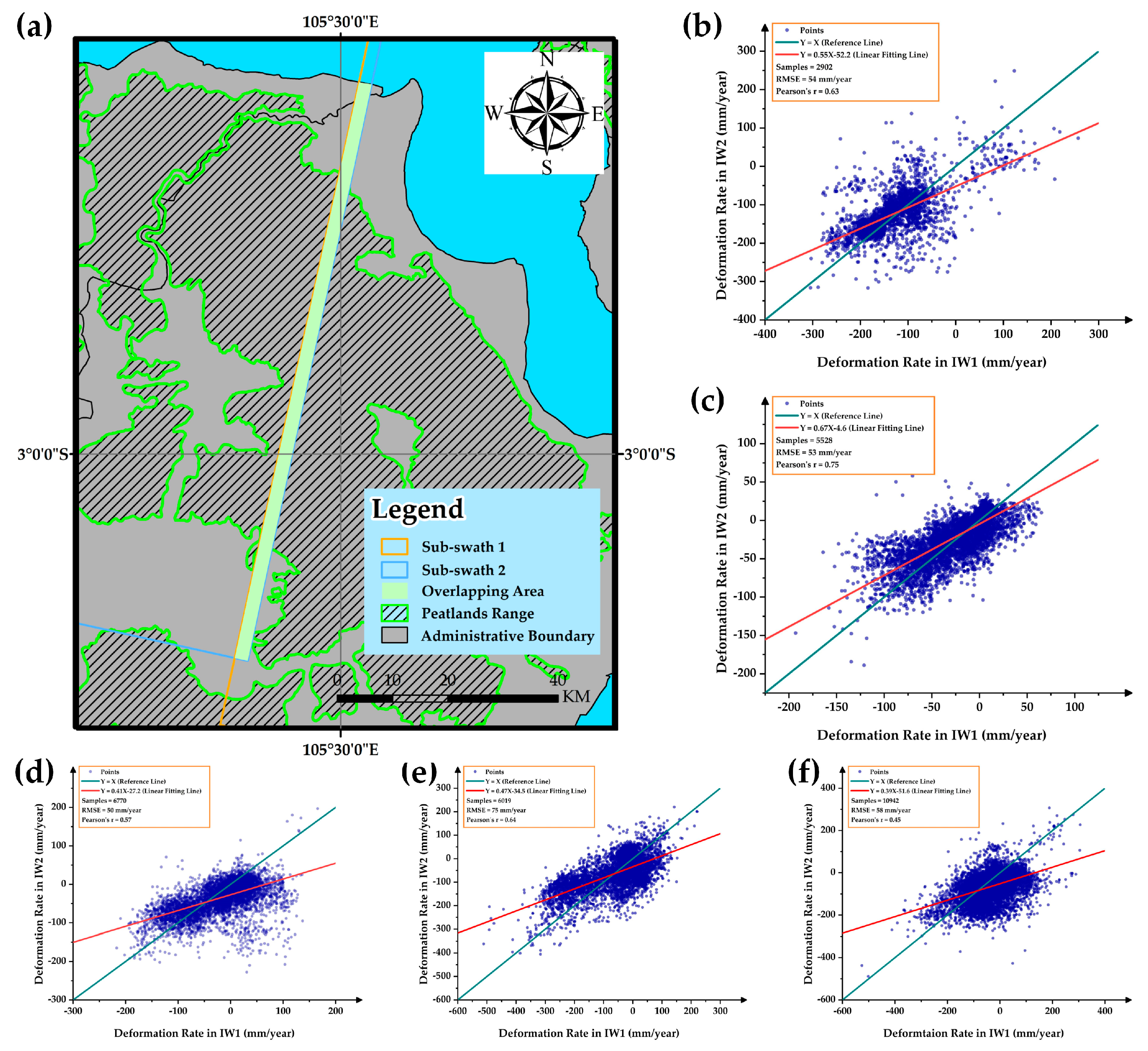
- Pearson’s r and RMSE in overlapping area’s deformation results ranged from 0.44 to 0.75 and 50 to 75 mm/year, respectively, which verified the reliability of the proposed method. In addition, compared with the deformation results obtained by SBAS-InSAR methods, the number of measurement points increases by about 2 to 127 times, and the ratio of coverage increases from 1.8% to 41.9%. New measurement points were always located in the areas that were difficult to monitor with SBAS-InSAR methods, which enhanced the monitoring ability of InSAR technology in tropical peatlands. At the same time, the number of interferograms and storage requirements were significantly reduced compared with the ISBAS method, which was conducive to meeting the requirements of calculation in a wider range.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, L.E.; Holden, J.; Palmer, S.M.; Johnston, K.; Ramchunder, S.J.; Grayson, R. Effects of fire on the hydrology, biogeochemistry, and ecology of peatland river systems. Freshw. Sci. 2015, 34, 1406–1425. [Google Scholar]
- Kirpotin, S.N.; Antoshkina, O.A.; Berezin, A.E.; Elshehawi, S.; Feurdean, A.; Lapshina, E.D.; Pokrovsky, O.S.; Peregon, A.M.; Semenova, N.M.; Tanneberger, F. Great Vasyugan Mire: How the world’s largest peatland helps addressing the world’s largest problems. Ambio 2021, 50, 2038–2049. [Google Scholar] [PubMed]
- Dohong, A.; Abdul Aziz, A.; Dargusch, P. A review of techniques for effective tropical peatland restoration. Wetlands 2018, 38, 275–292. [Google Scholar]
- Wu, J. Response of peatland development and carbon cycling to climate change: A dynamic system modeling approach. Environ. Earth Sci. 2012, 65, 141–151. [Google Scholar]
- Temmink, R.J.; Lamers, L.P.; Angelini, C.; Bouma, T.J.; Fritz, C.; van de Koppel, J.; Lexmond, R.; Rietkerk, M.; Silliman, B.R.; Joosten, H. Recovering wetland biogeomorphic feedbacks to restore the world’s biotic carbon hotspots. Science 2022, 376, eabn1479. [Google Scholar] [PubMed]
- Humpenöder, F.; Karstens, K.; Lotze-Campen, H.; Leifeld, J.; Menichetti, L.; Barthelmes, A.; Popp, A. Peatland protection and restoration are key for climate change mitigation. Environ. Res. Lett. 2020, 15, 104093. [Google Scholar]
- Dise, N.B. Peatland response to global change. Science 2009, 326, 810–811. [Google Scholar] [CrossRef]
- Gorham, E.; Lehman, C.; Dyke, A.; Clymo, D.; Janssens, J. Long-term carbon sequestration in North American peatlands. Quat. Sci. Rev. 2012, 58, 77–82. [Google Scholar]
- Page, S.E.; Rieley, J.O.; Banks, C.J. Global and regional importance of the tropical peatland carbon pool. Glob. Chang. Biol. 2011, 17, 798–818. [Google Scholar]
- Jauhiainen, J.; Hooijer, A.; Page, S. Carbon dioxide emissions from an Acacia plantation on peatland in Sumatra, Indonesia. Biogeosciences 2012, 9, 617–630. [Google Scholar]
- Miettinen, J.; Shi, C.; Liew, S.C. Land cover distribution in the peatlands of Peninsular Malaysia, Sumatra and Borneo in 2015 with changes since 1990. Glob. Ecol. Conserv. 2016, 6, 67–78. [Google Scholar] [CrossRef]
- Koh, L.P.; Miettinen, J.; Liew, S.C.; Ghazoul, J. Remotely sensed evidence of tropical peatland conversion to oil palm. Proc. Natl. Acad. Sci. USA 2011, 108, 5127–5132. [Google Scholar] [CrossRef] [PubMed]
- Hoyt, A.M.; Chaussard, E.; Seppalainen, S.S.; Harvey, C.F. Widespread subsidence and carbon emissions across Southeast Asian peatlands. Nat. Geosci. 2020, 13, 435–440. [Google Scholar] [CrossRef]
- Hooijer, A.; Page, S.; Canadell, J.; Silvius, M.; Kwadijk, J.; Wösten, H.; Jauhiainen, J. Current and future CO 2 emissions from drained peatlands in Southeast Asia. Biogeosciences 2010, 7, 1505–1514. [Google Scholar] [CrossRef]
- Moore, S.; Evans, C.D.; Page, S.E.; Garnett, M.H.; Jones, T.G.; Freeman, C.; Hooijer, A.; Wiltshire, A.J.; Limin, S.H.; Gauci, V. Deep instability of deforested tropical peatlands revealed by fluvial organic carbon fluxes. Nature 2013, 493, 660–663. [Google Scholar] [CrossRef]
- Hooijer, A.; Page, S.; Jauhiainen, J.; Lee, W.; Lu, X.; Idris, A.; Anshari, G. Subsidence and carbon loss in drained tropical peatlands. Biogeosciences 2012, 9, 1053–1071. [Google Scholar] [CrossRef]
- Sinclair, A.L.; Graham, L.L.; Putra, E.I.; Saharjo, B.H.; Applegate, G.; Grover, S.P.; Cochrane, M.A. Effects of distance from canal and degradation history on peat bulk density in a degraded tropical peatland. Sci. Total Environ. 2020, 699, 134199. [Google Scholar] [CrossRef]
- Othman, H.; Mohammed, A.T.; Darus, F.M.; Harun, M.H.; Zambri, M.P. Best management practices for oil palm cultivation on peat: Ground water-table maintenance in relation to peat subsidence and estimation of CO2 emissions at Sessang, Sarawak. J. Oil Palm Res. 2011, 23, 1078–1086. [Google Scholar]
- Evans, C.D.; Williamson, J.M.; Kacaribu, F.; Irawan, D.; Suardiwerianto, Y.; Hidayat, M.F.; Laurén, A.; Page, S.E. Rates and spatial variability of peat subsidence in Acacia plantation and forest landscapes in Sumatra, Indonesia. Geoderma 2019, 338, 410–421. [Google Scholar] [CrossRef]
- Updegraff, K.; Bridgham, S.D.; Pastor, J.; Weishampel, P.; Harth, C. Response of CO2 and CH4 emissions from peatlands to warming and water table manipulation. Ecol. Appl. 2001, 11, 311–326. [Google Scholar]
- Dawson, Q.; Kechavarzi, C.; Leeds-Harrison, P.; Burton, R. Subsidence and degradation of agricultural peatlands in the Fenlands of Norfolk, UK. Geoderma 2010, 154, 181–187. [Google Scholar] [CrossRef]
- Reeve, A.; Glaser, P.; Rosenberry, D.O. Seasonal changes in peatland surface elevation recorded at GPS stations in the Red Lake Peatlands, northern Minnesota, USA. J. Geophys. Res.-Biogeosci. 2013, 118, 1616–1626. [Google Scholar] [CrossRef]
- Webb, E.L.; Friess, D.A.; Krauss, K.W.; Cahoon, D.R.; Guntenspergen, G.R.; Phelps, J. A global standard for monitoring coastal wetland vulnerability to accelerated sea-level rise. Nat. Clim. Chang. 2013, 3, 458–465. [Google Scholar] [CrossRef]
- Zou, L.; Wang, C.; Tang, Y.; Zhang, B.; Zhang, H.; Dong, L. Interferometric SAR Observation of Permafrost Status in the Northern Qinghai-Tibet Plateau by ALOS, ALOS-2 and Sentinel-1 between 2007 and 2021. Remote Sens. 2022, 14, 1870. [Google Scholar] [CrossRef]
- Daout, S.; Doin, M.P.; Peltzer, G.; Socquet, A.; Lasserre, C. Large-scale InSAR monitoring of permafrost freeze-thaw cycles on the Tibetan Plateau. Geophys. Res. Lett. 2017, 44, 901–909. [Google Scholar] [CrossRef]
- Osmanoğlu, B.; Dixon, T.H.; Wdowinski, S.; Cabral-Cano, E.; Jiang, Y. Mexico City subsidence observed with persistent scatterer InSAR. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 1–12. [Google Scholar] [CrossRef]
- Hamling, I.J.; Hreinsdóttir, S.; Clark, K.; Elliott, J.; Liang, C.; Fielding, E.; Litchfield, N.; Villamor, P.; Wallace, L.; Wright, T.J. Complex multifault rupture during the 2016 M w 7.8 Kaikōura earthquake, New Zealand. Science 2017, 356, eaam7194. [Google Scholar] [CrossRef]
- Intrieri, E.; Raspini, F.; Fumagalli, A.; Lu, P.; Del Conte, S.; Farina, P.; Allievi, J.; Ferretti, A.; Casagli, N. The Maoxian landslide as seen from space: Detecting precursors of failure with Sentinel-1 data. Landslides 2018, 15, 123–133. [Google Scholar] [CrossRef]
- Wang, C.; Tang, Y.; Zhang, H.; You, H.; Zhang, W.; Duan, W.; Wang, J.; Dong, L.; Zhang, B. First mapping of China surface movement using supercomputing interferometric SAR technique. Sci. Bull. 2021, 66, 1608–1610. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Z.; Waldron, S.; Tanaka, A. InSAR time series analysis of L-band data for understanding tropical peatland degradation and restoration. Remote Sens. 2019, 11, 2592. [Google Scholar] [CrossRef]
- Izumi, Y.; Takeuchi, W.; Widodo, J.; Sulaiman, A.; Awaluddin, A.; Aditiya, A.; Razi, P.; Anggono, T.; Sumantyo, J.T.S. Temporal Subset SBAS InSAR Approach for Tropical Peatland Surface Deformation Monitoring Using Sentinel-1 Data. Remote Sens. 2022, 14, 5825. [Google Scholar] [CrossRef]
- Cigna, F.; Sowter, A.; Jordan, C.J.; Rawlins, B.G. Intermittent Small Baseline Subset (ISBAS) monitoring of land covers unfavourable for conventional C-band InSAR: Proof-of-concept for peatland environments in North Wales, UK. In Proceedings of the SPIE Remote Sensing, Amsterdam, The Netherlands, 11 November 2014; pp. 924305–924306. [Google Scholar]
- Umarhadi, D.A.; Widyatmanti, W.; Kumar, P.; Yunus, A.P.; Khedher, K.M.; Kharrazi, A.; Avtar, R. Tropical peat subsidence rates are related to decadal LULC changes: Insights from InSAR analysis. Sci. Total Environ. 2022, 816, 151561. [Google Scholar] [CrossRef]
- Marshall, C.; Large, D.J.; Athab, A.; Evers, S.L.; Sowter, A.; Marsh, S.; Sjögersten, S. Monitoring tropical peat related settlement using isbas insar, kuala lumpur international airport (klia). Eng. Geol. 2018, 244, 57–65. [Google Scholar] [CrossRef]
- Hrysiewicz, A.; Holohan, E.P.; Donohue, S.; Cushnan, H. SAR and InSAR data linked to soil moisture changes on a temperate raised peatland subjected to a wildfire. Remote Sens. Environ. 2023, 291, 113516. [Google Scholar] [CrossRef]
- Khakim, M.Y.N.; Bama, A.A.; Yustian, I.; Poerwono, P.; Tsuji, T.; Matsuoka, T. Peatland subsidence and vegetation cover degradation as impacts of the 2015 El niño event revealed by Sentinel-1A SAR data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101953. [Google Scholar] [CrossRef]
- Cigna, F.; Sowter, A. The relationship between intermittent coherence and precision of ISBAS InSAR ground motion velocities: ERS-1/2 case studies in the UK. Remote Sens. Environ. 2017, 202, 177–198. [Google Scholar] [CrossRef]
- Ferretti, A.; Colesanti, C.; Perissin, D.; Prati, C.; Rocca, F. Evaluating the effect of the observation time on the distribution of SAR permanent scatterers. In Proceedings of the Fringe Workshop, Frascati, Italy, 1–5 December 2003; p. 6. [Google Scholar]
- Hu, F.; Wu, J.; Chang, L.; Hanssen, R.F. Incorporating temporary coherent scatterers in multi-temporal InSAR using adaptive temporal subsets. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7658–7670. [Google Scholar] [CrossRef]
- Sowter, A.; Bateson, L.; Strange, P.; Ambrose, K.; Syafiudin, M.F. DInSAR estimation of land motion using intermittent coherence with application to the South Derbyshire and Leicestershire coalfields. Remote Sens. Lett. 2013, 4, 979–987. [Google Scholar] [CrossRef]
- Bateson, L.; Cigna, F.; Boon, D.; Sowter, A. The application of the Intermittent SBAS (ISBAS) InSAR method to the South Wales Coalfield, UK. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 249–257. [Google Scholar] [CrossRef]
- Cigna, F.; Novellino, A.; Jordan, C.J.; Sowter, A.; Ramondini, M.; Calcaterra, D. Intermittent SBAS (ISBAS) InSAR with COSMO-SkyMed X-band high resolution SAR data for landslide inventory mapping in Piana degli Albanesi (Italy). In Proceedings of the SAR Image Analysis, Modeling, and Techniques XIV, Amsterdam, The Netherlands, 21 October 2014; pp. 389–395. [Google Scholar]
- Novellino, A.; Cigna, F.; Sowter, A.; Ramondini, M.; Calcaterra, D. Exploitation of the Intermittent SBAS (ISBAS) algorithm with COSMO-SkyMed data for landslide inventory mapping in north-western Sicily, Italy. Geomorphology 2017, 280, 153–166. [Google Scholar] [CrossRef]
- Grebby, S.; Orynbassarova, E.; Sowter, A.; Gee, D.; Athab, A. Delineating ground deformation over the Tengiz oil field, Kazakhstan, using the Intermittent SBAS (ISBAS) DInSAR algorithm. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 37–46. [Google Scholar] [CrossRef]
- Gee, D.; Sowter, A.; Novellino, A.; Marsh, S.; Gluyas, J. Monitoring land motion due to natural gas extraction: Validation of the Intermittent SBAS (ISBAS) DInSAR algorithm over gas fields of North Holland, the Netherlands. Mar. Pet. Geol. 2016, 77, 1338–1354. [Google Scholar] [CrossRef]
- Perissin, D.; Ferretti, A. Urban-target recognition by means of repeated spaceborne SAR images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4043–4058. [Google Scholar] [CrossRef]
- Dogan, O.; Perissin, D. Detection of multitransition abrupt changes in multitemporal SAR images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 3239–3247. [Google Scholar] [CrossRef]
- Nurhayati, A.D.; Saharjo, B.H.; Sundawati, L.; Syartinilia, S.; Cochrane, M.A. Forest and peatland fire dynamics in South Sumatra Province. For. Soc. 2021, 5, 591–603. [Google Scholar] [CrossRef]
- Azizan, F.A.; Astuti, I.S.; Aditya, M.I.; Febbiyanti, T.R.; Williams, A.; Young, A.; Abdul Aziz, A. Using multi-temporal satellite data to analyse phenological responses of rubber (Hevea brasiliensis) to climatic variations in South Sumatra, Indonesia. Remote Sens. 2021, 13, 2932. [Google Scholar] [CrossRef]
- Ngadi, N.; Nagata, J. Oil Palm Land Use Change and Rice Sustainability in South Sumatra, Indonesia. Land 2022, 11, 669. [Google Scholar] [CrossRef]
- Irfan, M.; Virgo, F.; Khakim, M.; Ariani, M.; Sulaiman, A.; Iskandar, I. The dynamics of rainfall and temperature on peatland in South Sumatra during the 2019 extreme dry season. In Proceedings of the Journal of Physics: Conference Series, Padang, Indonesia, 23–24 July 2020; p. 012030. [Google Scholar]
- Ngadi, N.J. Development of the Oil Palm Plantation Sector in South Sumatra Province. Komaba Stud. Hum. Geogr. 2020, 23, 1–12. [Google Scholar]
- Miettinen, J.; Shi, C.; Liew, S.C. Fire distribution in Peninsular Malaysia, Sumatra and Borneo in 2015 with special emphasis on peatland fires. Environ. Manag. 2017, 60, 747–757. [Google Scholar] [CrossRef]
- Ardiansyah, M.; Boer, R.; Situmorang, A. Typology of land and forest fire in South Sumatra, Indonesia Based on Assessment of MODIS Data. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bogor, Indonesia, 25–26 October 2016; p. 012058. [Google Scholar]
- Sitanggang, I.; Asti, A.; Agmalaro, M. Haze in urban areas from peatland fires in Sumatra based on simulation using HYSPLIT. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bogor, Indonesia, 21 November 2017; p. 012004. [Google Scholar]
- Arjasakusuma, S.; Kusuma, S.S.; Vetrita, Y.; Prasasti, I.; Arief, R. Monthly Burned-Area Mapping using Multi-Sensor Integration of Sentinel-1 and Sentinel-2 and machine learning: Case Study of 2019’s fire events in South Sumatra Province, Indonesia. Remote Sens. Appl. Soc. Environ. 2022, 27, 100790. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Parizzi, A.; Cong, X.; Eineder, M. First Results from Multifrequency Interferometry. A comparison of different decorrelation time constants at L, C, and X Band. In Proceedings of the Fringe 2009 Workshop, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Morishita, Y.; Hanssen, R.F. Temporal decorrelation in L-, C-, and X-band satellite radar interferometry for pasture on drained peat soils. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1096–1104. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. EOS Trans. Am. Geophys. Union 2013, 92, 234. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Ribeiro, K.; Pacheco, F.S.; Ferreira, J.W.; de Sousa-Neto, E.R.; Hastie, A.; Krieger Filho, G.C.; Alvalá, P.C.; Forti, M.C.; Ometto, J.P. Tropical peatlands and their contribution to the global carbon cycle and climate change. Glob. Chang. Boil. 2021, 27, 489–505. [Google Scholar] [CrossRef]
- Murdiyarso, D.; Hergoualc’h, K.; Verchot, L.V. Opportunities for reducing greenhouse gas emissions in tropical peatlands. Proc. Natl. Acad. Sci. USA 2010, 107, 19655–19660. [Google Scholar] [CrossRef]



| Year | Path-Frame | Time Range | Number of SAR Images | Orbit Direction |
|---|---|---|---|---|
| 2019 | 120-600 | 8 January 2019–22 December 2019 | 23 | Descending |
| 2020 | 120-600 | 3 January 2020–28 December 2020 | 24 | Descending |
| 2021 | 120-600 | 9 January 2021–23 December 2021 | 22 | Descending |
| 2022 | 120-600 | 4 January 2022–30 December 2022 | 21 | Descending |
| Number | Path-Row | Data Acquisition Time | Sensor |
|---|---|---|---|
| 1 | 123-062 | 10 March 2019 | Landsat 8 |
| 2 | 123-062 | 13 April 2020 | Landsat 8 |
| 3 | 123-062 | 6 October 2020 | Landsat 8 |
| 4 | 123-062 | 9 October 2021 | Landsat 8 |
| 5 | 123-062 | 11 April 2022 | Landsat 9 |
| Master Image | Time Range | Number of SAR Images | |
|---|---|---|---|
| Subset 1 | 12 August 2019 | 2 August 2019–27 January 2020 | 15 |
| Subset 2 | 6 August 2020 | 6 August 2020–27 April 2021 | 23 |
| Subset 3 | 13 August 2021 | 13 August 2021–4 May 2022 | 13 |
| Subset 4 | 9 January 2021 | 9 January 2021–27 April 2021 | 10 |
| Subset 1 | Subset 2 | ||||||
| Region 1 | 0.5409 | 0.0794 | 19.9547 | Region 1 | 0.4683 | 0.081 | 18.006 |
| Region 2 | 0.5109 | 0.0873 | 13.3393 | Region 2 | 0.4961 | 0.0817 | 16.8464 |
| Region 3 | 0.6169 | 0.0828 | 23.0578 | Region 3 | 0.4589 | 0.081 | 16.1096 |
| Region 4 | 0.6624 | 0.0862 | 16.9992 | Region 4 | 0.3599 | 0.0787 | 30.9161 |
| Region 5 | 0.6323 | 0.0825 | 14.4918 | Region 5 | 0.3952 | 0.0823 | 28.2754 |
| Average | 0.59268 | 0.08364 | 17.56856 | Average | 0.43568 | 0.08094 | 22.0307 |
| Subset 3 | Subset 4 | ||||||
| Region 1 | 0.5534 | 0.0884 | 10.4404 | Region 1 | 0.676 | 0.0689 | 23.1483 |
| Region 2 | 0.5145 | 0.0843 | 9.6184 | Region 2 | 0.5854 | 0.0804 | 23.181 |
| Region 3 | 0.6645 | 0.0845 | 17.2163 | Region 3 | 0.5885 | 0.0787 | 26.3481 |
| Region 4 | 0.556 | 0.0843 | 25.1663 | Region 4 | 0.5986 | 0.0705 | 23.5385 |
| Region 5 | 0.4224 | 0.0893 | 17.6846 | Region 5 | 0.5106 | 0.0689 | 26.1949 |
| Average | 0.54216 | 0.08616 | 16.0252 | Average | 0.59182 | 0.07348 | 24.48216 |
| Sub-Swath 1 | Sub-Swath 2 | |||||
|---|---|---|---|---|---|---|
| No. | Time Range | Master Image | Number of Images (Inter 1) | Time Range | Master Image | Number of Images (Inter 1) |
| 1 | 8 January 2019–1 June 2019 | 9 March 2019 | 11 (15) | 8 January 2019–1 June 2019 | 9 March 2019 | 11 (15) |
| 2 | 2 August 2019–3 January 2020 | 23 October 2019 | 13 (23) | 2 August 2019–3 January 2020 | 23 October 2019 | 13 (23) |
| 3 | 5 September 2019–27 January 2020 | 16 November 2019 | 13 (23) | 5 September 2019–27 January 2020 | 16 November 2019 | 13 (23) |
| 4 | 3 March 2020–19 June 2020 | 8 April 2020 | 8 (10) | 3 March 2020–19 June 2020 | 8 April 2020 | 8 (10) |
| 5 | 6 August 2020–21 January 2021 | 17 October 2020 | 15 (27) | 6 August 2020–26 February 2021 | 29 October 2020 | 18 (33) |
| 6 | 30 August 2020–2 February 2021 | 10 November 2020 | 14 (25) | 30 August 2020–10 March 2021 | 4 December 2020 | 17 (31) |
| 7 | 23 September 2020–26 February 2021 | 4 December 2020 | 14 (25) | 23 September 2020–22 March 2021 | 16 December 2020 | 16 (29) |
| 8 | 17 October 2020–22 March 2021 | 28 December 2020 | 14 (25) | 17 October 2021–15 April 2021 | 9 January 2021 | 16 (29) |
| 9 | 10 November 2020–3 April 2021 | 9 Januray 2021 | 13 (23) | 10 November 2020–21 May 2021 | 2 February 2021 | 16 (28) |
| 10 | 4 December 2020–21 May 2021 | 14 February 2021 | 14 (24) | 13 August 2021–17 March 2022 | 5 November 2021 | 16 (24) |
| 11 | 13 August 2021–9 February 2022 | 24 October 2021 | 14 (22) | 6 September 2021–29 March 2022 | 11 December 2021 | 15 (22) |
| 12 | 6 September 2021–5 March 2022 | 17 November 2021 | 13 (19) | 30 September 2021–10 April 2022 | 23 December 2021 | 14 (20) |
| 13 | 30 September 2021–10 April 2022 | 23 December 2021 | 14 (20) | 24 October 2021–4 May 2022 | 16 January 2022 | 14 (20) |
| 14 | 24 October 2021–4 May 2022 | 16 Januray 2022 | 14 (20) | 8 August 2022–30 December 2022 | 7 October 2022 | 12 (15) |
| 15 | 8 August 2022–30 December 2022 | 7 October 2022 | 12 (15) | |||
| Reference Points | Sub-Swath | Location (Longitude, Latitude) | Land Use |
|---|---|---|---|
| 1 | (105°58′25.19″E, 3°18′4.92″S) | Urban | |
| 2 | (104°42′00.00″E, 2°54′7.02″S) | Urban (near to the GPS Station) |
| Min Subsidence Rate (mm/year) | Max Uplift Rate (mm/year) | |
|---|---|---|
| 2019 | −390 | 283 |
| 2020 | −324 | 436 |
| 2021 | −398 | 260 |
| 2022 | −735 | 327 |
| Whole | −567 | 347 |
| Number and coverage percent of measurement points in the comparative SBAS-InSAR experiments | ||||||
| 2019 | 2020 | 2021 | 2022 | Whole 1 | Whole 2 | |
| Sub-swath 1 (Points Number) | 38,221 | 39,195 | 40,080 | 29,122 | 5172 | 104,908 |
| Sub-swath 2 (Points Number) | 186,475 | 184892 | 195,595 | 209,057 | 124,467 | 303,075 |
| Coverage Percent in Sub-swath 1 (%) | 2.4 | 2.4 | 2.5 | 1.8 | 0.3 | 6.6 |
| Coverage Percent in Sub-swath 2 (%) | 4.4 | 4.3 | 4.6 | 4.9 | 2.9 | 7.1 |
| Number and coverage percent of measurement points in experiments based on the adaptive HCTSs SBAS-InSAR | ||||||
| 2019 | 2020 | 2021 | 2022 | Whole | ||
| Sub-swath 1 (Points Number) | 211,539 | 479,287 | 362,905 | 216,792 | 659,378 | |
| Sub-swath 2 (Points Number) | 542,354 | 561,776 | 416,772 | 434,282 | 773,624 | |
| Coverage Percent in Sub-swath 1 (%) | 13.4 | 30.4 | 23.1 | 13.8 | 41.9 | |
| Coverage Percent in Sub-swath 2 (%) | 12.9 | 13.3 | 9.9 | 10.2 | 18.3 | |
| Improvement of the number of measurement points (times) | ||||||
| Sub-swath 1 | 5.5 | 12.2 | 9.1 | 7.4 | 127.4 | 6.2 |
| Sub-swath 2 | 2.9 | 3 | 2.1 | 2.1 | 6.2 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Wang, C.; Tang, Y.; Zhang, H.; Li, T.; Zou, L.; Guan, S. Adaptive High Coherence Temporal Subsets SBAS-InSAR in Tropical Peatlands Degradation Monitoring. Remote Sens. 2023, 15, 4461. https://doi.org/10.3390/rs15184461
Zheng X, Wang C, Tang Y, Zhang H, Li T, Zou L, Guan S. Adaptive High Coherence Temporal Subsets SBAS-InSAR in Tropical Peatlands Degradation Monitoring. Remote Sensing. 2023; 15(18):4461. https://doi.org/10.3390/rs15184461
Chicago/Turabian StyleZheng, Xiaohan, Chao Wang, Yixian Tang, Hong Zhang, Tianyang Li, Lichuan Zou, and Shaoyang Guan. 2023. "Adaptive High Coherence Temporal Subsets SBAS-InSAR in Tropical Peatlands Degradation Monitoring" Remote Sensing 15, no. 18: 4461. https://doi.org/10.3390/rs15184461
APA StyleZheng, X., Wang, C., Tang, Y., Zhang, H., Li, T., Zou, L., & Guan, S. (2023). Adaptive High Coherence Temporal Subsets SBAS-InSAR in Tropical Peatlands Degradation Monitoring. Remote Sensing, 15(18), 4461. https://doi.org/10.3390/rs15184461








