Abstract
The traditional leveling, total station, and global navigation satellite system (GNSS) and the new differential interferometric synthetic aperture radar (DInSAR) and terrestrial laser scanning (TLS) systems have their own advantages and limitations in the deformation monitoring of mining areas. It is difficult to obtain accurate deformation information only using single-source measurement data. In this study, we propose an LOS deformation correction method for DInSAR in mining areas by fusing ground data without control points. Based on free space data, small deformations at the edges of mining influence areas accurately obtained using DInSAR. By combining leveling/GNSS and TLS methods, it was possible to obtain large deformations in central areas without the need for control points located outside the mining influence range. For overcoming the non-uniform coordinates of the “space–ground” data and the limited overlap of the effective measurement ranges, the subsidence prediction model was employed to assist in its fusion. In addition, in LOS deformation correction, we retained the non-full cycle phase of DInSAR and replaced the full cycle phase with the one from the data fusion. Engineering experiments have shown that the correction results preserve the differences in the LOS deformations at the edge areas of the mine influence range, and they recover the lost LOS deformations at the center areas. Using the difference in the LOS deformation before and after correction as the verification indicator, the maximum absolute value of the errors after correction was 143 mm, which was approximately 6.4% of the maximum LOS deformation. In addition, there were still two errors that were large (−112 mm and −89 mm, respectively), and the absolute values of errors were not more than 75 mm. For all errors, the mean absolute value was 36 mm. Compared with 399 mm before correction, the error was reduced by 91%. This study provides technical support and theoretical reference for deformation monitoring and control in mining areas.
1. Introduction
China, being the largest coal producer and consumer globally, holds approximately 76% and 66% of the primary energy production and consumption, respectively [1]. Heavy deformations are caused by high-intensity, large-scale, and rapid coal mining, resulting in significant damage to surface infrastructure and the ecological environment. Furthermore, they negatively impact the safety and wellbeing of the residents in the surrounding areas [2,3,4]. While new mining technologies, such as separation pouring mining and “mining-pouring-keeping” collaborative mining, offer some control over deformation [5,6], they have limited applicability and impose additional production burdens. Rapid subsidence, large deformation gradients, and a wide range of influences remain common occurrences in coal mining. Consequently, conducting deformation monitoring assumes great importance, as it provides vital production guidance for mining areas and aids in mitigating and forecasting damage [7].
The traditional deformation monitoring methods in mine areas are achieved through leveling, total station, and the global navigation satellite system (GNSS). These approaches typically require laying observation lines along the trend and tendency direction of the working faces. While this provides high accuracy, it requires establishing control points outside the mining influence areas as the starting points, which demands significant resources in terms of manpower and materials, and it is difficult to maintain them completely over an extended period [8]. In recent years, new measurement technologies, such as interferometric synthetic aperture radar (InSAR) and terrestrial laser scanning (TLS), have emerged for deformation monitoring [9,10]. InSAR enables the acquisition of surface deformation information and can separate surface deformations through interference processing [11]. Differential interferometric synthetic aperture radar (DInSAR), as an extension of InSAR, has become a mature method for monitoring deformations in mining areas [12,13,14]. However, incoherence arises due to large deformation gradients, causing notable discrepancies between the obtained line-of-sight (LOS) deformations and the actual values in the non-edge areas of the mining influence ranges. With the advancements in light detection and ranging, TLS has proven effective in achieving high-precision deformation monitoring that is largely unaffected by deformation gradients [15]. TLS possesses peculiarities when utilized for deformation monitoring in mining areas, namely, the need to scan from one station to another and the limited scanning range within a single station. While the deployment of measuring stations multiple times allows for their application in large-scale scenarios, obtaining deformation indicators within a mining area necessitates a combination of feature points, significantly limiting the measurement range [16].
The existing measurement methods in mining areas have their respective advantages and limitations. Fusing the characteristics of the measurement data is currently challenging, and it is a highly sought-after research topic for accurately determining deformations. In previous studies, an advantageous method was to use “measurement data + subsidence prediction model” [17,18,19]. However, in some areas of mining influence ranges, there is a lack of deformation constraints, leading to significant discrepancies between the obtained results and the actual deformations. Moreover, these measurements cannot accurately reflect the differences under the same deformation magnitudes. Nevertheless, based on local deformations in measurement data, it is possible to calculate the deformations for an entire mining influence range, which is the main reason why this method has been widely used [20,21,22,23]. Despite the efforts of some scholars to incorporate subsidence prediction models that better align with mining mechanisms, single-measurement data still struggle to overcome their inherent limitations and improve the accuracy of deformation determination. Recently, Yan et al. [24] proposed a “space-sky-ground” integrated collaborative monitoring framework in mining areas, and Jiang et al. [25] discussed the possibility of integrating other source measurement data with space data. These scholars have attempted to fuse other source measurement data in order to obtain high-precision deformation information, providing innovative research directions for deformation monitoring in mining areas [24,25,26].
With this background, this study proposes an LOS deformation correction method for DInSAR in mining areas by fusing ground data without control points. Based on free space data, small deformations at the edge of mining influence areas can be accurately obtained using DInSAR. By combining leveling/GNSS and TLS methods, it is possible to obtain large deformation information in central areas without the need for control points located outside the mining influence ranges. For overcoming the non-uniform coordinates of “space–ground” data and the limited overlap of effective measurement ranges, the subsidence prediction model was employed to assist in the fusion. In addition, in the LOS deformation correction, we retained the non-full cycle phase (NFCP) of the DInSAR and replaced the full cycle phase (FCP) with that of the data fusion. This helped to retrieve the large deformations lost in the DInSAR and preserve the differences in the small deformations.
The remaining content of this article is organized as follows: Section 2 describes the method used to correct the LOS deformations of the DInSAR. Then, in Section 3, we present the engineering experiments under the thick loose layer conditions that were used to verify the method. Discussions are provided in Section 4, and the conclusions are presented in Section 5.
2. Methods
2.1. Measurement of the Ground Data
In the ground data measurements of this method, leveling/GNSS and TLS were employed as the measurement approaches, and subsidence and horizontal displacements were used as the measurement indicators.
To calculate these indicators, it was imperative to have points with the same names. Consequently, the measurements required the artificial feature points (AFPs) and natural feature points (NFPs) to be combined. The detection of AFPs, which were embedded in the ground, was only possible when the scanning instrument was in close proximity, and they are typically measured through leveling/GNSS. The rural areas of China are predominantly characterized by coal mining activities. The infrastructure in the village, such as ground surfaces, brick–concrete buildings, streetlights, and tree trunks, could be used as the scanning objects and provided the most NFPs. Therefore, the NFPs were primarily measured using TLS.
As shown in Figure 1, the NFPs in the measurement scenario were mainly divided into three categories [27,28,29,30]:

Figure 1.
The NFPs in the measurement scenario: (a) the measurement scenario, (b) a point cloud image, (c) a class 1 NFP, (d) a class 2 NFP, and (e) a class 3 NFP.
- Grid nodes generated from the ground point clouds (for calculating subsidence)
- Corner points of building doors, windows, and walls (for calculating subsidence and horizontal displacements)
- Circle centers within cross-sections of the electric poles and tree trunks (for calculating horizontal displacements)
For the class 1 NFPs, after using cloth simulation filtering to obtain ground point clouds, the distance-weighted interpolation method could be used to calculate the elevation coordinates [31,32] with Equation (1). For the class 2 NFPs, the three-dimensional coordinates could be manually selected multiple times to determine the mean [33]. For the class 3 NFPs, the point clouds of the power poles and tree trunks perpendicular to the ground could be manually selected and the plane coordinates could be obtained by solving Equation (2) using the least squares method.
where ZGP is the elevation set of ground points within the neighborhood of grid nodes and Dis is the set of distances from these ground points to the grid nodes.
where (X, Y) is the plane coordinate of the center of the cross-section circle and (XTP, YTP) is the plane coordinate set of the individual electric pole or tree trunk point clouds.
Compared to TLS, which would require the presence of NFPs in the village, the AFPs widened the applicability of the leveling/GNSS. However, traditional leveling/GNSS typically requires setting up two or more control points outside the mining influence range as starting points, followed by measuring the AFP coordinates from the edge area to the center area. This approach is costly, time-consuming, and requires a large deployment volume of AFPs, which are difficult to preserve effectively over time. Therefore, in this study, the starting point was located in the village and converted to the TLS station coordinate system.
As shown in Figure 2, in addition to scanning objects with the NFPs, a scanning instrument should also be placed near the AFPs. At the same time, more than four target spheres should be placed near the scanning instrument to assist in merger and coordinate conversion. When an AFP is deployed on exposed ground, three-dimensional coordinates can be manually selected directly from the scanning point cloud. When there is vegetation coverage at the AFP deployment site, the target sphere can be erected above the AFP, with the plane coordinates of the AFP as its plane coordinates. Based on the ground points, distance-weighted interpolation is performed using Equation (1) to obtain the elevation coordinates. After obtaining the three-dimensional coordinates of the two AFPs and taking them as the starting points, the leveling instrument is used to measure the elevation coordinates and the GNSS receiver is used to measure the plane coordinates.
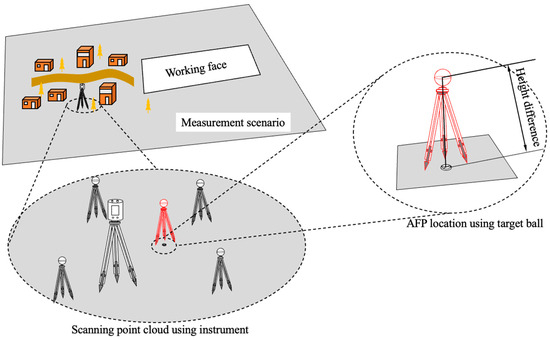
Figure 2.
Ground data measurement schematic.
In two adjacent measurements, based on Equations (3) and (4), the measurement index can be calculated by taking the difference of the coordinates of the feature points with the same name.
where ZFir and ZSec are the elevation coordinates of the feature points in the first and second phases, respectively.
where (XFir, YFir) and (XSec, YSec) are the plane coordinates of the feature points for the first and second phases, respectively, and φ is the vector direction for the horizontal displacement, which is usually the trend or tendency of the working face.
2.2. Fusion of the “Space–Ground” Data
To establish the correction benchmark of an LOS deformation for the complete mining influence range, the subsidence prediction model is used for the fusion of “space–ground” data. In this section, the used subsidence prediction model and data fusion background and steps are described in sequence.
2.2.1. BPM-EKTF Subsidence Prediction Model
In this study, the BPM-EKTF subsidence prediction model was used for the subsequent processing [21]. This model integrates the Boltzmann function prediction method (BPM) and the exponential Knothe time function (EKTF), taking the single-day mining range of the working face as the basic unit. Under the condition that the mining information and model parameters are known, the theoretical deformation of any point within the mining influence range can be obtained. When the working face is not fully mined, the subsidence and horizontal displacement (along the φ directions) are calculated using Equations (5) and (11), respectively.
where (x, y) is the ground coordinate in the working face coordinate system, t is the number of mining days, and W (x, y, i) is the final subsidence of the ground caused by the basic unit mined on day i. In fact, the final deformation is not instantaneous, and the subsidence of the basic unit on day t must be calculated using the time function.
where v is the mining speed of the working face.
where m is the thickness of the coal seam, q is the subsidence factor, and α is the dip angle of the coal seam.
where R = H/tanβ is the main influence radius, H is mined depth, β is the major influence angle, S1 and S2 are the deviations in the inflection points, and l is the length of the working face along the trend direction.
where S3 and S4 are the deviations in the inflection points.
where c and k are the time influence coefficients, respectively.
where B is the horizontal displacement factor and l is the length of the working face along the trend direction.
where L is the length of the working face along the tendency direction.
When the mining of the working face is completed, the subsidence and horizontal displacement are calculated using Equations (15) and (16), respectively.
where T is the time when the working face mining is completed.
2.2.2. Data Fusion Backgrounds and Steps
Surface deformation is a gradual process, and the maximum deformation cannot be achieved instantly. The newer the mining basic unit, the shorter the impact time on the surface. Consequently, during the advancing process of the working face, there is usually an asymmetry phenomenon where the deformation on one side of the advancing direction of the mined working face is always smaller than that on the opposite side [34,35].
In ground data, surface deformations near building clusters are obtained. However, in most engineering scenarios, it is difficult to ensure the presence of a building near both the mining and the stopping lines of the working face. It is common to only obtain deformations within a local range on one side of the already-mined working face. Discrete and small-scale ground data combined with the subsidence prediction model can be used to obtain the theoretical deformations within the complete mining impact ranges. However, in the advancement direction, the lack of data on one side of the already-mined working face makes the obtained theoretical deformations inconsistent with the asymmetry phenomenon. To establish the correction benchmark of an LOS deformation, it is not feasible to only combine ground data with subsidence prediction models.
For space data, DInSAR is the most commonly used and mature way to obtain deformations. However, the characteristic of large deformation gradients in mining areas makes the obtained deformation highly accurate only at the edges of the mining influence areas. By combining the accurate deformation of an edge area with the subsidence prediction model, the theoretical deformation obtained will conform to the asymmetry phenomenon. However, due to the lack of constraints on large deformations in non-edge regions, the maximum deformations in the center areas of a mining influence range cannot reach the ideal value.
At the same time, considering that “space–ground” data coordinates are not uniform and an effective measurement range has a low overlap, this study combined mining subsidence prediction models to fuse “space–ground” data for the establishment of correction benchmarks. The fusion steps are shown in Figure 3. According to the basic principle of mining subsidence, in the model parameters q, tanβ, B, θ, S1, S2, S3, S4, c, and k, c and k play major roles in the asymmetry phenomena. Considering that, in ground data, it is usually only possible to obtain deformation information within a local range on one side of a mined working face, solving c and k from the space data provides greater credibility. Similarly, and for to the same reason, the deviations in the inflection points S1, S2, S3, and S4 should also be solved using space data.

Figure 3.
The fusion steps of “space–ground” data.
Firstly, based on the above, the swarm intelligence algorithm was used as the solver, and the LOS deformation obtained from the DInSAR in the space data was used to solve the model parameters. Secondly, we fixed S1, S2, S3, S4, c, and k and solved the subsidence and horizontal displacement obtained from the ground data. Thirdly, the model parameters solved based on the space and ground data were combined to predict the theoretical subsidence, north–south horizontal displacement, and east–west horizontal displacement during the satellite follow-up period. According to the LOS projection principle, the relationship between the LOS deformation, subsidence, and horizontal displacement can be obtained using Equation (17). Finally, these subsidences and horizontal displacements were transformed into theoretical LOS deformations, and the fusion of the “space–ground” data was completed. There were differences between the three-dimensional deformations (subsidence + horizontal displacement) and the LOS deformations, and Equations (18) and (19) were used as the fitness functions of the solver, respectively.
where W is the subsidence, UNS and UWE are the horizontal displacements in the north–south and east–west directions, respectively, and θINC and θAZI are the incident angle and azimuth angle of the satellite, respectively.
where WP and WM are the predicted and measured subsidences, respectively, UP and UM are the predicted and measured horizontal displacements, respectively, and NW and NU are the numbers of the subsidences and horizontal displacements.
where LosP and LosM are the predicted and measured LOS deformations, respectively, and NL is the number of the LOS deformation values.
2.3. LOS Deformation Correction of the DInSAR
When using DInSAR, the recovered deformation phase (DP) based on the phase unwrapping can be used to calculate an LOS deformation using Equation (20). However, in practical applications, when the deformation gradients of adjacent pixels are too large, phase unwrapping can lead to FCP losses, resulting in accurate DInSAR results only at the edge areas of a mining influence range [36,37]. Within a full mining impact range, to achieve precise monitoring, it is necessary to correct the LOS deformation of the DInSAR.
where λ is the radar wavelength and ΦDEF is the DP.
In the previous section, the “space–ground” data were fused to obtain the theoretical LOS deformation within the complete mining impact range, but the subsidence prediction model is only a theoretical model, and the predicted theoretical deformation differed from the actual deformation to some extent. Therefore, this theoretical deformation was only used as a correction benchmark.
It should be noted that, in solving the model parameters, the time interval was the number of mining days. In the LOS deformation correction, the single-phase DInSAR result was the basic unit, and the time interval was the satellite follow-up period. This was also the reason why the fusion results were the theoretical LOS deformations during the satellite follow-up period.
After transforming the theoretical LOS deformation to the DP using Equation (20), it and the one of DInSAR values could be split into two parts: an FCP and an NFCP. Compared to the DInSAR, the FCP of the data fusion had lower credibility and the NFCP had higher credibility. The essence of LOS deformation correction is to retain the NFCP of the DInSAR and replace the FCP with that of the data fusion.
As shown in Figure 4, when correcting, we first converted the theoretical LOS deformations of the data fusion into the DPs. Second, we divided the DPs of the data fusion and the DInSAR into FCPs and NFCPs, and the results were obtained using Equations (21) and (22). Third, after replacing with , the corrected DP was obtained using Equation (23). When a deformation did not exceed λ/2, there was no need to correct it. Thus, we added an additional phase recovery step. Finally, after the DPs during the follow-up period were accumulated and converted into LOS deformations, the correction was completed.
where and are the NFCP and FCP, respectively, of the DInSAR during the n-th satellite follow-up period.
where and are the NFCP and FCP, respectively, of the data fusion during the n-th satellite follow-up period.
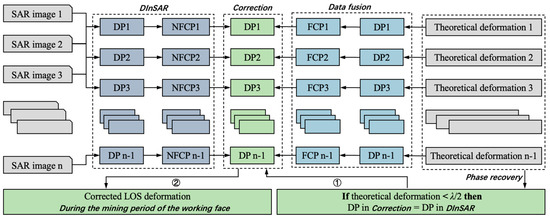
Figure 4.
Steps for LOS deformation correction.
3. Engineering Experiment
3.1. Experimental Area and Data
The experimental area was located in the Huainan Mining Area, Anhui Province, China, which is one of the five largest mining areas in China. The proven reserves are up to more than 40 billion tons, and the surface is rich in thick, loose layers. As shown in Figure 5, the mining on the working face started on 9 July 2019, with a mining direction of northwest to southeast and a mining speed of approximately 3.4 m/day. Compared to ZhaiMiao Village in GuQiao Town, which is located on the west side of the working face and has NFPs, there is farmland directly above the working face, and the AFPs need to be buried for monitoring. During the period of 9 July 2019 to 2 November of the same year, the “space–ground” data were used to obtain the surface deformations caused by mining.

Figure 5.
Overview of the experimental area.
Introduction to the ground data: The first measurement date was 9 July 2019, and the last measurement date was 25 October 2019. The measurement area and AFP positions are shown in Figure 5, and a total of five AFPs were deployed. The terrestrial laser scanner was an HD HS-650, the Dumpy level was a KLidar DL07, and the GNSS receiver was an HD V200. Starting from approximately 70 m away from the mining line, three TLS stations were set up along the mining direction, and the distance between each station was approximately 35 m. The distance between the AFPs as the starting points was approximately 15 m, and the distance between the remaining AFPs was approximately 50 m. CloudCompare was used to measure the subsidence and horizontal displacement calculations.
Introduction to the space data: From 9 July 2019 to 25 October 2019, 10 SAR images obtained from the Sentinel 1 satellite were employed. The main parameters of the SAR images used in the experiment are listed in Table 1. The DInSAR, which was implemented by GMTSAR, was used to obtain the LOS deformation measurement indicator, in which the precision orbital POD files, which were released 21 days after the SAR imaging, were used to attenuate the orbital phase error. The DEM used in the DInSAR was the 30 m resolution provided by NASA, and it was used to remove the reference terrain phase. The GACOS files provided by Newcastle University were used for the generic atmospheric correction.

Table 1.
Main parameters of the SAR images.
3.2. Results and Analysis of the Correction
Based on the geological mining experience of the site, 22 NFPs in the scanning area were selected for calculation measurement indexes. A total of 25 large deformations were obtained by combining the three AFPs (excluding the starting point), as shown in Figure 6. As shown in Figure 7, we plotted the LOS deformation of the DInSAR in the space data; a few monitoring points had low coherence and no deformation was obtained, so we plotted them after completing the distance-weighted interpolation.
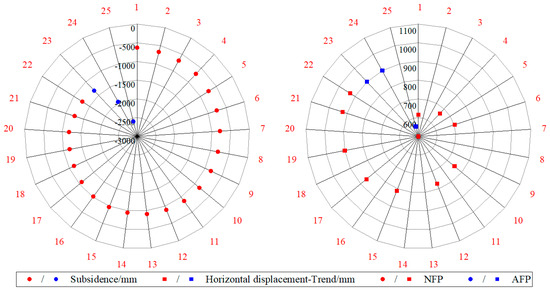
Figure 6.
Three-dimensional deformations in the ground data.
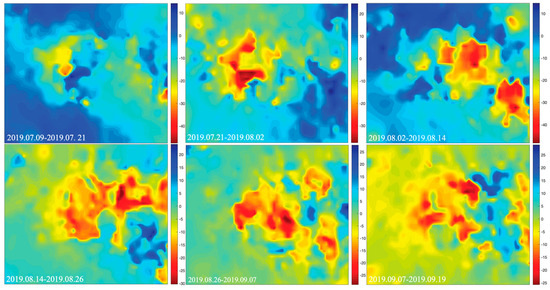
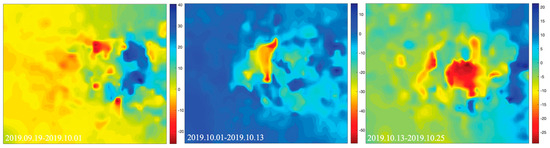
Figure 7.
LOS deformations of the DInSAR in the space data.
In the data fusion, a differential evolution algorithm was used as a model parameter solver [38]. Based on the correction benchmark established by the fusion (as shown in Figure 8), the corrected LOS deformation during the satellite follow-up period was obtained, as shown in Figure 9. In combination with Figure 6, it can be seen that before and after the correction, the trend of the central area of the mining influence area gradually moved to the southeast and the mining of the working face had not changed. However, after the fusion, the LOS deformation in the center area reached the maximum value under the geological and mining conditions. In addition, the deformation after fusion conformed to the asymmetry phenomenon in the advancing process of the working face, and it retained the difference in the LOS deformation at the edge of the deformed basin.
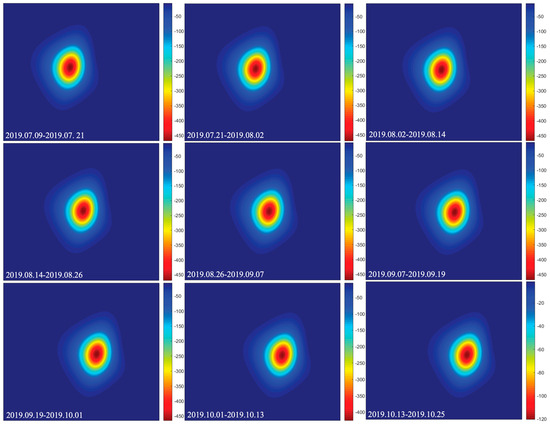
Figure 8.
LOS deformations of the data fusion in the space data.
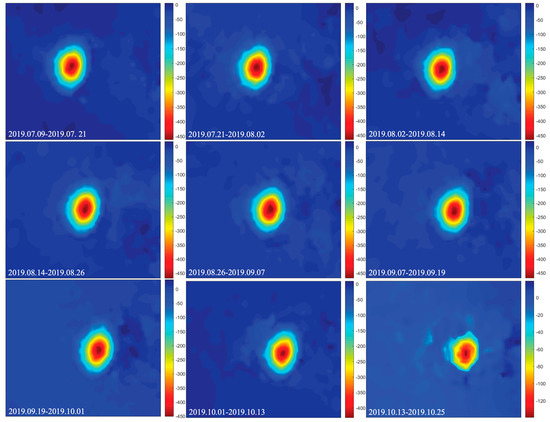
Figure 9.
LOS deformations after correction in the space data.
For verifying the correction accuracy, two observation lines were laid along the trend and tendency of the working face, as shown in Figure 5. After the three-dimensional deformations of the AFPs were converted to LOS deformations, the differences between the measurement values and the correction values were used as the indexes for verification. Since the coordinates of the AFPs and the DInSAR monitoring points were not uniform, four DInSAR monitoring points adjacent to each AFP were selected, and the corrected LOS deformations of the AFPs were obtained using the distance-weighted interpolation method. The coherence of the monitoring points in the rectangular region was low and the LOS deformation was not obtained, and so the AFPs in the region did not participate in the verification.
The accumulated LOS deformations and the correction accuracy are shown in Figure 10. Using the differences in the LOS deformations before and after the correction as the verification indicators, the maximum absolute value of the errors after correction was 143 mm, which was approximately 6.4% of the maximum LOS deformation. In addition, there were still two large errors (−112 mm and −89 mm), and the absolute values of the errors were not more than 75 mm. For all errors, the mean absolute value was 36 mm. Compared with the value of 399 mm before the correction, the error was reduced by 91%.
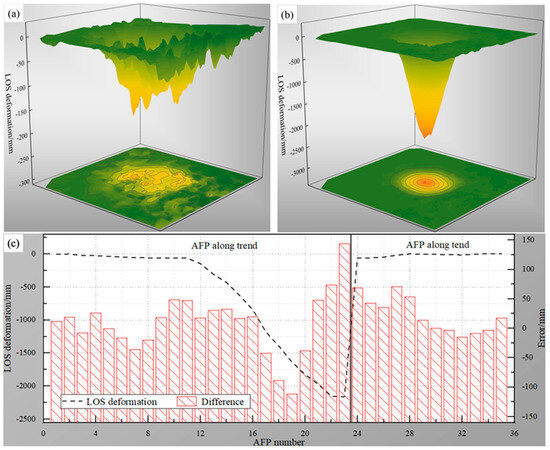
Figure 10.
Accumulated LOS deformations and the correction accuracy: (a) LOS deformations before correction; (b) LOS deformations after correction; and (c) LOS deformations and correction accuracies.
4. Discussion
4.1. Simulation Experiment Verification of the Data Fusion
In this study, the subsidence prediction model was used for the fusion of the “space–ground” data. In the LOS deformation simulation of the full mining influence area, the above BPM-EKTF subsidence prediction model was used. In order to simulate the inconsistency between the real surface deformation and the theoretical deformation predicted by the model, the LOS deformation was the combination of the two theoretical predicted deformations, and the combination ratio was 9:1. The relevant parameters are shown in Table 2. And, simulated LOS deformation is shown in Figure 11.

Table 2.
Relevant parameters in simulation experiment.
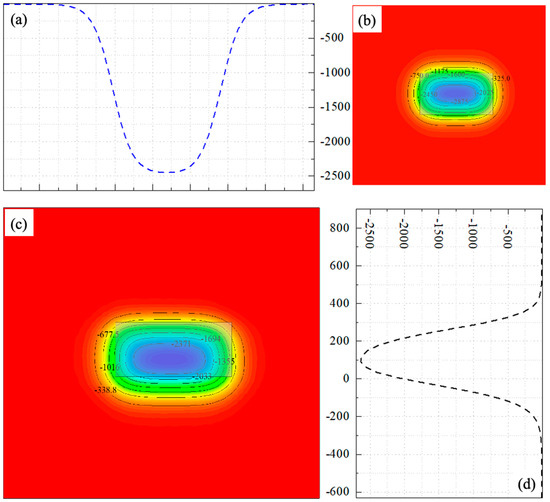
Figure 11.
Simulated deformations: (a) LOS deformations along the trend (mm), (b) subsidence (mm), (c) LOS deformations (mm), and (d) LOS deformations along the tendency (mm).
The existence of phase loss makes it possible for the Sentinel 1 satellite to have confidence only when the absolute value of an LOS deformation does not exceed 27.73 mm during the satellite follow-up period. In the space data simulation, only those values larger than −27.73 mm were selected for each period. Moreover, for simulating the data error, a random number ranging from −2 mm to 2 mm was added. In the ground data simulation, we deployed 21 simulated NFPs/AFPs along the trend from −50 m to 250 m on the left side of the working face mining line. For simulating the data error, random numbers ranging from −20 mm to 20 mm were added to the simulated subsidence and horizontal displacements of the NFPs and AFPs, respectively.
In this section, the LOS deformation differences between the fusion data and the simulation are used as the verification indexes. Combining the single-source data with the subsidence prediction model, the LOS deformations in the mining influence area could also be obtained. Therefore, verification indexes using only the space or ground data are also given. As can be seen in Figure 12, when only the space data were used, the errors were symmetrical along the direction of the working face. However, without the constraint of a large deformation in the non-edge region, the maximum absolute value of the errors was approximately 522 mm, which seriously deviated from the simulated LOS deformation. When using only the space data, due to the missing deformation on one side of the mined face, the theoretical deformation predicted by the model did not comply with the basic principles of the mining subsidence. Although the errors had decreased, the maximum absolute value was still as high as 383 mm. After fusion, the errors were symmetrical along the direction of the working face. The errors were effectively reduced, with a maximum absolute value of approximately 140 mm. Compared with the absolute mean errors of only using the space and ground data (37 mm and 29 mm, respectively) the mean absolute error after the data fusion was 16 mm, which reduced the errors by 56% and 45%, respectively. In addition, we also discussed the extension possibilities of the application scenarios and the correction strategies.

Figure 12.
Data fusion results of the simulation experiment: (a) differences in the data fusion (mm), (b) differences using only the space data (mm), (c) differences using only the ground data (mm), (d) differences along the trends (mm), and (e) differences along the tendencies (mm).
4.2. Possibility Analysis of the Method Extensions
This study proposed an LOS deformation correction method using DInSAR in a mining area by fusing the ground data without control points. However, due to experimental limitations, the extensible aspects of this method have not been described. Therefore, we discussed the following two aspects:
- Extension of the application scenarios
In the ground data, it was challenging to find points with the same name in the elevation from the cylinder, causing the tree trunks to be applied only for extracting the horizontal displacement. Additionally, most of the tree trunks were not suitable due to the requirement of being perpendicular to the ground. This was the reason why the data acquisition methods could not be used where building clusters did not exist. In recent research, Sun et al. [39] extracted the cross-sectional information of the tank, including the circle’s center within each cross-section. As shown in Figure 13, both the tree trunk and the tank belonged to cylinders. By utilizing this approach, the circle centers within various cross-sections could be used to fit a straight line that represented the inclination of a tree trunk. When combined with the ground point cloud, the circle center where the tree trunk connected with the ground could be determined, allowing for the simultaneous calculations of the subsidence and horizontal displacement. Consequently, the application scenarios of this method were extended.

Figure 13.
The forests and their point clouds: (a) forests in the mining area. (b) point clouds in the forest; the tree trunks are in green, and the DTM reconstructed based on ground points is brown [30].
- Extension of the correction strategies
In the LOS deformation correction, the missing large deformation in the DInSAR was recovered by replacing the FCP of the DInSAR with that of the data fusion. Recovering the lost FCP by unwrapping is a more systematic approach. To recover the lost LOS deformation, Jiang et al. [40] converted the theoretical deformation obtained by the “LOS deformation of DInSAR + subsidence prediction model” into a wrapped DP, and they removed it from the interferometric phase and unwrapped it again. Jiang et al. [26] adopted the same approach to extract large-gradient three-dimensional displacements in mining areas. However, they only used single-source space data. As shown in Figure 14, applying this approach to the method in this paper by utilizing the fused “space–ground” data may obtain better results.
Figure 14.
Extension strategy steps for the LOS deformation correction.
5. Conclusions
In this study, we proposed an LOS deformation correction method for DInSAR in mining areas by fusing ground data without control points. Based on free space data, small deformations iat the edge areas of the mining influence area were accurately obtained using DInSAR. By combining the leveling/GNSS and TLS methods, it was possible to obtain large deformations in the central area without the need for control points located outside the mining influence range. For overcoming the non-uniform coordinates of the “space–ground” data and the limited overlap of the effective measurement ranges, the subsidence prediction model was employed to assist in the fusion. In addition, in the LOS deformation correction, we retained the non-full cycle phase of the DInSAR and replaced the full cycle phase with that of the data fusion.
Engineering experiments showed that the correction results preserved the differences in the LOS deformations at the edge areas of the mine influence range, and we recovered the lost LOS deformation at the center area. Using the differences in the LOS deformations before and after correction as the verification indicators, the maximum absolute value of the errors after correction was 143 mm, which was approximately 6.4% of the maximum LOS deformation. In addition, there were still two large errors (−112 mm and −89 mm), and the absolute values of the errors were not more than 75 mm. For all the errors, the mean absolute value was 36 mm. Compared with the 399 mm value from before correction, the error was reduced by 91%.
In the discussion, the fusion of the “space–ground” data was verified based on the simulation experiments, and the LOS deformation differences between the fusion data and the simulation were used as the verification indexes. After fusion, the errors were symmetrical along the direction of the working face, and the errors had been effectively reduced, with a maximum absolute value of approximately 140 mm. Compared with the absolute mean error of only using the space and ground data (37 mm and 29 mm, respectively), the mean absolute error after the data fusion was 16 mm, which reduced the errors by 56% and 45%, respectively. In addition, we discussed the extension possibilities of the application scenarios and the correction strategies.
Author Contributions
Conceptualization, J.L.; methodology, J.L.; formal analysis, Y.Y. and J.C.; investigation, J.L.; resources, J.L.; writing—original draft, J.L.; writing—original review and editing, J.L., Y.Y. and J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51574242 (to Y.Y.) and the Fundamental Research Funds for the Central Universities, grant numbers 2022YJSDC20 and 2022YJSDC19 (to Y.Y.).
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the ESA/Copernicus for providing the Sentinel1A SAR images. The authors also thank all the reviewers for their valuable comments.
Conflicts of Interest
The authors declare that they have no competing interest.
References
- Yang, Q.; Tang, F.; Wang, F.; Tang, J.; Fan, Z.; Ma, T.; Su, Y.; Xue, J. A New Technical Pathway for Extracting High Accuracy Surface Deformation Information in Coal Mining Areas Using UAV LiDAR Data: An Example from the Yushen Mining Area in Western China. Measurement 2023, 218, 113220. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, X.; Wang, Y.; Wei, W.; Liu, B.; Jia, S.; Pang, T.; Bai, F.; Wei, Z. Long-Term Ground Multi-Level Deformation Fusion and Analysis Based on a Combination of Deformation Prior Fusion Model and OTD-InSAR for Longwall Mining Activity. Measurement 2020, 161, 107911. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, C.; Tomás, R.; Chen, L.; Yang, C.; Zhang, Y. Retrieving the Kinematic Process of Repeated-Mining-Induced Landslides by Fusing SAR/InSAR Displacement, Logistic Model, and Probability Integral Method. Remote Sens. 2023, 15, 3145. [Google Scholar] [CrossRef]
- Chi, S.; Wang, L.; Yu, X.; Lv, W.; Fang, X. Research on Dynamic Prediction Model of Surface Subsidence in Mining Areas with Thick Unconsolidated Layers. Energy Explor. Exploit. 2021, 39, 927–943. [Google Scholar] [CrossRef]
- Kong, D.; Pu, S.; Cheng, Z.; Wu, G.; Liu, Y. Coordinated Deformation Mechanism of the Top Coal and Filling Body of Gob-Side Entry Retaining in a Fully Mechanized Caving Face. Int. J. Geomech. 2021, 21, 04021030. [Google Scholar] [CrossRef]
- Pengtao, Z.; Haiqiao, W.; Long, W.; Xinlei, W.; Hongyu, M. Parameter Optimization of Constant Pressure Grouting Technology for Borehole Sealing with Inorganic Noncondensable Material in Tectonic Coalbed of South China. Geofluids 2023, 2023, 6053318. [Google Scholar] [CrossRef]
- Ma, S.; Qiu, H.; Yang, D.; Wang, J.; Zhu, Y.; Tang, B.; Sun, K.; Cao, M. Surface Multi-Hazard Effect of Underground Coal Mining. Landslides 2023, 20, 39–52. [Google Scholar] [CrossRef]
- Sevil, J.; Benito-Calvo, A.; Gutiérrez, F. Sinkhole Subsidence Monitoring Combining Terrestrial Laser Scanner and High-precision Levelling. Earth Surf. Process. Landforms 2021, 46, 1431–1444. [Google Scholar] [CrossRef]
- Jiang, N.; Li, H.; Hu, Y.; Zhang, J.; Dai, W.; Li, C.; Zhou, J.-W. A Monitoring Method Integrating Terrestrial Laser Scanning and Unmanned Aerial Vehicles for Different Landslide Deformation Patterns. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10242–10255. [Google Scholar] [CrossRef]
- Pawłuszek-Filipiak, K.; Wielgocka, N.; Tondaś, D.; Borkowski, A. Monitoring Nonlinear and Fast Deformation Caused by Underground Mining Exploitation Using Multi-Temporal Sentinel-1 Radar Interferometry and Corner Reflectors: Application, Validation and Processing Obstacles. Int. J. Digit. Earth 2023, 16, 251–271. [Google Scholar] [CrossRef]
- Gojković, Z.; Kilibarda, M.; Brajović, L.; Marjanović, M.; Milutinović, A.; Ganić, A. Ground Surface Subsidence Monitoring Using Sentinel-1 in the “Kostolac” Open Pit Coal Mine. Remote Sens. 2023, 15, 2519. [Google Scholar] [CrossRef]
- Manconi, A. How Phase Aliasing Limits Systematic Space-Borne DInSAR Monitoring and Failure Forecast of Alpine Landslides. Eng. Geol. 2021, 287, 106094. [Google Scholar] [CrossRef]
- Jiang, X.; Min, X.; Ye, T.; Li, X.; Hu, X. Monitoring the Subsidence at Different Periods in High Underground Water Level Coal Mine Areas Using Differential Interferometric Synthetic Aperture Radar (D-InSAR). Geocarto Int. 2023, 38, 2215730. [Google Scholar] [CrossRef]
- Monika; Govil, H.; Guha, S. Underground Mine Deformation Monitoring Using Synthetic Aperture Radar Technique: A Case Study of Rajgamar Coal Mine of Korba Chhattisgarh, India. J. Appl. Geophys. 2023, 209, 104899. [Google Scholar] [CrossRef]
- Kermarrec, G.; Lösler, M.; Guerrier, S.; Schön, S. The Variance Inflation Factor to Account for Correlations in Likelihood Ratio Tests: Deformation Analysis with Terrestrial Laser Scanners. J. Geod. 2022, 96, 86. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Huang, J. Wall Length-Based Deformation Monitoring Method of Brick-Concrete Buildings in Mining Area Using Terrestrial Laser Scanning. J. Civil Struct. Health Monit. 2023, 1–14. [Google Scholar] [CrossRef]
- Diao, X.; Wu, K.; Hu, D.; Li, L.; Zhou, D. Combining Differential SAR Interferometry and the Probability Integral Method for Three-Dimensional Deformation Monitoring of Mining Areas. Int. J. Remote Sens. 2016, 37, 5196–5212. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Preusse, A.; Yi, H.W.; Wang, Y.J.; Papst, M. An Extension of the InSAR-Based Probability Integral Method and Its Application for Predicting 3-D Mining-Induced Displacements Under Different Extraction Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3835–3845. [Google Scholar] [CrossRef]
- Wang, L.; Shangjun, Z.; Chuang, J.; Jingyu, L.; Kegui, J.; Chaoqun, T.; Tao, W.; Qing-biao, G. Research on 3D Laser Scanning Monitoring Method for Mining Subsidence Based on the Auxiliary for Probability Integral Method. KSCE J. Civ. Eng. 2021, 25, 4403–4416. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, L.; Yu, X.; Wei, T.; Chi, S.; Guo, Q. Prediction of 3D Deformation Due to Large Gradient Mining Subsidence Based on InSAR and Constraints of IDPIM Model. Int. J. Remote Sens. 2021, 42, 208–239. [Google Scholar] [CrossRef]
- Li, J.; Wang, L. Mining Subsidence Monitoring Model Based on BPM-EKTF and TLS and Its Application in Building Mining Damage Assessment. Environ. Earth Sci. 2021, 80, 396. [Google Scholar] [CrossRef]
- Hou, Z.; Yang, K.; Li, Y.; Gao, W.; Wang, S.; Ding, X.; Li, Y. Dynamic Prediction Model of Mining Subsidence Combined with D-InSAR Technical Parameter Inversion. Environ. Earth Sci. 2022, 81, 307. [Google Scholar] [CrossRef]
- Ding, X.; Yang, K.; Zhang, C.; Wang, S.; Hou, Z.; Zhao, H. Dynamic Prediction of Displacement and Deformation of Any Point on Mining Surface Based on B-Normal Model. Environ. Sci. Pollut. Res. 2023, 30, 78569–78597. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Li, M.; Dai, L.; Guo, J.; Dai, H.; Tang, W. Construction of “Space-Sky-Ground” Integrated Collaborative Monitoring Framework for Surface Deformation in Mining Area. Remote Sens. 2022, 14, 840. [Google Scholar] [CrossRef]
- Jiang, K.; Yang, K.; Zhang, Y.; Li, Y.; Li, T.; Zhao, X. An Extraction Method for Large Gradient Three-Dimensional Displacements of Mining Areas Using Single-Track InSAR, Boltzmann Function, and Subsidence Characteristics. Remote Sens. 2023, 15, 2946. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, Y.; Zhang, Y.; Zhang, W.; Kong, J.; Dai, A. Study on the Evolution Law of Overlying Strata Structure in Stope Based on “Space–Air–Ground” Integrated Monitoring Network and Discrete Element. Drones 2023, 7, 309. [Google Scholar] [CrossRef]
- Cheng, X.; Cheng, X.; Li, Q.; Ma, L. Automatic Registration of Terrestrial and Airborne Point Clouds Using Building Outline Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 628–638. [Google Scholar] [CrossRef]
- Zeng, F.; Li, L.; Wu, K. Extraction of Topographic Deformation Based on the 3D Information of Individual Trees. Int. J. Remote Sens. 2019, 40, 8668–8682. [Google Scholar] [CrossRef]
- Gu, Y.; Zhou, D.; Zhang, D.; Wu, K.; Zhou, B. Study on Subsidence Monitoring Technology Using Terrestrial 3D Laser Scanning without a Target in a Mining Area: An Example of Wangjiata Coal Mine, China. Bull. Eng. Geol. Environ. 2020, 79, 3575–3583. [Google Scholar] [CrossRef]
- Wang, X. GlobalMatch: Registration of Forest Terrestrial Point Clouds by Global Matching of Relative Stem Positions. ISPRS J. Photogramm. Remote Sens. 2023, 197, 71–86. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Chen, C.; Chang, B.; Li, Y.; Shi, B. Filtering Airborne LiDAR Point Clouds Based on a Scale-Irrelevant and Terrain-Adaptive Approach. Measurement 2021, 171, 108756. [Google Scholar] [CrossRef]
- Lian, X.; Dai, H.; Ge, L.; Cai, Y. Assessment of a House Affected by Ground Movement Using Terrestrial Laser Scanning and Numerical Modeling. Environ. Earth Sci. 2020, 79, 190. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Preusse, A.; Hu, J.; Feng, G.; Wang, Y.; Papst, M. An InSAR-Based Temporal Probability Integral Method and Its Application for Predicting Mining-Induced Dynamic Deformations and Assessing Progressive Damage to Surface Buildings. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 472–484. [Google Scholar] [CrossRef]
- Hu, Q.; Cui, X.; Liu, W.; Feng, R.; Ma, T.; Li, C. Quantitative and Dynamic Predictive Model for Mining-Induced Movement and Deformation of Overlying Strata. Eng. Geol. 2022, 311, 106876. [Google Scholar] [CrossRef]
- Maghsoudi, Y.; Hooper, A.J.; Wright, T.J.; Lazecky, M.; Ansari, H. Characterizing and Correcting Phase Biases in Short-Term, Multilooked Interferograms. Remote Sens. Environ. 2022, 275, 113022. [Google Scholar] [CrossRef]
- Olsen, K.M.; Calef, M.T.; Agram, P.S. Contextual Uncertainty Assessments for InSAR-Based Deformation Retrieval Using an Ensemble Approach. Remote Sens. Environ. 2023, 287, 113456. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Particle Swarm Optimization or Differential Evolution—A Comparison. Eng. Appl. Artif. Intell. 2023, 121, 106008. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Jin, F.; Li, Y.; Yang, Y. An Adaptive Cross-Section Extraction Algorithm for Deformation Analysis. Tunn. Undergr. Space Technol. 2022, 121, 104332. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, L.; Yu, X. Retrieving 3D Large Gradient Deformation Induced to Mining Subsidence Based on Fusion of Boltzmann Prediction Model and Single-Track InSAR Earth Observation Technology. IEEE Access 2021, 9, 87156–87172. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).