Learning-Based Optimization of Hyperspectral Band Selection for Classification
Abstract
:1. Introduction
- We introduce a constrained measurement learning network that learns a binary mask for band selection.
- The measurement learning network and the classification network are jointly learned to minimize the classification loss, leading to optimally selected bands directly for the classification task.
- The number of selected bands is an additional constraint for the measurement learning network, and the proposed architecture can learn binary masks for any desired number of bands.
- The proposed architecture is flexible enough to adapt a new classification network that takes selected bands as its input, meaning that any new back-propagation adaptable classification network that performs better compared to our proposed classification model can replace the classification part of the proposed architecture, leading to further improvements in the performance.
Abbreviations
2. Background and Related Work
2.1. Unsupervised Hyperspectral Band Selection
2.2. Supervised Hyperspectral Band Selection
2.3. Deep Neural Network-Based Measurement Learning
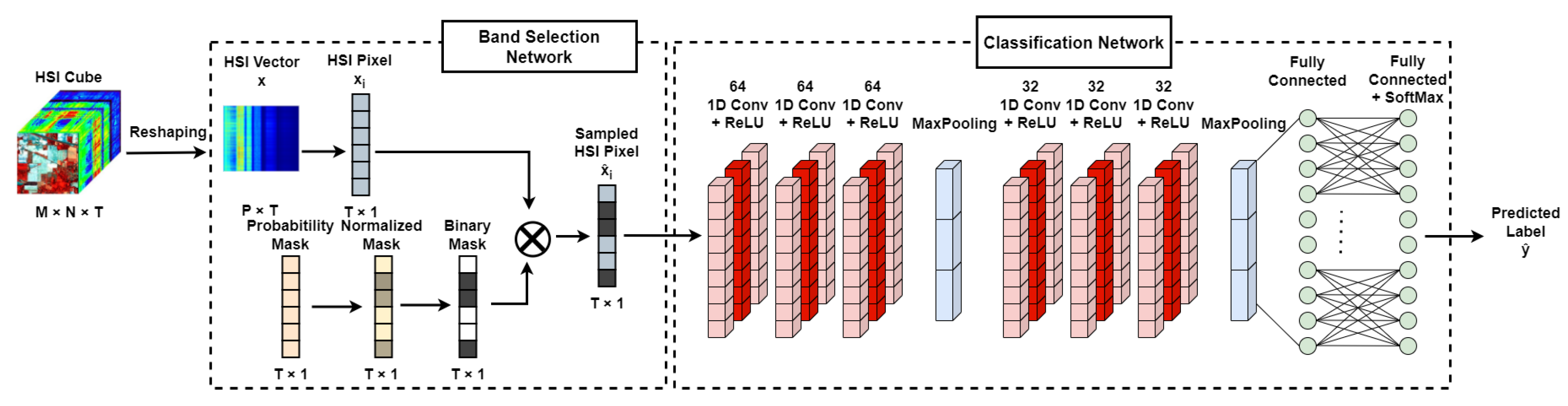
3. Proposed Method
3.1. Learning-Based Optimization of Band Selection Pattern
3.2. Classification Network
| Algorithm 1 MLBS Algorithm |
|
4. Datasets
5. Experimental Results
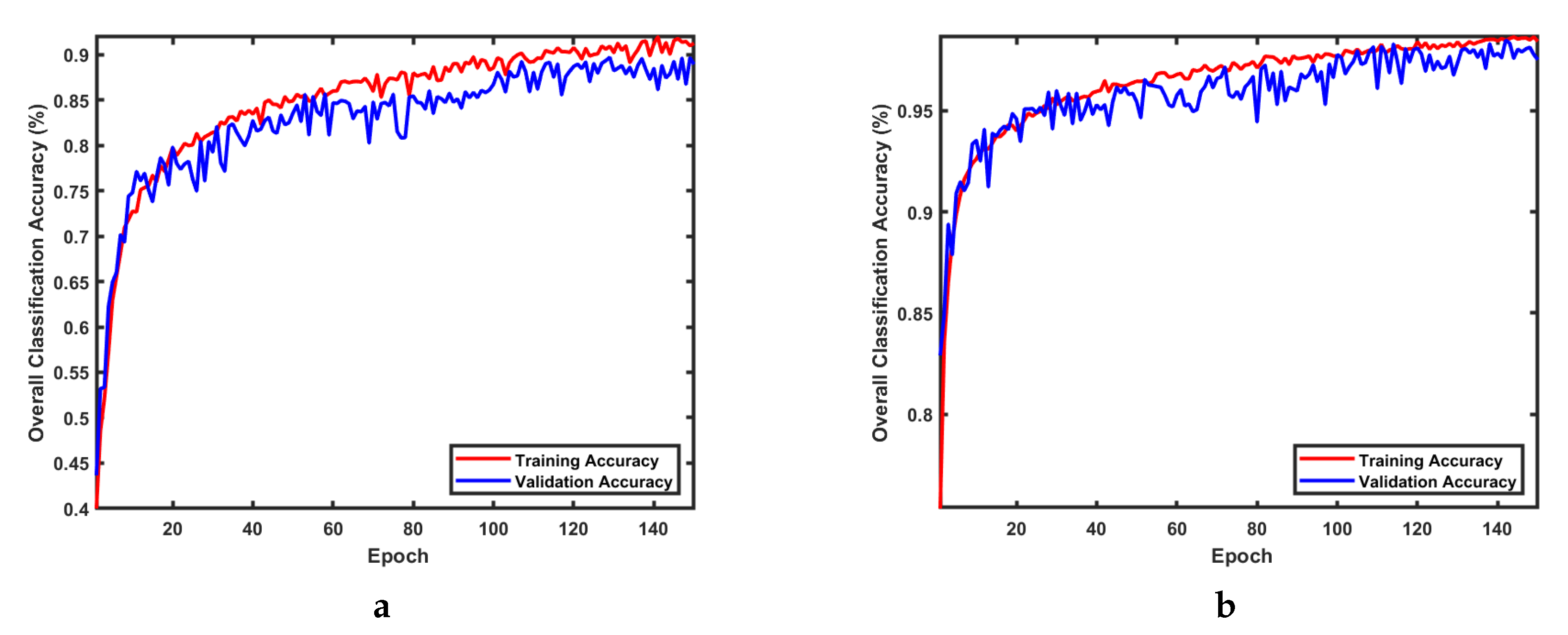
5.1. Experimental Setup
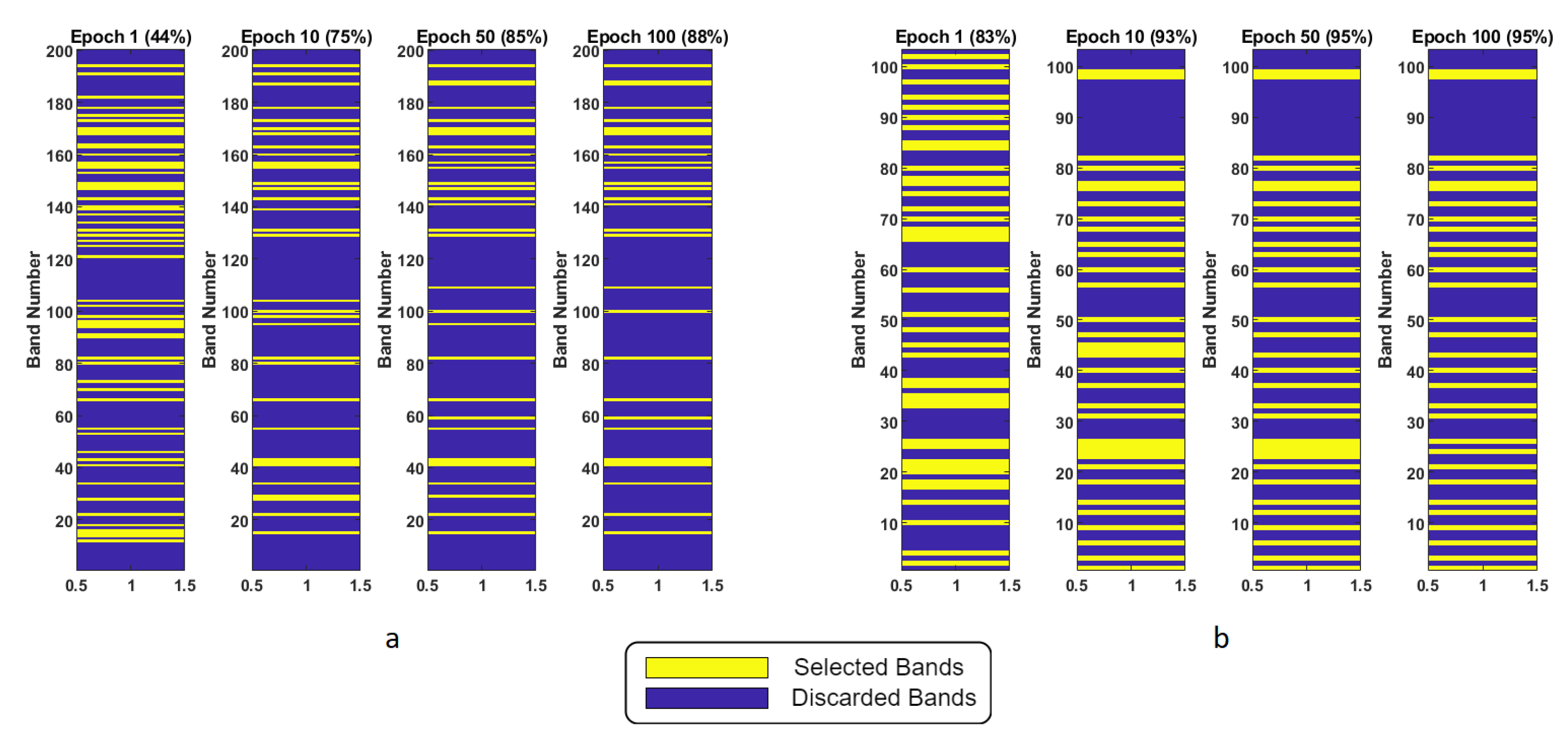
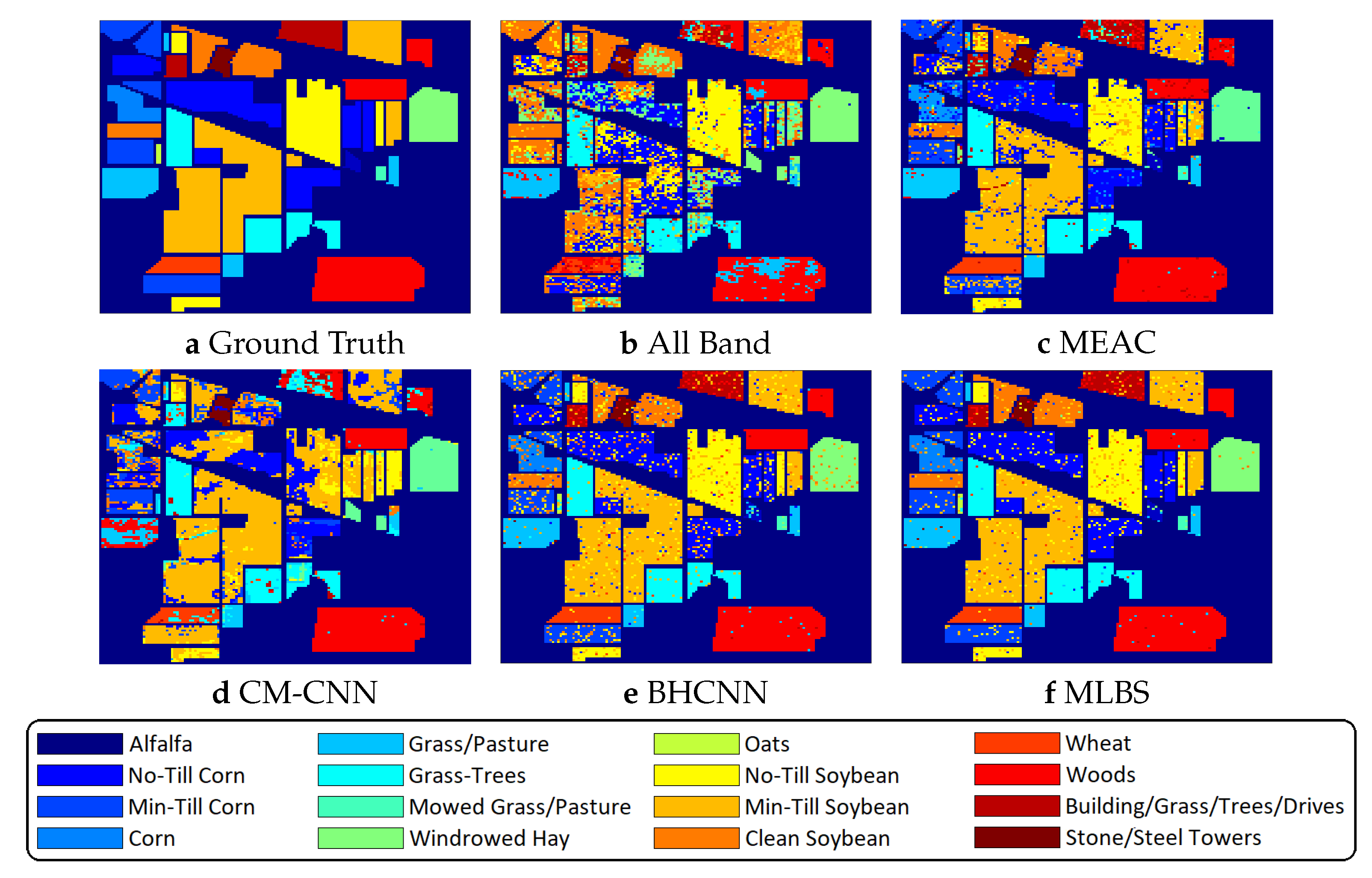
5.2. Joint Band Selection and Classification with MLBS
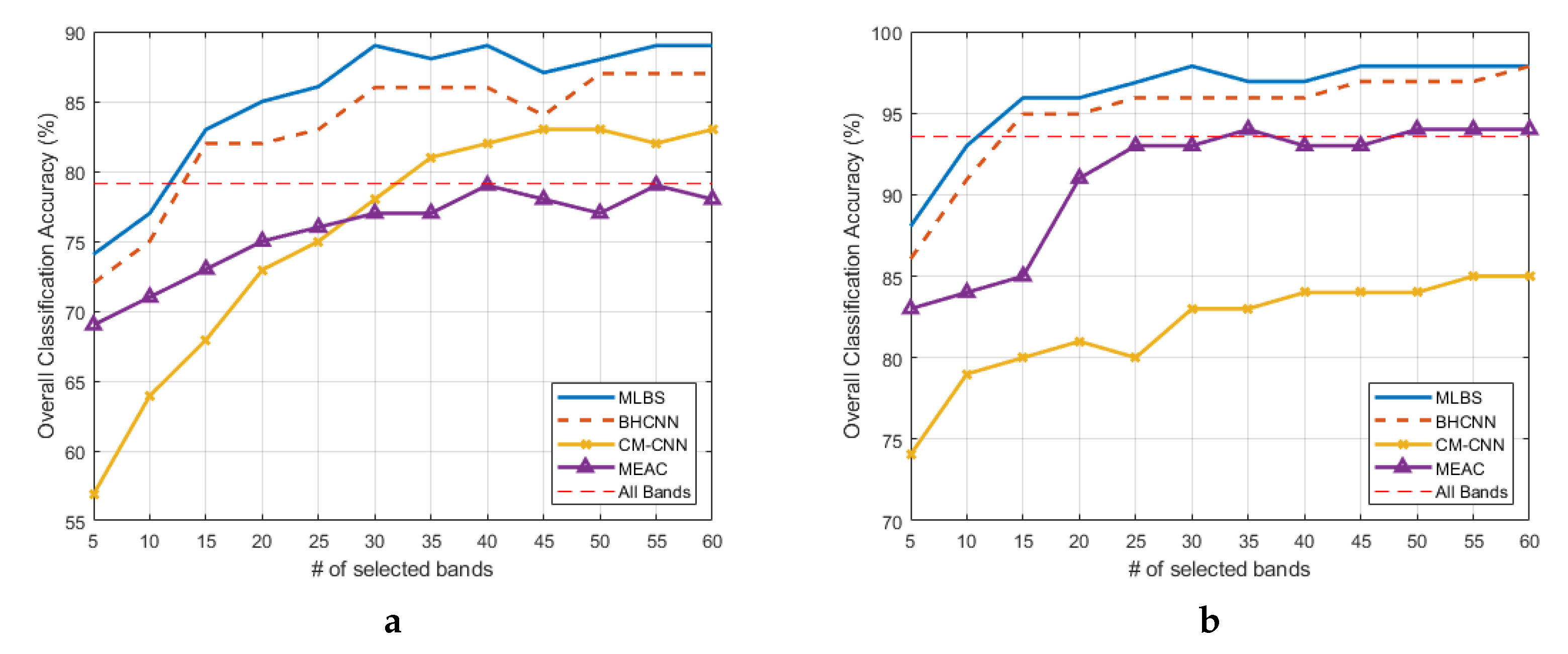
5.3. Quantitative Analysis and Comparisons
5.4. Computational Analysis
6. Discussion and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Yuen, P.W.; Richardson, M. An introduction to hyperspectral imaging and its application for security, surveillance and target acquisition. Imaging Sci. J. 2010, 58, 241–253. [Google Scholar] [CrossRef]
- Dale, L.M.; Thewis, A.; Boudry, C.; Rotar, I.; Dardenne, P.; Baeten, V.; Pierna, J.A.F. Hyperspectral imaging applications in agriculture and agro-food product quality and safety control: A review. Appl. Spectrosc. Rev. 2013, 48, 142–159. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Dopido, I.; Villa, A.; Plaza, A.; Gamba, P. A quantitative and comparative assessment of unmixing-based feature extraction techniques for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 421–435. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, J.; Huang, W. Attend in bands: Hyperspectral band weighting and selection for image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4712–4727. [Google Scholar] [CrossRef]
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Chang, C.I.; Liu, K.H. Progressive band selection of spectral unmixing for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2002–2017. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, J.; Yang, Y.; Kim, S.; Kim, H.S. Covariance-based band selection and its application to near-real-time hyperspectral target detection. Opt. Eng. 2017, 56, 053101. [Google Scholar] [CrossRef]
- Bajcsy, P.; Groves, P. Methodology for hyperspectral band selection. Photogramm. Eng. Remote Sens. 2004, 70, 793–802. [Google Scholar] [CrossRef]
- Chang, C.I.; Du, Q.; Sun, T.L.; Althouse, M.L. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Ifarraguerri, A.; Prairie, M.W. Visual method for spectral band selection. IEEE Geosci. Remote Sens. Lett. 2004, 1, 101–106. [Google Scholar] [CrossRef]
- He, Y.; Liu, D.; Yi, S. Recursive spectral similarity measure-based band selection for anomaly detection in hyperspectral imagery. J. Opt. 2010, 13, 015401. [Google Scholar] [CrossRef]
- Du, H.; Qi, H.; Wang, X.; Ramanath, R.; Snyder, W.E. Band selection using independent component analysis for hyperspectral image processing. In Proceedings of the 32nd Applied Imagery Pattern Recognition Workshop, Washington, DC, USA, 15–17 October 2003; pp. 93–98. [Google Scholar]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- MartÍnez-UsÓMartinez-Uso, A.; Pla, F.; Sotoca, J.M.; García-Sevilla, P. Clustering-based hyperspectral band selection using information measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Ahmad, M.; Haq, D.I.U.; Mushtaq, Q.; Sohaib, M. A new statistical approach for band clustering and band selection using K-means clustering. Int. J. Eng. Technol. 2011, 3, 606–614. [Google Scholar]
- Li, S.; Qiu, J.; Yang, X.; Liu, H.; Wan, D.; Zhu, Y. A novel approach to hyperspectral band selection based on spectral shape similarity analysis and fast branch and bound search. Eng. Appl. Artif. Intell. 2014, 27, 241–250. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhu, G.; Wang, Q. Hyperspectral band selection by multitask sparsity pursuit. IEEE Trans. Geosci. Remote Sens. 2014, 53, 631–644. [Google Scholar] [CrossRef]
- Du, Q.; Bioucas-Dias, J.M.; Plaza, A. Hyperspectral band selection using a collaborative sparse model. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3054–3057. [Google Scholar]
- Sun, W.; Zhang, L.; Du, B.; Li, W.; Lai, Y.M. Band selection using improved sparse subspace clustering for hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2784–2797. [Google Scholar] [CrossRef]
- Li, S.; Wu, H.; Wan, D.; Zhu, J. An effective feature selection method for hyperspectral image classification based on genetic algorithm and support vector machine. Knowl.-Based Syst. 2011, 24, 40–48. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A novel ranking-based clustering approach for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 88–102. [Google Scholar] [CrossRef]
- Sun, W.; Li, W.; Li, J.; Lai, Y.M. Band selection using sparse nonnegative matrix factorization with the thresholded earth’s mover distance for hyperspectral imagery classification. Earth Sci. Inform. 2015, 8, 907–918. [Google Scholar] [CrossRef]
- Tschannerl, J.; Ren, J.; Zabalza, J.; Marshall, S. Segmented autoencoders for unsupervised embedded hyperspectral band selection. In Proceedings of the 2018 7th European Workshop on Visual Information Processing (EUVIP), Tampere, Finland, 26–28 November 2018; pp. 1–6. [Google Scholar]
- Cai, R.; Yuan, Y.; Lu, X. Hyperspectral band selection with convolutional neural network. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Guangzhou, China, 23–26 November 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 396–408. [Google Scholar]
- Feng, J.; Chen, J.; Sun, Q.; Shang, R.; Cao, X.; Zhang, X.; Jiao, L. Convolutional neural network based on bandwise-independent convolution and hard thresholding for hyperspectral band selection. IEEE Trans. Cybern. 2020, 51, 4414–4428. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Du, Q.; Su, H.; Sheng, Y. An efficient method for supervised hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 2010, 8, 138–142. [Google Scholar] [CrossRef]
- Imbiriba, T.; Bermudez, J.C.M.; Richard, C.; Tourneret, J.Y. Band selection in RKHS for fast nonlinear unmixing of hyperspectral images. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 1651–1655. [Google Scholar]
- Feng, J.; Jiao, L.; Sun, T.; Liu, H.; Zhang, X. Multiple kernel learning based on discriminative kernel clustering for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6516–6530. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, H.; Bai, X.; Zhang, Z.; Zhou, J. Semi-supervised hyperspectral band selection via sparse linear regression and hypergraph models. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 1474–1477. [Google Scholar]
- Su, H.; Du, Q.; Chen, G.; Du, P. Optimized hyperspectral band selection using particle swarm optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2659–2670. [Google Scholar] [CrossRef]
- Ye, Z.; Cai, W.; Liu, S.; Liu, K.; Wang, M.; Zhou, W. A band selection approach for hyperspectral image based on a modified hybrid rice optimization algorithm. Symmetry 2022, 14, 1293. [Google Scholar] [CrossRef]
- Kavitha, K.; Jenifa, W. Feature selection method for classifying hyper spectral image based on particle swarm optimization. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 3–5 April 2018; pp. 119–123. [Google Scholar]
- Geng, X.; Sun, K.; Ji, L.; Zhao, Y. A fast volume-gradient-based band selection method for hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7111–7119. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A. A novel feature selection approach based on FODPSO and SVM. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2935–2947. [Google Scholar] [CrossRef]
- Wang, M.; Wan, Y.; Ye, Z.; Gao, X.; Lai, X. A band selection method for airborne hyperspectral image based on chaotic binary coded gravitational search algorithm. Neurocomputing 2018, 273, 57–67. [Google Scholar] [CrossRef]
- Archibald, R.; Fann, G. Feature selection and classification of hyperspectral images with support vector machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Khan, A.; Vibhute, A.D.; Mali, S.; Patil, C. A systematic review on hyperspectral imaging technology with a machine and deep learning methodology for agricultural applications. Ecol. Inform. 2022, 69, 101678. [Google Scholar] [CrossRef]
- Sharma, V.; Diba, A.; Tuytelaars, T.; Van Gool, L. Hyperspectral CNN for Image Classification & Band Selection, with Application to Face Recognition; Technical Report KUL/ESAT/PSI/1604; KU Leuven, ESAT: Leuven, Belgium, 2016. [Google Scholar]
- Zhan, Y.; Hu, D.; Xing, H.; Yu, X. Hyperspectral band selection based on deep convolutional neural network and distance density. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2365–2369. [Google Scholar] [CrossRef]
- Lorenzo, P.R.; Tulczyjew, L.; Marcinkiewicz, M.; Nalepa, J. Band selection from hyperspectral images using attention-based convolutional neural networks. arXiv 2018, arXiv:1811.02667. [Google Scholar]
- Shi, W.; Jiang, F.; Zhang, S.; Zhao, D. Deep Networks for Compressed Image Sensing. In Proceedings of the 2017 IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017. [Google Scholar]
- Mousavi, A.; Dasarathy, G.; Baraniuk, R.G. A Data-Driven and Distributed Approach to Sparse Signal Representation and Recovery. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Li, S.; Zhang, W.; Cui, Y.; Cheng, H.V.; Yu, W. Joint Design of Measurement Matrix and Sparse Support Recovery Method via Deep Auto-Encoder. IEEE Signal Process. Lett. 2019, 26, 1778–1782. [Google Scholar] [CrossRef]
- Mdrafi, R.; Gurbuz, A.C. Joint Learning of Measurement Matrix and Signal Reconstruction via Deep Learning. IEEE Trans. Comput. Imaging 2020, 6, 818–829. [Google Scholar] [CrossRef]
- Wu, S.; Dimakis, A.G.; Sanghavi, S.; Yu, F.X.; Holtmann-Rice, D.; Storcheus, D.; Rostamizadeh, A.; Kumar, S. Learning a Compressed Sensing Measurement Matrix via Gradient Unrolling. arXiv 2019, arXiv:1806.10175. [Google Scholar]
- Lohit, S.; Kulkarni, K.; Kerviche, R.; Turaga, P.; Ashok, A. Convolutional Neural Networks for Noniterative Reconstruction of Compressively Sensed Images. IEEE Trans. Comput. Imaging 2018, 4, 326–340. [Google Scholar] [CrossRef]
- Candès, E.; Romberg, J.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Comm. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef]
- MdRafi, R.; Gurbuz, A.C. Data Driven Learning of Constrained Measurement-Matrices for Signal Reconstruction. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 1591–1595. [Google Scholar]
- Mdrafi, R.; Gurbuz, A.C. Compressed Classification from Learned Measurements. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4038–4047. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical reparameterization with gumbel-softmax. arXiv 2016, arXiv:1611.01144. [Google Scholar]
- Maddison, C.J.; Mnih, A.; Teh, Y.W. The concrete distribution: A continuous relaxation of discrete random variables. arXiv 2016, arXiv:1611.00712. [Google Scholar]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Baumgardner, M.F.; Biehl, L.L.; Landgrebe, D.A. 220 band aviris hyperspectral image data set: June 12, 1992 indian pine test site 3. Purdue Univ. Res. Repos. 2015, 10, R7RX991C. [Google Scholar]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Measurement Learning-Based Band Selection (MLBS). 2023. Available online: https://github.com/msuimpress/mlbs_band_selection (accessed on 1 July 2023).
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Fuchs, M.H.P.; Demir, B. HySpecNet-11k: A Large-Scale Hyperspectral Dataset for Benchmarking Learning-Based Hyperspectral Image Compression Methods. arXiv 2023, arXiv:2306.00385. [Google Scholar]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- La Grassa, R.; Re, C.; Cremonese, G.; Gallo, I. Hyperspectral data compression using fully convolutional autoencoder. Remote Sens. 2022, 14, 2472. [Google Scholar] [CrossRef]
- Kuester, J.; Gross, W.; Schreiner, S.; Heizmann, M.; Middelmann, W. Transferability of convolutional autoencoder model for lossy compression to unknown hyperspectral prisma data. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–5. [Google Scholar]
- Patel, H.; Upla, K.P. A shallow network for hyperspectral image classification using an autoencoder with convolutional neural network. Multimed. Tools Appl. 2022, 81, 695–714. [Google Scholar] [CrossRef]
- He, K.; Sun, W.; Yang, G.; Meng, X.; Ren, K.; Peng, J.; Du, Q. A dual global–local attention network for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5527613. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Q.; Du, B.; Zhang, L. Weighted feature fusion of convolutional neural network and graph attention network for hyperspectral image classification. IEEE Trans. Image Process. 2022, 31, 1559–1572. [Google Scholar] [CrossRef] [PubMed]

| Method | HBS Approach | Category | Brief Description of the Strategy |
|---|---|---|---|
| MVPCA [11] | Unsupervised | Ranking-based | PCA-based ranking and high order selection |
| FDPC [23] | Unsupervised | Clustering-based | Distance clustering and density peak selection |
| WaluDI [16] | Unsupervised | Clustering-based | Information clustering and minmax optimization |
| ISSC [21] | Unsupervised | Sparsity-based | Domain transform and orthogonal rank search with L2-norm optimization |
| S-AEBS [25] | Unsupervised | Learning-based | Neural network-based autoencoder training and selecting highest contributing bands |
| MMCA [11] | Supervised | Ranking-based | Iterative band reduction with respect to misclassification error minimization |
| MEAC [28] | Supervised | Search-based | Iterative band selection with respect to covariance minimization |
| CM-CNN [26] | Supervised | Learning-based | Attention map generation with a neural network and selecting highest contributing bands |
| BHCNN [27] | Supervised | Learning-based | Band selection with hard tresholding, learning theshold jointly with HSI classification |
| Class Name | Method | ||||
|---|---|---|---|---|---|
| MEAC | BHCNN | CM-CNN | MLBS | All Bands | |
| Alfalfa | 76.47 | 69.05 | 65.22 | 70.39 | 36.59 |
| No-till corn | 71.24 | 76.92 | 70.31 | 78.43 | 75.41 |
| Minimal-till corn | 63.67 | 70.69 | 63.86 | 72.14 | 66.8 |
| Corn | 64.04 | 71.23 | 58.02 | 65.16 | 59.14 |
| Grass/pasture | 90.61 | 87.44 | 88.13 | 90.21 | 82.53 |
| Grass/trees | 94.34 | 97.54 | 97.21 | 98.08 | 96.04 |
| Mowed grass/pasture | 80.95 | 88.61 | 82.39 | 86 | 56 |
| Windrowed hay | 97.49 | 98.65 | 96.54 | 99.05 | 98.61 |
| Oats | 53.33 | 57.76 | 52.49 | 63.05 | 38.89 |
| No-till soybeans | 70.78 | 79.37 | 76.56 | 81.98 | 66.4 |
| Minimal-till soybean | 80.39 | 83.29 | 79.22 | 84.56 | 80.76 |
| Clean soybean | 64.49 | 84.08 | 81.63 | 86.34 | 69.85 |
| Wheat | 98.70 | 96.86 | 96.37 | 97.23 | 98.91 |
| Woods | 93.36 | 97.47 | 96.89 | 98.15 | 94.38 |
| Buildings/grass/trees/drives | 55.17 | 58.83 | 55.08 | 62.03 | 52.74 |
| Stone/steel towers | 94.29 | 92.49 | 85.44 | 93.34 | 89.29 |
| ACA | 78.08 | 81.89 | 77.84 | 82.88 | 72.65 |
| OCA | 78.90 | 87.74 | 78.06 | 89.08 | 79.12 |
| KC | 75.93 | 80.41 | 77.56 | 81.14 | 76.05 |
| Class Name | Method | ||||
|---|---|---|---|---|---|
| MEAC | BHCNN | CM-CNN | MLBS | All Bands | |
| Asphalt | 92.86 | 94.49 | 84.43 | 95.2 | 91.62 |
| Meadows | 96.43 | 98.28 | 97.31 | 98.65 | 98.16 |
| Gravel | 78.61 | 80.31 | 65.85 | 82.04 | 77.27 |
| Trees | 93.55 | 94.83 | 86.02 | 95.42 | 89.75 |
| Painted Metal Sheets | 99.59 | 99.38 | 93.43 | 99.03 | 98.95 |
| Bare Soil | 84.11 | 89.57 | 79.03 | 91.76 | 90.14 |
| Bitumen | 83.21 | 88.95 | 72.56 | 87.96 | 85.38 |
| Self-blocking Bricks | 84.70 | 92.78 | 72.89 | 93.85 | 90.2 |
| Shadows | 99.30 | 100 | 89.92 | 100 | 99.89 |
| ACA | 90.26 | 93.17 | 82.38 | 93.77 | 91.26 |
| OCA | 92.09 | 95.59 | 83.32 | 97.78 | 93.56 |
| KC | 89.49 | 93.55 | 87.46 | 93.21 | 91.42 |
| Dataset | Method | ||||
|---|---|---|---|---|---|
| MEAC | CM-CNN | BHCNN | MLBS | ||
| IP | Training | 1278 | 1275 s | 1293 s | 1216 s |
| Inference | 0.0904 s | 0.1406 | 0.1093 s | 0.0937 s | |
| UP | Training | 4959 s | 4877 s | 5625 s | 5050 s |
| Inference | 0.1099 s | 0.1939 s | 0.1406 s | 0.1249 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayna, C.O.; Mdrafi, R.; Du, Q.; Gurbuz, A.C. Learning-Based Optimization of Hyperspectral Band Selection for Classification. Remote Sens. 2023, 15, 4460. https://doi.org/10.3390/rs15184460
Ayna CO, Mdrafi R, Du Q, Gurbuz AC. Learning-Based Optimization of Hyperspectral Band Selection for Classification. Remote Sensing. 2023; 15(18):4460. https://doi.org/10.3390/rs15184460
Chicago/Turabian StyleAyna, Cemre Omer, Robiulhossain Mdrafi, Qian Du, and Ali Cafer Gurbuz. 2023. "Learning-Based Optimization of Hyperspectral Band Selection for Classification" Remote Sensing 15, no. 18: 4460. https://doi.org/10.3390/rs15184460
APA StyleAyna, C. O., Mdrafi, R., Du, Q., & Gurbuz, A. C. (2023). Learning-Based Optimization of Hyperspectral Band Selection for Classification. Remote Sensing, 15(18), 4460. https://doi.org/10.3390/rs15184460








