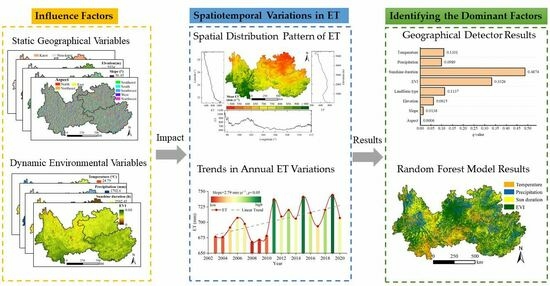
Spatiotemporal Variations in Evapotranspiration and Their Driving Factors in Southwest China between 2003 and 2020
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition and Processing
2.2.1. PML-V2 ET Data Product
2.2.2. Static Geographical Variables
2.2.3. Dynamic Environmental Variables
2.3. Data Analysis Methods
2.3.1. Trend Analysis
2.3.2. Geographical Detector
2.3.3. Partial Correlation Analysis
2.3.4. Random Forest Model
3. Results
3.1. Temporal and Spatial Distribution of ET
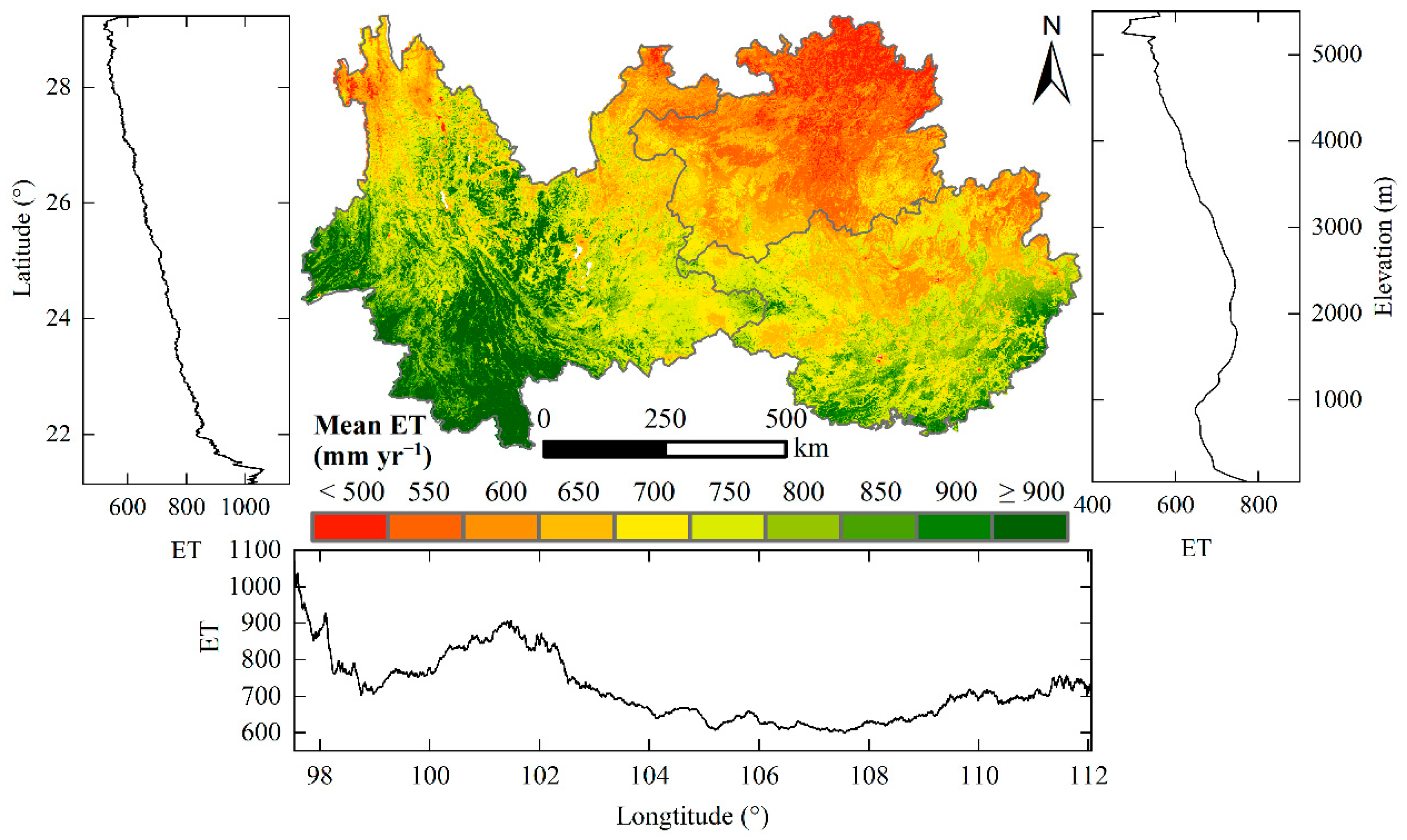
3.1.1. Spatial Distribution Pattern of ET
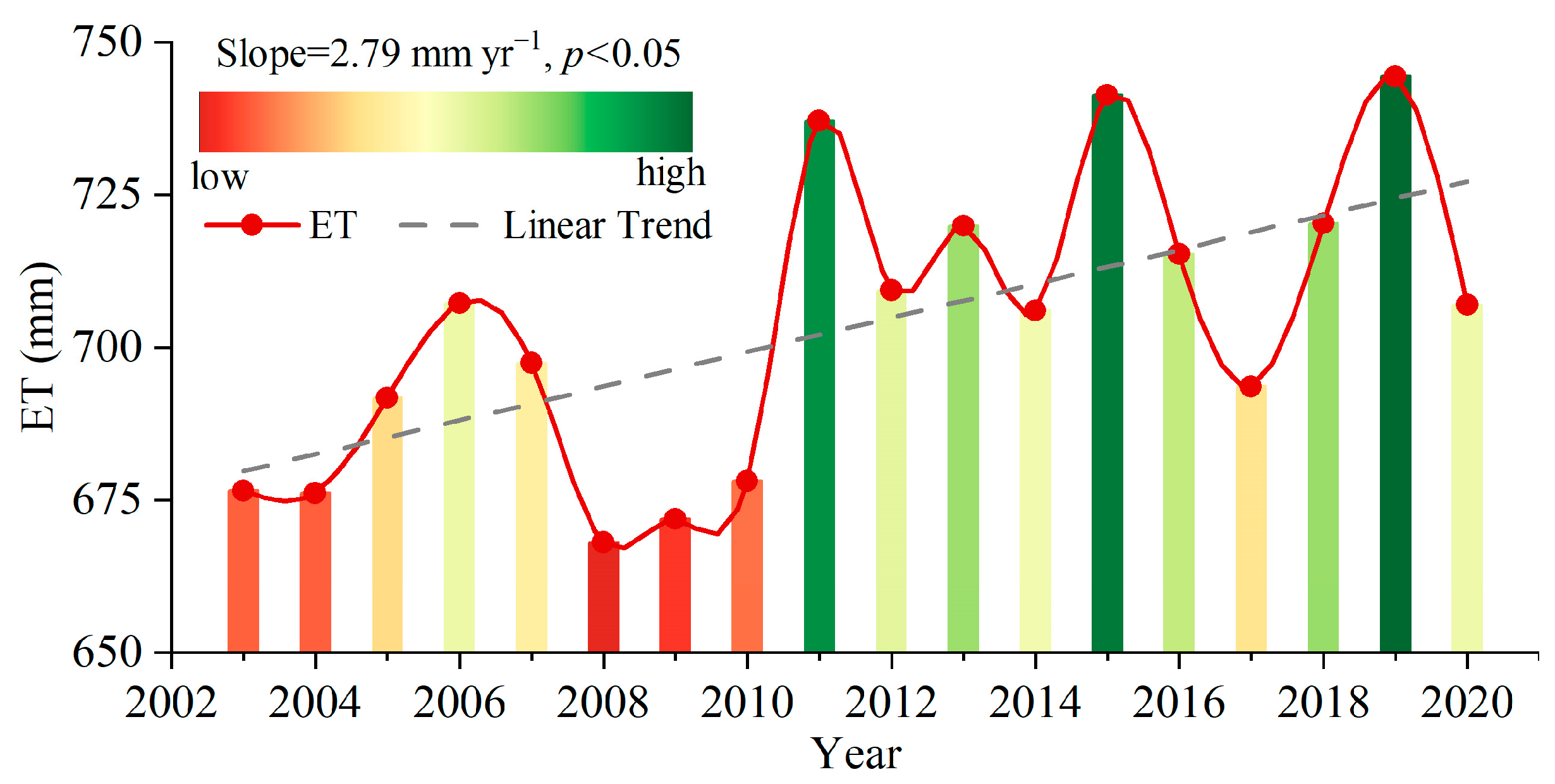
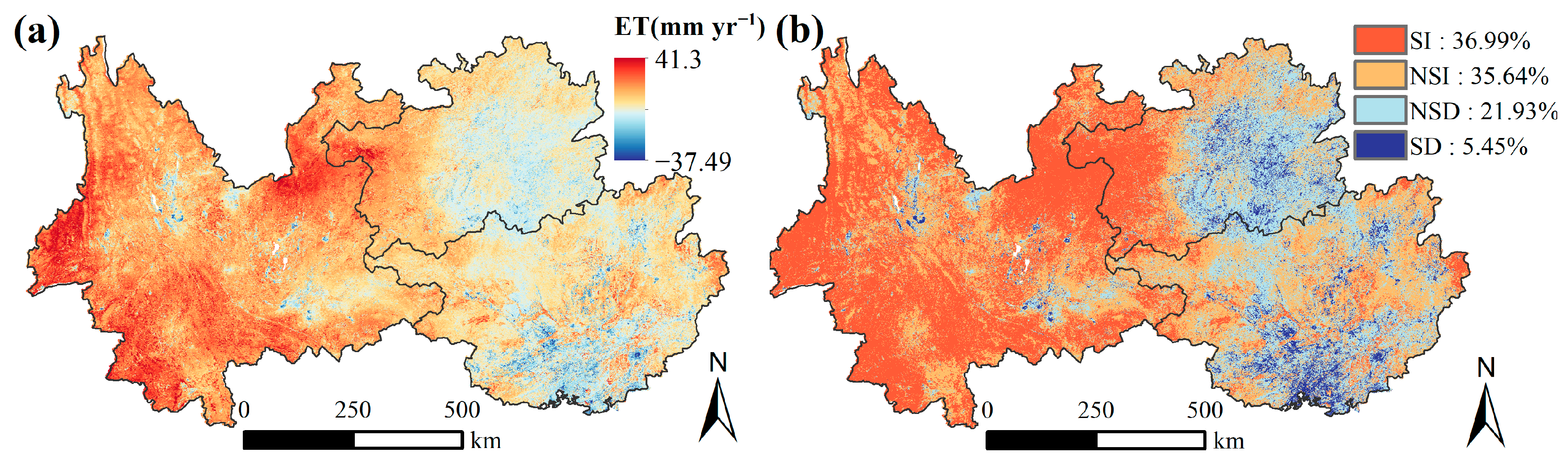
3.1.2. Trends in Annual ET Variations
3.2. Analysis of Geographical Detector Results
3.2.1. Independent Effects of Each Influencing Factor on Spatial Distribution Pattern of ET
3.2.2. Effects of Interaction between Influencing Factors on Spatial Distribution Pattern of ET
3.3. Partial Correlation Analysis Results
3.4. Analysis of Random Forest Model Results
4. Discussion
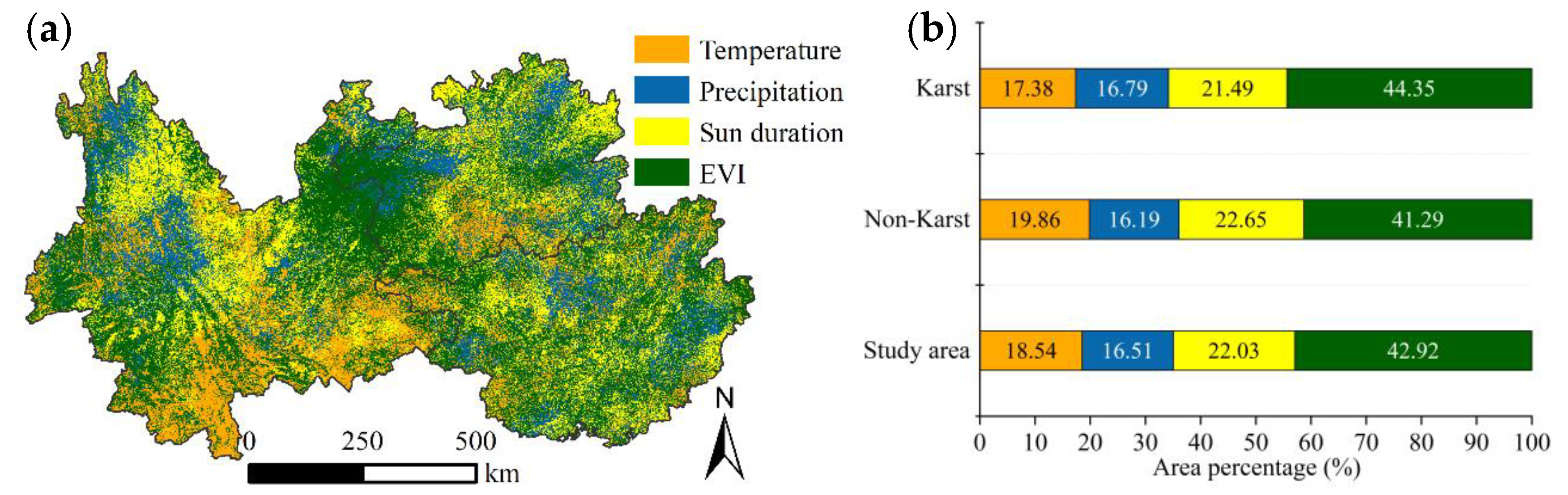
4.1. Key Factors Affecting Spatial Distribution Pattern of ET in Southwest China
4.2. Dominant Factors of ET Variations in Southwest China
4.3. Potential Inaccuracies, Limitations, and Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Oki, T.; Kanae, S. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. Causes of changes in actual evapotranspiration and terrestrial water storage over the Eurasian inland basins. Hydrol. Process. 2022, 36, e14482. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Yang, K.; Wang, C.; Walter, B.A.; Crétaux, J.-F. Lake storage variation on the endorheic Tibetan Plateau and its attribution to climate change since the new millennium. Environ. Res. Lett. 2018, 13, 064011. [Google Scholar] [CrossRef]
- Zhang, Y.; He, B.; Guo, L.; Liu, J.; Xie, X. The relative contributions of precipitation, evapotranspiration, and runoff to terrestrial water storage changes across 168 river basins. J. Hydrol. 2019, 579, 124194. [Google Scholar] [CrossRef]
- Cao, G.; Han, D.; Song, X. Evaluating actual evapotranspiration and impacts of groundwater storage change in the North China Plain. Hydrol. Process. 2014, 28, 1797–1808. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Hao, X.; Yue, P. Changes in Evapotranspiration Over Global Semiarid Regions 1984–2013. J. Geophys. Res. Atmos. 2019, 124, 2946–2963. [Google Scholar] [CrossRef]
- Liu, M.; Xu, X.; Wang, D.; Sun, A.Y.; Wang, K. Karst catchments exhibited higher degradation stress from climate change than the non-karst catchments in southwest China: An ecohydrological perspective. J. Hydrol. 2016, 535, 173–180. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W.; Hong, Y.; Gourley, J.J.; Yu, Z. Vegetation Greening and Climate Change Promote Multidecadal Rises of Global Land Evapotranspiration. Sci. Rep. 2015, 5, 15956. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef]
- Zeng, Z.; Piao, S.; Lin, X.; Yin, G.; Peng, S.; Ciais, P.; Myneni, R.B. Global evapotranspiration over the past three decades: Estimation based on the water balance equation combined with empirical models. Environ. Res. Lett. 2012, 7, 014026. [Google Scholar] [CrossRef]
- Tabari, H.; Hosseinzadeh Talaee, P. Sensitivity of evapotranspiration to climatic change in different climates. Glob. Planet. Chang. 2014, 115, 16–23. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Zhang, L.; Zhang, Q.; Gan, R.; Li, X. Attribution of Evapotranspiration Changes in Humid Regions of China from 1982 to 2016. J. Geophys. Res. Atmos. 2020, 125, e2020JD032404. [Google Scholar] [CrossRef]
- Mingyue, C.; Junbang, W.; Shaoqiang, W.; Hao, Y.; Yingnian, L. Temporal and Spatial Distribution of Evapotranspiration and Its Influencing Factors on Qinghai-Tibet Plateau from 1982 to 2014. J. Resour. Ecol. 2019, 10, 213–224. [Google Scholar]
- Ma, N.; Zhang, Y. Increasing Tibetan Plateau terrestrial evapotranspiration primarily driven by precipitation. Agric. For. Meteorol. 2022, 317, 108887. [Google Scholar] [CrossRef]
- Gao, X.; Sun, M.; Luan, Q.; Zhao, X.; Wang, J.; He, G.; Zhao, Y. The spatial and temporal evolution of the actual evapotranspiration based on the remote sensing method in the Loess Plateau. Sci. Total Environ. 2020, 708, 135111. [Google Scholar] [CrossRef]
- Jin, Z.; Liang, W.; Yang, Y.; Zhang, W.; Yan, J.; Chen, X.; Li, S.; Mo, X. Separating Vegetation Greening and Climate Change Controls on Evapotranspiration trend over the Loess Plateau. Sci. Rep. 2017, 7, 8191. [Google Scholar] [CrossRef]
- Trancoso, R.; Larsen, J.R.; McAlpine, C.; McVicar, T.R.; Phinn, S. Linking the Budyko framework and the Dunne diagram. J. Hydrol. 2016, 535, 581–597. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Van Niel, T.G. Less bluster ahead? Ecohydrological implications of global trends of terrestrial near-surface wind speeds. Ecohydrology 2012, 5, 381–388. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhu, A.X.; Yan, W.; Sun, Z. Impacts of forestland vegetation restoration on soil moisture content in humid karst region: A case study on a limestone slope. Ecol. Eng. 2022, 180, 106648. [Google Scholar] [CrossRef]
- Du, H.; Zeng, F.; Song, T.; Liu, K.; Wang, K.; Liu, M. Water depletion of climax forests over humid karst terrain: Patterns, controlling factors and implications. Agric. Water Manag. 2021, 244, 106541. [Google Scholar] [CrossRef]
- Jiang, S.Z.; Liang, C.; Cui, N.B.; Zhao, L.; Du, T.S.; Hu, X.T.; Feng, Y.; Guan, J.; Feng, Y. Impacts of climatic variables on reference evapotranspiration during growing season in Southwest China. Agric. Water Manag. 2019, 216, 365–378. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Gong, D.; Zhang, K. Spatiotemporal variation of reference evapotranspiration during 1954–2013 in Southwest China. Quat. Int. 2017, 441, 129–139. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Bai, X.; Tang, H.; Cao, Y.; Wang, M.; Wu, L. Inversion and spatiotemporal evolution of actual evapotranspiration in southwest China for the past 50 years. Acta Ecol. Sin 2018, 38, 8835–8848. [Google Scholar]
- Liu, Y.; Lian, J.; Luo, Z.; Chen, H. Spatiotemporal variations in evapotranspiration and transpiration fraction following changes in climate and vegetation in a karst basin of southwest China. J. Hydrol. 2022, 612, 128216. [Google Scholar] [CrossRef]
- Ersi, C.; Bayaer, T.; Bao, Y.; Bao, Y.; Yong, M.; Zhang, X. Temporal and Spatial Changes in Evapotranspiration and Its Potential Driving Factors in Mongolia over the Past 20 Years. Remote Sens. 2022, 14, 1856. [Google Scholar] [CrossRef]
- Luo, M.; Meng, F.; Wang, Y.; Sa, C.; Duan, Y.; Bao, Y.; Liu, T. Quantitative detection and attribution of soil moisture heterogeneity and variability in the Mongolian Plateau. J. Hydrol. 2023, 621, 129673. [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Sun, S.; Song, Z.; Chen, X.; Wang, T.; Zhang, Y.; Zhang, D.; Zhang, H.; Hao, Q.; Chen, B. Multimodel-based analyses of evapotranspiration and its controls in China over the last three decades. Ecohydrology 2020, 13, e2195. [Google Scholar] [CrossRef]
- Ahmadi, A.; Daccache, A.; Snyder, R.L.; Suvočarev, K. Meteorological driving forces of reference evapotranspiration and their trends in California. Sci. Total Environ. 2022, 849, 157823. [Google Scholar] [CrossRef]
- Tong, X.; Brandt, M.; Yue, Y.; Horion, S.; Wang, K.; Keersmaecker, W.D.; Tian, F.; Schurgers, G.; Xiao, X.; Luo, Y.; et al. Increased vegetation growth and carbon stock in China karst via ecological engineering. Nat. Sustain. 2018, 1, 44–50. [Google Scholar] [CrossRef]
- Qiao, Y.; Jiang, Y.; Zhang, C. Contribution of karst ecological restoration engineering to vegetation greening in southwest China during recent decade. Ecol. Indic. 2021, 121, 107081. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Leuning, R.; Zhang, Y.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, W10419. [Google Scholar] [CrossRef]
- Gan, R.; Zhang, Y.; Shi, H.; Yang, Y.; Eamus, D.; Cheng, L.; Chiew, F.H.S.; Yu, Q. Use of satellite leaf area index estimating evapotranspiration and gross assimilation for Australian ecosystems. Ecohydrology 2018, 11, e1974. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Ma, N.; Tian, J.; Kong, D.; Liu, C. A daily and 500 m coupled evapotranspiration and gross primary production product across China during 2000–2020. Earth Syst. Sci. Data 2022, 14, 5463–5488. [Google Scholar]
- Li, C.; Zhang, Y.; Shen, Y.; Yu, Q. Decadal water storage decrease driven by vegetation changes in the Yellow River Basin. Sci. Bull. 2020, 65, 1859–1861. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, M.F.; Xu, T. Anusplin version 4.2 user guide. In Centre for Resource and Environmental Studies; The Australian National University: Canberra, Australia, 2004; Volume 54. [Google Scholar]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Wu, G.; Lu, X.; Zhao, W.; Cao, R.; Xie, W.; Wang, L.; Wang, Q.; Song, J.; Gao, S.; Li, S.; et al. The increasing contribution of greening to the terrestrial evapotranspiration in China. Ecol. Model. 2023, 477, 110273. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Tegos, A.; Tyralis, H.; Koutsoyiannis, D.; Hamed, K. An R function for the estimation of trend significance under the scaling hypothesis-application in PET parametric annual time series. Open Water J. 2017, 4, 6. [Google Scholar]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GIScience Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Hussien, K.; Kebede, A.; Mekuriaw, A.; Beza, S.A.; Erena, S.H. Spatiotemporal trends of NDVI and its response to climate variability in the Abbay River Basin, Ethiopia. Heliyon 2023, 9, e14113. [Google Scholar] [CrossRef] [PubMed]
- Adeyeri, O.E.; Ishola, K.A. Variability and Trends of Actual Evapotranspiration over West Africa: The Role of Environmental Drivers. Agric. For. Meteorol. 2021, 308–309, 108574. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Zhou, Y.; Liu, D.; Wang, H. The dominant factors and influence of urban characteristics on land surface temperature using random forest algorithm. Sustain. Cities Soc. 2022, 79, 103722. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, L.; Zhang, Y.; Wang, Z.; Wu, J.; Li, L.; Li, S.; Paudel, B. Identification of impact factors for differentiated patterns of NDVI change in the headwater source region of Brahmaputra and Indus, Southwestern Tibetan Plateau. Ecol. Indic. 2021, 125, 107604. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, S.; Yang, S.; Fan, L.; Zhou, X. Spatio-Temporal Variations of Ecosystem Water Use Efficiency and Its Drivers in Southwest China. Land 2023, 12, 397. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, Q.; Tang, X.; Yan, W.; Chen, M. Changes in soil moisture caused solely by vegetation restoration in the karst region of southwest China. J. Hydrol. 2022, 613, 128460. [Google Scholar] [CrossRef]
- Sun, X.; Lai, P.; Wang, S.; Song, L.; Ma, M.; Han, X. Monitoring of Extreme Agricultural Drought of the Past 20 Years in Southwest China Using GLDAS Soil Moisture. Remote Sens. 2022, 14, 1323. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Z.; Song, Y.; Zhang, J. The unprecedented freezing disaster in January 2008 in southern China and its possible association with the global warming. Acta Meteorol. Sin. 2008, 22, 538–558. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Carter, C.; Liang, S. Comprehensive evaluation of empirical algorithms for estimating land surface evapotranspiration. Agric. For. Meteorol. 2018, 256–257, 334–345. [Google Scholar] [CrossRef]
- Mobilia, M.; Schmidt, M.; Longobardi, A. Modelling Actual Evapotranspiration Seasonal Variability by Meteorological Data-Based Models. Hydrology 2020, 7, 50. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In Symposia of the Society for Experimental Biology; Cambridge University Press (CUP): Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Hou, W.; Gao, J.; Wu, S.; Dai, E. Interannual Variations in Growing-Season NDVI and Its Correlation with Climate Variables in the Southwestern Karst Region of China. Remote Sens. 2015, 7, 11105–11124. [Google Scholar] [CrossRef]
- Song, Q.-H.; Braeckevelt, E.; Zhang, Y.-P.; Sha, L.-Q.; Zhou, W.-J.; Liu, Y.-T.; Wu, C.-S.; Lu, Z.-Y.; Klemm, O. Evapotranspiration from a primary subtropical evergreen forest in Southwest China. Ecohydrology 2017, 10, e1826. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Li, Y.-b.; Shao, J.-a.; Yang, H.; Bai, X.-y. The relations between land use and karst rocky desertification in a typical karst area, China. Environ. Geol. 2009, 57, 621–627. [Google Scholar] [CrossRef]
- Ma, Y.-J.; Li, X.-Y.; Liu, L.; Yang, X.-F.; Wu, X.-C.; Wang, P.; Lin, H.; Zhang, G.-H.; Miao, C.-Y. Evapotranspiration and its dominant controls along an elevation gradient in the Qinghai Lake watershed, northeast Qinghai-Tibet Plateau. J. Hydrol. 2019, 575, 257–268. [Google Scholar] [CrossRef]
- Pascolini-Campbell, M.; Reager, J.T.; Chandanpurkar, H.A.; Rodell, M. A 10 per cent increase in global land evapotranspiration from 2003 to 2019. Nature 2021, 593, 543–547. [Google Scholar] [CrossRef]
- Fu, J.; Gong, Y.; Zheng, W.; Zou, J.; Zhang, M.; Zhang, Z.; Qin, J.; Liu, J.; Quan, B. Spatial-temporal variations of terrestrial evapotranspiration across China from 2000 to 2019. Sci. Total Environ. 2022, 825, 153951. [Google Scholar] [CrossRef]
- Shao, R.; Shao, W.; Gu, C.; Zhang, B. Increased Interception Induced by Vegetation Restoration Counters Ecosystem Carbon and Water Exchange Efficiency in China. Earth’s Future 2022, 10, e2021EF002464. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Chen, H.; Yue, Y.; Zhang, W.; Zhang, M.; Qi, X.; Fu, Z. Karst landscapes of China: Patterns, ecosystem processes and services. Landsc. Ecol. 2019, 34, 2743–2763. [Google Scholar] [CrossRef]
- Zhang, X.; Yue, Y.; Tong, X.; Wang, K.; Qi, X.; Deng, C.; Brandt, M. Eco-engineering controls vegetation trends in southwest China karst. Sci. Total Environ. 2021, 770, 145160. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, C.R.; Sheffield, J.; Wood, E.F.; Gao, H. Quantifying uncertainty in a remote sensing-based estimate of evapotranspiration over continental USA. Int. J. Remote Sens. 2010, 31, 3821–3865. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Meynadier, R.; Sheffield, J.; Wood, E.F. Multi-model, multi-sensor estimates of global evapotranspiration: Climatology, uncertainties and trends. Hydrol. Process. 2011, 25, 3993–4010. [Google Scholar] [CrossRef]
- Chang, X.; Wang, Z.; Wei, F.; Xiao, P.; Shen, Z.; Lv, X.; Shi, Y. Determining the Contributions of Vegetation and Climate Change to Ecosystem WUE Variation over the Last Two Decades on the Loess Plateau, China. Forests 2021, 12, 1442. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X.; Ji, Y.; Luo, Y.; Yan, L.; Fan, Y.; Tan, D. China’s Greening Modulated the Reallocation of the Evapotranspiration Components during 2001–2020. Remote Sens. 2022, 14, 6327. [Google Scholar]
- Guo, X.; Wu, Z.; He, H.; Xu, Z. Evaluating the Potential of Different Evapotranspiration Datasets for Distributed Hydrological Model Calibration. Remote Sens. 2022, 14, 629. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Wang, J.; Feng, J.; Zhang, M. A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sens. 2021, 13, 2414. [Google Scholar] [CrossRef]
- Qing-ling, S.; Xian-feng, F.; Yong, G.; Bao-lin, L. Topographical effects of climate data and their impacts on the estimation of net primary productivity in complex terrain: A case study in Wuling mountainous area, China. Ecol. Inform. 2015, 27, 44–54. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Babaeian, E.; Paheding, S.; Siddique, N.; Devabhaktuni, V.K.; Tuller, M. Short- and mid-term forecasts of actual evapotranspiration with deep learning. J. Hydrol. 2022, 612, 128078. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiao, Q.; Sun, X. Ecological Risks Arising from the Impact of Large-scale Afforestation on the Regional Water Supply Balance in Southwest China. Sci. Rep. 2020, 10, 4150. [Google Scholar] [CrossRef] [PubMed]

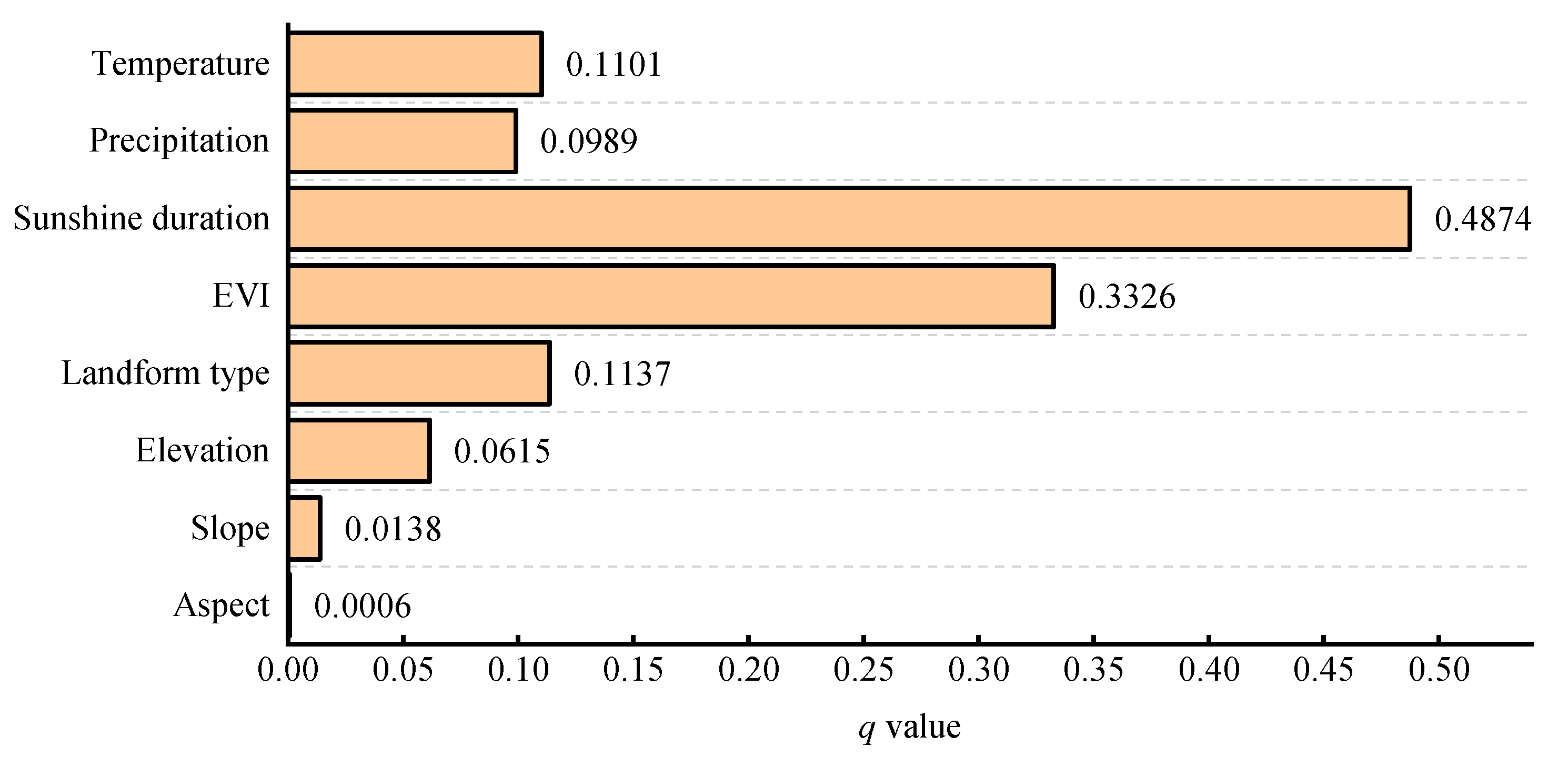


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhou, X.; Yang, S.; Ao, Y. Spatiotemporal Variations in Evapotranspiration and Their Driving Factors in Southwest China between 2003 and 2020. Remote Sens. 2023, 15, 4418. https://doi.org/10.3390/rs15184418
Zhang J, Zhou X, Yang S, Ao Y. Spatiotemporal Variations in Evapotranspiration and Their Driving Factors in Southwest China between 2003 and 2020. Remote Sensing. 2023; 15(18):4418. https://doi.org/10.3390/rs15184418
Chicago/Turabian StyleZhang, Ji, Xu Zhou, Shengtian Yang, and Yang Ao. 2023. "Spatiotemporal Variations in Evapotranspiration and Their Driving Factors in Southwest China between 2003 and 2020" Remote Sensing 15, no. 18: 4418. https://doi.org/10.3390/rs15184418
APA StyleZhang, J., Zhou, X., Yang, S., & Ao, Y. (2023). Spatiotemporal Variations in Evapotranspiration and Their Driving Factors in Southwest China between 2003 and 2020. Remote Sensing, 15(18), 4418. https://doi.org/10.3390/rs15184418