Next Article in Journal
TCNet: A Transformer–CNN Hybrid Network for Marine Aquaculture Mapping from VHSR Images
Previous Article in Journal
Spatio-Temporal Knowledge Graph-Based Research on Agro-Meteorological Disaster Monitoring
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 18
10.3390/rs15184407
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Synthetic Forest Stands and Point Clouds for Model Selection and Feature Space Comparison

by
Michelle S. Bester
1,*,
Aaron E. Maxwell
1,
Isaac Nealey
2,
Michael R. Gallagher
3,
Nicholas S. Skowronski
4 and
Brenden E. McNeil
1
1
Department of Geology and Geography, West Virginia University, Morgantown, WV 26505, USA
2
Department of Computer Science & Engineering, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
3
USDA Forest Service, Northern Research Station, New Lisbon, NJ 08064, USA
4
USDA Forest Service, Northern Research Station, 180 Canfield Street, Morgantown, WV 26505, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(18), 4407; https://doi.org/10.3390/rs15184407
Submission received: 1 August 2023 / Revised: 1 September 2023 / Accepted: 6 September 2023 / Published: 7 September 2023
(This article belongs to the Section Forest Remote Sensing)
Browse Figures
Review Reports Versions Notes

Abstract

:
The challenges inherent in field validation data, and real-world light detection and ranging (lidar) collections make it difficult to assess the best algorithms for using lidar to characterize forest stand volume. Here, we demonstrate the use of synthetic forest stands and simulated terrestrial laser scanning (TLS) for the purpose of evaluating which machine learning algorithms, scanning configurations, and feature spaces can best characterize forest stand volume. The random forest (RF) and support vector machine (SVM) algorithms generally outperformed k-nearest neighbor (kNN) for estimating plot-level vegetation volume regardless of the input feature space or number of scans. Also, the measures designed to characterize occlusion using spherical voxels generally provided higher predictive performance than measures that characterized the vertical distribution of returns using summary statistics by height bins. Given the difficulty of collecting a large number of scans to train models, and of collecting accurate and consistent field validation data, we argue that synthetic data offer an important means to parameterize models and determine appropriate sampling strategies.

Graphical Abstract

1. Introduction

Forests are one of the most biologically diverse terrestrial ecosystems globally. Consequently, they play a vital role in ecosystem processes, support numerous biological communities, offer a wealth of natural resources, and mitigate climate change through carbon sequestration and storage [1,2,3]. Furthermore, their physical attributes, including the quantity and arrangement of their biomass, influence how wildfires behave in natural areas [4,5]. Since the complexity of forest ecosystems and the associated numerous interactions contribute to a wide array of ecosystem processes that are essential for the health of the planet and its inhabitants, there is a need for accurate information for quantifying forest resources and monitoring their dynamics [6,7]. With recent advancements in remote sensing technologies, there have been considerable improvements in retrieving forest parameters. In particular, lidar (light detection and ranging) systems can characterize the three-dimensional structure of forests and provide estimates of key forest attributes [2,8,9].
Estimating tree- or plot-level characteristics is often accomplished using empirical or supervised learning methods, such as linear regression or machine learning. These methods require reliable, consistent, and unbiased reference data in order to yield trustworthy predictions of variables of interest [10,11]. Machine learning methods explored in this study, and described in more detail below, include the k-nearest neighbor (kNN), random forest (RF), and support vector machine (SVM) algorithms. kNN assigns a new data point to the majority class of its k nearest neighbors within the feature space based on a measure of distance. RF is an ensemble learning algorithm that combines multiple decision trees. It is applicable to both classification and regression tasks and is robust to a complex, high dimensional feature space. Similarly, SVM is applicable to both regression and classification tasks. It attempts to define an optimal hyperplane and is capable of modeling non-linear relationships [12,13].
It is not always practical, easy, or even possible to collect an adequate number of reference measurements using field methods, which limits the utility of traditional supervised learning. This has spurred interest in the further development of unsupervised and semi-supervised methods that are less reliant on reference data [10,14,15]. Another area of promise is generating synthetic data, artificially generated data that imitate the statistical and structural characteristics of real-world data, to train models and/or inform modeling parameterization or feature space development [16]. Synthetic data have the potential to provide data for diverse scenarios, which might be costly, time-consuming, or logistically challenging to replicate in the real world. They can also serve as part of benchmark datasets used for validating and comparing algorithms. For example, Fassnacht et al. [17] specifically explored the value of synthetic data for understanding how best to estimate tree- and plot-level biomass from lidar data. Moreover, synthetic data allow researchers to explore hypothetical scenarios, guiding the direction of future research and informing real-world data collection strategies. In a review of remote sensing technologies and methods to support forest inventories, White et al. [18] noted the value of synthetic data as a means to explore the effectiveness of laser scanning configurations, parameterizations, and summarization methods.
In this study, we specifically explore the utility of synthetic forest stands and associated simulated terrestrial laser scanning (TLS) data for assessing the impacts of scan density and position, the performance of different algorithms, and different means to summarize the point cloud to obtain a feature space for predicting the plot-level attribute of total vegetation volume. We argue that this experimental framework can be expanded to explore other research questions, such as the impact of noise, co-registration error, and field data uncertainty, and offer a means to overcome modeling challenges when reference data are absent or unreliable.

2. Background

Applying empirical modeling methods or supervised learning is challenging when the variable of interest is difficult to accurately and/or consistently quantify using field methods and/or when the study area is large or inaccessible. Prior studies have noted issues in the consistency of field methods due to sampling density variability, user bias, inconsistency of field protocols, and/or the general difficulty in measuring the variable of interest. For example, Sikkink and Keane [19] compared five field sampling techniques for estimating fuel loading and found that there were inconsistencies in estimates among each technique and that the technique that performed best required more than 2.5 km of transects to achieve the desired level of accuracy. As another example, Westfall and Woodal [20] documented inconsistencies in more than half of the measured forest fuel attributes in a large-scale sampling effort conducted as part of the Forest Inventory and Analysis (FIA) program of the United States Department of Agriculture (USDA) Forest Service. Practically, comprehensive field data collections are expensive, laborious, and time-consuming, and inconsistencies in collection methods often arise [5,17,21,22]. These issues are further exacerbated by the inability to directly measure some key attributes, such as biomass. Instead, field measurements such as diameter at breast height (DBH) are generally used to estimate these values using allometric equations, which are generally species-specific and derived using a small set of individual trees. This can further induce uncertainty in the reference data used to train models [23,24,25,26]. In summary, supervised, empirical modeling methods require reliable reference data, which are not always available or able to be collected using practical, accurate, and consistent field methods.
Since individual tree characteristics, as well as stand-level canopy and subcanopy densities, volumes, and biomass are valuable inputs to many ecological and fire modeling methods, prior studies have aimed to develop and/or assess technologies and data representations to obtain forest parameters as efficiently and accurately as possible. Specifically, studies have used lidar data to estimate heights, aboveground biomass, volume, density, basal area, and canopy attributes at the plot- or individual tree-level [2,18,21,27]. For example, Silva et al. [28] used canopy height profile statistics from airborne laser scanning (ALS) to predict the stem biomass of even-aged eucalyptus plantations in Brazil. Using TLS-based variables as opposed to aerial data, Mayamanikandan et al. [29] illustrated that vegetation volume can be predicted with relatively low (5.13%) errors relative to manual, field-based measurements. As another example, Saarinen et al. [30] investigated the feasibility of using TLS data for estimating individual tree volume. They documented that volume estimation accuracy increased as the number of scans increased and that accuracy depended on the distance of the TLS from the tree. Combining aerial and ground-based lidar has also been found to be useful; for example, Skowronski et al. [9] noted the value of using downward scanning aerial lidar in combination with upward sensing profiling lidar to better characterize the three-dimensional (3D) tree canopy structure in comparison to only using aerial data.
As with ground reference data, lidar-based measurements are also subject to some uncertainty, which can propagate from errors in the sensor position due to incorrect global navigation satellite system (GNSS) information, interference from the atmosphere, instrument effects such as after pulses (noise induced from laser firing), or sensor calibration issues [31,32,33]. The inherent complexity of forest stands at both the plot- and individual-tree levels, as well as terrain variability, also affect lidar acquisition accuracy [8,34]. For example, Clark et al. [35] documented that higher vegetation densities reduced the probability of detecting the ground surface and limited the ability to discriminate sub-canopy returns. Lidar-based estimations are further influenced by the point density, sensing distance, and angle of transmission of the TLS laser pulses. Specifically, TLS pulses that reach the uppermost part of the canopy have a larger footprint due to the beam divergence inherent to a specific instrument [36]. Further, the number of single location scans that are collected and subsequently merged to characterize a plot impacts the point cloud’s spatial resolution and, consequently, the amount of occlusion of and by vegetation structure [37]. Numerous studies have tried to minimize the impact of occlusion (e.g., Loudermilk et al. [4], Abegg et al. [38] and Rowell et al. [39,40,41]) by obtaining scans from multiple locations. However, these studies still note limitations; artifacts and errors are induced by external factors, such as weather conditions (wind, fog, or precipitation) and by mixed effects caused by laser pulses intersecting multiple small branches or compact, dense vegetation [9,25,26,27,28,29]. In summary, cleaning and filtering point cloud data to remove such anomalies is a complex process with some inherent uncertainty.
Finally, processing procedures, although necessary, can yield additional uncertainty. Common processing procedures include georeferencing, co-registration, merging, segmentation, subsetting, and classifying the point cloud data [42,43]. Geolocation errors refer to inaccuracies in determining the geographic coordinates of returns within the point cloud relative to a coordinate reference system. As an example of an attempt to quantify errors in a forestry context, Tao et al. [44] noted geolocation errors of up to 6 m for TLS-derived stem positions. Although the integration of multiple TLS scans uses sophisticated registration techniques, there are still errors. For example, Frazer et al. [45] investigated the uncertainty between plot size and co-registration and documented that the impact of co-registration errors was more pronounced in spatially heterogenous plots with taller vegetation in comparison to plots with more homogeneity. These studies highlight the complexity of lidar acquisition and processing, as well as the need to conduct the investigations of specific factors under more controlled conditions.
To overcome the abovementioned limitations, we propose using synthetic data and simulated lidar datasets to investigate the accuracy of lidar-derived estimations of plot-level characteristics, as well as the effect of occlusion within forest plots of varying complexity (i.e., tree and shrub density and configuration). These datasets are quantitatively similar to lidar datasets created within the “real” world, with the added advantage of having no positional noise within the point cloud, the ability to merge multiple scans without any co-registration error, and the ability to model against known stand-level metrics as opposed to those estimated using field methods [17,46]. This allows for comparisons between methods for estimating stand characteristics and provides a means to summarize three-dimensional point distributions. Moreover, it enables evaluations of techniques, algorithms, and workflows to empirically estimate metrics of interest in a standardized method without having the confounding variables of noise, errors, and a lack of accurate ground measurements to model against. There is also the added advantage of testing multiple configurations with little to no added expense, other than computational time, allowing for the manipulation of simulation parameters, such as scanning resolution, occlusion effects, and sensor characteristics, to understand their impact on results. Jiang et al. [47] demonstrated this by introducing a simulation program to create digital forest plots and simulating aerial and mobile laser scanning. By adjusting scanning parameters and vehicle speed, the scanned points were compared to original sampling points from the digital forest plots. The results indicated that scanning at different speeds and resolutions yielded varying point collection rates.
In a review on enhancing forest inventories using remote sensing, White et al. [48] commented that synthetic data could vastly improve our understanding of the relationship between forest structure and lidar attributes. The research of Yun et al. [49] offers an approach to quantitatively assess occlusion metrics and measure total leaf area in tree crowns using simulated multi-platform lidar data. This work highlights the potential of various scanning strategies to address occlusion challenges and enhance the accuracy of biophysical attribute estimation in forest canopies. Goodwin et al. [50] further emphasized the potential of synthetic data for testing forest metrics calculated from lidar data. We argue that such simulated studies can inform the best practices for designing field collection protocols and comparing methods for summarizing the point cloud and empirically estimating stand-level metrics. Simulated TLS allows researchers to set up controlled experiments with known ground truth. Thus, we further argue that exploring these problems in a synthetic space can inform expected accuracies and outcomes when using TLS to characterize real forest stands when modeling against real field reference data.
A few prior studies have proposed simulating the lidar data of forest stands using simplified ray-tracing methods. For example, Sun and Ranson [51] developed a full-waveform lidar simulator that captures the horizontal and vertical structure of geometrically simple (elliptical and conical) forest stands. Similarly, Wang et al. [46] used simple geometric shapes to generate artificial forest stands and simulate ALS sampling. However, they filtered out the understory and interpolated the canopy to a two-dimensional raster to calculate forest metrics [46]. In contrast to these aforementioned studies, Disney et al. [52] made use of more detailed tree models and ray-tracing canopy scattering methods to simulate lidar responses. They investigated canopy height retrieval under a range of conditions (different scan angles and sampling densities) and suggest that the simulated lidar height generally underestimated “real” canopy height; however, their research did not include any understory vegetation and they noted that their methodology needs further validation and testing as exact parameters were unknown [52].

3. Methods

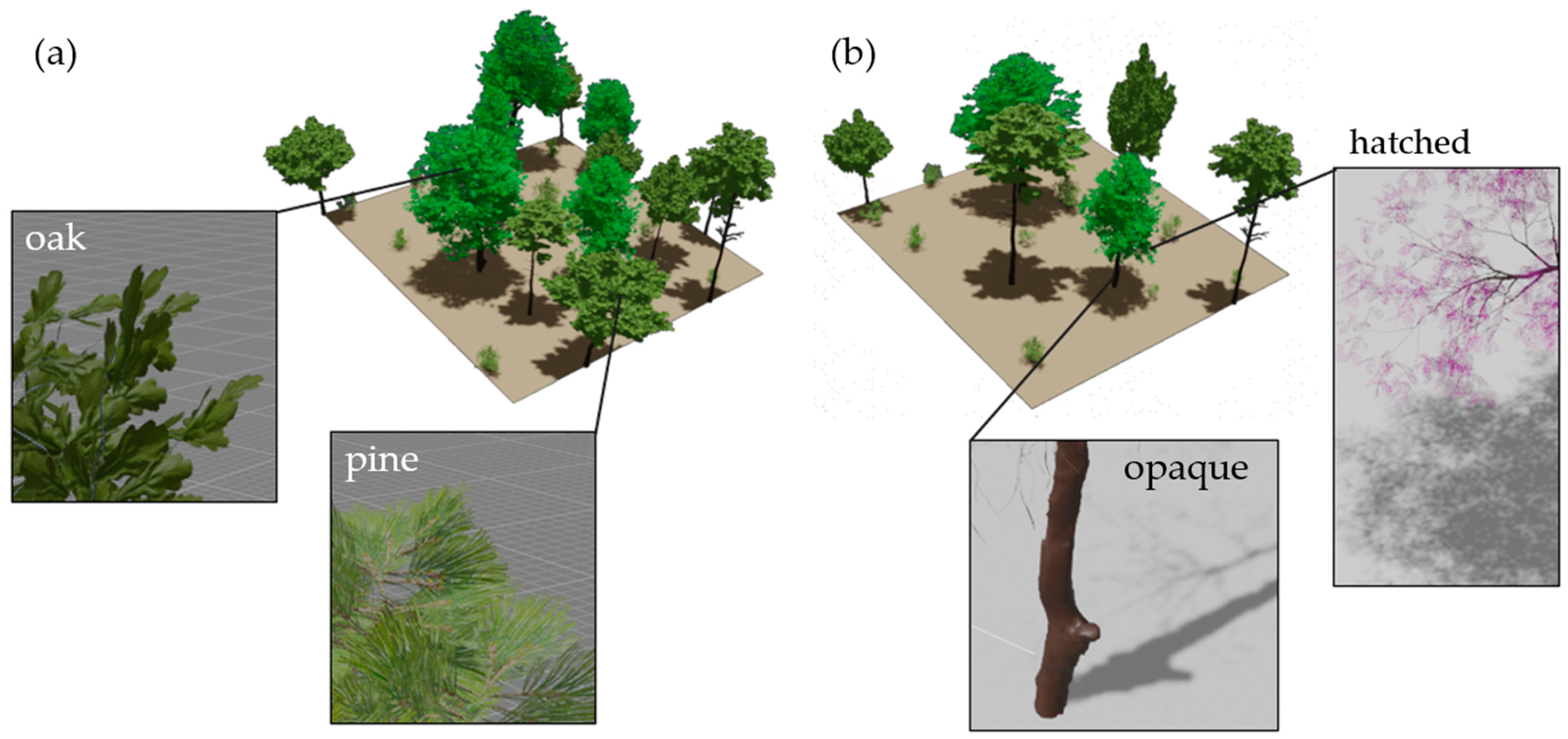
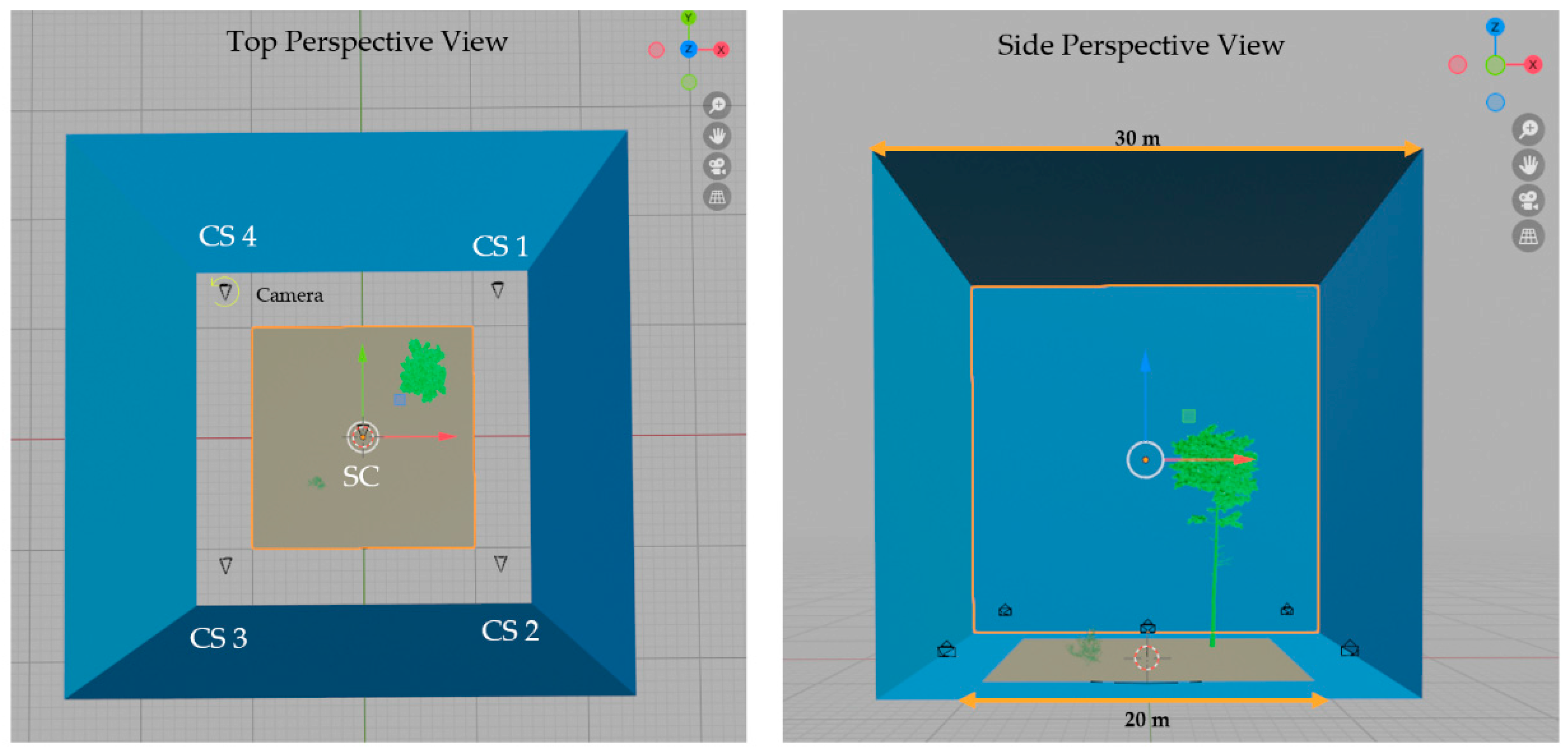
3.1. Synthetic Plot Generation

Real-world forest stands are complex terrestrial biomes, comprising diverse vegetation that frequently overlap, intertwine and can occur on rugged, variable terrain with varying levels of litter and downed woody debris. However, since our goal was to model forest attributes within the limitations of available 3D modeling software and to be able to account for all volumes without the overlap of objects and meshes, we generated simplified synthetic plots using a set of tree and shrub models randomly placed within a flat terrain such that there was no overlap between the meshes and objects. Since mixed evergreen–deciduous forests are one of the most abundant forest types in the Northern Hemisphere [53], we decided to imitate this natural forest for our study. Specifically, in North America, these forest ecosystems expand over a large portion of the eastern United States and southeastern Canada. Eastern United States mixed forests are dominated by evergreen conifers (eastern white pine (Pinus strobus) and Hemlock (Tsuga canadensis)) and broadleaf deciduous trees, including various oak (Quercus), maple (Acer) and hickory (Carya) species [54,55,56,57]. These forests form part of the World Wildlife Fund’s (WWF) global priority ecoregions for conservation due to their high levels of biodiversity of both fauna and flora [58]. From a modeling perspective, mixed evergreen deciduous forests provide a unique ecological setting that can be explored using synthetic data. These forests are rich in biodiversity due to the coexistence of two different types of trees with distinct ecological characteristics. Modeling the interactions between these species and other components can provide insights into a variety of ecological processes and dynamics. Synthetic models can help assess the trade-offs and synergies between different services under various management scenarios and enables us to observe how simulations interact with various tree species.
We developed our forest plots within the Blender™ version 3.10. (http://www.blender.org, accessed on 5 September 2023) open-source 3D model creation software (The Blender Foundation, Amsterdam, The Netherlands). The generation of these forest plots is a multi-step process. First, we constructed a 20 m × 20 m filled planar mesh as our forest floor (hereafter referred to as the ground plane). A mesh is a collection of faces, edges, and vertices that make up a 3D shape [59]. Our plots had flat terrain as the slope, and ruggedness would induce uncertainty and influence our accuracy assessment [60,61,62]. Blender™ uses a Cartesian coordinate system (X, Y, Z); as such, our plane center was located at (0, 0, 0). The initial tree models were imported from the ‘Tree Vegetation Pro V5’ (VegPro) add-on tool created by Bproduction (https://bproduction-3d.com/, accessed on 5 September 2023). VegPro contains an extensive 3D model library of diverse and varied trees, shrubs, tropical plants, tree hedges, and ornamental plants, all optimized for Blender™. We used two generic evergreen pine models and two broadleaf deciduous tree (maple and oak) models for our artificial overstory. We also included one woody holly shrub model with two stems for the understory.
In order to automate the synthetic plot creation process, we used the embedded Python application programming interface (API). The plot generation started by importing appropriate packages and declaring the various tree and shrub models as variables then randomizing (with predefined constraints) the number and placement of each tree/shrub model within the 20 m-by-20 m ground plane. We set a distance condition for the randomization such that no tree or shrub trunks or crowns overlapped. Although this type of distribution is unrealistic, it ensures discrimination between models and allows for the accurate calculations of forest parameters, such as volume, since no objects can share the same volume or overlap. Additionally, we customized each tree/shrub model by randomizing the scale, rotation, and crown size. These customizations change the orientation and minimum and maximum height and scale of the model crowns and trunk diameters by a percentage of the initial model (Mi) (original from VegPro). We set thresholds on the customization parameters to ensure model sizes are comparable to their real-world counterparts. The structural parameter thresholds for these models are summarized in Table 1.
Once a plot was generated, we ensured all trunks and leaves were assigned “materials”. The materials function describes the surface properties of the model, which defines how the model will appear when rendered and how the lidar simulator will interact with it. For example, the type of material (reflective or diffuse) will impact the intensity of the reflected beam, while the opacity of the model surface will determine the travel distance of the laser beam (i.e., for translucent objects, rays will continue past a model intersection point to simulate transmission). We assigned the same material properties to all models except the base color, where a slightly darker green hue was used for deciduous tree leaves. Our stem/trunk material was opaque, and we used the default VegPro stem/trunk surface parameters. The specular (brightness), roughness, and metallic parameters were 1.0, 0.55, and 0.0, respectively, on a scale from 0 to 1.0. Similarly, we used a default VegPro leaf material. However, we set the leaves to have a hatched transparency with 50% translucency, allowing light to disperse through the canopy. A hatched transparency allows for 50% of the light to be transmitted through the leaves. A specular reflection parameter value of 1.0 would have a high intensity, and the angle of incidence would be reflected in a single outgoing direction. Surface roughness and metallic values of 0 would represent a glossy object that is not metallic [63,64]. It should be noted that no spectral reflectance metrics were calculated from the TLS point cloud, so these color metrics were primarily used for visualization and not used to generate predictor variables as input to the modeling workflow.
We executed the script within a loop to create 200 randomized plots. After each iteration, we calculated each tree and shrub volume (see Section 3.3), saved the blender file in .blend format, and removed all tree and shrub models in the scene before initializing the next model iteration and subsequent plot generation. This was to ensure that no overlapping of trees or shrubs occurred and to clear processing memory. We illustrate an example of one densely packed and one sparse mixed-forest plot model in Figure 1 below. Some of the resulting scans were not included in subsequent analyses due to sparse vegetation cover; a total of 191 scans were used for the remaining phases of the experiment.

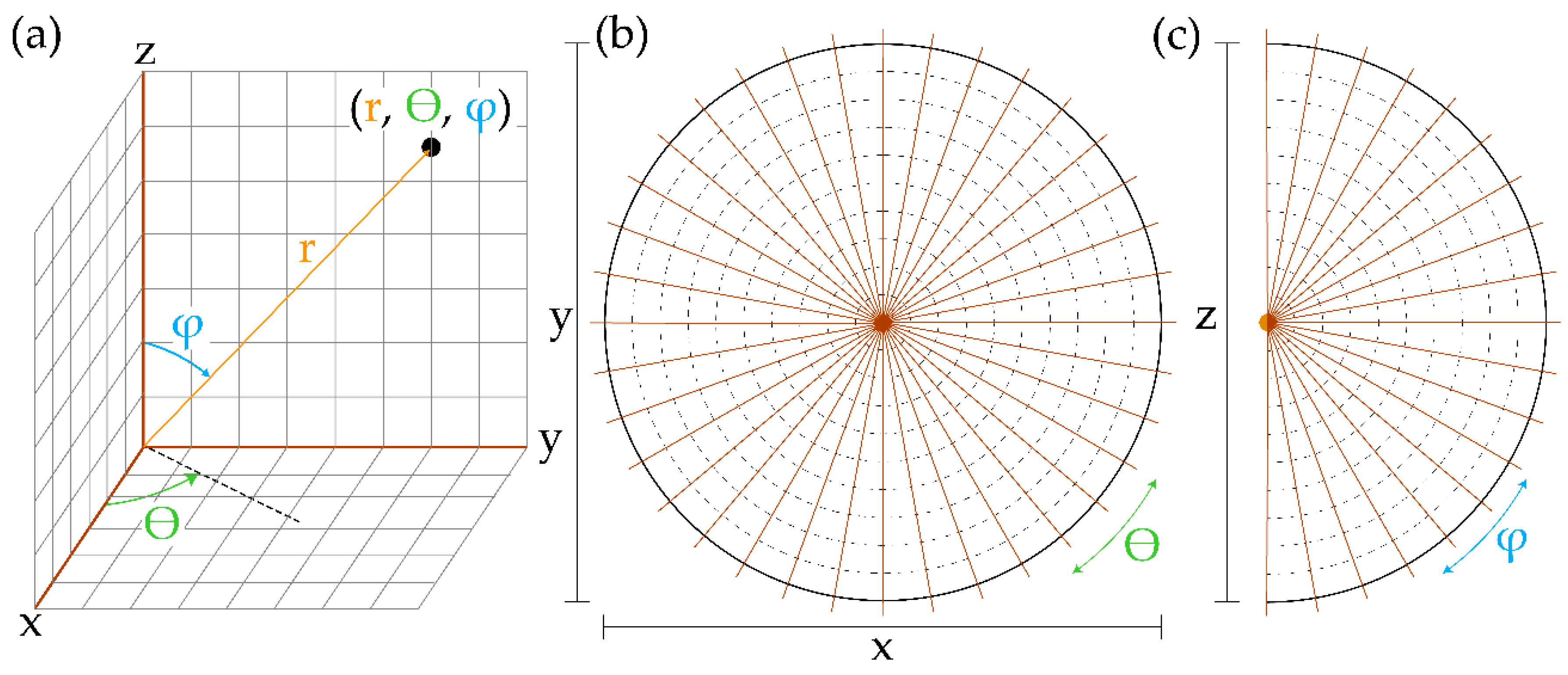
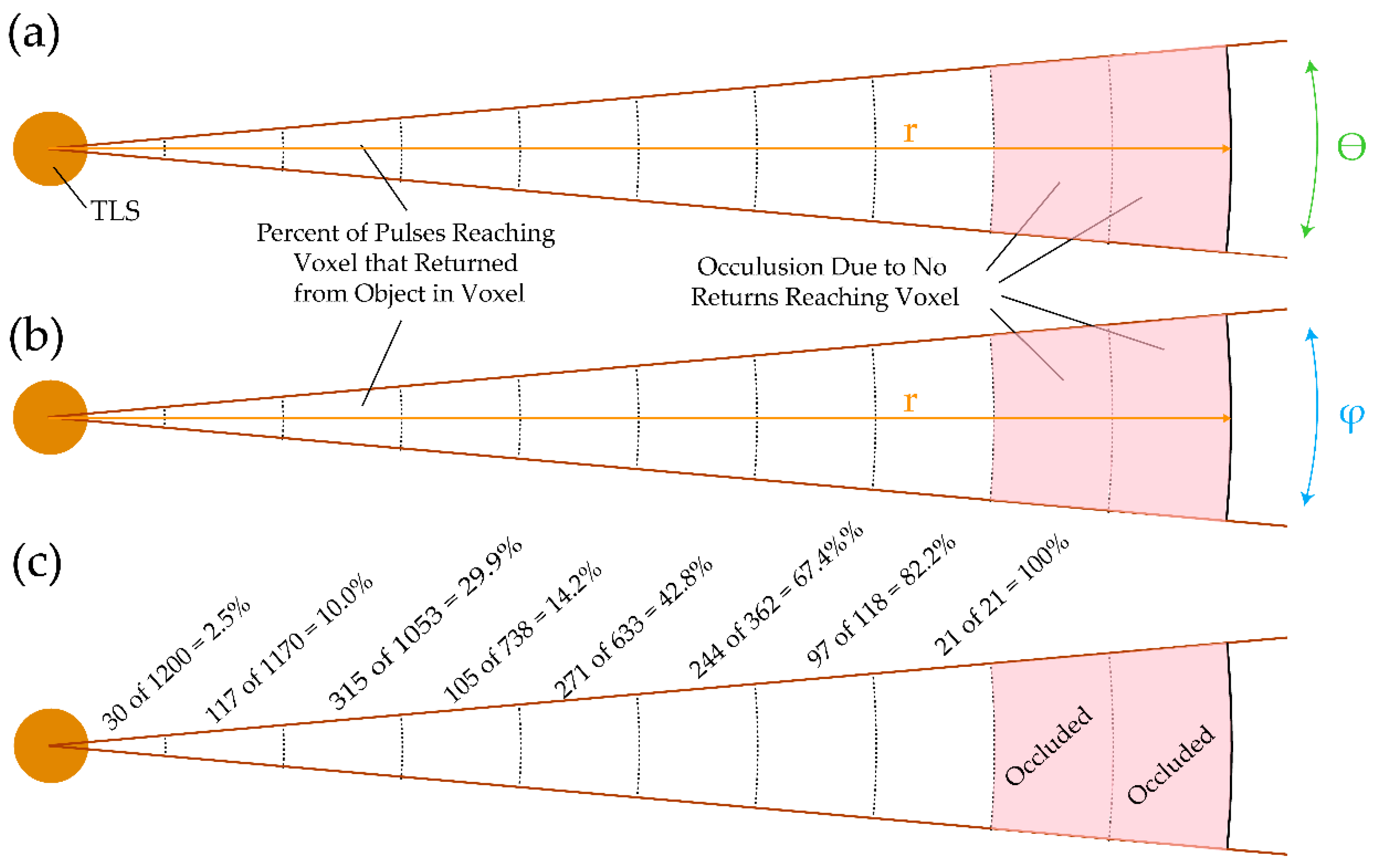
3.2. Simulated Lidar

Lidar works by emitting laser pulses and measuring the time it takes for them to return after potentially hitting surfaces. In Blender™, you can emulate this by using the Eevee real-time rendering engine. Eevee’s real-time rendering capabilities make it well-suited for visualizing point cloud data. You can manipulate objects, materials, lighting, and camera angles in the viewport and immediately observe how these changes affect the simulated point cloud. For this research, we simulated the TLS scans using a range scanner simulation add-on in Blender™ called Blainder, which is designed to work with the Eevee rendering engine [65]. Blainder was developed by Lorenzo Neumann and is freely available on github (https://github.com/ln-12/blainder-range-scanner, accessed on 5 September 2023). This add-on enables users to simulate the lidar, sonar and time of flight scanners within the Blender™ scene. We implemented the lidar functionality component of this add-on using its Python API within Blender™. The lidar functionality of Blainder is based on a ray-tracing approach. Ray tracing is a global illumination algorithm based on the emission of rays to determine the visibility of three-dimensional objects from a certain vantage point [49,66,67]. Previous works from Disney et al. [52,68] provide a detailed review of ray tracing for remote sensing and forestry studies. Briefly, the algorithm traces the beam path from the center of the scanner (camera) for each pixel on the screen, until it collides with an object in the virtual scene. When a collision occurs, the distance is calculated, and object attributes are recorded. Diffuse sampling beams are generated at an intersection with a scene object, sending further beams on possible routes by which they diffuse (scatter) based on the object’s material properties. After each measurement, the direction of the beam is adjusted horizontally and/or vertically according to the sensor configuration [50,65,68].
In our study, we set up cameras in the scene to serve as vantage points from which the lidar sensor would capture data. The position of the cameras emulated their real-world counterparts. We set up our sensor to use a rotating sensor type with a horizontal and vertical field of view of 360°, with a step size of 0.2° in both the X and Y direction. This yielded a total of 3.24 million points per scan. The step size determined the resolution of the sensor with smaller step sizes resulting in higher point densities. This approach assumes that there is no beam divergence resulting in a beam width that is constant. We simulated one scan from the center (SC = 0, 0, 0) of the forest plot at a height of 2 m (0, 0, 2) and a scan from each corner of the plot (CS 1–4) (Figure 2, triangles). For the corner plot scans, we placed the virtual camera (origin of the scanner) 2 m away from the ground plane. The coordinates (X, Y, Z) relative to the plot center were as follows: CS 1 = (12, 12, 2), CS 2 = (12, −12, 2), CS 3 = (−12, 12, 2) and CS 4 = (−12, 12, 2). We did not set a maximum distance limit that the beam could travel; instead, we enclosed our plot in a 30 × 30 × 30 m box (6 planes) with an opaque material (Figure 2, blue planes). This acted as a barrier and allowed us to capture all pulses that would otherwise have no associated return. Recording these points is helpful for determining occlusion and accounting for all transmitted laser pulses in subsequent calculations. We visualize the top and side view of our plot and camera setup in Figure 2. The final step was to save these scans to disk in .laz format for further analysis. Similar to the plot generation, we automated the lidar simulation process for all plots using the Python API.

3.3. Measured Metrics

To assess the impact of density and location of TLS data and also varying means to summarize the point cloud characteristics on forest parameter estimates, we calculated various summary metrics from the point cloud data. We calculated metrics based on only the center scan as well as the aggregation of all scans (center and four corners). Our analysis was performed on imported .las files within the R open-source data science environment and language (R Core Team, Vienna, Austria) [69]. We only used the coordinate information for our metric calculations; the true color (RGB) and intensity values would not be realistic since we manually assigned material properties to the woody and leaf objects. We also only calculated metrics using returns occurring within a box with lengths of 23.8 m along all three axes that was centered on the center scan and positioned at ground level. This subset of the data was used since only vegetation volumes within this box were calculated, as described below. We performed point cloud manipulation (filtering, clipping, etc.) using the lidR [70,71] and rlas [72] packages in the R language [69] and data science environment.
Within the clipped extent, we calculated the number of ground and non-ground returns along with the percent of the returns from the ground. The following metrics were calculated for just non-ground returns within the clipped extent: mean, median, standard deviation, skewness, and kurtosis of the height (Z) values. We also calculated the heights associated with the 10% to 90% percentiles with a step size of 10%. We next summarized the data relative to height strata. We filtered the point cloud data into height bins of 0.0–2.0 m, 2.0–4.0 m, 4.0–6.0 m, 6.0–8.0 m, and 8.0 to 23.8 m (Figure 3). We chose these height bins based on typical shrub and canopy heights within mixed deciduous forests. The following metrics were calculated for all non-ground returns within each height bin: return count; percentage of all non-ground returns in the current strata; and the mean, median, standard deviation, skewness, and kurtosis of the heights within the bin.
We also calculated a set of metrics using only the center scan and spherical, as opposed to Cartesian, coordinates, in which the sensor location was the center of the sphere (0, 0, 0). This was conducted to characterize the abundance of the occlusion of the plot volume by vegetation; our goal was to generate additional metrics to quantify what was not measured as a result of occlusion. This first required converting the X, Y, Z coordinates to angular measurements of theta (θ) (the angle of rotation from the X axis along the plane defined by the X and Y axes) and phi (φ) (the angle relative to the Z axis) and the radial distance (r) from the center of the sphere to the point measurement (Figure 4). Once the data were converted to spherical coordinates, data points were summarized relative to spherical voxels defined by a certain angle of θ and φ and a range of radial distances. As conceptualized in Figure 5 and using (1) the number of pulses passing through the volume, defined by angles of θ and φ, (2) the number of returns from the volume of interest, as defined by a given range of radial distances and the angles of θ and φ, and (3) the number of pulses being returned before reaching the volume of interest, it was possible to calculate the percent of pulses reaching a spherical voxel that returned from objects within that volume, and to also determine what spherical voxels had pulses passing through but no associated returns (i.e., true gaps or empty volumes), and those that had no returns passing through them due to occlusion (i.e., volumes that were not measured).
Figure 6 further conceptualizes the process of calculating metrics using spherical voxels. Once a synthetic plot (Figure 6a) is generated, it is synthetically scanned to create a point cloud in 3D Cartesian space (Figure 6b). These coordinates are then converted to spherical coordinates. By keeping track of the number of pulses passing through a given angle of θ and φ and the radial distance of each return from the sensor, it is possible to calculate the number of returns from each spherical voxel then normalize these values by the number of pulses passing through that volume. Volumes that have pulses passing through but no associated returns can be labeled as true gaps while those with no returns passing through, or where all available pulses were returned prior to reaching the volume of interest, can be labeled as areas of occlusion. In Figure 6c, all points represent the center of a spherical voxel. Pink points represent voxels that were occluded while green points represent voxels with returns. Figure 6d conceptualizes these results such that the X-axis shows angles of θ, the Y-axis shows angles of φ, and each image shows a range of radial distance from the scanner location. Blue represents gaps, pink represents areas of occlusion, and shades of green represent, for voxels that were not occluded or gaps, the proportion of pulses intersecting a voxel that were returned from that spherical voxel. It is important to note that performing these calculations required accounting for all transmitted pulses, not just those with an associated return. This was accomplished in the synthetic space by including barriers around each plot. If a pulse did not return from either the ground or an object in the plot, then it would return from the barriers. Such accounting of all transmitted pulses is more difficult using real TLS data since the pulses without associated returns and their associated angles of transmission are not always recorded or made available to the end user.
Using the spherical voxel-based analysis, we calculated the percent of the plot area that was occluded, the percent of the plot area that was true gaps, and the percent of the area that contained some returns (Table 2). We also partitioned the data into the same height bins defined for the Cartesian-based summarizations described above to calculate the same percentages by height strata and the mean proportion of pulses returned from those voxels that had associated returns. Calculations were made by dividing the space into spherical voxels covering 0.5° of θ and φ and a radial distance range of 1 m. Since spherical voxels do not have equal volumes, calculations required adjusting for relative voxel volume based on the range of radial distances associated with each voxel.

3.4. Modeling and Validation

The simulated plots include some regions that extend beyond the 20 m2 area, due to the nature of the tree and shrub placement. To obtain metrics, the plots needed to be consistently clipped such that volume measurements could be compared. Our approach was to clip each plot to within the bounds of a 20 m plot, then fill any resulting holes opened at the plot boundary. Failing to close the holes would result in errors when computing plot volume. The plots were imported into ParaView, Burlington, MA, USA [73,74] as object-based meshes (.STL files). ParaView is an open-source 3D interactive visualization and analysis software that employs the Visualization toolkit (VTK) for data processing [73,74]. A mesh quality filter was applied, and any gaps (holes) within the tree and shrub polygonal meshes were filled. We then calculated the volume of the synthetic vegetation in the plots using Python scripting within the ParaView software [73,74].
To assess how well the simulated point cloud metrics estimate total vegetation volume in the plot, we employed three machine learning algorithms, namely RF kNN, and SVM [11]. These models were trained using the metrics derived from the simulated lidar as the predictor variables and the volume from the 3D plots as the dependent variable. Machine learning-based algorithms have gained significant attention, especially in the field of remote sensing [13,54,75,76,77]. Since our study’s purpose was to predict plot-level total vegetation from a large set of predictor variables, we decided that machine learning algorithms would be better suited than statistical linear regression approaches for this study. Furthermore, these models could account for complex variable interactions, correlated predictor variables, and non-linear relationships [11].
SVM is a supervised learning algorithm that attempts to find the optimal hyperplane, defined as the boundary that provides the largest margin or separating distance between classes or groups, in n-dimensional space. When classes cannot be separated using a linear hyperplane, the data can be projected to a higher dimensional space, a process known as the kernel trick, in which the separating boundary may be more linear. This process can be augmented to allow for the prediction of a continuous variable, or a regression problem, as was the case in this study [77,78]. kNN is a non-parametric model that uses similarity (based on distance functions) to predict new data points; specifically, new samples are compared to the k closest samples from the training set within the multidimensional feature space [79]. RF regression models, developed by Breiman [80], are ensemble decision tree algorithms where the tree is ‘grown’ with some randomization [80]. Decision trees use recursive binary partitioning to split the data into more homogeneous subsets and generate rulesets to perform classification or regression. Within RF specifically, each tree in the ensemble uses a subset of the training samples, which are selected using bootstrapping (i.e., random sampling with replacement). Also, only a subset of the predictor variables is available for splitting at each decision node. The goal of using a subset of the training data and variables is to reduce the correlation between trees and minimize overfitting. In other words, a set of weak classifiers are collectively strong and generalize well due to reduced overfitting [67].
Models for predicting plot-level vegetation volume were trained in R [69] using the caret package [81]. kNN was executed within the caret package [81], RF was implemented through caret using the ranger package [80], and SVM was implemented using the kernlab package [82]. We included a center and scale pre-processing transformation for all models, since kNN and SVM make use of distance-based calculations and require all predictor variables to be consistently scaled. For RF, the number of random predictor variables available for splitting at each node hyperparameter (mtry) was uniquely optimized for each model or feature space using 10-fold cross-validation and a grid search to test ten values. The ntree parameter (number of trees to grow) was set to 500. In a review article by Belgiu et al. [83] on RF algorithms for remote sensing applications, they noted that a ntree of 500 provides stable predictions and satisfactory results [83]. For kNN and SVM algorithms, the k and cost parameters were optimized, respectively, and the best hyperparameter was selected based on the lowest average RMSE calculated from the withheld samples in each fold. Distance was calculated using Euclidean distance for the kNN models, and a radial basis function (RBF) kernel was used to map the data to a higher dimensional space for the SVM models.
To obtain multiple results and to characterize the variability in model performance, we trained and assessed 20 model replicates using different training and testing partitions, selected using a bootstrapping method in which a random subset of plots was used to train each model while the remaining plots were withheld for model validation. It should be noted that hyperparameter optimization was performed separately for each replicate so as not to induce data leakage by using the withheld samples for a specific run to perform the hyperparameter optimization or center and scaling. Using the withheld data, we calculated the R-squared and root-mean-square-error (RMSE) metrics using the yardstick [84] package in R [69] for model validation. Since multiple models were executed, this allowed us to obtain distributions for each assessment metric in order to assess model variability with changes in the training and validation partitions.

4. Results

We aimed to create randomized forest plots with varying densities. Table 3 provides descriptive statistics highlighting volume variability across the synthetic plots. Figure 7 shows the distribution of volume, as represented using violin and boxplots for all plots, as well as a histogram showing variability within individual plots. The mean volume across all plots was 593.56 m3. The least dense plot (plot 181) had a volume of 11.72 m3 while the densest plot (plot 140) had a volume of 2453 m3. Plot 181 only consisted of two pine trees and two small shrubs. In contrast, plot 140 consisted of 11 shrubs, 6 pine trees, and 9 deciduous trees.
Table 4 provides descriptive statistics that characterize the percentage of occluded surface area of the box enclosing the plot when using only the single, center scan and when combining all five scans. This was estimated as the percentage of all transmitted pulses that reached the exterior box as opposed to being returned from an object within the plot volume. With no objects in the scan space, or no occlusion, all returns should have reached the exterior box. Figure 8 illustrates the difference in the amount of occlusion in the plots when using only one scan versus using multiple scan locations (i.e., center scan and four corners). When using multiple scans the mean percentage of occlusion across all plots decreased nearly two-fold, from 10.53% to only 5.14%. Moreover, there is a large difference in the occlusion variance (33.21%) across plots when using only one scan. This suggests that density within the plot affects the occlusion from the center scan.
Figure 9 shows the distribution of the RMSE (Figure 9a) and predicted R-squared (Figure 9b) for estimating plot-level vegetation volume using 20 model replicates of each feature space and the algorithm combination, for a total of 240 models. Generally, the RF and SVM models performed similarly while outperforming the kNN models regardless of the feature space used. This could partially be attributed to kNN not being robust to a large feature space. Performing variable selection or variable reduction, such as principal component analysis (PCA), may have allowed for improved performance from the kNN algorithm. Given the large feature space provided and the correlation between predictor variables, RF and SVM were generally more appropriate algorithms for this specific task.
The metrics calculated from only the center, single scan and the same set of metrics calculated using all five scans generally showed similar performance. However, and especially for the RF and SVM algorithms, the multi-scan metrics generally provided slightly better performance. The multi-scan metrics provided a mean R-squared of 0.575 (RMSE = 321) for the SVM algorithm and 0.560 (RMSE = 324) for the RF algorithm, while the single-scan metrics yielded an R-squared of 0.554 (RMSE = 335) for the SVM algorithm and 0.541 (RMSE = 333) for the RF algorithm. The use of the spherical-based metrics generally provided substantial improvement in comparison to the multi- and single-scan metrics. Using only the spherical metrics and the SVM algorithm yielded a mean R-squared of 0.697 (RMSE = 272) and a R-squared of 0.738 (RMSE = 252) when using the RF algorithm. Incorporating the other single-scan metrics with the spherical metrics generally offered minimal improvements in comparison to just using the spherical-based metrics.
Figure 10 below provides scatterplots to visualize the relationship between plot-level vegetation volume and the six variables that were found to be most highly correlated with this measure, as estimated using the Spearman correlation coefficient, a measure of monotonic and non-linear correlation. The variable with the largest correlation with the vegetation volume was the percentage of the volume between 6 and 8 m above ground with returns (Spearman correlation coefficient = 0.880). The next two highest correlated variables were also derived using the spherical method, all with correlations higher than 0.850. The next two variables were derived using all five scans: the percentage of returns that were not ground returns and count of returns that were not ground returns. The last variable, with a Spearman correlation of 0.772, was the number of returns not ground returns calculated using only the single, center scan.
These results generally support the modeling results documented above. The variables with the highest correlation with total plot-level vegetation volume were all derived using the spherical voxel-based summarization, and the spherical-based features generally provided stronger model performance in comparison to the other feature spaces when using the SVM and RF models. 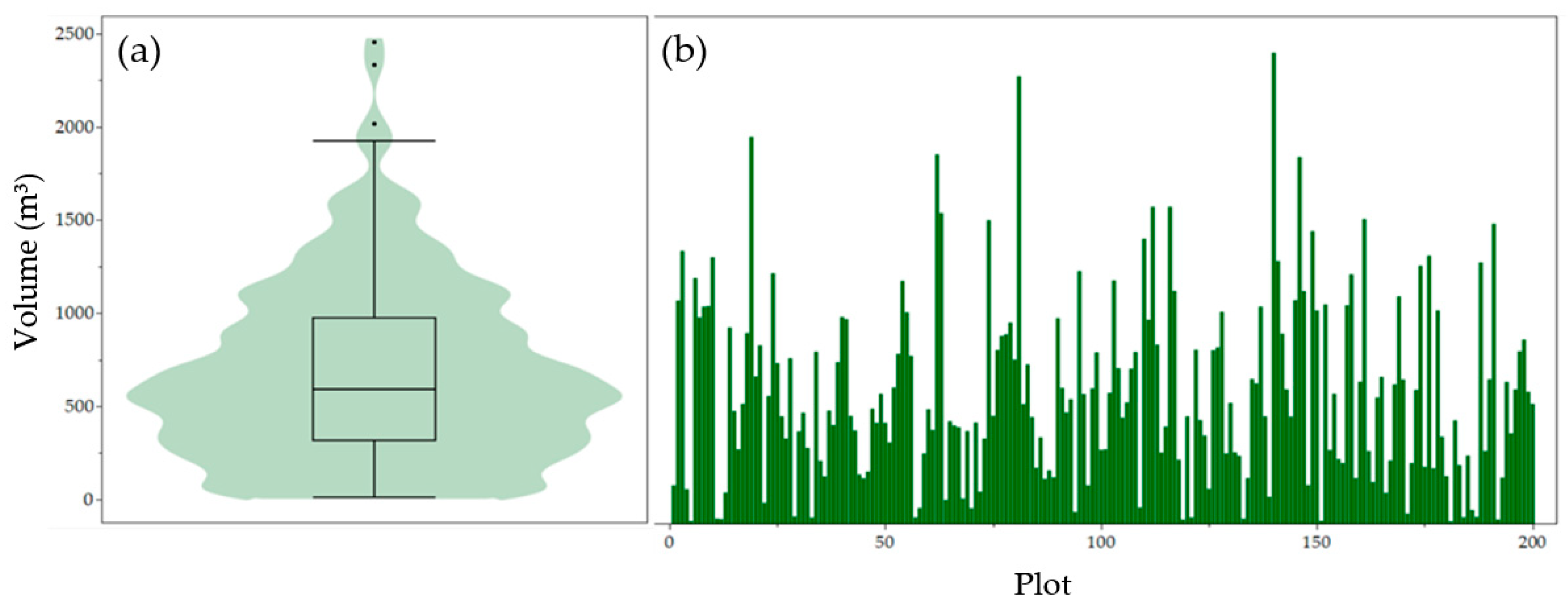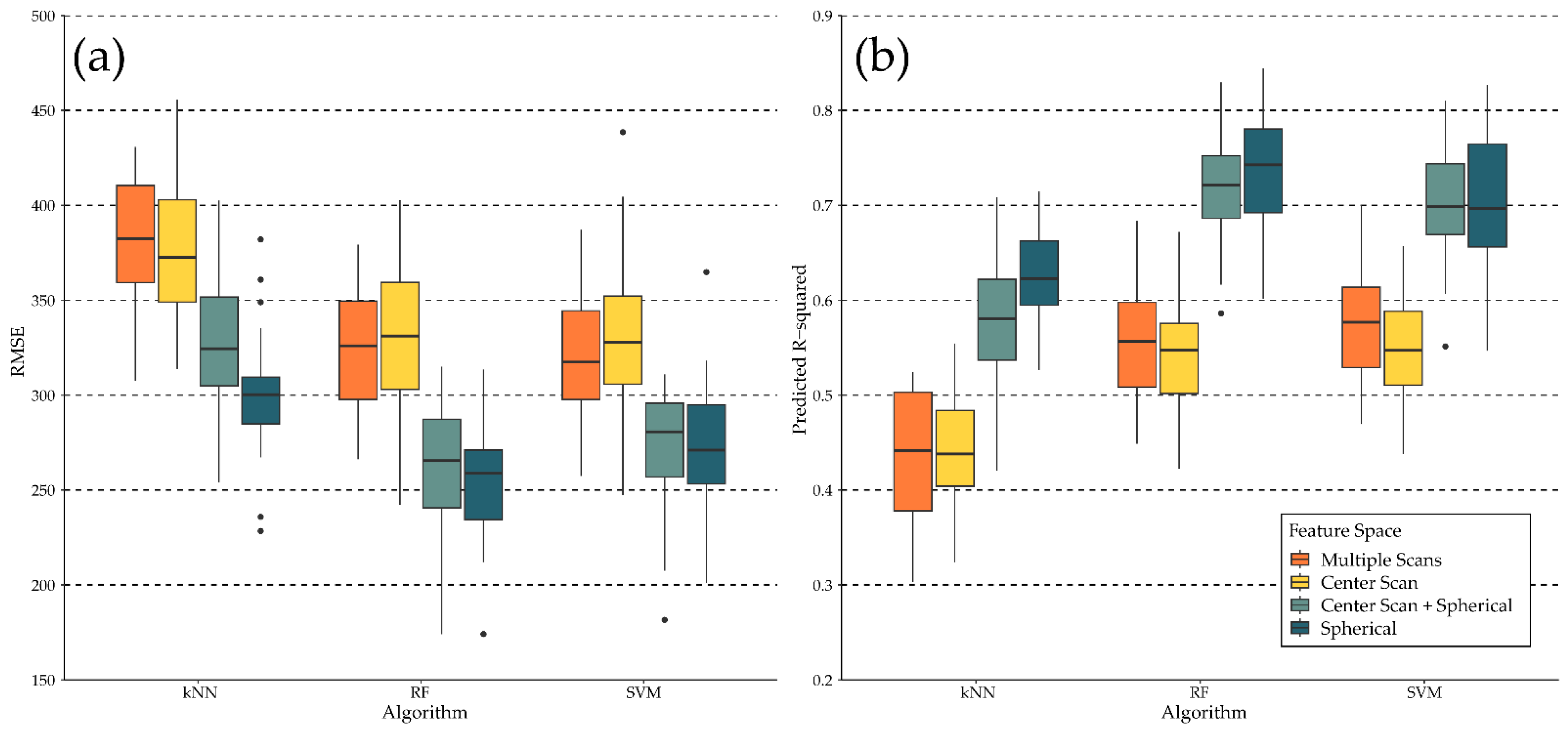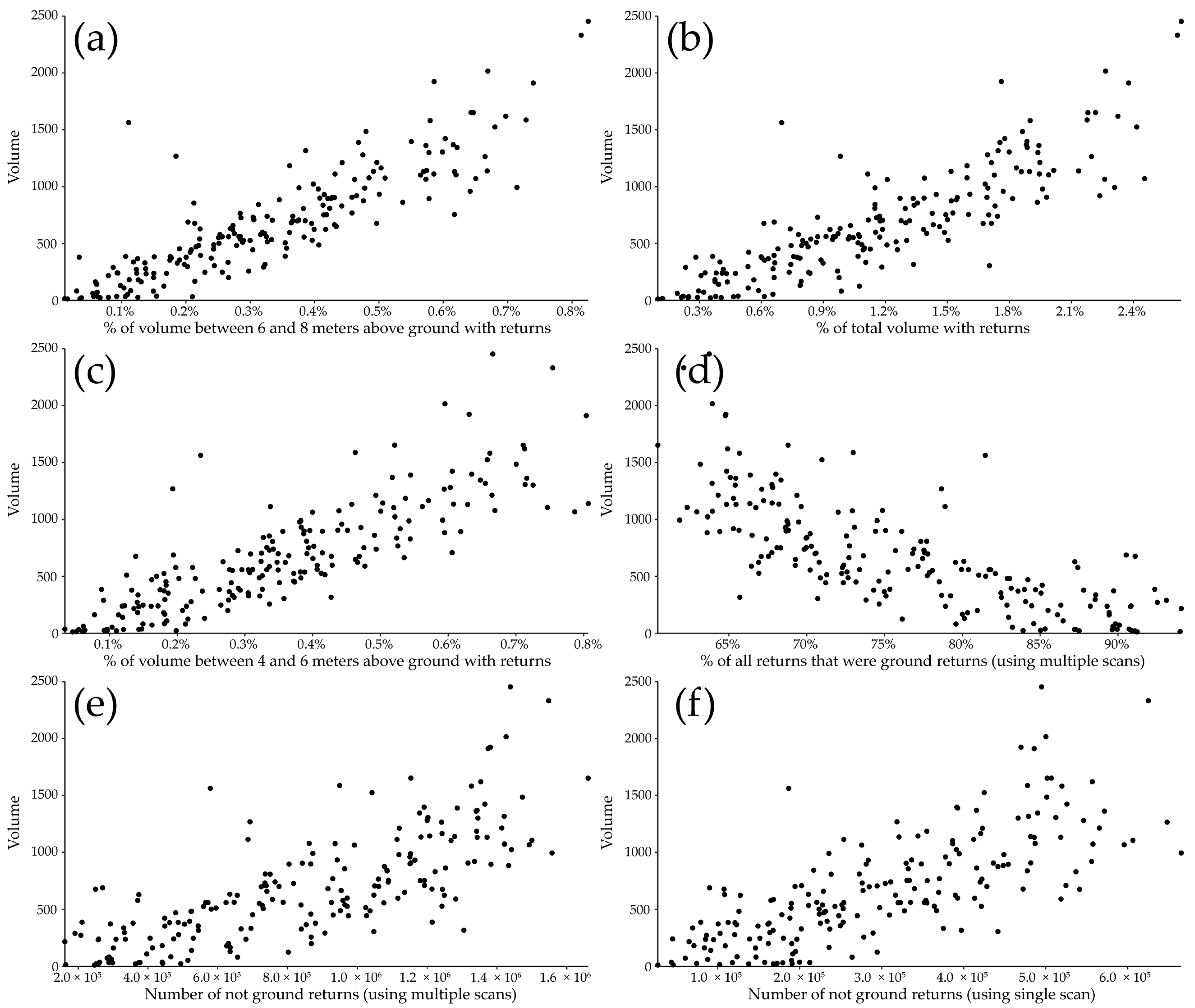Also, some of the multi-scan metrics were also shown to be highly correlated with the dependent variable, which makes sense since the multi-scan metrics generally outperformed the single-scan metrics.

5. Discussion and Future Work

Applications relying on point cloud data, either directly or using information derived from them for sustainable forest management, have increased over the last decade [48,62,85,86]. Thus, understanding how plot-scale forest structure and TLS scan location configuration and summarization methods influence the accuracy of estimated forest metrics is valuable for optimizing lidar acquisition for forest monitoring and remote sensing applications. This study describes a replicable, semi-automated approach for creating synthetic forest plots and simulating lidar point clouds. Furthermore, due to the benefit of known forest parameters, with set characteristics (materials and illumination source) and no noise within the simulated point cloud, it is possible to evaluate the impact of occlusion and performance of various methods and the errors associated with predictions. Conducting such experimentation is much more feasible than collecting field data and can also inform later field collections to optimize the value of the field data collected.
Our study specifically highlights variable algorithm performance, with the SVM and RF algorithms outperforming kNN for this specific task using the provided feature spaces. Further, the multi-scan metrics generally outperformed the single-scan metrics, even though the improvement was often marginal. In contrast, using metrics calculated from spherical voxels and designed to characterize areas of occlusion provided better predictive performance in comparison to more traditional summarization methods. This suggests that single-location scans may be adequate if summarized in a thoughtful manner.
Our results are similar to findings from studies based on “real-world” data [30,43,87,88]. For example, Wilkes et al. [89] investigated TLS sampling configurations for deriving forest plot-scale structure metrics and concluded that increasing the number of scan locations will always improve accuracy, regardless of scanner specifications or sampling approach. More similar to our approach, Yun et al. [49] adopted a computer simulation methodology to investigate virtual scanning patterns for estimating total leaf area. Their results suggest that only 25–38% of leaf area was retrieved and occlusion occurred on leaves distal to the scanner when the target tree was scanned from a single position. However, when three virtual scans were performed around a tree, the accuracy of leaf area recovery reached approximately 60–72%, and occlusion was restricted to just the crown center. Adding to these prior studies, our results highlight the value of considering alternative means to characterize the plot-level vegetation structure by using spherical voxels and metrics designed to characterize occlusion.
Predictor variables are required as input to models for estimating forest parameters from lidar. We used the metrics summarized in Table 2 to predict plot-level vegetation volume, while research using synthetic data for biomass estimations by Fassnacht et al. [17] did not consider any metrics derived from the point cloud, but instead restricted their analysis to metrics derived from canopy height models (only using the upper portion of lidar). Consequently, although they employed RF for predictions, a comparison between these two studies is difficult. Other studies have also made use of synthetic data to understand uncertainty and error propagation. Lovell et al. [90] modeled trees using simple geometric shapes (cones, ellipsoids, and cylinders), creating plantation stands, and simulated small footprint lidar data to determine the optimal acquisition parameters for measuring tree height. Disney et al. [52] used five experiments to quantify the impact of pulse density, scan angle, footprint size, and canopy structure for estimating canopy height and gave a detailed conclusion on each of these variables’ impact on canopy height estimation accuracy. However, different techniques were employed in both these studies to evaluate uncertainties. Therefore, comparisons between studies pose a challenge and highlight the need for a replicable method for evaluating uncertainty.
These results highlight some practical considerations for generating synthetic data in order to investigate the impact of collection characteristics and feature space. To conduct a similar experiment using real data would require selecting and measuring a large number of plots, collecting TLS data from multiple scan positions, and estimating the variable of interest, such as total above-ground-level biomass, using field methods, which may have a high level of uncertainty. This experiment using synthetic data generally suggest that the means of characterizing the plot-level conditions, in this case using more traditional versus spherical-based metrics, can have a large impact on predictive performance. Further, the spherical metrics, which were calculated using only the center scan, outperformed models created using data aggregated from all five scans. As a result, it may be possible to collect single scans and implement a more thoughtful summarization routine as opposed to collecting multiple scans of each field plot, which can greatly increase the cost and time of undertaking field campaigns. Further, multiple scans must be aligned and co-registered prior to the calculation of metrics, which increases the post-processing requirements and can induce errors resulting from imperfect co-registration or changes between scans, such as the movement of branches and leaves due to wind. It should be noted that these findings may not extrapolate to other parameters of interest or all forest community types with varying species compositions, ages, and structural characteristics.
Since we used this as a feasibility study for evaluating simulated lidar, some simplifications were made. This included using a limited number of vegetation species and having no overlapping trees and shrubs in the stand. In addition, all species had uniform foliage density and were assigned the same material characteristics, and we had flat ground terrain and a constant laser pulse. Future studies could develop more realistic forest stands with varying species compositions and landscape characteristics. Simulating a variety of landscapes would allow researchers to study how changes in species diversity and interactions impact ecosystem dynamics, health, and stability. It also allows researchers to explore a wide range of scenarios in a controlled environment, which could be beneficial for evaluating fire modeling and forest management practices. Moreover, researchers can investigate multifarious lidar-related aspects from acquisition to prediction. This could include investigating the effect of added noise to the point coordinates, for example, by simulating wind or beam divergence. How various scan configurations, including placement and scanner height, amount of overlap, and different vertical and horizonal field of views, impact prediction results could be investigated. Future research could also encompass exploring how prediction accuracy is influenced by the distance from the scanner, or how factors other than volume are affected by scan density. It would also be interesting to simulate terrain using digital elevation models (DEM) that represent the topography of the forest plot and evaluate how varying topography impacts model accuracy. It would also be useful to evaluate other metrics and algorithms for prediction. Simulated forest plots and TLS can also be used to test responses to extreme events, such as disasters or rare environmental conditions, without causing harm or damage in the real world, and to mimic long-term changes over short periods.
The focus of our future work will be to incorporate models of real-world objects, such as trees or shrubs modeled by quantitative structure models (QSMs), into the virtual space for further analysis, and work towards more realistic synthetic data sets, including terrain and topological features that are designed to mimic specific landscapes and serve as “digital twins” for experimentation and modeling.

6. Conclusions

In this study, we have presented a semi-automated approach for creating forest stands and simulating lidar. We have further investigated the impact of scan location and feature space for modeling forest parameters. Using the simulated lidar-derived metrics, we documented strong performances from the SVM (R-squared of 0.554) and RF (R-squared of 0.541) algorithms, slight improvements when combining multiple scans to calculate metrics, and more drastic improvements when incorporating spherical voxel-based metrics (R-squared of 0.697 and 0.738 for SVM and RF, respectively) designed to characterize occlusion.
Furthermore, we have highlighted the potential for using synthetic remote-sensing datasets to examine the lidar acquisition and scanning characteristics under controlled parameter sets that can be implemented across different forest stand complexities. This research allows us to reexamine existing methods and optimize workflows, data collection, and algorithm selection. Additionally, deep learning models are being incorporated into remote sensing applications, and the need for large datasets for training models is increasing; as such, synthetic datasets can provide a potential solution to this challenge as large realistic datasets can be generated in a precise, timely, and cost-effective manner. Synthetic modeling allows researchers to explore hypotheses that might be challenging to test directly in the field. It can also help identify gaps in current knowledge and guide further empirical research. Finally, it should be noted that the approach is not just limited to creating forest plots, but has a wider application in remote sensing as well as other fields.

Author Contributions

Conceptualization, M.S.B., A.E.M., M.R.G. and N.S.S.; data curation, M.S.B. and A.E.M.; formal analysis M.S.B., A.E.M. and I.N.; funding acquisition, A.E.M. and N.S.S.; investigation, M.S.B. and A.E.M.; supervision, A.E.M., N.S.S. and B.E.M.; writing—original draft preparation, M.S.B. and A.E.M.; validation, M.S.B., A.E.M. and M.R.G.; writing—review and editing, M.S.B., A.E.M., I.N., M.R.G., N.S.S. and B.E.M. All authors have read and agreed to the published version of the manuscript.

Funding

Funding was provided by the National Science Foundation (NSF) (Award Number: 2040676, “NSF Convergence Accelerator Track D: Artificial Intelligence and Community Driven Wildland Fire Innovation via a WIFIRE Commons Infrastructure for Data and Model Sharing”). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. This project was also funded by the USDA Forest Service Northern Research Station through joint venture agreement 20-JV-11242306-069 and the US Fish and Wildlife Service under grant number F21AC02192-00.

Data Availability Statement

Data and code associated with this study are available on the WV View webpage (https://www.wvview.org/research.html, accessed on 5 September 2023).

Acknowledgments

We would also like to thank 3 anonymous reviewers whose comments strengthened the work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Aravanopoulos, F.A. Conservation and Monitoring of Tree Genetic Resources in Temperate Forests. Curr. For. Rep. 2016, 2, 119–129. [Google Scholar] [CrossRef]
  2. Hu, T.; Sun, Y.; Jia, W.; Li, D.; Zou, M.; Zhang, M. Study on the Estimation of Forest Volume Based on Multi-Source Data. Sensors 2021, 21, 7796. [Google Scholar] [CrossRef]
  3. Waser, L.T.; Fischer, C.; Wang, Z.; Ginzler, C. Wall-to-Wall Forest Mapping Based on Digital Surface Models from Image-Based Point Clouds and a NFI Forest Definition. Forests 2015, 6, 4510–4528. [Google Scholar] [CrossRef]
  4. Loudermilk, E.L.; O’Brien, J.J.; Mitchell, R.J.; Cropper, W.P.; Hiers, J.K.; Grunwald, S.; Grego, J.; Fernandez-Diaz, J.C.; Loudermilk, E.L.; O’Brien, J.J.; et al. Linking Complex Forest Fuel Structure and Fire Behaviour at Fine Scales. Int. J. Wildland Fire 2012, 21, 882–893. [Google Scholar] [CrossRef]
  5. Parker, G.G.; Harding, D.J.; Berger, M.L. A Portable LIDAR System for Rapid Determination of Forest Canopy Structure. J. Appl. Ecol. 2004, 41, 755–767. [Google Scholar] [CrossRef]
  6. Liao, K.; Li, Y.; Zou, B.; Li, D.; Lu, D. Examining the Role of UAV Lidar Data in Improving Tree Volume Calculation Accuracy. Remote Sens. 2022, 14, 4410. [Google Scholar] [CrossRef]
  7. Vagizov, M.; Istomin, E.; Miheev, V.; Potapov, A. Visual Digital Forest Model Based on a Remote Sensing Data and Forest Inventory Data. Remote Sens. 2021, 13, 4092. [Google Scholar]
  8. Andersen, H.-E.; McGaughey, R.J.; Reutebuch, S.E. Estimating Forest Canopy Fuel Parameters Using LIDAR Data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
  9. Skowronski, N.S.; Clark, K.L.; Duveneck, M.; Hom, J. Three-Dimensional Canopy Fuel Loading Predicted Using Upward and Downward Sensing LiDAR Systems. Remote Sens. Environ. 2011, 115, 703–714. [Google Scholar] [CrossRef]
  10. James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
  11. Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6848-6. [Google Scholar]
  12. Alkhatib, R.; Sahwan, W.; Alkhatieb, A.; Schütt, B. A Brief Review of Machine Learning Algorithms in Forest Fires Science. Appl. Sci. 2023, 13, 8275. [Google Scholar] [CrossRef]
  13. Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
  14. Celebi, M.E.; Aydin, K. Unsupervised Learning Algorithms; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9. [Google Scholar]
  15. Hady, M.F.A.; Schwenker, F. Semi-Supervised Learning. Handb. Neural Inf. Process. 2013, 49, 215–239. [Google Scholar]
  16. Liu, W.; Liu, J.; Luo, B. Can Synthetic Data Improve Object Detection Results for Remote Sensing Images? arXiv 2020, arXiv:2006.05015. [Google Scholar]
  17. Fassnacht, F.E.; Latifi, H.; Hartig, F. Using Synthetic Data to Evaluate the Benefits of Large Field Plots for Forest Biomass Estimation with LiDAR. Remote Sens. Environ. 2018, 213, 115–128. [Google Scholar] [CrossRef]
  18. Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling Lidar-Derived Estimates of Forest Attributes over Space and Time: A Review of Approaches and Future Trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
  19. Sikkink, P.G.; Keane, R.E. A Comparison of Five Sampling Techniques to Estimate Surface Fuel Loading in Montane Forests. Int. J. Wildland Fire 2008, 17, 363–379. [Google Scholar] [CrossRef]
  20. Westfall, J.A.; Woodall, C.W. Measurement Repeatability of a Large-Scale Inventory of Forest Fuels. For. Ecol. Manag. 2007, 253, 171–176. [Google Scholar] [CrossRef]
  21. Xu, D.; Wang, H.; Xu, W.; Luan, Z.; Xu, X. LiDAR Applications to Estimate Forest Biomass at Individual Tree Scale: Opportunities, Challenges and Future Perspectives. Forests 2021, 12, 550. [Google Scholar] [CrossRef]
  22. Vandendaele, B.; Martin-Ducup, O.; Fournier, R.A.; Pelletier, G. Mobile and Terrestrial Laser Scanning for Tree Volume Estimation in Temperate Hardwood Forests. Available online: https://223.quebecconference.org/sites/223/files/documents/Extended_Abstract_Example_ICAG-CSRS_2022_Rev_02.pdf (accessed on 5 September 2023).
  23. Zhao, F.; Guo, Q.; Kelly, M. Allometric Equation Choice Impacts Lidar-Based Forest Biomass Estimates: A Case Study from the Sierra National Forest, CA. Agric. For. Meteorol. 2012, 165, 64–72. [Google Scholar] [CrossRef]
  24. Fehrmann, L.; Kleinn, C. General Considerations about the Use of Allometric Equations for Biomass Estimation on the Example of Norway Spruce in Central Europe. For. Ecol. Manag. 2006, 236, 412–421. [Google Scholar] [CrossRef]
  25. Basuki, T.; Van Laake, P.; Skidmore, A.; Hussin, Y. Allometric Equations for Estimating the above-Ground Biomass in Tropical Lowland Dipterocarp Forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
  26. Henry, M.; Bombelli, A.; Trotta, C.; Alessandrini, A.; Birigazzi, L.; Sola, G.; Vieilledent, G.; Santenoise, P.; Longuetaud, F.; Valentini, R.; et al. GlobAllomeTree: International Platform for Tree Allometric Equations to Support Volume, Biomass and Carbon Assessment. Iforest-Biogeosci. For. 2013, 6, 326. [Google Scholar] [CrossRef]
  27. Gao, T.; Gao, Z.; Sun, B.; Qin, P.; Li, Y.; Yan, Z. An Integrated Method for Estimating Forest-Canopy Closure Based on UAV LiDAR Data. Remote Sens. 2022, 14, 4317. [Google Scholar] [CrossRef]
  28. Silva, A.G.P.; Görgens, E.B.; Campoe, O.C.; Alvares, C.A.; Stape, J.L.; Rodriguez, L.C.E. Assessing Biomass Based on Canopy Height Profiles Using Airborne Laser Scanning Data in Eucalypt Plantations. Sci. Agric. 2015, 72, 504–512. [Google Scholar] [CrossRef]
  29. Mayamanikandan, T.; Reddy, R.S.; Jha, C. Non-Destructive Tree Volume Estimation Using Terrestrial Lidar Data in Teak Dominated Central Indian Forests. In Proceedings of the 2019 IEEE Recent Advances in Geoscience and Remote Sensing: Technologies, Standards and Applications (TENGARSS), Kochi, India, 17–20 October 2019; pp. 100–103. [Google Scholar]
  30. Saarinen, N.; Kankare, V.; Vastaranta, M.; Luoma, V.; Pyörälä, J.; Tanhuanpää, T.; Liang, X.; Kaartinen, H.; Kukko, A.; Jaakkola, A.; et al. Feasibility of Terrestrial Laser Scanning for Collecting Stem Volume Information from Single Trees. ISPRS J. Photogramm. Remote Sens. 2017, 123, 140–158. [Google Scholar] [CrossRef]
  31. Gonsalves, M.O. A Comprehensive Uncertainty Analysis and Method of Geometric Calibration for a Circular Scanning Airborne Lidar; The University of Southern Mississippi: Hattiesburg, MS, USA, 2010; ISBN 1-124-40472-4. [Google Scholar]
  32. Gonzalez, P.; Asner, G.P.; Battles, J.J.; Lefsky, M.A.; Waring, K.M.; Palace, M. Forest Carbon Densities and Uncertainties from Lidar, QuickBird, and Field Measurements in California. Remote Sens. Environ. 2010, 114, 1561–1575. [Google Scholar] [CrossRef]
  33. Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and Wood Classification Framework for Terrestrial LiDAR Point Clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
  34. Moorthy, I.; Miller, J.R.; Berni, J.A.J.; Zarco-Tejada, P.; Hu, B.; Chen, J. Field Characterization of Olive (Olea europaea L.) Tree Crown Architecture Using Terrestrial Laser Scanning Data. Agric. For. Meteorol. 2011, 151, 204–214. [Google Scholar] [CrossRef]
  35. Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-Footprint Lidar Estimation of Sub-Canopy Elevation and Tree Height in a Tropical Rain Forest Landscape. Remote Sens. Environ. 2004, 91, 68–89. [Google Scholar] [CrossRef]
  36. Disney, M. Terrestrial LiDAR: A Three-Dimensional Revolution in How We Look at Trees. New Phytol. 2019, 222, 1736–1741. [Google Scholar] [CrossRef]
  37. Malambo, L.; Popescu, S.C.; Horne, D.W.; Pugh, N.A.; Rooney, W.L. Automated Detection and Measurement of Individual Sorghum Panicles Using Density-Based Clustering of Terrestrial Lidar Data. ISPRS J. Photogramm. Remote Sens. 2019, 149, 1–13. [Google Scholar] [CrossRef]
  38. Abegg, M.; Boesch, R.; Schaepman, M.E.; Morsdorf, F. Impact of Beam Diameter and Scanning Approach on Point Cloud Quality of Terrestrial Laser Scanning in Forests. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8153–8167. [Google Scholar] [CrossRef]
  39. Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, S.; Seielstad, C.; Queen, L.l.; O’Brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling Terrestrial Laser Scanning with 3D Fuel Biomass Sampling for Advancing Wildland Fuels Characterization. For. Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
  40. Rowell, E.; Loudermilk, E.L.; Seielstad, C.; O’Brien, J.J. Using Simulated 3D Surface Fuelbeds and Terrestrial Laser Scan Data to Develop Inputs to Fire Behavior Models. Can. J. Remote Sens. 2016, 42, 443–459. [Google Scholar] [CrossRef]
  41. Rowell, E.M.; Seielstad, C.A.; Ottmar, R.D.; Rowell, E.M.; Seielstad, C.A.; Ottmar, R.D. Development and Validation of Fuel Height Models for Terrestrial Lidar—RxCADRE 2012. Int. J. Wildland Fire 2015, 25, 38–47. [Google Scholar] [CrossRef]
  42. Alonso-Benito, A.; Arroyo, L.; Arbelo, M.; Hernández-Leal, P. Fusion of WorldView-2 and LiDAR Data to Map Fuel Types in the Canary Islands. Remote Sens. 2016, 8, 669. [Google Scholar] [CrossRef]
  43. Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
  44. Tao, S.; Labrière, N.; Calders, K.; Fischer, F.J.; Rau, E.-P.; Plaisance, L.; Chave, J. Mapping Tropical Forest Trees across Large Areas with Lightweight Cost-Effective Terrestrial Laser Scanning. Ann. For. Sci. 2021, 78, 103. [Google Scholar] [CrossRef]
  45. Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated Impact of Sample Plot Size and Co-Registration Error on the Accuracy and Uncertainty of LiDAR-Derived Estimates of Forest Stand Biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
  46. Wang, L.; Birt, A.G.; Lafon, C.W.; Cairns, D.M.; Coulson, R.N.; Tchakerian, M.D.; Xi, W.; Popescu, S.C.; Guldin, J.M. Computer-Based Synthetic Data to Assess the Tree Delineation Algorithm from Airborne LiDAR Survey. Geoinformatica 2013, 17, 35–61. [Google Scholar] [CrossRef]
  47. Jiang, K.; Chen, L.; Wang, X.; An, F.; Zhang, H.; Yun, T. Simulation on Different Patterns of Mobile Laser Scanning with Extended Application on Solar Beam Illumination for Forest Plot. Forests 2022, 13, 2139. [Google Scholar] [CrossRef]
  48. White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
  49. Yun, T.; Cao, L.; An, F.; Chen, B.; Xue, L.; Li, W.; Pincebourde, S.; Smith, M.J.; Eichhorn, M.P. Simulation of Multi-Platform LiDAR for Assessing Total Leaf Area in Tree Crowns. Agric. For. Meteorol. 2019, 276, 107610. [Google Scholar] [CrossRef]
  50. Goodwin, N.; Coops, N.; Culvenor, D. Development of a Simulation Model to Predict LiDAR Interception in Forested Environments. Remote Sens. Environ. 2007, 111, 481–492. [Google Scholar] [CrossRef]
  51. Sun, G.; Ranson, K.J. Modeling Lidar Returns from Forest Canopies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2617–2626. [Google Scholar] [CrossRef]
  52. Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the Impact of Discrete-Return Lidar System and Survey Characteristics over Young Conifer and Broadleaf Forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
  53. Loidi Arregui, J.J.; Marcenò, C. The Temperate Deciduous Forests of the Northern Hemisphere. A Review. Mediterr. Bot. 2022, 43, e75527. [Google Scholar] [CrossRef]
  54. Hartley, F.M.; Maxwell, A.E.; Landenberger, R.E.; Bortolot, Z.J. Forest Type Differentiation Using GLAD Phenology Metrics, Land Surface Parameters, and Machine Learning. Geographies 2022, 2, 491–515. [Google Scholar] [CrossRef]
  55. Zhang, Z.; Li, X.; Liu, H. Biophysical Feedback of Forest Canopy Height on Land Surface Temperature over Contiguous United States. Environ. Res. Lett. 2022, 17, 034002. [Google Scholar] [CrossRef]
  56. Fei, S.; Yang, P. Forest Composition Change in the Eastern United States. In Proceedings of the 17th Central Hardwood Forest Conference, Lexington, KY, USA, 5–7 April 2010. [Google Scholar]
  57. U.S. National Park Service Eastern Deciduous Forest. Available online: https://www.nps.gov/im/ncrn/eastern-deciduous-forest.htm (accessed on 29 October 2022).
  58. Olson, D.M.; Dinerstein, E. The Global 200: Priority Ecoregions for Global Conservation. Ann. Mo. Bot. Gard. 2002, 89, 199–224. [Google Scholar] [CrossRef]
  59. van der Walt, L. What Are Meshes in 3D Modeling? Available online: http://wedesignvirtual.com/what-are-meshes-in-3d-modeling/ (accessed on 30 October 2022).
  60. Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Hermosilla, T. Analysis of the Factors Affecting LiDAR DTM Accuracy in a Steep Shrub Area. Int. J. Digit. Earth 2011, 4, 521–538. [Google Scholar] [CrossRef]
  61. Campbell, M.J.; Dennison, P.E.; Hudak, A.T.; Parham, L.M.; Butler, B.W. Quantifying Understory Vegetation Density Using Small-Footprint Airborne Lidar. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
  62. Contreras, M.A.; Staats, W.; Yiang, J.; Parrott, D. Quantifying the Accuracy of LiDAR-Derived DEM in Deciduous Eastern Forests of the Cumberland Plateau. J. Geogr. Inf. Syst. 2017, 9, 339–353. [Google Scholar] [CrossRef]
  63. Admin_Stanpro Reflection of Light: What Is Specular Reflection. Stanpro. 2018. Available online: https://www.standardpro.com/what-is-specular-reflection/ (accessed on 5 September 2023).
  64. Poirier-Quinot, D.; Noisternig, M.; Katz, B.F. EVERTims: Open Source Framework for Real-Time Auralization in VR. In Proceedings of the 12th International Audio Mostly Conference on Augmented and Participatory Sound and Music Experiences; 2017; pp. 1–5. Available online: https://dl.acm.org/doi/10.1145/3123514.3123559 (accessed on 5 September 2023).
  65. Reitmann, S.; Neumann, L.; Jung, B. BLAINDER—A Blender AI Add-on for Generation of Semantically Labeled Depth-Sensing Data. Sensors 2021, 21, 2144. [Google Scholar] [CrossRef] [PubMed]
  66. Gusmão, G.F.; Barbosa, C.R.H.; Raposo, A.B.; de Oliveira, R.C. A LiDAR System Simulator Using Parallel Raytracing and Validated by Comparison with a Real Sensor. J. Phys. Conf. Ser. 2021, 1826, 012002. [Google Scholar] [CrossRef]
  67. Scratchpixel An Overview of the Ray-Tracing Rendering Technique. Available online: https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-overview/ray-tracing-rendering-technique-overview (accessed on 3 November 2022).
  68. Disney, M.; Lewis, P.; North, P. Monte Carlo Ray Tracing in Optical Canopy Reflectance Modelling. Remote Sens. Rev. 2000, 18, 163–196. [Google Scholar] [CrossRef]
  69. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
  70. Roussel, J.-R.; Auty, D. Airborne LiDAR Data Manipulation and Visualization for Forestry Applications; R Package Version 3.1. 2022. Available online: https://cran.r-project.org/package=lidR (accessed on 5 September 2023).
  71. Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.-F.; De Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
  72. Roussel, J.-R.; De Boissieu, F. rlas: Read and Write ‘las’ and ‘laz’ Binary File Formats Used for Remote Sensing Data; R package version 1.6.2. 2023. Available online: https://CRAN.R-project.org/package=rlas (accessed on 5 September 2023).
  73. Paula, C. Sanematsu Interactive 3D Visualization and Post-Processing Analysis of Vertex-Based Unstructured Polyhedral Meshes with ParaView. bioRxiv 2021. [Google Scholar] [CrossRef]
  74. Brownlee, C.; DeMarle, D. Fast Volumetric Gradient Shading Approximations for Scientific Ray Tracing. In Ray Tracing Gems II: Next Generation Real-Time Rendering with DXR, Vulkan, and OptiX; Marrs, A., Shirley, P., Wald, I., Eds.; Apress: Berkeley, CA, USA, 2021; pp. 725–733. ISBN 978-1-4842-7185-8. [Google Scholar]
  75. Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine Learning in Geosciences and Remote Sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
  76. Yu, P. Research and Prediction of Ecological Footprint Using Machine Learning: A Case Study of China. In Proceedings of the 2022 International Conference on Big Data, Information and Computer Network (BDICN), Sanya, China, 20–22 January 2022; pp. 112–116. [Google Scholar]
  77. Hamilton, D.; Pacheco, R.; Myers, B.; Peltzer, B. KNN vs. SVM: A Comparison of Algorithms. In Proceedings of the Fire Continuum-Preparing for the Future of Wildland Fire, Missoula, MT, USA, 21–24 May 2018; Hood, S.M., Drury, S., Steelman, T., Steffens, R., Eds.; Proceedings RMRS-P-78. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2020; Volume 78, pp. 95–109. [Google Scholar]
  78. Fletcher, T. Support Vector Machines Explained. Tutor. Pap. 2009, 1–19. [Google Scholar]
  79. Duda, R.O.; Hart, P.E. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 81-265-1116-8. [Google Scholar]
  80. Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
  81. Kuhn, M. Caret: Classification and Regression Training; R Package Version 6.0-90. 2021. Available online: https://CRAN.R-project.org/package=caret (accessed on 5 September 2023).
  82. Karatzoglou, A.; Smola, A.; Hornik, K.; Karatzoglou, M.A.; SparseM, S.; Yes, L.; The Kernlab Package. Kernel-Based Machine Learning Lab. R Package Version 0.9.-22. 2017. Available online: https://cran.r-project.org/web/packages/kernlab (accessed on 4 November 2015).
  83. Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
  84. Kuhn, M.; Vaughan, D. Yardstick: Tidy Characterizations of Model Performance. 2021. Available online: https://cran.r-project.org/web/packages/yardstick/index.html (accessed on 5 September 2023).
  85. Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest Neighbor Imputation of Species-Level, Plot-Scale Forest Structure Attributes from LiDAR Data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
  86. Hernando, A.; Sobrini, I.; Velázquez, J.; García-Abril, A. The Importance of Protected Habitats and LiDAR Data Availability for Assessing Scenarios of Land Uses in Forest Areas. Land Use Policy 2022, 112, 105859. [Google Scholar] [CrossRef]
  87. Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of Methods of Small-footprint Airborne Laser Scanning for Extracting Forest Inventory Data in Boreal Forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
  88. Watt, P.J.; Donoghue, D.N.M. Measuring Forest Structure with Terrestrial Laser Scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
  89. Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; Gonzalez de Tanago, J.; Bartholomeus, H.; Brede, B.; Herold, M. Data Acquisition Considerations for Terrestrial Laser Scanning of Forest Plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
  90. Lovell, J.; Jupp, D.; Newnham, G.; Coops, N.; Culvenor, D. Simulation Study for Finding Optimal Lidar Acquisition Parameters for Forest Height Retrieval. For. Ecol. Manag. 2005, 214, 398–412. [Google Scholar] [CrossRef]
Remotesensing 15 04407 g001
Figure 1. (a) Example of a densely populated forest plot with zoomed insets of oak and pine leaf structure. (b) Example of a sparsely populated forest plot with zoomed insets illustrating an opaque trunk and hatched (50%) transparency for the canopy.
Figure 1. (a) Example of a densely populated forest plot with zoomed insets of oak and pine leaf structure. (b) Example of a sparsely populated forest plot with zoomed insets illustrating an opaque trunk and hatched (50%) transparency for the canopy.
Remotesensing 15 04407 g001
Remotesensing 15 04407 g002
Figure 2. Scanner location configuration within the virtual plot (light brown square) with 30 m square box (blue planes). For visualization purposes, the top view excludes the top and bottom sides of the box, while the side view excludes the front plane.
Figure 2. Scanner location configuration within the virtual plot (light brown square) with 30 m square box (blue planes). For visualization purposes, the top view excludes the top and bottom sides of the box, while the side view excludes the front plane.
Remotesensing 15 04407 g002
Remotesensing 15 04407 g003
Figure 3. Conceptualization of vertical height bins used to calculate summary metrics. Vegetation is represented as synthetic TLS point clouds.
Figure 3. Conceptualization of vertical height bins used to calculate summary metrics. Vegetation is represented as synthetic TLS point clouds.
Remotesensing 15 04407 g003
Remotesensing 15 04407 g004
Figure 4. Conceptualization of transformation into spherical coordinates (θ, φ, r) from Cartesian coordinates (X, Y, Z) relative to the sensor location. (a) θ, φ, r relative to X, Y, and Z axes. (b) Angles of θ relative to a plane defined by the X and Y axes. (c) Angle of φ defined by angle relative to the Z axis.
Figure 4. Conceptualization of transformation into spherical coordinates (θ, φ, r) from Cartesian coordinates (X, Y, Z) relative to the sensor location. (a) θ, φ, r relative to X, Y, and Z axes. (b) Angles of θ relative to a plane defined by the X and Y axes. (c) Angle of φ defined by angle relative to the Z axis.
Remotesensing 15 04407 g004
Remotesensing 15 04407 g005
Figure 5. Summarization of areas of gaps, areas of occlusion and percent of pulses reaching a spherical voxel that returned from that voxel using a spherical coordinate system. (a,b) represent angles of θ and φ segmented into ranges of r while (c) conceptualizes the calculation of the percentage of pulses returned from a volume and determination of what volumes were occluded.
Figure 5. Summarization of areas of gaps, areas of occlusion and percent of pulses reaching a spherical voxel that returned from that voxel using a spherical coordinate system. (a,b) represent angles of θ and φ segmented into ranges of r while (c) conceptualizes the calculation of the percentage of pulses returned from a volume and determination of what volumes were occluded.
Remotesensing 15 04407 g005
Remotesensing 15 04407 g006
Figure 6. Conceptualization of spherical voxels and summarization process. (a) Original synthetic plot; (b) scan of synthetic plot; (c) conversion to spherical voxels and calculation of occlusion; (d) summarization at different range distances.
Figure 6. Conceptualization of spherical voxels and summarization process. (a) Original synthetic plot; (b) scan of synthetic plot; (c) conversion to spherical voxels and calculation of occlusion; (d) summarization at different range distances.
Remotesensing 15 04407 g006
Remotesensing 15 04407 g007
Figure 7. Distribution of known forest metrics. (a) Violin plot of the distribution of surface volume across the plots and (b) histogram of individual plot volumes. Black dots in (a) represent samples that are further than 1.5 IQR from the 1st or 3rd quartile.
Figure 7. Distribution of known forest metrics. (a) Violin plot of the distribution of surface volume across the plots and (b) histogram of individual plot volumes. Black dots in (a) represent samples that are further than 1.5 IQR from the 1st or 3rd quartile.
Remotesensing 15 04407 g007
Remotesensing 15 04407 g008
Figure 8. Bar graph depicting the percentage of surface area occlusion for all scans (blue) and only the middle scan (green) per plot.
Figure 8. Bar graph depicting the percentage of surface area occlusion for all scans (blue) and only the middle scan (green) per plot.
Remotesensing 15 04407 g008
Remotesensing 15 04407 g009
Figure 9. Distribution of RMSE (a) and predicted R-squared (b) for 20 replicates of kNN, SVM, and RF models using four different feature spaces. Black dots represent samples that are further than 1.5 IQR from the 1st or 3rd quartile.
Figure 9. Distribution of RMSE (a) and predicted R-squared (b) for 20 replicates of kNN, SVM, and RF models using four different feature spaces. Black dots represent samples that are further than 1.5 IQR from the 1st or 3rd quartile.
Remotesensing 15 04407 g009
Remotesensing 15 04407 g010
Figure 10. (a–f) Scatterplots comparing the six predictor variables with the highest Spearman correlation coefficient with the dependent variable (total plot-level vegetation volume).
Figure 10. (a–f) Scatterplots comparing the six predictor variables with the highest Spearman correlation coefficient with the dependent variable (total plot-level vegetation volume).
Remotesensing 15 04407 g010
Table 1. Initial model dimensions and randomization thresholds of 3D models placed within a forest plot.
Table 1. Initial model dimensions and randomization thresholds of 3D models placed within a forest plot.
ModelMi * Height (Z)Mi Crown Dimensions (X, Y) Randomization Threshold (min, max) Random Rotation
(X, Y, Z)
Pine 115.0 m5.0 m, 6.0 m60%, 130%(±4°, ±4°, 360°)
Pine 210.0 m4.0 m, 4.5 m60%, 130%(±4°, ±4°, 360°)
Oak12.0 m5.0 m, 6.0 m60%, 130%(±4°, ±4°, 360°)
Maple8.0 m3.8 m, 3.8 m50%, 150%(±4°, ±4°, 360°)
Shrub1.5 m2.2 m, 1.8 m40%, 150%(±4°, ±4°, 360°)
* Mi is the initial model dimensions before randomization.
Table 2. Summary metrics generated from the point cloud data using only the center scan, all merged scans, and only the center scan summarized using spherical voxels.
Table 2. Summary metrics generated from the point cloud data using only the center scan, all merged scans, and only the center scan summarized using spherical voxels.
Metric SubsetVariableCount of Variables
All returnsGround return count2
Not ground count2
Percent ground2
All non-ground returnsMean Z2
Median Z2
Standard deviation Z2
Skewness Z2
Kurtosis Z2
Percentiles (10% to 9% by 10%)18
Non-ground returns by height strataReturn count10
Percent of all non-ground returns in strata10
Mean Z10
Median Z10
Standard Deviation Z10
Skewness Z10
Kurtosis Z10
Spherical-based
(total and by height bin)		Percent of area occluded6
Percent of area with returns6
Percent of area with gaps6
Spherical-based
(by height bin)		Mean proportion of pulses returned5
Total 127
Table 3. Descriptive statistics of known volume across the synthetic plots.
Table 3. Descriptive statistics of known volume across the synthetic plots.
Descriptive StatisticVolume (m3)
Minimum11.72
Maximum2453.66
1st Quartile324.56
Median593.56
3rd Quartile964.19
Mean679.22
Standard deviation475.44
Interquartile range (IQR)639.63
Table 4. Descriptive statistics of the percentage of surface area occlusion across the synthetic plots.
Table 4. Descriptive statistics of the percentage of surface area occlusion across the synthetic plots.
Descriptive StatisticMiddle Scan OnlyAll Scans
Minimum0.84%0.68%
Maximum25.84%13.26%
Mean10.53%5.14%
Variance33.21%6.15%
Standard deviation5.76%2.48%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bester, M.S.; Maxwell, A.E.; Nealey, I.; Gallagher, M.R.; Skowronski, N.S.; McNeil, B.E. Synthetic Forest Stands and Point Clouds for Model Selection and Feature Space Comparison. Remote Sens. 2023, 15, 4407. https://doi.org/10.3390/rs15184407

AMA Style

Bester MS, Maxwell AE, Nealey I, Gallagher MR, Skowronski NS, McNeil BE. Synthetic Forest Stands and Point Clouds for Model Selection and Feature Space Comparison. Remote Sensing. 2023; 15(18):4407. https://doi.org/10.3390/rs15184407

Chicago/Turabian Style

Bester, Michelle S., Aaron E. Maxwell, Isaac Nealey, Michael R. Gallagher, Nicholas S. Skowronski, and Brenden E. McNeil. 2023. "Synthetic Forest Stands and Point Clouds for Model Selection and Feature Space Comparison" Remote Sensing 15, no. 18: 4407. https://doi.org/10.3390/rs15184407

APA Style

Bester, M. S., Maxwell, A. E., Nealey, I., Gallagher, M. R., Skowronski, N. S., & McNeil, B. E. (2023). Synthetic Forest Stands and Point Clouds for Model Selection and Feature Space Comparison. Remote Sensing, 15(18), 4407. https://doi.org/10.3390/rs15184407

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop