Spatiotemporal Variation in Driving Factors of Vegetation Dynamics in the Yellow River Delta Estuarine Wetlands from 2000 to 2020
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Preprocessing
2.2.1. Remote Sensing Data
- (1)
- MODIS
- (2)
- Landsat
- (3)
- Remote Sensing Data Pre-Processing
2.2.2. Meteorological Data
2.2.3. Distribution Data of Spartina alterniflora
2.2.4. Runoff Data
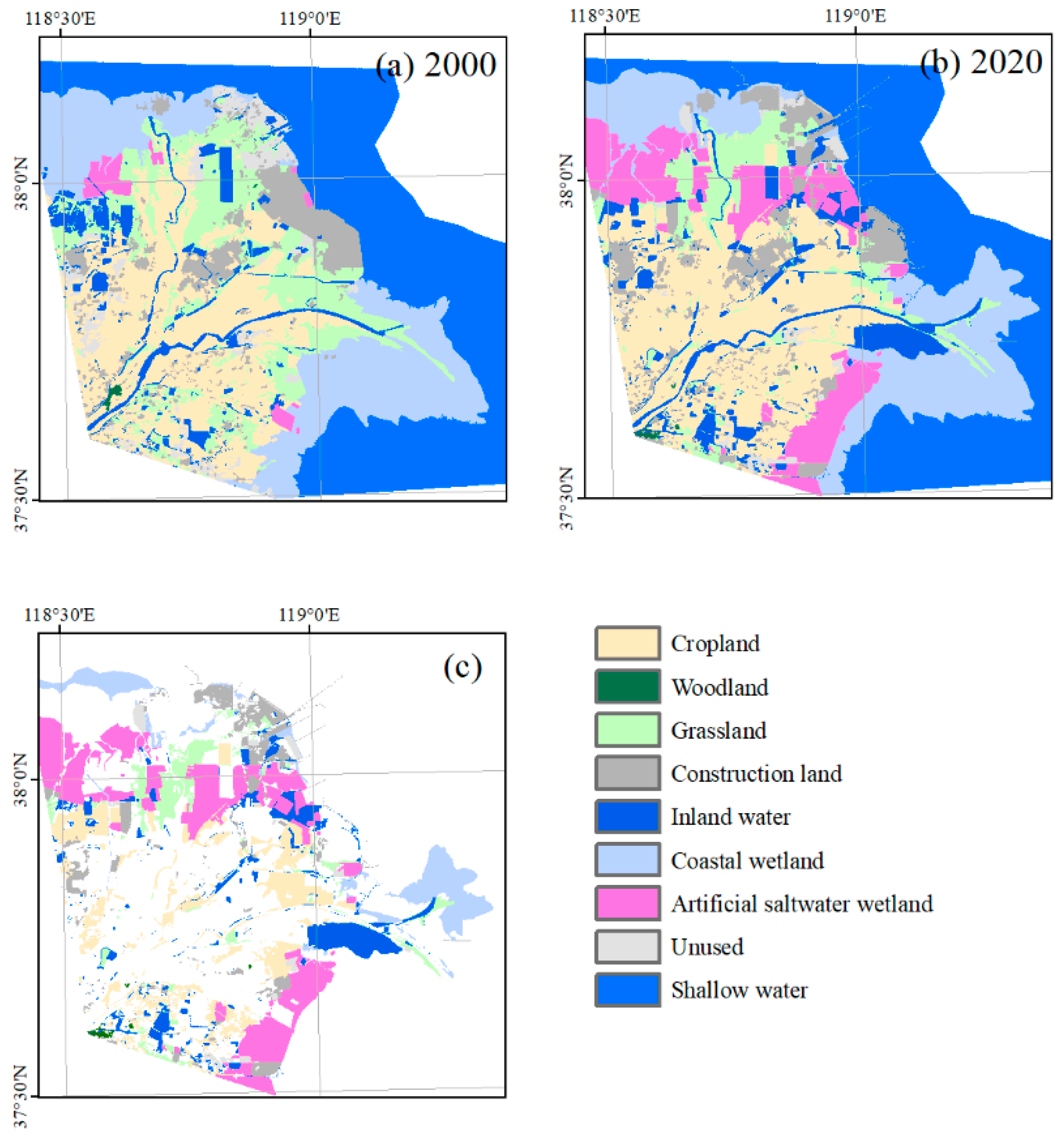
2.2.5. Landcover Data
2.3. Methods
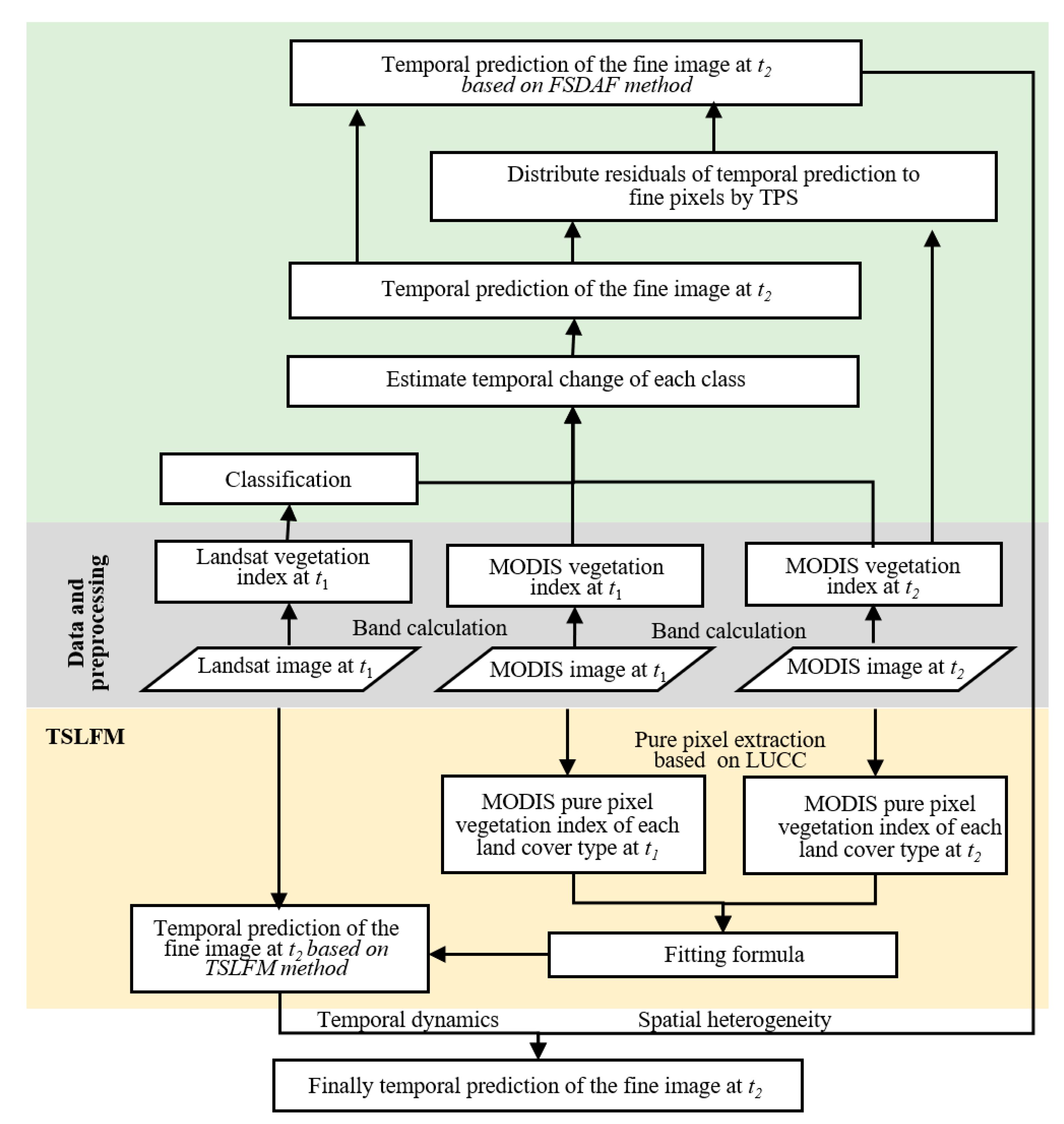
2.3.1. FSDAF Method
- (1)
- Classification of fine-resolution image
- (2)
- Temporal dynamics estimation
- (3)
- Prediction of fine-resolution image
- (4)
- Identify TPS interpolation to guide residual distribution
- (5)
- Distribute residuals to fine pixels
- (6)
- Robust prediction of fine image using neighborhood
2.3.2. TSLFM Method
- (1)
- Extraction of pure pixels
- (2)
- Construction of correlation function
- (3)
- Prediction of fine image
2.3.3. Integration of Simulation Results of FSDAF and TSLFM Methods
2.4. Statistical Analysis
3. Results
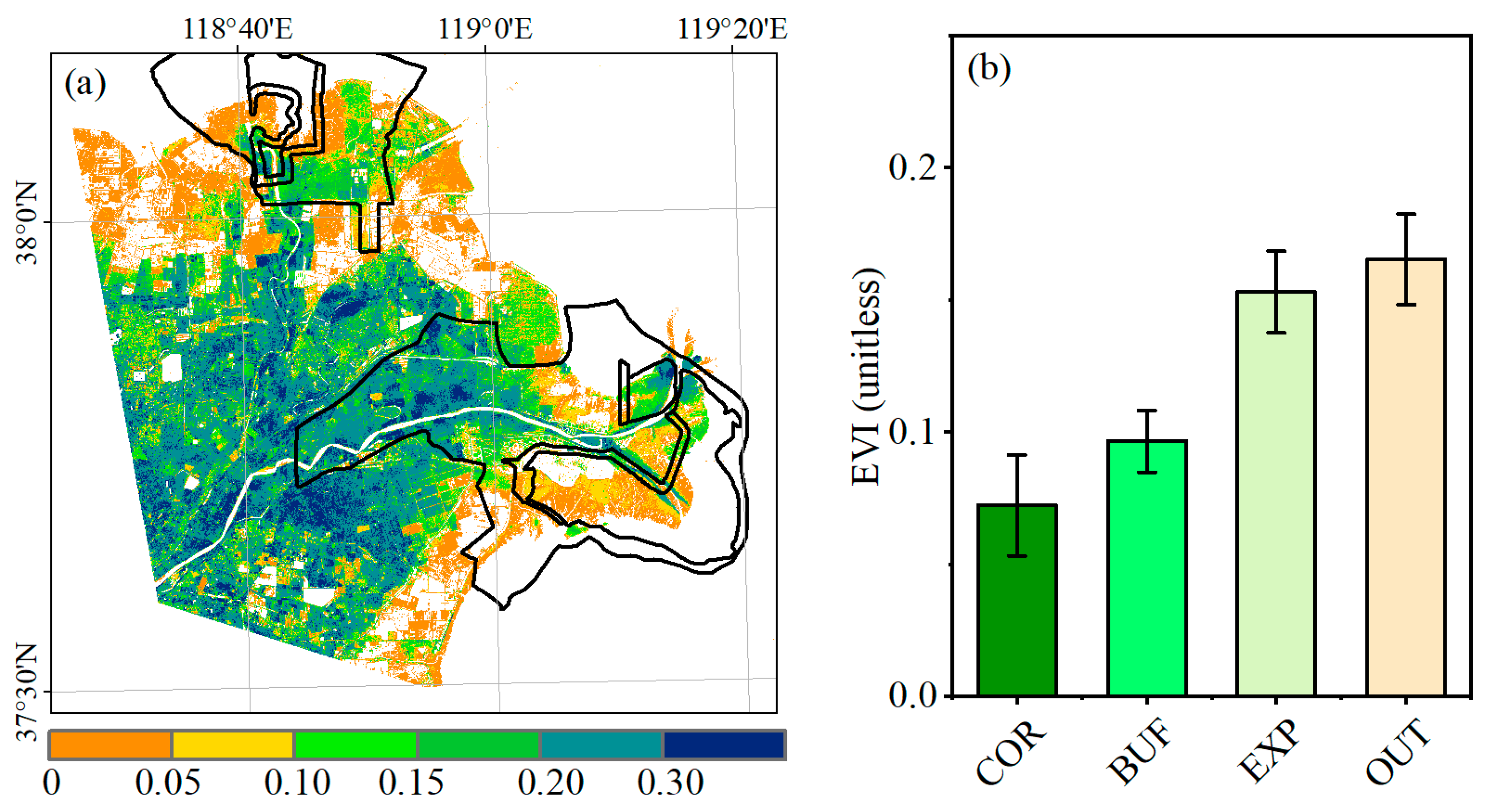
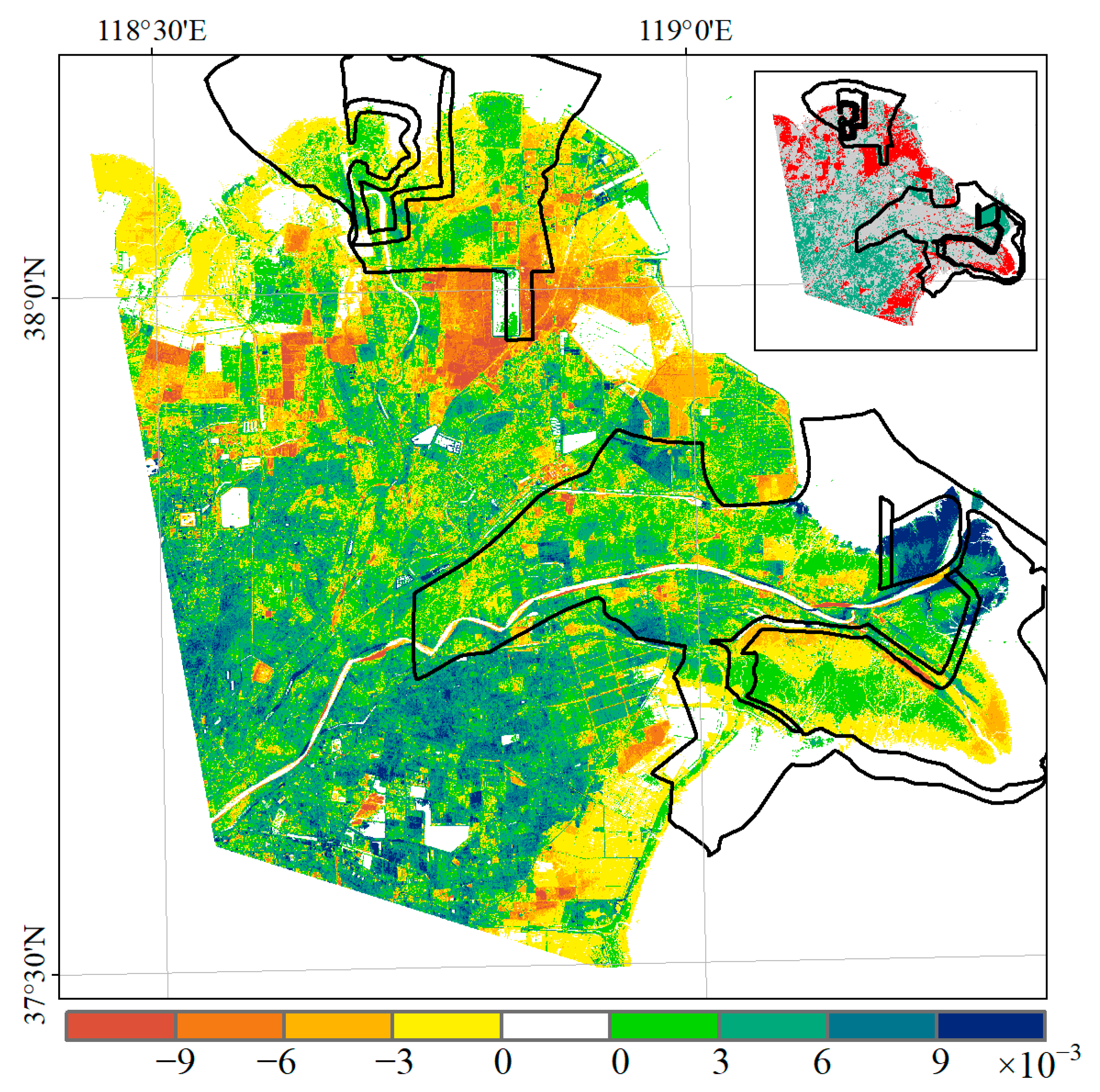
3.1. Spatial Pattern of Vegetation Variations
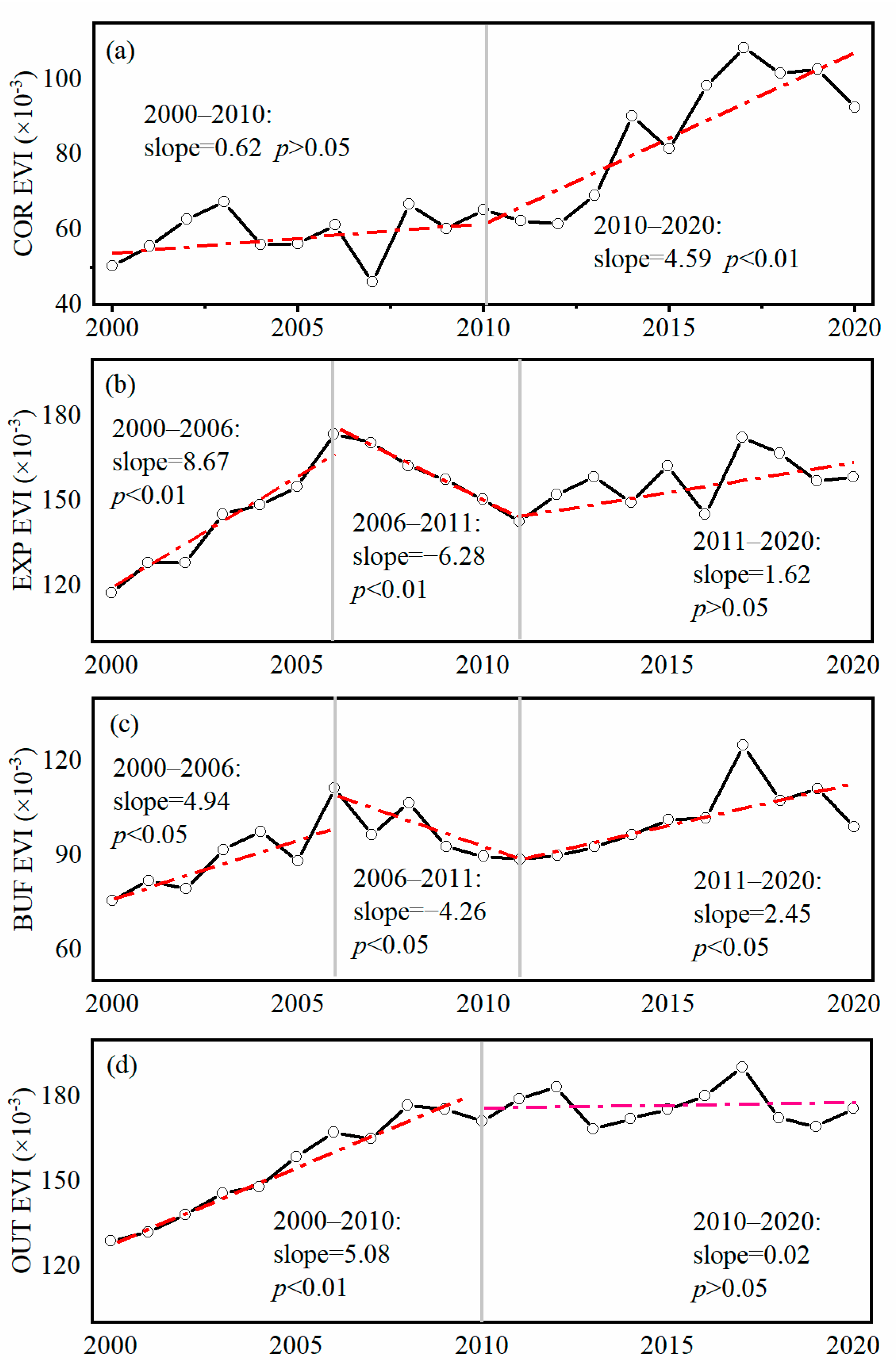
3.2. The Temporal Trends of the Fused EVI
3.3. The Driving Factors of Vegetation Variations in the YRD
4. Discussion
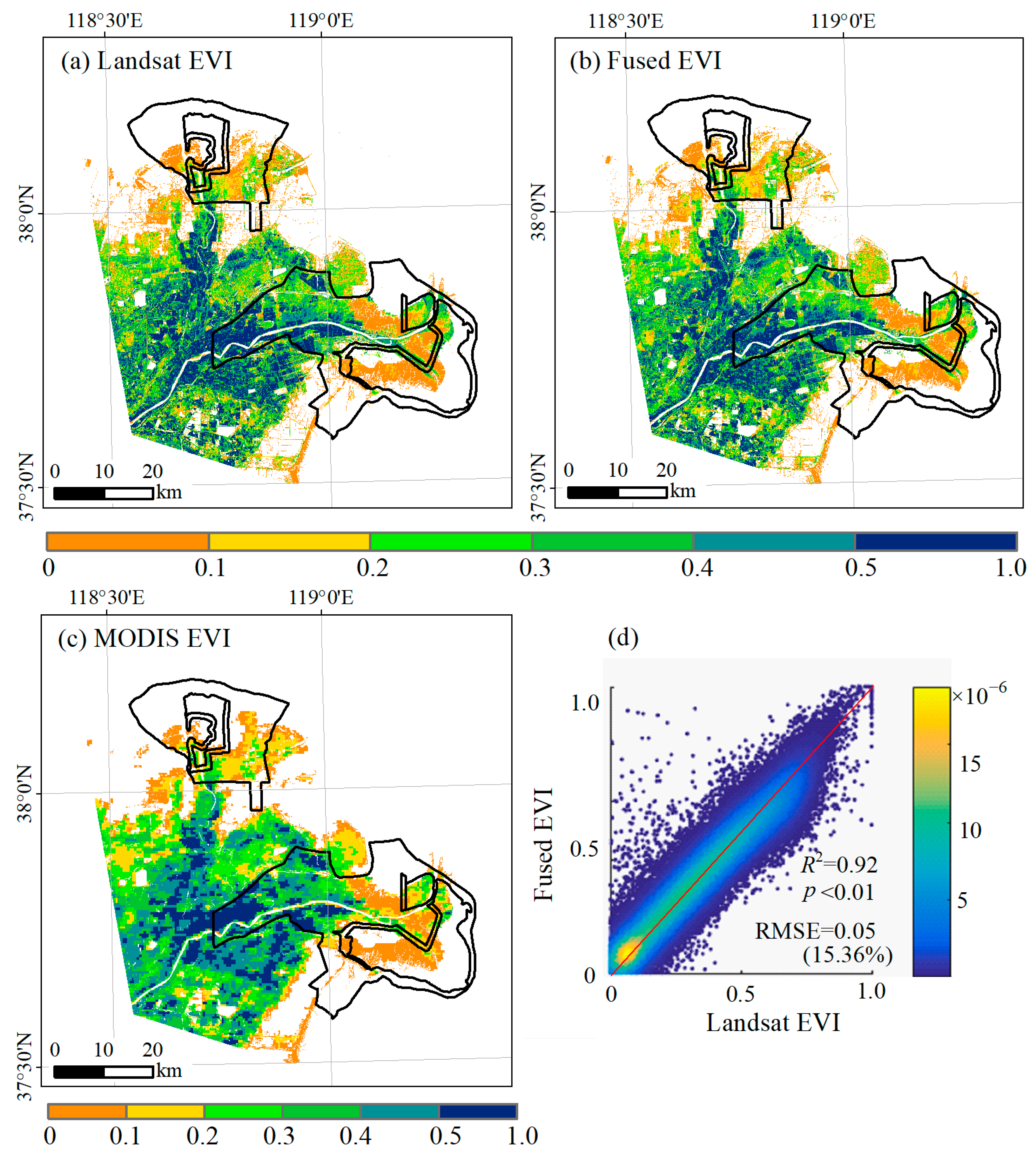
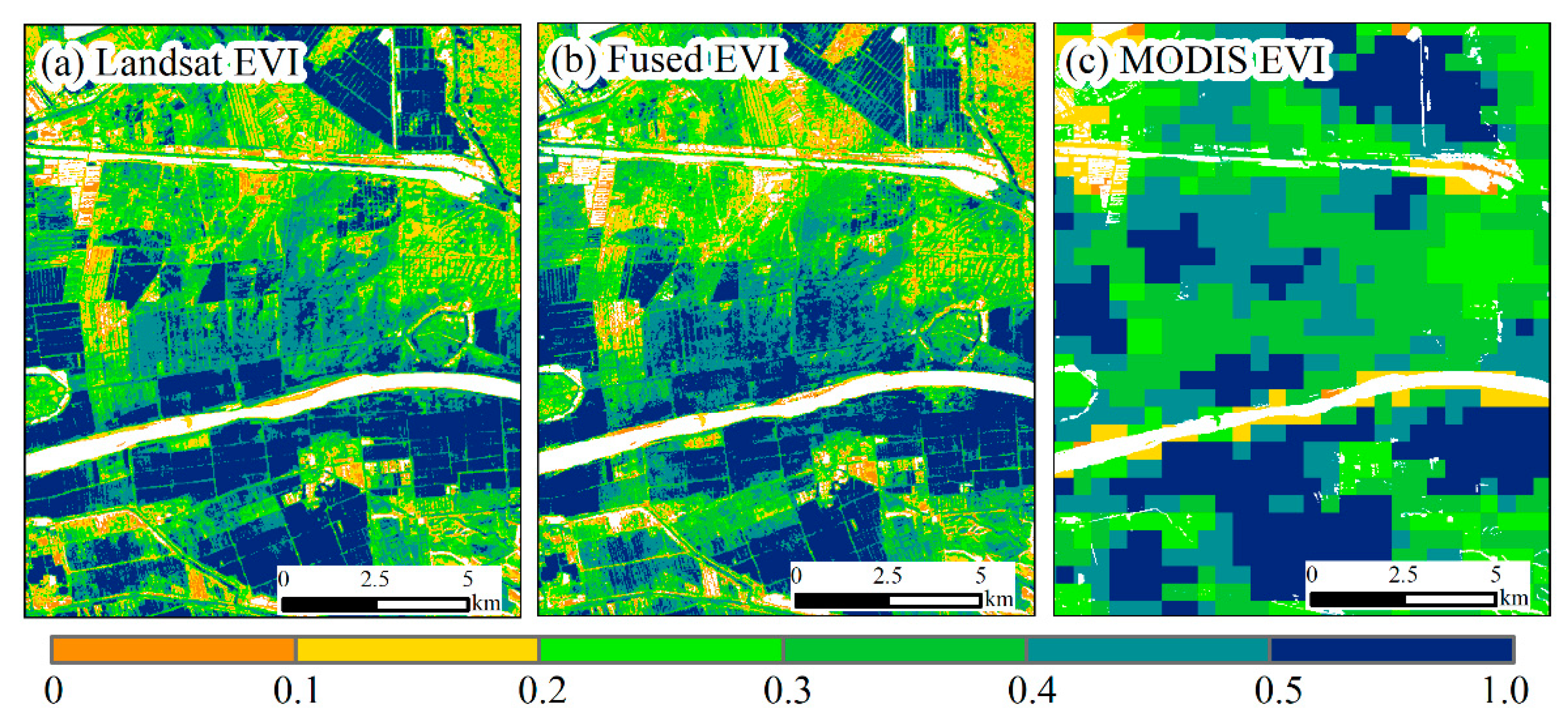
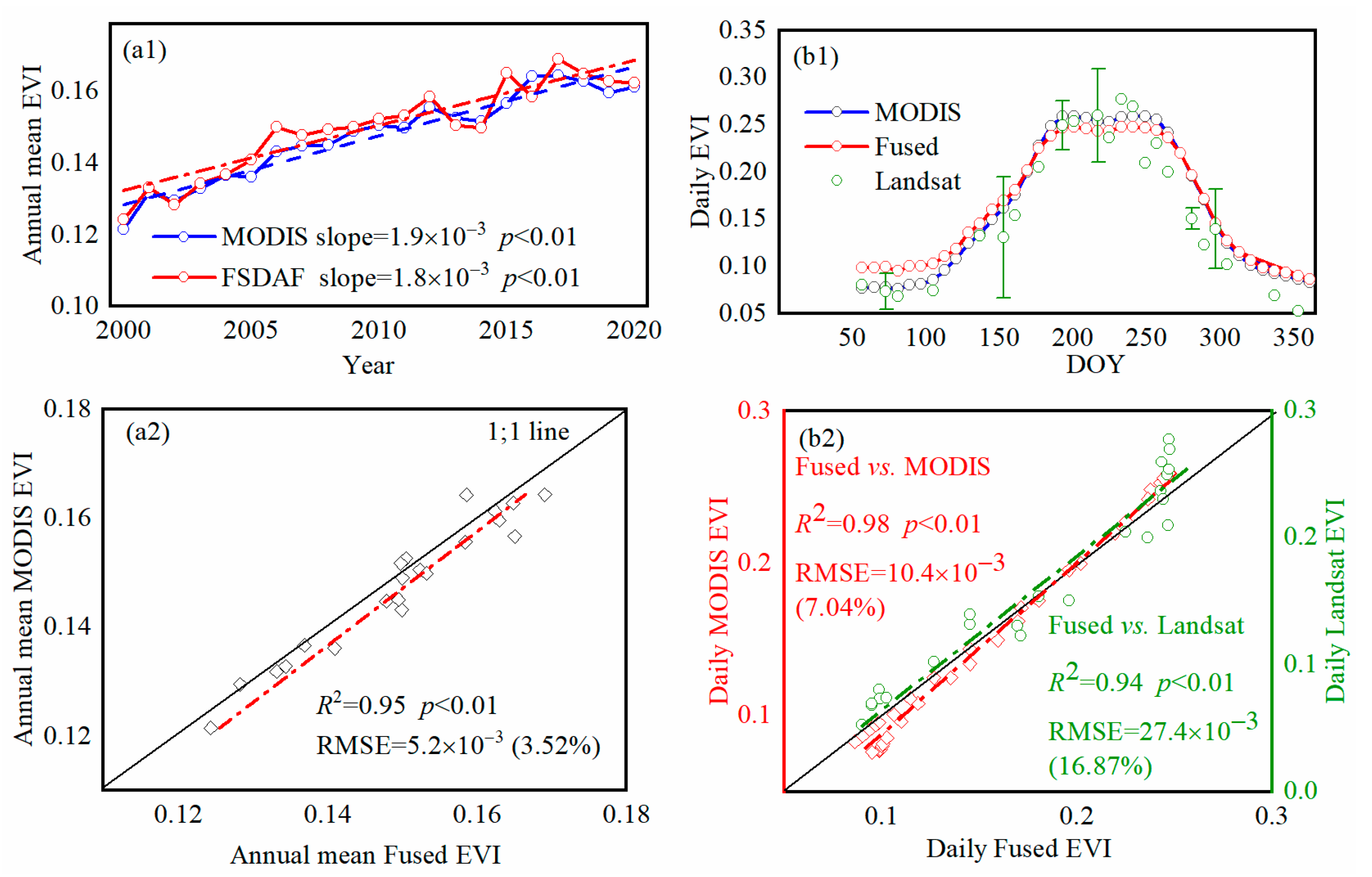
4.1. Accuracy of the Fused Data
4.2. Driving Factors of Vegetation Dynamics
5. Conclusions
- (1)
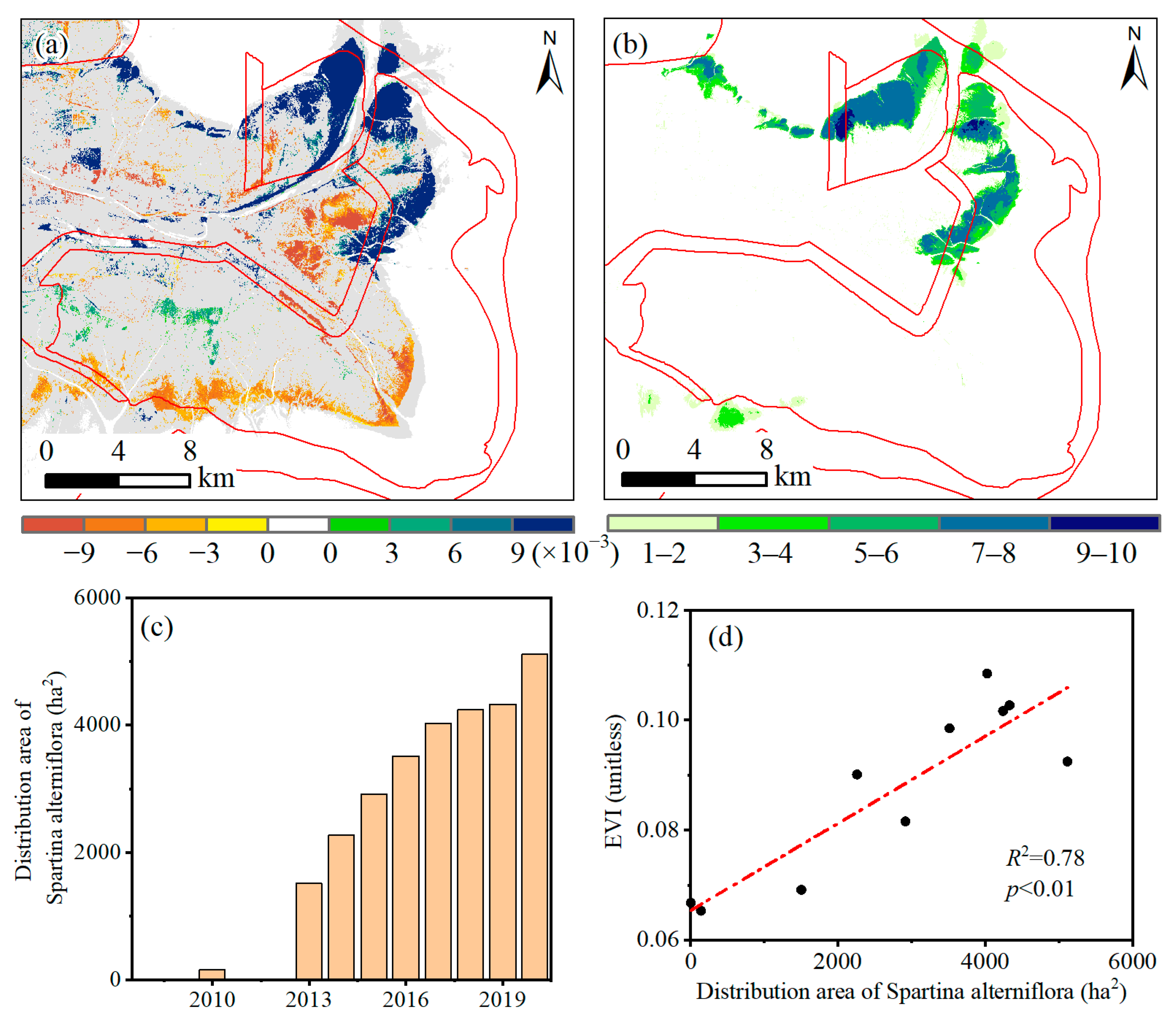
- In the core area of the YRDNRR, the fused EVI did not exhibit a significant trend before 2010, while a notable increasing trend was observed after 2010, with an annual increase of 7%; the invasion of Spartina alterniflora was identified as the primary driving factor, explaining 78% of the EVI increment.
- (2)
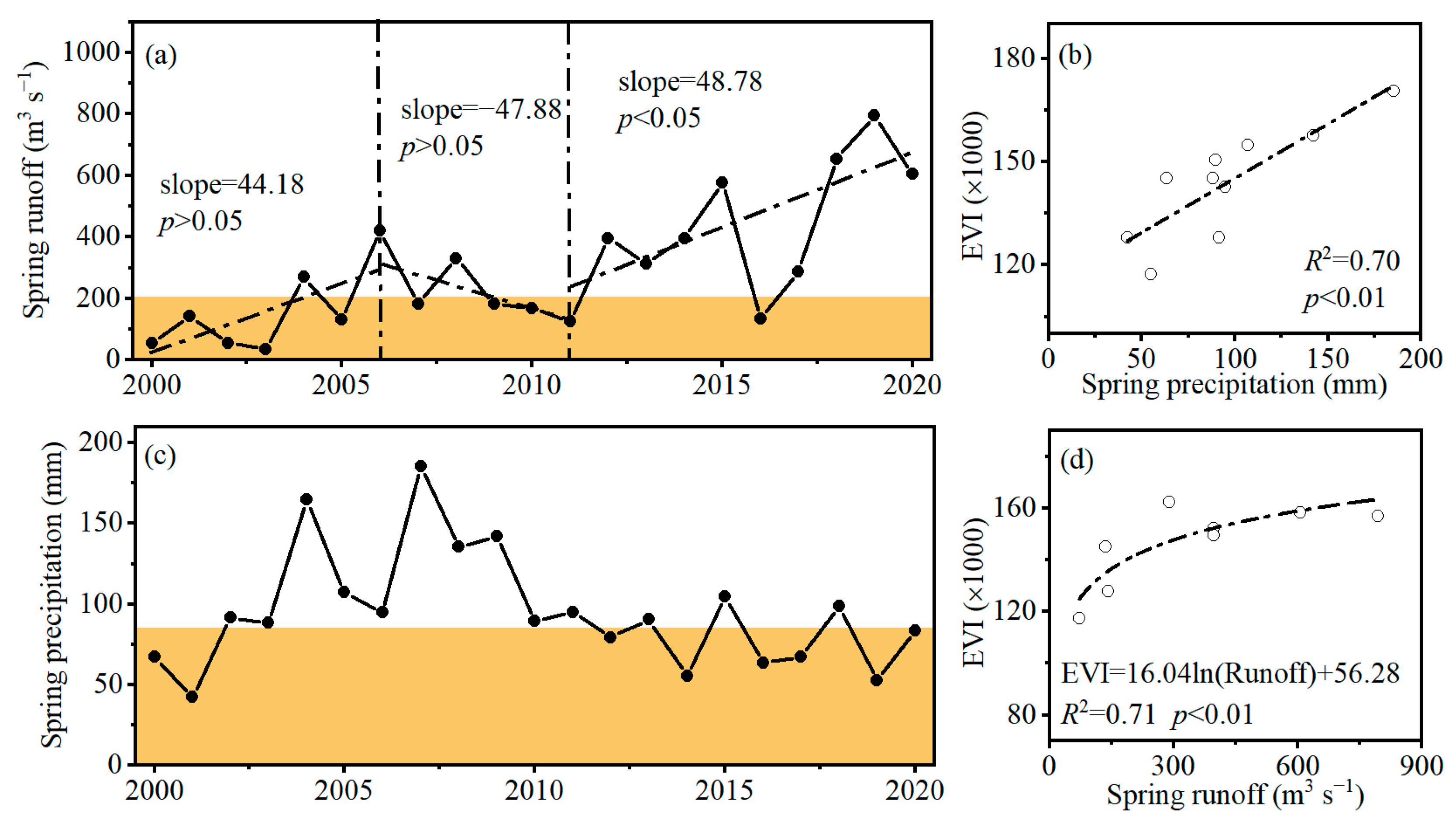
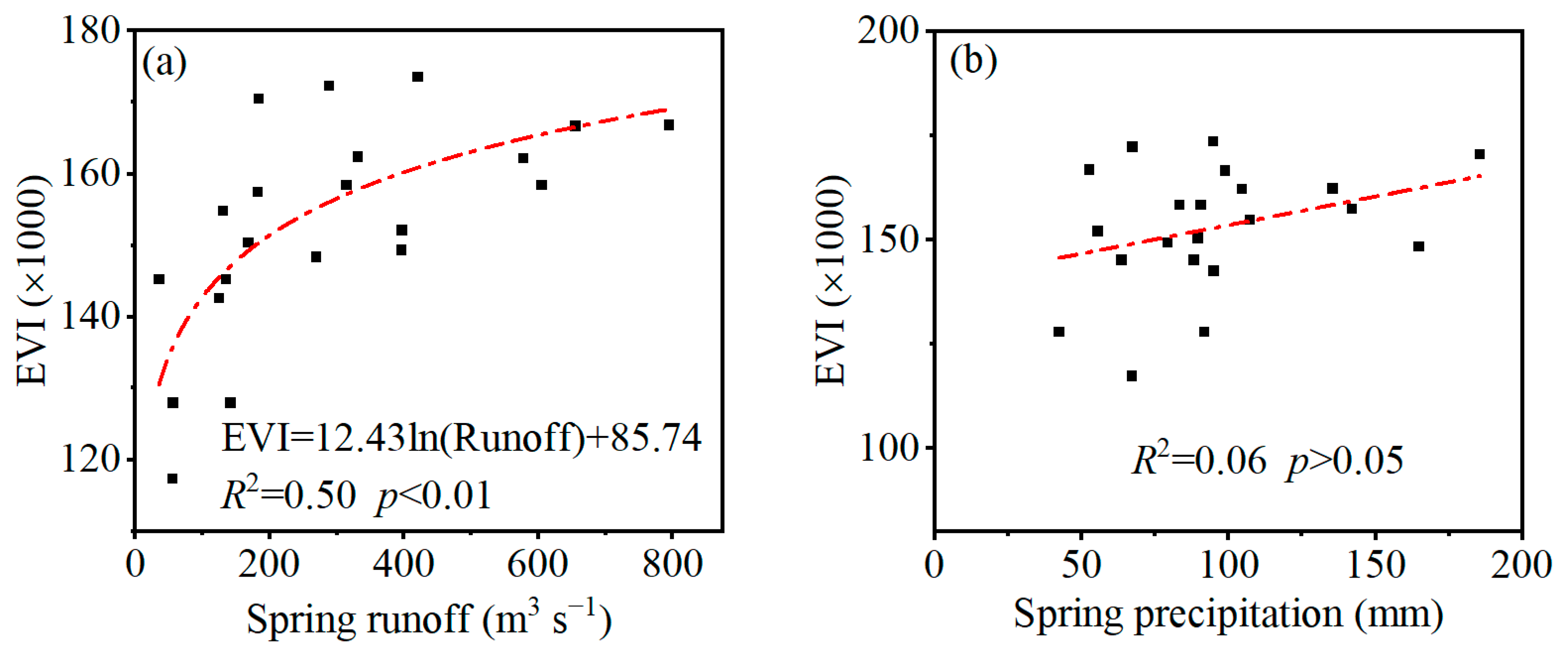
- In the experimental area of YRDNRR, the fused EVI showed a distinct interannual trend characterized by an initial increase (2000–2006, p < 0.01), followed by a subsequent decrease (2006–2011, p < 0.01) and, ultimately, a renewed increase (2011–2020, p > 0.05); the dynamics of fused EVI were mainly affected by the spring runoff (R2 = 0.71), while in years with lower runoff, they was also affected by the spring precipitation (R2 = 0.70).
- (3)
- Outside of the protected area, the fused EVI demonstrated a substantial increase from 2000 to 2010 due to the expansion of agricultural land and human management practices, followed by stabilization after 2010.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Xie, T.; Bai, J.; Cui, B. Degradation and Ecological Restoration of Estuarine Wetlands in China. Wetlands 2022, 42, 90. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, X.; Xu, X.; Zou, Z.; Chen, B.; Qin, Y.; Zhang, X.; Dong, J.; Liu, D.; Pan, L. Rebound in China’s coastal wetlands following conservation and restoration. Nat. Sustain. 2021, 4, 1076–1083. [Google Scholar] [CrossRef]
- Zhou, Y.; Tian, B.; Huang, Y.; Wu, W.; Qi, X.; Shu, M.; Xu, W.; Ge, F.; Wei, W.; Huang, G. Degradation of coastal wetland ecosystem in China: Drivers, impacts, and strategies. Bull. Chin. Acad. Sci. 2016, 31, 1157–1166. [Google Scholar]
- Hou, X.; Liu, J.; Song, Y.; Li, X. Environmental-ecological effect of development and utilization of China’s coastline and policy recommendations. Bull. Chin. Acad. Sci. 2021, 31, 1143–1150. [Google Scholar]
- Osland, M.J.; Chivoiu, B.; Enwright, N.M.; Thorne, K.M.; Guntenspergen, G.R.; Grace, J.B.; Dale, L.L.; Brooks, W.; Herold, N.; Day, J.W. Migration and transformation of coastal wetlands in response to rising seas. Sci. Adv. 2022, 8, eabo5174. [Google Scholar] [CrossRef]
- Guangxuan, H.; Weimin, S.; Peiguang, L.; Xiaojie, W.; Guangmei, W.; Xiaojing, C. Long-term ecological research support protection of coastal wetland ecosystems. Bull. Chin. Acad. Sci. (Chin. Version) 2020, 35, 218–228. [Google Scholar]
- Niu, B.; Zhang, Z.; Yu, X.; Li, X.; Wang, Z.; Loáiciga, H.A.; Peng, S. Regime shift of the hydroclimate–vegetation system in the Yellow River Delta of China from 1982 through 2015. Environ. Res. Lett. 2020, 15, 024017. [Google Scholar] [CrossRef]
- Gao, Y.; Song, X.; Li, W.; Wang, J.; He, J.; Jiang, X.; Feng, Y. Fusion classification of HSI and MSI using a spatial-spectral vision transformer for wetland biodiversity estimation. Remote Sens. 2022, 14, 850. [Google Scholar] [CrossRef]
- Du, P.; Hou, X.; Xu, H. Dynamic Expansion of Urban Land in China’s Coastal Zone since 2000. Remote Sens. 2022, 14, 916. [Google Scholar] [CrossRef]
- Su, H.; Yao, W.; Wu, Z.; Zheng, P.; Du, Q. Kernel low-rank representation with elastic net for China coastal wetland land cover classification using GF-5 hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2021, 171, 238–252. [Google Scholar] [CrossRef]
- Tang, Y.-N.; Ma, J.; Xu, J.-X.; Wu, W.-B.; Wang, Y.-C.; Guo, H.-Q. Assessing the Impacts of Tidal Creeks on the Spatial Patterns of Coastal Salt Marsh Vegetation and Its Aboveground Biomass. Remote Sens. 2022, 14, 1839. [Google Scholar] [CrossRef]
- Yu, L.; Zhuang, T.; Bai, J.; Wang, J.; Yu, Z.; Wang, X.; Zhang, G. Effects of water and salinity on soil labile organic carbon in estuarine wetlands of the Yellow River Delta, China. Ecohydrol. Hydrobiol. 2020, 20, 556–569. [Google Scholar] [CrossRef]
- LaFond-Hudson, S.; Sulman, B. Modeling strategies and data needs for representing coastal wetland vegetation in land surface models. New Phytol. 2023, 238, 938–951. [Google Scholar] [CrossRef] [PubMed]
- Woltz, V.L.; Stagg, C.L.; Byrd, K.B.; Windham-Myers, L.; Rovai, A.S.; Zhu, Z. Above-and Belowground Biomass Carbon Stock and Net Primary Productivity Maps for Tidal Herbaceous Marshes of the United States. Remote Sens. 2023, 15, 1697. [Google Scholar] [CrossRef]
- Chi, Y.; Shi, H.; Zheng, W.; Sun, J.; Fu, Z. Spatiotemporal characteristics and ecological effects of the human interference index of the Yellow River Delta in the last 30 years. Ecol. Indic. 2018, 89, 880–892. [Google Scholar] [CrossRef]
- Cong, P.; Chen, K.; Qu, L.; Han, J. Dynamic changes in the wetland landscape pattern of the Yellow River Delta from 1976 to 2016 based on satellite data. Chin. Geogr. Sci. 2019, 29, 372–381. [Google Scholar] [CrossRef]
- Lu, G.; Han, M.; Xu, Z.-H.; Zhu, J.-Q.; Niu, X.-R. Spatiotemporal variations of net primary productivity in new wetlands of the Yellow River Delta. Chin. J. Ecol. 2019, 38, 1113. [Google Scholar]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Luo, L.; Yan, H.; Niu, Z. Comparative Analysis on Three Multi-Source Remote Sensing Data Fusion Models in Monitoring Farmland Productivity. J. Geo-Inf. Sci. 2018, 20, 268–279. [Google Scholar]
- Gevaert, C.M.; García-Haro, F.J. A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion. Remote Sens. Environ. 2015, 156, 34–44. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Liu, M.; Yang, W.; Zhu, X.; Chen, J.; Chen, X.; Yang, L.; Helmer, E.H. An Improved Flexible Spatiotemporal DAta Fusion (IFSDAF) method for producing high spatiotemporal resolution normalized difference vegetation index time series. Remote Sens. Environ. 2019, 227, 74–89. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Song, H.; Huang, B. Spatiotemporal satellite image fusion through one-pair image learning. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1883–1896. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; Van Dijk, A.I. Assessing the accuracy of blending Landsat–MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, M.; Li, J.; Yuan, Q.; Wei, Y.; Zhang, L. Spatial–spectral fusion by combining deep learning and variational model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6169–6181. [Google Scholar] [CrossRef]
- Shen, H.; Meng, X.; Zhang, L. An integrated framework for the spatio–temporal–spectral fusion of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7135–7148. [Google Scholar] [CrossRef]
- Wu, J.; Lin, L.; Li, T.; Cheng, Q.; Zhang, C.; Shen, H. Fusing Landsat 8 and Sentinel-2 data for 10-m dense time-series imagery using a degradation-term constrained deep network. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102738. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, C.; Zhang, L.; Bai, J.; Zhou, D. Assessing spatiotemporal characteristics of native and invasive species with multi-temporal remote sensing images in the Yellow River Delta, China. Land Degrad. Dev. 2021, 32, 1338–1352. [Google Scholar] [CrossRef]
- Zhu, W.; Han, M.; Kong, X.; Li, Y.; Kong, F.; Wei, F.; Rong, J. Spatiotemporal characteristics of human activity intensity and its driving factors in the Yellow River Delta from 1990 to 2018. Res. Soil Water Conserv. 2021, 28, 287–292. [Google Scholar]
- Zhu, W.; Muhammad, A.; Han, M.; Li, Y.; Kong, X.; Kong, F. Spatial distribution and aggregation of human-environment coordination and optimal paths in the Yellow River Delta, China. Ecol. Indic. 2022, 143, 109380. [Google Scholar] [CrossRef]
- Jia, G.; Hu, W.; Zhang, B.; Li, G.; Shen, S.; Gao, Z.; Li, Y. Assessing impacts of the Ecological Retreat project on water conservation in the Yellow River Basin. Sci. Total Environ. 2022, 828, 154483. [Google Scholar] [CrossRef]
- Ren, L.; Li, Y.; Yu, M.; Yang, J.; Zhan, C.; Zhou, D. Evolution of artificial wetlands in the Yellow River Delta and related driving factors during 1984-2015. J. Agric. Resour. Environ. 2020, 37, 493–502. [Google Scholar]
- Jiang, D.; Fu, X.; Wang, K. Vegetation dynamics and their response to freshwater inflow and climate variables in the Yellow River Delta, China. Quat. Int. 2013, 304, 75–84. [Google Scholar] [CrossRef]
- Dou, X.; Guo, H.; Zhang, L.; Liang, D.; Zhu, Q.; Liu, X.; Zhou, H.; Lv, Z.; Liu, Y.; Gou, Y. Dynamic Changes of the Yellow River Delta Wetland and the Influence of Human Activities. Sci. Total Environ. 2023, 899, 166239. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Zhiyong, W.; Xiaodong, Z.; Liu, R. Monitoring and analysis of wetland change dynamics in the Yellow River Delta using multi-temporal remote sensing. Bull. Surv. Mapp. 2021, 4, 22–27. [Google Scholar]
- Ren, G.; Liu, Y.; Ma, Y.; Zhang, J. Spartina alterniflora monitoring and change analysis in Yellow River Delta by remote sensing technology. Acta Laser Biol. Sin 2014, 23, 596–603. [Google Scholar]
- Yang, J.; Ma, Y.; Ren, G.; Zhang, J.; Fan, Y. Monitoring method of invasive vegetation Spartina alterniflora in modern Yellow River delta based on gf remote sensing data. Mar. Environ. Sci. 2017, 36, 596–602. [Google Scholar]
- Wei, C.; Guo, B.; Lu, M.; Zang, W.; Yang, F.; Liu, C.; Wang, B.; Huang, X.; Liu, Y.; Yu, Y. The Changes in Dominant Driving Factors in the Evolution Process of Wetland in the Yellow River Delta during 2015–2022. Remote Sens. 2023, 15, 2858. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, M.; Zhang, W. Landscape pattern changes and its drivers inferred from salt marsh plant variations in the coastal wetlands of the Liao River Estuary, China. Ecol. Indic. 2022, 145, 109719. [Google Scholar] [CrossRef]
- Deng, S.; Chen, J.; Du, H. ENVI Remote Sensing Image Processing Method; Higher Education Press: Beijing, China, 2014. [Google Scholar]
- Peng, S. 1-km Monthly Precipitation Dataset for China (1901–2020); National Tibetan Plateau Data Center: Beijing, China, 2020. [Google Scholar]
- Peng, S. 1-km Monthly Mean Temperature Dataset for China (1901–2017); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Hu, J.; Gong, Z.; Zhang, C.; Qiu, H. Development of a Dataset of the Spatiotemporal Distribution of Typical Salt Marsh Vegetation in the Yellow River Delta (1999–2020). J. Glob. Change Data Discov. 2022, 5, 217–224. [Google Scholar] [CrossRef]
- Hou, X.; Di, X.; Hou, W.; Wu, L.; Liu, J.; Wang, J.; Su, H.; Lu, X.; Ying, L.; Yu, X.; et al. Accuracy Evaluation of Land Use Mapping Using Remote Sensing Techniques in Coastal Zone of China. J. Geo-Inf. Sci. 2018, 20, 1478–1488. [Google Scholar]
- Yan, H.; Du, W.; Zhou, Y.; Luo, L.; Niu, Z.E. Satellite-based evidences to improve cropland productivity on the high-standard farmland project regions in Henan Province, China. Remote Sens. 2022, 14, 1724. [Google Scholar] [CrossRef]
- Dubrule, O. Comparing splines and kriging. Comput. Geosci. 1984, 10, 327–338. [Google Scholar] [CrossRef]
- Liang, W.; Yang, Y.; Fan, D.; Guan, H.; Zhang, T.; Long, D.; Zhou, Y.; Bai, D. Analysis of spatial and temporal patterns of net primary production and their climate controls in China from 1982 to 2010. Agric. For. Meteorol. 2015, 204, 22–36. [Google Scholar] [CrossRef]
- Toms, J.D.; Lesperance, M.L. Piecewise regression: A tool for identifying ecological thresholds. Ecology 2003, 84, 2034–2041. [Google Scholar] [CrossRef]
- Curnutt, J.L. Host-area specific climatic-matching: Similarity breeds exotics. Biol. Conserv. 2000, 94, 341–351. [Google Scholar] [CrossRef]
- Shi, D.; Tian, J.; Chen, Y. Biological and ecological characteristics of an invasive alien species Spartina in Yellow River Delta. J. Binzhou Univ. 2009, 25, 27–32. [Google Scholar]
- McFarlin, C.R.; Bishop, T.D.; Hester, M.W.; Alber, M. Context-dependent effects of the loss of Spartina alterniflora on salt marsh invertebrate communities. Estuar. Coast. Shelf Sci. 2015, 163, 218–230. [Google Scholar] [CrossRef]
- Zhu, X.; Meng, L.; Zhang, Y.; Weng, Q.; Morris, J. Tidal and meteorological influences on the growth of invasive Spartina alterniflora: Evidence from UAV remote sensing. Remote Sens. 2019, 11, 1208. [Google Scholar] [CrossRef]
- Ren, G.; Zhao, Y.; Wang, J.; Wu, P.; Ma, Y. Ecological effects analysis of Spartina alterniflora invasion within Yellow River delta using long time series remote sensing imagery. Estuar. Coast. Shelf Sci. 2021, 249, 107111. [Google Scholar] [CrossRef]
- Wu, D.; Liu, J.; Wang, W.; Ding, W.; Wang, R. Mutiscale analysis of vegetation index and topographic variables in the Yellow River Delta of China. J. Plant Ecol. (Chin. Version) 2009, 33, 237–245. [Google Scholar]
- Cui, B.; Yang, Q.; Zhang, K.; Zhao, X.; You, Z. Responses of saltcedar (Tamarix chinensis) to water table depth and soil salinity in the Yellow River Delta, China. Plant Ecol. 2010, 209, 279–290. [Google Scholar] [CrossRef]
- Cui, B.; Yang, Q.; Yang, Z.; Zhang, K. Evaluating the ecological performance of wetland restoration in the Yellow River Delta, China. Ecol. Eng. 2009, 35, 1090–1103. [Google Scholar] [CrossRef]
- Wang, X.; Lian, Y.; Huang, C.; Wang, X.; Wang, R.; Shan, K.; Pedroli, B.; van Eupen, M.; ElMahdi, A.; Ali, M. Environmental flows and its evaluation of restoration effect based on LEDESS model in Yellow River Delta wetlands. Mitig. Adapt. Strateg. Glob. Change 2012, 17, 357–367. [Google Scholar] [CrossRef]
- Yeling, L.; Bin, H.; Qing, W.; Jizeng, D.; Baoshan, C.; Wei, Y. Temporal and spatial evolution of hydrological connectivity in River-Lake-Swamps in high efficiency eco-economic zone at the Yellow River Delta from 1970–2015. J. Beijing Norm. Univ. (Nat. Sci.) 2021, 57, 2–11. [Google Scholar]



| ID | Data Source | Data | ID | Data Source | Data |
|---|---|---|---|---|---|
| 1 | Landsat5 TM | 20 February 2000 | 23 | Landsat5 TM | 27 January 2009 |
| 2 | Landsat5 TM | 11 June 2000 | 24 | Landsat5 TM | 19 May 2009 |
| 3 | Landsat5 TM | 4 December 2000 | 25 | Landsat5 TM | 4 June 2009 |
| 4 | Landsat5 TM | 30 June 2001 | 26 | Landsat5 TM | 14 January 2010 |
| 5 | Landsat5 TM | 8 January 2002 | 27 | Landsat5 TM | 7 June 2010 |
| 6 | Landsat5 TM | 21 September 2002 | 28 | Landsat5 TM | 2 February 2011 |
| 7 | Landsat5 TM | 12 February 2003 | 29 | Landsat5 TM | 22 March 2011 |
| 8 | Landsat5 TM | 7 August 2003 | 30 | Landsat5 TM | 7 June 2011 |
| 9 | Landsat5 TM | 15 February 2004 | 31 | Landsat8 OLI | 3 September 2013 |
| 10 | Landsat5 TM | 10 September 2004 | 32 | Landsat8 OLI | 25 January 2014 |
| 11 | Landsat5 TM | 28 October 2004 | 33 | Landsat8 OLI | 14 March 2014 |
| 12 | Landsat5 TM | 16 January 2005 | 34 | Landsat8 OLI | 12 January 2015 |
| 13 | Landsat5 TM | 12 August 2005 | 35 | Landsat8 OLI | 5 June 2015 |
| 14 | Landsat5 TM | 15 October 2005 | 36 | Landsat8 OLI | 27 October 2015 |
| 15 | Landsat5 TM | 4 February 2006 | 37 | Landsat8 OLI | 30 December 2015 |
| 16 | Landsat5 TM | 16 September 2006 | 38 | Landsat8 OLI | 3 March 2016 |
| 17 | Landsat5 TM | 7 February 2007 | 39 | Landsat8 OLI | 20 January 2018 |
| 18 | Landsat5 TM | 17 July 2007 | 40 | Landsat8 OLI | 31 July 2018 |
| 19 | Landsat5 TM | 13 March 2008 | 41 | Landsat8 OLI | 23 January 2019 |
| 20 | Landsat5 TM | 14 April 2008 | 42 | Landsat8 OLI | 19 August 2019 |
| 21 | Landsat5 TM | 20 August 2008 | 43 | Landsat8 OLI | 23 January 2020 |
| 22 | Landsat5 TM | 7 October 2008 | 44 | Landsat8 OLI | 20 July 2020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Z.; Si, B.; Li, D.; Zhao, Y.; Hou, X.; Li, L.; Wang, B.; Song, B.; Zhang, M.; Li, X.; et al. Spatiotemporal Variation in Driving Factors of Vegetation Dynamics in the Yellow River Delta Estuarine Wetlands from 2000 to 2020. Remote Sens. 2023, 15, 4332. https://doi.org/10.3390/rs15174332
Niu Z, Si B, Li D, Zhao Y, Hou X, Li L, Wang B, Song B, Zhang M, Li X, et al. Spatiotemporal Variation in Driving Factors of Vegetation Dynamics in the Yellow River Delta Estuarine Wetlands from 2000 to 2020. Remote Sensing. 2023; 15(17):4332. https://doi.org/10.3390/rs15174332
Chicago/Turabian StyleNiu, Zhongen, Bingcheng Si, Dong Li, Ying Zhao, Xiyong Hou, Linlin Li, Bin Wang, Bing Song, Mengyu Zhang, Xiyu Li, and et al. 2023. "Spatiotemporal Variation in Driving Factors of Vegetation Dynamics in the Yellow River Delta Estuarine Wetlands from 2000 to 2020" Remote Sensing 15, no. 17: 4332. https://doi.org/10.3390/rs15174332
APA StyleNiu, Z., Si, B., Li, D., Zhao, Y., Hou, X., Li, L., Wang, B., Song, B., Zhang, M., Li, X., Zeng, N., Zhu, X., Lv, Y., & Mai, Z. (2023). Spatiotemporal Variation in Driving Factors of Vegetation Dynamics in the Yellow River Delta Estuarine Wetlands from 2000 to 2020. Remote Sensing, 15(17), 4332. https://doi.org/10.3390/rs15174332








