Carotenoid Content Estimation in Tea Leaves Using Noisy Reflectance Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Measurements
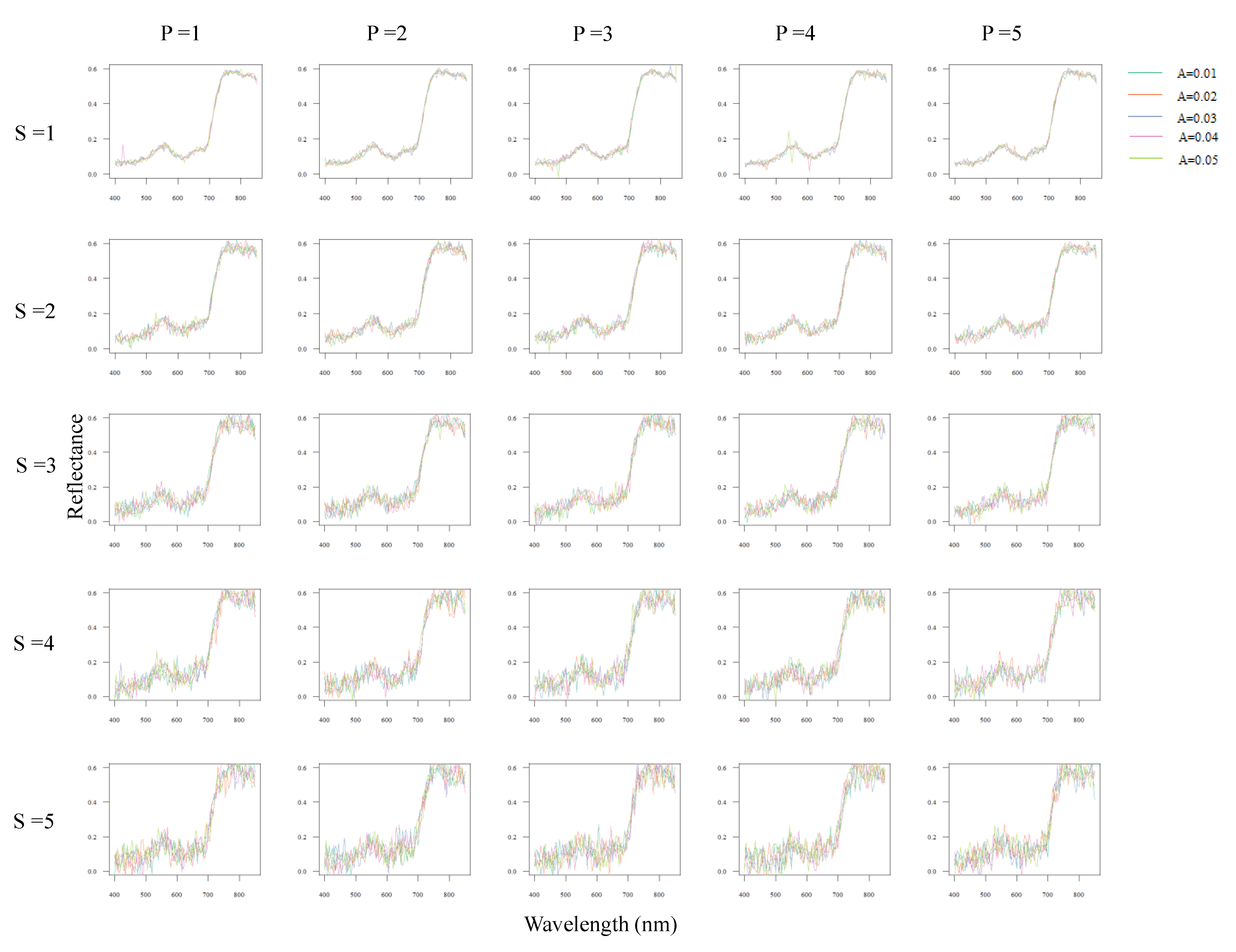
2.2. Adding Noise
2.3. Regression Models Based on Machine Learning Algorithms
2.4. Performance Assessment
3. Results
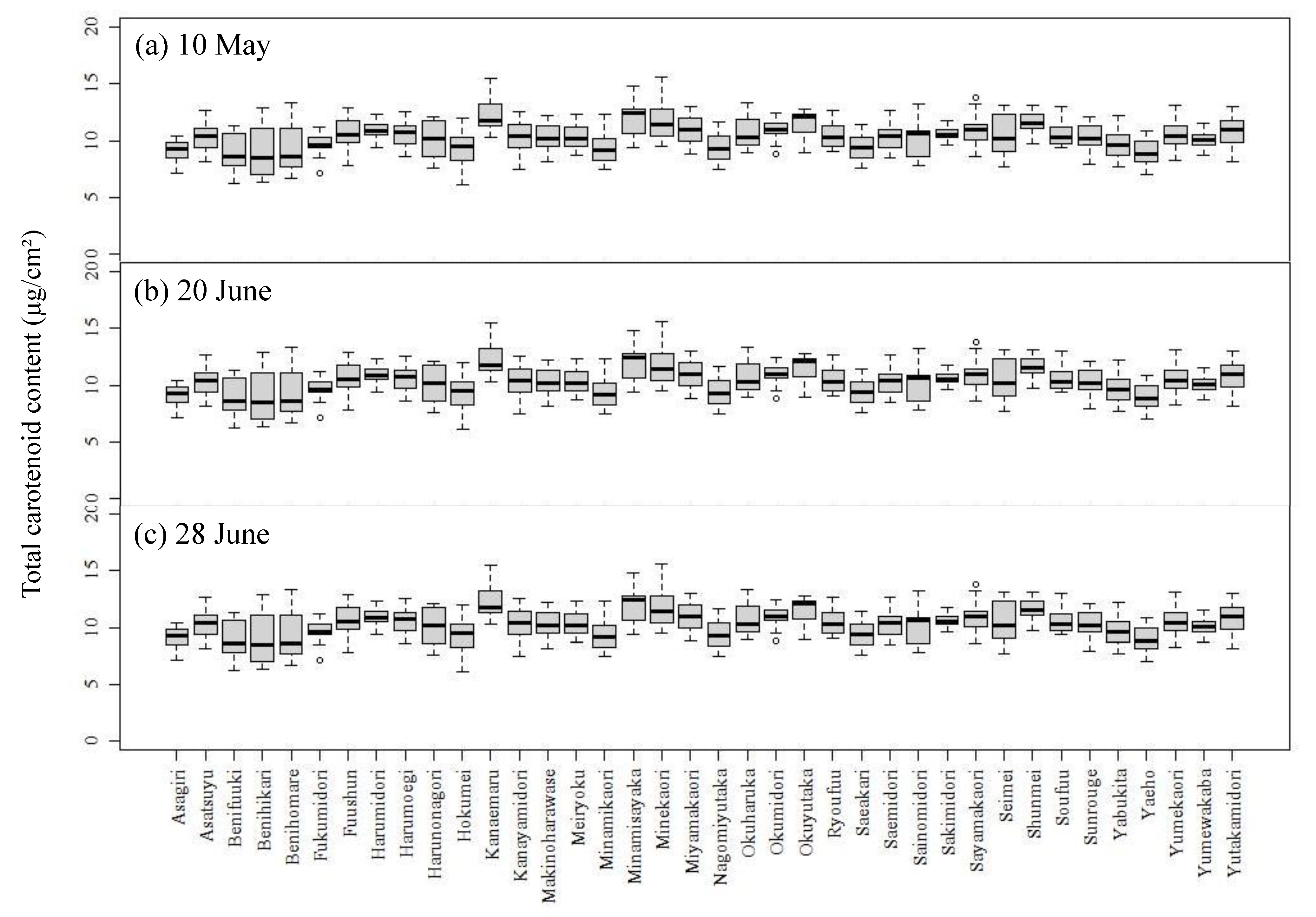
3.1. Carotenoid Content for Each Cultivar
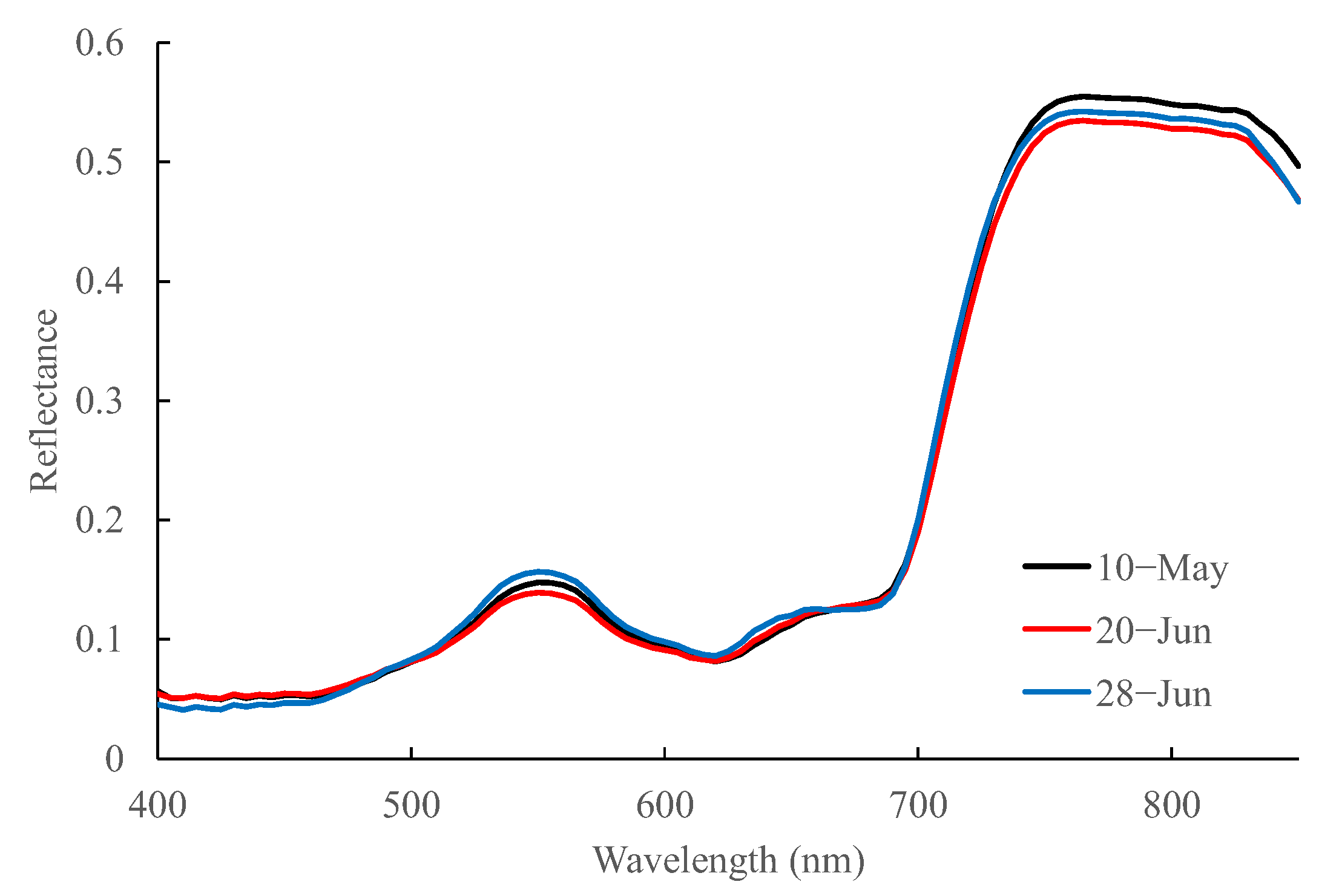
3.2. Spectral Reflectance
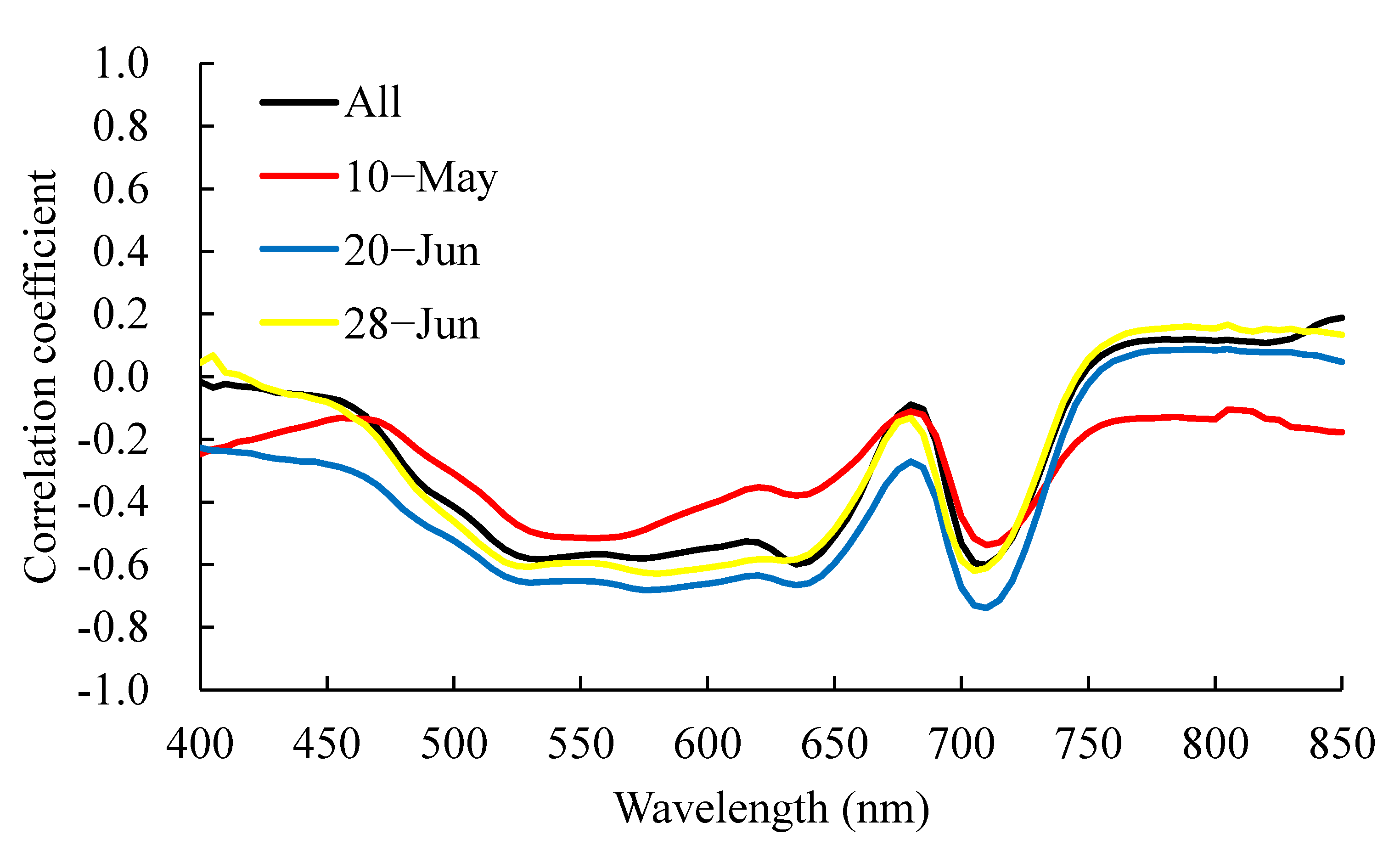
3.3. Correlation between Carotenoid Content and Reflectance
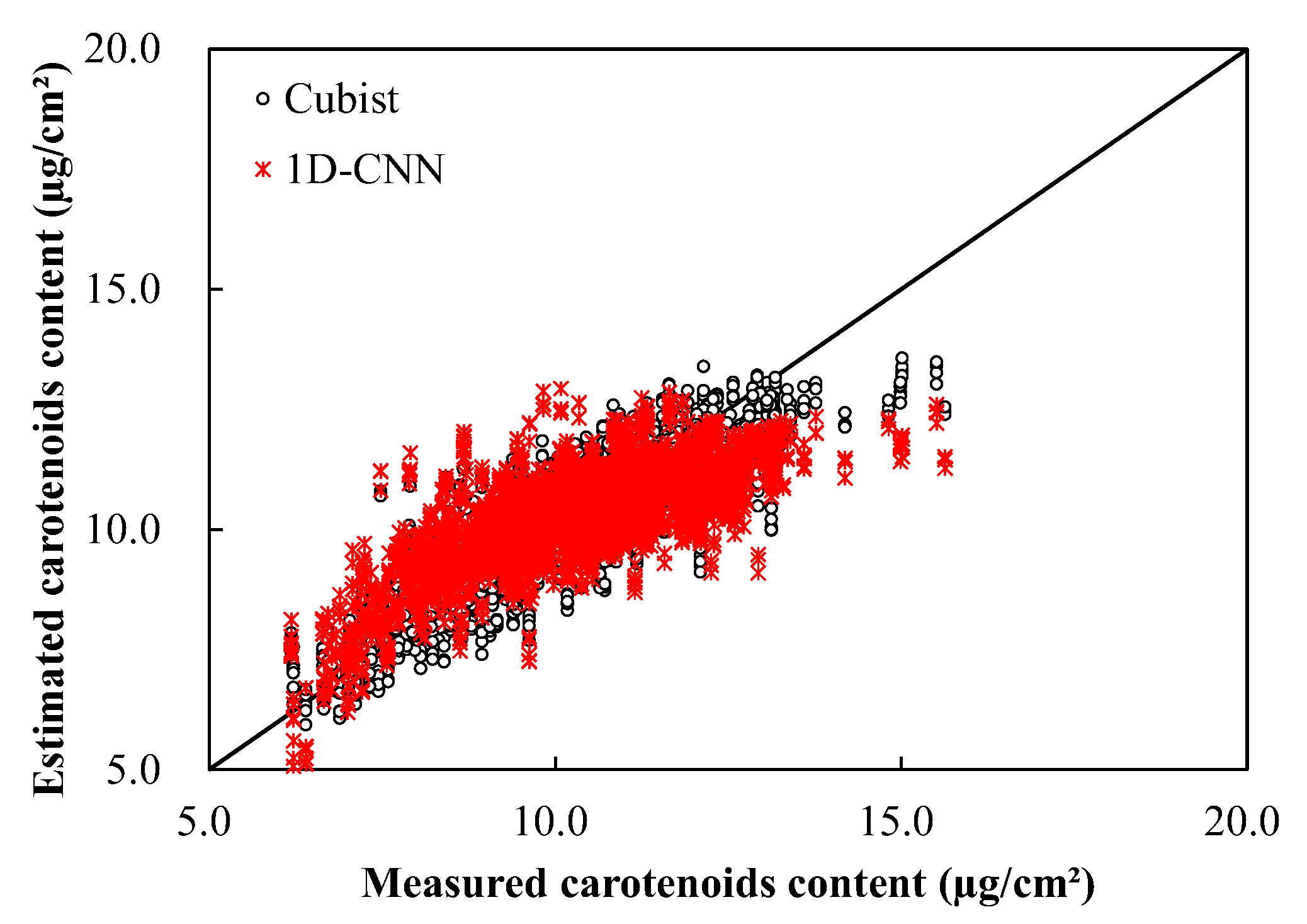
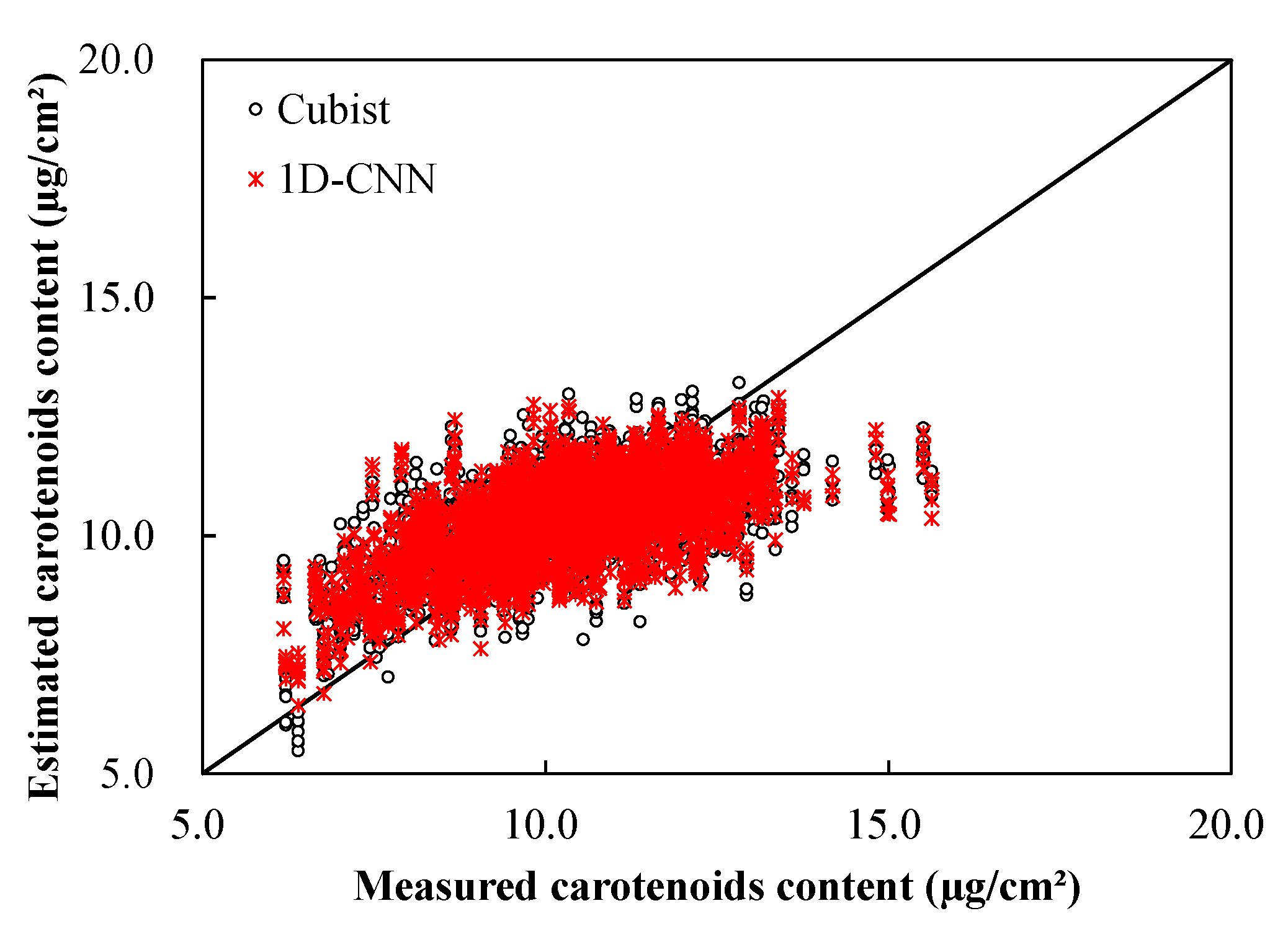
3.4. Accuracy Assessment
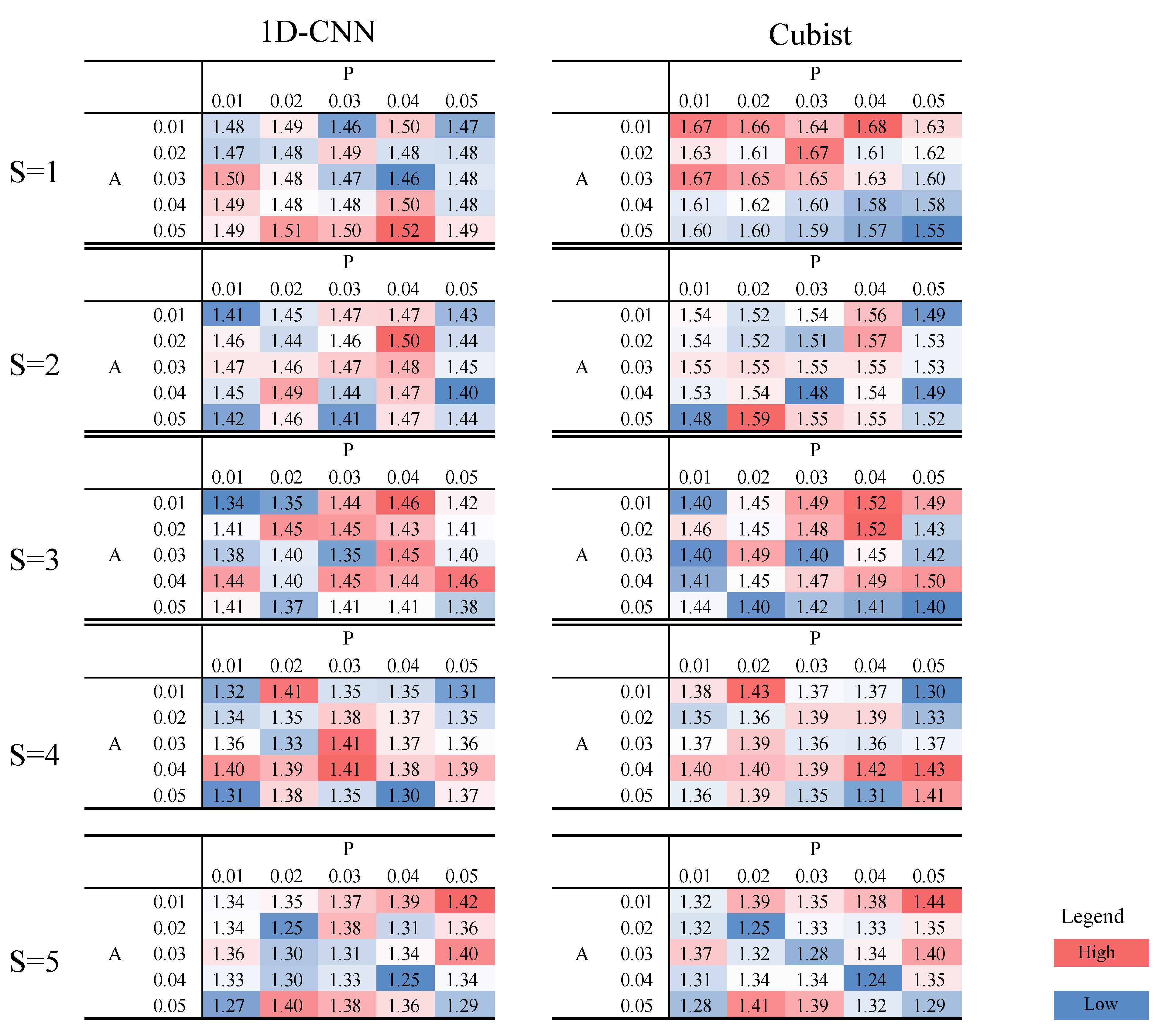
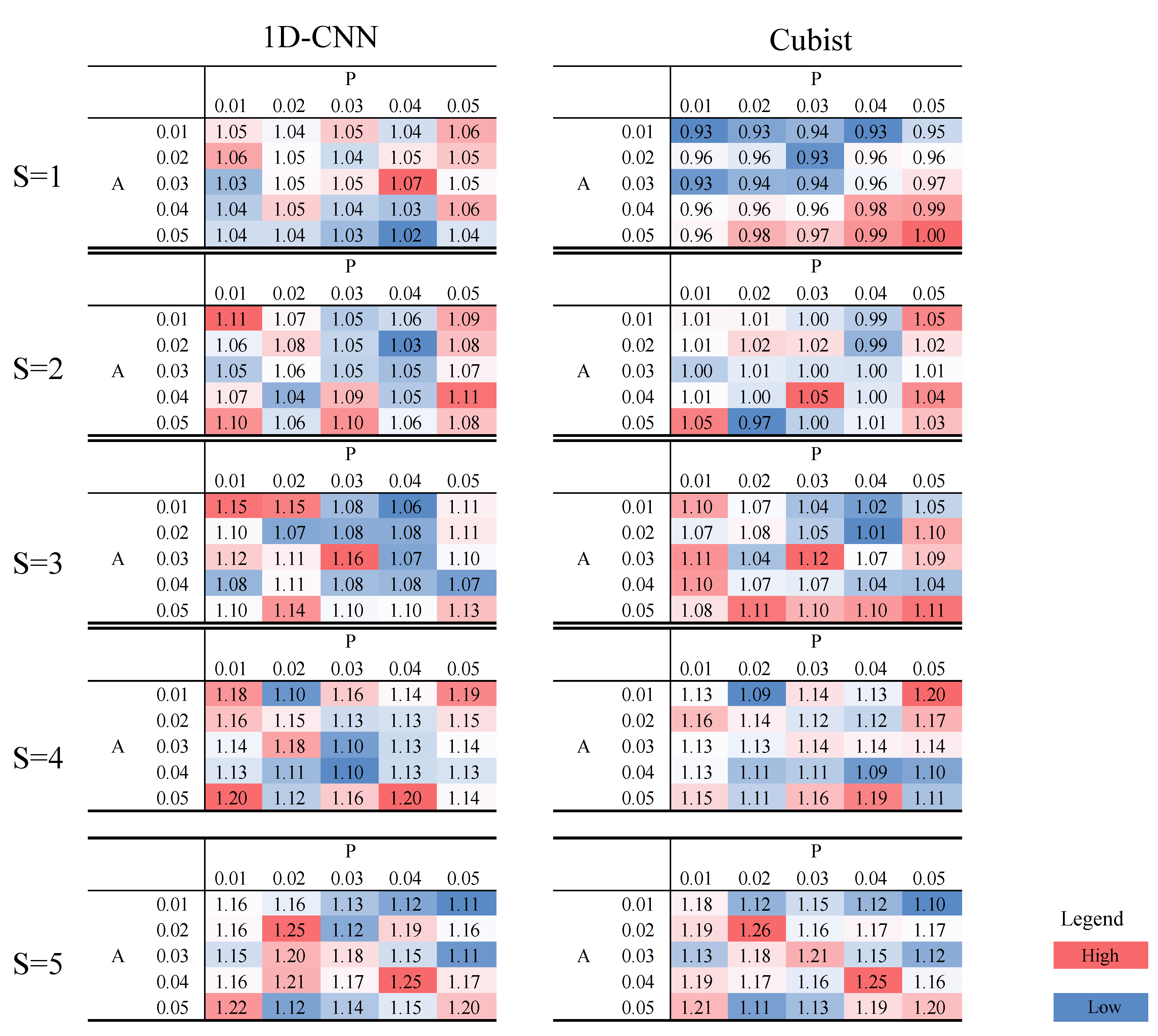
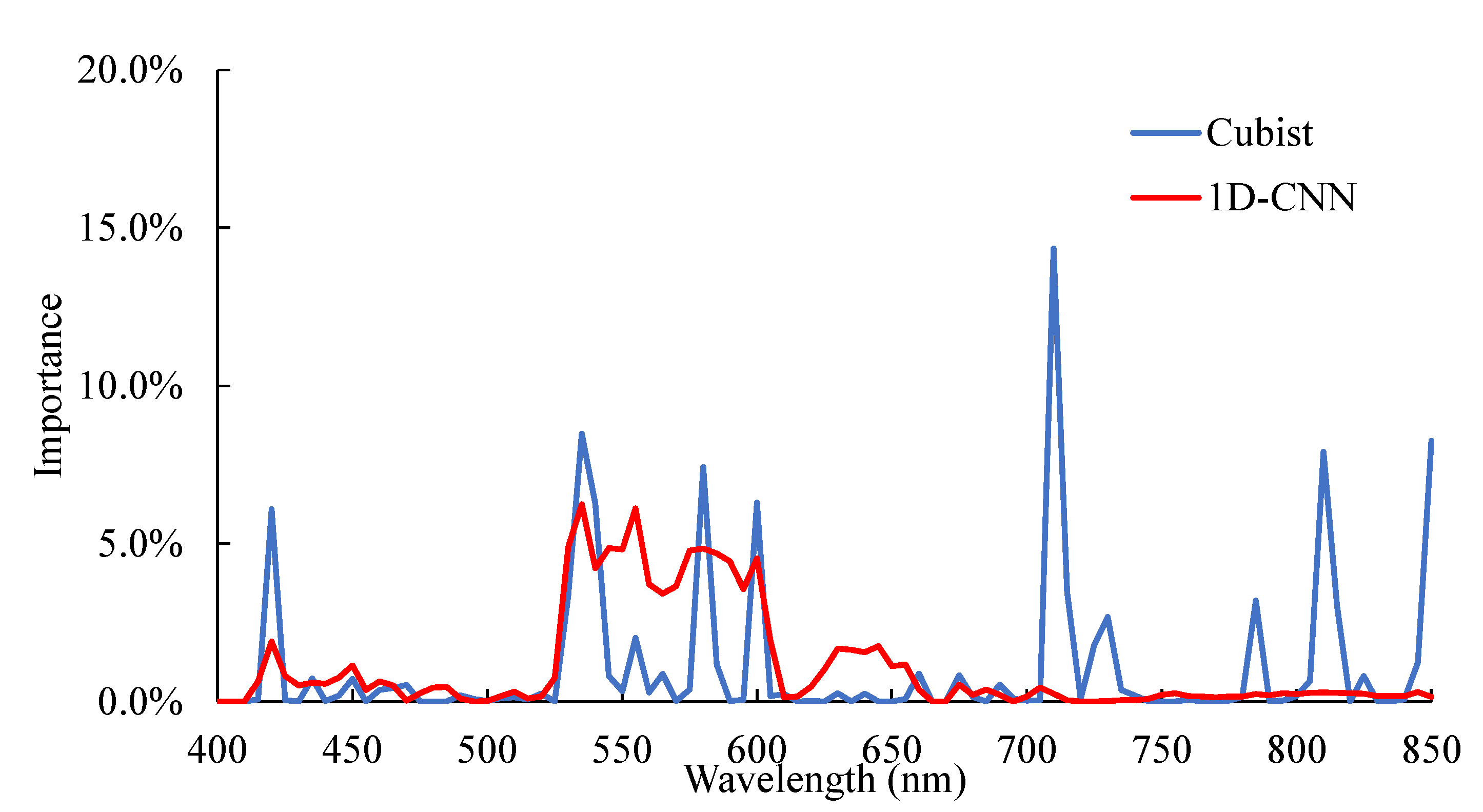
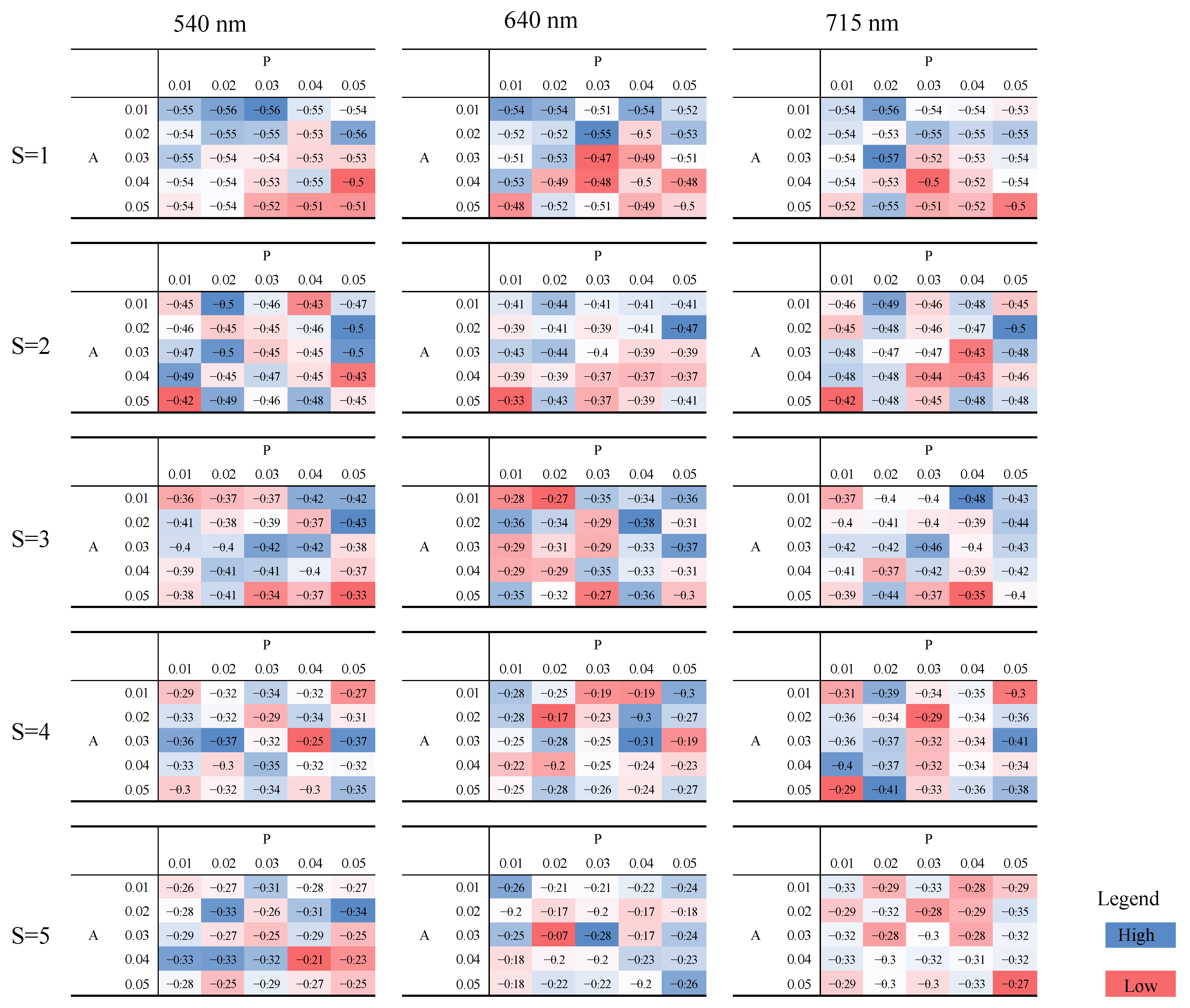
3.5. Sensitivity Analysis
4. Discussion
4.1. Accuracy Assessment
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palace, V.P.; Khaper, N.; Qin, Q.; Singal, P.K. Antioxidant potentials of vitamin A and carotenoids and their relevance to heart disease. Free. Radic. Biol. Med. 1999, 26, 746–761. [Google Scholar] [CrossRef] [PubMed]
- Maoka, T. Carotenoids as natural functional pigments. J. Nat. Med. 2020, 74, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Crupi, P.; Faienza, M.F.; Naeem, M.Y.; Corbo, F.; Clodoveo, M.L.; Muraglia, M. Overview of the Potential Beneficial Effects of Carotenoids on Consumer Health and Well-Being. Antioxidants 2023, 12, 1069. [Google Scholar] [CrossRef] [PubMed]
- Elvira-Torales, L.I.; García-Alonso, J.; Periago-Castón, M.J. Nutritional Importance of Carotenoids and Their Effect on Liver Health: A Review. Antioxidants 2019, 8, 229. [Google Scholar] [CrossRef] [PubMed]
- Demmig-Adams, B.; Gilmore, A.M.; Adams, W.W. Carotenoids 3: In Vivo Function of Carotenoids in Higher Plants. FASEB J. 1996, 10, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Edge, R.; McGarvey, D.; Truscott, T. The carotenoids as anti-oxidants—A review. J. Photochem. Photobiol. B Biol. 1997, 41, 189–200. [Google Scholar] [CrossRef]
- Yang, Y.-Z.; Li, T.; Teng, R.-M.; Han, M.-H.; Zhuang, J. Low temperature effects on carotenoids biosynthesis in the leaves of green and albino tea plant (Camellia sinensis (L.) O. Kuntze). Sci. Hortic. 2021, 285, 110164. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, S.; Deng, X.; Song, Q.; He, L.; Bai, D.; He, Y. Genome-wide association study of leaf-related traits in tea plant in Guizhou based on genotyping-by-sequencing. BMC Plant Biol. 2023, 23, 196. [Google Scholar] [CrossRef]
- Baker, R.; Günther, C. The Role of Carotenoids in Consumer Choice and the Likely Bene Wts from Their Inclusion into Products for Human Consumption. Trends Food Sci. Technol. 2004, 15, 484–488. [Google Scholar] [CrossRef]
- Smith, R.M. High-Performance Liquid Chromatography—Advances and Perspectives. J. Pharm. Biomed. Anal. 1984, 2, 567. [Google Scholar] [CrossRef]
- Wellburn, A.R. The Spectral Determination of Chlorophylls a and b, as well as Total Carotenoids, Using Various Solvents with Spectrophotometers of Different Resolution. J. Plant Physiol. 1994, 144, 307–313. [Google Scholar] [CrossRef]
- Seoudi, R.; El-Bahy, G.; El Sayed, Z. Ultraviolet and visible spectroscopic studies of phthalocyanine and its complexes thin films. Opt. Mater. 2006, 29, 304–312. [Google Scholar] [CrossRef]
- Prasad, K.A.; Gnanappazham, L.; Selvam, V.; Ramasubramanian, R.; Kar, C.S. Developing a spectral library of mangrove species of Indian east coast using field spectroscopy. Geocarto Int. 2015, 30, 580–599. [Google Scholar] [CrossRef]
- Cristóbal, J.; Graham, P.; Prakash, A.; Buchhorn, M.; Gens, R.; Guldager, N.; Bertram, M. Airborne Hyperspectral Data Acquisition and Processing in the Arctic: A Pilot Study Using the Hyspex Imaging Spectrometer for Wetland Mapping. Remote Sens. 2021, 13, 1178. [Google Scholar] [CrossRef]
- Qamar, F.; Sharma, M.S.; Dobler, G. The Impacts of Air Quality on Vegetation Health in Dense Urban Environments: A Ground-Based Hyperspectral Imaging Approach. Remote Sens. 2022, 14, 3854. [Google Scholar] [CrossRef]
- Shaik, R.U.; Periasamy, S.; Zeng, W. Potential Assessment of PRISMA Hyperspectral Imagery for Remote Sensing Applications. Remote Sens. 2023, 15, 1378. [Google Scholar] [CrossRef]
- Sonobe, R.; Miura, Y.; Sano, T.; Horie, H. Monitoring Photosynthetic Pigments of Shade-Grown Tea from Hyperspectral Reflectance. Can. J. Remote Sens. 2018, 44. [Google Scholar] [CrossRef]
- Sonobe, R.; Sano, T.; Horie, H. Using spectral reflectance to estimate leaf chlorophyll content of tea with shading treatments. Biosyst. Eng. 2018, 175, 168–182. [Google Scholar] [CrossRef]
- Sonobe, R.; Hirono, Y.; Oi, A. Non-Destructive Detection of Tea Leaf Chlorophyll Content Using Hyperspectral Reflectance and Machine Learning Algorithms. Plants 2020, 9, 368. [Google Scholar] [CrossRef]
- Sonobe, R.; Hirono, Y.; Oi, A. Quantifying chlorophyll-a and b content in tea leaves using hyperspectral reflectance and deep learning. Remote Sens. Lett. 2020, 11, 933–942. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; De Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Gautam, D.; Lucieer, A.; Watson, C.; McCoull, C. Lever-arm and boresight correction, and field of view determination of a spectroradiometer mounted on an unmanned aircraft system. ISPRS J. Photogramm. Remote Sens. 2019, 155, 25–36. [Google Scholar] [CrossRef]
- Sonobe, R.; Hirono, Y. Applying Variable Selection Methods and Preprocessing Techniques to Hyperspectral Reflectance Data to Estimate Tea Cultivar Chlorophyll Content. Remote Sens. 2023, 15, 19. [Google Scholar] [CrossRef]
- Sonobe, R.; Yamashita, H.; Nofrizal, A.Y.; Seki, H.; Morita, A.; Ikka, T. Use of spectral reflectance from a compact spectrometer to assess chlorophyll content in Zizania latifolia. Geocarto Int. 2022, 37, 5363–5375. [Google Scholar] [CrossRef]
- Shao, Y.; He, Y.; Bao, Y.; Mao, J. Near-Infrared Spectroscopy for Classification of Oranges and Prediction of the Sugar Content. Int. J. Food Prop. 2009, 12, 644–658. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Jamshidi, B.; Minaei, S.; Mohajerani, E.; Ghassemian, H. Reflectance Vis/NIR spectroscopy for nondestructive taste characterization of Valencia oranges. Comput. Electron. Agric. 2012, 85, 64–69. [Google Scholar] [CrossRef]
- Mishra, P.; Karami, A.; Nordon, A.; Rutledge, D.N.; Roger, J.-M. Automatic de-noising of close-range hyperspectral images with a wavelength-specific shearlet-based image noise reduction method. Sens. Actuators B Chem. 2019, 281, 1034–1044. [Google Scholar] [CrossRef]
- Karami, A.; Heylen, R.; Scheunders, P. Band-Specific Shearlet-Based Hyperspectral Image Noise Reduction. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5054–5066. [Google Scholar] [CrossRef]
- Vorasayan, P.; Suwanwela, N.C.; Auethavekiat, S.; Chinrungrueng, C.; Sa-Ing, V. Multiscale adaptive regularisation Savitzky–Golay method for speckle noise reduction in ultrasound images. IET Image Process. 2018, 12, 105–112. [Google Scholar] [CrossRef]
- Zimmermann, B.; Kohler, A. Optimizing Savitzky-Golay Parameters for Improving Spectral Resolution and Quantification in Infrared Spectroscopy. Appl. Spectrosc. 2013, 67, 892–902. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Zur, Y.; Chivkunova, O.B.; Merzlyak, M.N. Assessing Carotenoid Content in Plant Leaves with Reflectance Spectroscopy. Photochem. Photobiol. 2002, 75, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-Empirical Indices to Assess Carotenoids/Chlorophyll a Ratio from Leaf Spectral Re-flectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Féret, J.-B.; Gitelson, A.; Noble, S.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Sonobe, R.; Miura, Y.; Sano, T.; Horie, H. Estimating leaf carotenoid contents of shade-grown tea using hyperspectral indices and PROSPECT–D inversion. Int. J. Remote Sens. 2018, 39, 1306–1320. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Sirsat, M.; Cernadas, E.; Alawadi, S.; Barro, S.; Febrero-Bande, M. An extensive experimental survey of regression methods. Neural Netw. 2019, 111, 11–34. [Google Scholar] [CrossRef]
- Alkhayrat, M.; Aljnidi, M.; Aljoumaa, K. A comparative dimensionality reduction study in telecom customer segmentation using deep learning and PCA. J. Big Data 2020, 7, 9. [Google Scholar] [CrossRef]
- Sakurada, M.; Yairi, T. Anomaly Detection Using Autoencoders with Nonlinear Dimensionality Reduction. In Proceedings of the ACM International Conference Proceeding Series, Montreal, QC, Canada, 8–13 December 2014; Volume 2. [Google Scholar]
- Ng, W.; Minasny, B.; Montazerolghaem, M.; Padarian, J.; Ferguson, R.; Bailey, S.; McBratney, A.B. Convolutional neural network for simultaneous prediction of several soil properties using visible/near-infrared, mid-infrared, and their combined spectra. Geoderma 2019, 352, 251–267. [Google Scholar] [CrossRef]
- Pullanagari, R.; Dehghan-Shoar, M.; Yule, I.J.; Bhatia, N. Field spectroscopy of canopy nitrogen concentration in temperate grasslands using a convolutional neural network. Remote Sens. Environ. 2021, 257, 112353. [Google Scholar] [CrossRef]
- Malvern Panalytical. ASD Plant Probe. Available online: https://www.azom.com/equipment-details.aspx?EquipID=5412 (accessed on 19 July 2023).
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 19 July 2023).
- Ruppert, D. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. J. Am. Stat. Assoc. 2004, 99, 567. [Google Scholar] [CrossRef]
- Kuhn, M.; Weston, S.; Keefer, C.; Coulter, N.; Quinlan, R. Rulequest Research Pty Ltd. Package ‘Cubist’. Available online: https://cran.r-project.org/web/packages/Cubist/Cubist.pdf (accessed on 19 July 2023).
- Kawamura, K.; Nishigaki, T.; Andriamananjara, A.; Rakotonindrina, H.; Tsujimoto, Y.; Moritsuka, N.; Rabenarivo, M.; Razafimbelo, T. Using a One-Dimensional Convolutional Neural Network on Visible and Near-Infrared Spectroscopy to Improve Soil Phosphorus Prediction in Madagascar. Remote Sens. 2021, 13, 1519. [Google Scholar] [CrossRef]
- Bisong, E. Google Colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform; Apress: Berkeley, CA, USA, 2019. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Linow, F. Near-Infrared Technology in the Agriculture and Food Industries. Herausgegeben von P. Williams und K. Norris. 330 Seiten, zahlr. Abb. und Tab. American Association of Cereal Chemists, Inc., St. Paul, Minnesota, USA, 1987. Preis: 175,90 $ (USA 169,00 $). Food Nahr. 1988, 32, 803. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R., Jr. Near-Infrared Reflectance Spectroscopy-Principal Components Regression Analyses of Soil Properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Pan, L.; Lu, R.; Zhu, Q.; Tu, K.; Cen, H. Predict Compositions and Mechanical Properties of Sugar Beet Using Hyperspectral Scattering. Food Bioprocess Technol. 2016, 9, 1177–1186. [Google Scholar] [CrossRef]
- Shi, S.; Xu, L.; Gong, W.; Chen, B.; Chen, B.; Qu, F.; Tang, X.; Sun, J.; Yang, J. A convolution neural network for forest leaf chlorophyll and carotenoid estimation using hyperspectral reflectance. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102719. [Google Scholar] [CrossRef]
- Lamsal, K.; Malenovský, Z.; Woodgate, W.; Waterman, M.; Brodribb, T.J.; Aryal, J. Spectral Retrieval of Eucalypt Leaf Biochemical Traits by Inversion of the Fluspect-Cx Model. Remote Sens. 2022, 14, 567. [Google Scholar] [CrossRef]
- Sonobe, R.; Yamashita, H.; Mihara, H.; Morita, A.; Ikka, T. Estimation of Leaf Chlorophyll a, b and Carotenoid Contents and Their Ratios Using Hyperspectral Reflectance. Remote Sens. 2020, 12, 3265. [Google Scholar] [CrossRef]
- Chlap, P.; Min, H.; Vandenberg, N.; Dowling, J.; Holloway, L.; Haworth, A. A review of medical image data augmentation techniques for deep learning applications. J. Med. Imaging Radiat. Oncol. 2021, 65, 545–563. [Google Scholar] [CrossRef] [PubMed]
- Caicedo, J.P.R.; Verrelst, J.; Munoz-Mari, J.; Moreno, J.; Camps-Valls, G. Toward a Semiautomatic Machine Learning Retrieval of Biophysical Parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1249–1259. [Google Scholar] [CrossRef]
- DeVries, T.; Taylor, G.W. Improved Regularization of Convolutional Neural Networks with Cutout. arXiv 2017, arXiv:1708.04552. [Google Scholar]
- Brendel, W.; Rauber, J.; Bethge, M. Decision-Based Adversarial Attacks: Reliable Attacks against Black-Box Machine Learning Models. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Saif-Ul-Allah, M.W.; Khan, J.; Ahmed, F.; Salman, C.A.; Gillani, Z.; Hussain, A.; Yasin, M.; Ul-Haq, N.; Khan, A.U.; Bazmi, A.A.; et al. Computationally Inexpensive 1D-CNN for the Prediction of Noisy Data of NOx Emissions From 500 MW Coal-Fired Power Plant. Front. Energy Res. 2022, 10, 945769. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Sonobe, R.; Yamashita, H.; Mihara, H.; Morita, A.; Ikka, T. Hyperspectral reflectance sensing for quantifying leaf chlorophyll content in wasabi leaves using spectral pre-processing techniques and machine learning algorithms. Int. J. Remote Sens. 2021, 42, 1311–1329. [Google Scholar] [CrossRef]
- Hashimoto, H.; Uragami, C.; Cogdell, R.J. Carotenoids and Photosynthesis. Subcell Biochem. 2016, 79, 111–139. [Google Scholar] [CrossRef]
- Kirilovsky, D.; Kerfeld, C.A. The Orange Carotenoid Protein: A blue-green light photoactive protein. Photochem. Photobiol. Sci. 2013, 12, 1135–1143. [Google Scholar] [CrossRef]
- Hamamatsu Photonics. Mini-Spectrometer. Available online: http://www.farnell.com/datasheets/2822646.pdf (accessed on 19 July 2023).
- Udelhoven, T.; Schlerf, M.; Segl, K.; Mallick, K.; Bossung, C.; Retzlaff, R.; Rock, G.; Fischer, P.; Müller, A.; Storch, T.; et al. A Satellite-Based Imaging Instrumentation Concept for Hyperspectral Thermal Remote Sensing. Sensors 2017, 17, 1542. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, G.; Pan, Y.; Yang, X.; Chen, L.; Zhao, C. A Review of Advanced Technologies and Development for Hy-perspectral-Based Plant Disease Detection in the Past Three Decades. Remote Sens. 2020, 12, 3188. [Google Scholar] [CrossRef]




| RPD | RMSE (µg/cm2) | R2 | |||
|---|---|---|---|---|---|
| 1D-CNN | Cubist | 1D-CNN | Cubist | 1D-CNN | Cubist |
| 1.50 | 2.05 | 1.03 | 0.76 | 0.56 | 0.76 |
| Sample | Accuracy | Algorithm | Reference |
|---|---|---|---|
| Forest leaves included in ANGERS (measured with ASD FieldSpec) | RMSE = 2.6019 μg/m2 R2 = 0.74 | Convolution neural network | [54] |
| Australian eucalypt species (measured with ASD FieldSpec 3) | RMSE = 3.83 μg/m2 NRMSE = 30.82% | Inversion of the Fluspect-Cx Model | [55] |
| Japanese horseradish (measured with ASD FieldSpec 4) | RPD = 1.63–3.32 RMSE = 0.31–1.89 μg/m2 | SNV and Cubist | [56] |
| Maple and chestnut (measured with Hitachi 150-20 spectrophotometer), beech (measured with Shimatzu 2101 PC spectrophotometer) | R2 = 0.71 RMSE = 1.86 nmol/cm2 | Spectral indices | [32] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sonobe, R.; Hirono, Y. Carotenoid Content Estimation in Tea Leaves Using Noisy Reflectance Data. Remote Sens. 2023, 15, 4303. https://doi.org/10.3390/rs15174303
Sonobe R, Hirono Y. Carotenoid Content Estimation in Tea Leaves Using Noisy Reflectance Data. Remote Sensing. 2023; 15(17):4303. https://doi.org/10.3390/rs15174303
Chicago/Turabian StyleSonobe, Rei, and Yuhei Hirono. 2023. "Carotenoid Content Estimation in Tea Leaves Using Noisy Reflectance Data" Remote Sensing 15, no. 17: 4303. https://doi.org/10.3390/rs15174303
APA StyleSonobe, R., & Hirono, Y. (2023). Carotenoid Content Estimation in Tea Leaves Using Noisy Reflectance Data. Remote Sensing, 15(17), 4303. https://doi.org/10.3390/rs15174303









