A Multi-Correlation Peak Phase Deblurring Algorithm for BeiDou B1C Signals in Urban Environments
Abstract
:1. Introduction
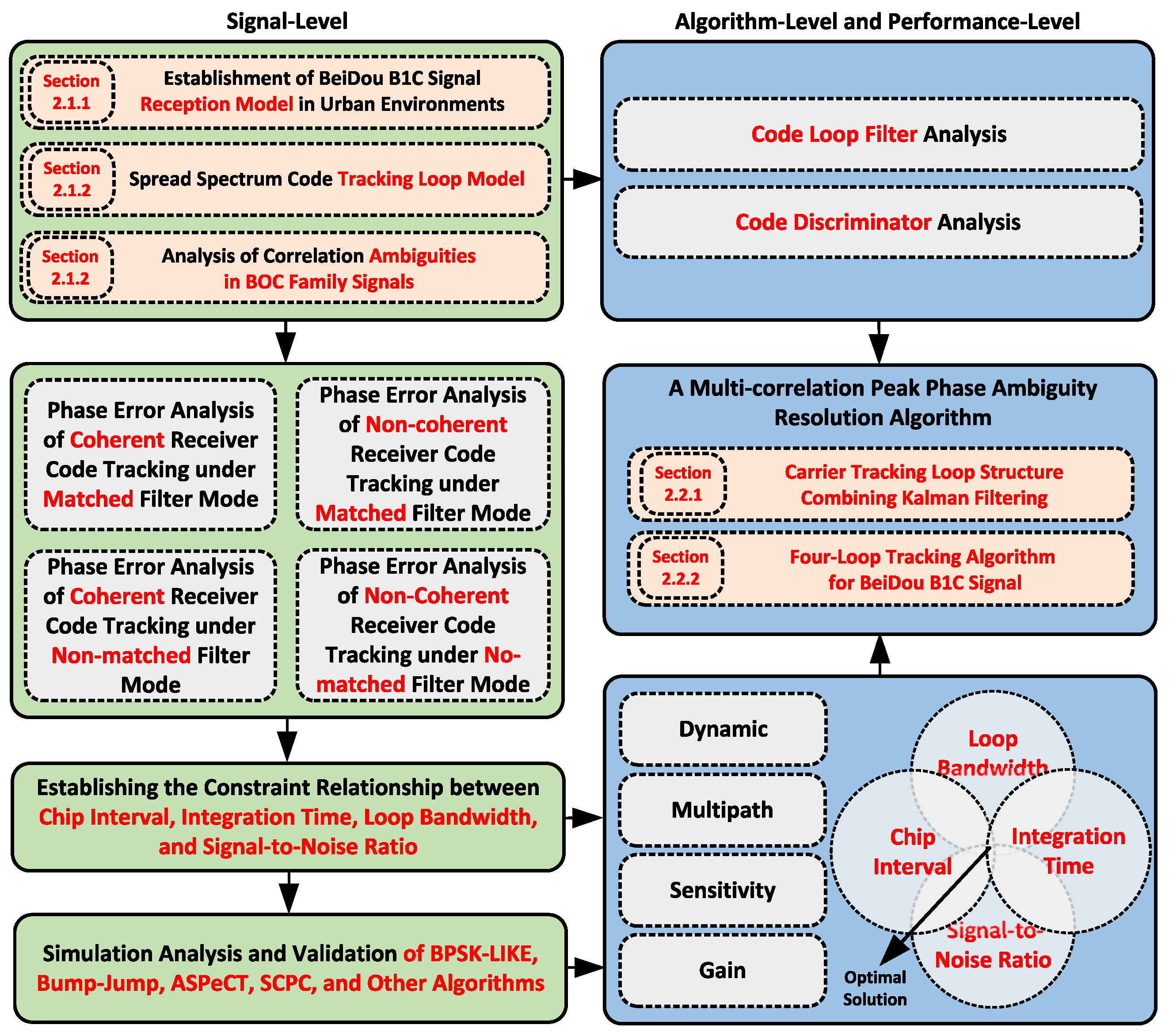
- This paper constructs a mathematical model and structure for the BeiDou B1C signal, exploring autocorrelation properties and power spectrum density characteristics, and it addresses ambiguity in BOC signals. This foundational research informs the design and validation of the tracking loop synchronization algorithm.
- This study introduces a custom multi-loop structure for synchronized B1C signal tracking, along with a specialized multi-peak phase deblurring algorithm tailored to urban BeiDou B1C signals. This coordinated design ensures accurate pseudocode phase estimation and stable tracking.
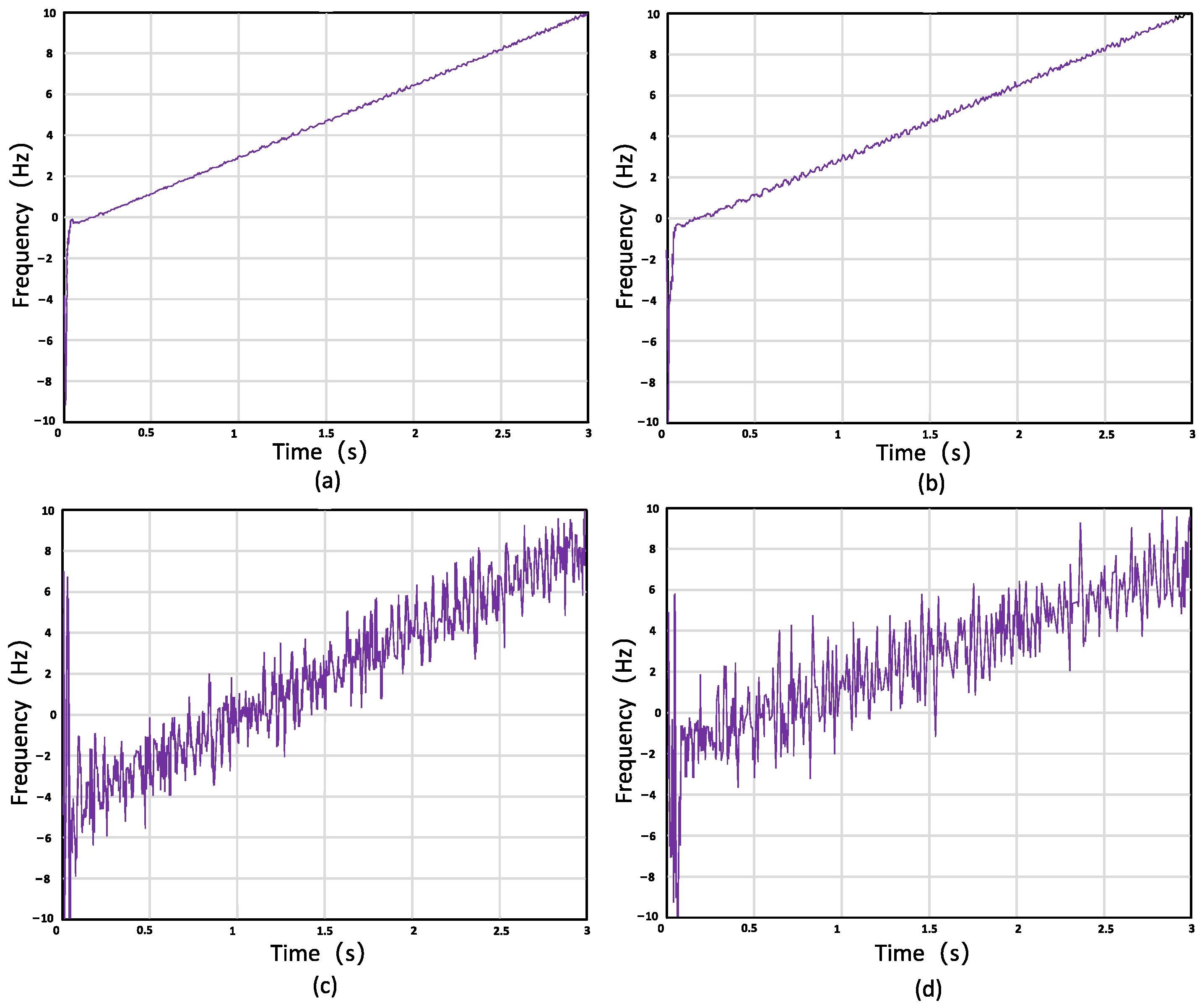
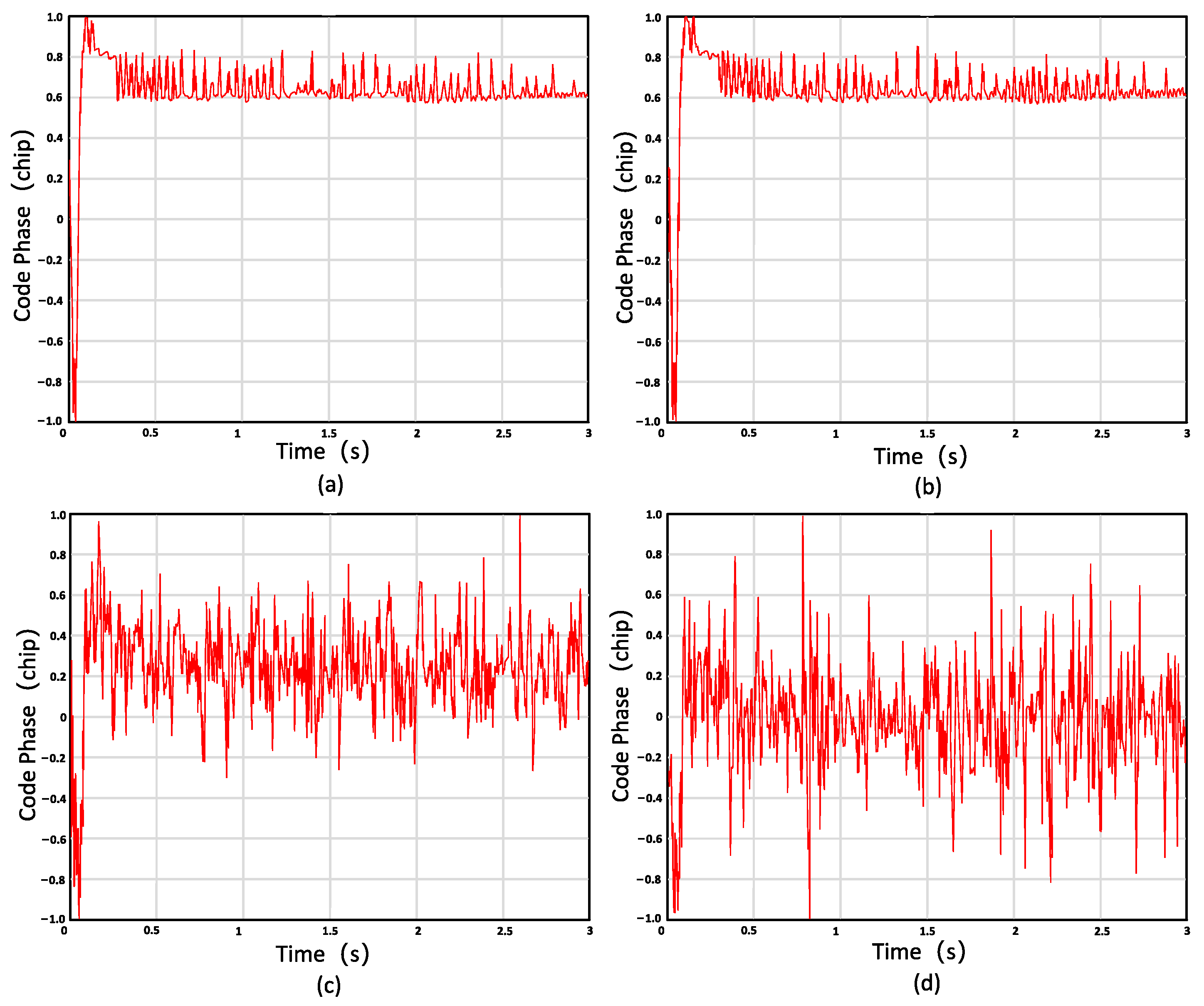
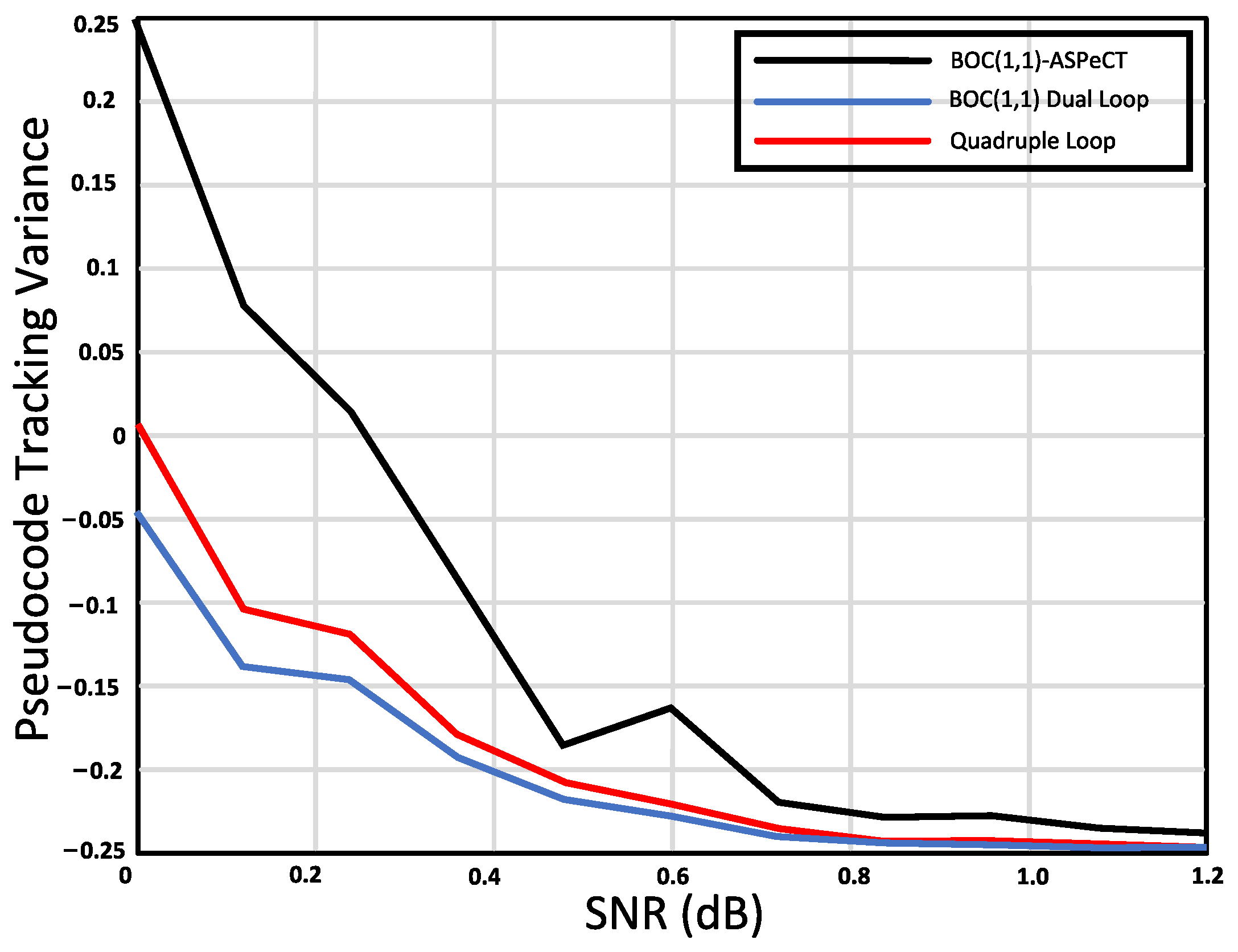
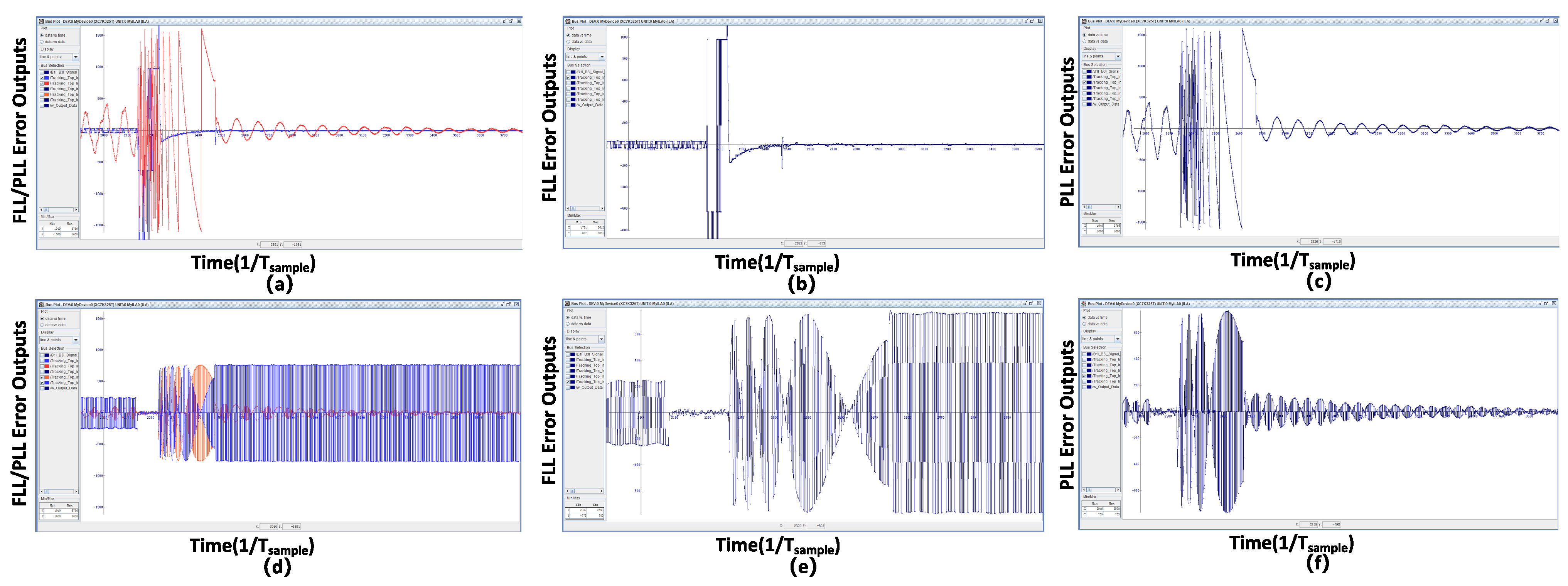
- This study simulated tracking algorithm performance in urban environments at −20 dB SNR, assessing it across four dimensions: coherent integration, non-coherent integration, Doppler frequency error, and code phase estimation. Subcarrier tracking was also analyzed.
2. Proposed Method
2.1. The Characteristics of BeiDou B1C Signal Structure
2.1.1. The Model and Structure of the BeiDou B1C Signal
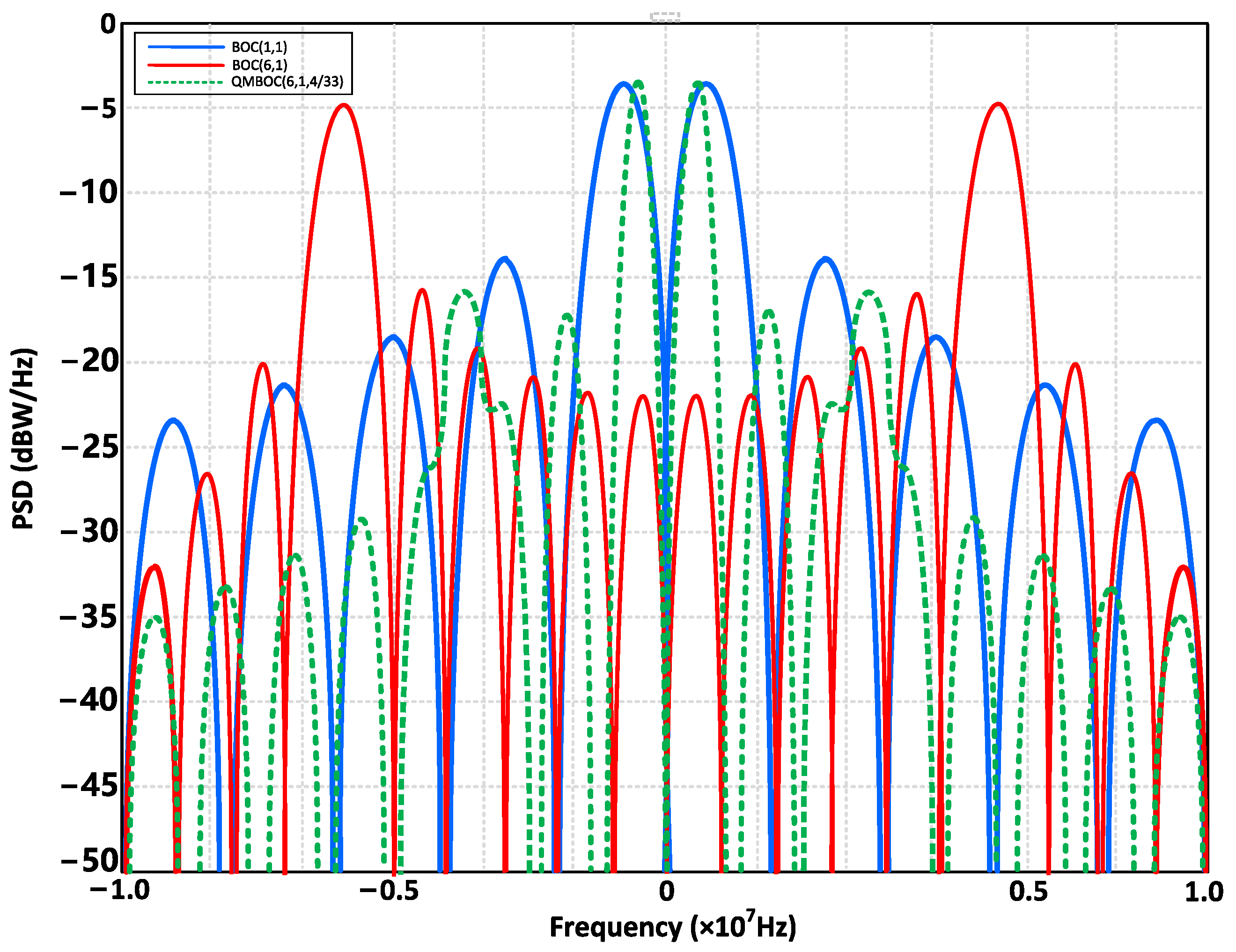
2.1.2. Characteristics Analysis of the BeiDou B1C Signal
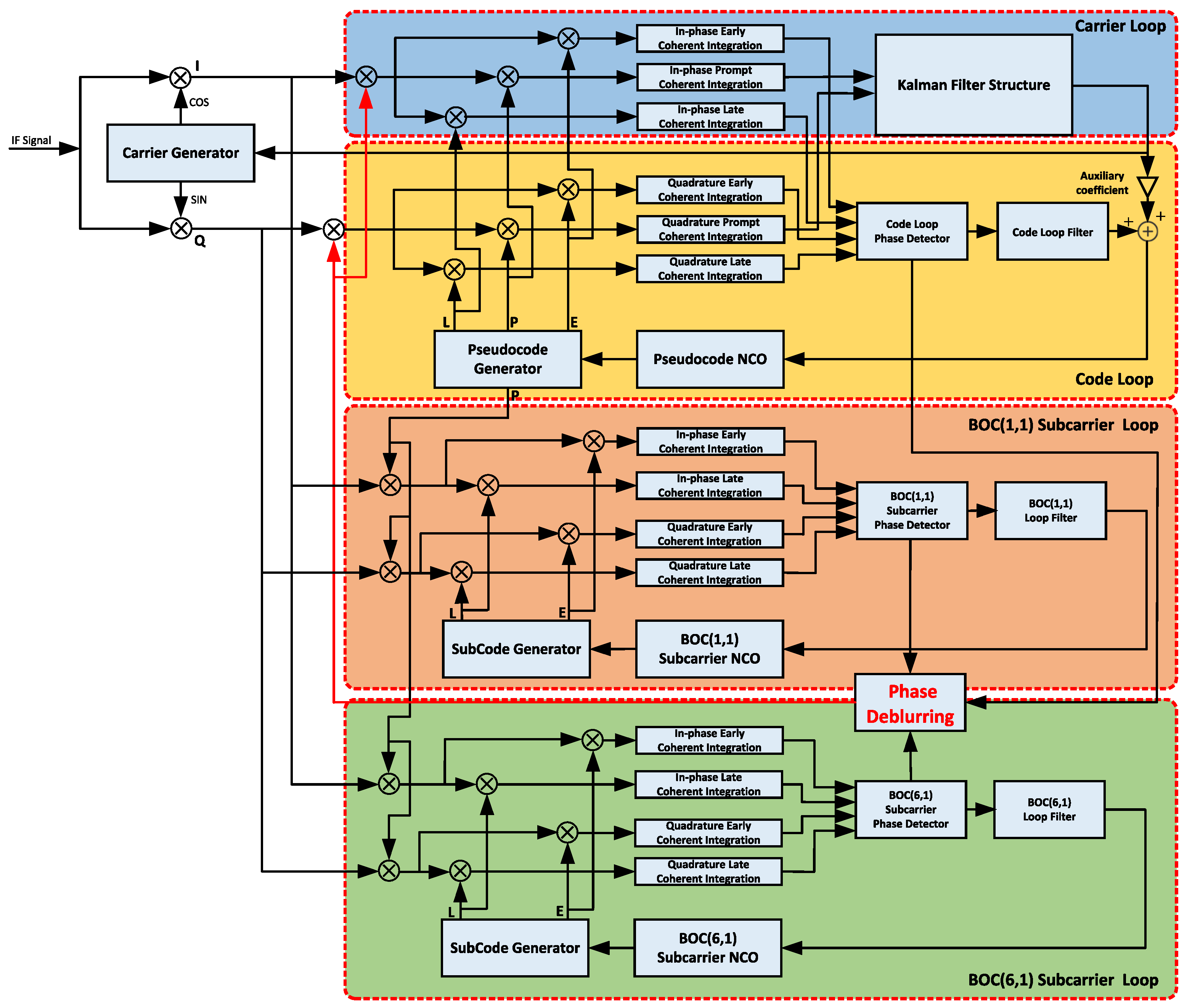
2.2. Multi-Correlation Peak Phase Deblurring Algorithm Design
2.2.1. Carrier Loop Design
2.2.2. Code Loop Design
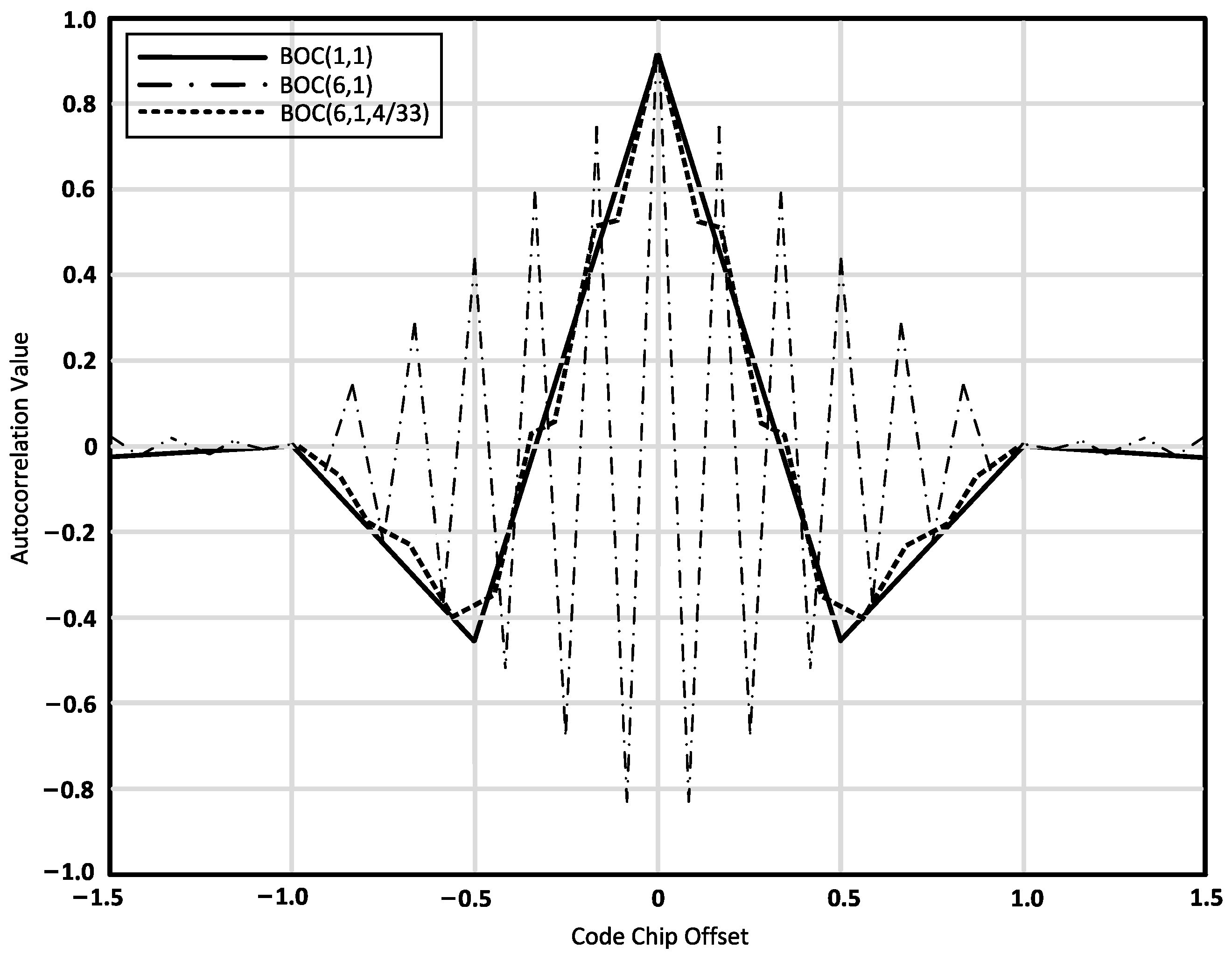
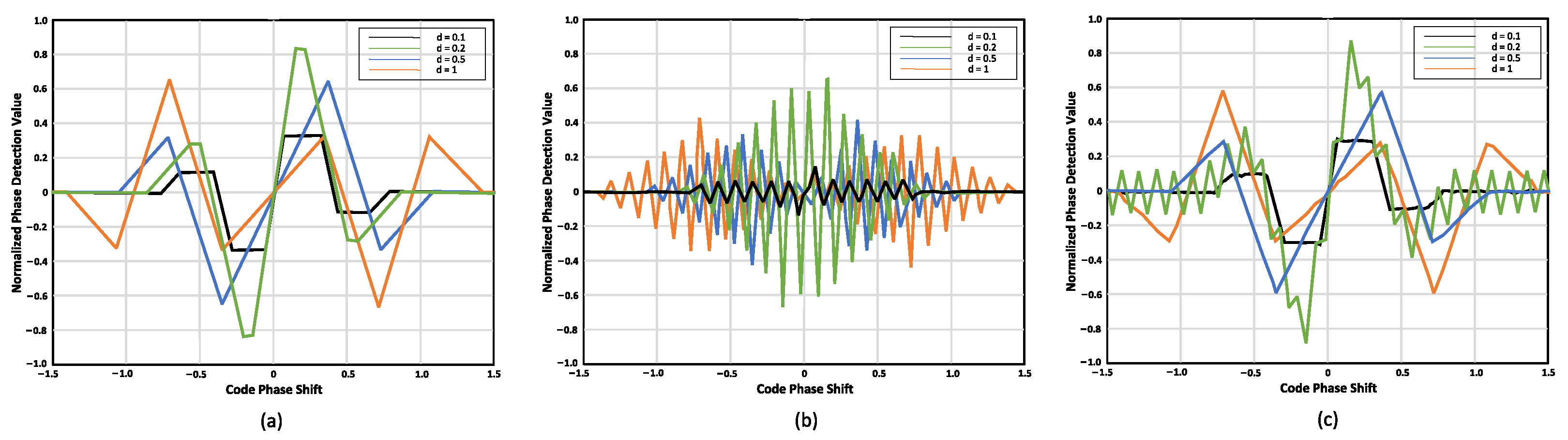
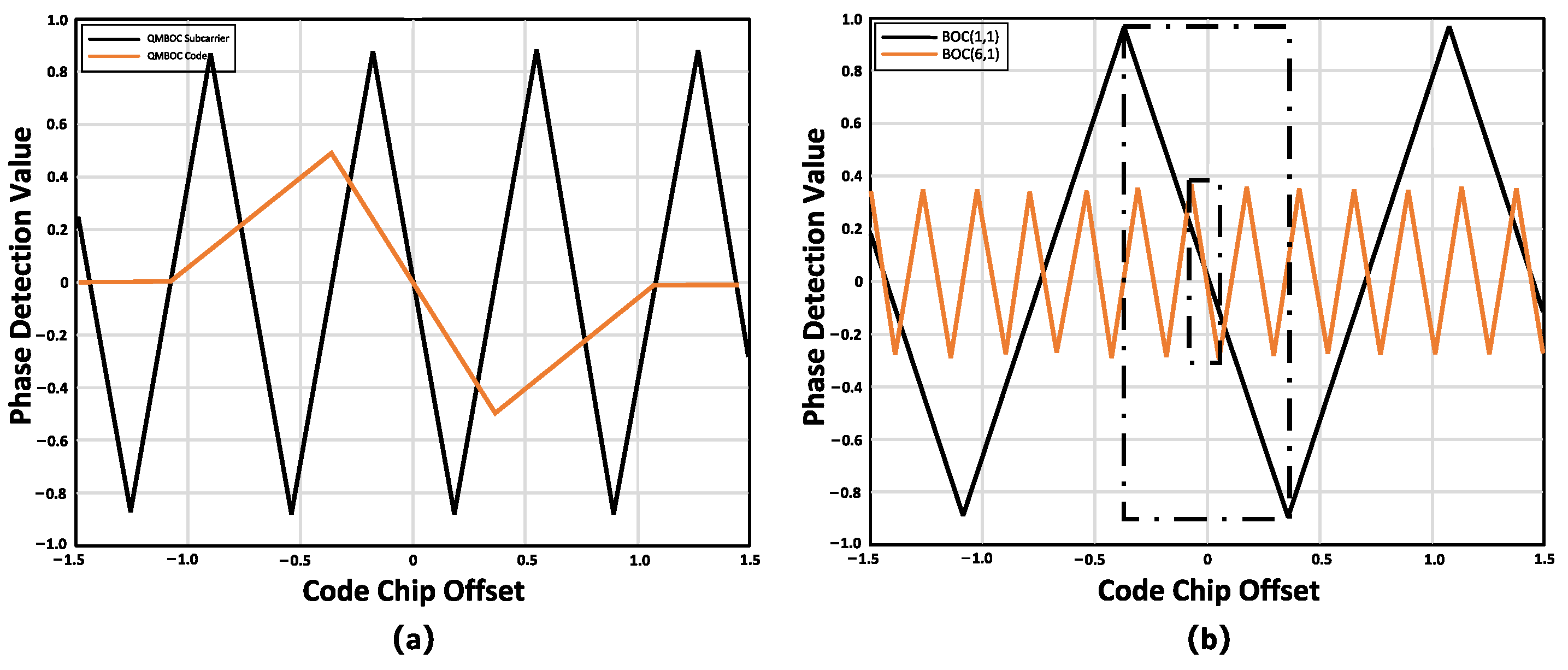
- The higher the modulation order of the BOC signal, the higher the level of ambiguity (the greater the number of zero-crossings in phase detection).
- As the correlation interval becomes smaller, the phase detection accuracy increases.
- In the pseudocode domain, the correlation peaks only reflect the pseudocode correlation, with sharp peaks but low precision and no ambiguity. Due to the influence of subcarrier correlation values, there are pseudocode correlation values both above and below the peak.
- On the other hand, in the subcarrier domain, the subcarrier has a higher frequency, resulting in narrower peaks and higher phase detection accuracy. However, there is ambiguity present, leading to multiple peaks.
3. Results
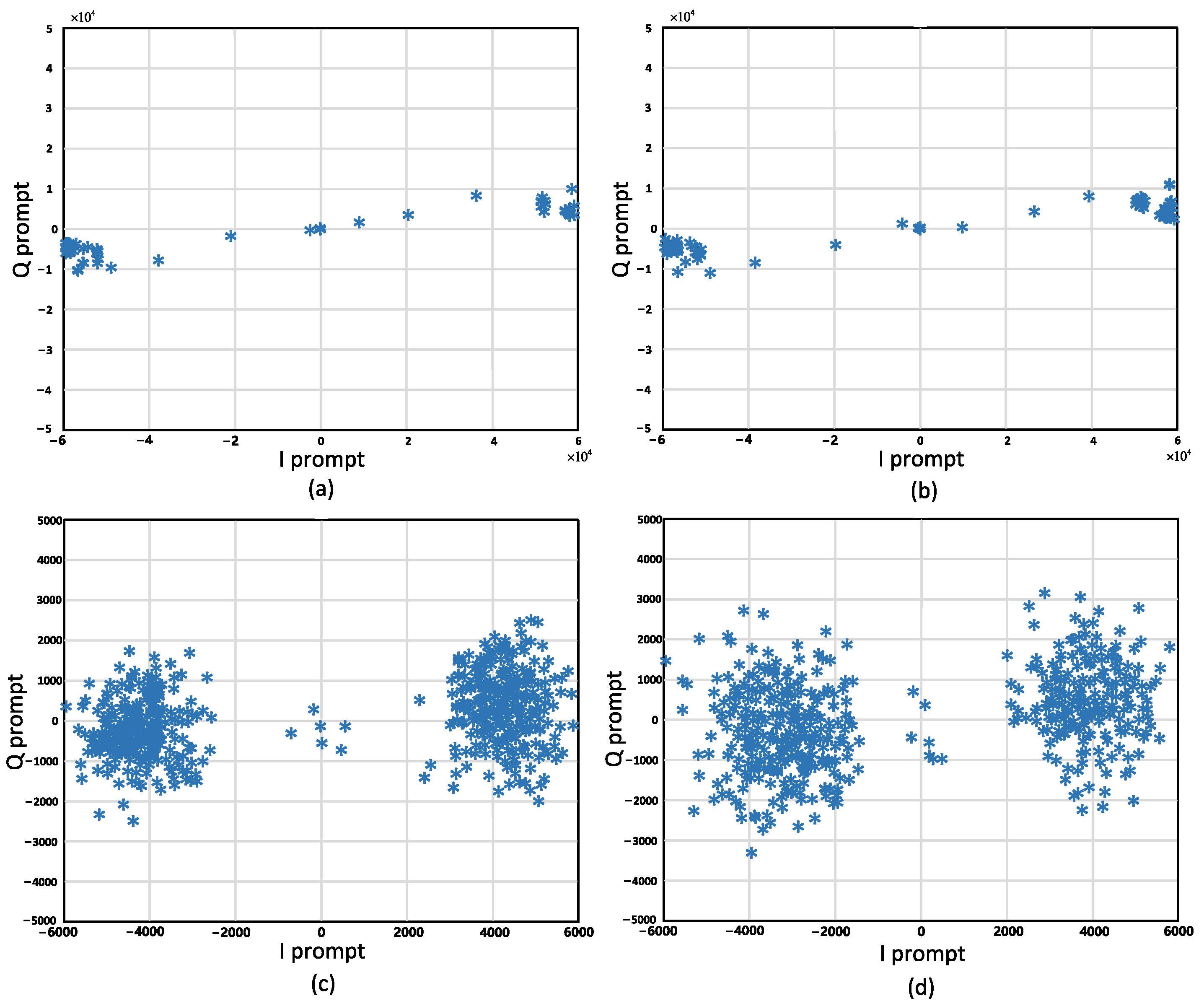
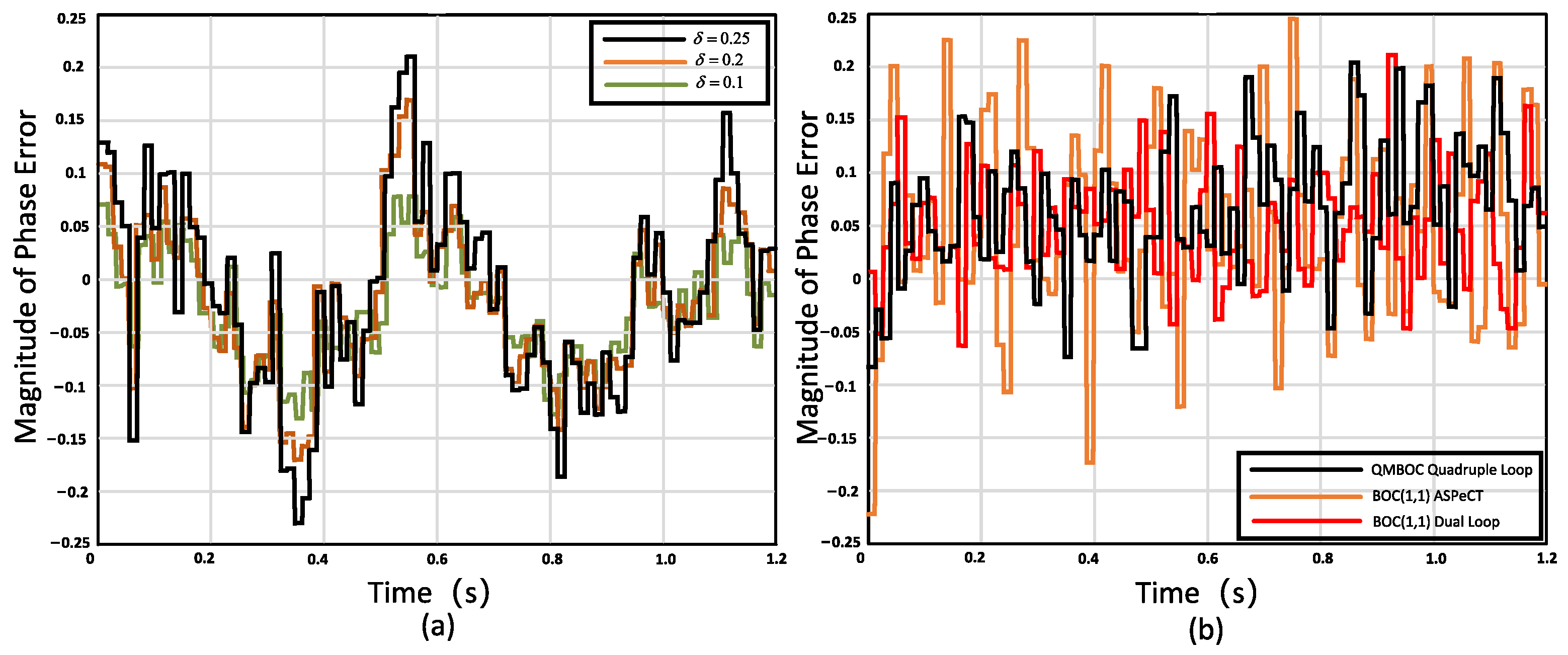
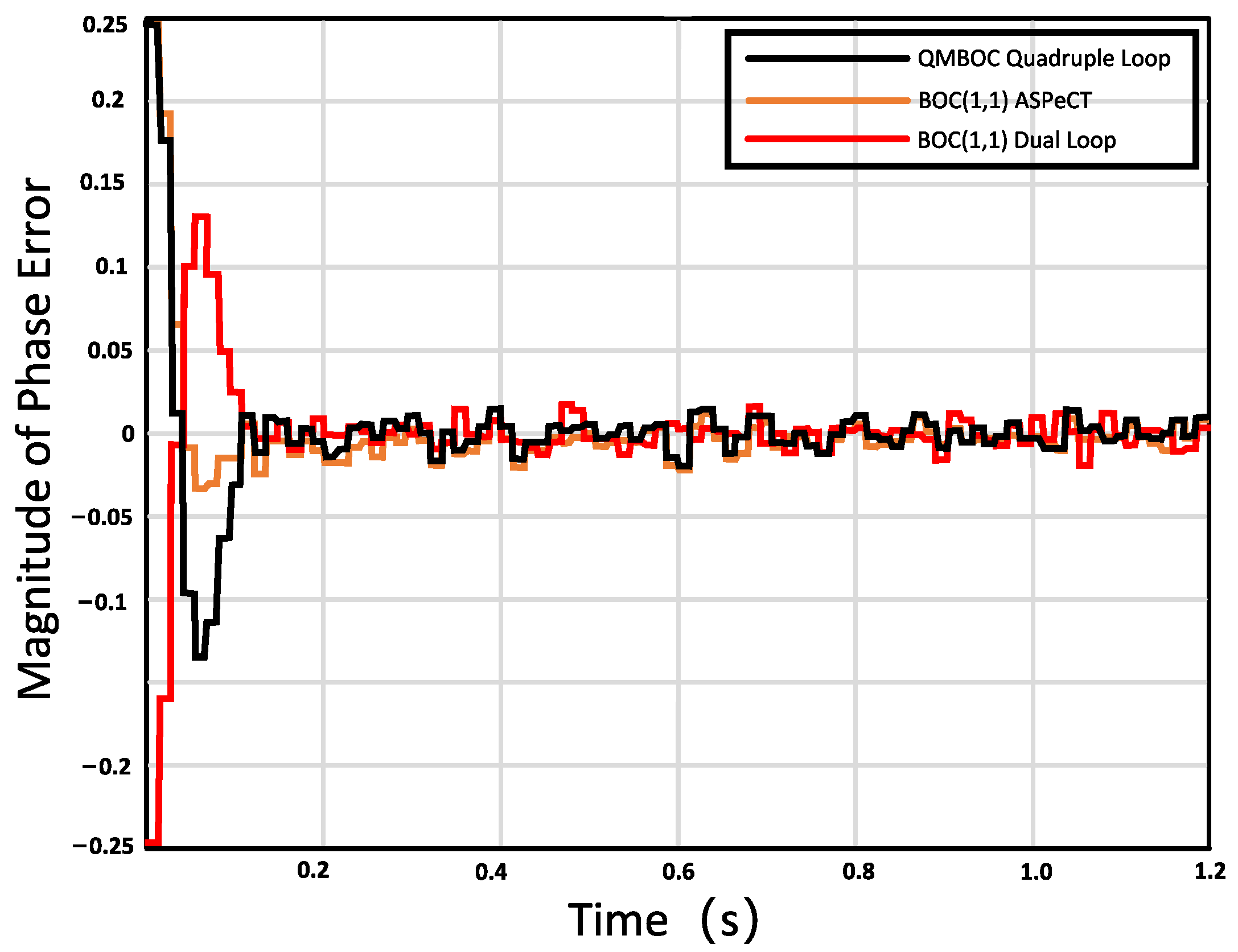
3.1. Simulation and Analysis
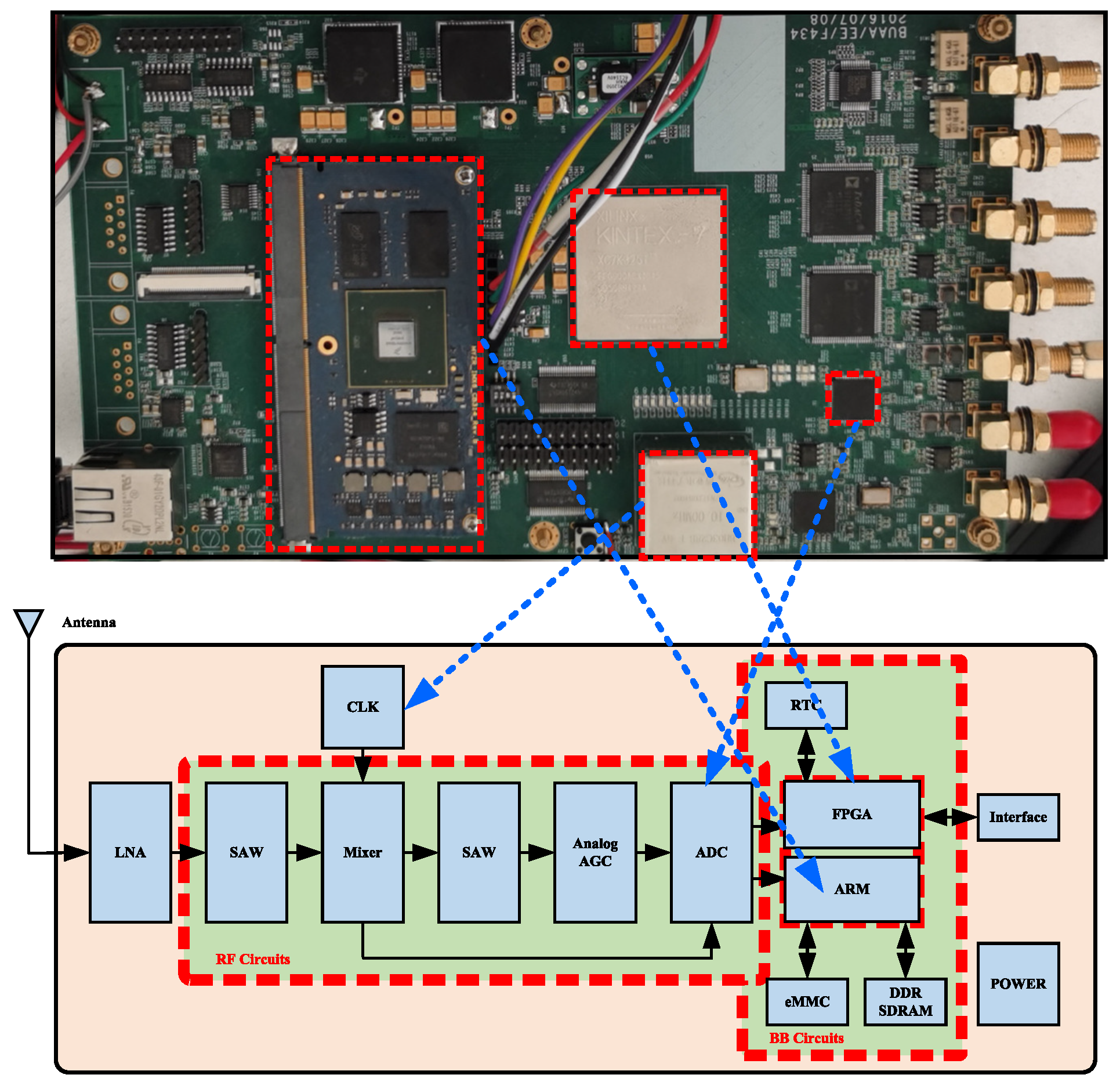
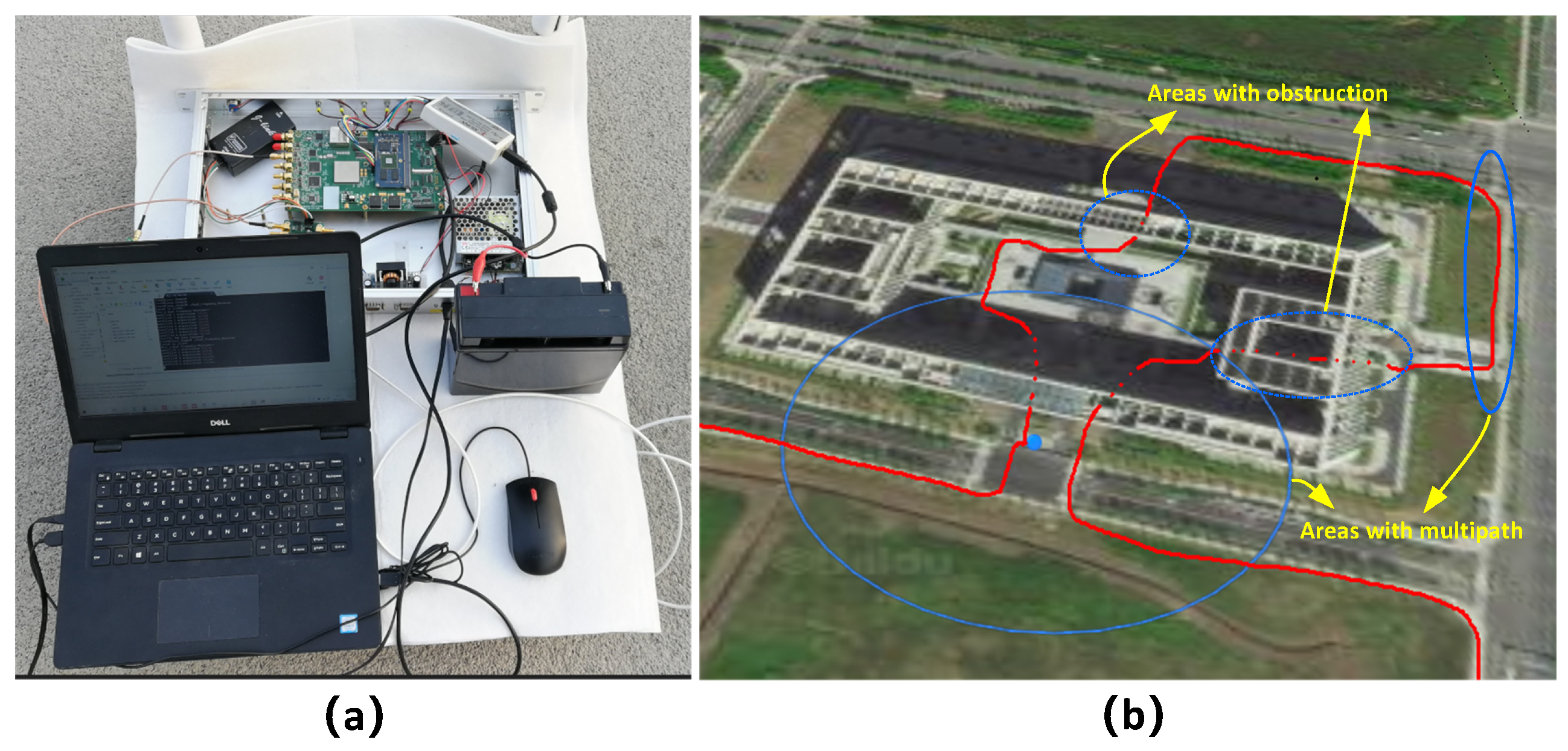
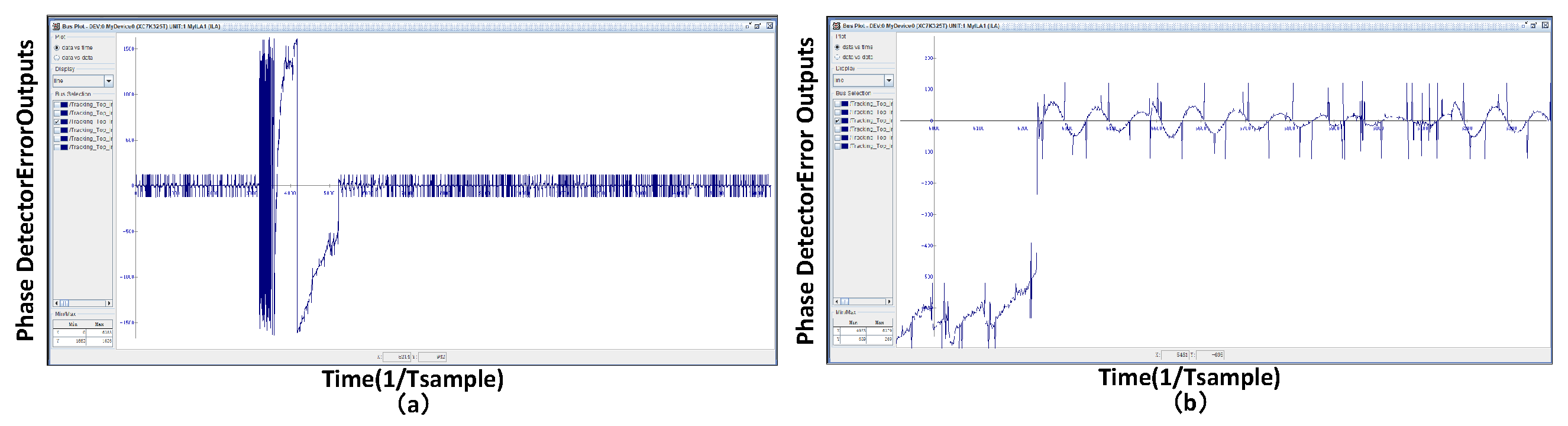
3.2. Practical Testing
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | Autocorrelation Function |
| ADC | Analog-to-Digital Converter |
| AGC | Automatic Gain Control |
| AltBOC | Alternative Binary Offset Carrier |
| ASPeCT | Adaptive Subspace Power Estimation and Cancellation Technique |
| BDS | BeiDou Navigation Satellite System |
| BOC | Binary Offset Carrier |
| BPSK | Binary Phase Shift Keying |
| BPSK-R | Binary Phase Shift Keying-Rectangular |
| CBOC | Composite Binary Offset Carrier |
| CAT | Cross-Assisted Tracking |
| CDMA | Code Division Multiple Access |
| CNR | Carrier to Noise Ratio |
| CWIs | Continuous Wave Interferences |
| DPE | Dual Phase Estimator |
| DLL | Delay Lock Loop |
| DRAM | Dynamic Random Access Memory |
| DSP | Digital Signal Processing |
| DSPs | Digital Signal Processors |
| DSSS-CDMA | Direct Sequence Spread Spectrum-Code Division Multiple Access |
| DualQPSK | Dual-Quadrature Phase Shift Keying |
| EKF | Extend Kalman Filter |
| ELS | Early Late Slope |
| EMLA | Early Minus Late Amplitude |
| EPL | Early-Prompt-Late |
| FDD | Frequency Division Duplexing |
| FIFO | First Input First Output |
| FIR | Finite Impulse Response |
| FLL | Frequency Locked Loop |
| FPGA | Field Programmable Gate Array |
| Galileo | Galileo Navigation Satellite System |
| GLONASS | GLONASS Navigation Satellite System |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| GPU | Graphics Processing Unit |
| HRC | High Resolution Correlator |
| IF | Intermediate Frequency |
| IFFT | Inverse Fast Fourier Transformation |
| LNA | Low Noise Amplifier |
| LPF | Low Pass Filter |
| MCMM | Mixed Mode Clock Manager |
| MBOC | Multiplexed Binary Offset Carrier |
| NELP | Non-coherent Early-Late Power |
| PLL | Phase Lock Loop |
| PRN | Pseudorandom Noise |
| PSD | Power Spectral Density |
| QMBOC | Quadrature Multiplexed Binary Offset Carrier |
| SCBOC | Single-Sideband Complex Binary Offset Carrier |
| SCPC | Sub Carrier Phase Cancellation |
| SDR | Software-Defined Radio |
| SLL | Subcarrier Lock Loop |
| SOPC | System On Programmable Chip |
| TMBOC | Time-Multiplexed Binary Offset Carrier |
References
- Anantharamu, P.B.; Borio, D.; Lachapelle, G. Sub-carrier shaping for BOC modulated GNSS signals. EURASIP J. Adv. Signal Process. 2011, 2011, 133. [Google Scholar] [CrossRef]
- Camacho-Lara, S. Current and future GNSS and their augmentation systems. In Handbook of Satellite Applications; Springer: Cham, Switzerland, 2017; pp. 781–819. [Google Scholar]
- Foucras, M.; Ngayap, U.; Bacard, F.; Ekambi, B. Acquisition performance comparison of new generation of GNSS BOC-modulated signals. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 107–119. [Google Scholar]
- Kao, T.L.; Juang, J.C. Weighted discriminators for GNSS BOC signal tracking. GPS Solut. 2012, 16, 339–351. [Google Scholar] [CrossRef]
- Harris, R.B.; Lightsey, E.G. A general model of multipath error for coherently tracked BOC modulated signals. IEEE J. Sel. Top. Signal Process. 2009, 3, 682–694. [Google Scholar] [CrossRef]
- Rusu-Casandra, A.; Lohan, E.S.; Seco-Granados, G.; Marghescu, I. Investigation of narrowband interference filtering algorithms for galileo CBOC signal. In Proceedings of the the ISI Conference Proceedings of the 3rd European Conference of Communications, Paris, France, 17–18 October 2012; pp. 274–279. [Google Scholar]
- Zhang, K. Generalised constant-envelope DualQPSK and AltBOC modulations for modern GNSS signals. Electron. Lett. 2013, 49, 1335–1337. [Google Scholar] [CrossRef]
- Yan, T.; Wei, J.; Tang, Z.; Zhou, Z.; Xia, X. General AltBOC modulation with adjustable power allocation ratio for GNSS. J. Navig. 2016, 69, 531–560. [Google Scholar] [CrossRef]
- Yang, C. Sharpen the correlation peak: A novel gnss receiver architecture with variable if correlation. Navig. J. Inst. Navig. 2016, 63, 249–265. [Google Scholar] [CrossRef]
- Attia, S.; Rouabah, K.; Chikouche, D.; Flissi, M. Side peak cancellation method for sine-BOC (m, n)-modulated GNSS signals. EURASIP J. Wirel. Commun. Netw. 2014, 2014, 34. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, E.; Yin, L.; Liu, W.; Yang, L.; Arain, Q.A. An unambiguous tracking technique for sine-BOC (kn, n) modulated GNSS signals. Wirel. Pers. Commun. 2018, 103, 1101–1112. [Google Scholar] [CrossRef]
- Sun, X.; Song, S.; Ji, Y.; Gan, X.; Yan, S.; Jia, X. An Unambiguous Synchronization Scheme for GNSS BOC Signals Based on Reconstructed Correlation Function. Sensors 2021, 21, 1982. [Google Scholar] [CrossRef]
- Chengtao, X.; Zhe, L.; Xiaomei, T.; Feixue, W. Strobe double phase estimator: A multipath mitigating technique for BOC signal in GNSS based on double phase estimator. Int. J. Satell. Commun. Netw. 2017, 35, 249–261. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Lu, X.; Rao, Y.; He, C. Algorithm research on high-precision tracking of beidou-3 B1C signal. In Proceedings of the China Satellite Navigation Conference (CSNC) 2019 Proceedings: Volume I, Beijing, China, 22–25 May 2019; Springer: Singapore, 2019; pp. 452–464. [Google Scholar]
- Gao, Y.; Yao, Z.; Lu, M. Exploring the ultra-high-precision ranging potential of BDS B1 signal. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Virtual, 22–25 September 2020; pp. 3626–3646. [Google Scholar]
- Hao, Z.; He, C.; Guo, J.; Lu, X.; Rao, Y.; Wang, M. A New Joint Tracking Method of BeiDou B1C Signal and Its Influence on Signal Quality Evaluation. In Proceedings of the Wireless and Satellite Systems: 11th EAI International Conference, WiSATS 2020, Nanjing, China, 17–18 September 2020; Proceedings, Part I. Springer: Cham, Switzerland, 2021; pp. 449–467. [Google Scholar]
- Hao, W.; Gong, W. Research on Tracking Algorithm of Beidou B1C Signal. In Proceedings of the 2019 IEEE 9th International Conference on Electronics Information and Emergency Communication (ICEIEC), IEEE, Beijing, China, 12–14 July 2019; pp. 226–229. [Google Scholar]
- Wang, H. Research on BDS B1C Signal Synchronization Method. In Proceedings of the CIBDA 2022, 3rd International Conference on Computer Information and Big Data Applications, VDE, Wuhan, China, 25–27 March 2022; pp. 1–4. [Google Scholar]
- Liu, X.; Yin, C.; Yu, Q.; Li, B. Implementation of PMF and FFT acquisition design for B1C signal based on ASPeCT. In Journal of Physics: Conference Series; IOP Publishing: Dalian, China, 2021; Volume 1952, p. 042135. [Google Scholar]
- Sun, X.; Liu, Z.; Ji, Y.; Yan, S.; Liang, W. Sub cross-correlation shift cancellation technique for unambiguous tracking of BOC (kn, n) signals. In Proceedings of the 2020 8th International Conference on Digital Home (ICDH), IEEE, Dalian, China, 20–22 September 2020; pp. 239–247. [Google Scholar]
- Hao, W.; Gong, W. Research on Beidou B1C Signal Joint Tracking Algorithm Based on Pseudo Correlation Function. In Journal of Physics: Conference Series; IOP Publishing: Suzhou, China, 2020; Volume 1544, p. 012013. [Google Scholar]
- Gao, Y.; Yao, Z.; Lu, M. High-precision unambiguous tracking technique for BDS B1 wideband composite signal. Navigation 2020, 67, 633–650. [Google Scholar] [CrossRef]
- LI, W.; HUANG, C.; WANG, Y. Strobe Pulse Design for Quadrature Multiplexed Binary Offset Carrier Modulation in BeiDou B1C Signal. J. Electron. Inf. Technol. 2018, 40, 2438–2446. [Google Scholar]
- Wu, M.; Zhao, L.; Ding, J.; Gao, Y.; Li, Y.; Kang, Y. A BDS-3 B1C/B2a dual-frequency joint tracking architecture based on adaptive Kalman filter and extended integration time. GPS Solut. 2020, 24, 1–16. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, S.; Liu, T.; Chen, Y.; Dong, Q. Performance analysis of cross-frequency Doppler-assisted carrier phase tracking. GPS Solut. 2023, 27, 105. [Google Scholar] [CrossRef]
- Wu, M.; Zhao, L.; Ding, J.; Kang, Y.; Luo, Z. Design and performance analysis of Doppler-aided Beidou B1C/B2a joint tracking algorithm. In Proceedings of the China Satellite Navigation Conference (CSNC) 2019 Proceedings: Volume II, Beijing, China, 22–25 May 2019; Springer: Singapore, 2019; pp. 463–476. [Google Scholar]
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1C (Version 1.0); China Satellite Navigation Office: Beijing, China, 2017. [Google Scholar]
- Zhang, H.; He, Z.; Ye, L.; Ma, H. The Analysis And Comparison of The Performance of The Equi - Length Weil and Gold Codes. Comput. Simul. 2019, 36, 71–76. [Google Scholar]
- Yan, Z.; Chen, X.; Tang, X.; Ruotsalainen, L. A novel carrier loop based on adaptive LM-QN method in GNSS receivers. IEEE Trans. Veh. Technol. 2022, 71, 5259–5271. [Google Scholar] [CrossRef]
- Razavi, A.; Gebre-Egziabher, D.; Akos, D.M. Carrier loop architectures for tracking weak GPS signals. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 697–710. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Psiaki, M.L.; Ledvina, B.M.; Cerruti, A.P.; Kintner, P.M. Data-driven testbed for evaluating GPS carrier tracking loops in ionospheric scintillation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1609–1623. [Google Scholar] [CrossRef]
- Qi, Y.; Yao, Z.; Lu, M. General Design Method for Two-dimensional Multi-correlator Anti-multipath Tracking Loop for BOC Signals. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 871–885. [Google Scholar] [CrossRef]
- Song, Y.J.; Pany, T.; Won, J.H. Theoretical Upper and Lower Limits for Normalized Bandwidth of Digital Phase-Locked Loop in GNSS Receivers. Sensors 2023, 23, 5887. [Google Scholar] [CrossRef]
- Zhou, W.; Lv, Z.; Wu, W.; Shang, X.; Ke, Y. Anti-Spoofing Technique Based on Vector Tracking Loop. IEEE Trans. Instrum. Meas. 2023, 72, 8504516. [Google Scholar] [CrossRef]
- Lopes, R.A.; Antreich, F.; Fohlmeister, F.; Kriegel, M.; Kuga, H.K. Ionospheric Scintillation Mitigation with Kalman PLLs Employing Radial Basis Function Networks. IEEE IEEE Trans. Aerosp. Electron. Syst. 2023; early access. [Google Scholar]
- Dey, A.; Iyer, K.; Xu, B.; Sharma, N.; Hsu, L.T. Carrier-aided dual-frequency vectorized tracking architecture for NavIC signals. IEEE Trans. Instrum. Meas. 2022, 71, 8500513. [Google Scholar] [CrossRef]
- Khalife, J.; Neinavaie, M.; Kassas, Z.M. The first carrier phase tracking and positioning results with Starlink LEO satellite signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1487–1491. [Google Scholar] [CrossRef]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Acquisition, Doppler tracking, and positioning with Starlink LEO satellites: First results. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2606–2610. [Google Scholar] [CrossRef]






| Component | Modulation | Phase Relationship | Power Ratio | |
|---|---|---|---|---|
| 0 | 1/4 | |||
| 90 | 29/44 | |||
| 0 | 1/11 | |||
| Parameter | Value |
|---|---|
| Sampling Rate | 120 MHz |
| Signal Duration | 5 s |
| PRN Number | 20 |
| Initial Code Phase | 4120th chip |
| Initial Doppler Frequency | 800 Hz |
| Doppler Frequency Shift | 4 Hz per second |
| Signal-to-Noise Ratio (SNR) | −20 dB |
| Code Phase Correlation Interval | 0.5 chip |
| BOC (1,1) Subcarrier Correlation Interval | 0.5 chip |
| BOC (6,1) Subcarrier Correlation Interval | 0.2 chip |
| Loop Noise Bandwidth | 5 Hz |
| Carrier Loop Bandwidth | 20 Hz |
| Damping Coefficient | 0.707 |
| Test Route Conditions | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Visible Satellites Number | Code Correlation Interval (chip) | Subcarrier Correlation Interval (chip) | Loop Noise Bandwidth (Hz) | Carrier Loop Bandwidth (Hz) | SNR (dB) | Typical Scenarios | Average Tracking Time (ms) | Average Tracking Sensitivity (dBm) | Average Tracking Error (chip) |
| ≥−20 | Open Environments | ≤50 | −153.72 | 0.03 | |||||
| ≥10 | 0.5 | 0.5 | 5 | 20 | −30∼−20 | Multipath Environments | ≤50 | −150.32 | 0.25 |
| ≤−40 | Obstructed Environments | ≤100 | −142.17 | 0.73 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Feng, W.; Zhuang, C.; Wang, Q.; Yang, X.; Yang, Z. A Multi-Correlation Peak Phase Deblurring Algorithm for BeiDou B1C Signals in Urban Environments. Remote Sens. 2023, 15, 4300. https://doi.org/10.3390/rs15174300
Yang X, Feng W, Zhuang C, Wang Q, Yang X, Yang Z. A Multi-Correlation Peak Phase Deblurring Algorithm for BeiDou B1C Signals in Urban Environments. Remote Sensing. 2023; 15(17):4300. https://doi.org/10.3390/rs15174300
Chicago/Turabian StyleYang, Xu, Wenquan Feng, Chen Zhuang, Qiang Wang, Xu Yang, and Zhe Yang. 2023. "A Multi-Correlation Peak Phase Deblurring Algorithm for BeiDou B1C Signals in Urban Environments" Remote Sensing 15, no. 17: 4300. https://doi.org/10.3390/rs15174300
APA StyleYang, X., Feng, W., Zhuang, C., Wang, Q., Yang, X., & Yang, Z. (2023). A Multi-Correlation Peak Phase Deblurring Algorithm for BeiDou B1C Signals in Urban Environments. Remote Sensing, 15(17), 4300. https://doi.org/10.3390/rs15174300