Abstract
The fusion of hyperspectral and LiDAR images plays a crucial role in remote sensing by capturing spatial relationships and modeling semantic information for accurate classification and recognition. However, existing methods, such as Graph Convolutional Networks (GCNs), face challenges in constructing effective graph structures due to variations in local semantic information and limited receptiveness to large-scale contextual structures. To overcome these limitations, we propose an Invariant Attribute-driven Binary Bi-branch Classification (IABC) method, which is a unified network that combines a binary Convolutional Neural Network (CNN) and a GCN with invariant attributes. Our approach utilizes a joint detection framework that can simultaneously learn features from small-scale regular regions and large-scale irregular regions, resulting in an enhanced structural representation of HSI and LiDAR images in the spectral–spatial domain. This approach not only improves the accuracy of classification and recognition but also reduces storage requirements and enables real-time decision making, which is crucial for effectively processing large-scale remote sensing data. Extensive experiments demonstrate the superior performance of our proposed method in hyperspectral image analysis tasks. The combination of CNNs and GCNs allows for the accurate modeling of spatial relationships and effective construction of graph structures. Furthermore, the integration of binary quantization enhances computational efficiency, enabling the real-time processing of large-scale data. Therefore, our approach presents a promising opportunity for advancing remote sensing applications using deep learning techniques.
1. Introduction
Geospatial classification plays a pivotal role in diverse applications such as Earth monitoring, ecological studies, and woodland administration. Sensor technology advancements have offered various data resources to aid in categorization assignments. Among these options, HyperSpectral Imaging (HSI) distinguishes itself due to its extensive range of spectral bands, providing comprehensive insights into land surface characteristics. Nevertheless, its passive imaging methodology renders it susceptible to the impact of overcast weather conditions and challenges the differentiation of objects with similar spectral reflectance. On the other hand, the active collection of LIght Detection And Ranging (LiDAR) data is relatively immune to the influence of weather conditions. LiDAR data facilitate the collection of altitude data, assisting in the assessment of the dimensions and contours of particular entities. Presently, there is an increasing inclination towards employing a fusion of HSI and LiDAR data to achieve the precise classification of land cover. Numerous collaborative models have been examined to offer a thorough understanding of this research area.
In the past few decades, numerous machine-learning-based classifiers have been designed for the integration of HSI and LiDAR in classification tasks. Among these classifiers, Convolutional Neural Networks (CNNs) have become the prevailing tool for extracting spectral–spatial characteristics from HSI and LiDAR imagery. Different variants of CNNs, including 1D-CNNs [1], 2D-CNNs [2], and 3D-CNNs [3,4], have been suggested to augment the capacity for learning spectral–spatial characteristics. Additionally, combining the advantages of different structural networks to enhance feature information extraction and improve classification accuracy has also been validated [5,6,7]. However, these experiments indicated a limited improvement from the inclusion of extra branches, potentially due to suboptimal compatibility among distinct network branches. To tackle this problem, Hao et al. [8] suggested the adaptive learning of fusion weights for diverse categories to equalize the features extracted by distinct branches. Compared to traditional feature-level fusion methods that are artificially designed, deep feature fusion methodologies based on CNNs possess the ability to autonomously and flexibly acquire representative features. This offers significant potential for improving the task of multimodal image classification. Nevertheless, although the current CNN-based approaches for the joint classification of HSI and LiDAR excel in extracting spatial–spectral features at a local level, they overlook the complete utilization of the overarching sequential characteristics inherent in spatial–spectral features. Graph Convolutional Networks (GCNs) are popular and emerging network architectures that effectively manage graph-structured data by capturing connections between instances (vertices). As a result, GCNs can inherently simulate the global spatial–spectral relationships within images, which are not accounted for in CNNs. Shahraki and Prasad [9] integrated 1D CNNs and GCNs for HSI classification. Wan et al. [10,11] used super-pixel segmentation technology on the HSI, enabling the adjacency matrix to be dynamically updated throughout the iterations of the network. Qin et al. [12] devised an innovative approach to constructing graphs by concurrently combining spatial and spectral neighborhoods in second-order versions, which enhanced the efficacy of remote sensing image classification. Hong et al. [13] introduced miniGCN, which utilizes mini-batch learning to train a GCN with a fixed scale for the purpose of reducing computational expenses and enhancing classification accuracy. However, GCNs have some potential drawbacks in the subsequent areas and are not extensively employed in the remote sensing community for multimodal data classification.
As shown in Figure 1, variations in the local semantic information around target pixels, such as scene composition and relative positions between objects, lead to significant feature variations when modeling spatial information. This results in inaccurate graph structure construction in GCN networks, where effective connections cannot be established among pixels belonging to identical categories in spatial contexts. Therefore, we put forward an approach to solve this problem by extracting invariant features from images at a local level in both the spatial and frequency domains by employing the method of invariant attribute configuration. While CNNs have the ability to learn local spatial–spectral features at the pixel level, their receptive fields are generally constrained to small square windows, making it difficult to capture large-scale contextual structures in images. We propose the integration of CNNs and GCNs in a unified network architecture, where the CNN branch learns fine-grained features at the pixel level within small regular regions, while the GCN branch models capture high-level semantic features within irregular regions of the image. By doing so, we combine the advantages of both CNNs and GCNs. Additionally, because of the imaging mechanism and high-dimensional characteristics of hyperspectral bands, the resource costs are high. Henceforth, our CNN network is designed as a binary-quantized network to address the computational challenges and enhance the inference speed of the CNN model. Binary quantization offers several advantages, including a significant reduction in storage requirements, as binary values consume less memory compared to floating-point values. Moreover, by adopting binary quantization, we are able to alleviate resource constraints and facilitate real-time decision-making capabilities, which are essential for effectively handling extensive data in remote sensing applications.
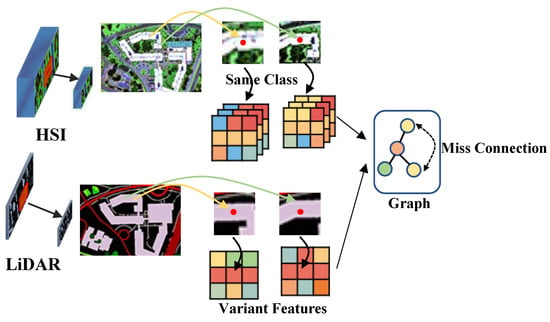
Figure 1.
The graph structure construction is influenced by feature variations in the same class field.
- We systematically analyze the sensitivity of CNNs and GCNs to variations such as rotation, translation, and semantic information. To the best of our understanding, this is the first investigation in the community to explore the importance of spatial invariance in CNN and GCN networks. By extracting invariant features, we address the problem of feature variations caused by local semantic changes in spatial information modeling, thereby improving the accuracy of graph structure construction in the GCN network.
- By leveraging the advantages of both CNN and GCN, our proposed method has the ability to concurrently acquire features from fine-grained regular regions as well as coarse-grained irregular regions, leading to an enhanced structure representation of HSI and LiDAR images in the spectral–spatial domain. This improvement contributes to an overall enhancement in the classification accuracy of the network.
- To address the challenges posed by the high-dimensional nature of hyperspectral data and computational resource limitations, we introduce a lightweight binary CNN architecture that significantly reduces the number of parameters and computational requirements while still maintaining a high level of classification performance.
The structure of the paper is outlined as follows. Section 2 reviews the existing literature on multimodal classification and network compression. Section 3 elaborates on the proposed IABC approach. The experimental outcomes and thorough analysis of the approach are presented in Section 3. Section 4 then discusses the implications and draws conclusions based on the findings of our method.
2. Related Work
In this section, we provide a concise overview of two crucial aspects that are pertinent to our work: multimodal classification and network compression.
2.1. Multimodal Classification
Multimodal image fusion can be further classified based on existing image classification algorithms into (1) classical deep learning algorithms and (2) transformer algorithms. CNNs as a traditional deep learning structure have become the most commonly used tool for extracting spectral–spatial features from HSI and LiDAR data. In terms of spectral learning, previous studies such as Hu et al. [1] utilized 1D CNNs to extract spectral features and classify HSIs by inputting the pixel vector, derived from available samples, into the models. For spatial learning, Chen et al. [2] introduced a 2D CNN-based framework for HSI classification. While satisfactory results were achieved through using 1D and 2D CNN, there was a need to effectively combine the spectral and spatial information in HSIs to achieve more robust abstraction. This led to the incorporation of 3D CNNs in HSI processing frameworks. Chen et al. [2] introduced a basic 3D CNN for HSI classification. Zhong et al. [3] introduced a 3D framework that systematically extracted spectral and spatial features in a sequential manner. Another example is the work of Ying et al. [4], who proposed a 3D CNN that utilizes three-dimensional convolution to learn spectral–spatial features. Xu et al. [5] employed 1D and 2D CNNs in parallel for spectral and spatial learning. Yang et al. [6] presented a dual-channel CNN (TCCNN) that integrates one-dimensional and two-dimensional convolution branches to capture spectral and spatial features. Furthermore, Chen et al. [7] designed a multichannel CNN (MCCNN) with an additional 3D convolution branch based on TCCNN. Hao et al. [8] proposed the adaptive learning of fusion weights for different categories to equalize the features extracted by distinct branches. Fusion based on convolutional neural networks can yield compact modal representations. For instance, Hong et al. [14] proposed a deep encoder–decoder network architecture for HSI and LiDAR data classification. Liu et al. [15] introduced a novel heterogeneous deep network using both CNN and GCN branches to learn features from small-scale regular regions and large-scale irregular regions. Although traditional methods are easy to implement, they may suffer from classification errors and low-level features, which can potentially degrade overall accuracy. Recently, transformer networks [16,17] have been introduced into classification tasks, leveraging the distinct and robust global modeling capabilities to produce desirable results. Roy et al. [18] developed a novel multimodal fusion transformer network that integrates external classification markers from other multimodal data into the transformer encoders, leading to improved generalization performance. Yao et al. [19] extended conventional ViT with minimal modifications.
In this study, we present a novel algorithm for multimodal remote sensing image classification using a miniature convolutional network. Our approach incorporates a joint feature extraction framework that combines a miniature convolutional network and a two-dimensional convolutional neural network. By leveraging this framework, we aim to enhance the extraction of high-level information representations to overcome the limitations posed by the weak robustness of feature information and single-feature information, ultimately improving the classification performance.
2.2. Network Compression
Multiple approaches have been proposed to tackle the memory footprint and inference latency issues of neural networks. These methods include knowledge distillation [20,21], model pruning [22], and model quantization [23,24,25]. Our particular focus is on model quantization, which aims to reduce memory and computation requirements by representing weights and activations in low-bit data types. Quantization has been extensively researched for compressing and accelerating deep neural networks in computer vision. Han et al. [26] reduced model sizes by quantizing network weights using rule-based strategies. Jacob et al. [27] quantized weight values and activation values using 8-bit integers. Courbariaux et al. [28] devised a binary quantization method where network weights were binarized into , achieving high compression ratios by using only one bit for weights or activations. While quantization research in computer vision is extensive, there is limited research specifically focusing on quantizing neural networks for remote sensing tasks.
In this study, we applied binary quantization operations to the input and output layers of the multilayer perceptron in the spectral attention mechanism, as well as to the convolutional layers and each downsampling layer in the spatial attention mechanism within the network structure. Furthermore, performing quantization operations at different levels on the weights and activations proves beneficial for improving the model’s accuracy.
3. Proposed Method
3.1. Invariant Attribute Consistency Fusion
As shown in Figure 2, the Invariant Attribute Consistency Fusion includes two parts: Invariant Attribute Extraction (IAE) and Spatial Consistency Fusion (SCF). Extracting invariant attribute features can counteract local semantic changes caused by pixel rotation and movement or local regional composition changes. We utilize the Invariant Attribute Profiles (IAPs) [29] for feature extraction to enhance the diversity of features and model the invariant behaviors in multimodal data. This approach generates robust feature extraction for various semantic changes in multimodal remote sensing data. Isotropic filtering [30] is a well-known and powerful tool in image processing that can robustly tackle rotational or shift variations in image patches and effectively eliminates other variabilities such as salt-and-pepper noise and the absence of local information. Hence, the multimodal remote sensing images are filtered using isotropic filters to obtain spatial invariant features, which can be expressed as follows:
where H represents the HSI and L represents the LiDAR image. is the input remote sensing image, and represents isotropic filtering, achieved by convolving with , thereby extracting spatially invariant features from local space. Moreover, the robustness of the features is further enhanced through the utilization of super-pixel segmentation methods [31]. These methods prioritize the spatial invariance of the features by taking into account object semantics, including edges, shapes, and their inherent invariance, which can be expressed by
where represents the segmentation of super pixels. The final attribute features for the HSI and LiDAR images can be obtained by
where is the channel concatenation operation. To achieve invariance to translation and rotation in the frequency domain, we construct a continuous histogram of oriented gradients in Fourier polar coordinates. By utilizing the Fourier-based continuous Histogram of Oriented Gradients (HOG) [32], we ensure invariant feature extraction in polar coordinates. This approach accurately captures rotation behaviors at any angle. Therefore, by mapping the translation or rotation of image blocks in Fourier polar coordinates, discrete attribute features are transformed into continuous contours. Consequently, we obtain Frequency Invariant Features (FIF) in the frequency domain.
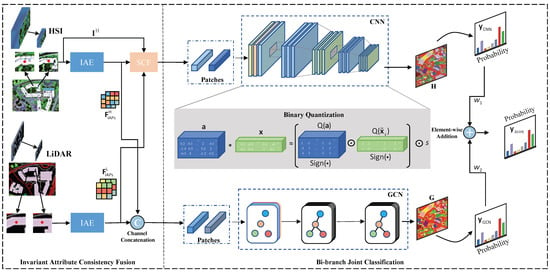
Figure 2.
The architecture of the proposed IABC. The invariant attributes are captured by Invariant Attribute Extraction (IAE) and then transformed to construct an effective graph structure for the GCN. The Spatial Consistency Fusion (SCF) is designed to enhance the consistency of similar features in the observed area’s terrain feature information for the CNN. The collaboration between the CNN and GCN improves the classification performance while the CNN with binary weights reduces storage requirements and enables accelerating speed.
By utilizing the extracted spatially invariant features, and , along with the frequency invariant features, and , we obtain the joint invariant attribute features, denoted as :
Spatial Consistency Fusion is designed to enhance the consistency of similar features in the observed area’s terrain feature information. We employ the Generalized Graph-Based Fusion (GGF) method [33] to jointly extract consistent feature information of different modalities’ invariant attributes.
where and , , and represent HSI, invariant features of HSI, and invariant features of LiDAR, respectively. The HSI is specifically used to capture the consistency information in the spectral dimension. is the fusion result. denotes the transformation matrix used to reduce the dimensionality of the feature maps, fuse the feature information, preserve local neighborhood information, and detect manifolds embedded in a high-dimensional feature space.
Initially, a graph structure is constructed to describe the correlation between spatial sample points and obtain the edge consistency information of the graph structure for different features:
where , , and are defined as the edges of the graph structures , , and , respectively, which describe the connections between any two points in the spatial domain. They are obtained through the k-nearest neighbors (k-NN) method. When the distance between two sample points is large (weak correlation), . When two sample points i and j are close in distance (strong correlation), . ⊙ is an XNOR operation to obtain the edge consistency information from these three features , , and . The likelihood of a data point having similar features to its nearest neighbor is greater than with those points that are far away. Therefore, it is necessary to add a distance constraint when calculating graph edges. This can be defined as
where refers to the matrix of pairwise distances between the individual data points of . The operator “” denotes logical negation. When the element in is 0, this indicates that the edges in , , and are not consistent. We impose a constraint on the maximum distance in , which helps to reduce the correlation between pairs of vertices in the graph structure. Then, , the diagonal matrix, is computed based on . Subsequently, the Laplacian matrix is obtained through this process:
By combining the known feature information , the Laplacian matrix , and the diagonal matrix , we can use the following generalized eigenvalue calculation formula to obtain different eigenvalues and their corresponding eigenvectors :
where denotes the transpose matrix of , represents the eigenvalue, and with indicate the number of eigenvalues. Since each eigenvector has its own unique eigenvalue, we can obtain . Finally, based on all the eigenvectors, we can obtain the desired transformation matrix :
where represents an eigenvector corresponding to the i-th eigenvalue. The fusion result is finally obtained using Equation (5) with .
3.2. Bi-Branch Joint Classification
The GCN and CNN are architectural designs used to extract distinct representations of salient information from multimodal remote sensing images. The CNN specializes in capturing intricate local spatial features, while the GCN excels at extracting abundant global spectral feature information from multimodal remote sensing images by utilizing spectral vectors as input. Additionally, the GCN can simulate the topological relationships between samples in graph-structured data. We design a bi-branch joint classification combining the advantages of the GCN and CCN to offer feature diversity.
Traditional GCNs effectively model the relationships between samples to simulate long-range spatial relationships in remote sensing images. However, inputting all samples into the network at once leads to significant memory overhead. To address these issues, the Mini Graph Convolutional Network (MiniGCN) [13] is introduced to find robust locally optimal feature information by utilizing a sampler for small-sample sampling, dividing the original input graph-structured data into multiple subgraphs. The graph-structured multimodal fused image data are input into the MiniGCN in a matrix form for training. During the training process, the input data are processed and features are extracted and outputted in mini batches. The classification output can be represented by the following equation:
where is the modified adjacency matrix after adding a unit matrix and an adjacency matrix of spatial-frequency-invariant attribute features . represents the weight of the l-th layer in the graph convolutional network. denotes the diagonal matrix of . represents the ReLU non-linear activation function. represents the feature output of the l-th layer in the graph convolutional network during the feature extraction process. When , corresponds to the original input features . represents the feature output of the -th layer in the graph convolutional network, which serves as the final output spectral features.
In addition, we utilize a simple CNN structure [34], which can be defined as
where the base structure includes the convolutional layer, batch normalization layer, max-pooling layer, and ReLU layer. When , corresponds to the original input features . We use adaptive coefficients to combine the detection results of the two networks, which can be represented as
where represents the classification head function, while and refer to the features extracted by the GCN and the CNN, respectively. The and are learnable parameters of the network to balance the weight of the bi-branch results.
3.3. Binary Quantization
We introduce the Libra Parameter Binarization (Libra-PB) technique [35], which incorporates both quantization error and information loss. During forward propagation, the full-precision weights are initially adjusted by computing the difference between the weight and the weights’ mean. This adjustment aims to distribute the quantized values uniformly and normalize the weight, thereby enhancing training stability and mitigating any negative effects caused by weight magnitude. The resultant standardized balanced weight, denoted as , can be obtained through the following operations:
In the above equation, represents the standard deviation, while is the mean of the weights. Generally, the quantization of weights and activations can be defined as
where and a represent the floating-point parameters of weights and activations. The function is commonly employed to obtain binary values. s is an integer parameter employed to enhance the representation capability of binary weights.
Here, n represents the dimension of the vector and denotes its L1 norm. The main operations during the forward propagation of the binary network, involving quantized weights and activations , can be expressed as
During backward propagation, due to the discontinuity introduced by binarization, gradient approximation becomes necessary, which can be expressed as
where is the loss function, corresponds to the approximation of the , and represents its derivative. In our paper, we use the following approximation function:
3.4. Loss Function
The output of , , and passing a softmax classification layer is used to predict the probability distribution. The overall network is trained using the following loss function:
Here, refers to the label of the dataset, s is the softmax operation, and is the cumulative L2 norm, utilized to determine the weights across all network layers. This approach is employed to address the issue of overfitting, which arises when there is an excessive number of model parameters.
3.5. Experimental Setup
Data Description: (1) Houston2013 Data: Experiments were carried out using HyperSpectral Imaging (HSI) and Digital Surface Model (DSM) data that were obtained in June 2012 over the University of Houston campus and the adjacent urban area. The HSI data consisted of 144 spectral bands and covered a wavelength range from 380 to 1050 nm, with a spatial resolution of 2.5 m that was consistent with the DSM data. The entire dataset covered an area of pixels and included 15 classes of natural and artificial objects, which were determined through photo interpretation by the DFTC. The LiDAR data were collected at an average sensor height of 2000 feet, while the HSI was collected at an average height of 5500 feet. The scene contained various natural objects such as water, soil, trees, and grass, as well as artificial objects such as parking lots, railways, highways, and roads. The land-cover classes and their respective counts in the training and testing samples are provided in Table 1.

Table 1.
A list of the number of training and testing samples for each class in the Houston2013 and Trento datasets.
(2) Trento Data: This dataset comprises 1 HSI with 63 spectral bands and 1 set of LiDAR data, captured in a rural area located in southern Trento, Italy. The HSI was obtained through the AISA Eagle sensor, while the corresponding LiDAR data were collected using the Optech Airborne Laser Terrain Mapper (ALTM) 3100EA sensor. Both datasets were of size pixels with a spatial resolution of 1 m, while the wavelength range of HSI was from 0.42 to 0.99 m. This particular dataset consisted of a total of 30,214 ground-truth samples, with research conducted on 6 distinguishable category labels. The land-cover classes and their respective counts in the training and testing samples are provided in Table 1.
Evaluation Metrics: To comprehensively evaluate the performance of multimodal remote sensing image classification algorithms, this article analyzes and compares various algorithms based on their classification prediction maps and accuracy. While the classification prediction map is subject to a certain degree of subjectivity and may not accurately measure the impact of an algorithm on classification performance, this study employs quantitative evaluation metrics such as overall accuracy (OA), average accuracy (AA), and Kappa coefficient to better measure and compare the performance of different algorithms. A higher value of any of these three indicators represents higher classification accuracy and an overall better performance of the algorithm. Among these three evaluation metrics, Overall Accuracy (OA) refers to the ratio of correctly classified test samples to the total number of test samples. Average Accuracy (AA) refers to the ratio of correctly classified test samples to the total number of test samples in a specific category.
Furthermore, we employ the Bit-Operations (BOPs) count [36] and parameters [37] as metrics to evaluate the compression performance.
Implementation Details: Our proposed approach is executed in Python and trained on a single RTX 3090 card. All the networks analyzed in this paper are implemented using the Pytorch framework. Throughout this procedure, we configure the batch size to 32, employ the Adam optimizer with an initial learning rate of 0.001, and conduct the procedure over a total of 200 epochs. The current learning rate is adapted using an exponential learning rate scheme, where the learning rate is multiplied by every 50 epochs. Furthermore, we apply weight regularization employing the L2 norm to stabilize network training and mitigate overfitting.
3.6. Ablation Study
An ablation study is conducted to demonstrate the validity of the proposed components by evaluating several variants of the IABC on HSI and LiDAR datasets.
Invariant Attribute Consistency Fusion: In Table 2, we discuss the impact of using IACF (IAE structure and SCF module) on CNN and GNN networks in remote sensing image classification tasks and provide a comparison between multimodal and single-modal HSI and LiDAR data. The Houston2013 dataset is used for evaluation. Firstly, the experimental results for HSI data show that both GCN and CNN networks achieve a certain level of accuracy in classification but differ in precision. The introduction of the IAE structure improves classification performance, increasing OA and AA from 79.04% and 81.15% to 91.15% and 91.78%, respectively. This indicates the effectiveness of the IAE structure in improving the accuracy of remote sensing image classification. Secondly, the experimental results for LiDAR data demonstrate a lower classification accuracy when using GCN or CNN networks alone. However, the introduction of the IAE structure significantly improves classification performance. For example, OA increases from 22.74% to 35.46% for the GCN network on the LiDAR dataset. This confirms the effectiveness of the IAE structure in processing LiDAR data. Lastly, fusion experiments are conducted with HSI and LiDAR data. The results show that fusing HSI and LiDAR data further improves classification performance. In particular, when combining the IAE structure and SCF structure on the CNN network, the Overall Accuracy (OA) performance increases from 89.46% (with only the IAE structure) to 91.88%, resulting in a significant improvement of 2.43%.

Table 2.
Ablation study of our proposed IACF on the Houston2013 dataset.
Similarly, on the Trento dataset, similar conclusions were obtained, as shown in Table 3. In the case of HSI data, when only GCN or CNN was used, the Overall Accuracy (OA) was 83.96% and 96.06%, respectively. However, when the IAE structure was introduced for invariant feature extraction, the OA accuracy improved to 95.34% (an increase of 11.38%) and 96.93% (an increase of 0.87%) for GCN and CNN, respectively. This indicates that the extraction of spatially invariant attributes can reduce the heterogeneity in extracting pixel features of the same class by CNN and GNN networks, enhancing the discriminative ability for the same class. Moreover, the extraction of invariant attributes has a more significant effect on improving the classification accuracy of the GCN network. When classifying LiDAR data, due to the characteristics of LiDAR data, the performance is relatively low, with only the GCN network achieving an OA of 48.31%. Introducing IAE can improve the GCN network OA by 11.94%. However, introducing IAE to the CNN network instead results in a decrease in classification performance from 90.81% to 68.81%. This might be due to the large size of areas with the same class in the Trento dataset, resulting in minimal elevation changes in the LiDAR images over a considerable area, leading to similar invariant attributes for different classes and interfering with the CNN network’s ability to extract and discriminate local information. This situation can be alleviated by using multimodal data (HSI + LiDAR) for classification. Considering the information from both the HSI and LiDAR, better performance can be observed. The highest classification accuracy (OA 98.05%) was attained when CNN introduced the IAE structure and SCF module. This further demonstrates that SCF can enhance the classification accuracy of the CNN network.

Table 3.
Ablation study of our proposed IACF on the Trento dataset.
In summary, these experiments prove that the introduction of the IAE structure significantly improves the classification performance of CNN and GNN networks in remote sensing image classification tasks. Additionally, SCF enhances the classification performance of the CNN network. Furthermore, the fusion of multimodal data can further improve classification accuracy.
Bi-Branch Joint Classification: To analyze the performance of the bi-branch joint network for classification, we compare the different networks in the two datasets in Table 4. The GCNs and CNNs demonstrate different advantages on different datasets. The GCN obtained a better classification performance at an OA of 92.60% compared with the CNN at an OA of 91.88% on the Houston dataset. However, the results show that the CNN achieved a high OA (98.05%), while the GCN obtained a lower OA (97.66%). This indicates that when dealing with sparsely categorized images, such as Trento, extracting local spatial information is useful. However, when dealing with densely distributed categories, such as Houston, extracting global spectral features has greater potential. In contrast, the joint approach yielded the top-performing classification outcomes on the Houston dataset, with an OA of 92.78%, and on the Trento dataset, with an OA of 98.14%. The experimental results demonstrate that using the bi-branch joint network can combine the advantages of CNN and GCN networks, resulting in excellent classification performance in land classification tasks using remote sensing images.

Table 4.
Validation of bi-branch joint network on Houston2013 and Trento datasets.
Binary Quantization: With the application of binary quantization, we can effectively address resource limitations and enable real-time decision-making capabilities in the context of processing large-scale data in remote sensing applications. To analyze the performance differences, we conducted a comparative study on classification accuracy and computational resources using different quantization strategies on the IABC network. In Table 5, 32w and 32a denote the full precision of the weight and activation, while 1w and 1a represent the binary quantization of the weight and activation. The binary quantization module achieved OA accuracies of 98.14%, 98.16%, 85.33%, and 83.44% at different computational levels. Notably, the difference in OA accuracy between the 1w32a quantization level and the full-precision network is relatively small. Additionally, for the CNN network at the 1w32a quantization level, the parameter count is 32.675 KB, which accounts for only 3% of the parameter count of the full-precision network. Likewise, the BOPs are approximately 3% of the BOPs in the full-precision network. As the quantity of quantization bits decreases, there is a corresponding decrease in the accuracy of the classification model, as observed. The decrease in accuracy can be attributed to the reduction in model parameters, which leads to the loss of crucial layer information and subsequently causes a decline in accuracy. It is observed that the binary quantization of the activations has a significantly negative influence on the accuracy of classification, and the OA decreases by 12.81% compared with the full-precision network and 12.53% compared with the quantization weight only (1w32a). In particular, when using the 1w1a network exclusively, the impact is notably significant, with a resulting accuracy reduction of 14.7% compared to a full-precision network. Hence, we only consider the binary quantization of the weights 1w32a in our experiment.

Table 5.
Validation of binary quantization for CNN on the Trento dataset.
3.7. Quantitative Comparison with the State-of-the-Art Classification Network
To validate the effectiveness of the proposed IABC, we compare the experimental results of the IABC on both HSI and LiDAR datasets with those of other competitive classifiers: MDL_RS_FC [34], EndNet [14], RNN [38], CALC [39], ViT [17], MFT [18], HCT [40], and Exvit [19]. The parameters of the whole compared algorithms are optimized on the same server. Additionally, the training and testing samples we utilize are identical and our proposed IABC network abstains from utilizing any data augmentation operations to ensure a fair comparison. Table 6 and Table 7 show the classification outcomes of various networks on two datasets. The most favorable results are emphasized using bold highlighting. The superiority of the proposed IABC over other methods is evident. For instance, when considering the Houston2013 dataset, IABC exhibits substantial improvements in Overall Accuracy (OA) for various approaches: MDL_RS_FC sees an improvement of approximately 7.67%, Endnet by 7.6%, RNN by 20.32%, CALC by 2.84%, ViT by 7.58%, MFT by 3.03%, HCT by 2.21%, and Exvit by 1.36%. RNN performs the worst, with only 72.31% OA. The MDL_RS_FC method achieves better performance, with an Overall Accuracy (OA) of 84.96%, thanks to its meticulously designed cross-fusion approach, which facilitates the more effective interaction of information during the fusion, resulting in improved performance. The conventional classifier EndNet works by leveraging deep neural networks to enhance the ability of feature extraction for spectral and spatial features. The CALC method achieves a ranking of three with an OA of 89.79%, fully harnessing and extracting semantic information as well as complementary information. The transformer-based methods ViT and MFT, with their strong feature expression ability in high-level sequential abstract representation, achieve higher accuracy than the traditional deep learning networks (such as Endnet and MDL_RS_FC). In contrast, our IABC method obtains the optimal performance by using spatial–spectral CNN and relation-enhanced GCN features with invariant attribute enhancement. For the Trento dataset, IABC provides approximately 10.36%, 7.54%, 2.20%, 0.52%, 2.16%, 0.31%, 10.41%, and 0.05% OA improvements for MDL_RS_FC, Endnet, RNN, CALC, ViT, MFT, HCT, and Exvit, respectively. The performance of the RNN network on the Trento dataset is noticeably better compared with the result on the Houston2013 dataset, while the MDL_RS_FC method performance is worse on the Trento dataset. It is proven that the generalization performance of these two methods is comparatively poor. The performance of other algorithms is consistent with the performance on the Houston2013 dataset.

Table 6.
Comparison of the classification accuracy (%) using the Houston2013 dataset.

Table 7.
Comparison of the classification accuracy (%) using the Trento dataset.
Figure 3 and Figure 4 illustrate a range of visual results, including hyperspectral false-color data, LiDAR images, ground truths, and classification maps acquired using various methods. Each category is accompanied by its respective color scheme. Upon thorough evaluation and comparison, it is clear that the proposed methods yield superior results with significantly reduced noise compared to alternative approaches. Deep learning models excel in capturing the nonlinear relationship between input and output features, thanks to their remarkable ability to extract learnable features. Hence, all the methods generate relatively smooth classification maps, effectively distinguishing between different land-use and land-cover classes. Notably, Vit, MFT, HCT, and Exvit demonstrate their efficacy in classification by extracting high-level sequential abstract representations from images. Consequently, the classification maps exhibit better visual quality compared to fully connecting, CNN, and RNN networks. By enhancing neighboring spatial–spectral information and facilitating the effective transmission of relation-augmented information across layers, the proposed IABC method achieves highly desirable classification maps, particularly in terms of texture and edge details, surpassing CALC, ViT, MFT, HCT, and Exvit.
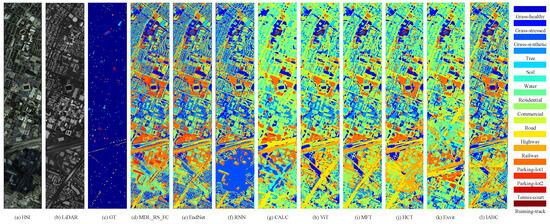
Figure 3.
Classification maps of different methods for the Houston2013 dataset.

Figure 4.
Classification maps of different methods for the Trento dataset.
4. Conclusions
In conclusion, our proposed unified network, combining CNNs and GCNs, presents a promising solution for hyperspectral image and LiDAR image fusion in remote sensing. By employing a joint detection framework, our approach effectively captures spatial relationships and models semantic information. Hence, an improved representation can be obtained in the spectral–spatial domain. Our method successfully addresses the limitations in constructing graph structures and showcases superior performance in hyperspectral image analysis. The utilization of CNNs and GCNs ensures the accurate modeling of local spatial–spectral relationships and the construction of effective global graph structures. Moreover, the cooperation of binary quantization improves computational effectiveness, facilitating the real-time handling of extensive datasets. Furthermore, systematic analysis sheds light on the significance of spatial invariance and examines the sensitivity of CNN and GCN neural networks to variations, contributing to the overall understanding of the research community. Additionally, our introduction of a lightweight binary CNN architecture effectively tackles the challenges posed by high-dimensional hyperspectral data and computational limitations while maintaining a high level of classification performance.
Overall, our method offers a potential opportunity to improve remote sensing applications through the implementation of deep learning techniques. It significantly improves accuracy, diminishes storage demands, and enables instantaneous decision making, which facilitates the real-time processing of extensive remote sensing data.
Author Contributions
J.Z. and W.X. conceived the study; J.Z. devised the approach; J.Z. conducted the experiments and scrutinized the resulting data; D.L. explored the relevant literature; W.X. and J.L. provided suggestions for paper revision; J.Z. and D.L. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant No. 62071360.
Data Availability Statement
Our experiments employ open datasets in [34].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HSI | Hyperspectral image |
| CNN | Convolutional neural network |
| GCN | Graph convolutional network |
| KNN | K-nearest neighbors |
| OA | Overall accuracy |
| AA | Average accuracy |
| BOPs | Bit-operations |
| Params | Parameters |
References
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2017, 56, 937–949. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Learning and transferring deep joint spectral–spatial features for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, J.J.; Zheng, C.H.; Yan, Q.; Xun, L.N. Classification of hyperspectral data using a multi-channel convolutional neural network. In Intelligent Computing Methodologies, Proceedings of the 14th International Conference, ICIC 2018, Wuhan, China, 15–18 August 2018; Part III; Springer: Cham, Switzerland, 2018; pp. 81–92. [Google Scholar]
- Hao, S.; Wang, W.; Ye, Y.; Nie, T.; Bruzzone, L. Two-stream deep architecture for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2349–2361. [Google Scholar] [CrossRef]
- Shahraki, F.F.; Prasad, S. Graph convolutional neural networks for hyperspectral data classification. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–28 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 968–972. [Google Scholar]
- Wan, S.; Gong, C.; Zhong, P.; Pan, S.; Li, G.; Yang, J. Hyperspectral image classification with context-aware dynamic graph convolutional network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 597–612. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multiscale dynamic graph convolutional network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3162–3177. [Google Scholar] [CrossRef]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y.Y. Spectral–spatial graph convolutional networks for semisupervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 241–245. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Hang, R.; Zhang, B.; Chanussot, J. Deep encoder–decoder networks for classification of hyperspectral and LiDAR data. IEEE Geosci. Remote Sens. Lett. 2020, 19, 5500205. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, L.; Yang, J.; Wei, Z. CNN-enhanced graph convolutional network with pixel-and superpixel-level feature fusion for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 8657–8671. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Roy, S.K.; Deria, A.; Hong, D.; Rasti, B.; Plaza, A.; Chanussot, J. Multimodal fusion transformer for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5515620. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, B.; Li, C.; Hong, D.; Chanussot, J. Extended Vision Transformer (ExViT) for Land Use and Land Cover Classification: A Multimodal Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5514415. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Wang, L.; Yoon, K.J. Knowledge distillation and student-teacher learning for visual intelligence: A review and new outlooks. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3048–3068. [Google Scholar] [CrossRef]
- Zhu, M.; Gupta, S. To prune, or not to prune: Exploring the efficacy of pruning for model compression. arXiv 2017, arXiv:1710.01878. [Google Scholar]
- Cai, Z.; He, X.; Sun, J.; Vasconcelos, N. Deep learning with low precision by half-wave gaussian quantization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5918–5926. [Google Scholar]
- Yang, J.; Shen, X.; Xing, J.; Tian, X.; Li, H.; Deng, B.; Huang, J.; Hua, X.S. Quantization networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7308–7316. [Google Scholar]
- Han, T.; Li, D.; Liu, J.; Tian, L.; Shan, Y. Improving low-precision network quantization via bin regularization. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 5261–5270. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2704–2713. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks: Training deep neural networks with weights and activations constrained to + 1 or -1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Hong, D.; Wu, X.; Ghamisi, P.; Chanussot, J.; Yokoya, N.; Zhu, X.X. Invariant attribute profiles: A spatial-frequency joint feature extractor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3791–3808. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Ghamisi, P.; Li, W.; Tao, R. MsRi-CCF: Multi-scale and rotation-insensitive convolutional channel features for geospatial object detection. Remote Sens. 2018, 10, 1990. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Skibbe, H.; Schmidt, T.; Blein, T.; Palme, K.; Brox, T.; Ronneberger, O. Rotation-invariant HOG descriptors using Fourier analysis in polar and spherical coordinates. Int. J. Comput. Vis. 2014, 106, 342–364. [Google Scholar] [CrossRef]
- Liao, W.; Pižurica, A.; Bellens, R.; Gautama, S.; Philips, W. Generalized graph-based fusion of hyperspectral and LiDAR data using morphological features. IEEE Geosci. Remote Sens. Lett. 2014, 12, 552–556. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More diverse means better: Multimodal deep learning meets remote-sensing imagery classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4340–4354. [Google Scholar] [CrossRef]
- Qin, H.; Gong, R.; Liu, X.; Shen, M.; Wei, Z.; Yu, F.; Song, J. Forward and backward information retention for accurate binary neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2250–2259. [Google Scholar]
- Wang, Y.; Lu, Y.; Blankevoort, T. Differentiable joint pruning and quantization for hardware efficiency. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 259–277. [Google Scholar]
- Zhang, J.; Lei, J.; Xie, W.; Li, Y.; Yang, G.; Jia, X. Guided Hybrid Quantization for Object Detection in Remote Sensing Imagery via One-to-one Self-teaching. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5614815. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Lu, T.; Ding, K.; Fu, W.; Li, S.; Guo, A. Coupled adversarial learning for fusion classification of hyperspectral and LiDAR data. Inform. Fusion 2023, 93, 118–131. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, Q.; Sun, L.; Wu, Z.; Pan, C.; Jeon, B. Joint classification of hyperspectral and lidar data using a hierarchical cnn and transformer. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5500716. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).