The CNES Solutions for Improving the Positioning Accuracy with Post-Processed Phase Biases, a Snapshot Mode, and High-Frequency Doppler Measurements Embedded in Recent Advances of the PPP-WIZARD Demonstrator
Abstract
:1. Introduction
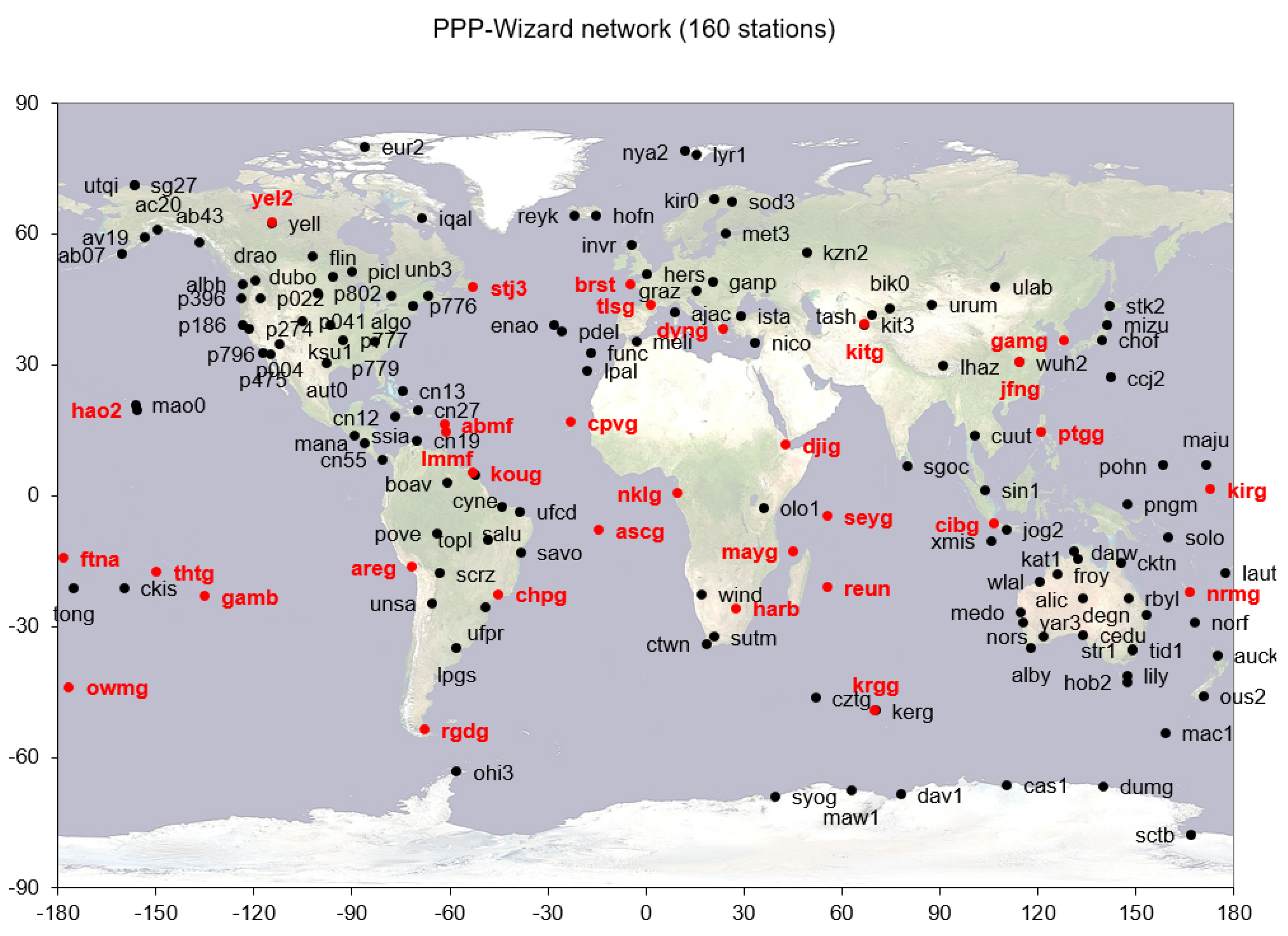
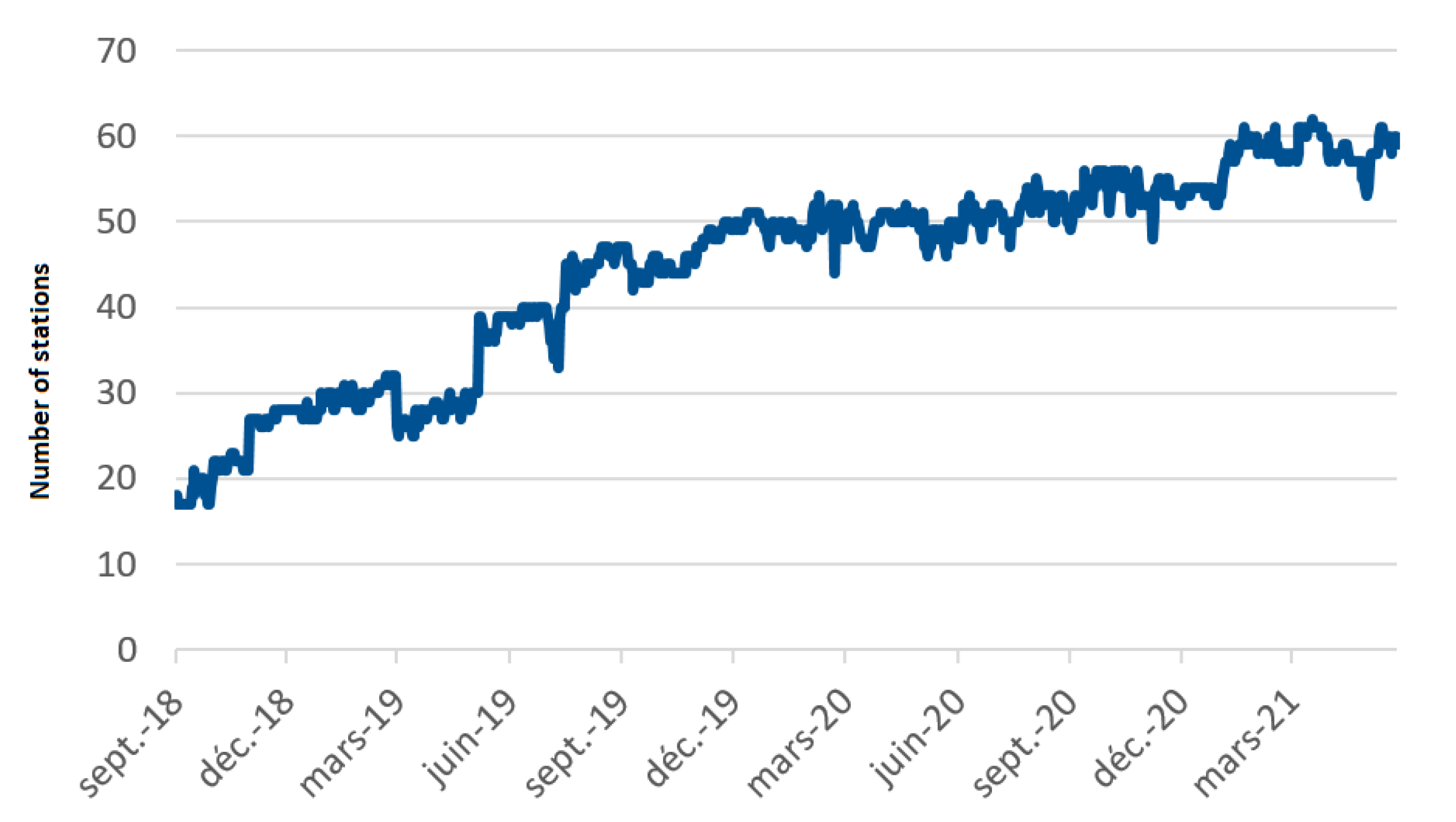
2. The CNES PPP-WIZARD Demonstrator
- on the network side, also named server side, raw data are collected thanks to a global network of stations, then the main processing software Orbit Determination and Time Synchronization (ODTS) computes all the necessary corrections (orbits, clocks, biases, ionosphere) that are compatible with the ambiguity resolution on the user side;
- the corrections are disseminated over the network in an open standard, RTCM, or SSR;
- on the user side, the PPP-User software estimates the position of the receiver by means of a stochastic filter, leading to centimeter-level PPP by fixing the integer ambiguities of the phase measurements.
2.1. The Network Side of the Demonstator
2.2. Dissemination Standards
- stream SSRA00CNE0 (IGS standard),
- stream SSRA00CNE1 (RTCM standard).
2.3. The User Side of the Demonstrator
2.3.1. Measurement Modeling in the User
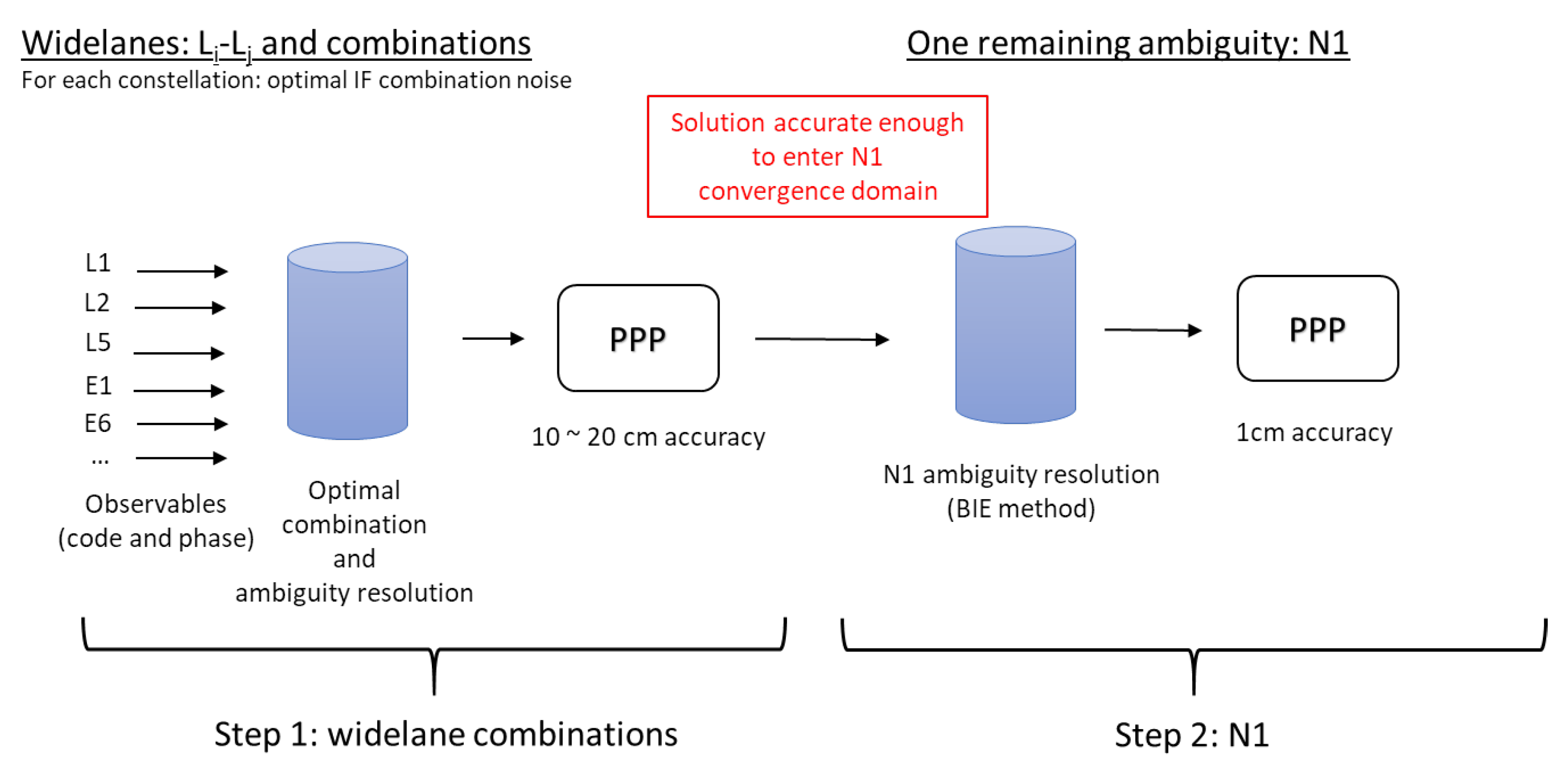
2.3.2. Instantaneous Ambiguity Resolution
- all the widelanes can easily be solved;
- the obtained solution is accurate enough to enter the narrowlane convergence domain, leading to centimeter accuracy.
2.3.3. The PPP-Snapshot Concept
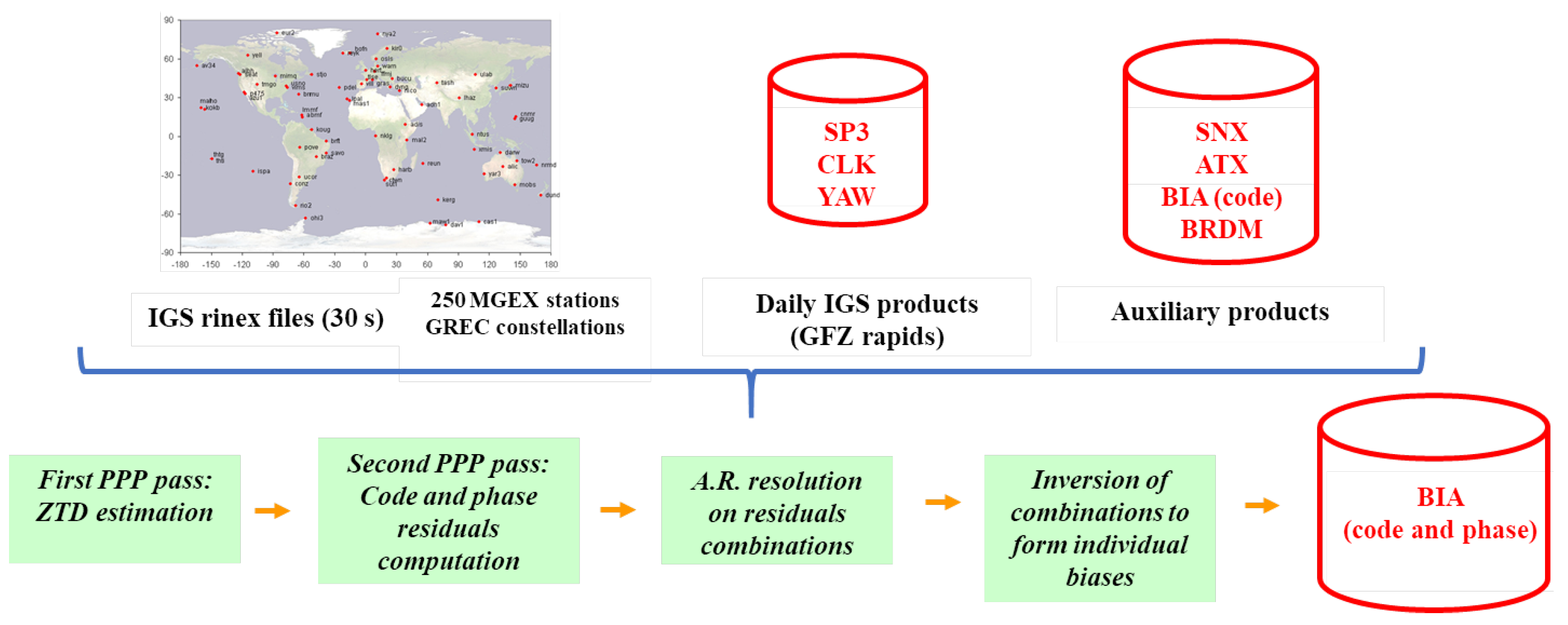
2.4. Computation of the post-processed Phase Biases
- a first PPP pass (forward, backward) to compute the troposphere elongation of the stations;
- the computation of the observed minus computed (OmC) values of all the code and phase observables;
- the resolution of ambiguities on a chosen set of the OmC values combinations (the output of this process is the satellite fractional phase biases of the combinations) in the same way as the one done for the production of the real-time products;
- the inversion of the combined fractional phase biases to recover individual phase biases.
3. Phase-Bias Results Assessment
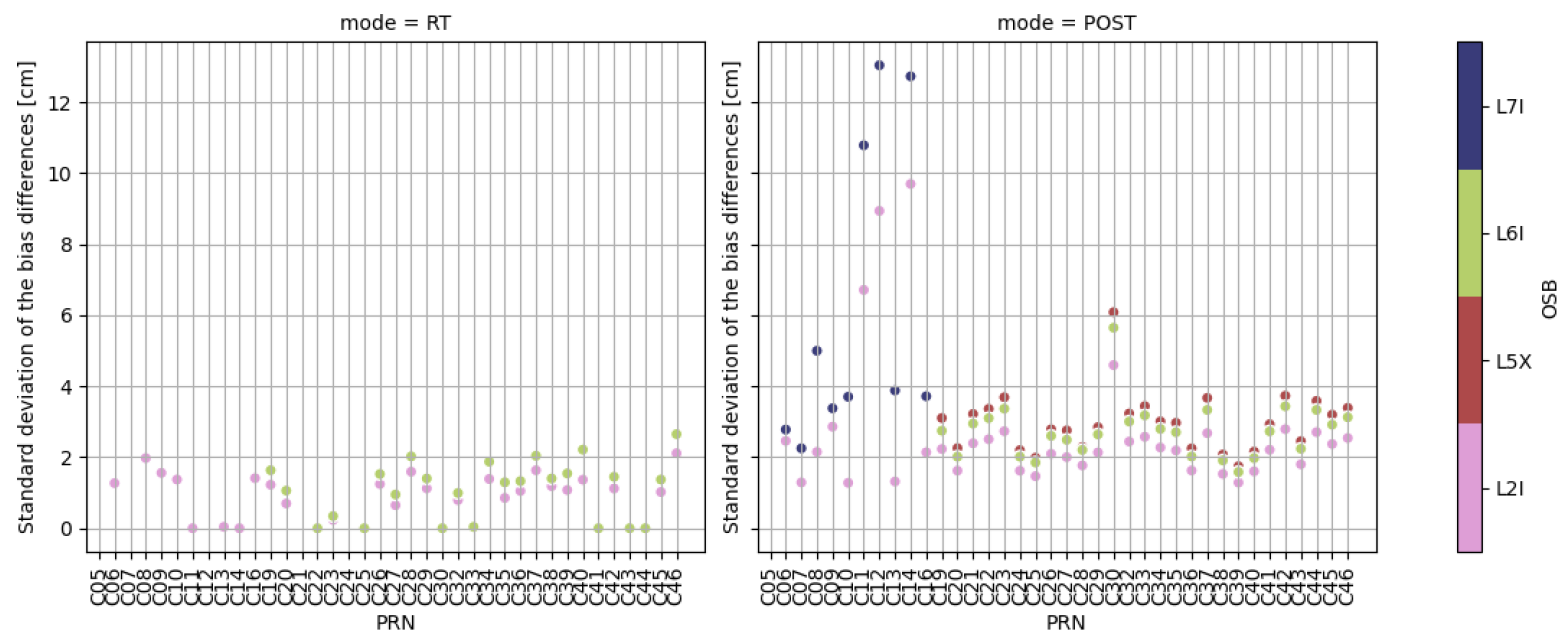
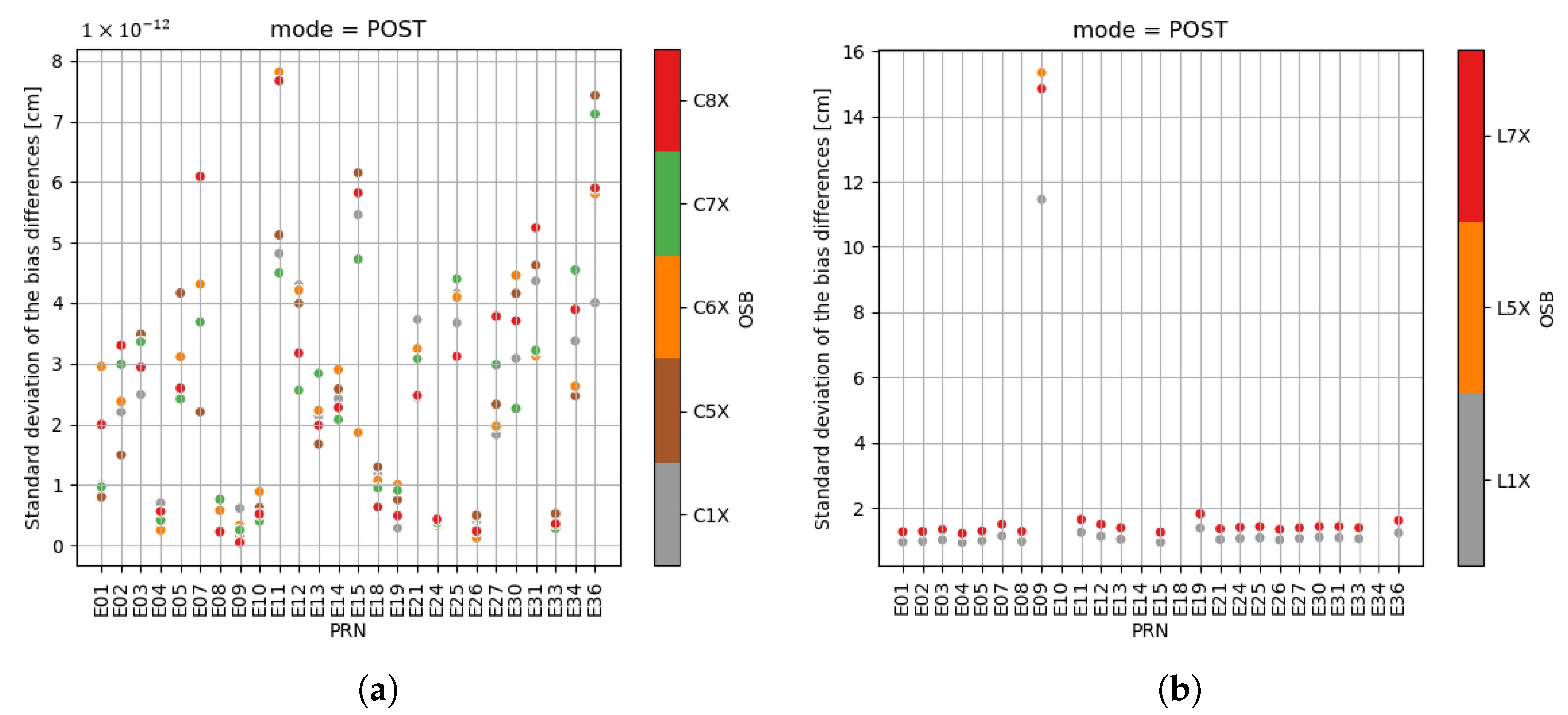
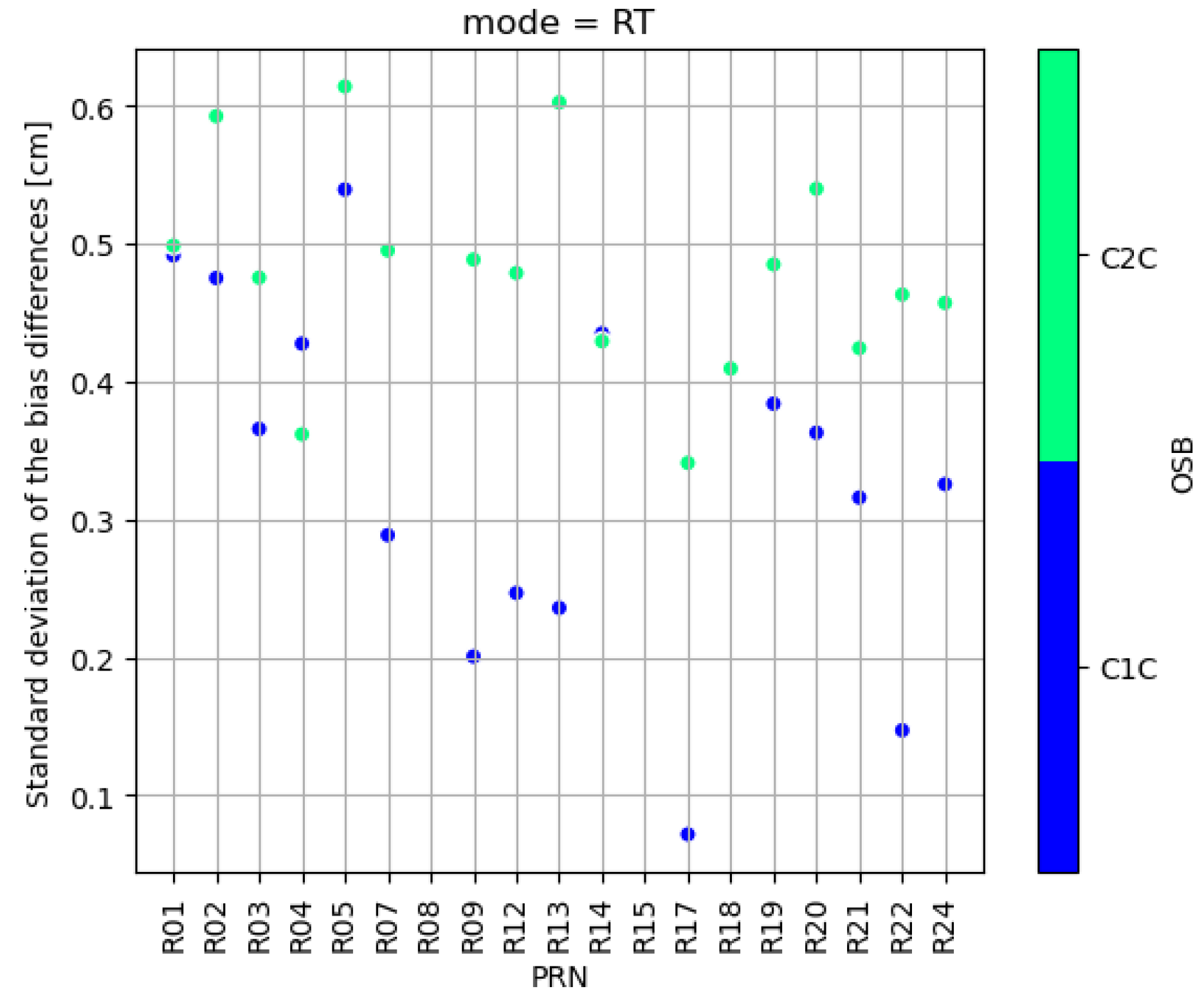
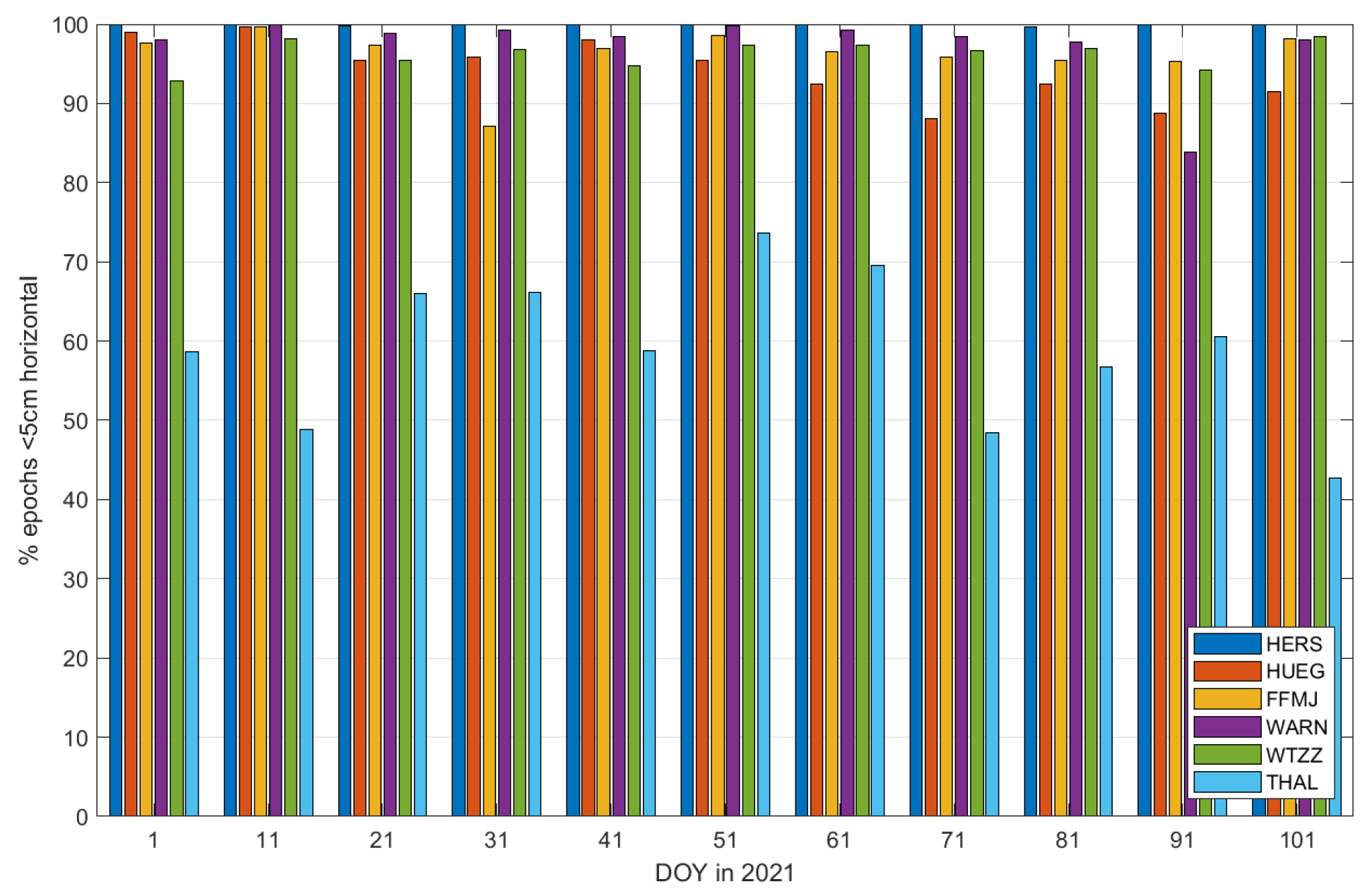
3.1. Assessment of the CNES Phase Biases
3.2. Comparison of the CNES Phase Biases
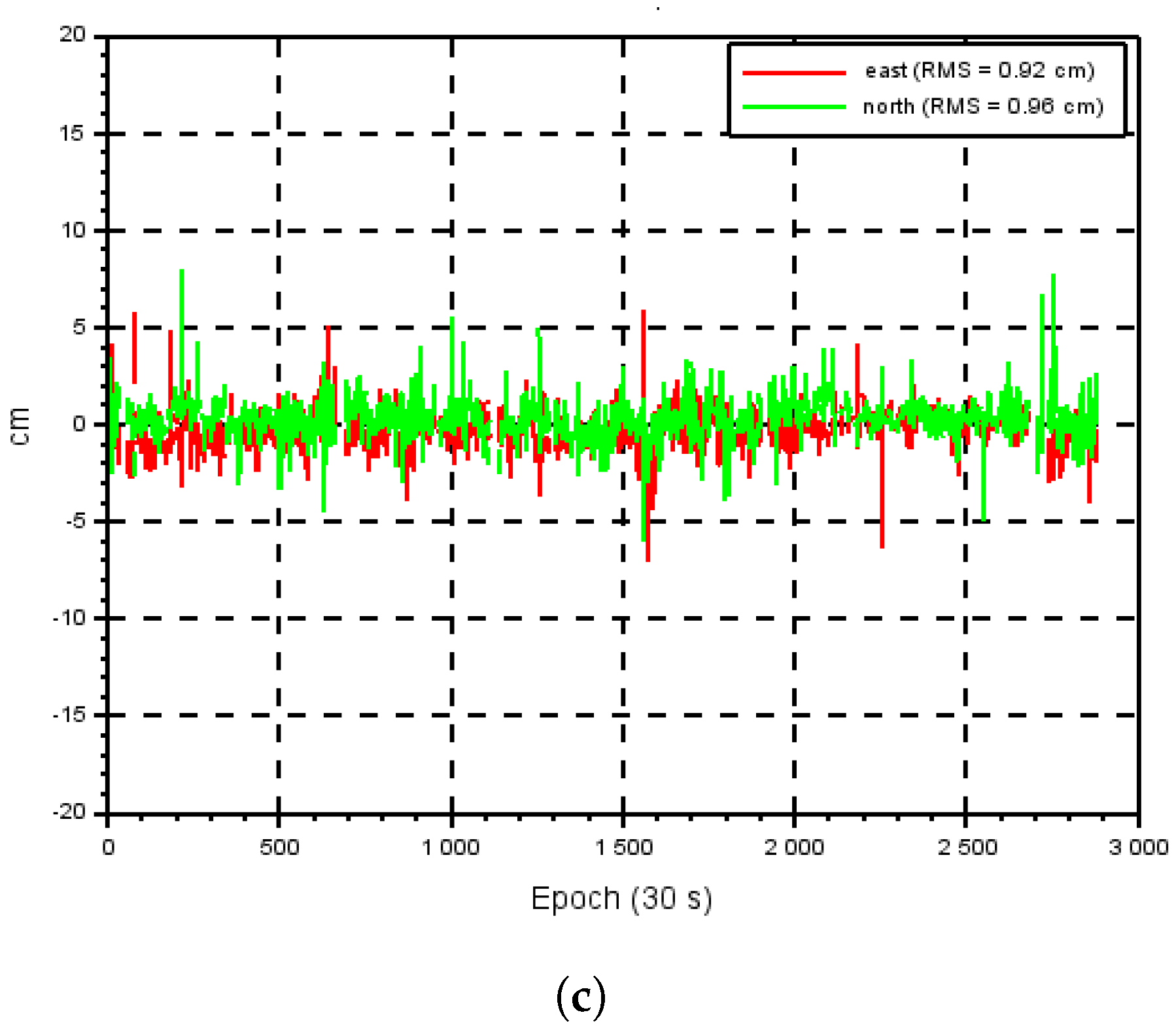
4. Precise Point Positioning Results
4.1. CNES Evaluation
- in the first case, called static (STA), the velocity process noise standard deviation and the velocity a priori standard deviation are set to zero, in such a way that the velocity is not estimated by the filter;
- in the second case, called kinematic (KIN), the velocity a priori and process noise standard deviations are not zero, and the position process noise standard deviation is set to zero.
4.2. Academic Comparison
4.3. Commercial Service Comparison
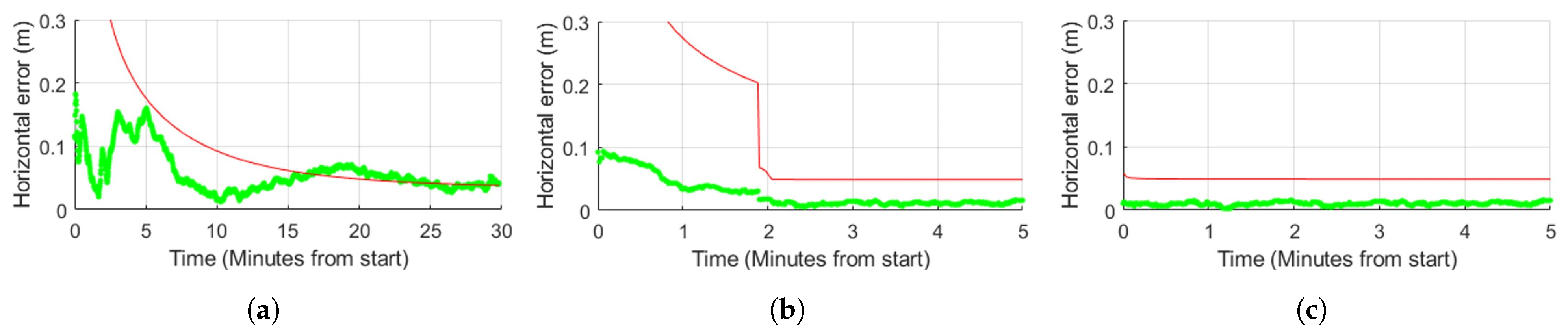
- This is the typical convergence in float mode. The process takes about 30 min to attain full convergence.
- The results are similar to those presented in [30]. With partial ambiguity fixing, 10 cm of accuracy is achieved instantaneously, and fully ambiguity fixing at the centimeter level is obtained after 2 min of convergence.
- With the addition of Beidou signals, full ambiguity resolution is instantaneous. Note that a better noise combination can be chosen for Beidou (namely B1c/B2a/B3) but has not been used here.
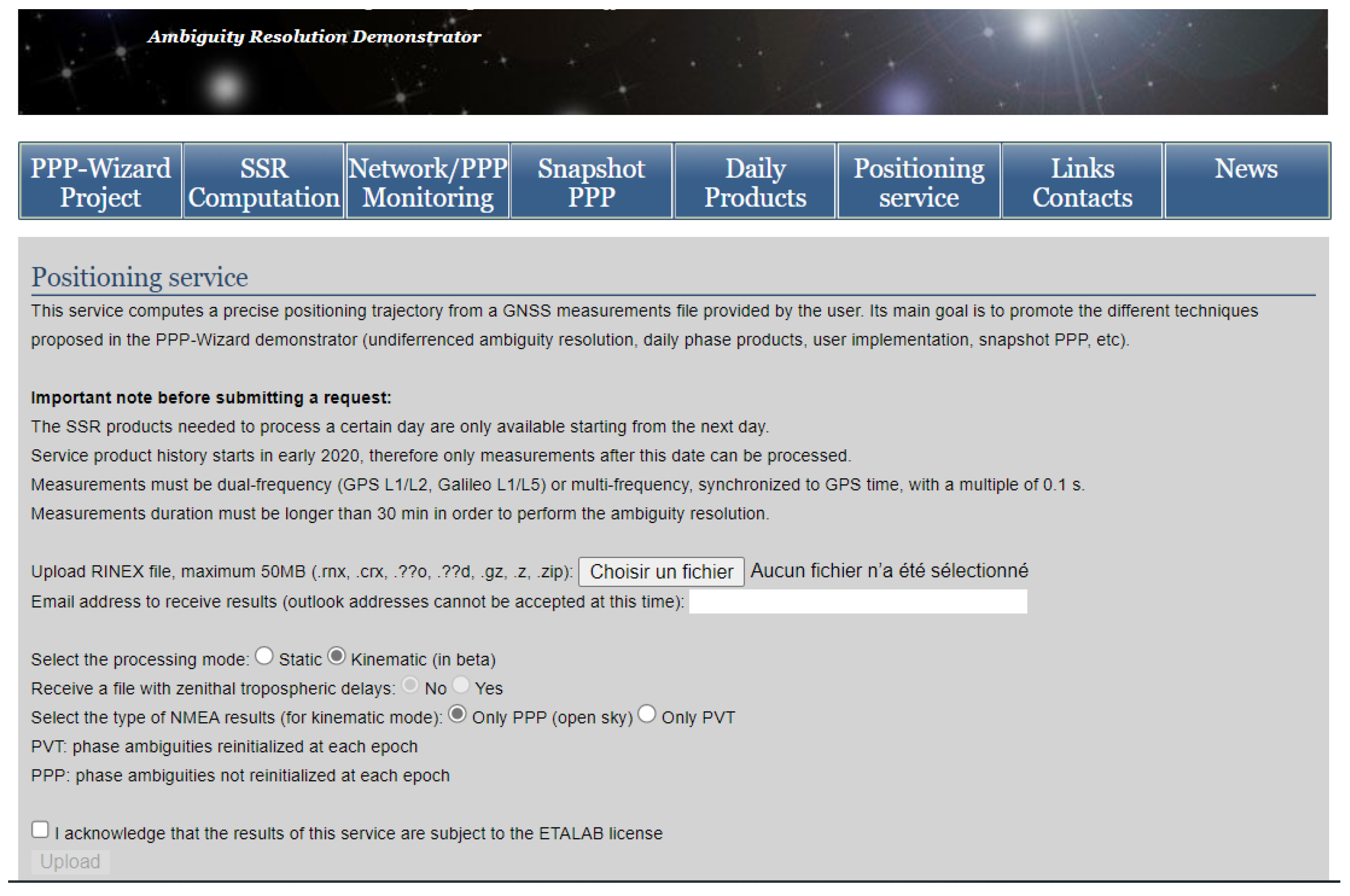
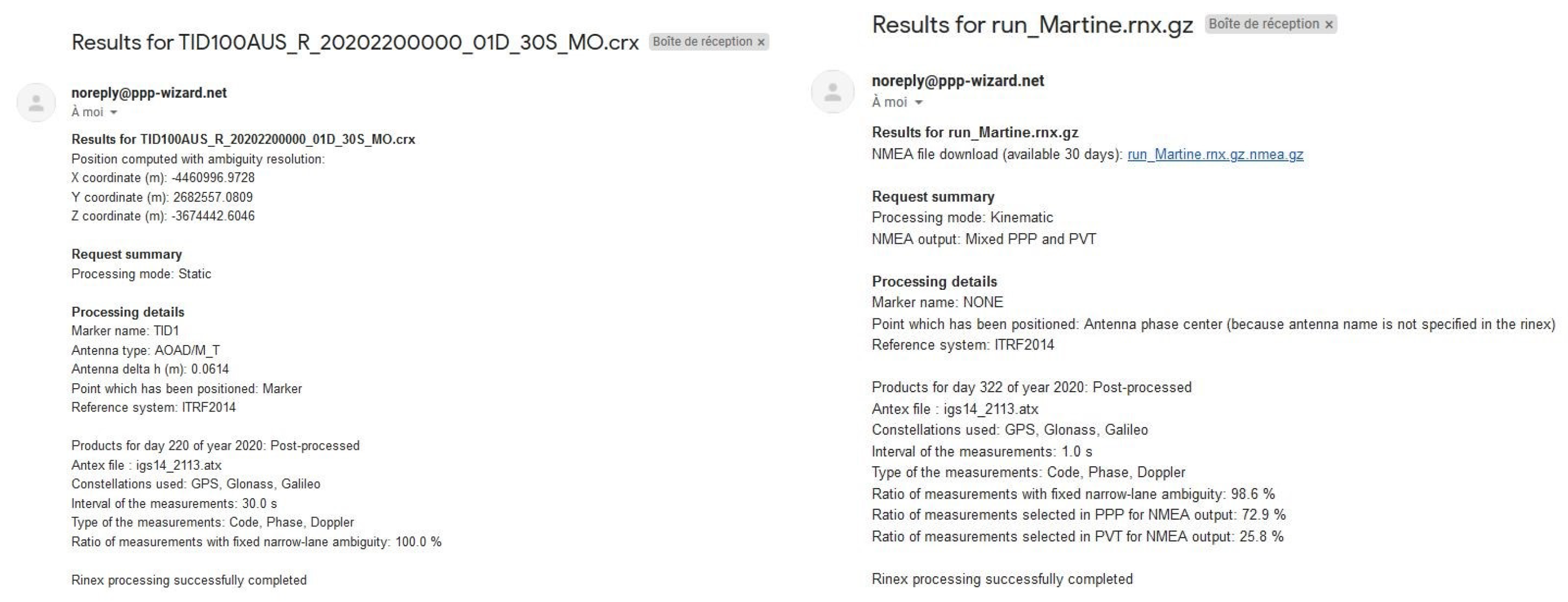
5. Online Positioning Service
- a general description of the demonstrator, including descriptions of the new concepts such as the “PPP-Snapshot” mode,
- a set of PPP monitoring stations (for each station, an instance of the PPP-User software is running), the website displays the errors of the obtained solution with respect to an accurate reference and they are updated in real time and reflect the current performance of the demonstrator from the user side,
- links to download daily corrections (real-time or post-processed),
- an online positioning service,
- links to the presentations of the method,
- news of the project.
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS—Principles and Applications, 2nd ed.; Artech House Inc.: Norwood, MA, USA, 2006. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House Inc.: Boston, MA, USA, 2008. [Google Scholar]
- Malys, S.; Jensen, P.A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. GPS precise point positioning using IGS orbit products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Hirokawa, R.; Fernández-Hernández, I. Open format specifications for PPP/PPP-RTK services: Overview and interoperability assessment. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 21–25 September 2020; pp. 1268–1290. [Google Scholar]
- Hamza, V.; Stopar, B.; Sterle, O.; Pavlovčič-Prešeren, P. Low-Cost Dual-Frequency GNSS Receivers and Antennas for Surveying in Urban Areas. Sensors 2023, 23, 2861. [Google Scholar] [CrossRef] [PubMed]
- Vana, S.; Bisnath, S. Low-Cost, Triple-Frequency, Multi-GNSS PPP and MEMS IMU Integration for Continuous Navigation in Simulated Urban Environments. Navigation—J. Inst. Navig. 2023, 70, navi.578. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. In Proceedings of the 2008 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2008; pp. 720–732. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.A.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389. [Google Scholar] [CrossRef]
- Nie, Z.; Liu, F.; Gao, Y. real-time precise point positioning with a low-cost dual-frequency GNSS device. GPS Solut. 2020, 24, 9. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The international GNSS service. In Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 967–982. [Google Scholar]
- Velut, C.; Jolivet, L.; Garayt, B.; Donal, T.; Cardaliaguet, J. Regina, A CNES/IGN worldwide GNSS receivers network for IGS and navigation: Overview and perspectives. In Proceedings of the 6th International Colloquium–Scientific and Fundamental Aspects of the Galileo Programme, Valencia, Spain, 25–27 October 2017; pp. 25–27. [Google Scholar]
- Laurichesse, D. The CNES real-time PPP with undifferenced integer ambiguity resolution demonstrator. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011; pp. 654–662. [Google Scholar]
- Laurichesse, D.; Banville, S. Innovation: Instantaneous centimeter-level multi-frequency precise point positioning. GPS World 2018, 4, 42–47. [Google Scholar]
- NRCAN Online PPP Service. Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php (accessed on 20 June 2023).
- The Automatic Precise Positioning Service of the Global Differential GPS (GDGPS) System. Available online: https://pppx.gdgps.net// (accessed on 20 June 2023).
- AUSPOS Online GPS Processing Service. Available online: https://gnss.ga.gov.au/auspos (accessed on 20 June 2023).
- Laurichesse, D. Phase biases estimation for undifferenced ambiguity resolution. In PPP-RTK & Open Standards Symposium; GIM International: Lemmer, The Netherlands, 2012; pp. 12–13. [Google Scholar]
- Teunissen, P.J.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10. [Google Scholar]
- Caissy, M.; Agrotis, L.; Weber, G.; Fisher, S. The IGS real-time service. In Proceedings of the EGU General Assembly, Vienna, Austria, 7–12 April 2013; p. EGU2013–11168. Available online: https://www.igs.org/rts (accessed on 30 June 2023).
- Laurichesse, D.; Mercier, F. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and its Application to PPP. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 839–848. [Google Scholar]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Bijac, J. Real time zero-difference ambiguities fixing and absolute RTK. In Proceedings of the 2008 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2008; pp. 747–755. [Google Scholar]
- Mercier, F.; Laurichesse, D. Receiver/Payload hardware biases stability requirements for undifferenced Widelane ambiguity blocking. In Proceedings of the Scientifics and Fundamental Aspects of the Galileo Program Colloquium, Toulouse, France, 1–4 October 2007. [Google Scholar]
- Laurichesse, D.; Cerri, L.; Berthias, J.; Mercier, F. Real time precise GPS constellation and clocks estimation by means of a Kalman filter. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 1155–1163. [Google Scholar]
- Subirana, J.S.; Zornoza, J.J.; Hernandez-Pajares, M. GNSS Data Processing, Vol. I: Fundamentals and Algorithms; ESA Communications: Oakville, ON, Canada, 2013; p. 6. [Google Scholar]
- Melbourne, W.G. The case for ranging in GPS-based geodetic systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wübbena, G. Software developments for geodetic positioning with GPS using TI-4100 code and carrier measurements. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; Volume 19, pp. 403–412. [Google Scholar]
- Laurichesse, D.; Langley, R. Handling the biases for improved triple-frequency PPP convergence. GPS World 2015, 26, 42–49. [Google Scholar]
- Laurichesse, D.; Privat, A. An open-source PPP client implementation for the CNES PPP-WIZARD demonstrator. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; pp. 2780–2789. [Google Scholar]
- Vincent, F.; Vilà-Valls, J.; Besson, O.; Medina, D.; Chaumette, E. Doppler-aided positioning in GNSS receivers—A performance analysis. Signal Process. 2020, 176, 107713. [Google Scholar] [CrossRef]
- Li, L.; Zhong, J.; Zhao, M. Doppler-aided GNSS position estimation with weighted least squares. IEEE Trans. Veh. Technol. 2011, 60, 3615–3624. [Google Scholar] [CrossRef]
- Bierman, G.J. Factorization Methods for Discrete Sequential Estimation; Courier Corporation: North Chelmsford, MA, USA, 2006. [Google Scholar]
- Thornton, C. Triangular Covariance Factorizations for Kalman Filtering. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1976. [Google Scholar]
- Asl, H.G.; Pourtakdoust, S. UD covariance factorization for unscented Kalman filter using sequential measurements update. World Acad. Sci. Eng. Technol. 2007, 34, 368–376. [Google Scholar]
- Teunissen, P.; Joosten, P.; Tiberius, C. A comparison of TCAR, CIR and LAMBDA GNSS ambiguity resolution. In Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2002), Portland, OR, USA, 24–27 September 2002; pp. 2799–2808. [Google Scholar]
- Teunissen, P. Theory of integer equivariant estimation with application to GNSS. J. Geod. 2003, 77, 402–410. [Google Scholar] [CrossRef]
- Carcanague, S.; Julien, O.; Vigneau, W.; Macabiau, C. Undifferenced ambiguity resolution applied to RTK. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011; pp. 663–678. [Google Scholar]
- Zhao, L.; Blunt, P.; Yang, L. Performance Analysis of Zero-Difference GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 Point Positioning Using CNES Uncombined Bias Products. Remote Sens. 2022, 14, 650. [Google Scholar] [CrossRef]
- Laurichesse, D.; Blot, A. Fast PPP convergence using multi-constellation and triple-frequency ambiguity resolution. In Proceedings of the 29th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 2082–2088. [Google Scholar]
- Geng, J.; Wen, Q.; Zhang, Q.; Li, G.; Zhang, K. GNSS observable-specific phase biases for all-frequency PPP ambiguity resolution. J. Geod. 2022, 96, 11. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O.; Steigenberger, P.; Martini, I.; Fernandez-Hernandez, I. Orbit determination of Sentinel-6A using the Galileo high accuracy service test signal. GPS Solut. 2022, 26, 120. [Google Scholar] [CrossRef]
- Naciri, N.; Yi, D.; Bisnath, S.; de Blas, F.J.; Capua, R. Assessment of Galileo High Accuracy Service (HAS) test signals and preliminary positioning performance. GPS Solut. 2023, 27, 73. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Chen, H.; Chen, Q.; Jiang, W.; Laurichesse, D.; An, X.; Geng, T. Characteristics of phase bias from CNES and its application in multi-frequency and multi-GNSS precise point positioning with ambiguity resolution. GPS Solut. 2021, 25, 58. [Google Scholar] [CrossRef]
- Du, S.; Shu, B.; Xie, W.; Huang, G.; Ge, Y.; Li, P. Evaluation of real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES. Remote Sens. 2022, 14, 4970. [Google Scholar] [CrossRef]

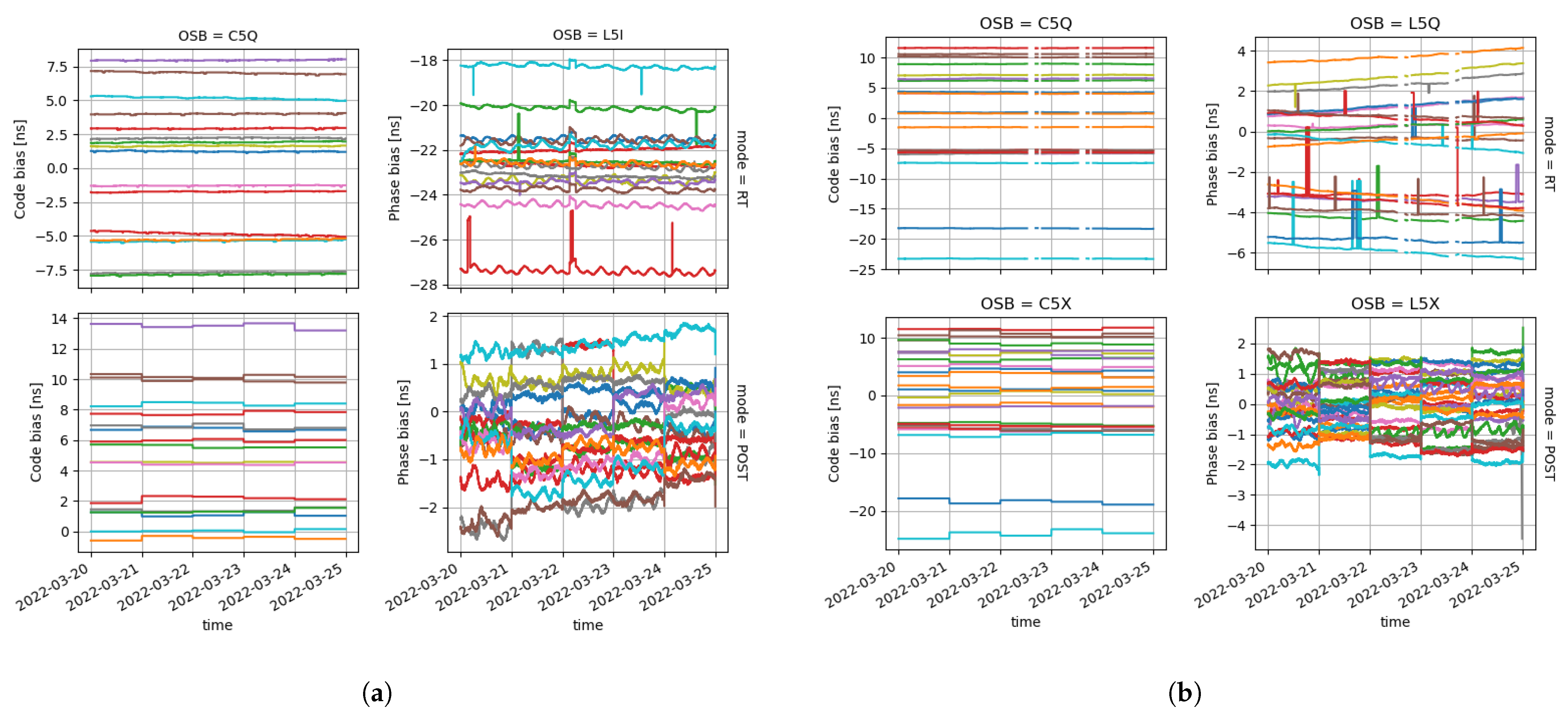
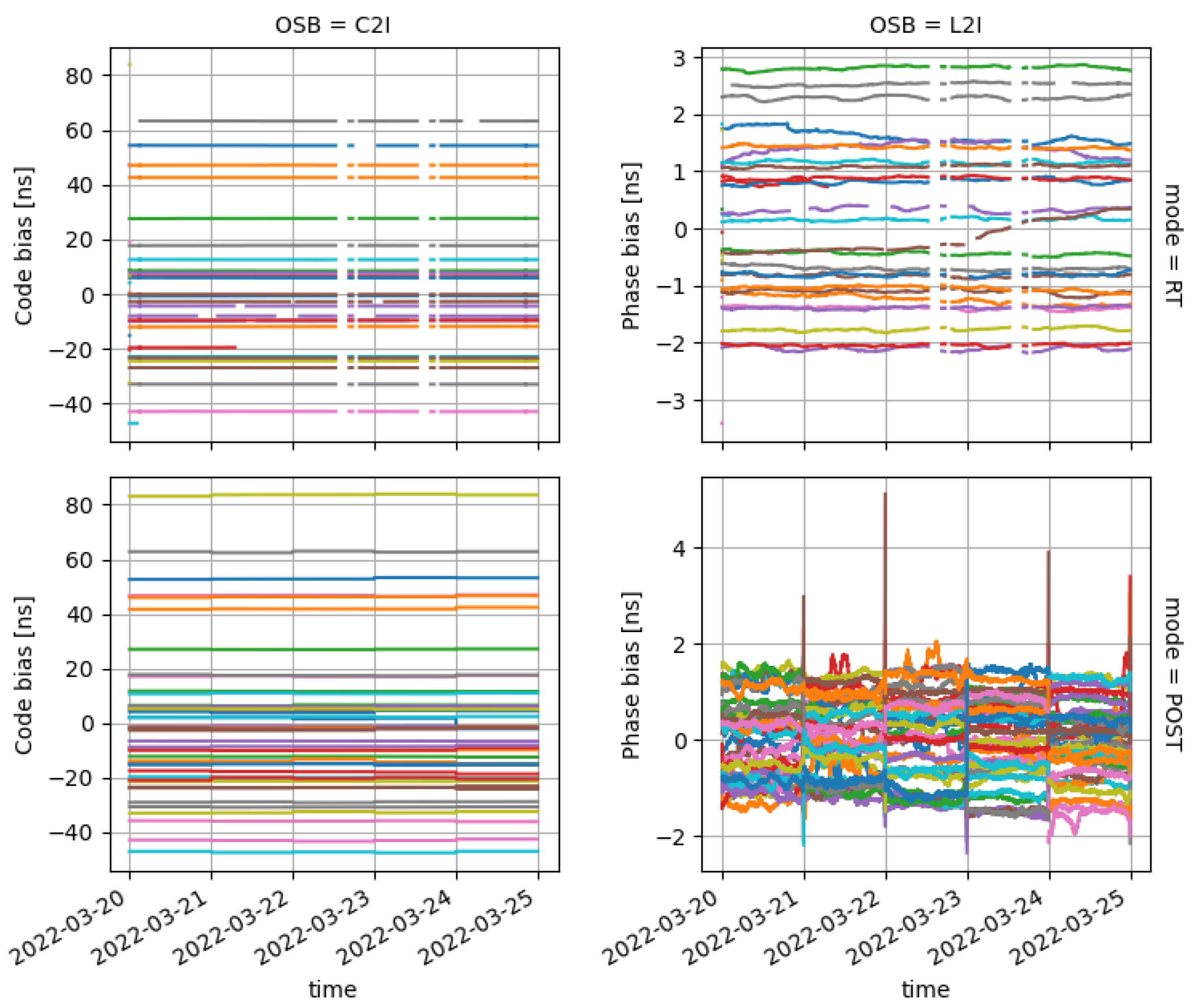

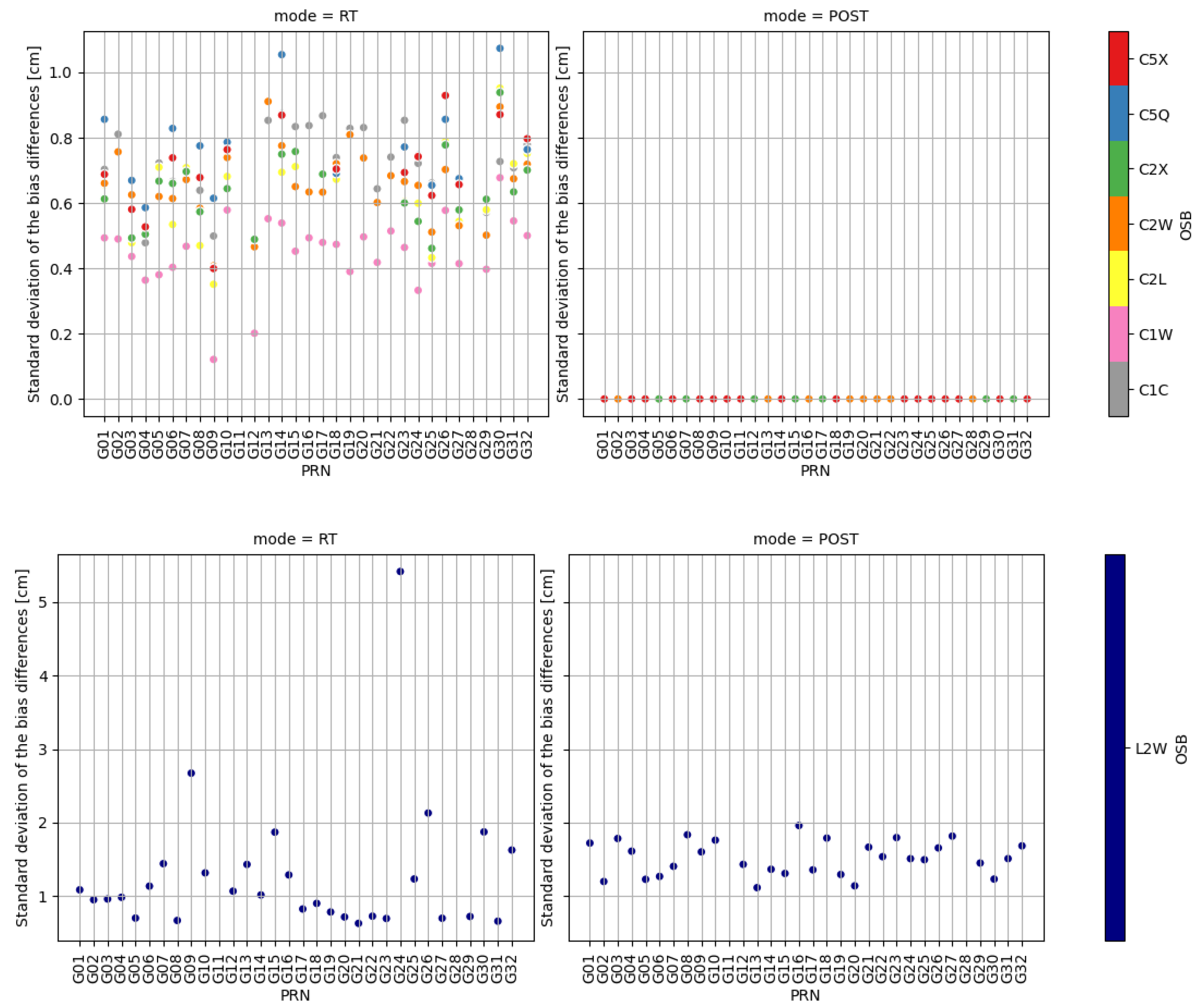
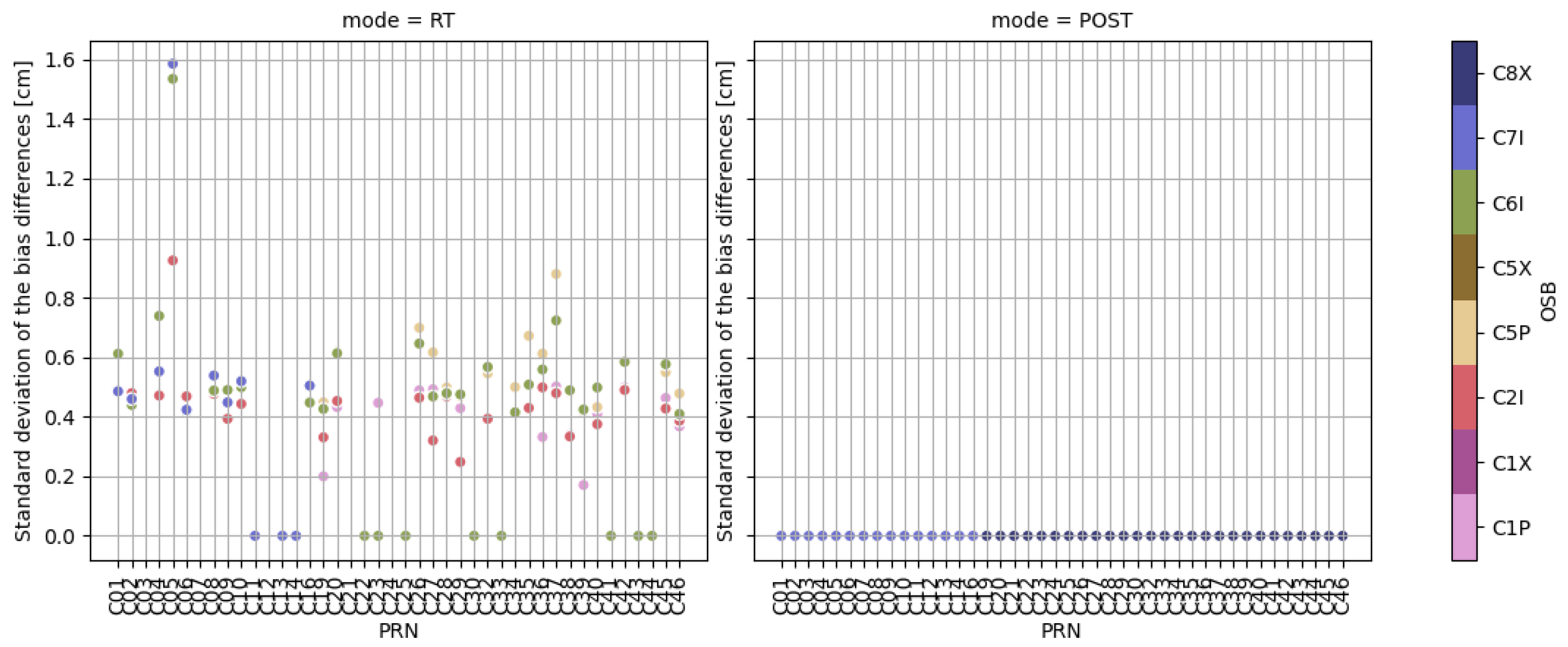




| Constellation | Nature | RTCM Message | IGS Message | Occurrence (s) |
|---|---|---|---|---|
| GPS | orbits/clocks | 1060 | 23 | 5 |
| code biases | 1059 | 25 | 5 | |
| phase biases (L1, L2, L5), all ambiguities | 1265 | 26 | 5 | |
| Glonass | orbits/clocks | 1066 | 43 | 5 |
| code biases | 1065 | 45 | 5 | |
| phase biases (yaw) | 1266 | 46 | 5 | |
| Galileo | orbits/clocks | 1243 | 63 | 5 |
| code biases | 1242 | 65 | 5 | |
| phase biases (E1, E5a, E5b, E6), all ambiguities | 1267 | 66 | 5 | |
| Beidou 2-3 | orbits/clocks | 1261 | 103 | 5 |
| code biases | 1260 | 105 | 5 | |
| phase biases (B1, B2, B3), widelane ambiguities | 1270 | 106 | 5 | |
| Ionosphere VTEC | 1264 | 201 | 60 |
| Constellation | Ranging Noise of Optimal Widelanes Combination (cm) |
|---|---|
| GPS (L1, L2, L5) | 30 |
| GAL (E1, E5a, E5b, E6) | 19 |
| BEI-2 (B1I, B2I, B3I) | 33 |
| BEI-3 (B1I, B1C, B2a, B2b, B3I) | 20 |
| MW WL | IF | WL IF | WL IF | WL IF | |
|---|---|---|---|---|---|
| GPS | F1/F2 | F1/F2 | F1/F2/F5 | − | − |
| GAL | E1/E5a | E1/E5a | E1/E5a/E6 | E1/E5a/E5b | − |
| BEI | B1I/B3I | B1I/B3I | B1I/B3I/B2I | B1I/B3I/B1c | B1I/B3I/B2a |
| System | Frequency | Code Bias | Phase Bias | ||
|---|---|---|---|---|---|
| RT | POST | RT | POST | ||
| GPS | L1 | C1C, C1P, C1W | C1C, C1W | L1C | L1C |
| L2 | C2S, C2L, C2X | C2C, C2S, C2L, C2W | L2W | L2W | |
| L5 | C5Q, C5X | C5Q, C5X | L5I | L5I | |
| GAL | E1 | C1C | C1X | L1C | L1X |
| E5a | C5Q | C5X | L5Q | L58X | |
| E5b | C7Q | C7X | L7Q | L7X | |
| E6 | C6C | C6X | L6C | L6X | |
| BEI | B1C | C1P | C1P, C1X | – | L1X |
| B1I | C2I | C2I | L2I | L2I | |
| B2a | C5P | C5X | – | L5X | |
| B3A | C6I | C6I | L6I | L6I | |
| B2b | C7I | C7I, C7Z | L7I | L7I | |
| GLO | G1 | C1C | C1C | – | – |
| G2 | C2C | C2C | – | – | |
| PVT | WL Only | All Ambiguities | |
|---|---|---|---|
| RMS East error [cm] | |||
| RMS North error [cm] |
| GPS observables | Code, carrier phase, Doppler shift | |
| Galileo observables | Code, carrier phase, Doppler shift | |
| Beidou observables | Code, carrier phase, Doppler shift | |
| Glonass observables | Code, Doppler shift | |
| Iono a priori standard deviation [m] | 10 | |
| Iono process noise standard deviation [m] | 0.025 | |
| Tropo model | Saastamoinen | |
| Wet tropo a priori standard deviation [m] | 0.5 | |
| Wet tropo model standard deviation [m] | ||
| Galileo code measurements standard deviation [m] | 0.5 | |
| GPS code measurements standard deviation [m] | 1 | |
| Beidou code measurements standard deviation [m] | 10 | |
| Carrier phase measurements standard deviation [cm] | 5 | |
| Doppler shift measurements standard deviation [cm/s] | 5 | |
| STA | KIN | |
| Position a priori standard deviation [m] | 10.0 | 10.0 |
| Position process noise standard deviation [m] | 1.0 | 0.0 |
| Velocity a priori standard deviation [m/s] | 0.0 | 1.0 |
| Velocity process noise standard deviation [m/s] | 0.0 | 0.025 horizontal |
| 0.05 vertical | ||
| Real-Time Products | ||||||||
|---|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | |||||||
| mean | std. | mean | std. | |||||
| PPP-float | KIN STA | Pos. error [cm] | ||||||
| Vel. error [cm/s] | ||||||||
| Pos. error [cm] | ||||||||
| PPP-AR | KIN STA | Pos. error [cm] | ||||||
| Vel. error [cm/s] | ||||||||
| Pos. error [cm] | ||||||||
| PPP-Snapshot | KIN STA | Pos. error [cm] | ||||||
| Vel. error [cm/s] | ||||||||
| Pos. error [cm] | ||||||||
| Post-Processed Products | ||||||||
| Horizontal | Vertical | |||||||
| mean | std. | mean | std. | |||||
| PPP-float | KIN STA | Pos. error [cm] | ||||||
| Vel. error [cm/s] | ||||||||
| Pos. error [cm] | ||||||||
| PPP-AR | KIN STA | Pos. error [cm] | ||||||
| Vel. error [cm/s] | ||||||||
| Pos. error [cm] | ||||||||
| PPP-Snapshot | KIN STA | Pos. error [cm] | ||||||
| Vel. error [cm/s] | ||||||||
| Pos. error [cm] | ||||||||
| Horizontal Convergence [min] | Vertical Convergence [min] | |||
|---|---|---|---|---|
| STA Mode | KIN Mode | STA Mode | KIN Mode | |
| RT products | 54 | 55 | 72 | 73 |
| POST products | 25 | 31 | 25 | 29 |
| Position Results | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Post-Processed Products | Real-Time Products | ||||||||||||
| PPP-AR | PPP-Snapshot | PPP-AR | PPP-Snapshot | ||||||||||
| mean | std. | mean | std. | mean | std. | mean | std. | ||||||
| 1 Hz | C/P [m] | ||||||||||||
| C/P/D [m] | |||||||||||||
| Rel. diff. [%] | |||||||||||||
| 10 Hz | C/P [m] | ||||||||||||
| C/P/D [m] | |||||||||||||
| Rel. diff. [%] | |||||||||||||
| Velocity Results | |||||||||||||
| Post-Processed Products | Real-Time Products | ||||||||||||
| PPP-AR | PPP-Snapshot | PPP-AR | PPP-Snapshot | ||||||||||
| mean | std. | mean | std. | mean | std. | mean | std. | ||||||
| 1 Hz | C/P [m/s] | ||||||||||||
| C/P/D [m/s] | |||||||||||||
| Rel. diff. [%] | |||||||||||||
| 10 Hz | C/P [m/s] | ||||||||||||
| C/P/D [m/s] | |||||||||||||
| Rel. diff. [%] | |||||||||||||
| Post-Processed Products | Real-Time Products | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PPP-AR | PPP-Snapshot | PPP-AR | PPP-Snapshot | ||||||||||
| EWL | WL | NL | EWL | WL | NL | EWL | WL | NL | EWL | WL | NL | ||
| 1 Hz | C/P [%] | ||||||||||||
| C/P/D [%] | |||||||||||||
| 10 Hz | C/P [%] | ||||||||||||
| C/P/D [%] | |||||||||||||
| Test Case | 1 | 2 | 3 |
|---|---|---|---|
| GNSS Measurements | GPS + GAL + BDS | GPS + GAL + BDS | GPS + GAL + BDS |
| Biases applied | Only code biases were applied for the three systems | GPS: code and phase biases, GAL: code and phase biases, BDS: code biases only | Code and phase biases were applied for the three systems |
| Hor. mean [cm] | 5.8 | 1.3 | 1.0 |
| Hor. RMS [cm] | 6.7 | 1.8 | 1.1 |
| Hor [cm] | 13.6 | 3.2 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gazzino, C.; Blot, A.; Bernadotte, E.; Jayle, T.; Laymand, M.; Lelarge, N.; Lacabanne, A.; Laurichesse, D. The CNES Solutions for Improving the Positioning Accuracy with Post-Processed Phase Biases, a Snapshot Mode, and High-Frequency Doppler Measurements Embedded in Recent Advances of the PPP-WIZARD Demonstrator. Remote Sens. 2023, 15, 4231. https://doi.org/10.3390/rs15174231
Gazzino C, Blot A, Bernadotte E, Jayle T, Laymand M, Lelarge N, Lacabanne A, Laurichesse D. The CNES Solutions for Improving the Positioning Accuracy with Post-Processed Phase Biases, a Snapshot Mode, and High-Frequency Doppler Measurements Embedded in Recent Advances of the PPP-WIZARD Demonstrator. Remote Sensing. 2023; 15(17):4231. https://doi.org/10.3390/rs15174231
Chicago/Turabian StyleGazzino, Clément, Alexis Blot, Elodie Bernadotte, Théo Jayle, Marion Laymand, Nicolas Lelarge, Aude Lacabanne, and Denis Laurichesse. 2023. "The CNES Solutions for Improving the Positioning Accuracy with Post-Processed Phase Biases, a Snapshot Mode, and High-Frequency Doppler Measurements Embedded in Recent Advances of the PPP-WIZARD Demonstrator" Remote Sensing 15, no. 17: 4231. https://doi.org/10.3390/rs15174231
APA StyleGazzino, C., Blot, A., Bernadotte, E., Jayle, T., Laymand, M., Lelarge, N., Lacabanne, A., & Laurichesse, D. (2023). The CNES Solutions for Improving the Positioning Accuracy with Post-Processed Phase Biases, a Snapshot Mode, and High-Frequency Doppler Measurements Embedded in Recent Advances of the PPP-WIZARD Demonstrator. Remote Sensing, 15(17), 4231. https://doi.org/10.3390/rs15174231








