Estimation of Soil Moisture Using Multi-Source Remote Sensing and Machine Learning Algorithms in Farming Land of Northern China
Abstract
:1. Introduction
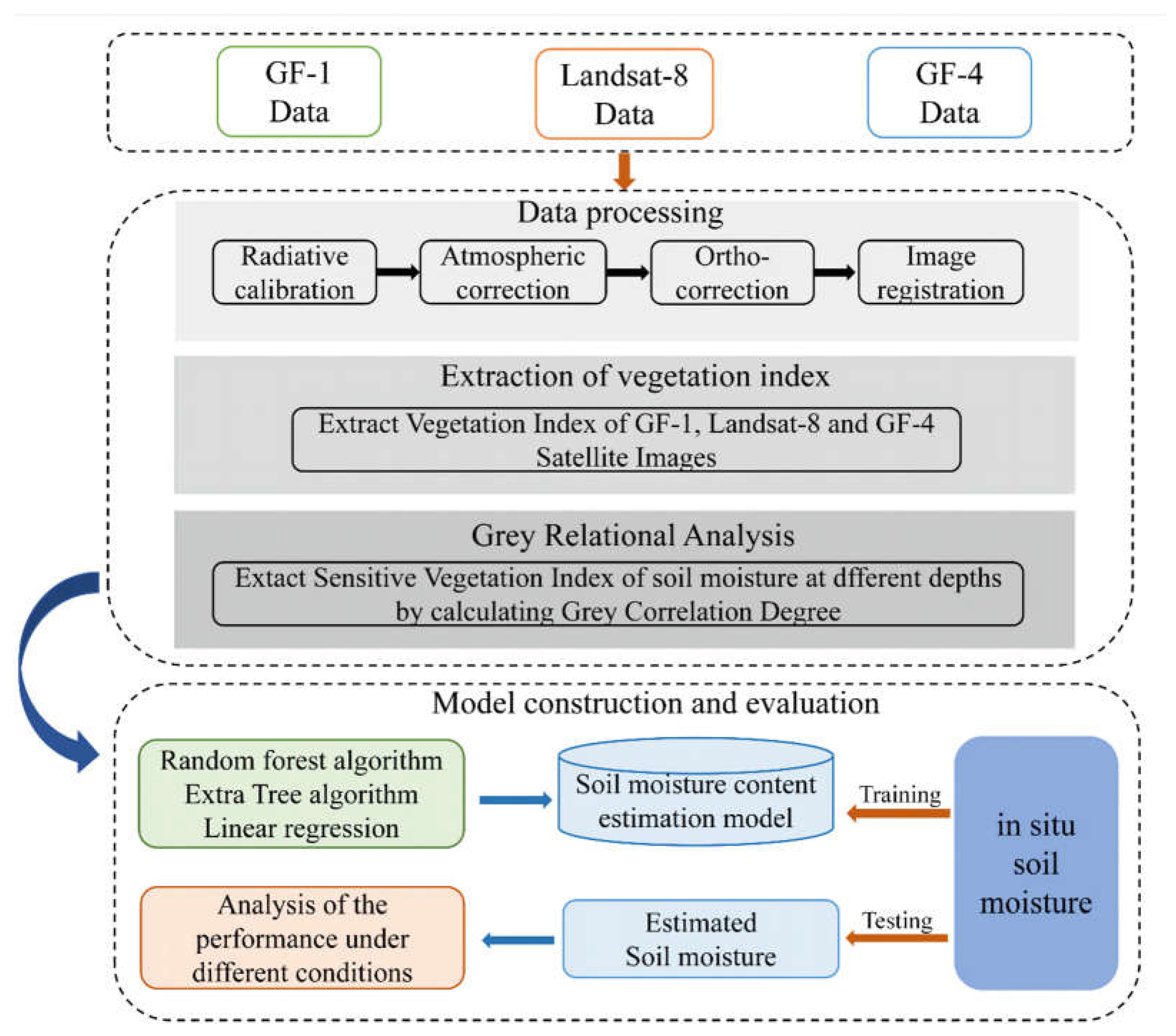
2. Materials and Methods
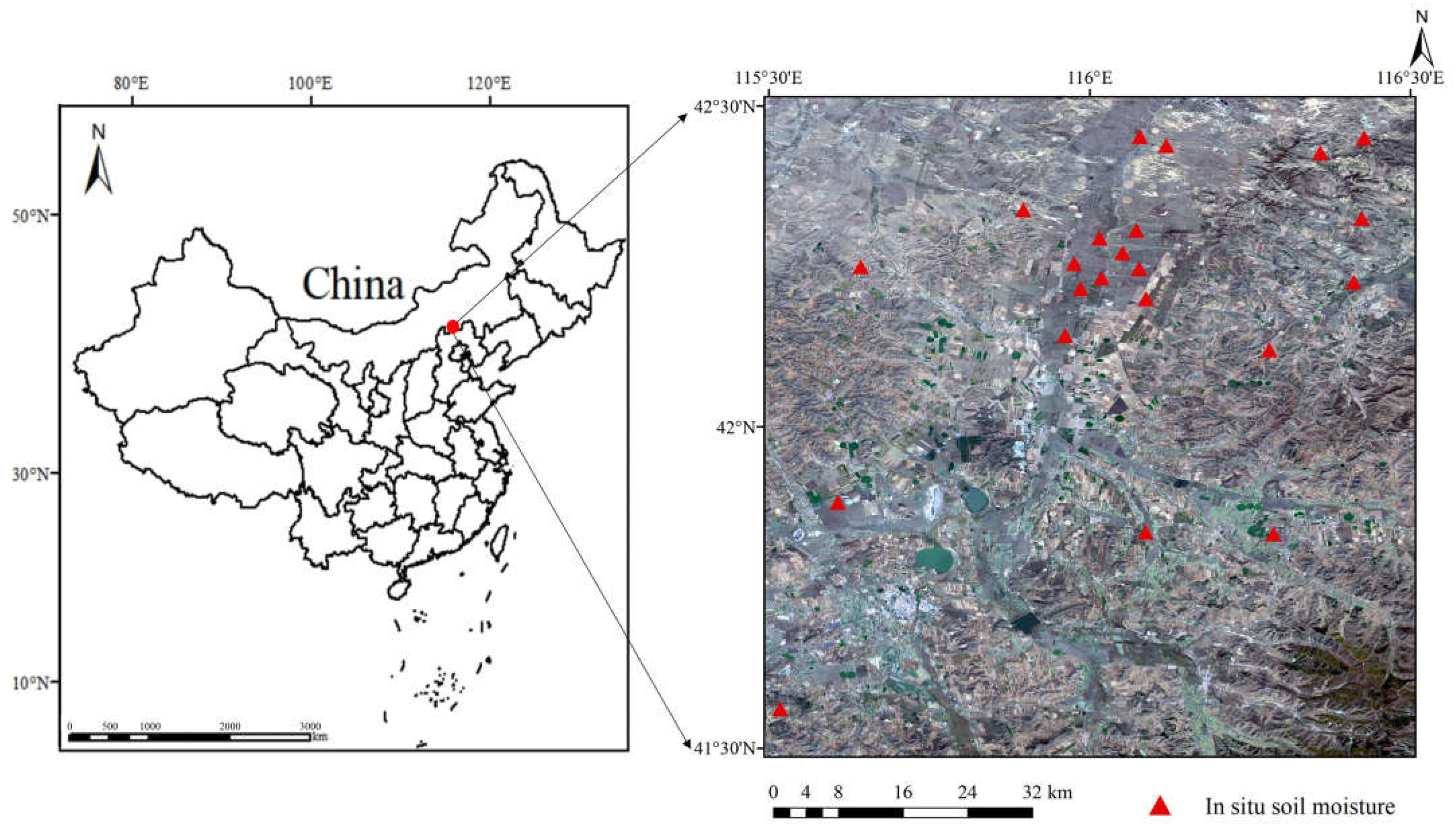
2.1. Study Area
2.2. Data Sources and Processing
2.2.1. Ground Data
2.2.2. Satellite Data and Preprocessing
2.2.3. Remote Sensing Vegetation Indices
2.3. Methodology
2.3.1. Gray Relational Analysis
2.3.2. Machine Learning Algorithms
2.3.3. Model Evaluation
3. Results
3.1. Sensitive Vegetation Index Selection of Soil Moisture Based on GRA
3.2. Estimation of Soil Moisture at Different Depths Using Multi-Source Remote Sensing Data and Machine Learning Methods
3.3. Comprehensive Evaluation of Soil Moisture Estimation Accuracy Based on Different Remote Sensing Imagery and Machine Learning Models
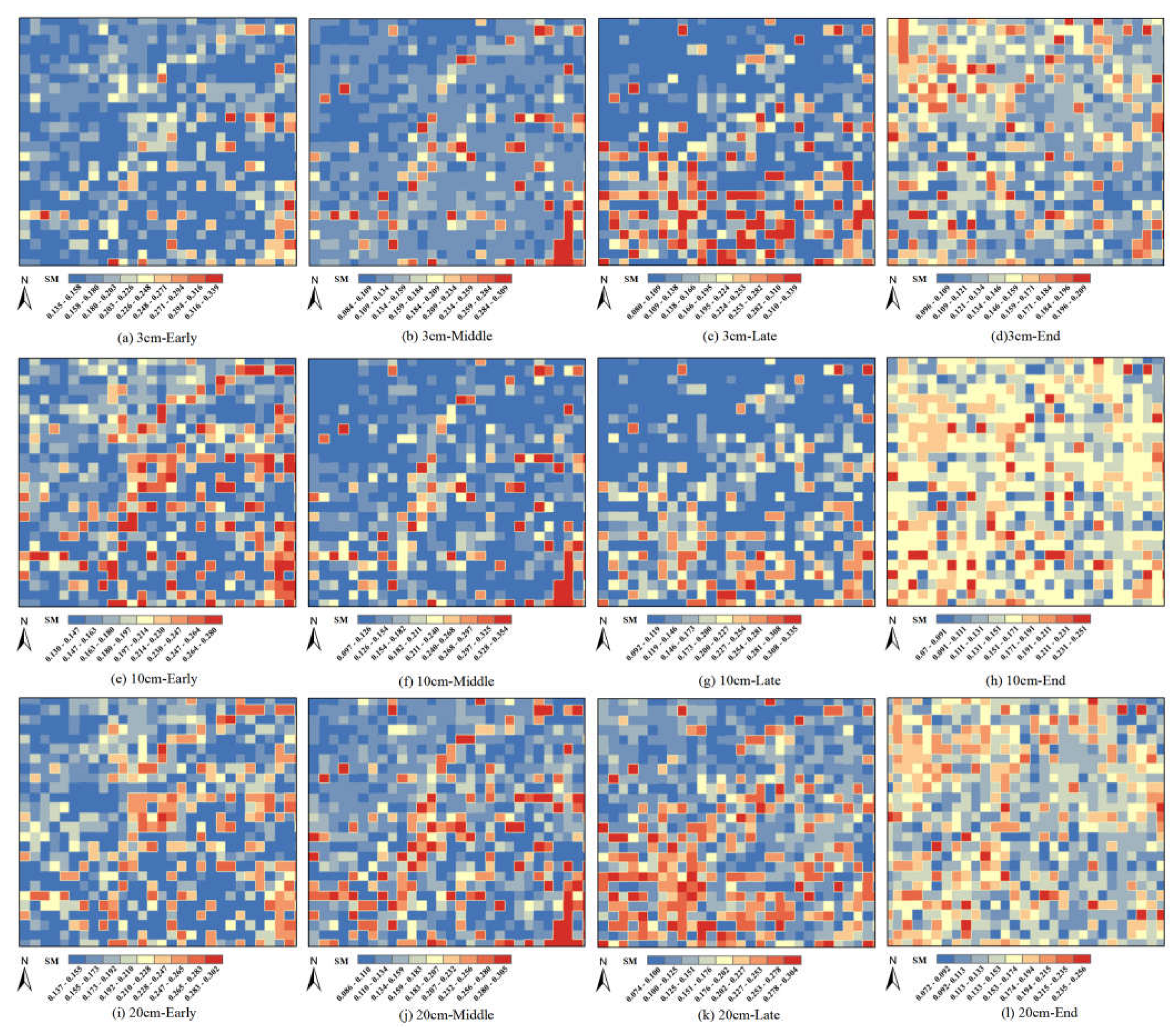
3.4. Spatial and Temporal Distribution of Soil Moisture in Shandian River Basin
4. Discussion
4.1. The Sensitive Vegetation Indices of Different Screening Periods Are Obviously Different
4.2. Multisource Remote Sensing Data and Machine Learning Model Had Significant Differences in Soil Water Estimation Accuracy at Different Depths
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pangaluru, K.; Velicogna, I.; Geruo, A.; Mohajerani, Y.; Ciracì, E.; Cpepa, S.; Basha, G.; Rao, S.V.B. Soil Moisture Variability in India: Relationship of Land Surface–Atmosphere Fields Using Maximum Covariance Analysis. Remote Sens. 2019, 11, 335. [Google Scholar] [CrossRef]
- Zheng, X.; Feng, Z.; Li, L.; Li, B.; Jiang, T.; Li, X.; Li, X.; Chen, S. Simultaneously estimating surface soil moisture and roughness of bare soils by combining optical and radar data. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102345. [Google Scholar] [CrossRef]
- West, H.; Quinn, N.; Horswell, M.; White, P. Assessing Vegetation Response to Soil Moisture Fluctuation under Extreme Drought Using Sentinel-2. Water. 2018, 10, 838. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Pachepsky, Y.; Montzka, C.; van der Kruk, J.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhao, B.; Chanussot, J.; Hong, D.; Yao, J.; Gao, L. Progress and Challenges in Intelligent Remote Sensing Satellite Systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1814–1822. [Google Scholar] [CrossRef]
- Nie, Y.; Tan, Y.; Deng, Y.; Yu, J. Suitability Evaluation of Typical Drought Index in Soil Moisture Retrieval and Monitoring Based on Optical Images. Remote Sens. 2020, 12, 2587. [Google Scholar] [CrossRef]
- Fan, J.; Luo, M.; Han, Q.; Liu, F.; Huang, W.; Tan, S. Evaluation of SMOS, SMAP, AMSR2 and FY-3C soil moisture products over China. PLoS ONE 2022, 17, e266091. [Google Scholar] [CrossRef]
- Yao, Z.; Cui, Y.; Geng, X.; Chen, X.; Li, S. Mapping Irrigated Area at Field Scale Based on the OPtical TRApezoid Model (OPTRAM) Using Landsat Images and Google Earth Engine. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4409011. [Google Scholar] [CrossRef]
- Chai, X.; Zhang, T.; Shao, Y.; Gong, H.; Liu, L.; Xie, K. Modeling and Mapping Soil Moisture of Plateau Pasture Using RADARSAT-2 Imagery. Remote Sens. 2015, 7, 1279–1299. [Google Scholar] [CrossRef]
- Al-Bakri, J.; Suleiman, A.; Berg, A. A comparison of two models to predict soil moisture from remote sensing data of RADARSAT II. Arab. J. Geosci. 2014, 7, 4851–4860. [Google Scholar] [CrossRef]
- Jing, W.; Song, J.; Zhao, X. Evaluation of Multiple Satellite-Based Soil Moisture Products over Continental U.S. Based on In Situ Measurements. Water Resour. Manag. 2018, 32, 3233–3246. [Google Scholar] [CrossRef]
- Menenti, M.; Li, X.; Jia, L.; Yang, K.; Pellicciotti, F.; Mancini, M.; Shi, J.; Escorihuela, M.J.; Zheng, C.; Chen, Q.; et al. Multi-Source Hydrological Data Products to Monitor High Asian River Basins and Regional Water Security. Remote Sens. 2021, 13, 5122. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, J.X.; Yue, H. Comprehensive Evaluation of Sentinel-2 Red Edge and Shortwave-Infrared Bands to Estimate Soil Moisture. Ieee J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 7448–7465. [Google Scholar] [CrossRef]
- Cao, M.; Chen, M.; Liu, J.; Liu, Y. Assessing the performance of satellite soil moisture on agricultural drought monitoring in the North China Plain. Agric. Water Manag. 2022, 263, 107450. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Yang, J.; Deng, Y. Time-Lag Effect of Vegetation Response to Volumetric Soil Water Content: A Case Study of Guangdong Province, Southern China. Remote Sens. 2022, 14, 1301. [Google Scholar] [CrossRef]
- Bayad, M.; Chau, H.W.; Trolove, S.; Muller, K.; Condron, L.; Moir, J.; Yi, L. Time series of remote sensing and water deficit to predict the occurrence of soil water repellency in New Zealand pastures. Isprs-J. Photogramm. Remote Sens. 2020, 169, 292–300. [Google Scholar] [CrossRef]
- Koley, S.; Jeganathan, C. Estimation and evaluation of high spatial resolution surface soil moisture using multi-sensor multi-resolution approach. Geoderma 2020, 378, 114618. [Google Scholar] [CrossRef]
- Carranza, C.; Nolet, C.; Pezij, M.; van der Ploeg, M. Root zone soil moisture estimation with Random Forest. J. Hydrol. 2021, 593, 125840. [Google Scholar] [CrossRef]
- Hosoda, M.; Tokonami, S.; Suzuki, T.; Janik, M. Machine learning as a tool for analysing the impact of environmental parameters on the radon exhalation rate from soil. Radiat. Meas. 2020, 138, 106402. [Google Scholar] [CrossRef]
- Senanayake, I.P.; Yeo, I.Y.; Walker, J.P.; Willgoose, G.R. Estimating catchment scale soil moisture at a high spatial resolution: Integrating remote sensing and machine learning. Sci. Total Environ. 2021, 776, 145924. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, X.; Sun, Z.; Liang, D.; An, X.; Chen, L.; Yang, G.; Huang, L.; Xu, S.; Yang, M. Estimation of Winter Wheat Residue Coverage Based on GF-1 Imagery and Machine Learning Algorithm. Agronomy. 2022, 12, 1051. [Google Scholar] [CrossRef]
- Cheng, M.; Li, B.; Jiao, X.; Huang, X.; Fan, H.; Lin, R.; Liu, K. Using multimodal remote sensing data to estimate regional-scale soil moisture content: A case study of Beijing, China. Agric. Water Manag. 2022, 260, 107298. [Google Scholar] [CrossRef]
- Adab, H.; Morbidelli, R.; Saltalippi, C.; Moradian, M.; Ghalhari, G.A.F. Machine Learning to Estimate Surface Soil Moisture from Remote Sensing Data. Water 2020, 12, 3223. [Google Scholar] [CrossRef]
- Zhao, T.J.; Shi, J.C.; Xu, H.X.; Sun, Y.L.; Chen, D.Q.; Cui, Q.; Jia, L.; Huang, S.; Niu, S.D.; Li, X.W.; et al. Comprehensive remote sensing experiment of water cycle and energy balance in the Shandian river basin. Natl. Remote Sens. Bull. 2021, 25, 871–887. [Google Scholar] [CrossRef]
- Zhao, T.; Ji, D.; Jiang, L.; Cui, Q.; Chen, D.; Zheng, J.; Zhang, Z.; Hu, L.; Shi, J. In-Situ Measurement Data Set (2019) of the Soil Moisture and Temperature Wireless Sensor Network within the Shandian River Basin; National Tibetan Plateau Data Center: Lanzhou, China, 2021. [Google Scholar]
- Luo, L.; Wang, X.; Lasaponara, R.; Xiang, B.; Zhen, J.; Zhu, L.; Yang, R.; Liu, D.; Liu, C. Auto-Extraction of Linear Archaeological Traces of Tuntian Irrigation Canals in Miran Site (China) from Gaofen-1 Satellite Imagery. Remote Sens. 2018, 10, 718. [Google Scholar] [CrossRef]
- Sánchez, N.; Alonso-Arroyo, A.; Martínez-Fernández, J.; Piles, M.; González-Zamora, Á.; Camps, A.; Vall-llosera, M. On the Synergy of Airborne GNSS-R and Landsat 8 for Soil Moisture Estimation. Remote Sens. 2015, 7, 9954–9974. [Google Scholar] [CrossRef]
- Sun, Z.; Wei, J.; Zhang, N.; He, Y.; Sun, Y.; Liu, X.; Yu, H.; Sun, L. Retrieving High-Resolution Aerosol Optical Depth from GF-4 PMS Imagery in Eastern China. Remote Sens. 2021, 13, 3752. [Google Scholar] [CrossRef]
- Gadi, V.K.; Garg, A.; Rattan, B.; Raj, P.; Gaurav, S.; Sreedeep, S.; Sahoo, L.; Berretta, C.; Peng, L. Growth dynamics of deciduous species during their life period: A case study of urban green space in India. Urban For. Urban Green. 2019, 43, 126380. [Google Scholar] [CrossRef]
- Fernández-Buces, N.; Siebe, C.; Cram, S.; Palacio, J.L. Mapping soil salinity using a combined spectral response index for bare soil and vegetation: A case study in the former lake Texcoco, Mexico. J. Arid Environ. 2006, 65, 644–667. [Google Scholar] [CrossRef]
- Xu, L.Y.; Xie, X.D.; Li, S. Correlation analysis of the urban heat island effect and the spatial and temporal distribution of atmospheric particulates using TM images in Beijing. Environ. Pollut. 2013, 178, 102–114. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wu, W. The Generalized Difference Vegetation Index (GDVI) for Dryland Characterization. Remote Sens. 2014, 6, 1211–1233. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J.L. Advanced vegetation indices optimized for up-coming sensors: Design, performance, and applications. Ieee Trans. Geosci. Remote Sensing. 2000, 38, 2489–2505. [Google Scholar]
- Ranjan, R.; Chopra, U.K.; Sahoo, R.N.; Singh, A.K.; Pradhan, S. Assessment of plant nitrogen stress in wheat (Triticum aestivum L.) through hyperspectral indices. Int. J. Remote Sens. 2012, 33, 6342–6360. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, G. Determination of green aboveground biomass in desert steppe using litter-soil-adjusted vegetation index. Eur. J. Remote Sens. 2014, 47, 611–625. [Google Scholar] [CrossRef]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Schnell, J.A. Monitoring the Vernal Advancement and Retrogradation (Greenwave Effect) of Natural Vegetation; NASA/GSFCT Type Final Report; NASA: Pasadena, CA, USA, 1974. [Google Scholar]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Weisz, R. Aerial Color Infrared Photography for Determining Late-Season Nitrogen Requirements in Corn. Agron. J. 2005, 97, 1443–1451. [Google Scholar] [CrossRef]
- Noborio, K. Measurement of soil water content and electrical conductivity by time domain reflectometry: A review. Comput. Electron. Agric. 2001, 31, 213–237. [Google Scholar] [CrossRef]
- Williamson, H.D. Reflectance from shrubs and under-shrub soil in a semiarid environment. Remote Sens. Environ. 1989, 29, 263–271. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Schneider, P.; Roberts, D.A.; Kyriakidis, P.C. A VARI-based relative greenness from MODIS data for computing the Fire Potential Index. Remote Sens. Environ. 2008, 112, 1151–1167. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Tao, J.; Sun, X.H.; Cao, Y.; Ling, M.H. Evaluation of water quality and its driving forces in the Shaying River Basin with the grey relational analysis based on combination weighting. Environ. Sci. Pollut. Res. 2022, 29, 18103–18115. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Ren, G.; Yang, G.; Feng, Y. Analysis of the spatiotemporal variability of droughts and the effects of drought on potato production in northern China. Agric. For. Meteorol. 2019, 264, 334–342. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Karmakar, C.; Datcu, M. A Framework for Interactive Visual Interpretation of Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4509105. [Google Scholar] [CrossRef]
- Xie, J.; Qi, T.; Hu, W.; Huang, H.; Chen, B.; Zhang, J. Retrieval of Live Fuel Moisture Content Based on Multi-Source Remote Sensing Data and Ensemble Deep Learning Model. Remote Sens. 2022, 14, 4378. [Google Scholar] [CrossRef]
- Rhee, J.; Yang, H. Drought Prediction for Areas with Sparse Monitoring Networks: A Case Study for Fiji. Water 2018, 10, 788. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Wang, S.; Ning, Y.; Shi, H. A new uncertain linear regression model based on equation deformation. Soft Comput. 2021, 25, 12817–12824. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, Z.; Xu, C.; Ma, Y.; Yao, Z.; Wei, G.; Li, Y. Soil water content inversion model in field maize root zone based on UAV multispectral remote sensing. Trans. Chin. Soc. Agric. Eng. 2020, 36, 63–74. [Google Scholar]
- Nguyen, T.T.; Ngo, H.H.; Guo, W.; Chang, S.W.; Nguyen, D.D.; Nguyen, C.T.; Zhang, J.; Liang, S.; Bui, X.T.; Hoang, N.B. A low-cost approach for soil moisture prediction using multi-sensor data and machine learning algorithm. Sci. Total Environ. 2022, 833, 155066. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.; Jin, T.; Chang, X.; Zhu, Y.; Li, Y.; Sun, J.; Li, D. Comparative Analysis of Landsat-8, Sentinel-2, and GF-1 Data for Retrieving Soil Moisture over Wheat Farmlands. Remote Sens. 2020, 12, 2708. [Google Scholar] [CrossRef]
- Qun’Ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval model for total nitrogen concentration based on UAV hyper spectral remote sensing data and machine learning algorithms—A case study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- Jeon, G.; Bellandi, V.; Chehri, A. Editorial for the Special Issue Advanced Machine Learning for Time Series Remote Sensing Data Analysis. Remote Sens. 2020, 12, 2815. [Google Scholar] [CrossRef]
- Zhou, P.; Du, L.; Liu, X.; Shen, Y.; Fan, M.; Li, X. Self-Paced Clustering Ensemble. Ieee Trans. Neural Netw. Learn. Syst. 2021, 32, 1497–1511. [Google Scholar] [CrossRef]
- He, L.; Cheng, Y.; Li, Y.X.; Li, F.; Fan, K.L.; Li, Y.Z. An Improved Method for Soil Moisture Monitoring With Ensemble Learning Methods Over the Tibetan Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2833–2844. [Google Scholar] [CrossRef]
- Zhao, J.H.; Zhang, C.Y.; Min, L.; Guo, Z.W.; Li, N. Retrieval of Farmland Surface Soil Moisture Based on Feature Optimization and Machine Learning. Remote Sens. 2022, 14, 5102. [Google Scholar] [CrossRef]
- Cheng, M.H.; Jiao, X.Y.; Liu, Y.D.; Shao, M.C.; Yu, X.; Bai, Y.; Wang, Z.X.; Wang, S.Y.; Tuohuti, N.; Liu, S.B.; et al. Estimation of soil moisture content under high maize canopy coverage from UAV multimodal data and machine learning. Agric. Water Manag. 2022, 264, 107530. [Google Scholar] [CrossRef]
- Han, Z.Y.; Zhu, X.C.; Fang, X.Y.; Wang, Z.Y.; Wang, L.; Zhao, G.X.; Jiang, Y.M. Hyperspectral Estimation of Apple Tree Canopy LAI Based on SVM and RF Regression. Spectrosc. Spectr. Anal. 2016, 36, 800–805. [Google Scholar]
- Breiman. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yuan, H.H.; Yang, G.J.; Li, C.C.; Wang, Y.J.; Liu, J.G.; Yu, H.Y.; Feng, H.K.; Xu, B.; Zhao, X.Q.; Yang, X.D. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Alfian, G.; Syafrudin, M.; Fahrurrozi, I.; Fitriyani, N.L.; Atmaji, F.T.D.; Widodo, T.; Bahiyah, N.; Benes, F.; Rhee, J. Predicting Breast Cancer from Risk Factors Using SVM and Extra-Trees-Based Feature Selection Method. Computers 2022, 11, 136. [Google Scholar] [CrossRef]
- Ganaie, M.A.; Tanveer, M.; Suganthan, P.N.; Snasel, V. Oblique and rotation double random forest. Neural Netw. 2022, 153, 496–517. [Google Scholar] [CrossRef]
- Negahbani, S.; Momeni, M.; Moradizadeh, M. Improving the Spatiotemporal Resolution of Soil Moisture through a Synergistic Combination of MODIS and LANDSAT8 Data. Water Resour. Manag. 2022, 36, 1813–1832. [Google Scholar] [CrossRef]


| Satellite | GF-1 WFV | Landsat-8 OLI | GF-4 PMS |
|---|---|---|---|
| Spectral range (μm) | 0.450–0.520 | 0.433–0.453 (b1) | 0.450–0.900 (b1) |
| 0.520–0.590 (b2) | 0.450–0.515 (b2) | 0.450–0.520 (b2) | |
| 0.630–0.690 (b3) | 0.525–0.600 (b3) | 0.520–0.600 (b3) | |
| 0.770–0.890 (b4) | 0.630–0.680 (b4) | 0.630–0.690 (b4) | |
| 0.845–0.885 (b5) | 0.760–0.900 (b5) | ||
| 1.560–1.660 (b6) | |||
| 2.100–2.300 (b7) | |||
| 0.500–0.680 (b8) | |||
| 1.360–1.390 (b9) | |||
| Spatial resolution (m) | 16 | 30 | 50 |
| Width (km) | 60 | 185 | 400 |
| Revisit time (d) | 4 | 16 | 1 |
| Growth Stage | Satellite | Date |
|---|---|---|
| Early | GF-1 | 14 April 2019 |
| Landsat-8 | 2 April 2019 | |
| GF-4 | 14 April 2019 | |
| Middle | GF-1 | 14 June 2019 |
| Landsat-8 | 24 August 2019 | |
| GF-4 | 24 August 2019 | |
| Late | GF-1 | 29 September 2019 |
| Landsat-8 | 25 September 2019 | |
| GF-4 | 28 September 2019 | |
| End of growth | GF-1 | 31 October 2019 |
| Landsat-8 | 27 October 2019 | |
| GF-4 | 30 October 2019 |
| Vegetation Index | Abbreviation | Formula | References |
|---|---|---|---|
| Comprehensive spectral response index | COSRI | (B + G) × (NIR − R)/(R + NIR)2 | [30] |
| Differential vegetation index | DVI | NIR − R | [31] |
| Enhanced vegetation index | EVI | 2.5(NIR − R)/(1 + NIR + 6R − 7.5B) | [32] |
| Green DVI | GDVI | NIR − G | [33] |
| Green leaf index | GLI | (2G – B − R)/(2G + B + R) | [34] |
| Green NDVI | GNDVI | (NIR − G)/(NIR + G) | [35] |
| Green OSAVI | GOSAVI | (NIR − G)/(NIR + G + 0.16) | [36] |
| Green RVI | GRVI | NIR/G | [37] |
| Green SAVI | GSAVI | (NIR − G)/(NIR + G + 0.5) | [38] |
| Infrared vegetation index | IPVI | NIR/(NIR + R) | [39] |
| Modified soil-adjusted vegetation index | MSAVI2 | NIR + 0.5 − 0.5 × [(2NIR + 1)2 − 8(NIR − R)]0.5 | [40] |
| Normalized difference vegetation index | NDVI | (NIR − R)/(NIR + R) | [41] |
| Normalized NIR | NNIR | NIR/(NIR + R + G) | [42] |
| Normalized Red | NR | R/(NIR + R + G) | [43] |
| Optimized soil-adjusted vegetation index | OSAVI | (NIR − R)/(NIR + R + 0.16) | [36] |
| Red vegetation index | RI | (R − G)/(R + G) | [44] |
| Ratio vegetation index | RVI | NIR/R | [45] |
| Transformed vegetation index | TVI | 60(NIR − G) − 100(R − G) | [46] |
| Visible atmospheric resistance index | VARI | (G − R)/(G + R − B) | [47] |
| Wide dynamic range vegetation index | WDRVI | (0.12NIR − R)/(0.12NIR + R) | [48] |
| Satellite | Growth Stages | 3 cm | 10 cm | 20 cm | |||
|---|---|---|---|---|---|---|---|
| VIs | GCD | VIs | GCD | VIs | GCD | ||
| GF-1 | Early | NR | 0.934 | NR | 0.938 | IPVI | 0.926 |
| WDRVI | 0.932 | WDRVI | 0.931 | NR | 0.924 | ||
| GLI | 0.931 | IPVI | 0.931 | NNIR | 0.923 | ||
| IPVI | 0.926 | GLI | 0.930 | GLI | 0.922 | ||
| NNIR | 0.924 | GOSAVI | 0.929 | MSAVI2 | 0.922 | ||
| Middle | EVI | 0.898 | OSAVI | 0.907 | OSAVI | 0.891 | |
| COSRI | 0.894 | TVI | 0.897 | EVI | 0.888 | ||
| OSAVI | 0.882 | EVI | 0.896 | TVI | 0.884 | ||
| DVI | 0.882 | NDVI | 0.895 | COSRI | 0.878 | ||
| NDVI | 0.878 | COSRI | 0.894 | DVI | 0.878 | ||
| Late | COSRI | 0.802 | EVI | 0.798 | GLI | 0.884 | |
| EVI | 0.802 | COSRI | 0.791 | EVI | 0.884 | ||
| MSAVI2 | 0.801 | RVI | 0.788 | MSAVI2 | 0.884 | ||
| RVI | 0.801 | OSAVI | 0.786 | GOSAVI | 0.883 | ||
| IPVI | 0.800 | MSAVI2 | 0.786 | IPVI | 0.882 | ||
| End | EVI | 0.755 | EVI | 0.767 | COSRI | 0.707 | |
| GLI | 0.755 | COSRI | 0.755 | MSAVI2 | 0.704 | ||
| COSRI | 0.754 | NDVI | 0.751 | NNIR | 0.704 | ||
| GSAVI | 0.752 | OSAVI | 0.750 | EVI | 0.704 | ||
| MSAVI2 | 0.750 | GLI | 0.748 | IPVI | 0.703 | ||
| Landsat-8 | Early | WDRVI | 0.720 | WDRVI | 0.743 | IPVI | 0.688 |
| NR | 0.719 | NR | 0.742 | COSRI | 0.685 | ||
| GLI | 0.710 | GLI | 0.736 | NR | 0.684 | ||
| GDVI | 0.704 | COSRI | 0.734 | WDRVI | 0.684 | ||
| IPVI | 0.700 | IPVI | 0.731 | NNIR | 0.683 | ||
| Middle | NNIR | 0.978 | GRVI | 0.976 | GNDVI | 0.970 | |
| IPVI | 0.978 | NDVI | 0.975 | GSAVI | 0.970 | ||
| MSAVI2 | 0.978 | OSAVI | 0.975 | GOSAVI | 0.970 | ||
| GLI | 0.977 | NNIR | 0.975 | GRVI | 0.970 | ||
| COSRI | 0.976 | TVI | 0.975 | NNIR | 0.970 | ||
| Late | COSRI | 0.806 | GLI | 0.798 | COSRI | 0.748 | |
| GLI | 0.805 | COSRI | 0.796 | GLI | 0.744 | ||
| IPVI | 0.800 | IPVI | 0.792 | MSAVI2 | 0.743 | ||
| MSAVI2 | 0.798 | MSAVI2 | 0.789 | IPVI | 0.742 | ||
| NNIR | 0.797 | NNIR | 0.789 | EVI | 0.74 | ||
| End | GLI | 0.767 | GLI | 0.770 | NNIR | 0.702 | |
| IPVI | 0.757 | VARI | 0.763 | MSAVI2 | 0.702 | ||
| VARI | 0.756 | IPVI | 0.763 | IPVI | 0.701 | ||
| NR | 0.756 | RI | 0.762 | GLI | 0.701 | ||
| WDRVI | 0.754 | MSAVI2 | 0.762 | EVI | 0.700 | ||
| GF-4 | Early | NR | 0.827 | WDRVI | 0.813 | IPVI | 0.790 |
| WDRVI | 0.827 | NR | 0.813 | NNIR | 0.790 | ||
| GLI | 0.825 | IPVI | 0.813 | MSAVI2 | 0.790 | ||
| IPVI | 0.824 | GLI | 0.812 | GRVI | 0.790 | ||
| NNIR | 0.823 | COSRI | 0.812 | RVI | 0.789 | ||
| Middle | RVI | 0.945 | COSRI | 0.939 | RVI | 0.924 | |
| COSRI | 0.944 | RVI | 0.936 | GRVI | 0.923 | ||
| MSAVI2 | 0.944 | GRVI | 0.936 | NNIR | 0.923 | ||
| IPVI | 0.942 | GNDVI | 0.935 | IPVI | 0.922 | ||
| NNIR | 0.942 | OSAVI | 0.935 | MSAVI2 | 0.922 | ||
| Late | COSRI | 0.850 | RVI | 0.841 | MSAVI2 | 0.838 | |
| RVI | 0.847 | MSAVI2 | 0.839 | IPVI | 0.838 | ||
| NDVI | 0.847 | COSRI | 0.836 | NNIR | 0.837 | ||
| OSAVI | 0.846 | IPVI | 0.835 | GNDVI | 0.837 | ||
| MSAVI2 | 0.845 | NNIR | 0.835 | GRVI | 0.837 | ||
| End | GLI | 0.907 | GLI | 0.905 | GLI | 0.880 | |
| IPVI | 0.906 | GRVI | 0.905 | WDRVI | 0.880 | ||
| WDRVI | 0.906 | NNIR | 0.904 | NNIR | 0.879 | ||
| NNIR | 0.905 | IPVI | 0.904 | IPVI | 0.879 | ||
| GRVI | 0.905 | MSAVI2 | 0.904 | NR | 0.878 | ||
| Satellite | Machine Learning Algorithm | Depth (cm) | Training | Testing | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |||
| GF-1 | Random Forest | 3 | 0.764 | 0.024 | 0.588 | 0.044 |
| 10 | 0.814 | 0.026 | 0.463 | 0.044 | ||
| 20 | 0.769 | 0.026 | 0.404 | 0.055 | ||
| Extra Tree | 3 | 0.812 | 0.019 | 0.601 | 0.041 | |
| 10 | 0.818 | 0.027 | 0.518 | 0.037 | ||
| 20 | 0.762 | 0.034 | 0.496 | 0.03 | ||
| Linear Regression | 3 | 0.158 | 0.05 | 0.129 | 0.059 | |
| 10 | 0.345 | 0.039 | 0.162 | 0.054 | ||
| 20 | 0.155 | 0.053 | 0.149 | 0.078 | ||
| Landsat-8 | Random Forest | 3 | 0.759 | 0.024 | 0.308 | 0.059 |
| 10 | 0.748 | 0.028 | 0.261 | 0.054 | ||
| 20 | 0.79 | 0.027 | 0.239 | 0.054 | ||
| Extra Tree | 3 | 0.753 | 0.029 | 0.296 | 0.046 | |
| 10 | 0.798 | 0.026 | 0.28 | 0.047 | ||
| 20 | 0.764 | 0.022 | 0.117 | 0.077 | ||
| Linear Regression | 3 | 0.292 | 0.043 | 0.306 | 0.055 | |
| 10 | 0.247 | 0.045 | 0.23 | 0.064 | ||
| 20 | 0.173 | 0.052 | 0.108 | 0.058 | ||
| GF-4 | Random Forest | 3 | 0.826 | 0.035 | 0.349 | 0.063 |
| 10 | 0.802 | 0.046 | 0.255 | 0.054 | ||
| 20 | 0.803 | 0.04 | 0.225 | 0.082 | ||
| Extra Tree | 3 | 0.848 | 0.035 | 0.451 | 0.051 | |
| 10 | 0.823 | 0.038 | 0.384 | 0.075 | ||
| 20 | 0.820 | 0.033 | 0.372 | 0.091 | ||
| Linear Regression | 3 | 0.389 | 0.048 | 0.232 | 0.084 | |
| 10 | 0.249 | 0.063 | 0.07 | 0.076 | ||
| 20 | 0.153 | 0.096 | 0.086 | 0.052 | ||
| Satellite | Machine Learning Algorithm | Depth (cm) | Training | Testing | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |||
| GF-1 | Random Forest | 3 | 0.926 | 0.019 | 0.876 | 0.039 |
| 10 | 0.913 | 0.021 | 0.874 | 0.061 | ||
| 20 | 0.852 | 0.03 | 0.814 | 0.056 | ||
| Extra Tree | 3 | 0.928 | 0.021 | 0.885 | 0.024 | |
| 10 | 0.913 | 0.026 | 0.828 | 0.034 | ||
| 20 | 0.879 | 0.028 | 0.803 | 0.065 | ||
| Linear Regression | 3 | 0.708 | 0.03 | 0.566 | 0.068 | |
| 10 | 0.733 | 0.039 | 0.606 | 0.064 | ||
| 20 | 0.612 | 0.057 | 0.612 | 0.048 | ||
| Landsat-8 | Random Forest | 3 | 0.803 | 0.041 | 0.731 | 0.024 |
| 10 | 0.837 | 0.032 | 0.719 | 0.059 | ||
| 20 | 0.717 | 0.05 | 0.427 | 0.064 | ||
| Extra Tree | 3 | 0.794 | 0.033 | 0.748 | 0.06 | |
| 10 | 0.809 | 0.035 | 0.723 | 0.07 | ||
| 20 | 0.79 | 0.044 | 0.602 | 0.048 | ||
| Linear Regression | 3 | 0.221 | 0.062 | 0.167 | 0.091 | |
| 10 | 0.208 | 0.071 | 0.174 | 0.102 | ||
| 20 | 0.183 | 0.089 | 0.116 | 0.065 | ||
| GF-4 | Random Forest | 3 | 0.832 | 0.028 | 0.716 | 0.064 |
| 10 | 0.83 | 0.031 | 0.701 | 0.073 | ||
| 20 | 0.745 | 0.047 | 0.629 | 0.061 | ||
| Extra Tree | 3 | 0.839 | 0.028 | 0.72 | 0.052 | |
| 10 | 0.834 | 0.022 | 0.7 | 0.08 | ||
| 20 | 0.753 | 0.046 | 0.682 | 0.055 | ||
| Linear Regression | 3 | 0.185 | 0.041 | 0.17 | 0.12 | |
| 10 | 0.179 | 0.042 | 0.131 | 0.14 | ||
| 20 | 0.128 | 0.089 | 0.129 | 0.077 | ||
| Satellite | Machine Learning Algorithm | Depth (cm) | Training | Testing | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |||
| GF-1 | Random Forest | 3 | 0.838 | 0.038 | 0.776 | 0.027 |
| 10 | 0.856 | 0.035 | 0.728 | 0.051 | ||
| 20 | 0.796 | 0.036 | 0.495 | 0.08 | ||
| Extra Tree | 3 | 0.854 | 0.037 | 0.8 | 0.031 | |
| 10 | 0.829 | 0.038 | 0.828 | 0.071 | ||
| 20 | 0.823 | 0.04 | 0.612 | 0.054 | ||
| Linear Regression | 3 | 0.277 | 0.066 | 0.275 | 0.083 | |
| 10 | 0.231 | 0.085 | 0.248 | 0.062 | ||
| 20 | 0.213 | 0.076 | 0.215 | 0.083 | ||
| Landsat-8 | Random Forest | 3 | 0.838 | 0.038 | 0.606 | 0.024 |
| 10 | 0.811 | 0.032 | 0.776 | 0.062 | ||
| 20 | 0.811 | 0.029 | 0.62 | 0.077 | ||
| Extra Tree | 3 | 0.808 | 0.033 | 0.693 | 0.056 | |
| 10 | 0.862 | 0.031 | 0.698 | 0.082 | ||
| 20 | 0.832 | 0.031 | 0.568 | 0.073 | ||
| Linear Regression | 3 | 0.284 | 0.078 | 0.21 | 0.045 | |
| 10 | 0.334 | 0.078 | 0.216 | 0.058 | ||
| 20 | 0.216 | 0.075 | 0.219 | 0.094 | ||
| GF-4 | Random Forest | 3 | 0.845 | 0.037 | 0.693 | 0.028 |
| 10 | 0.8 | 0.042 | 0.689 | 0.043 | ||
| 20 | 0.771 | 0.044 | 0.652 | 0.051 | ||
| Extra Tree | 3 | 0.797 | 0.035 | 0.778 | 0.06 | |
| 10 | 0.835 | 0.03 | 0.751 | 0.079 | ||
| 20 | 0.818 | 0.032 | 0.748 | 0.08 | ||
| Linear Regression | 3 | 0.115 | 0.073 | 0.152 | 0.082 | |
| 10 | 0.245 | 0.044 | 0.172 | 0.118 | ||
| 20 | 0.147 | 0.086 | 0.131 | 0.074 | ||
| Satellite | Machine Learning Algorithm | Depth (cm) | Training | Testing | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |||
| GF-1 | Random Forest | 3 | 0.849 | 0.025 | 0.623 | 0.05 |
| 10 | 0.793 | 0.03 | 0.462 | 0.078 | ||
| 20 | 0.779 | 0.036 | 0.579 | 0.072 | ||
| Extra Tree | 3 | 0.836 | 0.035 | 0.736 | 0.046 | |
| 10 | 0.813 | 0.034 | 0.732 | 0.049 | ||
| 20 | 0.804 | 0.036 | 0.693 | 0.068 | ||
| Linear Regression | 3 | 0.214 | 0.059 | 0.255 | 0.063 | |
| 10 | 0.3 | 0.066 | 0.414 | 0.054 | ||
| 20 | 0.276 | 0.063 | 0.269 | 0.088 | ||
| Landsat-8 | Random Forest | 3 | 0.748 | 0.022 | 0.316 | 0.08 |
| 10 | 0.735 | 0.031 | 0.312 | 0.079 | ||
| 20 | 0.769 | 0.04 | 0.348 | 0.071 | ||
| Extra Tree | 3 | 0.772 | 0.026 | 0.477 | 0.062 | |
| 10 | 0.766 | 0.028 | 0.479 | 0.075 | ||
| 20 | 0.743 | 0.044 | 0.472 | 0.061 | ||
| Linear Regression | 3 | 0.117 | 0.057 | 0.1 | 0.078 | |
| 10 | 0.178 | 0.06 | 0.151 | 0.082 | ||
| 20 | 0.101 | 0.068 | 0.101 | 0.107 | ||
| GF-4 | Random Forest | 3 | 0.734 | 0.034 | 0.233 | 0.063 |
| 10 | 0.746 | 0.037 | 0.22 | 0.067 | ||
| 20 | 0.725 | 0.04 | 0.216 | 0.085 | ||
| Extra Tree | 3 | 0.799 | 0.033 | 0.285 | 0.045 | |
| 10 | 0.78 | 0.038 | 0.256 | 0.063 | ||
| 20 | 0.758 | 0.048 | 0.189 | 0.041 | ||
| Linear Regression | 3 | 0.188 | 0.058 | 0.138 | 0.078 | |
| 10 | 0.102 | 0.071 | 0.071 | 0.073 | ||
| 20 | 0.129 | 0.059 | 0.048 | 0.114 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Wu, Z.; Cui, N.; Jin, X.; Zhu, S.; Jiang, S.; Zhao, L.; Gong, D. Estimation of Soil Moisture Using Multi-Source Remote Sensing and Machine Learning Algorithms in Farming Land of Northern China. Remote Sens. 2023, 15, 4214. https://doi.org/10.3390/rs15174214
Liu Q, Wu Z, Cui N, Jin X, Zhu S, Jiang S, Zhao L, Gong D. Estimation of Soil Moisture Using Multi-Source Remote Sensing and Machine Learning Algorithms in Farming Land of Northern China. Remote Sensing. 2023; 15(17):4214. https://doi.org/10.3390/rs15174214
Chicago/Turabian StyleLiu, Quanshan, Zongjun Wu, Ningbo Cui, Xiuliang Jin, Shidan Zhu, Shouzheng Jiang, Lu Zhao, and Daozhi Gong. 2023. "Estimation of Soil Moisture Using Multi-Source Remote Sensing and Machine Learning Algorithms in Farming Land of Northern China" Remote Sensing 15, no. 17: 4214. https://doi.org/10.3390/rs15174214
APA StyleLiu, Q., Wu, Z., Cui, N., Jin, X., Zhu, S., Jiang, S., Zhao, L., & Gong, D. (2023). Estimation of Soil Moisture Using Multi-Source Remote Sensing and Machine Learning Algorithms in Farming Land of Northern China. Remote Sensing, 15(17), 4214. https://doi.org/10.3390/rs15174214









