An Investigation on the Ionospheric Response to the Volcanic Explosion of Hunga Ha’apai, 2022, Based on the Observations from the Meridian Project: The Plasma Drift Variations
Abstract
1. Introduction
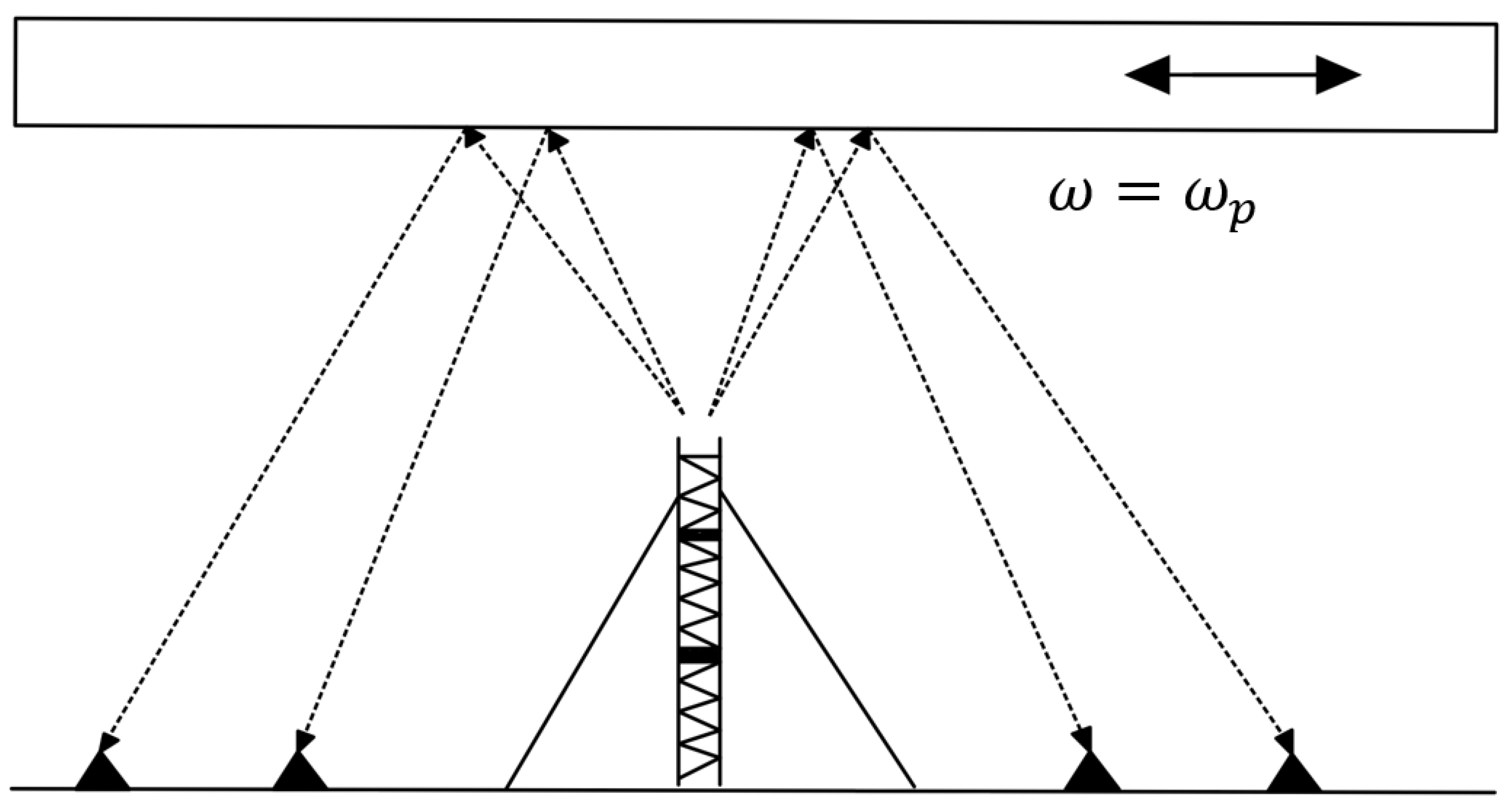
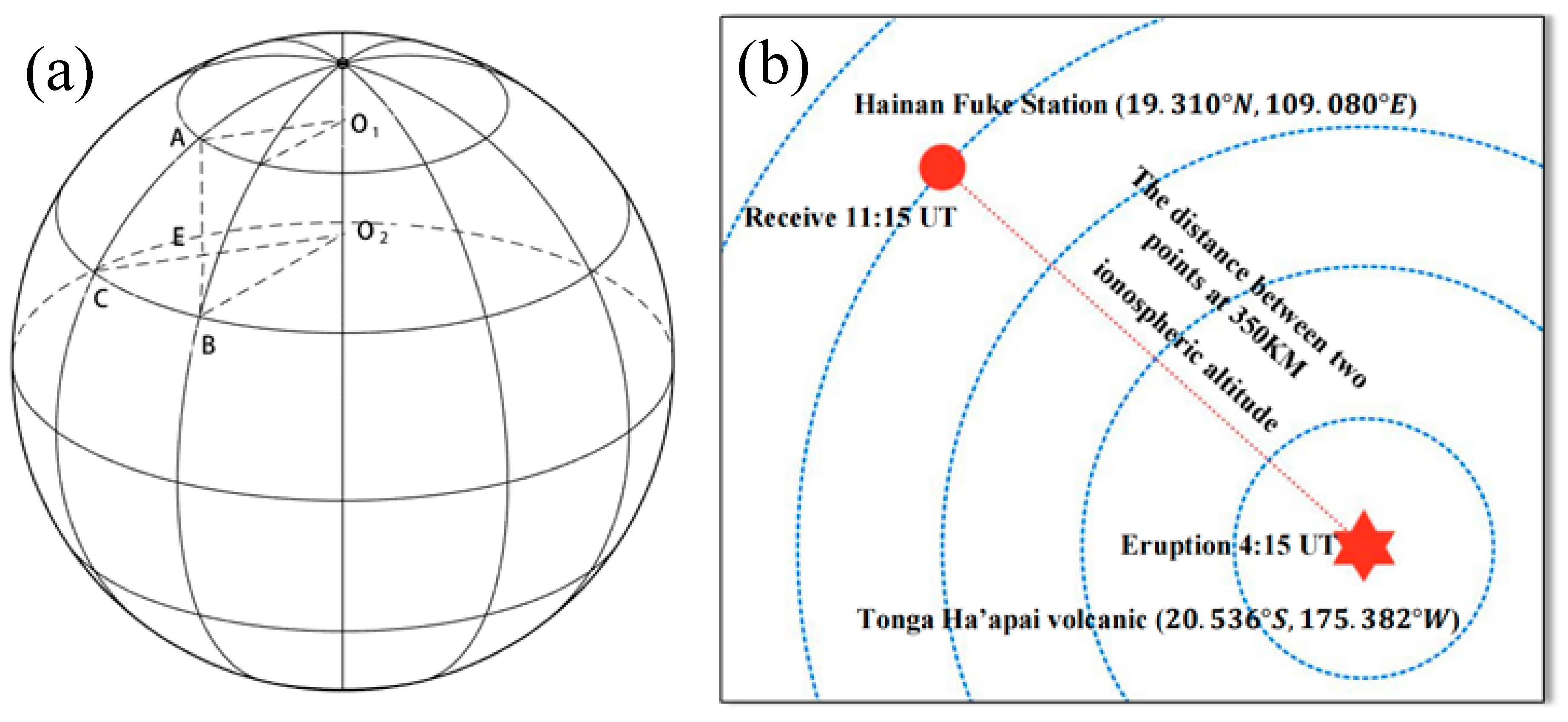
2. Materials and Methods
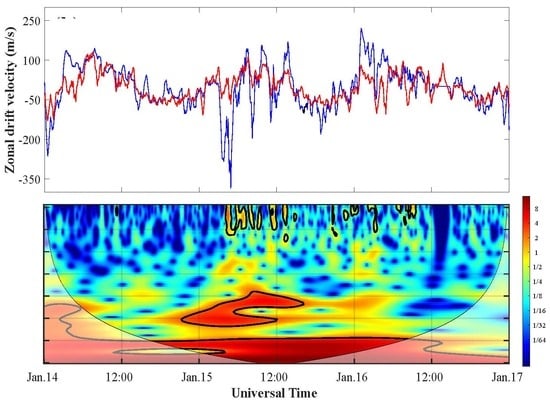
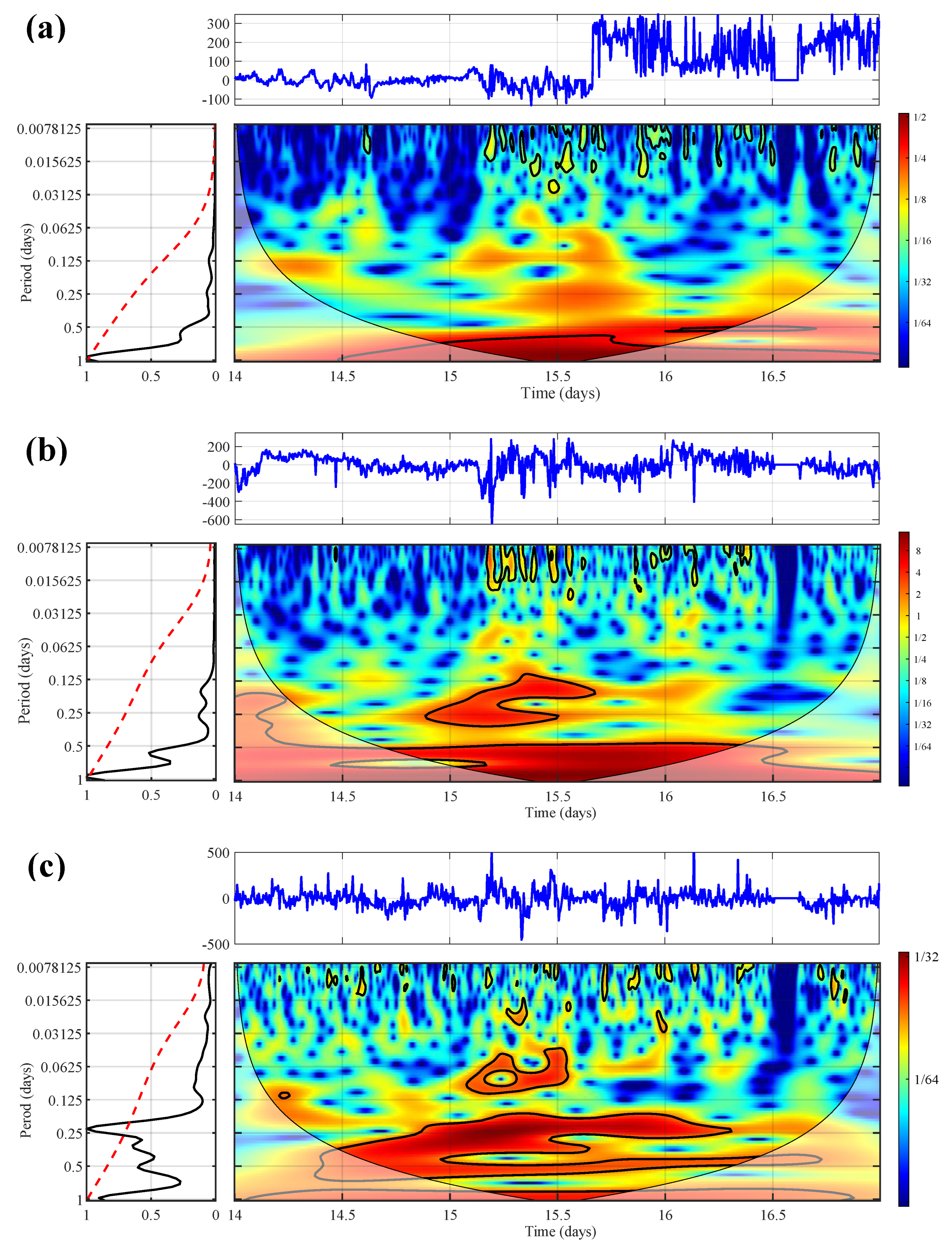
3. Observations and Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bittencourt, J.A. Fundamentals of Plasma Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; Volume 38. [Google Scholar]
- Lysak, R.L. Introduction to Space Physics. Eos Trans. Am. Geophys. Union 1995, 49, 57–58. [Google Scholar] [CrossRef]
- Zhang, R.L.; Liu, L.B.; Chen, Y.D.; Hui, J. The dawn enhancement of the equatorial ionospheric vertical plasma drift. J. Geophys. Res. Space Phys. 2015, 120, 10688–10697. [Google Scholar] [CrossRef]
- Kremeyer, K.; Nazarenko, S.; Newell, A. The role of vorticity in shock propagation through inhomogeneous media. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. [Google Scholar]
- Hong, Y.; Wang, G.J.; Shi, J.K.; Wang, X.; Cheng, W.Z.; Wang, Z.; Shang, S.P. Response of ionospheric plasma drift to geomagnetic activity at low latitudes (Hainan). J. Space Sci. 2019, 39, 8. [Google Scholar] [CrossRef]
- Chao-Song Huang, J.C.; Foster, J.; Holt, J. Westward plasma drift in the midlatitude ionospheric F region in the midnight-dawn sector. Pract. Stat. Med. Res. 2001, 106, 30349–30362. [Google Scholar]
- Liu, L.B.; Wan, W.X. Recent ionospheric investigations in China (2018–2019). Earth Planet. Phys. 2020, 4, 179–205. [Google Scholar] [CrossRef]
- Cai, J.T.; Zhao, G.Z.; Zhan, Y.; Tang, J.; Chen, X.B. Study of ionospheric disturbance phenomena during earthquakes. Prog. Geophys. 2007, 22, 695–701. [Google Scholar]
- Eccles, J.V.; Stmaurice, J.; Schunk, R.W. Reviewing the Mechanisms Underlying the Pre-reversal Enhancement of the Vertical Plasma Drift in the Low Latitude Ionosphere. AGU Fall Meet. Abstr. 2011, 120, 4950–4970. [Google Scholar]
- Farley, D.T.; Bonelli, E.; Fejer, B.G.; Larsen, M.F. The prereversal enhancement of the zonal electric field in the equatorial ionosphere. J. Geophys. Res. Atmos. 1986, 91, 13723–13728. [Google Scholar] [CrossRef]
- Navarro, L.A.; Fejer, B.G. Storm-time coupling of equatorial nighttime F-region neutral winds and plasma drifts. J. Geophys. Res. Space Phys. 2020, 125, 2169–9380. [Google Scholar] [CrossRef]
- Huang, C.-S.; de La Beaujardiere, O.; Pfaff, R.F.; Retterer, J.M.; Roddy, P.A.; Hunton, D.E.; Su, Y.-J.; Su, S.-Y.; Rich, F.J. Zonal drift of plasma particles inside equatorial plasma bubbles and its relation to the zonal drift of the bubble structure. J. Geophys. Res. Space Phys. 2010, 115, A7. [Google Scholar] [CrossRef]
- Fejer, B.G.; Olson, M.E.; Chau, J.L.; Stolle, C.; Lühr, H.; Goncharenko, L.P.; Yumoto, K.; Nagatsuma, T. Lunar-dependent equatorial ionospheric electrodynamic effects during sudden stratospheric warmings. J. Geophys. Res. Space Phys. 2010, 115, A00G03. [Google Scholar] [CrossRef]
- Li, J.Y. Study of Seismic Ionospheric TEC Anomalies Using GPS Data; Institute of Earthquake Prediction, China Earthquake Administration: Beijing, China, 2010.
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Muto, F.; Horie, T.; Maekawa, S.; Hobara, Y.; Rozhnoi, A.A.; Solovieva, M.; Molchanov, O.A. A statistical study on the correlation between lower ionospheric perturbations as seen by subionospheric VLF/LF propagation and earthquakes. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Bondur, V.G.; Tsidilina, M.N.; Gaponova, M.V. Verification of the concept of seismoionospheric coupling under quiet heliogeomagnetic conditions, using the Wenchuan (China) earthquake of May 12, 2008, as an example. Geomagn. Aeron. 2010, 50, 231–242. [Google Scholar] [CrossRef]
- Zhang, X.M.; Shen, X.H.; Zhao, S.F.; Liu, J.; Ouyang, X.Y.; Lou, W.Y. Research progress of seismic ionospheric sounding technology and its application. J. Seismol. 2016, 38, 20. [Google Scholar]
- Liu, J.Y.; Liu, L. A statistical analysis of ionospheric anomalies before 736 M6.0+ earthquakes during 2002–2010. J. Geophys. Res. 2011, 116, A02303. [Google Scholar] [CrossRef]
- Aoyama, T.; Iyemori, T.; Nakanishi, K.; Nishioka, M.; Rosales, D.; Veliz, O.; Safor, E.V. Localized field-aligned currents and 4-min TEC and ground magnetic oscillations during the 2015 eruption of Chile’s Calbuco volcano. Earth Planets Space 2016, 68, 148. [Google Scholar] [CrossRef]
- Cahyadi, M.N.; Handoko, E.Y.; Rahayu, R.W.; Heki, K. Comparison of volcanic explosions in Japan using impulsive ionospheric disturbances. Earth Planets Space 2021, 73, 228. [Google Scholar] [CrossRef]
- Cahyadi, M.N.; Rahayu, R.W.; Heki, K.; Nakashima, Y. Harmonic ionospheric oscillation by the 2010 eruption of the Merapi volcano, Indonesia, and the relevance of its amplitude to the mass eruption rate. J. Volcanol. Geotherm. Res. 2020, 405, 107047. [Google Scholar] [CrossRef]
- Heki, K.; Fujimoto, T. Atmospheric modes excited by the 2021 August eruption of the Fukutoku-Okanoba volcano, Izu–Bonin Arc, observed as harmonic TEC oscillations by QZSS. Earth Planets Space 2022, 74, 112. [Google Scholar] [CrossRef]
- Li, W.; Guo, J.; Yue, J.; Shen, Y.; Yang, Y. Total electron content anomalies associated with global VEI4 + volcanic eruptions during 2002–2015. J. Volcanol. Geotherm. Res. 2016, 325, 98–109. [Google Scholar] [CrossRef]
- Lin, J.W. Ionospheric Anomaly due to the volcanic eruption in Colima, Mexico, 06 January 2013: Two-Dimensional Principal Component Analysis. Eur. J. Remote Sens. 2017, 46, 689–698. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Q.; Shah, M.; Hong, Z. Atmospheric-ionospheric disturbances following the April 2015 Calbuco volcano from GPS and OMI observations. Adv. Space Res. 2017, 60, 2836–2846. [Google Scholar] [CrossRef]
- Maletckii, B.; Astafyeva, E. Near-Real-Time Analysis of the Ionospheric Response to the 15 January 2022 Hunga Tonga-Hunga Ha’apai Volcanic Eruption. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030735. [Google Scholar] [CrossRef]
- Manta, F.; Occhipinti, G.; Hill, E.M.; Perttu, A.; Assink, J.; Taisne, B. Correlation Between GNSS-TEC and Eruption Magnitude Supports the Use of Ionospheric Sensing to Complement Volcanic Hazard Assessment. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020726. [Google Scholar] [CrossRef]
- Pandara, D.P.; Muslim, B.; Sunardi, B.; Ferdy; Pasau, G.; Mananohas, M.; Ango, C. Analysis of Ionosphere disturbance caused by the Lokon Volcano Eruption using GPS TEC data. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1115, 012062. [Google Scholar] [CrossRef]
- Saito, S. Ionospheric disturbances observed over Japan following the eruption of Hunga Tonga-Hunga Ha’apai on 15 January 2022. Earth Planets Space 2022, 74, 57. [Google Scholar] [CrossRef]
- Toman, I.; Bri, D.; Kos, S. Contribution to the Research of the Effects of Etna Volcano Activity on the Features of the Ionospheric Total Electron Content Behaviour. Remote Sens. 2021, 13, 1006. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Vierinen, J.; Aa, E.; Goncharenko, L.P.; Erickson, P.J.; Rideout, W.; Coster, A.J.; Spicher, A. 2022 Tonga Volcanic Eruption Induced Global Propagation of Ionospheric Disturbances via Lamb Waves. Front. Astron. Space Sci. 2022, 9, 871275. [Google Scholar] [CrossRef]
- Gokhberg MB, G.; Gershenzon, N.I.; Pilipenko, V.A. Electromagnetic effects during rupture of the Earth’s Crust. Phys. Solid Earth 1985, 21, 52–63. [Google Scholar]
- Lockner, D.A.; Johnston, M.J.S.; Byerlee, J.D. A mechanism to explain the generation of earthquake lights. Nature 1983, 302, 28–33. [Google Scholar] [CrossRef]
- Parrot, M.; Benoist, D.; Berthelier, J.; Błęcki, J.; Chapuis, Y.; Colin, F.; Elie, F.; Fergeau, P.; Lagoutte, D.; Lefeuvre, F.; et al. The magnetic field experiment IMSC and its data processing onboard DEMETER: Scientific objectives, description and first results. Planet. Space Sci. 2006, 54, 441–455. [Google Scholar] [CrossRef]
- Parrot, M.; Berthelier, J.J.; Lebreton, J.P.; Sauvaud, J.A.; Santolik, O.; Blecki, J. Examples of unusual ionospheric observations made by the DEMETER satellite over seismic regions. Phys. Chem. Earth Parts A/B/C 2006, 31, 486–495. [Google Scholar] [CrossRef]
- Zhang, X.M.; Liu, J.; Qian, J.D.; Shen, X.H.; Zhao, S.F. Ionospheric electromagnetic disturbance before Gaize earthquake with MS 6.9 Tibet. Earthquake 2008, 28, 14–22. [Google Scholar]
- Poli, P.; Shapiro, N.M. Rapid Characterization of Large Volcanic Eruptions: Measuring the Impulse of the Hunga Tonga Ha’apai Explosion from Teleseismic Waves. Geophys. Res. Lett. 2022, 49, e2022GL098123. [Google Scholar] [CrossRef]
- Robin, S.; Matoza David, F.; Jelle, D.; Alexandra, M.; David, N.; Keehoon, K. Atmospheric waves and global seismoacoustic observations of the January 2022 Hunga eruption, Tonga. Science 2022, 377, 95–100. [Google Scholar]
- Amores, A.; Monserrat, S.; Marcos, M.; Argüeso, D.; Villalonga, J.; Jordà, G.; Gomis, D. Numerical Simulation of Atmospheric Lamb Waves Generated by the 2022 Hunga-Tonga Volcanic Eruption. Geophys. Res. Lett. 2022, 49, e2022GL098240. [Google Scholar] [CrossRef]
- Global Volcanism Program. Report on Hunga Tonga-Hunga Ha’apai (Tonga); Bennis, K.L., Venzke, E., Eds.; Bulletin of the Global Volcanism Network, 47:3; Smithsonian Institution: Washington, DC, USA, 2022. [Google Scholar] [CrossRef]
- IGS. About IGS. 2022. Available online: https://igs.org/about/ (accessed on 8 August 2023).
- INGV. La Grande Eruzione del Vulcano Hunga Tonga–Hunga Ha’apai. 2022. Available online: https://ingvvulcani.com/2022/01/17/grande-eruzione-vulcano-hunga-tonga-hunga-haapai/ (accessed on 8 August 2023).
- Kusky, T.M. Déjà vu: Might Future Eruptions of Hunga Tonga-Hunga Ha’apai Volcano be a Repeat of the Devastating Eruption of Santorini, Greece (1650 BC)? J. Earth Sci. 2022, 33, 229–235. [Google Scholar] [CrossRef]
- Lin, J.T.; Rajesh, P.K.; Lin CC, H.; Chou, M.Y.; Liu, J.Y.; Yue, J. Rapid Conjugate Appearance of the Giant Ionospheric Lamb Wave Signatures in the Northern Hemisphere After Hunga-Tonga Volcano Eruptions. Geophys. Res. Lett. 2022, 49, e2022GL098222. [Google Scholar] [CrossRef]
- NASA. Hunga Tonga-Hunga Ha‘apai Erupts. 2022. Available online: https://earthobservatory.nasa.gov/images/149347/hunga-tonga-hunga-haapai-erupts (accessed on 8 August 2023).
- NPR. NASA Scientists Estimate Tonga Blast at 10 Megatons. 2022. Available online: https://www.npr.org/2022/01/18/1073800454/nasa-scientists-estimate-tonga-blast-at-10-megatons (accessed on 8 August 2023).
- Tatsuya, K.; Tatsuhiko, S.; Kiwamu, N. Global fast-traveling tsunamis driven by atmospheric Lamb waves on the 2022 Tonga eruption. Science 2022, 377, 91–94. [Google Scholar]
- Wright, C.J.; Hindley, N.P.; Alexander, M.J.; Barlow, M.; Hoffmann, L.; Mitchell, C.N. Surface-to-space atmospheric waves from Hunga Tonga–Hunga Ha’apai eruption. Nature 2022, 609, 741–746. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Wang, W.; Wang, G.; Ruohoniemi, J.M.; Shinbori, A.; Nishitani, N.; Wang, C.; Deng, X.; Lan, A.; et al. Oscillations of the Ionosphere Caused by the 2022 Tonga Volcanic Eruption Observed with SuperDARN Radars. Geophys. Res. Lett. 2022, 49, e2022GL100555. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2022GL100555 (accessed on 8 August 2023). [CrossRef]
- Nagano, I.; Mambo, M.; Shimbo, T.; Kimura, I. Propagation characteristics in the earth-ionosphere waveguide for VLF waves emitted from trapping cones at high latitudes. Memoirs of National Institute of Polar Research. Spec. Issue 1987, 47, 183–191. [Google Scholar]
- Olwendo, J.; Cilliers, P.J.; Ming, O. Comparison of ground-based ionospheric scintillation observations with in situ electron density variations as measured by the Swarm satellites. Radio Sci. 2019, 54, 852–866. [Google Scholar] [CrossRef]
- Cheng, J.; Shi, J.K. Comparison of ionospheric detection methods. In Proceedings of the Twentieth Annual Meeting of the Chinese Geophysical Society, Xi’an, China, 16 October 2003. [Google Scholar]
- Wang, X.; Shi, J.K.; Wang, X. Ionospheric drift characteristics at low latitudes in China (Hainan). J. Radio Wave Sci. 2005, 20, 5. [Google Scholar]
- Astafyeva, E. Ionospheric detection of natural hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
- Kan, L.; Fang, Y.; Han, J.; Li, Y.; Yang, X. Design and validation of space-based GPS ionospheric sounding technology. In Proceedings of the China Satellite Navigation Academic Conference, Shanghai, China, 25 May 2017. [Google Scholar]
- Zhang, M.L.; Shi, J.K.; Wang, X.; Wu, S.Z.; Zhang, S.R. Comparative study of ionospheric characteristic parameters obtained by DPS-4 digisonde with IRI2000 for low latitude station in China. Adv. Space Res. 2004, 33, 869–873. [Google Scholar] [CrossRef]
- Wang, X. Study of Ionospheric Variability and Disturbance Characteristics in the Low-Latitude (Hainan) Region; Graduate School of Chinese Academy of Sciences (Center for Space Science and Applications Research): Beijing, China, 2004. [Google Scholar]
- Chapman, S. The absorption and dissociative or ionizing effect of monochromatic radiation in an atmosphere on a rotating earth. Proc. Phys. Soc. 1931, 43, 26–45. [Google Scholar] [CrossRef]
- Adam, D. Tonga Volcano Created Puzzling Atmospheric Ripples. Nature 2022, 602, 2022. [Google Scholar]
- Astafyeva, E.; Maletckii, B.; Mikesell, T.D.; Munaibari, E.; Ravanelli, M.; Coisson, P.; Manta, F.; Rolland, L. The 15 January 2022 Hunga Tonga Eruption History as Inferred from Ionospheric Observations. Geophys. Res. Lett. 2022, 49, e2022GL098827. [Google Scholar] [CrossRef]
- Lynett, P.; McCann, M.; Zhou, Z.; Renteria, W.; Borrero, J.; Greer, D.; Fa’anunu, O.; Bosserelle, C.; Jaffe, B.; La Selle, S.; et al. Diverse tsunamigenesis triggered by the Hunga Tonga-Hunga Ha’apai eruption. Nature 2022, 609, 728–733. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.B.; Le, H.J. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257–275. [Google Scholar] [CrossRef]
- Liang, B.; Li, J.; Ma, S. Progress of ionospheric research in China. Chin. J. Geophys. 1994, 37 (Suppl. S1), 51–73. [Google Scholar]
- Hong, Y.; Wang, G.J.; Shi, J.K.; Wang, Z.; Wang, X. Comparative Study of Ionospheric Drift at Hainan Station during Different Solar Activity Years; China Electronics Society, Member of the National Natural Science Foundation of China, Xi’an University of Electronic Science and Technology: Xi’an, China, 2017. [Google Scholar]
- Liu, L.B.; Lei, J.H.; Liu, J. Ionospheric Investigations Conducted by Chinese Mainland Scientists in 2020–2021. Chin. J. Space Sci. 2022, 42, 653–683. [Google Scholar] [CrossRef]
- Wan, W.X.; Nin, B.Q.; Yuan, H. Observation of ionospheric disturbances with GPS beacons. Chin. J. Space Sci. 1998, 18, 247–252. [Google Scholar]

| Date | Receive Time (UT) | Longitudinal Velocity (m/s) | Latitudinal Velocity (m/s) | Horizontal Velocity (m/s) | Vertical Velocity (m/s) | |
|---|---|---|---|---|---|---|
| 1 | 15 January 2022 | 16:02:02 | 52.64 | −138.75 | 148.40 | 290.90 |
| 2 | 15 January 2022 | 16:07:02 | −40.44 | −111.87 | 118.95 | 250.78 |
| 3 | 15 January 2022 | 16:12:02 | 81.54 | −130.52 | 153.90 | 302.49 |
| 4 | 15 January 2022 | 16:17:02 | 11.85 | −26.30 | 28.84 | 288.31 |
| 5 | 15 January 2022 | 16:22:02 | −46.08 | −92.49 | 103.33 | 242.83 |
| 6 | 15 January 2022 | 16:27:02 | 36.21 | −24.76 | 43.87 | 305.03 |
| 7 | 15 January 2022 | 16:32:02 | 31.45 | −119.53 | 123.60 | 284.41 |
| 8 | 15 January 2022 | 16:37:02 | 61.08 | −119.65 | 134.34 | 297.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Shi, M.; Wang, X.; Zhang, Z.; Soon, W.; Velasco Herrera, V.M. An Investigation on the Ionospheric Response to the Volcanic Explosion of Hunga Ha’apai, 2022, Based on the Observations from the Meridian Project: The Plasma Drift Variations. Remote Sens. 2023, 15, 4181. https://doi.org/10.3390/rs15174181
Qiu S, Shi M, Wang X, Zhang Z, Soon W, Velasco Herrera VM. An Investigation on the Ionospheric Response to the Volcanic Explosion of Hunga Ha’apai, 2022, Based on the Observations from the Meridian Project: The Plasma Drift Variations. Remote Sensing. 2023; 15(17):4181. https://doi.org/10.3390/rs15174181
Chicago/Turabian StyleQiu, Shican, Mengxi Shi, Xinye Wang, Zhanming Zhang, Willie Soon, and Victor Manuel Velasco Herrera. 2023. "An Investigation on the Ionospheric Response to the Volcanic Explosion of Hunga Ha’apai, 2022, Based on the Observations from the Meridian Project: The Plasma Drift Variations" Remote Sensing 15, no. 17: 4181. https://doi.org/10.3390/rs15174181
APA StyleQiu, S., Shi, M., Wang, X., Zhang, Z., Soon, W., & Velasco Herrera, V. M. (2023). An Investigation on the Ionospheric Response to the Volcanic Explosion of Hunga Ha’apai, 2022, Based on the Observations from the Meridian Project: The Plasma Drift Variations. Remote Sensing, 15(17), 4181. https://doi.org/10.3390/rs15174181