Influential Topographic Factor Identification of Soil Heavy Metals Using GeoDetector: The Effects of DEM Resolution and Pollution Sources
Abstract
:1. Introduction
2. Materials and Methods
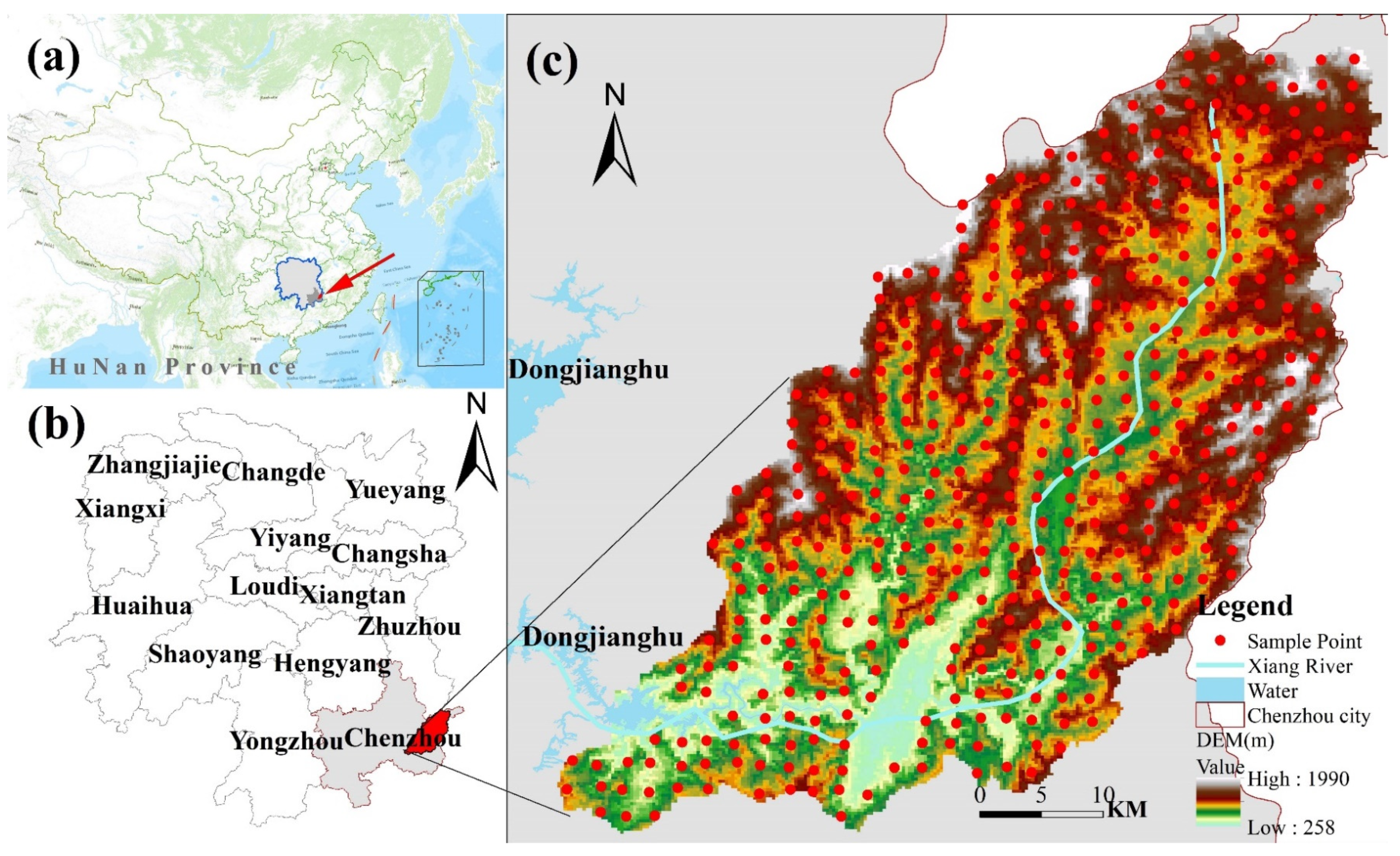
2.1. Study Area and Soil Sampling
2.2. Methods
2.2.1. DEM Gradient Generation
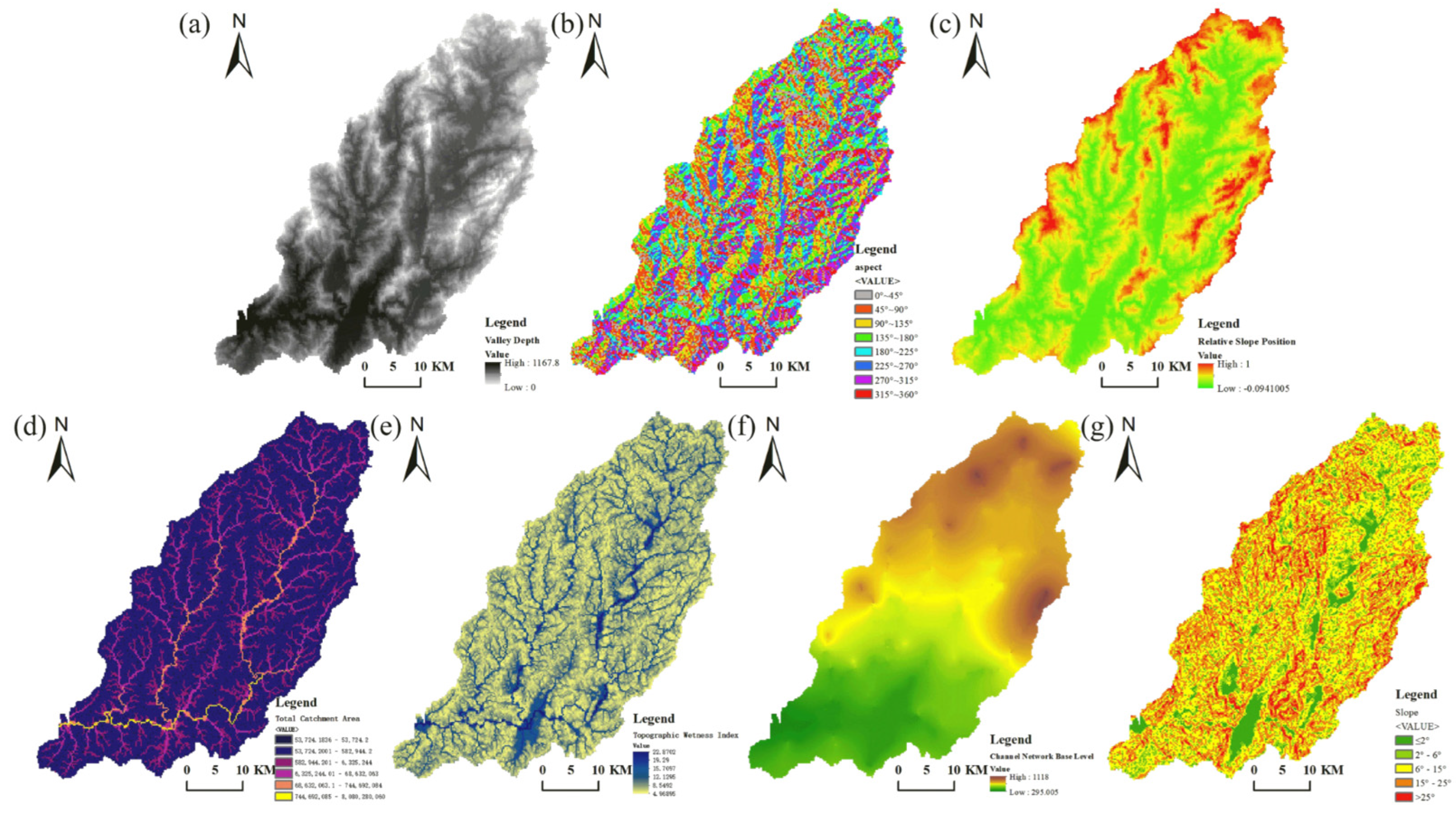
2.2.2. Topographic Factors
2.2.3. GeoDetector Model
- Factor detector:
- 2.
- Ecological detector:
- 3.
- Optimal Parameters-based Geographical Detector Model (OPGD)
2.2.4. Source Apportionment Model—Positive Matrix Factorization Model
3. Results and Discussion
3.1. Spatial Distribution Characteristics of HMs and Topographic Factor
3.1.1. Statistics of Soil HM Concentration
3.1.2. Topographic Factors at Different Resolutions
3.2. Explanatory Power of Topographic Factors at Different Resolutions Using GeoDetector
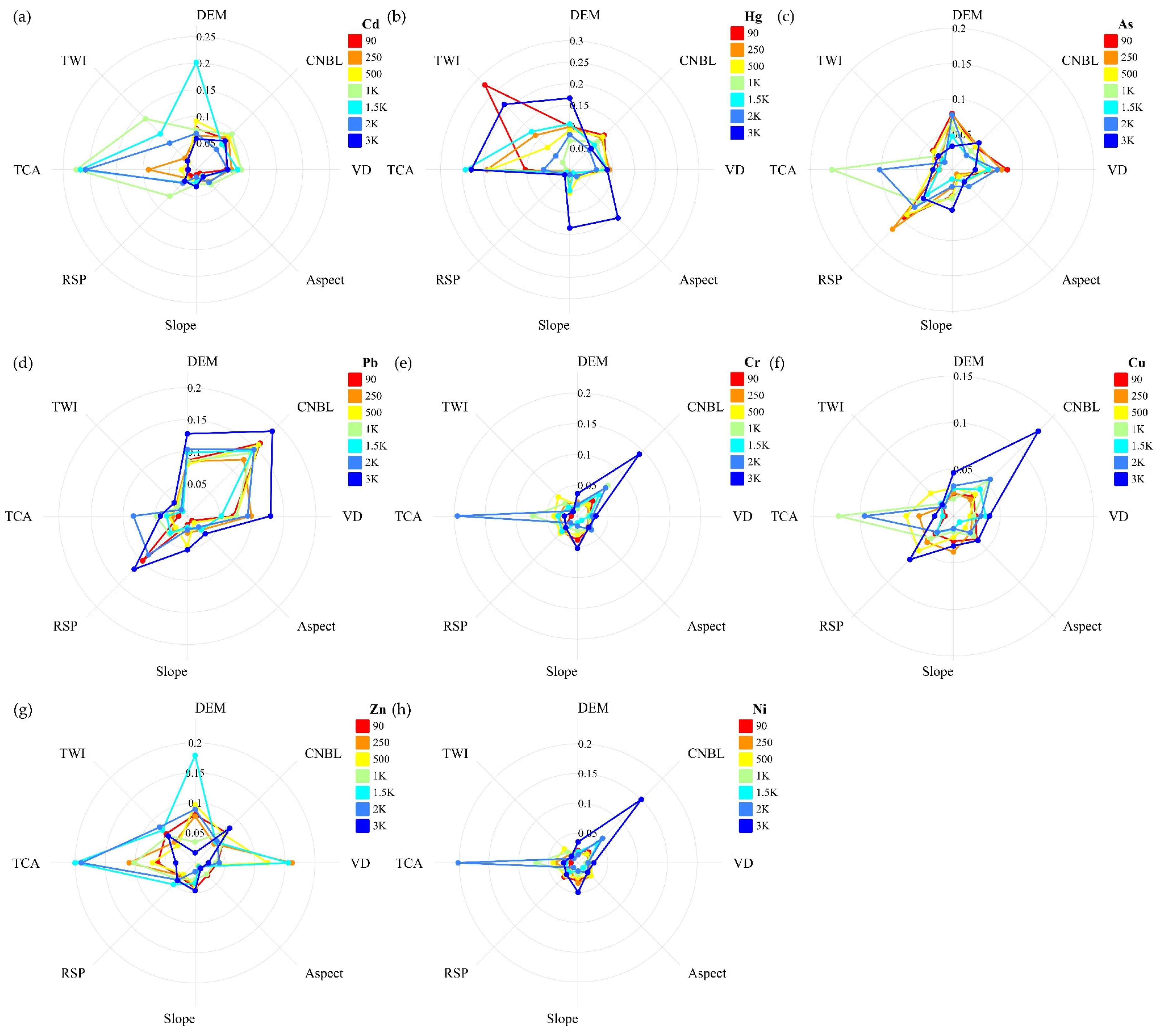
3.2.1. The Inconsistent q Results of Topographic Factors
3.2.2. Test of an Optimal Resolution for Each Topographic Factor
3.3. Possible Explanation for the Inconsistency of the Optimal Resolution
3.3.1. The Source Appointment of Soil HMs Using PMF
3.3.2. Different Sources (Processes) Lead to Inconsistent Optimal Resolution Results
- Strategy 1 is applicable to the scenario in which the dominant pollution source is well known, such as the Hg and As in this study. By jointly analyzing the physicochemical properties of Hg and As, and the corresponding sensitivity factors for the source and process, the possible OR of the factors can be effectively determined.
- Strategy 2 is for scenarios where the HM’s sources and corresponding processes are known but they are level-pegged. For example, Cr is the main HM in both S2 and S5 in this study, thus its OR performance is jointly composed of the preferences of all the sources it contains, and thus cannot be determined by the OR preferences of a single source alone. Strategy 2 is also applicable to scenarios where one specific TF differs in its representation of sources and processes at different spatial scales. Such an example can be found in the TWI for Hg in S1 and Pb in S3. A fine-scale TWI may be more conducive to highlighting flexible processes such as atmospheric deposition sources and accompanying soil transport, while large-scale TWI may be able to adequately characterize mineral dusts and their subsequent transport. In these cases, further comparison and evaluation at different resolutions should be conducted before GeoDetector analysis.
- Strategy 3 is mainly suitable for scenarios where pollution source analysis is not available, as was the case in most previous studies. We recommend trying at least several different resolutions to select the most explanatory resolutions possible.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- O’Connor, D.; Hou, D. More Haste, Less Speed in Replenishing China’s Groundwater. Nature 2019, 569, 487. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Chang, Q.; Liu, J.; Clevers, J.G.P.W.; Kooistra, L. Identification of Soil Heavy Metal Sources and Improvement in Spatial Mapping Based on Soil Spectral Information: A Case Study in Northwest China. Sci. Total Environ. 2016, 565, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Shao, S.; Ni, H.; Fu, Z.; Hu, L.; Zhou, Y.; Min, X.; She, S.; Chen, S.; Huang, M.; et al. Current Status, Spatial Features, Health Risks, and Potential Driving Factors of Soil Heavy Metal Pollution in China at Province Level. Environ. Pollut. 2020, 266, 114961. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.; Teng, Y.; Chen, H.; Wang, Y. A Partition Computing-Based Positive Matrix Factorization (PC-PMF) Approach for the Source Apportionment of Agricultural Soil Heavy Metal Contents and Associated Health Risks. J. Hazard. Mater. 2020, 388, 121766. [Google Scholar] [CrossRef] [PubMed]
- Xiang, M.; Li, Y.; Yang, J.; Lei, K.; Li, Y.; Li, F.; Zheng, D.; Fang, X.; Cao, Y. Heavy Metal Contamination Risk Assessment and Correlation Analysis of Heavy Metal Contents in Soil and Crops. Environ. Pollut. 2021, 278, 116911. [Google Scholar] [CrossRef]
- Khosravi, K.; Rezaie, F.; Cooper, J.R.; Kalantari, Z.; Abolfathi, S.; Hatamiafkoueieh, J. Soil Water Erosion Susceptibility Assessment Using Deep Learning Algorithms. J. Hydrol. 2023, 618, 129229. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, H.; Sun, J.; Tang, R.; Cai, B.; Song, X.; Huang, X.; Huang, J.; Fan, Z. Spatio-Temporal Characteristics of Soil Cd Pollution and Its Influencing Factors: A Geographically and Temporally Weighted Regression (GTWR) Method. J. Hazard. Mater. 2023, 446, 130613. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, L.; Lv, J. Spatial Assessment Models to Evaluate Human Health Risk Associated to Soil Potentially Toxic Elements. Environ. Pollut. 2021, 268, 115699. [Google Scholar] [CrossRef]
- Hudson-Edwards, K. Tackling Mine Wastes. Science 2016, 352, 288–290. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, X.; Teng, M.; Wu, F.; Meng, Y.; Wu, Y.; Byrne, P.; Abbaspour, K.C. Model-Based Evaluation of Reduction Strategies for Point and Nonpoint Source Cd Pollution in a Large River System. J. Hydrol. 2023, 622, 129701. [Google Scholar] [CrossRef]
- Thompson, J.A.; Bell, J.C.; Butler, C.A. Digital Elevation Model Resolution: Effects on Terrain Attribute Calculation and Quantitative Soil-Landscape Modeling. Geoderma 2001, 100, 67–89. [Google Scholar] [CrossRef]
- Fang, S.; Jia, X.; Qian, Q.; Cui, J.; Cagle, G.; Hou, A. Reclamation History and Development Intensity Determine Soil and Vegetation Characteristics on Developed Coasts. Sci. Total Environ. 2017, 586, 1263–1271. [Google Scholar] [CrossRef] [PubMed]
- Fei, X.; Christakos, G.; Xiao, R.; Ren, Z.; Liu, Y.; Lv, X. Improved Heavy Metal Mapping and Pollution Source Apportionment in Shanghai City Soils Using Auxiliary Information. Sci. Total Environ. 2019, 661, 168–177. [Google Scholar] [CrossRef] [PubMed]
- Lv, J. Multivariate Receptor Models and Robust Geostatistics to Estimate Source Apportionment of Heavy Metals in Soils. Environ. Pollut. 2019, 244, 72–83. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An Optimal Parameters-Based Geographical Detector Model Enhances Geographic Characteristics of Explanatory Variables for Spatial Heterogeneity Analysis: Cases with Different Types of Spatial Data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Huang, S.; Xiao, L.; Zhang, Y.; Wang, L.; Tang, L. Interactive Effects of Natural and Anthropogenic Factors on Heterogenetic Accumulations of Heavy Metals in Surface Soils through Geodetector Analysis. Sci. Total Environ. 2021, 789, 147937. [Google Scholar] [CrossRef]
- Qiao, P.; Yang, S.; Lei, M.; Chen, T.; Dong, N. Quantitative Analysis of the Factors Influencing Spatial Distribution of Soil Heavy Metals Based on Geographical Detector. Sci. Total Environ. 2019, 664, 392–413. [Google Scholar] [CrossRef]
- Shi, T.; Hu, Z.; Shi, Z.; Guo, L.; Chen, Y.; Li, Q.; Wu, G. Geo-Detection of Factors Controlling Spatial Patterns of Heavy Metals in Urban Topsoil Using Multi-Source Data. Sci. Total Environ. 2018, 643, 451–459. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, X.; Han, Z.; Tian, M.; Wang, Q.; Wu, H.; Liu, F. Geodetector Based Identification of Influencing Factors on Spatial Distribution Patterns of Heavy Metals in Soil: A Case in the Upper Reaches of the Yangtze River, China. Appl. Geochem. 2022, 146, 105459. [Google Scholar] [CrossRef]
- Liu, Z.; Fei, Y.; Shi, H.; Mo, L.; Qi, J. Prediction of High-Risk Areas of Soil Heavy Metal Pollution with Multiple Factors on a Large Scale in Industrial Agglomeration Areas. Sci. Total Environ. 2022, 808, 151874. [Google Scholar] [CrossRef]
- Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the Effects of Digital Elevation Model Resolution in Urban Fluvial Flood Modelling. J. Hydrol. 2021, 596, 126088. [Google Scholar] [CrossRef]
- Qiao, P.; Dong, N.; Lei, M.; Yang, S.; Gou, Y. An Effective Method for Determining the Optimal Sampling Scale Based on the Purposes of Soil Pollution Investigations and the Factors Influencing the Pollutants. J. Hazard. Mater. 2021, 418, 126296. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, R.; Seibert, J. Effects of DEM Resolution on the Calculation of Topographical Indices: TWI and Its Components. J. Hydrol. 2007, 347, 79–89. [Google Scholar] [CrossRef]
- Tang, G.; Zhao, M.; Li, T.; Liu, Y.; Xie, Y. Modeling Slope Uncertainty Derived from DEMs in Loess Plateau. Acta Geol. Sin. 2003, 58, 824–830. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of Errors of Derived Slope and Aspect Related to DEM Data Properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- López-Vicente, M.; Álvarez, S. Influence of DEM Resolution on Modelling Hydrological Connectivity in a Complex Agricultural Catchment with Woody Crops: Modelling Hydrological Connectivity in Woody Crops. Earth Surf. Process. Landf. 2018, 43, 1403–1415. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, H. Monitoring of Gully Erosion on the Loess Plateau of China Using a Global Positioning System. CATENA 2005, 63, 154–166. [Google Scholar] [CrossRef]
- Zhang, J.X.; Chang, K.; Wu, J.Q. Effects of DEM Resolution and Source on Soil Erosion Modelling: A Case Study Using the WEPP Model. Int. J. Geogr. Inf. Sci. 2008, 22, 925–942. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Jiménez-Hornero, F.J.; Gutiérrez De Ravé, E. Influence of DEM Resolution on Drainage Network Extraction: A Multifractal Analysis. Geomorphology 2015, 241, 243–254. [Google Scholar] [CrossRef]
- Saksena, S.; Merwade, V. Incorporating the Effect of DEM Resolution and Accuracy for Improved Flood Inundation Mapping. J. Hydrol. 2015, 530, 180–194. [Google Scholar] [CrossRef]
- Li, M.; Zhao, Y.; Gao, G.; Ding, G.; Yu, N. Effects of DEM Resolution on the Accuracy of Topographic Factor Derived from DEM. Sci. Soil Water Conserv. 2016, 14, 15–22. (In Chinese) [Google Scholar]
- Zhang, J.G.; Chen, H.S.; Su, Y.R.; Kong, X.L.; Zhang, W.; Shi, Y.; Liang, H.B.; Shen, G.M. Spatial Variability and Patterns of Surface Soil Moisture in a Field Plot of Karst Area in Southwest China. Plant Soil Environ. 2011, 57, 409–417. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, X.; Meng, Y.; Fei, Y.; Teng, M.; Song, F.; Wu, F. Identification Priority Source of Soil Heavy Metals Pollution Based on Source-Specific Ecological and Human Health Risk Analysis in a Typical Smelting and Mining Region of South China. Ecotoxicol. Environ. Saf. 2022, 242, 113864. [Google Scholar] [CrossRef] [PubMed]
- NASA. The Shuttle Radar Topography Mission (SRTM) Collection User Guide. Available online: https://lpdaac.usgs.gov/documents/179/SRTM_User_Guide_V3.pdf (accessed on 1 July 2023).
- Tian, Q.; Huhns, M.N. Algorithms for Subpixel Registration. Comput. Vis. Graph. Image Process. 1986, 35, 220–233. [Google Scholar] [CrossRef]
- Xu, F.; Dong, G.; Wang, Q.; Liu, L.; Yu, W.; Men, C.; Liu, R. Impacts of DEM Uncertainties on Critical Source Areas Identification for Non-Point Source Pollution Control Based on SWAT Model. J. Hydrol. 2016, 540, 355–367. [Google Scholar] [CrossRef]
- Schleiss, M. A New Discrete Multiplicative Random Cascade Model for Downscaling Intermittent Rainfall Fields. Hydrol. Earth Syst. Sci. 2020, 24, 3699–3723. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Guo, Z.; Adhikari, K.; Chellasamy, M.; Greve, M.B.; Owens, P.R.; Greve, M.H. Selection of Terrain Attributes and Its Scale Dependency on Soil Organic Carbon Prediction. Geoderma 2019, 340, 303–312. [Google Scholar] [CrossRef]
- Peckham, S.D. Profile, Plan and Streamline Curvature: A Simple Derivation and Applications. Proc. Geomorphometry 2011, 4, 27–30. [Google Scholar]
- Gruber, S.; Peckham, S. Chapter 7 Land-Surface Parameters and Objects in Hydrology. In Developments in Soil Science; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 171–194. ISBN 9780123743459. [Google Scholar]
- Kopecký, M.; Macek, M.; Wild, J. Topographic Wetness Index Calculation Guidelines Based on Measured Soil Moisture and Plant Species Composition. Sci. Total Environ. 2021, 757, 143785. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and Prospective. Acta Geogr. Sin. 2017, 72, 116–134. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A Measure of Spatial Stratified Heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Paatero, P.; Tapper, U. Positive Matrix Factorization: A Non-Negative Factor Model with Optimal Utilization of Error Estimates of Data Values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
- Brown, S.G.; Eberly, S.; Paatero, P.; Norris, G.A. Methods for Estimating Uncertainty in PMF Solutions: Examples with Ambient Air and Water Quality Data and Guidance on Reporting PMF Results. Sci. Total Environ. 2015, 518–519, 626–635. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Fu, B.; Wang, J.; Chen, L. Variability of the Soil Physical Properties on the Loess Plateau. Acta Geogr. Sin. 2002, 57, 587–594. (In Chinese) [Google Scholar]
- CNEMC (China National Environmental Monitoring Center). Soil Element Background Values in China; China Environmental Science Press: Beijing, China, 1990. [Google Scholar]
- Vázquez, R.F.; Feyen, J. Assessment of the Effects of DEM Gridding on the Predictions of Basin Runoff Using MIKE SHE and a Modelling Resolution of 600 m. J. Hydrol. 2007, 334, 73–87. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R. On the Effect of Digital Elevation Model Accuracy on Hydrology and Geomorphology. Water Resour. Res. 1999, 35, 2259–2268. [Google Scholar] [CrossRef]
- Wu, W.; Fan, Y.; Wang, Z.; Liu, H. Assessing Effects of Digital Elevation Model Resolutions on Soil–Landscape Correlations in a Hilly Area. Agric. Ecosyst. Environ. 2008, 126, 209–216. [Google Scholar] [CrossRef]
- Zhang, W.; Montgomery, D.R. Digital Elevation Model Grid Size, Landscape Representation, and Hydrologic Simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- The United Nations Environment Programme. Global Mercury Assessment. 2018. Available online: https://www.unep.org/resources/publication/global-mercury-assessment-2018 (accessed on 1 July 2023).
- Jiang, X.; Wang, F. Mercury Emissions in China: A General Review. Waste Dispos. Sustain. Energy 2019, 1, 127–132. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, Y.; Tian, H.; Gao, X.; Zhang, Y.; Wu, X.; Zhu, C.; Gao, J. Atmospheric Emission Characteristics and Control Policies of Five Precedent-Controlled Toxic Heavy Metals from Anthropogenic Sources in China. Environ. Sci. Technol. 2015, 49, 1206–1214. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Guo, S.; Wei, X.-X.; Cao, Y. The Effect of Atmosphere on Elemental Mercury Release During Thermal Treatment of Two Bituminous Coals. J. Braz. Chem. Soc. 2016, 27, 2210–2215. [Google Scholar] [CrossRef]
- Fang, G.-C.; Lin, Y.-H.; Chang, C.-Y.; Zheng, Y.-C. Concentrations of Particulates in Ambient Air, Gaseous Elementary Mercury (GEM), and Particulate-Bound Mercury (Hg(p)) at a Traffic Sampling Site: A Study of Dry Deposition in Daytime and Nighttime. Env. Geochem Health 2014, 36, 605–612. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Deng, L.; Guo, Y.; Guo, G.; Wang, L.; Zhou, G.; Huan, Y.; Liang, T. The Spatial Analysis, Risk Assessment and Source Identification for Mercury in a Typical Area with Multiple Pollution Sources in Southern China. Env. Geochem Health 2023, 45, 4057–4069. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Ma, J.; Zhang, Z.; Zhu, Y.; Hou, H.; Zhao, L.; Sun, Z.; Xue, W.; Shi, H. Linkage between Human Population and Trace Elements in Soils of the Pearl River Delta: Implications for Source Identification and Risk Assessment. Sci. Total Environ. 2018, 610–611, 944–950. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Xu, Z.; Ren, M.; Guo, Q.; Hu, X.; Hu, G.; Wan, H.; Peng, P. Source Identification of Eight Hazardous Heavy Metals in Agricultural Soils of Huizhou, Guangdong Province, China. Ecotoxicol. Environ. Saf. 2012, 78, 2–8. [Google Scholar] [CrossRef]
- Najmeddin, A.; Keshavarzi, B.; Moore, F.; Lahijanzadeh, A. Source Apportionment and Health Risk Assessment of Potentially Toxic Elements in Road Dust from Urban Industrial Areas of Ahvaz Megacity, Iran. Env. Geochem. Health 2018, 40, 1187–1208. [Google Scholar] [CrossRef]
- Dong, S.; Zhou, Y.; Liang, Z.; Zhou, T.; An, Y.; Gu, Y. Geochemical Characteristics and Its Geological Significance of the Qingshan Group Siliceous Rocks in Lingshan Island Shandong. Bull. Mineral. Petrol. Geochem. 2019, 8, 3623–3633. (In Chinese) [Google Scholar] [CrossRef]
- Xie, G.; Hu, R.; Fang, W.; Qi, L. Geochemical Characteristics of Cherts in Mojiang Gold Deposit. Acta Mineral. Sin. 2001, 1, 95–101. (In Chinese) [Google Scholar]
- Li, J.; Zhu, L.; Zhan, M.; Yang, Z.; Zhong, C. The Geochemical Distribution Characteristics and Source Analysis of Heavy Metals in the Typical Hilly Acidic Soil Region of South China. Acta Geol. Sin. 2016, 90, 1978–1987. (In Chinese) [Google Scholar]
- Xiao, X.; Chen, T.; Liao, X.; Wu, B.; Yan, X.; Zhai, L.; Xie, H.; Wang, L. Regional Distribution of Arsenic Contained Minerals and Arsenic Pollution in China. Geogr. Res. 2008, 27, 201–212. (In Chinese) [Google Scholar]
- Si, R.; Gu, X.; Xiao, C.; Yu, H.; Wang, Z.; Chen, Y.; Qiu, N. Geochemical Character of Trace Elements in Sphalerite from Fule Pb-Zn Deposit, Yunnan Provence. J. Mineral. Petrol. 2011, 31, 34–40. (In Chinese) [Google Scholar] [CrossRef]
- He, X.; Wang, Y.; Fang, Z.; Cui, X.; Zhang, S. Pollution Characteristics and Pollution Risk Evaluation of Heavy Metals in Soil of Lead-Zinc Mining Area. J. Environ. Eng. 2016, 6, 476–483. (In Chinese) [Google Scholar]
- Cao, G. Arsenic, the Claws of Ecological Life—Chenzhou City Arsenic Pollution War Never Stops, Chenzhou Environmental Protection Bureau. Environ. Econ. 2006, 9, 32–36. (In Chinese) [Google Scholar]
- Zhang, L.; Zhou, P.; Cao, S.; Zhao, Y. Atmospheric Mercury Deposition over the Land Surfaces and the Associated Uncertainties in Observations and Simulations: A Critical Review. Atmos. Chem. Phys. 2019, 19, 15587–15608. [Google Scholar] [CrossRef]
- Van Der Does, M.; Korte, L.F.; Munday, C.I.; Brummer, G.-J.A.; Stuut, J.-B.W. Particle Size Traces Modern Saharan Dust Transport and Deposition across The equatorial North Atlantic. Atmos. Chem. Phys. 2016, 16, 13697–13710. [Google Scholar] [CrossRef]






| Topographic Factors (Abbreviations) | Brief Description/Arithmetic | |
|---|---|---|
| Topographic undulation | Digital elevation model (DEM) | LiDAR-generated surface elevation. |
| Valley Depth (VD) | Valley depth [39] is defined as the relative height difference to the immediate adjacent channel lines: where CND stands for channel network depth. This compares elevation at a given cell to the highest ridge within its channel network [38]. | |
| Ground roughness | Aspect (Aspect) | The cardinal direction the prevailing slope faces [40]. |
| Relative Slope Position (RSP) | Relative slope position is defined as the position of one point relative to the ridge and valley of a slope, with a value of 0 for the bottom of the valley and 1 for the top of the ridge: where is the elevation, is the elevation of the valley, and is the elevation of the ridge [39]. | |
| Soil wetness | Total Catchment Area (TCA) | The total catchment area represents the cumulative upslope area that drains through the cell, and is calculated with the flow routing algorithm [41]. |
| Topographic Wetness Index (TWI) | Incorporation of slope, upstream drainage area (), and the length of a contour that is orthogonal to the flow from the cell (). It quantifies the topographic-driven variation in soil moisture [42]. Here, the gradient is either the slope of the focal cell or the slope between the focal cell and a cell further downslope. | |
| Other factor | Channel Network Base Level (CNBL) | The base level of the channel network is a grid in which the value of each cell is the distance to the channel network, either defined by overland flow or to its interpolated base level, which then might be used to estimate, e.g., the groundwater level [38,39]. In our study, CNBL was used to estimate the effect of groundwater level on soil wetness. |
| Slope (Slope) |
| Cd | Hg | As | Pb | Cr | Cu | Zn | Ni | |
|---|---|---|---|---|---|---|---|---|
| Mean | 0.21 | 0.16 | 19.14 | 39.92 | 63.13 | 27.58 | 77.91 | 23.39 |
| Min | 0.09 | 0.04 | 1.12 | 12.00 | 5.00 | 3.00 | 26.00 | 1.20 |
| Max | 1.53 | 3.87 | 308.27 | 141.00 | 308.00 | 90.00 | 278.00 | 131.40 |
| Median | 0.17 | 0.13 | 12.33 | 36.00 | 61.00 | 26.00 | 75.00 | 21.96 |
| Skewness | 5.07 | 11.59 | 5.16 | 1.50 | 1.19 | 1.01 | 2.08 | 1.66 |
| SDa | 0.14 | 0.22 | 25.24 | 15.37 | 32.92 | 13.98 | 23.22 | 13.29 |
| CVb | 0.66 | 1.35 | 1.32 | 0.39 | 0.52 | 0.51 | 0.30 | 0.57 |
| BVc | 0.13 | 0.12 | 15.70 | 29.70 | 71.40 | 27.30 | 94.40 | 31.90 |
| Aspect | CNBL | DEM | RSP | Slope | TWI | TCA | VD | |
|---|---|---|---|---|---|---|---|---|
| Cd | 1K | 1K/250/500 | 1.5K | NS a | 3K | 1K | 1K/1.5K/2K | 1K/500/1.5K |
| Hg | 3K | 90/250/500 | 3K | NS | 3K | 90 | 1.5K/3K | 250/90/500/1.5K/3K |
| As | 2K | 3K/250 | 90/250/2K | 250 | 3K | 90/500 | 1K | 90/250 |
| Pb | 3K | 3K | 3K | 3K | NS | NS | 2K | 3K |
| Zn | 90 | 3K | 1.5K | NS | 3K | 1.5K | 1.5K/2K | 250/1.5K |
| Cr | 2K/90/1K | 3K | 3K | NS | 250 | 500 | 2K | 3K |
| Cu | 3K/90 | 3K | 3K | 3K | 250 | 500 | 1K | 1.5K |
| Ni | 250 | 3K | 3K | 90 | 3K | 500 | 2K | 3K |
| Aspect | CNBL | DEM | RSP | Slope | TWI | TCA | VD | |
|---|---|---|---|---|---|---|---|---|
| S1 | 3K* | 90*/250*/500* | 3K* | 3K*/2K* | 3K* | 90* | 1.5K*/3K* | 250*/90*/500*/1.5K*/3K* |
| S2 | 2K*/250* | 3K* | 3K* | 500 | 3K* | 500*/1K* | 2K* | 3K* |
| S3 | 3K* | 3K* | 3K* | 3K* | 3K*/500 | 500/250 | 2K* | 3K* |
| S4 | 2K* | 250*/90*/500*/3K* | 90*/250* | 250* | 3K* | 500* | 1K* | 90*/250* |
| S5 | 2K*/3K | 3K* | 1.5K*/500* | 1K/3K* | 3K* | 1K* | 1K* | 500*/1K*/1.5K*/3K* |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhou, L.; Meng, Y.; Lin, Q.; Fei, Y. Influential Topographic Factor Identification of Soil Heavy Metals Using GeoDetector: The Effects of DEM Resolution and Pollution Sources. Remote Sens. 2023, 15, 4067. https://doi.org/10.3390/rs15164067
Wu Y, Zhou L, Meng Y, Lin Q, Fei Y. Influential Topographic Factor Identification of Soil Heavy Metals Using GeoDetector: The Effects of DEM Resolution and Pollution Sources. Remote Sensing. 2023; 15(16):4067. https://doi.org/10.3390/rs15164067
Chicago/Turabian StyleWu, Yating, Lingfeng Zhou, Yaobin Meng, Qigen Lin, and Yang Fei. 2023. "Influential Topographic Factor Identification of Soil Heavy Metals Using GeoDetector: The Effects of DEM Resolution and Pollution Sources" Remote Sensing 15, no. 16: 4067. https://doi.org/10.3390/rs15164067
APA StyleWu, Y., Zhou, L., Meng, Y., Lin, Q., & Fei, Y. (2023). Influential Topographic Factor Identification of Soil Heavy Metals Using GeoDetector: The Effects of DEM Resolution and Pollution Sources. Remote Sensing, 15(16), 4067. https://doi.org/10.3390/rs15164067









