Abstract
Marine heatwaves (MHWs) are extreme events characterized by abnormally high sea surface temperatures, and they have significant impacts on marine ecosystems and human society. The rapid and accurate forecasting of MHWs is crucial for preventing and responding to the impacts they can lead to. However, the research on relevant forecasting methods is limited, and a dedicated forecasting system specifically tailored for the South China Sea (SCS) region has yet to be reported. This study proposes a novel forecasting system utilizing U-Net and ConvLSTM models to predict MHWs in the SCS. Specifically, the U-Net model is used to forecast the intensity of MHWs, while the ConvLSTM model is employed to predict the probability of their occurrence. The indication of an MHW relies on both the intensity forecasted by the U-Net model exceeding threshold T and the occurrence probability predicted by the ConvLSTM model surpassing threshold P. Incorporating sensitivity analysis, optimal thresholds for T are determined as 0.9 °C, 0.8 °C, 1.0 °C, and 1.0 °C for 1-, 3-, 5-, and 7-day forecast lead times, respectively. Similarly, optimal thresholds for P are identified as 0.29, 0.30, 0.20, and 0.28. Employing these thresholds yields the highest forecast accuracy rates of 0.92, 0.89, 0.88, and 0.87 for the corresponding forecast lead times. This innovative approach gives better predictions of MHWs in the SCS, providing invaluable reference information for marine management authorities to make well-informed decisions and issue timely MHW warnings.
1. Introduction
Marine heatwaves (MHWs) are characterized as extended periods of exceptionally high sea surface temperatures (SSTs) lasting for a minimum of five consecutive days [,,]. The intensification and frequency of MHWs are gradually increasing due to global climate warming. In the past two decades, the occurrence probability of impactful MHWs has escalated more than 20-fold in terms of their duration, intensity, and cumulative intensity [].
Research indicates that marine organisms and ecosystems are highly vulnerable to MHWs, making them a potent disruptive force capable of reshaping entire ecosystems [,,,,,]. For instance, MHWs can decrease chlorophyll concentrations in tropical and mid-latitude regions while increasing them in high-latitude areas, thereby influencing marine primary productivity []. In the aftermath of MHWs in 2010/11, 36% of seagrass meadows in Shark Bay experienced damage []. Unprecedented MHWs in the North Pacific Ocean from 2014 to 2016 triggered significant changes in the Gulf of Alaska ecosystem, resulting in a 71% decline in Pacific cod abundance compared to the previous period []. MHWs also have the potential to affect phytoplankton species composition, resulting in increased mortality among higher trophic-level organisms, such as marine mammals and seabirds []. In 2016, MHWs significantly impacted the surface picoplankton community and facilitated the proliferation of potentially pathogenic bacteria in the Great Barrier Reef []. Moreover, MHWs have been identified as a potential cause for large-scale coral bleaching events in the South China Sea (SCS), particularly near Weizhou Island []. It is evident that MHWs have emerged as severe oceanic disasters capable of reshaping marine ecosystems.
The ocean is a complex system that encompasses numerous dynamic and thermodynamic processes []. Thus, the occurrence and intensity of MHWs are influenced by multiple driving factors []. For instance, subtropical extreme MHWs are frequently initiated by persistent high-pressure systems and anomalously weak wind speeds []. Moreover, certain regions may experience the occurrence of MHWs induced by more intricate local processes []. The SCS is one of the largest semi-enclosed marginal seas globally, spanning approximately 3.5 million square kilometers. It is renowned for its complex and diverse dynamical environment [,,,,,,,]. Recent research indicates that the SCS is a hotspot for MHWs []. These MHWs have already inflicted significant impacts on marine ecosystems, such as coral reefs [], undermining the establishment of marine pastures in this region [].
MHWs in the SCS are predominantly concentrated in the Nansha Islands and the Beibu Gulf region. The weakening of coastal upwelling is identified as a crucial factor that triggers summer MHWs in the SCS []. Additionally, the occurrence of MHWs in the SCS is strongly influenced by El Niño-Southern Oscillation events []. Moreover, on the northern continental shelf of the SCS, the net heat flux at the sea surface is recognized as another significant factor that initiates MHWs []. A study utilizing data from OISSTV2 and five selected models from CMIP6 revealed significantly increasing trends in various MHW characteristics in the SCS, including duration, annual cumulative duration, mean intensity, and maximum intensity [].
Given the severe damage caused by MHWs to marine ecosystems, accurate prediction of MHWs plays a crucial role in enabling marine stakeholders to mitigate the negative impacts of these events [,]. Traditional numerical-modeling-based forecasting is an important approach for predicting MHWs as well as studying other disaster processes [,]. Jacox et al. [] use an ensemble output from a global climate prediction system to examine the relationship between the skill of MHW predictions and the underlying mechanisms of MHW evolution in the California Current System from 2014 to 2016. They find that the predictability of different types or aspects of MHWs varies depending on the driving mechanisms involved. Benthuysen et al. [] assess the Australian Community Climate and Earth System Simulator Seasonal Version 1, a traditional forecasting tool, to evaluate its ability to capture the severity, duration, and spatial extent of MHWs. They emphasize the importance of assessing daily to weekly predictions of extreme ocean temperatures at sub-seasonal time scales as a crucial step in developing operational forecast products for extreme MHWs.
However, numerical model-based forecasts encounter several challenges, such as: (1) Complex model architectures requiring extensive preparation of input data (wind speed, longwave radiation, shortwave radiation, atmospheric pressure, sensible heat flux, latent heat flux, oceanic flow fields, marine topography, etc.). (2) The effectiveness of model predictions relies on the selection of various parameterization schemes, making them difficult to optimize. (3) The computational demands of model calculations are substantial, especially as model resolutions increase. This leads to extended computation times, which can hinder the delivery of timely and efficient MHW forecasts. (4) Poor model portability is observed due to the reliance of numerical models on seafloor topography data specific to the simulated area. Models designed for a particular region often struggle to be directly applied to other regions.
Conversely, the development of artificial intelligence (AI) technology has introduced new approaches to address these issues. Firstly, AI models yield forecasts without necessitating intricate input data, simplifying the model execution process. Secondly, many parameters in AI models training can be automatically optimized, reducing the need for subjective expertise. Thirdly, one of the most notable advantages of AI models is their rapid computational efficiency, which enables the timely provision of forecasts. Lastly, AI models could operate independently of seafloor topography data, facilitating seamless model adaptation across diverse regions. In fact, AI technology has been employed in various studies related to many marine phenomena [,,,,,,,], including wave height prediction [,,,,], chlorophyll concentration forecasting [], intelligent urban green space detection [], cloud detection in high-brightness scenes [], automatic modulation classification [], and the prediction of MHWs [].
As stated by Giamalaki et al. [], they are able to forecast MHWs in the Northeast Pacific Ocean with a 7-day lead time utilizing a random forest model grounded in atmospheric and oceanic conditions. Their developed model achieved an average accuracy of 76% in predicting the presence or absence of MHWs. However, when it comes to predicting the intensity of MHWs, the accuracy of the forecasts dropped to 38%. This indicates that while the model performs reasonably well in identifying the occurrence of MHWs, it encounters greater difficulties in accurately gauging their intensity. Additionally, their random forest model incorporates various features beyond time (a specific day of the year) and spatial information (longitude–latitude). These features encompass sea surface pressure, net heat flux, SSTs, and wind speed anomalies. The inclusion of numerous input variables not only complicates model training and extends the requisite training time but also undoubtedly reduces efficiency in MHW forecasting. To tackle this challenge, this study aims to predict MHWs using a minimal set of training variables, focusing solely on sea surface temperature anomaly (SSTA) data.
In summary, past research has highlighted the potential of employing AI methods for forecasting marine phenomena. Given the projected increase in the intensity, frequency, and duration of MHWs in the future, coupled with their escalating impact on marine ecosystems, particularly in the coral-rich SCS, there exists an urgent necessity for a dedicated prediction system. To the best of the author’s knowledge, such a system has not yet been established for this specific area. Thus, the establishment of a specialized MHW prediction system for the SCS becomes imperative. In this study, we propose the division of MHW prediction into intensity and probability forecasts, forming a comprehensive prediction system. The core objective of this system is to provide essential predictions to marine fisheries management authorities, facilitating the mitigation of MHW-related impacts. Furthermore, this prediction system has the potential to make substantial contributions to the preservation of marine biodiversity and the enhancement of local aquaculture endeavors.
The article is structured into the following sections. The Section 2 introduces the utilized data and outlines methodologies employed in constructing the MHWs forecasting system. The Section 3 is dedicated to evaluating the U-Net method’s efficacy in predicting MHW intensity, focusing on specific cases across various days. Additionally, the performance of MHW probability forecasting using the ConvLSTM method is assessed. Subsequently, the article evaluates the comprehensive prediction performance of the proposed forecasting system. The Section 4 discusses the challenges encountered during the model training and proposes potential solutions. This section also highlights areas that require improvement for future intelligent MHW forecasting. The conclusive insights are presented in the Section 5 of the article.
2. Materials and Methods
2.1. OISSTV2.1
This study utilizes the Optimum Interpolation Sea Surface Temperature version 2.1 (OISSTV2.1) dataset, derived from Advanced Very High-Resolution Radiometer infrared satellite data provided by the National Oceanic and Atmospheric Administration (NOAA), for the detection of MHWs [,,,,]. The OISSTV2.1 dataset is an optimally interpolated product that combines data from satellites, ships, buoys, and Argo floats. Biases between satellite and in situ observations are corrected, and data gaps are filled using interpolation methods to ensure accuracy []. The dataset has a spatial resolution of 0.25° and a daily temporal resolution. The OISST product, including versions V2.0 and V2.1, has been widely used in the analysis and research of MHWs in various ocean regions, such as the Tasman Sea [,], the SCS [], the tropical Indian Ocean [], the marginal seas of China [], the Northwest Pacific Ocean [], and global oceans [,,,,,].
It is evident that the OISSTV2.1 dataset is advantageous for this study due to its: (1) Data Quality and Accuracy: NOAA-provided data with validated SSTs from diverse sources ensure high accuracy. (2) Temporal Range and Global Coverage: Encompassing September 1981 to the present, it offers global coverage, enabling comprehensive analysis. (3) Data Consistency: Uniform temporal and spatial resolutions facilitate streamlined data analysis. (4) Data Accessibility and Openness: Freely accessible through NOAA, reducing data-related burdens and promoting replication of findings. To ensure that both the training and validation datasets consist of complete annual data, the analysis in this study covers the period from 1 January 1982, to 31 December 2021. The selected analysis region spans from 105.125°E to 124.125°E longitude and 0.125°N to 24.875°N latitude, which covers the entire SCS region. The detected MHW data from 1982 to 2019 are used to create the training dataset for the model, while the data from 2020 to 2021 are utilized to construct the validation dataset.
2.2. Definition of Marine Heatwave
In this study, we adhere to the same definition for MHWs and their intensity as outlined by Hobday et al. []. Specifically, an MHW event is defined as a period of at least five consecutive days during which the sea surface temperature (SST) surpasses a specific threshold. The difference between satellite-observed SST and climatological mean temperature is taken as the intensity of MHWs. Simply, the determination of MHWs involves the following three steps.
Step 1: Select the time duration of the climatological baseline period. In this study, the period from 1982 to 2021, spanning 40 years, is chosen as the climatological baseline period.
Step 2: Calculate the 90th percentile and mean value of SSTs at any grid point during the climatological baseline period. For each day of the year, a window spanning 11 days, including 5 days before and after the given day, is considered. Within this window, SST data for each year are extracted and arranged in ascending order. The 90th percentile value and the mean value of all data are calculated. Once the threshold and mean values for each day throughout the year are obtained, a 31-day moving average is applied to each of them, resulting in the final threshold and climatological mean values. This methodology ensures an adequate sample size for accurate calculations, allowing the derived climate state and threshold to effectively capture the multi-year average, upper limit characteristics, and seasonal variations of SST in the region.
Step 3: Compare the satellite-observed data with the climatological baseline and define an MHW event if the SST remains above the baseline for five consecutive days. Consecutive events within a maximum interval of one day are considered part of the same event.
2.3. Construction of the South China Sea Marine Heatwave Forecasting System
The overall structure of the MHW forecasting system is shown in Figure 1, which comprises three components: the intensity forecast module (Figure 1a), the probability forecast module (Figure 1b), and the decision module (Figure 1c). The intensity forecast module is based on the U-Net architecture, a deep convolutional neural network structure proposed by Ronneberger et al. []. It consists of two main components: a contracting path and a symmetric expanding path. The role of the contracting path is to extract features from the input and progressively reduce the size of the feature maps, a process known as down-sampling. This contracting path effectively enlarges the model’s receptive field, enabling the extraction of potential teleconnections. With each step, the number of channels in the feature maps is doubled to enhance the feature capture across various scales. To align with the original image, the expanding path utilizes up-sampling operations to restore the feature maps. Additionally, this path incorporates skip connections to blend local and global features, empowering the network to simultaneously utilize features from different scales. This approach significantly bolsters forecast accuracy. The U-Net model is effective for semantic segmentation, dividing images based on content. Our goal is to segment SSTA images into MHW intensity regions. The U-Net captures patterns and classifies pixels well. The U-Net’s deep architecture and skip connections handle complex intensity variations. It aligns with our research for predicting MHW in the SCS.
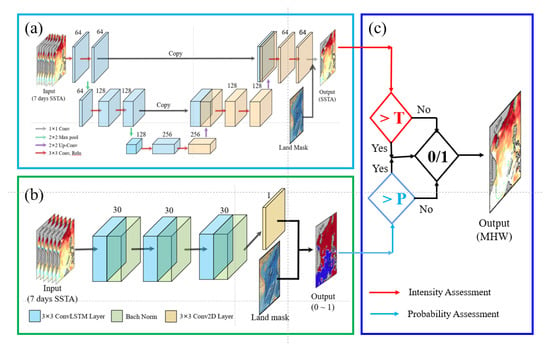
Figure 1.
Schematic diagram of the algorithm flow for the marine heatwave forecasting system: (a) illustrates the prediction of sea surface temperature anomalies using the U-Net; (b) depicts the forecast of marine heatwave occurrence probability using the ConvLSTM; (c) demonstrates the final determination and prediction of marine heatwaves based on the previous two forecasts.
The contracting path is constructed through iterative application of two sets of 3 by 3 convolutions, succeeded by a Leaky ReLU activation, followed by down-sampling facilitated by a 2 by 2 max pooling with a stride of 2. In the symmetric expanding path, each stage encompasses an up-sampling of the feature map, followed by a 2 by 2 convolution and two consecutive 3 by 3 convolutions, each accompanied by a Leaky ReLU activation. The output layer incorporates a 1 × 1 convolution followed by a linear operation. Within the intensity forecast module, the single-step forecast mode is adopted. This mode employs sea surface temperature anomaly (SSTA) data as both input and output data. The SSTA indicates the disparity between observed SST and the threshold temperature, which is calculated based on climatological data spanning from 1982 to 2021 (the detailed calculation method is referenced in Section 2.2). To define the input tensor, we designate it as , with dimensions of . The output tensor is defined as , with dimensions of 100 by 80. Here, “” represents the duration of input data, and “step” denotes the lead time. The numbers 100 and 80 represent the number of grids in latitude and longitude directions, respectively.
The probability forecast module relies on the ConvLSTM, an advanced model that extends LSTM capabilities to retain spatial information while processing sequential data. In our research, we aim to predict the probability of MHW occurrences by forecasting the likelihood of MHW events within a specific time frame using SSTA sequences. The ConvLSTM’s spatial-temporal modeling capacity suits this probability prediction task well, as it effectively captures spatial features from SSTA images while retaining the chronological sequence information. The ConvLSTM algorithm was initially introduced by Shi et al. [] and is applied to precipitation forecasting, showcasing its superior ability to capture spatiotemporal correlations. Subsequently, Zhou et al. [] and Han et al. [], respectively applied the ConvLSTM model to forecast two-dimensional wave heights in the South and East China Seas, as well as effective wave heights in the SCS region, respectively. These applications validated the ConvLSTM algorithm’s effectiveness in predicting time-series-related phenomena.
In the ConvLSTM architecture, both the input and output data are represented as 3D tensors, incorporating the dimensions of time, width (longitude), and height (latitude). This design empowers ConvLSTM to directly handle data with spatiotemporal variations. The pivotal innovation of ConvLSTM is the substitution of traditional LSTM’s fully connected layer operations with convolutional operations. The architecture comprises three ConvLSTM layers, with the concluding layer being a Conv2D layer. To amplify the model’s forecasting performance and tackle gradient vanishing challenges, Batch Normalization is integrated between the ConvLSTM layers. Each layer incorporates 30 filters and employs a kernel size of 3 by 3. The activation function applied in each layer is Leaky ReLU, introducing non-linearity into the model. Similar to the intensity forecast module, the input data for this module are also based on SSTA. However, we adopt a labeled dataset that distinguishes locations where MHWs occur (labeled as 1) from those where MHWs do not occur (labeled as 0).
In both above two modules, this study uses the past 7 days of data as input. Sensitivity experiments reveal that the model achieves optimal forecasting performance with a 7-day input data, striking a balance between retaining sufficient historical information and minimizing computational overhead. The system is designed to predict the intensity and probability of MHW occurrence for 1-, 3-, 5-, and 7-day in the future. The objective function in the U-Net and ConvLSTM is mean square error (MSE), which measures the difference between the predicted and actual probability values. Before calculating the MSE at each step, the predicted value on land needs to be set to 0, which could avoid the missing value affecting the weight update.
It is worth noting that both the U-Net and ConvLSTM models are trained using the early stopping mechanism to prevent overfitting, with a patience value set to 30. The model combines the results of the intensity forecast and probability forecast (Figure 1c). It determines the occurrence of an MHW only when both the intensity and probability forecasts meet the set threshold values. Moreover, to optimize GPU memory usage, the model adopts a single-step prediction strategy instead of using a sequence-to-sequence prediction form.
2.4. Evaluation Parameters for Marine Heatwave Forecasting
The subsequent parameters are utilized to assess the forecasting performance of the model on MHWs.
- (1)
- Forecast bias (FB):
Here, N signifies the overall count of predictions generated by the model using the validation set (722 times for a lead time of 7 days). Furthermore, and denote the grid point indices for the longitude and latitude of the SCS, respectively. represents the forecasted SSTA at spatial point in the kth forecast instance. represents the observed SSTA derived from OISSTV2.1 at the corresponding position. FB measures the difference between the forecasted MHWs intensity and the observed values.
- (2)
- Mean absolute forecast bias (MAFB):
The symbols and expressions employed here mirror those in Equation (1). The MAFB provides a direct measure of the difference between the forecasted results and the observed values. By negating the impact of positive and negative biases, this measure renders the evaluation outcomes more objective and conducive to comparison.
- (3)
- Root Mean Square Error (RMSE):
RMSE calculates the square root of the average squared forecast biases. It amplifies larger biases, making it effective in detecting significant prediction discrepancies.
- (4)
- Correlation Coefficient (R):
In the formula, the numerator represents covariance between model predictions and observations, while the denominator represents the product of standard deviations of model predictions and observations. and represent their respective average values. The correlation coefficient gauges the linear relationship between the forecasted MHWs intensity and the observed values.
- (5)
- True Positive Rate (TPR):
TPR, also known as sensitivity, evaluates the rate of accurately predicted MHW occurrences relative to the total number of actual occurrences. The formula for calculating TPR is as follows:
In the equation, TP denotes the count of predictions accurately identified as MHW occurrences, while FN represents the count of false negatives, instances in which the model predicted no MHW occurrence despite it actually occurring.
- (6)
- True Negative Rate (TNR):
TNR, also recognized as specificity, represents the proportion of correctly predicted non-MHW occurrences out of all actual non-MHW samples. It is calculated using the formula:
TN represents the count of correctly predicted non-MHW occurrences, while FP represents the count of instances in which the model incorrectly forecasted MHW occurrence despite its absence.
- (7)
- Forecast Accuracy Rate (FAR)
FAR represents the rate of accurately predicted samples to the total number of samples within a classification model. The formula for calculating FAR is as follows:
The symbols and expressions employed are consistent with those in Equations (5) and (6).
3. Results
3.1. Individual Case of Marine Heatwave Intensity Forecast
Figure 2 portrays the spatial distribution of observed SSTA in the SCS on 15 April 2021 (Figure 2a,d,g,j), model forecasts (Figure 2b,e,h,k), and the deviation between the two (forecast minus observed, Figure 2c,f,i,l). Each row illustrates the outcomes for varying lead times: 1 day (Figure 2a–c), 3 days (Figure 2d–f), 5 days (Figure 2g–i), and 7 days (Figure 2j–l) in advance. The model’s predicted MHWs intensity generally exhibits commendable spatial consistency with the observed values derived from OISSTV2.1. Both reveal substantial positive anomalies in the northern region of the SCS, particularly concentrated within the shallow waters of the continental slope (within 200 m) and along the western side of the Luzon Strait. In the central SCS region, a marked decline in MHW intensity is evident, with a noticeable low-value region between Vietnam and Hainan Island (Figure 2a,d,g,j). Evidently, the MHW intensity forecasting model constructed using the U-Net network adeptly captures these spatial patterns (Figure 2b,e,h,k).
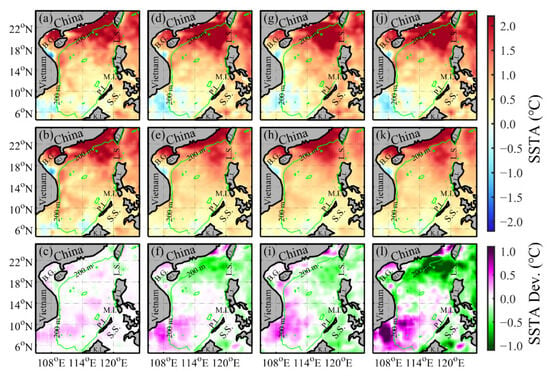
Figure 2.
Spatial distribution of sea Surface temperature anomalies in the South China Sea on 15 April 2021. The top row (a,d,g,j) depicts the outcomes computed using OISSTV2.1. The middle row (b,e,h,k) displays the projections made by the U-Net network with forecast lead times of 1, 3, 5, and 7 days. The bottom row (c,f,i,l) illustrates the deviation between the model predictions and the observed values. The green curve represents the 200 m isobath in the South China Sea. The figure employs abbreviations to denote specific geographical locations: B.G. for Beibu Gulf, H.I. for Hainan Island, T.I. for Taiwan Island, L.S. for Luzon Strait, L.I. for Luzon Island, M.I. for Mindoro Island, P.I. for Palawan Island, S.S. for Sulu Sea, and K.I. for Kalimantan Island.
The distribution maps depicting the differences between observations and forecasts (Figure 2c,f,i,l) distinctly indicate that as the lead time lengthens, ranging from 1-day ahead to 7-day ahead, the model’s predictive accuracy gradually decreases. This trend is particularly evident on the western side of the Luzon Strait. In the initial 1-day lead time forecast, the model tends to overestimate intensity, but as the lead time extends, it progressively underestimates intensity. In the southern region of the SCS and along its western marginal seas, the model’s forecasts generally exhibit higher values compared to the observations. This overestimation is notably more pronounced in the southern region of Vietnam.
With the exception of the 1-day lead time forecast, the outcomes for 3-, 5-, and 7-day lead times consistently exhibit a noticeable north–south dipole pattern. In the northern expanse of the SCS, the forecasted MHW intensities are relatively weaker, while in the southern waters of the SCS, they tend to be stronger. The model demonstrates a propensity to underestimate the intensity of strong MHWs in the northern region and overestimate the intensity of weak MHWs in the southern region. In summary, the model inclines towards tempering the intensity of MHWs, making strong events weaker and weak occurrences stronger. This phenomenon of underestimating MHW intensity in forecasts, as mentioned, corresponds with observations in the study conducted by Giamalaki et al. []. The underlying reason for this bias might be attributed to the limited occurrence of high-intensity MHWs in the training samples, leading to a deficiency in adequate training data.
3.2. Determining Thresholds for Marine Heatwave
There are three approaches that can be utilized to determine the occurrence of MHWs. The first approach involves leveraging predictions from the U-Net model by selecting a specific temperature anomaly threshold. This method relies on the U-Net model’s SSTA predictions to indirectly anticipate the occurrence of MHWs. As depicted in Figure 3a, the highest FAR can be attained by configuring temperature thresholds of 1.0 °C, 1.0 °C, 1.0 °C, and 1.1 °C for lead times of 1, 3, 5, and 7 days. The FARs associated with these thresholds are 0.91, 0.89, 0.88, and 0.86, respectively.
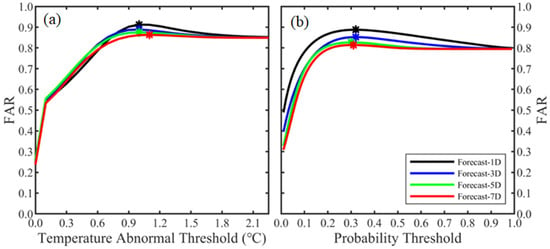
Figure 3.
Distribution curves of forecast accuracy rates obtained using temperature anomaly thresholds (a) and probability thresholds (b) methods, presented separately. The curves are color-coded as black, blue, green, and red, respectively, corresponding to the results of 1-, 3-, 5-, and 7-day forecasts. The asterisks depicted in the figure represent the points where the maximum forecast accuracy rates are attained.
The second approach involves using the probability outcomes from the ConvLSTM forecasting model to determine the occurrence of MHWs. By selecting a suitable probability threshold, instances where the predicted probability exceeds this threshold are classified as MHW occurrences. This method solely depends on the probability forecast results, disregarding the results from the U-Net model. As shown in Figure 3b, the highest accuracy can be achieved by configuring probability thresholds of 0.32, 0.32, 0.30, and 0.31 for lead times of 1, 3, 5, and 7 days, respectively. Correspondingly, the corresponding FARs are 0.89, 0.85, 0.83, and 0.81. It is worth noting that using this approach only provides information about the occurrence of an MHW, without yielding any insight into its intensity.
The third approach employed in this study amalgamates the results of the previous two methods. It requires that the SSTA predicted by the U-Net surpasses a designated temperature anomaly threshold (T), and the predicted probability value by the ConvLSTM exceeds another set probability threshold (P). Only when both conditions are fulfilled, the occurrence of MHWs is affirmed. The analysis underscores that the MHW forecast accuracy achieved through this combined approach surpasses that of utilizing the two previous methods in isolation. For 1-, 3-, 5-, and 7-day lead times, the highest FARs are 0.92, 0.89, 0.88, and 0.87, respectively. The corresponding temperature anomaly thresholds (probability thresholds) for these levels of accuracies are 0.9 °C (0.29), 0.8 °C (0.30), 1.0 °C (0.20), and 1.0 °C (0.28). Notably, the synergy of both methods in the combined approach yields elevated forecast accuracy rates compared to employing either method in isolation.
Additionally, it is noteworthy that both Figure 3a,b exhibit a tendency where the FAR stabilizes as the threshold value increases up to a certain point. This phenomenon can be attributed to the data imbalance among different data types within the model’s training dataset []. Specifically, the training dataset displays an imbalance in the occurrence of MHWs, with occurrences accounting for only a quarter of the grid points in comparison to non-occurrence instances. This signifies that approximately 80% of the grid points fall into the non-occurrence category of MHWs. This matter warrants further investigation, and forthcoming studies will delve into a more comprehensive analysis of this phenomenon.
3.3. Analysis of the Forecast Performance of the Marine Heatwave Prediction System
We comprehensively evaluated the overall forecasting performance of the model in predicting MHWs across the entire validation dataset spanning from 2020 to 2021. Figure 4 presents the spatial distribution of the time-averaged FBs for different lead times. It is important to emphasize that this assessment is grounded in the ultimate output of the forecast system, which amalgamates both the intensity forecast and the probability forecast. To ensure meaningful comparison across various lead times, adjustments have been made to the color bar range, given the relatively smaller magnitude of the average forecast bias for a 1-day lead time.
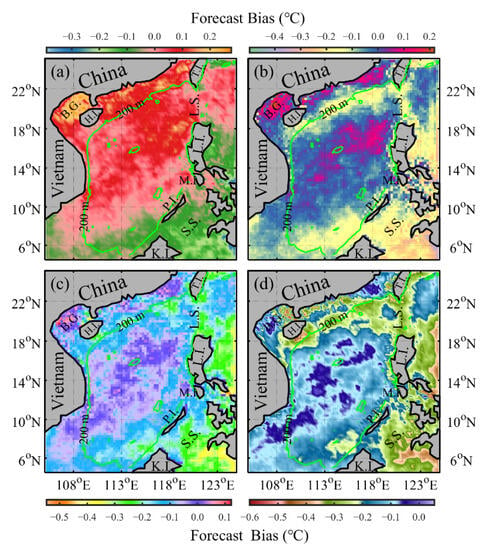
Figure 4.
Spatial distribution of forecast biases in MHWs intensity. Panels (a–d) correspond to the forecast biases for lead times of 1, 3, 5, and 7 days, respectively. The green curve represents the 200 m isobath within the South China Sea. In the figure, the abbreviations represent specific geographical locations: B.G. for Beibu Gulf, H.I. for Hainan Island, T.I. for Taiwan Island, L.S. for Luzon Strait, L.I. for Luzon Island, M.I. for Mindoro Island, P.I. for Palawan Island, S.S. for Sulu Sea, and K.I. for Kalimantan Island.
In general, a discernible trend is observed wherein the intensity FB of MHWs tends to diminish near the 200 m isobath within the northern region of the SCS, a trend that becomes more pronounced with extended lead times (Figure 4). In terms of spatial distribution, the magnitude of the FB notably amplifies within the shallow waters that are characterized by depths within 200 m, in contrast to the more expansive central open ocean areas of the SCS. This discrepancy could be attributed to the higher frequency of MHWs in the shallow waters and the diverse physical mechanisms influencing MHWs in these specific areas []. The adjacency of land to these shallow waters could potentially introduce disturbances during model training, contributing to the observed variations. For example, when training the U-Net model on SSTA data, the absence of data on land grid points (which is substituted with data to zero) introduces discrepancies in the model’s accuracy. The extreme FB values for 1-, 3-, 5-, and 7-day lead times are −0.39 °C, −0.49 °C, −0.55 °C, and −0.60 °C, respectively, situated near the 200 m isobath to the right of Hainan Island in the northern region of the SCS.
The MAFB offers a direct measurement of the discrepancy between the forecasted MHWs and the observed values, disregarding positive or negative biases. Figure 5a–d illustrate the spatial distribution of MAFB for the model’s MHW intensity forecasts, spanning 1-, 3-, 5-, and 7-day lead times. With increasing lead times, MAFB values gradually rise (transitioning from Figure 5a–d), but the consistent spatial distribution trend remains. A notable pattern emerges in the figures, characterized by a northeast-southwest directional distribution of MAFB values. Notably elevated values are discernible along the northern slope region of the SCS. The area extending between the Luzon Strait and Vietnam, particularly at depths exceeding 200 m, exhibits intermediate MAFB values. Conversely, the southeastern SCS demonstrates the lowest MAFB values. As the forecast lead time extends, the MAFB within the SCS correspondingly grows. Specifically, the mean MAFB for 1-, 3-, 5-, and 7-day lead times are 0.10 ± 0.08 °C, 0.14 ± 0.11 °C, 0.17 ± 0.13 °C, and 0.18 ± 0.14 °C, respectively.
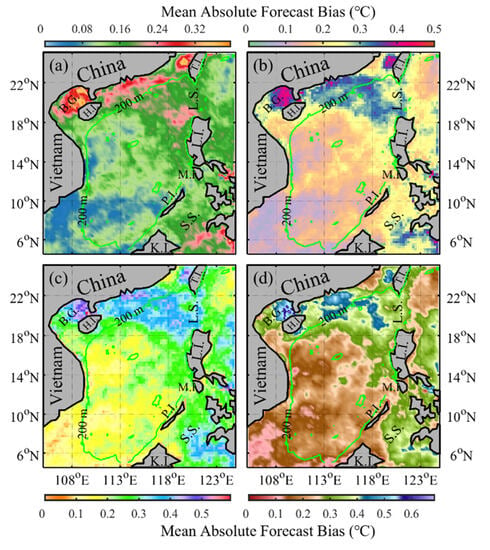
Figure 5.
Spatial distribution of the mean absolute forecast bias for the model-predicted MHWs intensity. Panels (a–d) represent the forecast results for 1-, 3-, 5-, and 7-day lead times, respectively. The green curve represents the 200 m isobath in the South China Sea. In the figure, the abbreviations correspond to specific geographical locations: B.G. for Beibu Gulf, H.I. for Hainan Island, T.I. for Taiwan Island, L.S. for Luzon Strait, L.I. for Luzon Island, M.I. for Mindoro Island, P.I. for Palawan Island, S.S. for Sulu Sea, and K.I. for Kalimantan Island.
The RMSE serves as a commonly used metric that quantifies the overall disparity between predicted values and their corresponding observed values, thereby providing an assessment of prediction performance. In our study, RMSE offers insights into spatial variations in prediction accuracy. Specifically, it exhibits higher values in the shallow waters of the northwestern shelf and the Luzon Strait, while lower values are observed in other regions (Figure 6). Analogous to the descriptions of FB and MAFB, RMSE also exhibits the characteristic of increasing values with longer forecast lead times. For instance, in the shallow waters of the northwestern SCS, RMSE reaches its maximum values of 0.87 °C, 0.89 °C, 1.08 °C, and 1.23 °C for 1-, 3-, 5-, and 7-day forecast lead times, respectively. The spatial averaged RMSE for each forecast lead time are 0.27 ± 0.18 °C, 0.33 ± 0.22 °C, 0.37 ± 0.24 °C, and 0.40 ± 0.27 °C, respectively. These results outcomes provide valuable insights into the model’s performance across different forecast lead times and spatial locations in the SCS.
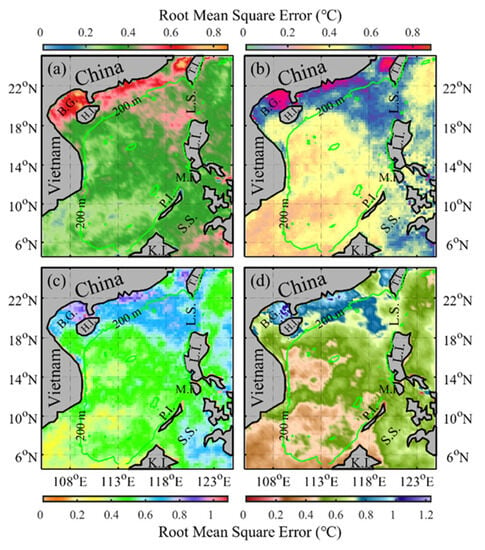
Figure 6.
Spatial distribution of the root means square error in the model’s forecast of MHWs. Panels (a–d) represent the forecast results for 1-, 3-, 5-, and 7-day lead times, respectively. The green curve represents the 200 m isobath in the South China Sea. In the figure, the abbreviations denote specific geographical locations: B.G. for Beibu Gulf, H.I. for Hainan Island, T.I. for Taiwan Island, L.S. for Luzon Strait, L.I. for Luzon Island, M.I. for Mindoro Island, P.I. for Palawan Island, S.S. for Sulu Sea, and K.I. for Kalimantan Island.
In the SCS, there is generally a strong positive correlation between the model-predicted MHW intensity and the observed MHW intensity (Figure 7). However, it is important to note that the spatial distribution pattern of these correlation coefficients differs from that of FB, MAFB, and RMSE. Unlike the latter metrics, the 200 m isobath does not serve as a clear boundary for categorizing the correlation coefficient into strong and weak categories. Instead, the Luzon Strait area shows notably lower correlation coefficients compared to other regions in the SCS. This difference may be attributed to various factors, including the intrusion of the Kuroshio near the Luzon Strait. Such processes may give rise to different mechanisms for MHW occurrences in that specific area compared to other regions. Further exploration and analysis of this specific issue will be conducted in future research as it extends beyond the scope of the current study. Regions with relatively high correlation coefficients are distributed in the central open waters of the SCS. The spatial average correlation coefficients for 1-, 3-, 5-, and 7-day forecast lead times across the entire SCS region are 0.73 ± 0.13, 0.56 ± 0.17, 0.43 ± 0.20, and 0.34 ± 0.20, respectively.
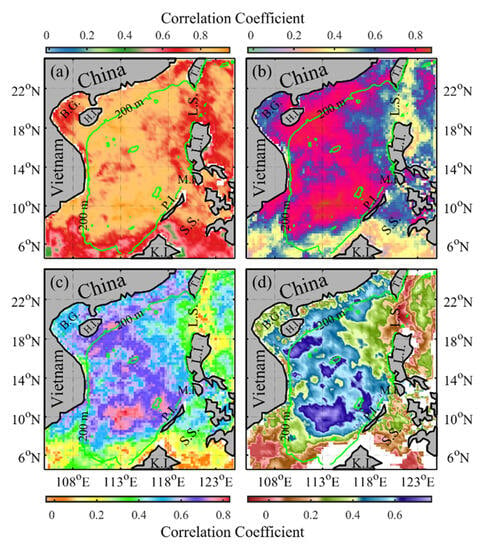
Figure 7.
Spatial distribution of the correlation coefficient between the model-predicted and the observed MHWs intensity. Panels (a–d) correspond to the forecast results for 1-, 3-, 5-, and 7-day lead times, respectively. The green curve represents the 200 m isobath in the South China Sea. In the figure, the abbreviations denote specific geographical locations: B.G. for Beibu Gulf, H.I. for Hainan Island, T.I. for Taiwan Island, L.S. for Luzon Strait, L.I. for Luzon Island, M.I. for Mindoro Island, P.I. for Palawan Island, S.S. for Sulu Sea, and K.I. for Kalimantan Island.
Figure 8 depicts the spatial distribution of TPR in Figure 8a,d,g,j, TNR in Figure 8b,e,h,k, and FAR in Figure 8c,f,i,l for 1-day (Figure 8a–c), 3-day (Figure 8d–f), 5-day (Figure 8g–i), and 7-day (Figure 8j–l) forecast lead times. The TPRs exhibit a notable decline in areas shallower than 200 m, particularly in the southern region of the SCS, when compared to the open waters. As the forecast lead time increases, a clear downward trend in TPRs is observed. The spatial average of TPRs across the entire SCS for l 1-, 3-, 5-, and 7-day lead times are 0.64 ± 0.25, 0.53 ± 0.25, 0.32 ± 0.22, and 0.22 ± 0.19, respectively. This indicates forecasting performance requires improvement for lead times of 5 days or longer.
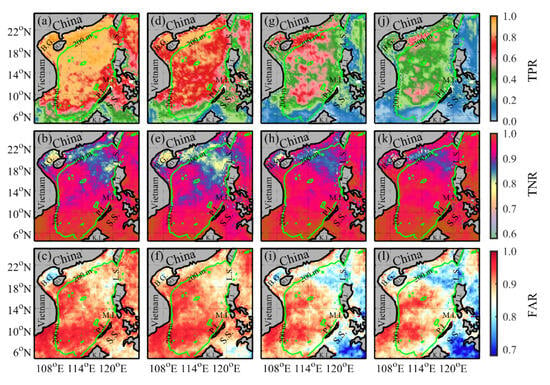
Figure 8.
Spatial distribution of the true positive rate, true negative rate and forecast accuracy rate in the South China Sea marine heatwave prediction system. The top row (a,d,g,j), middle row (b,e,h,k), and bottom row (c,f,i,l) depict the spatial distribution of true positive rate, true negative rate, and forecast accuracy rate for forecasts made 1 day in advance (a–c), 3 days in advance (d–f), 5 days in advance (g–i), and 7 days in advance (j–l), respectively. The green curve represents the 200 m isobath in the South China Sea. In the figure, the abbreviations denote specific geographical locations: B.G. for Beibu Gulf, H.I. for Hainan Island, T.I. for Taiwan Island, L.S. for Luzon Strait, L.I. for Luzon Island, M.I. for Mindoro Island, P.I. for Palawan Island, S.S. for Sulu Sea, and K.I. for Kalimantan Island.
Conversely, the corresponding TNRs exhibit considerable elevation (Figure 8b,d,f,h), with spatial average values of 0.96 ± 0.05, 0.95 ± 0.05, 0.96 ± 0.04, and 0.97 ± 0.04 for 1-, 3-, 5-, and 7-day forecast lead times, respectively. TNRs are noticeably reduced in the northern shallow water region of the SCS and on the western side of the Luzon Strait in comparison to other areas. Particularly within the Beibu Gulf region, a clear central area of low TNR values is observed.
The FAR serves as a composite metric that takes both TPR and TNR into account, offering an encompassing evaluation of performance within a probability forecast model. Figure 8c,f,i,l illustrate that the spatial distribution pattern of FAR generally aligns with that of TNR, with distinctly lower FARs observed in the Beibu Gulf and the western region of the Luzon Strait. Across the entirety of the SCS, the average FARs for 1-, 3-, 5-, and 7-day forecast lead times are 0.94 ± 0.05, 0.91 ± 0.07, 0.90 ± 0.08, and 0.89 ± 0.09, respectively.
Figure 9 depicts the probability density distributions of four evaluation parameters at different forecast lead times. The correlation coefficients for forecasts with 1-, 3-, 5-, and 7-day lead times display skewness (kurtosis) values of −1.58 (6.77), −0.67 (2.88), −0.38 (2.12), and −0.21 (2.03), respectively (Figure 9a). Negative skewness indicates a left-skewed distribution, implying that there is a higher frequency of data points below the mean in the correlation coefficient data compared to those above it. Kurtosis reflects the concentration of data around the mean, as well as the thickness and heaviness of the tails. A positive kurtosis indicates a relatively sharp distribution, with values deviating further from 3, which is the kurtosis value of a standard normal distribution, indicating a greater departure from the standard normal distribution.
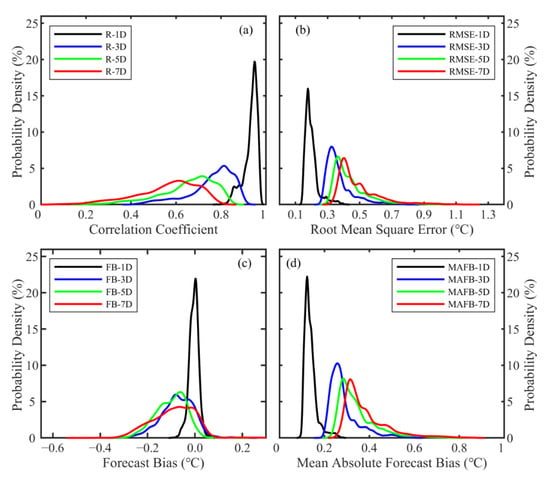
Figure 9.
Probability density distributions of the correlation coefficient (a), root mean square error (b), forecast bias (c), and mean absolute forecast bias (d) for different lead forecast periods. The black, blue, green, and red curves represent the results for 1-, 3-, 5-, and 7-day lead forecast periods, respectively.
The probability density distribution of RMSE also exhibits similar characteristics, with an increasing mean value as the forecast lead time extends (Figure 9b). The skewness (kurtosis) values of the RMSE for 1-, 3-, 5-, and 7-day lead time forecasts are 0.83 (4.51), 0.35 (3.13), 0.38 (3.22), and 0.48 (3.67), respectively. The positive skewness of the RMSE indicates that the distribution of data points is skewed to the right, suggesting that there are more data points with larger values compared to the mean.
Figure 9c presents the skewness (kurtosis) values of the forecast bias for 1-, 3-, 5-, and 7-day lead time forecasts as −0.26 (4.49), −0.85 (3.72), −0.85 (3.12), and −0.53 (2.49), respectively. The noticeable left-skewness in the data indicates a tendency for the forecast results to underestimate the intensity of MHWs. Furthermore, Figure 9d displays the probability density distribution of the MAFB, showing an increasing trend in the peak value with longer forecast lead times. The skewness (kurtosis) values of MAFB for 1-, 3-, 5-, and 7-day forecasts are 0.79 (3.99), 0.33 (2.56), 0.39 (2.65), and 0.42 (2.84), respectively. The identification of these values is valuable for subsequent systematic bias correction of the model forecasts.
4. Discussion
Based on the above analysis, it is evident that the forecast performance of MHWs is significantly influenced by various factors, including threshold selection, spatial location, forecast lead time, and others. For instance, this study does not differentiate the occurrence time of MHWs, meaning that the selection of temperature anomaly thresholds does not account for seasonal variations. In reality, MHWs in the SCS do exhibit seasonal variations. During the winter and spring seasons, the intensity of MHWs typically exceeds 1 °C, while in the summer and autumn seasons, it is usually around 0.5 °C []. Therefore, considering these seasonal variations could be advantageous for further refining and enhancing the accuracy of MHW forecasts in the SCS.
Moreover, the probability density distribution of the forecast bias in Figure 9c highlights a consistent trend where the model consistently underestimates the intensity of MHWs, indicating a systematic bias towards lower forecasted intensities. Addressing this bias through systematic corrections could prove advantageous in future model development, leading to enhanced accuracy in MHW predictions. Additionally, another critical factor that demands consideration is the data type imbalance within the model training datasets. A notable discrepancy exists between the abundance of non-MHW data and the relatively fewer instances of MHW data, potentially introducing disruptions to the model’s learning process. Specifically, within the confines of the model training dataset, a substantial proportion of grid points represent occurrences devoid of MHWs, while only about a fifth corresponds to locations where MHWs manifest. This prevailing imbalance tends to skew the model’s inclinations toward more frequently classifying forecasted grid points as non-MHW occurrences while allocating fewer grid points to represent actual MHW events [].
The study underscores a robust correlation between the model’s forecasting performance for MHWs and the geographic location of the region. Notably, within the northern slope region of the SCS within 200 m, the model tends to exhibit elevated values in forecast bias, mean absolute forecast bias, and root mean square error. In contrast, these metrics demonstrate relatively smaller magnitudes in the central part of the SCS. One possible reason explanation for this divergence could be attributed to the edge effects encountered during model training. The constrained availability of oceanic points in the proximity of the slope region might compromise the model’s training efficacy, consequently influencing the accuracy of the forecasts within that particular area.
Moreover, it is noteworthy that a majority of studies have conventionally embraced the definition proposed by Hobday et al. [] for MHWs. This definition characterizes an MHW as an event at a specific point in space, overlooking the contextual surroundings. This “micro-scale” vantage point in the MHW definition imparts a drawback of generating a fragmented spatial distribution of MHWs. Consequently, certain MHW instances appear isolated, inadvertently intensifying the challenge of model assimilation. In essence, what researchers are interested in is a broader perspective of the “macro-scale” MHWs. This concept alludes to the aggregation of individual “micro-scale” MHWs, thereby forming interconnected spatial domains of contiguous MHW activity []. This distinction is pivotal in refining our understanding of MHW dynamics.
Indeed, the influence of a solitary “micro-scale” MHW occurrence at an individual spatial point is relatively minimal and might even be inconsequential. The true impact only materializes when these isolated “micro-scale” MHWs expand to cover a certain spatial scope, at which point their ecological and other consequences become significant. Consequently, in forthcoming research endeavors, it might prove imperative to embrace a “macro-scale” definition of MHWs that operates within a comprehensive spatio-temporal framework []. This paradigm shift can streamline the intricacies of forecasting and ultimately enhance predictive prediction by acknowledging the interconnected nature of MHWs across a broader spatial expanse.
5. Conclusions
In the face of increasing global warming, the escalating detrimental consequences of MHWs on marine ecosystems, along with their growing frequency and intensity, present difficult challenges. The imperative for timely and effective MHW prediction has risen to the forefront for marine management entities. To address this issue, this study develops an artificial intelligence forecasting system tailored for predicting MHWs in the SCS. The system is comprised of three integral components:
- (1)
- SSTA (intensity) prediction through the U-Net network: This initial facet is designed to predict SSTA values, which act as pivotal indicators of MHWs. It uses the U-Net network architecture to achieve accurate and dependable predictions.
- (2)
- MHW occurrence probability prediction based on ConvLSTM network: The second facet employs the ConvLSTM model to forecast the probability of MHW occurrence, incorporating the temporal correlations intrinsic to the SCS.
- (3)
- Holistic MHW determination through SSTA and occurrence probability thresholds: The goal centers on a comprehensive determination of MHWs, achieved by applying predefined thresholds for both SSTA and the probability of occurrence.
Through the seamless integration of these three components, the forecasting system aims to provide precise and timely MHWs predictions in the SCS. This equips marine management authorities with the tools to proactively address and alleviate the impacts associated with these events.
The model’s training dataset is meticulously constructed from MHW data obtained from the OISSTV2.1 dataset, spanning the time frame of 1982–2019. This data compilation forms the basis for model learning. To rigorously evaluate the model’s forecasting ability, the detection outcomes for 2020 and 2021 are used as the validation set. The findings of the sensitivity testing underscore a crucial insight: the best forecasting performance is obtained when both the SSTA threshold method and the occurrence probability threshold method are combined. In particular, when setting the temperature threshold values at 0.9 °C, 0.8 °C, 1.0 °C, and 1.0 °C, coupled with probability threshold values of 0.29, 0.30, 0.20, and 0.28 for 1-, 3-, 5-, and 7-day forecast lead times, respectively, the forecast accuracy reaches is highest. Consequently, the corresponding maximum forecast accuracy rates are 0.92, 0.89, 0.88, and 0.87.
Given the paramount importance of the SCS in activities such as nearshore aquaculture, marine ranching, fishing, and coral reef conservation, the establishment of an MHW forecasting system carries important practical implications. The innovative forecasting system proposed in this study stands as a pivotal solution to provide timely MHW alert information to pertinent management authorities. It plays a pivotal role in shaping disaster prevention and mitigation policies, which are of paramount significance in addressing the escalating risks posed by MHWs. The distinctive aspect of this forecasting system lies in its direct utilization of SSTA data, avoiding the incorporation of meteorological variables. This quality endows it with heightened transferability, positioning it as a reference model for the construction of MHW prediction systems in diverse regions. The research brings to the fore critical issues, such as the imbalance in MHW data and the potential influence of coastal land points during model training. These findings provide invaluable insights that pave the way for the development of more finely tuned artificial intelligence-based MHW prediction systems in subsequent endeavors. Furthermore, a forward-looking dimension emerges by acknowledging that MHWs are influenced by a confluence of oceanic dynamics and thermodynamics. Integrating these underlying physical constraints into AI models, thereby constructing interpretable forecasting networks, constitutes a promising avenue for future research endeavors.
Author Contributions
Conceptualization, W.S. and S.Z.; methodology, W.S.; software, W.S.; validation, W.S., J.Y. and J.J.; formal analysis, W.S.; investigation, W.S.; resources, W.S.; data curation, S.Z. and X.G.; writing—original draft preparation, W.S.; writing—review and editing, W.S.; visualization, S.Z.; supervision, C.D.; project administration, C.D.; funding acquisition, C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), grant number SML2020SP007; the National Natural Science Foundation of China, grant number 42192562; the Open Fund of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, MNR, grant number QNHX2231; the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), grant number 311020004 and the China Scholarship Council, grant number 202008320195.
Data Availability Statement
The daily optimum interpolation SSTs from the infrared and microwave radiometers were produced by NOAA (https://www.ncdc.noaa.gov/oisst/data-access, accessed on 1 January 2023). All schema data used in this study can be obtained by contacting the corresponding author via email.
Acknowledgments
The authors would like to wholeheartedly express their gratitude to Kenny T.C. Lim Kam Sian (Nanjing University of Information Science and Technology) for his invaluable contributions in editing and refining the English language of the manuscript. Additionally, the authors wish to extend their sincere appreciation to the editor and the four anonymous reviewers for their insightful comments, constructive feedback, and valuable suggestions on the earlier version of this manuscript. Their collective input has played a pivotal role in elevating the overall quality and clarity of the research presented.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pearce, A.; Lenanton, R.; Jackson, G.; Moore, J.; Feng, M.; Gaughan, D. The marine heat wave off Western Australia during the summer of 2010/11. In Fisheries Research Report No. 222; Department of Fisheries: South Fremantle, Australia, 2011; 40p. [Google Scholar]
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Feng, M.; et al. A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef]
- Oliver, E.; Benthuysen, J.A.; Darmaraki, S.; Donat, M.G.; Hobday, A.J.; Holbrook, N.J.; Schlegel, R.W.; Gupta, A.S. Marine heatwaves. Ann. Rev. Mar. Sci. 2021, 13, 313–342. [Google Scholar] [CrossRef] [PubMed]
- Laufkötter, C.; Zscheischler, J.; Frölicher, T.L. High-impact marine heatwaves attributable to human-induced global warming. Science 2020, 369, 1621–1625. [Google Scholar] [CrossRef] [PubMed]
- Frölicher, T.L.; Laufkötter, C. Emerging risks from marine heat waves. Nat. Commun. 2018, 9, 650. [Google Scholar] [CrossRef]
- Smale, D.A.; Wernberg, T.; Oliver, E.C.J.; Thomsen, M.; Harvey, B.P.; Straub, S.C.; Burrows, M.T.; Alexander, L.V.; Benthuysen, J.A.; Donat, M.G.; et al. Marine heatwaves threaten global biodiversity and the provision of ecosystem services. Nat. Clim. Change 2019, 9, 306–312. [Google Scholar] [CrossRef]
- Smith, K.E.; Burrows, M.T.; Hobday, A.J.; King, N.G.; Moore, P.J.; Gupta, S.A.; Thomsen, M.S.; Wernberg, T.; Smale, D.A. Biological impacts of marine heatwaves. Annu. Rev. Mar. Sci. 2022, 15, 119–145. [Google Scholar] [CrossRef]
- McCabe, R.M.; Hickey, B.M.; Kudela, R.M.; Lefebvre, K.A.; Adams, N.G.; Bill, B.D.; Gulland, F.M.D.; Thomson, R.E.; Cochlan, W.P.; Trainer, V.L. An unprecedented coastwide toxic algal bloom linked to anomalous ocean conditions. Geophys. Res. Lett. 2016, 43, 10366–10376. [Google Scholar] [CrossRef]
- Cavole, L.; Demko, A.; Diner, R.; Giddings, A.; Koester, I.; Pagniello, C.; Paulsen, M.L.; Ramirez-Valdez, A.; Schwenck, S.; Yen, N.; et al. Biological impacts of the 2013–2015 warm-water anomaly in the Northeast Pacific: Winners, losers, and the future. Oceanography 2016, 29, 273–285. [Google Scholar] [CrossRef]
- Santora, J.A.; Mantua, N.J.; Schroeder, I.D.; Field, J.C.; Hazen, E.L.; Bograd, S.J.; Sydeman, W.J.; Wells, B.K.; Calambokidis, J.; Saez, L.; et al. Habitat compression and ecosystem shifts as potential links between marine heatwave and record whale entanglements. Nat. Commun. 2020, 11, 536. [Google Scholar] [CrossRef]
- Noh, K.M.; Lim, H.; Kug, J. Global chlorophyll responses to marine heatwaves in satellite ocean color. Environ. Res. Lett. 2022, 17, 64034. [Google Scholar] [CrossRef]
- Arias, O.A.; Serrano, O.; Masqué, P.; Lavery, P.S.; Mueller, U.; Kendrick, G.A.; Rozaimi, M.; Esteban, A.; Fourqurean, J.W.; Marbà, N.; et al. A marine heatwave drives massive losses from the world’s largest seagrass carbon stocks. Nat. Clim. Change 2018, 8, 338–344. [Google Scholar] [CrossRef]
- Barbeaux, S.J.; Holsman, K.; Zador, S. Marine heatwave stress test of ecosystem-based fisheries management in the Gulf of Alaska Pacific cod fishery. Front. Mar. Sci. 2020, 7, 703. [Google Scholar] [CrossRef]
- Arteaga, L.A.; Rousseaux, C.S. Impact of Pacific Ocean heatwaves on phytoplankton community composition. Commun. Biol. 2023, 6, 263. [Google Scholar] [CrossRef] [PubMed]
- Doni, L.; Oliveri, C.; Lasa, A.; Di, C.A.; Petrin, S.; Martinez-Urtaza, J.; Coman, F.; Richardson, A.; Vezzulli, L. Large-scale impact of the 2016 marine heatwave on the plankton-associated microbial communities of the Great Barrier Reef (Australia). Mar. Pollut. Bull. 2023, 188, 114685. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Bethel, B.J.; Dong, C.; Zhao, H.; Yao, Y.; Yu, Y. Marine heatwave events near Weizhou Island, Beibu Gulf in 2020 and their possible relations to coral bleaching. Sci. Total Environ. 2022, 823, 153414. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, W.; Li, T. Impact of the Indian Ocean Dipole on evolution of the subsequent ENSO: Relative roles of dynamic and thermodynamic processes. J. Clim. 2021, 34, 3591–3607. [Google Scholar] [CrossRef]
- Holbrook, N.; Scannell, H.A.; Gupta, S.A.; Benthuysen, J.A.; Feng, M.; Oliver, E.C.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Hobday, A.J.; et al. A global assessment of marine heatwaves and their drivers. Nat. Commun. 2019, 10, 2624. [Google Scholar] [CrossRef]
- Gupta, S.A.; Thomsen, M.; Benthuysen, J.A.; Hobday, A.J.; Oliver, E.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Feng, M.; Holbrook, N.J.; et al. Drivers and impacts of the most extreme marine heatwave events. Sci. Rep. 2020, 10, 19359. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, J.; Yin, J.; Zou, X. Marine heatwaves in China’s marginal seas and adjacent offshore waters: Past, present, and future. J. Geophys. Res. 2020, 125, e2019JC015801. [Google Scholar] [CrossRef]
- Zhuang, W.; Xie, S.; Wang, D.; Taguchi, B.; Aiki, H.; Sasaki, H. Intraseasonal variability in sea surface height over the South China Sea. J. Geophys. Res. 2010, 115, C04010. [Google Scholar] [CrossRef]
- Shu, Y.; Wang, Q.; Zu, T. Progress on shelf and slope circulation in the northern South China Sea. Sci. China Earth Sci. 2018, 61, 560–571. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, J.; Wang, Y.; Li, S.; Xu, T.; Wei, Z.; Qu, T. Overview of the multi-layer circulation in the South China Sea. Prog. Oceanogr. 2019, 175, 171–182. [Google Scholar] [CrossRef]
- Mao, H.; Qi, Y.; Qiu, C.; Luan, Z.; Wang, X.; Cen, X.; Yu, L.; Lian, S.; Shang, X. High-Resolution observations of upwelling and front in daya bay, South China Sea. J. Mar. Syst. Eng. 2021, 9, 657. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, W.; Wang, H.; Zhang, X. Assessing the spatio-temporal features and mechanisms of symmetric instability activity probability in the central part of the South China Sea based on a regional ocean model. J. Mar. Syst. Eng. 2023, 11, 431. [Google Scholar] [CrossRef]
- Wu, M.; Xue, H.; Chai, F. Asymmetric chlorophyll responses enhanced by internal waves near the Dongsha Atoll in the South China Sea. J. Oceanol. Limnol. 2023, 41, 418–426. [Google Scholar] [CrossRef]
- Chen, C.; Wang, S.; Wang, B.; Pai, S. Nutrient budgets for the South China Sea basin. Mar. Chem. 2001, 75, 281–300. [Google Scholar] [CrossRef]
- Geng, B.; Xiu, P.; Liu, N.; He, X.; Chai, F. Biological response to the interaction of a mesoscale eddy and the river plume in the northern South China Sea. J. Geophys. Res. 2021, 126, e2021J–e17244J. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, C. Variations in summer marine heatwaves in the South China Sea. J. Geophys. Res. 2021, 126, e2021JC017792. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, S.; Zhang, X.; Chen, P.; Tian, T.; Chen, T. Strategic thinking on the construction of modern marine ranching in China. J. Fish. China 2019, 43, 1255–1262. [Google Scholar] [CrossRef]
- Liu, K.; Xu, K.; Zhu, C.; Liu, B. Diversity of marine heatwaves in the South China Sea regulated by ENSO phase. J. Clim. 2022, 35, 877–893. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, B.; Zeng, L.; He, Y.; Wu, Z.; Chen, J. Properties and drivers of marine heat waves in the northern South China Sea. J. Phys. Oceanogr. 2022, 52, 917–927. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, W.; Yang, J.; Lim, K.S.K.T.C.; Ji, J.; Dong, C. Analysis and prediction of marine heatwaves in the Western North Pacific and Chinese coastal region. Front. Environ. Sci. 2022, 9, 1048557. [Google Scholar] [CrossRef]
- Jacox, M.G.; Alexander, M.A.; Bograd, S.J.; Scott, J.D. Thermal displacement by marine heatwaves. Nature 2020, 584, 82–86. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.E.; Burrows, M.T.; Hobday, A.J.; Gupta, S.A.; Moore, P.J.; Thomsen, M.; Wernberg, T.; Smale, D.A. Socioeconomic impacts of marine heatwaves: Global issues and opportunities. Science 2021, 374, 419. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Peng, Y. Seismic performance assessment of unsaturated soil slope in different groundwater levels. Landslides 2021, 18, 2813–2833. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wu, X.; Jakob, Z.; Guo, S.; Chen, X. A standardized index for assessing sub-monthly compound dry and hot conditions with application in China. Hydrol. Earth Syst. Sci. 2021, 25, 1587–1601. [Google Scholar] [CrossRef]
- Jacox, M.G.; Tommasi, D.; Alexander, M.A.; Hervieux, G.; Stock, C.A. Predicting the evolution of the 2014–2016 California current system marine heatwave from an ensemble of coupled global climate forecasts. Front. Environ. Sci. 2019, 6, 497. [Google Scholar] [CrossRef]
- Benthuysen, J.A.; Smith, G.A.; Spillman, C.M.; Steinberg, C.R. Subseasonal prediction of the 2020 Great Barrier Reef and Coral Sea marine heatwave. Environ. Res. Lett. 2021, 16, 124050. [Google Scholar] [CrossRef]
- Anderson, G.J.; Lucas, D.D. Machine learning predictions of a multiresolution climate model ensemble. Geophys. Res. Lett. 2018, 45, 4273–4280. [Google Scholar] [CrossRef]
- Dong, C.; Xu, G.; Han, G.; Bethel, B.J.; Xie, W.; Zhou, S. Recent developments in artificial intelligence in oceanography. Ocean-Land-Atmos. Res. 2022, 2022, 9870950. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, C.; Yang, W.; Xie, W.; Kong, L.; Hang, R.; Ma, F.; Dong, C.; Yang, J. Oceanic eddy identification using an AI scheme. Remote Sens. 2019, 11, 1349. [Google Scholar] [CrossRef]
- Xu, G.; Xie, W.; Dong, C.; Gao, X. Application of three deep learning schemes into oceanic eddy detection. Front. Environ. Sci. 2021, 8, 672334. [Google Scholar] [CrossRef]
- Jia, X.; Ji, Q.; Han, L.; Liu, Y.; Han, G.; Lin, X. Prediction of sea surface temperature in the east China sea based on LSTM neural network. Remote Sens. 2022, 14, 3300. [Google Scholar] [CrossRef]
- Han, Y.; Sun, K.; Yan, J.; Dong, C. The CNN-GRU model with frequency analysis module for sea surface temperature prediction. Soft Comput. 2023, 27, 8711–8720. [Google Scholar] [CrossRef]
- Martin, S.A.; Manucharyan, G.E.; Klein, P. Synthesizing sea surface temperature and satellite altimetry observations using deep learning improves the accuracy and resolution of gridded sea surface height anomalies. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003589. [Google Scholar] [CrossRef]
- Wu, X.; Guo, S.; Qian, S.; Wang, Z.; Lai, C.; Li, J.; Liu, P. Long-range precipitation forecast based on multipole and preceding fluctuations of sea surface temperature. Int. J. Climatol. 2022, 42, 8024–8039. [Google Scholar] [CrossRef]
- O’Donncha, F.; Zhang, Y.; Chen, B.; James, S.C. Ensemble model aggregation using a computationally lightweight machine-learning model to forecast ocean waves. J. Mar. Syst. 2019, 199, 103206. [Google Scholar] [CrossRef]
- Wu, T.; Cao, Y.; Wu, Z.; Wu, J.; Qu, T.; Zhang, J. Deep learning for inversion of significant wave height based on actual sea surface backscattering coefficient model. Multimed Tools Appl. 2020, 79, 34173–34193. [Google Scholar] [CrossRef]
- Jörges, C.; Berkenbrink, C.; Stumpe, B. Prediction and reconstruction of ocean wave heights based on bathymetric data using LSTM neural networks. Ocean Eng. 2021, 232, 109046. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, W.; Lu, Y.; Wang, Y.; Zhou, Y.; Hui, N.; Dong, C. ConvLSTM-Based wave forecasts in the South and East China Seas. Front. Mar. Sci. 2021, 8, 680079. [Google Scholar] [CrossRef]
- Han, L.; Ji, Q.; Jia, X.; Liu, Y.; Han, G.; Lin, X. Significant wave height prediction in the South China Sea based on the ConvLSTM algorithm. J. Mar. Syst. Eng. 2022, 10, 1683. [Google Scholar] [CrossRef]
- Cen, H.; Jiang, J.; Han, G.; Lin, X.; Liu, Y.; Jia, X.; Ji, Q.; Li, B. Applying deep learning in the prediction of chlorophyll-a in the East China Sea. Remote Sens. 2022, 14, 5461. [Google Scholar] [CrossRef]
- Chen, Y.; Weng, Q.; Tang, L.; Wang, L.; Xing, H.; Liu, Q. Developing an intelligent cloud attention network to support global urban green spaces mapping. ISPRS J. Photogramm. Remote Sens. 2023, 198, 197–209. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, L.; Huang, W.; Guo, J.; Yang, G. A novel spectral indices-driven spectral-spatial-context attention network for automatic cloud detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3092–3103. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Li, Y.; Wang, H.; Yang, Y. Spectrum interference-based two-level data augmentation method in deep learning for automatic modulation classification. Neural Comput. Appl. 2021, 33, 7723–7745. [Google Scholar] [CrossRef]
- Giamalaki, K.; Beaulieu, C.; Prochaska, J.X. Assessing predictability of marine heatwaves with random forests. Geophys. Res. Lett. 2022, 49, e2022GL099069. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Michael, G.S. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Chin, T.M.; Liu, C.; Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling and environmental studies. Earth Syst. Sci. Data. 2016, 8, 165–176. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Freeman, E.; Graham, G.; Smith, T.; Zhang, H. Assessment and Intercomparison of NOAA Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 7421–7441. [Google Scholar] [CrossRef]
- Le, G.N.; Zscheischler, J.; Rodgers, K.B.; Yamaguchi, R.; Frölicher, T.L. Hotspots and drivers of compound marine heatwaves and low net primary production extremes. Biogeosciences 2022, 19, 5807–5835. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Benthuysen, J.A.; Bindoff, N.L.; Hobday, A.J.; Holbrook, N.J.; Mundy, C.N.; Perkins-Kirkpatrick, S.E. The unprecedented 2015/16 Tasman Sea marine heatwave. Nat. Commun. 2017, 8, 16101. [Google Scholar] [CrossRef] [PubMed]
- Elzahaby, Y.; Schaeffer, A.; Roughan, M.; Delaux, S. Oceanic circulation drives the deepest and longest marine heatwaves in the east Australian current system. Geophys. Res. Lett. 2021, 48, e2021GL094785. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, Y.; Feng, M.; Hu, S. Long-lasting marine heatwaves instigated by ocean planetary waves in the tropical Indian ocean during 2015–2016 and 2019–2020. Geophys. Res. Lett. 2021, 48, e2021GL095350. [Google Scholar] [CrossRef]
- Frölicher, T.L.; Fischer, E.M.; Gruber, N. Marine heatwaves under global warming. Nature 2018, 560, 360–364. [Google Scholar] [CrossRef]
- Ren, X.; Liu, W. The role of a weakened Atlantic Meridional Overturning circulation in modulating marine heatwaves in a warming climate. Geophys. Res. Lett. 2021, 48, e2021GL095941. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, C.; Fu, Y. Global marine heatwaves and cold-spells in present climate to future projections. Earth’s Future 2022, 10, e2022EF002787. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Wang, Y.; Zhang, C.; Tian, S.; Chen, Q.; Li, S.; Zeng, J.; Wei, Z.; Xie, S. Seasonal cycle of marine heatwaves in the northern South China Sea. Clim. Dynam. 2023, 1–11. [Google Scholar] [CrossRef]
- Bonino, G.; Masina, S.; Galimberti, G.; Moretti, M. Southern Europe and western Asian marine heatwaves (SEWA-MHWs): A dataset based on macroevents. Earth Syst. Sci. Data 2023, 15, 1269–1285. [Google Scholar] [CrossRef]
- Sun, D.; Jing, Z.; Li, F.; Wu, L. Characterizing global marine heatwaves under a spatio-temporal framework. Prog. Oceanogr. 2023, 211, 102947. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).