Abstract
Accurately estimating hydrological parameters is crucial for comprehending global water resources and climate dynamics. This study addresses the challenge of quantifying uncertainties in the global land data assimilation system (GLDAS) model and enhancing the accuracy of downscaled gravity recovery and climate experiment (GRACE) data. Although the GLDAS models provide valuable information on hydrological parameters, they lack uncertainty quantification. To enhance the resolution of GRACE data, a spectral downscaling approach can be employed, leveraging uncertainty estimates. In this study, we propose a novel approach, referred to as method 2, which incorporates parameter magnitudes to estimate uncertainties in the GLDAS model. The proposed method is applied to downscale GRACE data over Alberta, with a specific focus on December 2003. The groundwater storage extracted from the downscaled terrestrial water storage (TWS) are compared with measurements from piezometric wells, demonstrating substantial improvements in accuracy. In approximately 80% of the wells, the root mean square (RMS) and standard deviation (STD) were improved to less than 5 mm. These results underscore the potential of the proposed approach to enhance downscaled GRACE data and improve hydrological models.
1. Introduction
The gravity recovery and climate experiment (GRACE) mission, as described by Tapley et al. [1], comprises a pair of satellite missions that provide precise measurements of temporal and spatial variations in the Earth’s gravity field. The monthly global gravity models derived from these missions include spherical harmonic coefficients and associated errors. These models have proven valuable for estimating variations in terrestrial water storage (TWS) at a large scale, thereby facilitating the assessment of surface and groundwater storage (GWS) [2,3,4,5]. However, the application of GRACE models is limited when it comes to monitoring changes at smaller scales, thereby limiting their utility for local water management authorities due to their low spatial and temporal resolutions (approximately 200,000 km2 and one month, respectively) [6,7]. Hydrogeologists and researchers have acknowledged these limitations [8,9] and recognise the need for high-resolution GRACE data products, especially in regions with insufficient in situ monitoring networks, such as the northern regions of Canada. Mohamed et al. [10] discussed water scarcity challenges in north and central Africa, focusing on Chad, due to climate change and human activities. By integrating GRACE data, climatic model outputs, and precipitation information, the study examines spatial and temporal mass fluctuations caused by groundwater variations, providing valuable insights for water resource management in the region.
Downscaling techniques can be employed to obtain high-resolution GRACE data products. Downscaling refers to the reconstruction of variations at a finer scale, assuming that the values observed at a larger scale are representative averages of those at smaller scales [11]. Numerous downscaling techniques have been proposed, broadly categorised into two groups: deterministic (dynamical) and statistical downscaling. Deterministic approaches, including data assimilation techniques, utilise high-resolution models within limited areas when compared to GRACE (such as global climate models or general circulation models) and are driven by lateral boundary conditions to derive information at smaller scales [12,13,14]. Although these methods offer physical consistency, their computationally intensive nature restricts their applicability [15]. Statistical downscaling methods, on the other hand, establish statistical relationships between large-scale and small-scale parameters to predict finer-scale details [16]. These methods offer flexibility in utilising various spatiotemporal datasets and enable the estimation of uncertainties in the model outputs. Various statistical techniques have been applied and studied in the downscaling literature, including classification-based methods, empirical and statistical regression models [17,18], correlative relation methods [19], and Markov chains. In recent years, statistical inversion using machine learning algorithms has been widely employed for downscaling GRACE observations [20,21,22,23,24], including random forest [25,26], artificial neural networks [27,28,29], support vector machines [30], and multiple linear regression [31] models. However, statistical methods require access to large datasets and rely on the assumptions that the observed data and small-scale information accurately capture the dynamics of the system under study and that these dynamics remain valid beyond the observation period [32].
An iterative adjustment method has gained popularity as a novel approach for downscaling GRACE data. Zhong et al. [33] applied this method spatially, using a self-calibrating variance–component model to downscale coarse resolution GRACE observations (300 km) to a finer resolution of 5 km. Their method also estimated uncertainties in high-resolution TWS and GWS variations. Additionally, Zhong et al. [34] developed an iterative adjustment method that holds promise for downscaling GRACE-derived TWS both spatially and temporally. Their approach enhances the spatiotemporal resolution of TWS variations from the original coarse resolution GRACE data in two stages: spatially from a 3-degree spherical cap (~300 km) to 5 km, and temporally from monthly to daily. However, further verification of the model’s performance is required due to the absence of precise and comparable observations. Arshad et al. [35] employed geographically weighted regression and a soil and water assessment tool (SWAT) model for downscaling. They reported promising results. Another study by Ali et al. [36] utilised machine learning techniques, including random forest, support vector machine, artificial neural network, and extreme gradient boosting (XGBoost), to downscale GRACE TWS and GWS datasets. The XGBoost model outperformed other methods, accurately reproducing local groundwater behaviour. Ali et al. [37] have also studied this method further and applied it over the Indus Basin.
In this study, we employ spectral combination theory [38,39,40] for downscaling GRACE models. Previous researchers [41,42,43,44] have successfully applied this theory primarily in gravity field modelling. Unlike existing downscaling methods, spectral combination or spectral downscaling, operates in the spectral domain [45,46]. Fatolazadeh et al. [45] utilised this method to spatially downscale GRACE models using the global land data assimilation system (GLDAS) model and later extended it to simultaneous spatiotemporal downscaling. Spectral downscaling involves employing an estimator in spectral form that incorporates GRACE observations, hydrological models, and their spectral uncertainties. The parameters of the estimator are determined using a least-squares approach to minimise the global mean square error. In this paper, we expand on previous research by considering both low- and high-frequency signal components of the GRACE and GLDAS system. We compare two approaches for estimating uncertainties in the GLDAS models: Method 1, previously used by Fatolazadeh et al. [12,46], and Method 2, a novel method developed in this study. Method 2 incorporates a condition adjustment approach that does not require additional information and considers the magnitudes of the hydrological parameters during uncertainty estimation. Both methods are employed to estimate the uncertainties of the GLDAS models, which are then applied in the spectral downscaling of GRACE gravity models over the province of Alberta for December 2003. The effectiveness and accuracy of the two methods are compared to assess their performance.
2. Methodology
The methodology for downscaling GRACE products is illustrated in Figure 1, and it incorporates the consideration of magnitudes of hydrological parameters during uncertainty estimation. Two distinct methods are utilised to estimate the uncertainties of the global land data assimilation system (GLDAS) models, which are subsequently applied in the spectral downscaling of GRACE products.
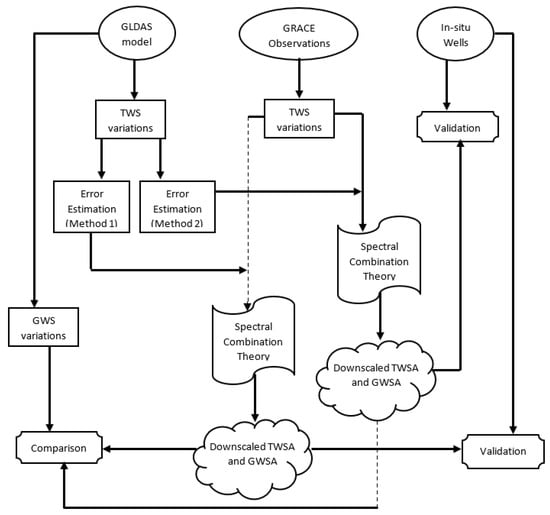
Figure 1.
Technical flowchart for the spectral downscaling of GRACE products.
2.1. Gravity Field and Terrestrial Water Storage from GRACE Models
The monthly gravity models derived from the gravity recovery and climate experiment (GRACE) provide valuable information on Earth’s gravity field. These models can be used to compute terrestrial water storage (TWS) in land areas using the spherical harmonic coefficients (SHCs) of the GRACE data. The conversion from SHCs to TWS is based on the spherical harmonic expression presented by Wahr et al. [47] and further mathematically elaborated by Eshagh [48]:
where G = 6.67 ×10 −11 represents the Newtonian gravitational constant, R is the radius of the spherical Earth, denotes the normal gravity, represents the Love number of degree n, corresponds to the SHCs of the gravitational potential, the SHCs of the terrestrial water storage, and represents the fully normalised spherical harmonics with the arguments of co-latitude (θ) and longitude (λ). The parameters n and m denote the degree and order of the spherical harmonic function, respectively.
The fully normalised associated Legendre functions, denoted by , are employed in Equation (2) to calculate the spherical harmonics:
The orthogonality property of the spherical harmonic functions is given by Equation (3), where δij represents Kronecker’s delta; see e.g., [49]:
In Equation (3), Ω denotes the sphere on which the surface integration is performed and dΩ represents the surface integration element.
The GRACE monthly models also provide uncertainties associated with the SHCs of the Earth’s gravitational potential. By applying the error propagation law of random errors to Equation (1), the error of SHCs of TWS () can be derived:
In Equation (4), represents the error of SHCs of the GRACE monthly models. These equations provide the theoretical framework for computing TWS from the GRACE models and estimating the associated uncertainties.
2.2. Terrestrial Water Storage from Hydrological Models
In addition to the GRACE gravity models, TWS can also be estimated using hydrological models such as the GLDAS. This later provides information on various components of the water cycle, including groundwater storage (GWS), snow water equivalent (SWE), canopy water (CAN), soil moisture (SM), and TWS. These data are typically available in gridded forms with a specific resolution, such as 0.25 × 0.25 degrees. To estimate TWS from the GLDAS model, we can use the spherical harmonic expansion of TWS () as presented by Eshagh [48]:
represents the SHCs of , which can be derived using the orthogonality property of the spherical harmonics (Equation (3)):
To derive , a global grid of with a specific resolution is needed; for each degree n and order m of spherical harmonics, the corresponding frequency of of the same degree and order () is computed. This principle can be simply presented in the following vectorised model:
In fact, Equation (6) is discretised and converted to the multiplication of two vectors of : the vector of discretised integral and the gridded data of converted to the column vector .
2.3. Error Estimation of GLDAS Components
The uncertainties of the hydrological parameters play a significant role in the spectral combination of the GLDAS and GRACE models. In this section, two approaches are presented for the estimation of uncertainties for the hydrological parameters. The first one deals with the case where the same uncertainty is considered for all parameters, but the second one, which is new and more advanced, estimates the uncertainties based on the magnitudes of the hydrological parameters.
2.3.1. Conventional Method of Uncertainty Estimation (Method 1)
Theoretically, the relationship of the hydrological parameters is expressed by the following mathematical formula:
where again stands for the TWS signal, and , , , , and are, respectively, the soil moisture (SM), snow water equivalent (SWE), canopy water (CAN), surface water (SW), and groundwater storage (GWS).
Equation (8) is valid in the case of absence of any error associated with in situ measurement networks and other data sources that were being considered. However, this condition is not satisfied in practice.
Let us rewrite Equation (8) in the following form:
Let us consider the following matrix for this equation:
where stands for statistical expectation, is the a priori variance factor, Q the co-factor matrix with a dimension of six, B is the coefficient matrix, and is a vector of , , , , , and , which are errors of , , , , , and , respectively. Furthermore, []T is the transposition operator, w is the misclosure of the equation, and L is the vector of , , , , , and . The vectors of Equation (10) are the following:
and
The minimum norm solution of Equation (10) when Q = I is the following:
The assumption Q = I and mean to consider one value for uncertainties of all of the hydrological parameters. can be used for adjusting the parameters. The a posteriori variance factor of the model (10), which is an overall estimate of variance, is the following [50]:
The square root of is a global uncertainty value for the uncertainties of the hydrological parameters for each point.
2.3.2. New Method for Uncertainty Estimation (Method 2)
One problem with the previous method, which was applied by Fatolazadeh et al. [46] (2022b, 2022c), is related to estimating one value for hydrological parameters with different magnitudes. For example, soil moisture (SM) can have a stronger signal than the canopy (CAN) water, estimating one value for their uncertainties is thus not fair. Estimating the same uncertainty for all signals can lead to a situation where weaker signals, such as canopy, lose their statistical significance as their errors may surpass the signal itself. In such cases, the signal is wrongly categorised as noise, when, in fact, it is weak but not entirely noise. Hence, a more pragmatic approach is necessary for estimating uncertainties that considers the magnitude of the signals. By doing so, a more realistic assessment of the actual signal strength can be achieved. Therefore, the magnitudes of the parameters are considered.
Let us consider the following co-factor matrix in Equation (10):
where , , , , , and are the uncertainties of SM, SWE, CAN, GWS, SW, and TWS, respectively, and diag() means a diagonal matrix.
The a posteriori variance factor, which considers the co-factor matrix (15), is (cf. [50]) the following:
So far, we considered w as a vector since we wanted to use matrix algebra, but in our special case of this study, w contains only the element w. Then, Equation (16) can be further simplified. From Equations (11), (12), and (15), the following equation is concluded:
After rearranging Equation (17) we obtain the following:
The left-hand side is the summation of absolute uncertainties; if they are replaced with the relative uncertainties, Equation (18) will change to the following:
This is a new system of equations with the relative uncertainties as the unknowns. There are infinite numbers of solutions to this equation. In order to solve this system, we write it in the following matrix form:
where
Matrix A has only one row as there is only one condition equation for each point, and the unknown parameters are variances of the hydrological parameters. Therefore, there is no redundancy in the created system of equation, and it cannot be solved using the least-squares method. However, since the unknown parameters of the system are variances of the hydrological parameters, it is rational to estimate vector x in Equation (19) in such a way that the quadratic norm is minimised; in other words, the quadratic form of variances is minimised with the weight . Such a solution considering the co-factor matrix (15) is the following:
The solution (24) can be written in a short general formula:
which is the estimated relative uncertainty for each hydrological parameter; it is not difficult to conclude that the absolute uncertainty of each parameter is the following:
As observed, Equation (26) is the uncertainty of a hydrological parameter, which depends on the magnitude of the parameter in addition to the misclosure w. In practice, we consider =1, which means that our assumption is that the uncertainties of the parameters are in balance/statistical agreement with the size of misclosure.
All these uncertainties are used point by point over the land area based on the resolution of the GLDAS model, and thereafter, they are transferred to spherical harmonic domain for each degree and order based on the method presented in Section 2.2.
2.4. Spectral Combination of GRACE and GLDAS TWSA
Here, the main goal is to see if our new method (Method 2) for estimating the uncertainties of the GLDAS model can improve the GRACE downscaling using spectral combination, compared to the former method applied by Fatolazadeh et al. [46]. Therefore, we use the GLDAS models as extra information for downscaling the monthly TWS derived from the GRACE models to the daily TWS. The beauty of the spectral combination is to weigh the data based on the quality of their frequencies. This means that prior information about the uncertainties of the TWS from both GRACE and GLDAS models are required. In Section 2.1 and Section 2.2, the methods for estimating the signal spectra or the SHCs of the TWS from these models were presented and discussed. Now, assume that the SHCs of the TWS of both models and their uncertainties are available. Fatolazadeh et al. [46] proposed the following estimator for the daily TWS from a GRACE monthly model:
where is the spectral coefficients of the estimator, which should be estimated in such a way that the mean square error (MSE) of the estimator is minimised; is the SHCs of the ratio of the daily and monthly variation in the TWS, from external information, such as hydrological models, which can be derived by the following equation:
where means the monthly average of the TWS from the hydrological model, and K is the column vector of ratio of daily to monthly TWS of the hydrological model. The uncertainties of can be estimated from the error propagation law of random errors to the vectorised model:
and is the variance–covariance matrix of the error of .
The optimal estimation of is [46] the following:
where
and where and are, respectively, the daily TWS estimated from GRACE (unknown in this case). The daily TWS that is obtained from the hydrological model, and and , are their monthly averages. To shorten the mathematical derivations, we considered and .
In fact, we used the initial idea presented by Zhong et al. [34] and assumed that the daily frequency behaviour of GLDAS used to form monthly averages is similar to the daily frequency of our estimator. In the case that , then the daily TWS of GRACE and the hydrological model would be identical, which is not the case in practice. In fact, is a scale factor (a constant at each point) transforming the monthly TWS to daily values when the errors in TWS of the hydrological models are available. This means that changes from one point to another. Based upon the error propagation law of random errors, the variance of is the following:
where is the variance of daily TWS from the hydrological models. stands for the total number of days in the months.
As observed, the uncertainty of the TWS in the GLDAS model influences our estimator via the spectral coefficients an. On the other hand, in Method 2 of uncertainty estimation, each hydrological parameter possesses its own estimated uncertainty, while our estimator only utilises the uncertainty of the TWS from the GLDAS and GRACE models, requiring only the TWS data and their respective uncertainties. It is essential to note that estimating the uncertainty of the GLDAS TWS solely is not possible without considering the other hydrological parameters.
The output of our estimator provides downscaled TWS, which facilitates the determination of GWS by subtracting canopy, soil moisture, snow water equivalent, and surface water signals. In this process, considering the uncertainties of these parameters would enable a more comprehensive estimation of the uncertainty of groundwater storage. Nevertheless, for the purposes of this study, we have not accounted for these uncertainties.
3. The Area and Data
In this section, we present the study area, Alberta (Canada), and provide the rationale behind its selection, considering its unique hydrological and geological characteristics. Subsequently, we describe the data sources employed in our analysis, namely GRACE, GLDAS, and piezometric wells.
3.1. The Area
Alberta, located in western Canada, lies between the latitudes 49° and 60° north and longitudes 110° and 120° west. This province encompasses a vast and diverse landscape characterised by its dominant topography, which comprises the Rocky Mountains to the west, the boreal forest in the north, and the rolling plains in the south. The hydrology of Alberta is heavily influenced by the province’s geographical features, including numerous rivers and lakes. In fact, Alberta’s hydrology is characterised by a complex network of rivers, lakes, wetlands, and aquifers, shaped by its diverse geography and climate. The province’s hydrological system plays a crucial role in supporting various ecosystems, agriculture, industry, and human settlements. Alberta is well known for its extensive river systems, with major rivers such as the Athabasca, Bow, and North and South Saskatchewan flowing through the province. These rivers are primarily fed by melting snowpack in the Rocky Mountains and rainfall. The spring melt from the mountains contributes to seasonal fluctuations in river flow, providing a crucial source of water for downstream regions and reservoirs for both human and ecological needs. Alberta is also dotted with numerous lakes and wetlands, which contribute to the region’s biodiversity and act as important habitats for various plant and animal species (e.g., Lake Athabasca, Lesser Slave Lake, and Lake Claire). The hydrology in the region is also influenced by an extensive network of aquifers, which are essential for providing water to wells, supplying water for agricultural irrigation, industrial processes, and supporting rural communities.
Alberta’s hydrology faces several challenges, including water scarcity and variability, especially during drought periods. The province’s semi-arid regions can experience water stress, impacting agriculture and ecosystems. Climate change further compounds these challenges, altering precipitation patterns, snowmelt timing, and potentially leading to more extreme weather events. Therefore, Alberta is not exempt from the challenges of groundwater depletion. The province has witnessed significant groundwater extraction for various purposes, such as agriculture, industrial processes, and municipal water supply, leading to concerns about the sustainability of this resource. Studies have highlighted the impacts of groundwater depletion on aquifer levels, water quality, and the long-term availability of this vital resource [51,52,53].
3.2. GRACE, GLDAS and Piezometric Wells Data
In this study, we utilised the monthly gravity field models of GRACE release-06, which consist of the spherical harmonic coefficients (SHCs) of the field along with their uncertainties up to degree and order 60. These models were obtained from the Centre for Space Research, University of Texas at Austin (UTCSR), for the period ranging from the 1st to 31st of December 2003 as an example for showing the performance of our methods. All the necessary processes, such as the replacement of degrees 1 and 2 (as described by Cheng et al. [54]), correction of leakage errors, implementation of glacial isostatic adjustment (GIA), and determination of de-stripping error, have already been applied to these models; see [55] for details.
The GLDAS hydrological system comprises several hydrological variables that are effective in analysing the water cycle, such as SM, SWE, CAN, GWS, and TWS anomalies. Our research utilises the GLDAS products that are based on the catchment land surface model (LSM) L4 daily 0.25° × 0.25° (GLDAS_CLSM025_DA1_D 2.2). These products have higher spatial resolution and temporal resolutions as compared to GRACE (3° × 3°). It is worth mentioning that this study utilises the only GLDAS LSM that contains the GWS variable. To align with the GRACE model’s temporal resolution, GLDAS daily data needs to be averaged out monthly. However, it is important to note that GLDAS products lack the surface water body variables necessary for accurately reconstructing water balance equations.
In addition to GRACE and GLDAS data, we used in situ measurements to validate the results that were obtained following the application of the approach. For instance, 16 active unconfined piezometric wells were used to validate our downscaled GRACE GWS anomalies. Validation was limited to the province of Alberta, based upon the wells that were available. Figure 2 shows the locations of the piezometric wells over the topographic map of Alberta. As the figure shows, there are 16 wells over the area and their distribution is denser in the south-east and the north-west over flat areas and close to residents.
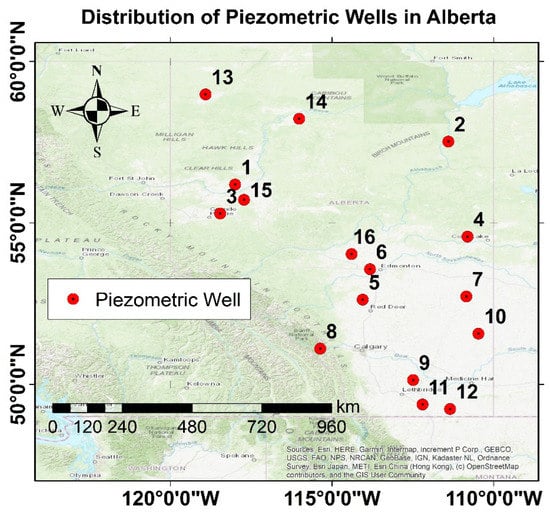
Figure 2.
Distribution of piezometric wells in Alberta.
4. Numerical Results
In this section, we present the analysis of two key datasets: GRACE TWS and GLDAS TWS/GWS. Subsequently, we discuss the results of the uncertainty estimation for the GLDAS TWS using both Method 1 and Method 2. To downscale the GRACE TWS data, we apply the spectral combination method. Next, we compare the GWS derived from the subtraction of the hydrological parameters of GLDAS, excluding TWS from the downscaled GRACE TWS. Finally, we evaluate and compare the GWS data obtained from the piezometric wells in the study area.
4.1. GRACE TWS before Downscaling and GLDAS TWS/GWS
Figure 3a is the map of the TWS storage computed by Equation (1) and the GRACE gravity model of December 2003. High values (about 65 mm) are seen in the north-east of the area and low values (about −98 mm) in the south-east over the urban areas. The map of the TWS is rather smooth and does not show any detail as it shows monthly TWS, which is an average value of TWS at each point during December 2003. Figure 3b is the map of uncertainties of the GRACE TWS, generated from errors of the SHCs given in the gravity model of the month. The uncertainties are computed using Equation (4) and range from 16.7 to 17.3 mm. Although larger uncertainties are seen in the north-west of the area, the difference between the maximum and minimum of the errors is extremely small and seems to be insignificant.
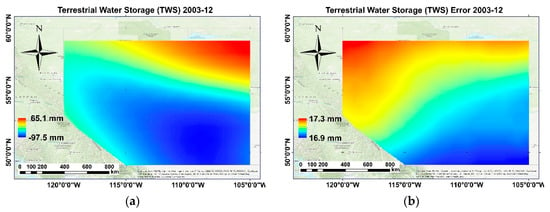
Figure 3.
(a) Terrestrial water storage (TWS) and (b) TWS error computed from the GRACE model in December 2003 over the Alberta province.
Figure 4 illustrates the maps of monthly GLDAS TWS in December 2003. The range of values was between about 293 mm and −182 mm. In fact, all daily values of TWS during this month are averaged to generate this map. Generally, comparison of this figure with the GRACE TWS map (Figure 3a) shows almost similar spatial patterns with high and low values over the north-east and south-east areas, but the maximum values are not seen in the same places. Since the GLDAS TWS has a higher spatial resolution compared to the GRACE, more details are observed in the map. However, we should state that our goal for presenting Figure 4 is to give a general idea about the TWS regime in comparison with the GRACE model, presented in Figure 3a.
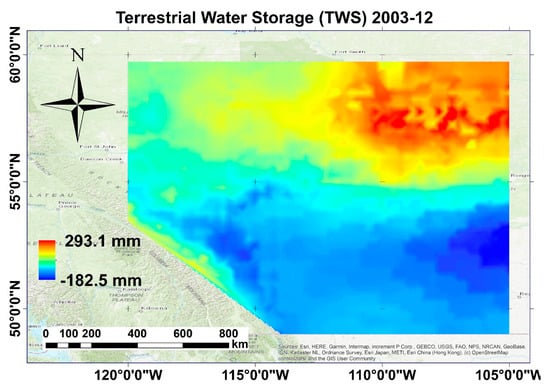
Figure 4.
Average value of terrestrial water storage (TWS) of the GLDAS daily models in December 2003 over the Alberta province.
Because the daily TWS of the GLDAS model (and not the monthly ones) are used in the calculations for downscaling the GRACE TWS model to daily products, producing these daily TWSs is part of this process. However, as December has 31 days, providing 31 maps for the daily TWS of the GLDAS is impractical for this paper. Therefore, we have chosen to display only one day (15 December 2003) for illustrative purposes. Figure 5a,b are the maps of TWS anomalies (TWSA) and GWS anomalies (GWSA) of the GLDAS model in Alberta on 15 December 2003. The maximum and minimum variations in GLDAS TWS in this day are about +8 mm and −9 mm, respectively.
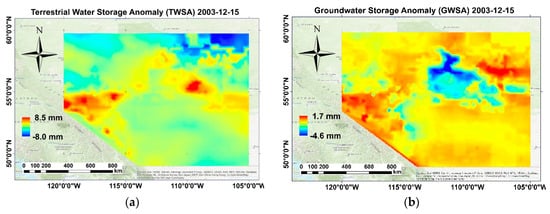
Figure 5.
(a) Terrestrial water storage anomaly (TWSA) and (b) groundwater storage anomaly (GWSA) of the GLDAS model on 15 December 2003 in Alberta.
It must be noted that the GWSA from GLDAS model are not included in the process of spectral combination. We will see in the following sub-section that by proposing two methods of GLDAS errors, two different downscaled results of GRACE-based TWS/GWS will be extracted (reference to the provided flowchart in Figure 1). Therefore, showing the variations in GWS derived from GLDAS is only to understand which downscaled GRACE GWS are similar to the GWS derived from GLDAS.
The misclosures derived from Equation (12) play a significant role for estimation of quality of the hydrological parameters including TWSA. In fact, our two proposed methods of GLDAS TWSA error estimation are based on two different strategies from these misclosures. Figure 6 is the map of these misclosures in Alberta on 15 December 2003. We only interpret this map and the rest of misclosure maps for other days of the month can be explained similarly.
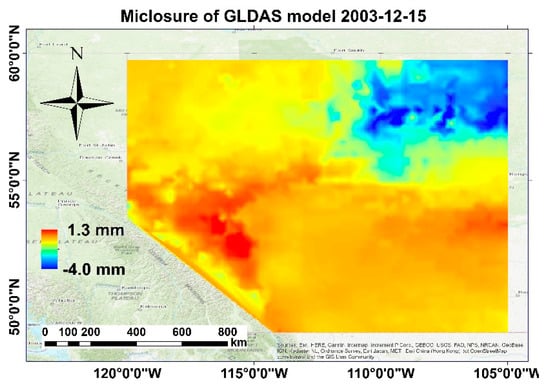
Figure 6.
Map of misclosures of the GLDAS TWSA in Alberta on 15 December 2003.
According to Equation (12), an ideal case would have c = 0, indicating that the summation of all hydrological parameters is equal to the TWS. Therefore, areas on the map in Figure 6 with values close to zero suggest good quality parameters with smaller estimated errors. However, large negative values north-east of Alberta indicate that the value of TWS is greater than the sum of the other hydrological parameters. Hence, it is reasonable to estimate larger errors for parameters in this region.
4.2. GLDAS TWS Error Estimation Proposed by Two Theories
The spectral combination method can be seen as a generalised form of spectral averaging, where the uncertainties of the GRACE and GLDAS signals’ spectra play a vital role. In this process, certain frequencies may be upweighted or downweighted based on their respective uncertainties. For instance, if the signal quality at a particular frequency in the GLDAS model is deemed poor, the estimator will weigh it down and take more signal from the GRACE model and vice versa. In this study, the mathematical formulas for computing the errors of the GRACE (Equation (4)) and GLDAS TWS models (Section 2.3) have been presented. The uncertainties of the GRACE TWS are mapped in Figure 3b, while those of the GLDAS model on the 15th of December are presented in Figure 7. Precisely, Figure 7a is the map of the estimated uncertainties using Method 1 in Alberta on the selected day, (15 December 2003) and Figure 7b is a similar map using Method 2.
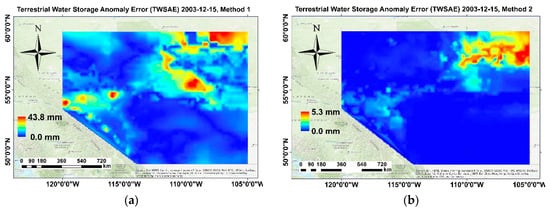
Figure 7.
(a) estimated uncertainty for the GLDAS TWSA in Alberta on 15 December 2003 using (a) Method 1 and (b) Method 2.
It is interesting to note that the map depicted in Figure 7b bears a stronger resemblance to the map of misclosures presented in Figure 6 rather than in Figure 7a. The map of misclosures highlights the presence of significantly negative values in the north-east region, indicating a higher degree of uncertainty regarding the hydrological parameters in that area. However, Figure 7a indicates that there are large uncertainties in the south-east region, with maximum values reaching about 44 mm. However, as shown in Figure 7b, this maximum value is only approximately 5 mm. This leads to the conclusion that Method 2, which is a more sophisticated and complex technique for estimating uncertainties in GLDAS models, is superior to Method 1. Method 2 considers the size of the hydrological parameters and distributes the misclosures such that larger parameters receive higher uncertainties. This approach is reasonable because assigning the same level of uncertainty to soil moisture (which has a strong signal and contribution to TWS) and canopy water (which has a weak signal and contribution to TWS) is not appropriate. In contrast, Method 1 estimates only the uncertainty value for all hydrological parameters, including the TWSA, at each point. It is also expected that by using Method 2 to estimate uncertainties, the spectral downscaling of the GRACE TWSA based on the GLDAS TWSA will yield more realistic results.
The downscaling method uses a form of spectral combination that requires transforming the TWSA of GRACE and GLDAS, along with their respective errors, to the spectral domain. Figure 8 displays the signal and error spectra, along with degree variances, of the TWSA derived from GRACE in December and those of GLDAS on the 15th of the month. It is important to note that our interpretation of this plot is specific to this day; however, the principle remains the same for all days. Method 1 delivers larger uncertainties of the GLDAS TWSA than Method 2, except for low degrees. In the spectral combination, our estimator gives higher weights to the GRACE TWSA than to those of the GLDAS. The GLDAS TWSA role is more pronounced in higher degrees.
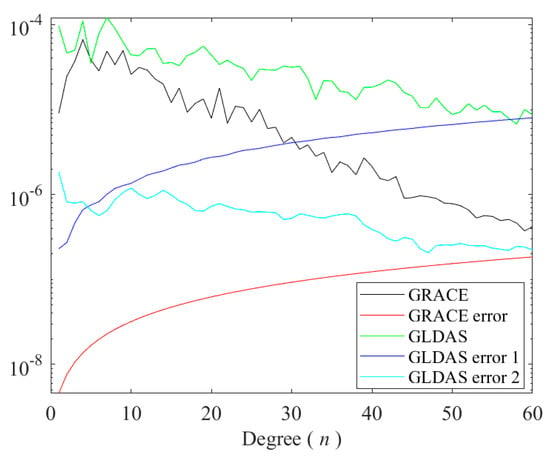
Figure 8.
Signal and error degree variances of TWSA of GRACE and GLDAS on 15 December 2003 [mm].
4.3. Results of Spectral Combination to Downscale GRACE TWS/GWS
Without incorporating supplementary data containing higher spatial and temporal frequencies than those present in the GRACE models, it is not feasible to downscale them. Without such data, mathematical and statistical methods would only act as interpolators without including significant high-frequency signals. In this study, we employed GRACE models and their uncertainties in conjunction with simulated hydrological products from GLDAS to downscale GRACE-based TWS and GWS changes. The uncertainty of GLDAS TWS was derived in the spatial domain and later, by performing a spherical harmonic analysis using Equations (14) and (26), they are transferred to the spectral domain. Later, the spectra of the daily GLDAS TWSAs and their respective errors in conjunction with GRACE TWS were used in the estimator (Equation (27)) for downscaling TWSA. In this section, we select only 15 December 2003 for illustrating the downscaled TWSA and GWSA.
Figure 9 illustrates the fluctuations in the spectral coefficient () on December 15, 2003, with both Method 1 and Method 2 employed to estimate the downscaled GRACE TWSA. The range of is between 0 and 1, and because it is multiplied to the spectra of the GRACE TWSA, it can either amplify or reduce the power of the signals at different frequencies. The downweighting effect of this spectral coefficient differs between the two methods, and in fact, they act in opposite directions.
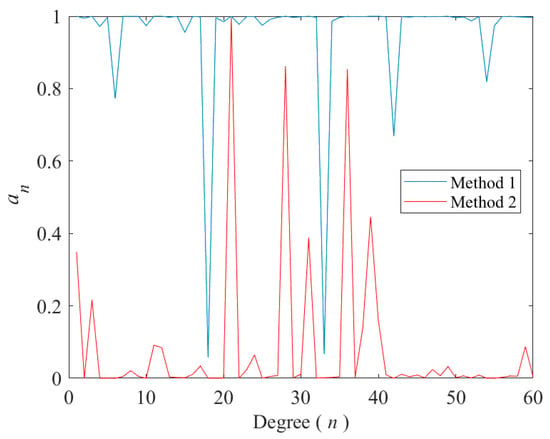
Figure 9.
Estimated spectral coefficient for the estimator (Equation (30)) when the error spectral of the GLDAS TWSA on 15 December 2003 is computed using Method 1 (the blue line) and Method 2 (the red line).
Figure 10 presents a graph depicting the changes in the mean squared error (MSE) of the estimator (Equation (27)) as the degree of combination increases. According to the least-squares principle, it is expected that the MSE will decrease with increasing data, in this case, the signal frequencies. The plot in Figure 10 shows a decreasing trend, except for very low degrees. This can be attributed to the limited amount of data over the oceans in the GLDAS model. Nevertheless, the estimator displays an RMS of approximately 10 mm when considered up to degree 360. As expected, our new method for uncertainty estimation, Method 2, leads to a smaller RMS for the spectral downscaling estimator than Method 1. The MSE is smaller for degrees higher than degree 300 when using Method 1 for downscaling, but this result was anticipated, considering that the estimated uncertainty spectra of the TWS exhibit greater independence when Method 1 is employed, in contrast to the case when Method 2 is used. The incorporation of the magnitude of hydrological parameters in Method 2 for estimating uncertainties restricts the uncertainty spectra from decaying rapidly.
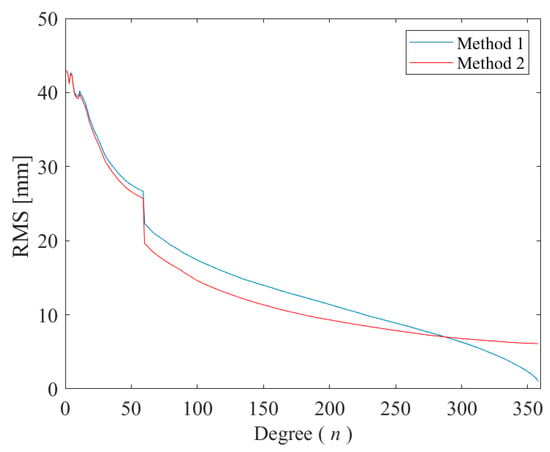
Figure 10.
Behaviour of the MSE of the estimator (27) by increasing the degree of combination from 0 to 360 [mm].
Figure 11a shows the downscaled daily TWSA of the GRACE model, when Method 1 is applied to estimate the uncertainties of the GLDAS daily models; Figure 11b depicts a similar map but based on the new strategy, i.e., Method 2, presented in this research. These figures show how different the result will be when the errors of the GLDAS models are estimated in different ways. When Method 1 is applied, the high TWSAs are seen mainly on the western part of the area (with maximum and minimum values of about 6 mm and −16 mm, respectively), but when Method 2 is used they are mainly in the north-west part (with the maximum and minimum amounts of 4 mm and 1 mm, respectively).
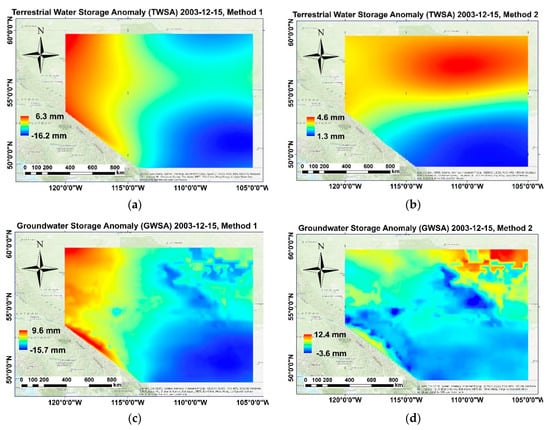
Figure 11.
Daily downscaled TWSA of GRACE using (a) Method 1 and (b) Method 2, and downscaled GWSA of GRACE using (c) Method 1 and (d) Method 2 on 15 December 2003 over Alberta.
Figure 11c,d are the maps of the downscaled GWSA of GRACE based on our spectral downscaling method in which Method 1 and Method 2 are, respectively, used for uncertainty estimation of the GLDAS TWSA up to degree and order 60. When Method 1 is used, the GWSA ranges from about −17 mm to 10 mm, but from about −4 mm to 13 mm when Method 2 is used although the maps are similar but the values of GWSA are different. It can be seen that the GWSA presented in Figure 11d, Method 2, are more similar to the GLDAS GWSA (Figure 5b). It could be expected that the uncertainties of the GLDAS TWSA estimated by Method 2 are more realistic when compared to those in Method 1.
4.4. Validation with Piezometric Wells
In order to show the performance of our methods on all days of the month and the external evaluation of our results, the downscaled GWSA of GRACE are compared with those 16 piezometric wells in Alberta. Here, the GWSA of these wells are considered as the reference information and the estimated downscaled GRACE GWSA are compared to them. Table 1 summarises the statistics of the differences between the use of each one of our methods in GRACE GWS downscaling and these wells in the study areas for the average of 31 days of December 2003.

Table 1.
Statistical metrics between the downscaled GRACE GWSA computed by the two proposed uncertainty methods and piezometric wells in Alberta (in the unit of mm in whole metrics except for correlation).
The well number and its geographic coordinates are given in the first three columns, see Figure 2. It should be stated that the compared wells are at a specific position are scattered and the downscaled GWSAs are in grid forms with much lower resolution. We had to linearly interpolate the GRACE GWSA to find the corresponding values. Table 1 shows that the downscaling based on Method 2 leads to a smaller standard deviation (STD) and root mean squares (RMS) of differences between the downscaled GRACE GWSA and those of wells in most of the wells (about 13 wells out of 16 wells). Moreover, the Pearson correlation extracted from Method 2 showed better consistency with wells when compared to Method 1 (11 wells in Method 2 had higher correlation compared to wells in Method 1). This means that the spectral downscaling based on the uncertainty estimation for the GLDAS model using Method 2 delivers closer GRACE GWSA to those of the piezometric wells.
In order to show the behaviour of the time series of the changes in a meaningful way, we have normalised the GWSA of wells and the interpolated downscaled one by subtracting their respective mean values and dividing the result to their standard deviations. In other words, we have standardised them for better visualisation. Some of these time series have been shown in Figure 12. Generally, the estimated GRACE GWSA have good agreements with those of the wells. Figure 12a–f are, respectively, the time series of variation in GWSA at wells number 1, 3, 6, 13, 14, and 15. We observe the significance of a proper uncertainty estimation strategy for the GLDAS hydrological parameters in spectral downscaling of GRACE models for estimating GWSA. As all these time series show, the variations in the GWSA where Method 2 was used for uncertainty estimation are closer to those of the wells than Method 1.
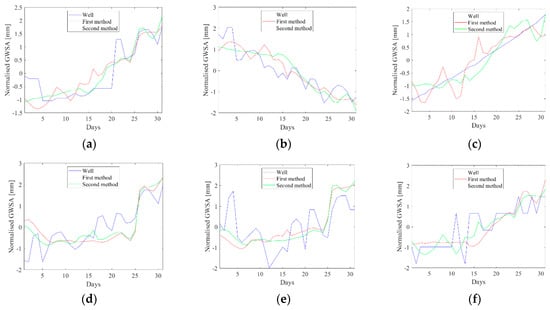
Figure 12.
Normalised time series of GWSA of wells and downscaled GRACE model extracted from two proposed methods of uncertainties, for wells number (a) 1, (b) 3, (c) 6, (d), 13, (e) 14, and (f) 15.
5. Discussion
The downscaling of GRACE data based on hydrological information has been the subject of various research studies. One approach proposed by Fatolazadeh et al. [8] is the application of spectral combination theory, which has been successfully used for the spatial downscaling of GRACE data over the Canadian prairies. This method was further developed to enable spatial and temporal downscaling of GRACE data, allowing for the estimation of daily TWSA and GWSA using monthly GRACE TWSA data in the spectral domain; see [9].
An important aspect of our methods, referred to as spectral downscaling in this study, is the estimation of uncertainties. The quality of hydrological parameters, particularly TWSA, plays a significant role in weighting GRACE and GLDAS TWSA data. However, this issue has not been adequately addressed in most studies on downscaling GRACE data. Merging data of different types with varying frequency content is problematic, and merging and combining data based on least-squares approaches or machine learning algorithms would only be meaningful if the differences between the merged data types were purely random in nature. It is crucial to consider the type of signal being input to the method and what is being obtained as a result. Here, we can refer to the work by Arshad et al. [35], where they downscale GRACE-based GWS variations using geographically weighted regression combined with results from a calibrated soil and water assessment tool (SWAT) model. While their results are promising, like other downscaling methods, the difference here is that we have considered the frequency contents of the signals. Another study by Ali et al. [36] used various machine learning techniques to downscale GRACE TWS and GWS datasets from 1° to 0.25° resolution. They obtained the best results with the extreme gradient boosting model. Ali et al. [37] also conducted a related study on this subject. While these methods are largely stochastic, ours is more deterministic or semi-stochastic. It is important to note that uncertainty estimation was not the primary focus in these studies, and the uncertainties of machine learning results were estimated by comparing them with a percentage of data not used in the training step. For a specific focus on uncertainty in GRACE-based GWS, Li et al. [56] conducted a study, primarily addressing the uncertainty of the GRACE models rather than the hydrological parameters.
In spectral downscaling, different signals at the same frequencies are combined considering their uncertainties. Therefore, realistic estimation of these uncertainties is essential. In this study, we propose a new method to address this goal and apply it to spectral downscaling of GRACE data. However, this method can also be applied to estimate the uncertainties of the GLDAS hydrological parameters for other purposes.
Finally, the results of correlation between GWSA derived from GRACE and wells proved that the quality of the results in the northern part of Alberta is better than the southern part. Some potential factors could explain this. First, the hydrogeological characteristics in the northern part of Alberta might be more homogeneous or exhibit more consistent groundwater behaviour compared to the southern region, resulting in a stronger correlation between the GRACE GWSA and well measurements. Second, groundwater extraction practices and patterns of water usage can differ between the north and south of Alberta, as there are fewer water-intensive activities or less groundwater extraction in the northern region. It may result in less interference with natural groundwater storage variations, and this reduced human influence can lead to a stronger correlation between satellite data and well measurements in the north. Finally, the northern part of Alberta may experience climate conditions that favour more reliable and consistent rainfall or snowmelt, resulting in a more pronounced correlation between GRACE satellite-derived GWSA and in situ well data.
One significant advantage of our downscaling method, when compared to other studies and methods, is that it operates in the spectral domain, allowing us to examine the frequency content of the TWS. In many other studies, errors in the hydrological models are not considered, and downscaling is performed in the spatial domain without considering the frequency characteristics of the hydrological and GRACE TWS signals.
Our uncertainty estimation methods can be enhanced by calibrating the estimated uncertainties using reliable sources. In our study, we made an assumption to create condition models, where the summation of soil moisture, snow water equivalent, canopy, and surface water equals terrestrial water storage (TWS). This assumption is a valid one in hydrology. However, when the summation is close to the TWS value, the misclosure approaches zero, which may lead to unrealistically small uncertainties, potentially falling below the sensor’s precision level in certain areas.
Further improvements to our method could be achieved by developing an integral estimator. However, since hydrological data is unavailable over oceans, we currently set the grid data over these regions to zero when estimating the signal and uncertainty spectral of the TWS. Unfortunately, the presence of zeroes in the spherical harmonic analysis, which is a global averaging process, weakens the signal. A potential improvement lies in creating a method for locally estimating the spectral properties of the hydrological parameters and their uncertainties. Certainly, such a precise theory and method, combined with future satellite gravity missions, which will provide high spatial and temporal resolution and precision, will significantly advance our understanding of the hydrological nature of the Earth’s system.
6. Conclusions
This study introduces a novel method for estimating the uncertainties in hydrological parameters within the GLDAS model. This method considers the magnitude of parameters to ensure a more accurate assessment of their quality. To evaluate these uncertainties, they were utilised in the spectral combination-based downscaling of GRACE products. The spectral combination method is highly sensitive to the uncertainties associated with merged data. Our comparative analysis revealed that spectral downscaling of GRACE data yielded superior results when employing this new method, method 2, for estimating the uncertainties within the GLDAS hydrological model. The downscaled groundwater storage anomalies and measurements from 16 piezometric wells in Alberta during December 2003 exhibited smaller standard deviations and root mean square errors when using this approach when compared with the older method, referred to as method 1 in our study. It is worth noting that the optimal uncertainties derived from our study can be readily applied to the spectral downscaling of GRACE data. Moreover, they can be incorporated into other downscaling techniques that require an accurate estimation of the uncertainties associated with the GLDAS parameters.
The findings presented in this paper are expected to make significant contributions to the advancement of downscaling methodologies and offer valuable insights for enhancing the accuracy of hydrological models. The proposed method provides a more robust framework for estimating uncertainties in GLDAS parameters, consequently enhancing the overall quality of downscaled GRACE data. Based on our comprehensive study, which revealed noteworthy uncertainties in daily GLDAS TWS data and monthly GRACE TWS data at a global scale, we recommend that policymakers allocate resources to improve data collection and measurement techniques for these variables. Furthermore, we advocate for efforts to transfer the GLDAS TWS data and its associated uncertainties into the spectral domain. This process will facilitate further analysis and application of our downscaling estimator, ultimately leading to improved accuracy in water resource management. Given the dynamic nature of hydrological conditions in various regions, our research findings can serve as essential inputs to inform decision-making processes. By incorporating the proposed downscaling methodology and addressing data uncertainties, policymakers can better respond to challenges posed by changing hydrological conditions and implement more effective water resource management strategies.
Author Contributions
Conceptualization, M.E. and F.F.; methodology, M.E.; software, F.F.; validation, M.E. and F.F.; formal analysis, M.E.; investigation, M.E.; resources, F.F.; data curation, F.F.; writing—original draft preparation, M.E.; writing—review and editing, F.F. and K.G.; visualization, M.E.; supervision, M.E. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by grants from the Natural Sciences and Engineering Research Council of Canada (NSERC Discovery Grant Number: RGPIN-2018-06101; and NSERC Create Grant: 543360-2020). We thank all data and product providers, University of Texas at Austin, Natural Resources Canada, and the Goddard Earth Sciences Data and Information Services Center (Greenbelt, MD, USA).
Data Availability Statement
The data that support the findings of this study are available upon reasonable request. Data are available from the authors farzam.fatolazadeh@usherbrooke.ca for researchers who meet the criteria for access to confidential data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Chao, N.; Jin, T.; Cai, Z.; Chen, G.; Liu, X.; Wang, Z.; Yeh, P.J.-F. Estimation of component contributions to total terrestrial water storage change in the Yangtze River Basin. J. Hydrol. 2021, 595, 125661. [Google Scholar] [CrossRef]
- Famiglietti, J. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Z.; Sang, Y.F.; Qian, J.; Feng, W.; Chen, X.; Zhou, Q. Temporal and spatial variations in the terrestrial water storage across Central Asia based on multiple satellite datasets and global hydrological models. J. Hydrol. 2021, 596, 126013. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Alley, W.M.; Konikow, L.F. Bringing GRACE down to earth. Groundwater 2015, 53, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Long, D.; Yang, W.; Li, X.; Pan, Y. Reconstruction of GRACE data on changes in total water storage over the global land surface and 60 basins. Water Resour. Res. 2020, 56, e2019WR026250. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Voosoghi, B.; Raoofian Naeeni, M. Wavelet and Gaussian approaches for estimation of groundwater variations using GRACE data. Groundwater 2015, 54, 74–81. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Goïta, K. Mapping terrestrial water storage changes in Canada using GRACE and GRACE-FO. Sci. Total Environ. 2021, 779, 146435. [Google Scholar] [CrossRef]
- Mohamed, A.; Abdelrady, A.; Alarifi, S.S.; Othman, A. Geophysical and Remote Sensing Assessment of Chad’s Groundwater Resources. Remote Sens. 2023, 15, 560. [Google Scholar] [CrossRef]
- Becker, A.; Braun, P. Disaggregation, aggregation and spatial scaling in hydrological modeling. J. Hydrol. 1999, 217, 239–252. [Google Scholar] [CrossRef]
- Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awange, J.L.; Schmidt, M.; Omondi, P.; Famiglietti, J. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote Sens. Environ. 2014, 140, 580–595. [Google Scholar] [CrossRef]
- Gemitzi, A.; Koutsias, N.; Venkataraman, L. A spatial downscaling methodology for GRACE total water storage anomalies using GPM IMERG precipitation estimates. Remote Sens. 2021, 13, 5149. [Google Scholar] [CrossRef]
- Zaitchik, B.; Rodell, M.; Reichle, R. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Schoof, J. Statistical downscaling in climatology. Geogr. Compass 2013, 7, 249–265. [Google Scholar] [CrossRef]
- Wilby, R.L.; Wigley, T.M.L.; Conway, D.; Jones, P.D.; Hewitson, B.C.; Main, J.; Wilks, D.S. Statistical downscaling of general circulation model output: A comparison of methods. Water Resour. Res. 1998, 34, 2995–3008. [Google Scholar] [CrossRef]
- Ning, S.; Ishidaira, H.; Wang, J. Statistical downscaling of GRACE-derived terrestrial water storage using satellite and GLDAS products. J. Japan Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2014, 70, I_133–I_138. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Zhang, J.; Sneeuw, N. Downscaling GRACE total water storage change using partial least squares regression. Sci. Data 2021, 8, 95. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Zhang, M.; Wang, J.; Han, S.-C. Statistical downscaling of GRACE-derived groundwater storage using ET data in the North China Plain. J. Geophys. Res. Atmos. 2018, 123, 5973–5987. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pham, Q.B.; Rahaman, M.M.; Dang, T.D.; Anh, D.T. Improving the resolution of GRACE data for spatio-temporal groundwater storage assessment. Remote Sens. 2021, 13, 3513. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Zhang, G.; Zhang, J. Improving the spatial resolution of GRACE-derived terrestrial water storage changes in small areas using the Machine Learning Spatial Downscaling Method. Remote Sens. 2021, 13, 4760. [Google Scholar] [CrossRef]
- He, H.; Yang, K.; Wang, S.; Petrosians, H.A.; Liu, M.; Li, J.; Marcato, J.J.; Goncalves, W.N.; Wang, L.; Li, J. Deep learning approaches to spatial downscaling of GRACE Terrestrial Water Storage Products using EALCO Model over Canada. Can. J. Remote Sens. 2021, 47, 657–675. [Google Scholar] [CrossRef]
- Milewski, A.M.; Thomas, M.B.; Seyoum, W.M.; Rasmussen, T.C. Spatial downscaling of GRACE TWSA data to identify spatiotemporal groundwater level trends in the Upper Floridan Aquifer, Georgia, USA. Remote Sens. 2019, 11, 2756. [Google Scholar] [CrossRef]
- Seyoum, W.; Kwon, D.; Milewski, A. Downscaling GRACE TWSA data into high-resolution groundwater level anomaly using machine learning-based models in a glacial aquifer system. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef]
- Chen, L.; He, Q.; Liu, K.; Li, J.; Jing, C. Downscaling of GRACE-derived groundwater storage based on the Random Forest model. Remote Sens. 2019, 11, 2979. [Google Scholar] [CrossRef]
- Zuo, J.; Xu, J.; Chen, Y.; Li, W. Downscaling simulation of groundwater storage in the Tarim River Basin in Northwest China based on GRACE data. Phys. Chem. Earth 2021, 123, 103042. [Google Scholar] [CrossRef]
- Lavado, C.J.; Maneta, M.; Schnabel, S. Prediction of near-surface soil moisture at large scale by digital terrain modeling and neural networks. Environ. Monit. Assess. 2006, 121, 213–232. [Google Scholar] [CrossRef]
- Miro, M.; Famiglietti, J. Downscaling GRACE remote sensing datasets to high-resolution groundwater storage change maps of California’s Central Valley. Remote Sens. 2018, 10, 143. [Google Scholar] [CrossRef]
- Seyoum, W.M.; Milewski, A.M. Improved methods for estimating local terrestrial water dynamics from GRACE in the Northern High Plains. Adv. Water Resour. 2017, 110, 279–290. [Google Scholar] [CrossRef]
- Shang, Q.; Liu, X.; Deng, X.; Zhang, B. Downscaling of GRACE datasets based on relevance vector machine using InSAR time series to generate maps of groundwater storage changes at local scale. J. Appl. Remote Sens. 2019, 13, 048503. [Google Scholar] [CrossRef]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.A.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T.M. Statistical applications to downscale GRACE-derived terrestrial water storage data and to fill temporal gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef]
- Wilby, R.L.; Charles, S.P.; Zorita, E.; Timbal, B.; Whetton, P.; Mearns, L.O. Guidelines for Use of Climate Scenarios Developed from Statistical Downscaling Methods. Task Group of Data and Scenario Support for Impacts and Climate Analysis (TGICA). Intergovernmental Panel on Climate Change. 2004. Available online: http://www.ipcc-data.org/guidelines/dgm_no1_v1_10-2003.pdf (accessed on 20 August 2017).
- Zhong, D.; Wang, S.; Li, J. A self-calibration variance-component model for spatial downscaling of GRACE observations using Land Surface Model outputs. Water Resour. Res. 2021, 57, e28944. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, S.; Li, J. Spatiotemporal downscaling of GRACE Total Water Storage using Land Surface Model outputs. Remote Sens. 2021, 13, 900. [Google Scholar] [CrossRef]
- Arshad, A.; Mirchi, A.; Samimi, M.; Ahmad, B. Combining downscaled-GRACE data with SWAT to improve the estimation of groundwater storage and depletion variations in the Irrigated Indus Basin (IIB). Sci. Total Environ. 2022, 838 Pt 2, 156044. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Jehanzeb, M.; Cheema, M.; Chandra Pal, S.; Arshad, A.; Bao, Q.P.; Zhang, L. Constructing high-resolution groundwater drought at spatio-temporal scale using GRACE satellite data based on machine learning in the Indus Basin. J. Hydrol. 2022, 612 Pt C, 128295. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Least squares combination of satellite harmonics and integral formulas in physical geodesy. Gerlands Beitr. Geophys. 1980, 89, 371–377. [Google Scholar]
- Sjöberg, L.E. Least squares combination of satellite and terrestrial data in physical geodesy. Ann. Geophys. 1981, 37, 25–30. [Google Scholar]
- Wenzel, H.G. Geoid computation by least squares spectral combination using integral kernels. In Proceedings of the International General Meeting of IAG, Tokyo, Japan, 7–15 May 1982; pp. 438–453. [Google Scholar]
- Eshagh, M. Spectral combination of vector gravimetric boundary value problems. Eng. J. Geospat. Inf. Syst. 2011, 1, 33–50. [Google Scholar] [CrossRef][Green Version]
- Eshagh, M. Spectral combination of spherical gradiometric boundary-value problems: A theoretical study. Pure Appl. Geophys. 2012, 169, 2201–2215. [Google Scholar] [CrossRef]
- Pitoňák, M.; Eshagh, M.; Šprlák, M.; Tenzer, R.; Novák, P. Spectral combination of spherical gravitational curvature boundary-value problems. Geophys. J. Int. 2018, 214, 773–791. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Eshagh, M. A theory on geoid modelling by spectral combination of data from satellite gravity gradiometry, terrestrial gravity and an Earth gravitational model. Acta Geod. Geophys. Hung. 2012, 47, 13–28. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Eshagh, M.; Goïta, K. New spectro-spatial downscaling approach for terrestrial and groundwater storage variations estimated by GRACE models. J. Hydrol. 2022, 615 Pt A, 128635. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Eshagh, M.; Goïta, K.; Wang, S. A new Spatiotemporal estimator to downscale GRACE gravity models for terrestrial and groundwater storage variations. Remote Sens. 2022, 14, 5991. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Eshagh, M. Satellite Gravimetry and the Solid Earth; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W H Freeman: San Francisco, CA, USA, 1967. [Google Scholar]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Gan, T.Y. Reducing vulnerability of water resources of Canadian Prairies to potential droughts and possible climatic warming. Water Resour. Manag. 2000, 14, 111–135. [Google Scholar] [CrossRef]
- Kromm, D.E. Water conservation in the irrigated prairies of Canada and the United States. Can. Water Resour. J. 1993, 18, 451–458. [Google Scholar] [CrossRef]
- Larocque, M.; Broda, S. Groundwater-surface water interactions in Canada. Can. Water Resour. J. 2016, 41, 451–454. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef]
- Fatolazadeh, F.; Goïta, K. Reconstructing groundwater storage variations from GRACE observations using a new Gaussian-Han-Fan (GHF) smoothing approach. J. Hydrol. 2022, 604, 127234. [Google Scholar] [CrossRef]
- Li, Q.; Pan, Y.; Zhang, C.; Gong, H. Quantifying Multi-Source Uncertainties in GRACE-Based Estimates of Groundwater Storage Changes in Mainland China. Remote Sens. 2023, 15, 2744. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).