Tracking Low-Frequency Variations in Land–Sea Water Mass Redistribution during the GRACE/GRACE-FO Era
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.1.1. GRACE/GRACE-FO-Derived Water Mass Data
2.1.2. ERA5 Reanalysis Data
2.2. Methods
2.2.1. Empirical Orthogonal Function (EOF)
2.2.2. Maximum Covariance Analysis (MCA)
2.2.3. Sea-Level Equation (SLE)
2.2.4. Pearson’s Correlation Coefficient (PCC)
2.2.5. Space-Similarity Coefficient (SC)
3. Results
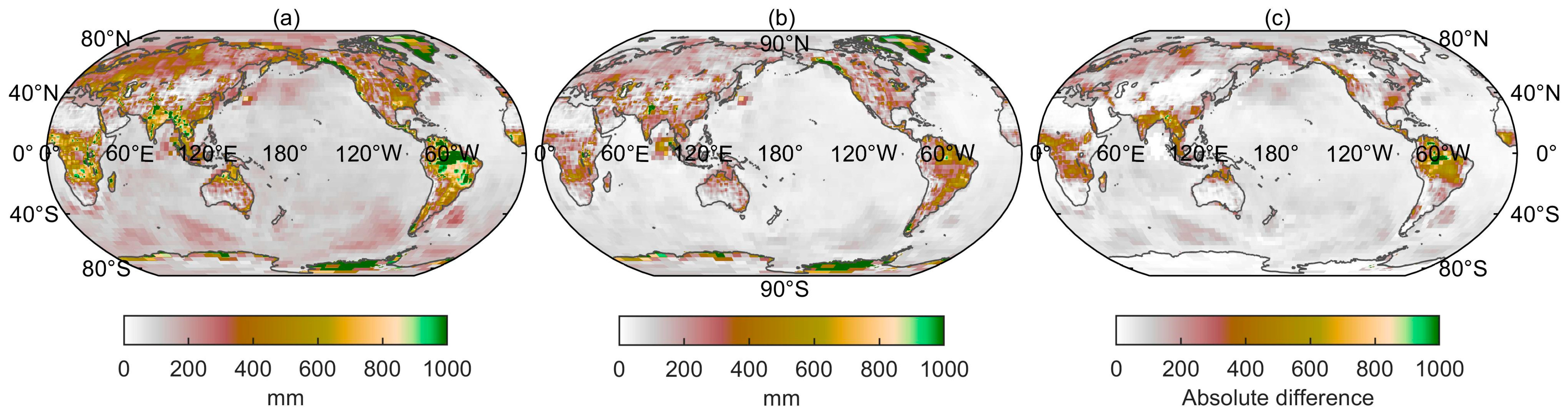
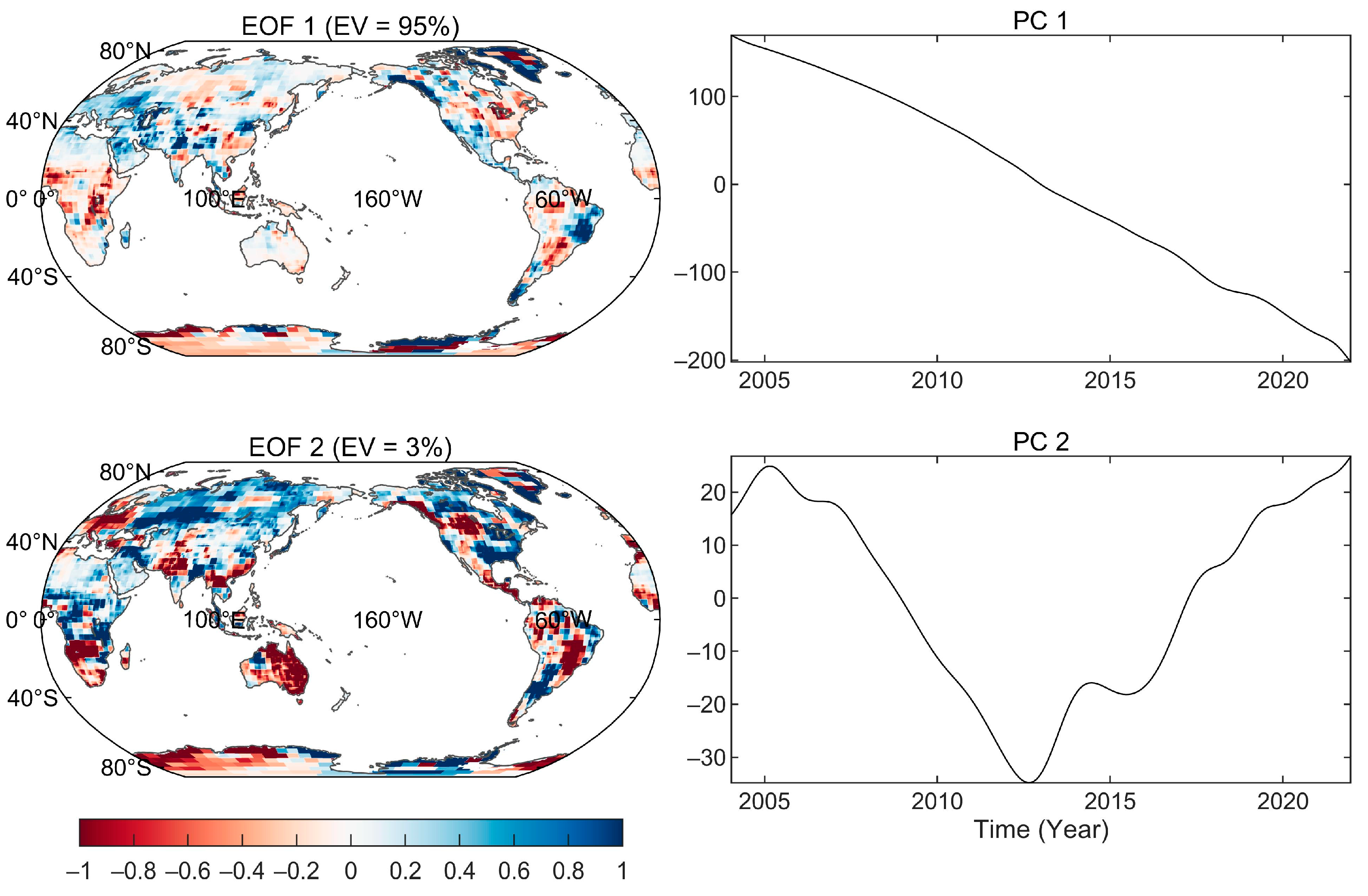
3.1. Spatio-Temporal Evolutionary Characteristics in TWS Anomalies
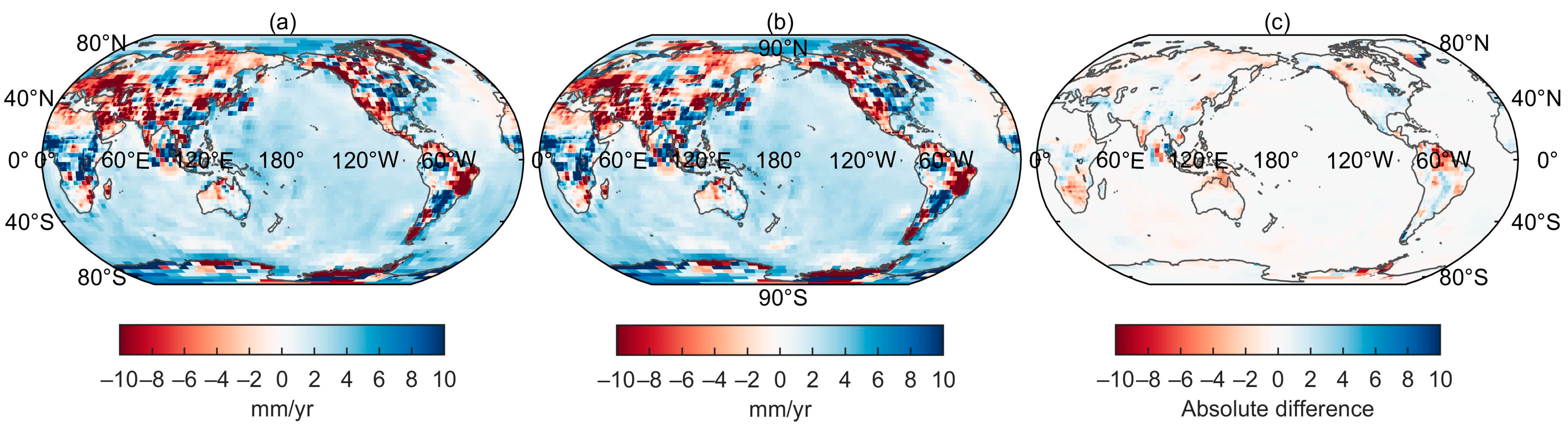
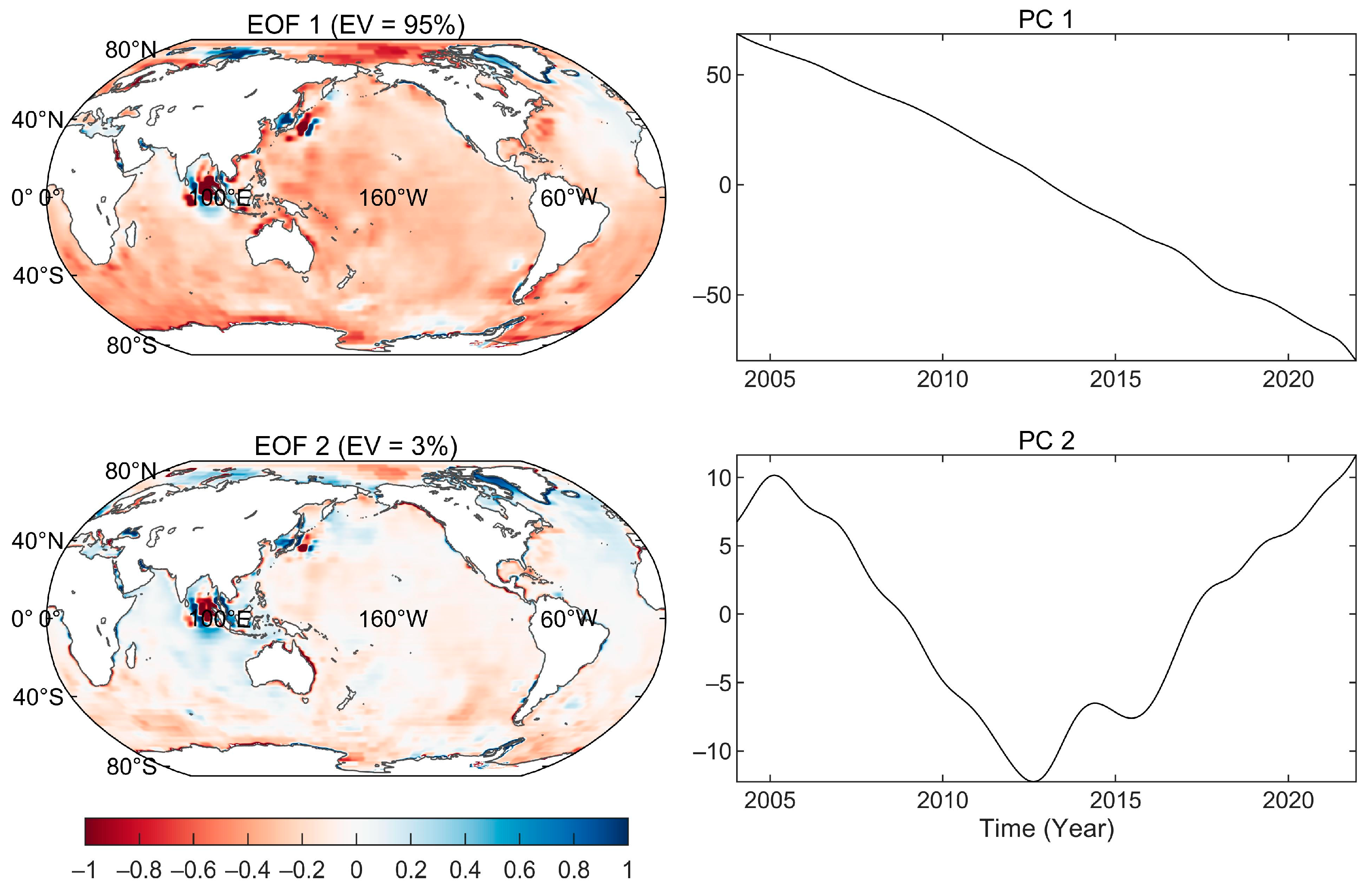
3.2. Spatio-Temporal Characteristics of Ocean Water Mass Anomalies
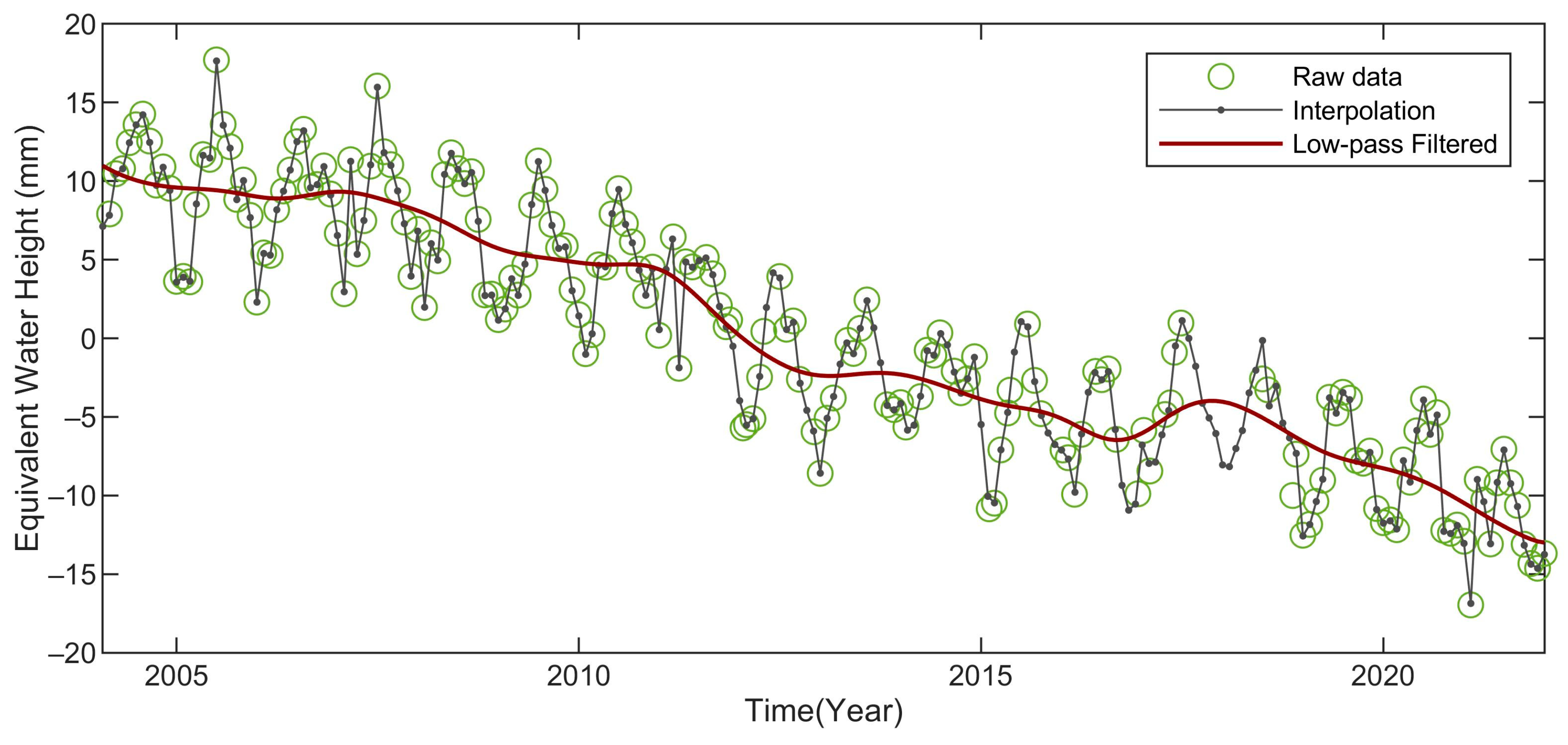
3.3. Low-Frequency Dynamic Ocean Mass Redistribution
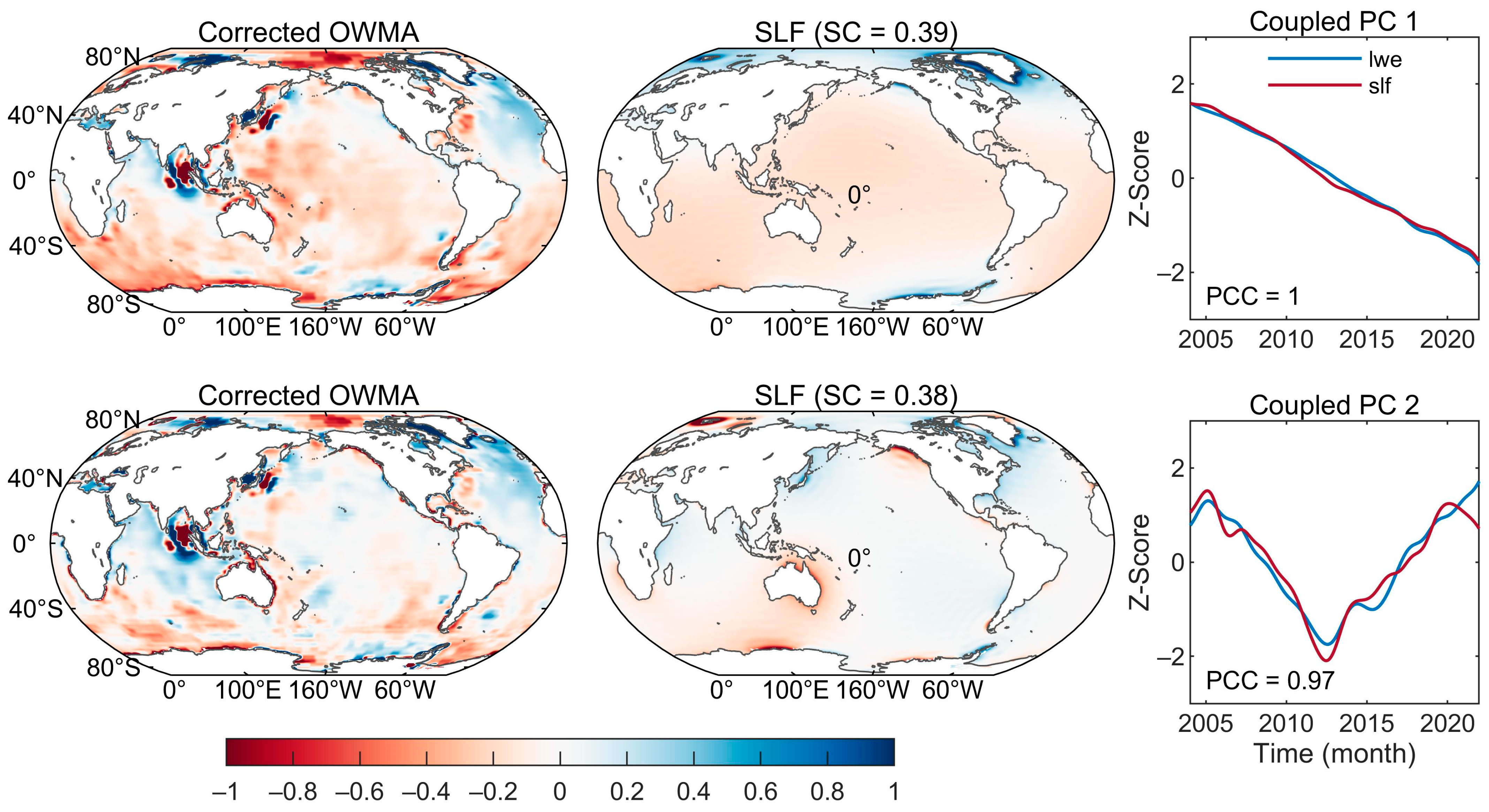
3.4. TWS-Related Ocean Water Mass Anomalies
3.5. Residuals of GRACE/GRACE-FO-Derived Ocean Mass Anomalies
4. Discussion
4.1. Impact of Climate Change and Human Activities on TWS
4.2. Attribution of Ocean Water Mass Redistribution
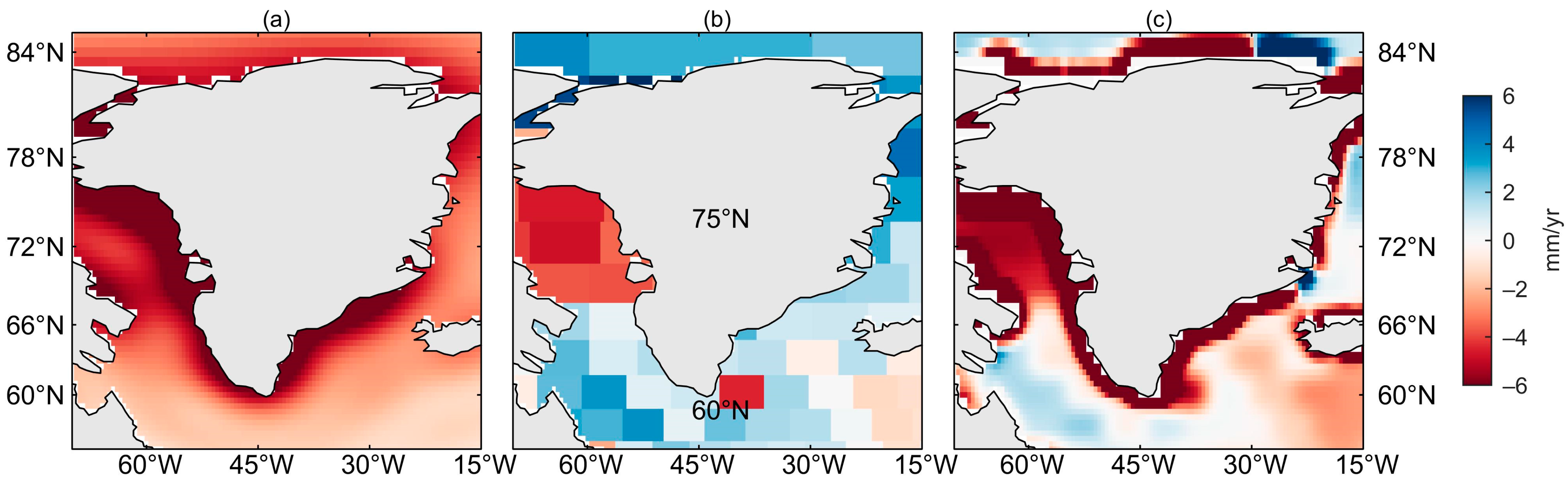
4.3. Comparing the SLFs Derived from Satellite Gravity and Satellite Altimetry
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, S.; Liu, S.; Mo, X.; Jiang, L.; Bauer-Gottwein, P. Polar drift in the 1990s explained by terrestrial water storage changes. Geophys. Res. Lett. 2021, 48, e2020GL092114. [Google Scholar] [CrossRef]
- Deng, S.; Liu, Y.; Zhang, W. A Comprehensive Evaluation of GRACE-Like Terrestrial Water Storage (TWS) Reconstruction Products at an Interannual Scale During 1981–2019. Water Resour. Res. 2023, 59, e2022WR034381. [Google Scholar] [CrossRef]
- Frederikse, T.; Landerer, F.; Caron, L.; Adhikari, S.; Parkes, D.; Humphrey, V.W.; Dangendorf, S.; Hogarth, P.; Zanna, L.; Cheng, L.; et al. The causes of sea-level rise since 1900. Nature 2020, 584, 393–397. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2021: The Physical Science Basis; Douville, H., Raghavan, K., Renwick, J., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Seo, K.-W.; Ryu, D.; Eom, J.; Jeon, T.; Kim, J.-S.; Youm, K.; Chen, J.; Wilson, C.R. Drift of Earth’s Pole Confirms Groundwater Depletion as a Significant Contributor to Global Sea Level Rise 1993–2010. Geophys. Res. Lett. 2023, 50, e2023GL103509. [Google Scholar] [CrossRef]
- Deng, S.; Liu, S.; Mo, X. Assessment of Three Common Methods for Estimating Terrestrial Water Storage Change with Three Reanalysis Datasets. J. Clim. 2020, 33, 511–525. [Google Scholar] [CrossRef]
- Deng, S.; Liu, S.; Mo, X. Assessment and attribution of China’s droughts using an integrated drought index derived from GRACE and GRACE-FO data. J. Hydrol. 2021, 603, 127170. [Google Scholar] [CrossRef]
- Farrell, W.E.; Clark, J.A. On Postglacial Sea Level. Geophys. J. R. Astron. Soc. 1976, 46, 647–667. [Google Scholar] [CrossRef]
- Haubrich, R., Jr.; Munk, W. The pole tide. J. Geophys. Res. 1959, 64, 2373–2388. [Google Scholar] [CrossRef]
- Coulson, S.; Dangendorf, S.; Mitrovica, J.X.; Tamisiea, M.E.; Pan, L.; Sandwell, D.T. A detection of the sea level fingerprint of Greenland Ice Sheet melt. Science 2022, 377, 1550–1554. [Google Scholar] [CrossRef]
- Adhikari, S.; Ivins, E.R.; Frederikse, T.; Landerer, F.W.; Caron, L. Sea-level fingerprints emergent from GRACE mission data. Earth Syst. Sci. Data 2019, 11, 629–646. [Google Scholar] [CrossRef]
- Gregory, J.M.; Griffies, S.M.; Hughes, C.W.; Lowe, J.A.; Church, J.A.; Fukimori, I.; Gomez, N.; Kopp, R.E.; Landerer, F.; Cozannet, G.L.; et al. Concepts and Terminology for Sea Level: Mean, Variability and Change, Both Local and Global. Surv. Geophys. 2019, 40, 1251–1289. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, S.-K.; Landerer, F.W.; Lumpkin, R. Decade-long deep-ocean warming detected in the subtropical South Pacific. Geophys. Res. Lett. 2017, 44, 927–936. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Gornitz, V. Global coastal hazards from future sea level rise. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1991, 89, 379–398. [Google Scholar] [CrossRef]
- Hauer, M.E.; Fussell, E.; Mueller, V.; Burkett, M.; Call, M.; Abel, K.; McLeman, R.; Wrathall, D. Sea-level rise and human migration. Nat. Rev. Earth Environ. 2020, 1, 28–39. [Google Scholar] [CrossRef]
- Melet, A.; Teatini, P.; Le Cozannet, G.; Jamet, C.; Conversi, A.; Benveniste, J.; Almar, R. Earth Observations for Monitoring Marine Coastal Hazards and Their Drivers. Surv. Geophys. 2020, 41, 1489–1534. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Velicogna, I. Detection of sea level fingerprints derived from GRACE gravity data. Geophys. Res. Lett. 2017, 44, 8953–8961. [Google Scholar] [CrossRef]
- Jeon, T.; Seo, K.-W.; Kim, B.-H.; Kim, J.-S.; Chen, J.; Wilson, C.R. Sea level fingerprints and regional sea level change. Earth Planet. Sci. Lett. 2021, 567, 116985. [Google Scholar] [CrossRef]
- Moreira, L.; Cazenave, A.; Barnoud, A.; Chen, J. Sea-Level Fingerprints Due to Present-Day Water Mass Redistribution in Observed Sea-Level Data. Remote Sens. 2021, 13, 4667. [Google Scholar] [CrossRef]
- Uebbing, B.; Rietbroek, R.; Kusche, J. Investigating global and regional sea level budgets by combining GRACE (-FO) and altimetry data in a joint fingerprint inversion. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-2190. [Google Scholar]
- Rietbroek, R.; Brunnabend, S.-E.; Kusche, J.; Schröter, J.; Dahle, C. Revisiting the contemporary sea-level budget on global and regional scales. Proc. Natl. Acad. Sci. USA 2016, 113, 1504–1509. [Google Scholar] [CrossRef] [PubMed]
- Zlotnicki, V.; Wahr, J.; Fukumori, I.; Song, Y.T. Antarctic Circumpolar Current Transport Variability during 2003–05 from GRACE. J. Phys. Oceanogr. 2007, 37, 230–244. [Google Scholar] [CrossRef]
- Bergmann, I.; Dobslaw, H. Short-term transport variability of the Antarctic Circumpolar Current from satellite gravity observations. J. Geophys. Res. Ocean. 2012, 117, C5. [Google Scholar] [CrossRef]
- Volkov, D.L.; Landerer, F.W. Nonseasonal fluctuations of the Arctic Ocean mass observed by the GRACE satellites. J. Geophys. Res. Ocean. 2013, 118, 6451–6460. [Google Scholar] [CrossRef]
- Petrick, C.; Dobslaw, H.; Bergmann-Wolf, I.; Schön, N.; Matthes, K.; Thomas, M. Low-frequency ocean bottom pressure variations in the North Pacific in response to time-variable surface winds. J. Geophys. Res. Ocean. 2014, 119, 5190–5202. [Google Scholar] [CrossRef]
- Yu, Y.; Chao, B.F.; García-García, D.; Luo, Z. Variations of the Argentine Gyre Observed in the GRACE Time-Variable Gravity and Ocean Altimetry Measurements. J. Geophys. Res. Ocean. 2018, 123, 5375–5387. [Google Scholar] [CrossRef]
- Rietbroek, R. Retrieval of Sea Level and Surface Loading Variations from Geodetic Observations and Model Simulations. Ph.D. Thesis, Universitäts-und Landesbibliothek Bonn, Bonn, Germany, 2014. [Google Scholar]
- Sun, Y.; Riva, R.; Ditmar, P.; Rietbroek, R. Using GRACE to explain variations in the Earth’s oblateness. Geophys. Res. Lett. 2019, 46, 158–168. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Tamisiea, M.E.; Save, H.; Wilson, C.; Bettadpur, S.; Seo, K.-W. Error Assessment of GRACE and GRACE Follow-On Mass Change. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022124. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Lorenz, E.N. Empirical Orthogonal Functions and Statistical Weather Prediction; Massachusetts Institute of Technology, Department of Meteorology: Cambridge, MA, USA, 1956; Volume 1. [Google Scholar]
- Barreto, N.J.C.; Mesquita, M.d.S.; Mendes, D.; Spyrides, M.H.C.; Pedra, G.U.; Lucio, P.S. Maximum covariance analysis to identify intraseasonal oscillations over tropical Brazil. Clim. Dyn. 2017, 49, 1583–1596. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.; Tapley, B. Satellite gravity measurements confirm accelerated melting of Greenland ice sheet. Science 2006, 313, 1958–1960. [Google Scholar] [CrossRef]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, L19503. [Google Scholar] [CrossRef]
- Rignot, E.; Velicogna, I.; van den Broeke, M.R.; Monaghan, A.; Lenaerts, J.T. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 2011, 38, L05503. [Google Scholar] [CrossRef]
- Sasgen, I.; Wouters, B.; Gardner, A.S.; King, M.D.; Tedesco, M.; Landerer, F.W.; Dahle, C.; Save, H.; Fettweis, X. Return to rapid ice loss in Greenland and record loss in 2019 detected by the GRACE-FO satellites. Commun. Earth Environ. 2020, 1, 8. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Quinn, K.J.; Ponte, R.M. Satellite-derived interannual ocean bottom pressure variability and its relation to sea level. Geophys. Res. Lett. 2013, 40, 3106–3110. [Google Scholar] [CrossRef]
- Naveira Garabato, A.C.; Dotto, T.S.; Hooley, J.; Bacon, S.; Tsamados, M.; Ridout, A.; Frajka-Williams, E.E.; Herraiz-Borreguero, L.; Holland, P.R.; Heorton, H.D.B.S.; et al. Phased Response of the Subpolar Southern Ocean to Changes in Circumpolar Winds. Geophys. Res. Lett. 2019, 46, 6024–6033. [Google Scholar] [CrossRef]
- Delforge, D.; de Viron, O.; Durand, F.; Dehant, V. The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records. Remote Sens. 2022, 14, 1861. [Google Scholar] [CrossRef]
- Zavialov, P.; Kostianoy, A.; Emelianov, S.; Ni, A.; Ishniyazov, D.; Khan, V.; Kudyshkin, T. Hydrographic survey in the dying Aral Sea. Geophys. Res. Lett. 2003, 30, 1659. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.H.; de Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef]
- Wang, J.; Song, C.; Reager, J.T.; Yao, F.; Famiglietti, J.S.; Sheng, Y.; MacDonald, G.M.; Brun, F.; Schmied, H.M.; Marston, R.A.; et al. Recent global decline in endorheic basin water storages. Nat. Geosci. 2018, 11, 926–932. [Google Scholar] [CrossRef]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef]
- Cheng, G.D.; Li, X. Integrated research methods in watershed science. Sci. China Earth Sci. 2015, 58, 1159–1168. [Google Scholar] [CrossRef]
- Ghobadi-Far, K.; Han, S.-C.; Allgeyer, S.; Tregoning, P.; Sauber, J.; Behzadpour, S.; Mayer-Gürr, T.; Sneeuw, N.; Okal, E. GRACE gravitational measurements of tsunamis after the 2004, 2010, and 2011 great earthquakes. J. Geod. 2020, 94, 65. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, S.; Jian, Z.; Liu, Y.; Yi, C.; Chen, Y.; Zhang, W. Tracking Low-Frequency Variations in Land–Sea Water Mass Redistribution during the GRACE/GRACE-FO Era. Remote Sens. 2023, 15, 4248. https://doi.org/10.3390/rs15174248
Deng S, Jian Z, Liu Y, Yi C, Chen Y, Zhang W. Tracking Low-Frequency Variations in Land–Sea Water Mass Redistribution during the GRACE/GRACE-FO Era. Remote Sensing. 2023; 15(17):4248. https://doi.org/10.3390/rs15174248
Chicago/Turabian StyleDeng, Shanshan, Zhenlong Jian, Yuxin Liu, Chushun Yi, Yi Chen, and Wenxi Zhang. 2023. "Tracking Low-Frequency Variations in Land–Sea Water Mass Redistribution during the GRACE/GRACE-FO Era" Remote Sensing 15, no. 17: 4248. https://doi.org/10.3390/rs15174248
APA StyleDeng, S., Jian, Z., Liu, Y., Yi, C., Chen, Y., & Zhang, W. (2023). Tracking Low-Frequency Variations in Land–Sea Water Mass Redistribution during the GRACE/GRACE-FO Era. Remote Sensing, 15(17), 4248. https://doi.org/10.3390/rs15174248








