Antarctic Time-Variable Regional Gravity Field Model Derived from Satellite Line-of-Sight Gravity Differences and Spherical Cap Harmonic Analysis
Abstract
1. Introduction
- GRACE (Gravity Recovery and Climate Experiment) was a joint mission between NASA and the German Aerospace Center. It consisted of two satellites in a polar orbit that provided highly accurate measurements of the Earth’s gravity field. Research such as [2,3,4,5,6] used GRACE data to estimate regional gravitational field models.
- Champ (Challenging Minisatellite Payload) was a German satellite that operated between 2000 and 2010. It also provided highly accurate gravity measurements and has been utilized by research such as [7] to estimate regional gravitational field models.
- GOCE (Gravity field and steady-state Ocean Circulation Explorer) was a European Space Agency mission that operated from 2009 to 2013. It was designed specifically for gravity measurements and provided highly accurate data. Research such as [8,9,10,11] used GOCE data to estimate regional gravitational field models.
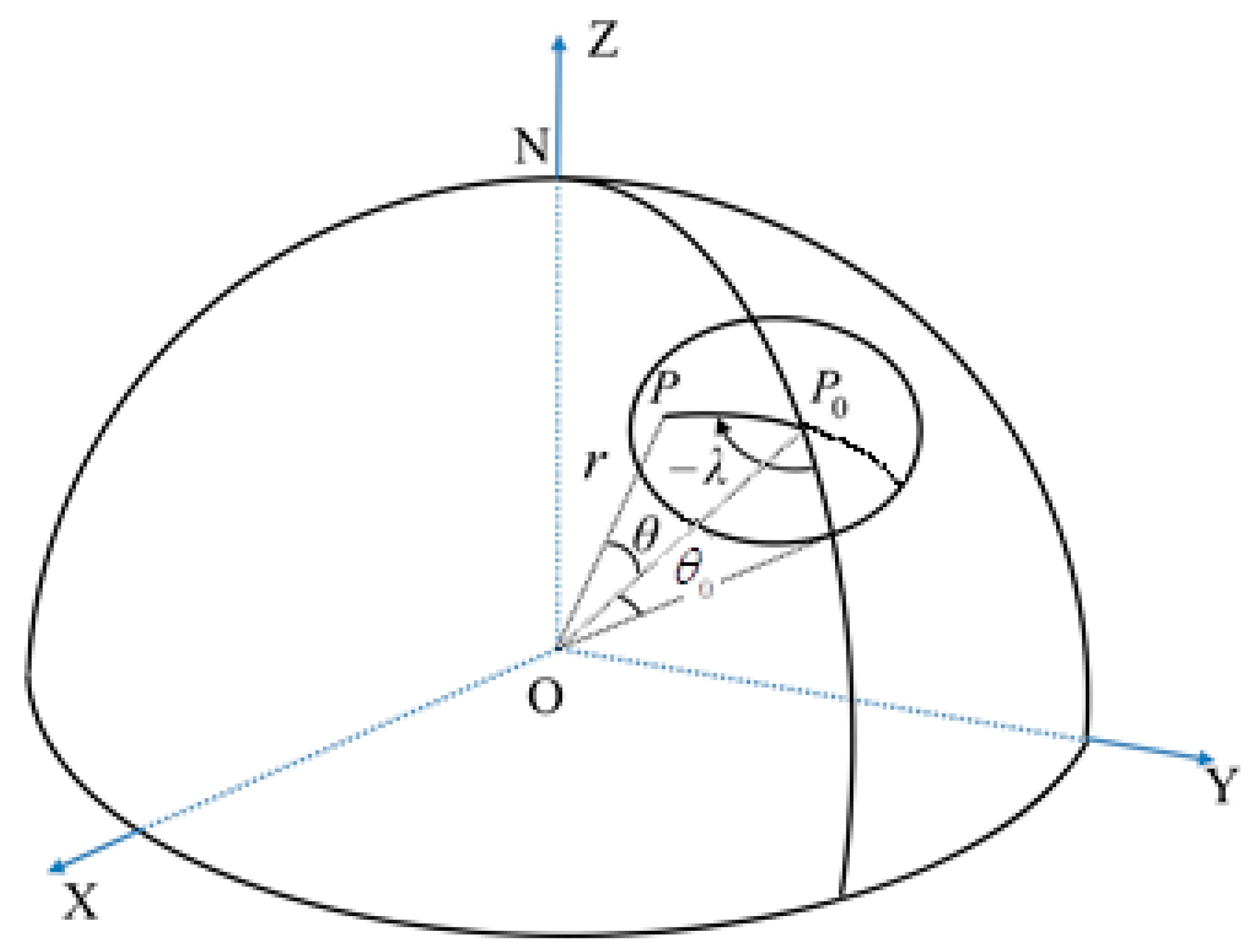
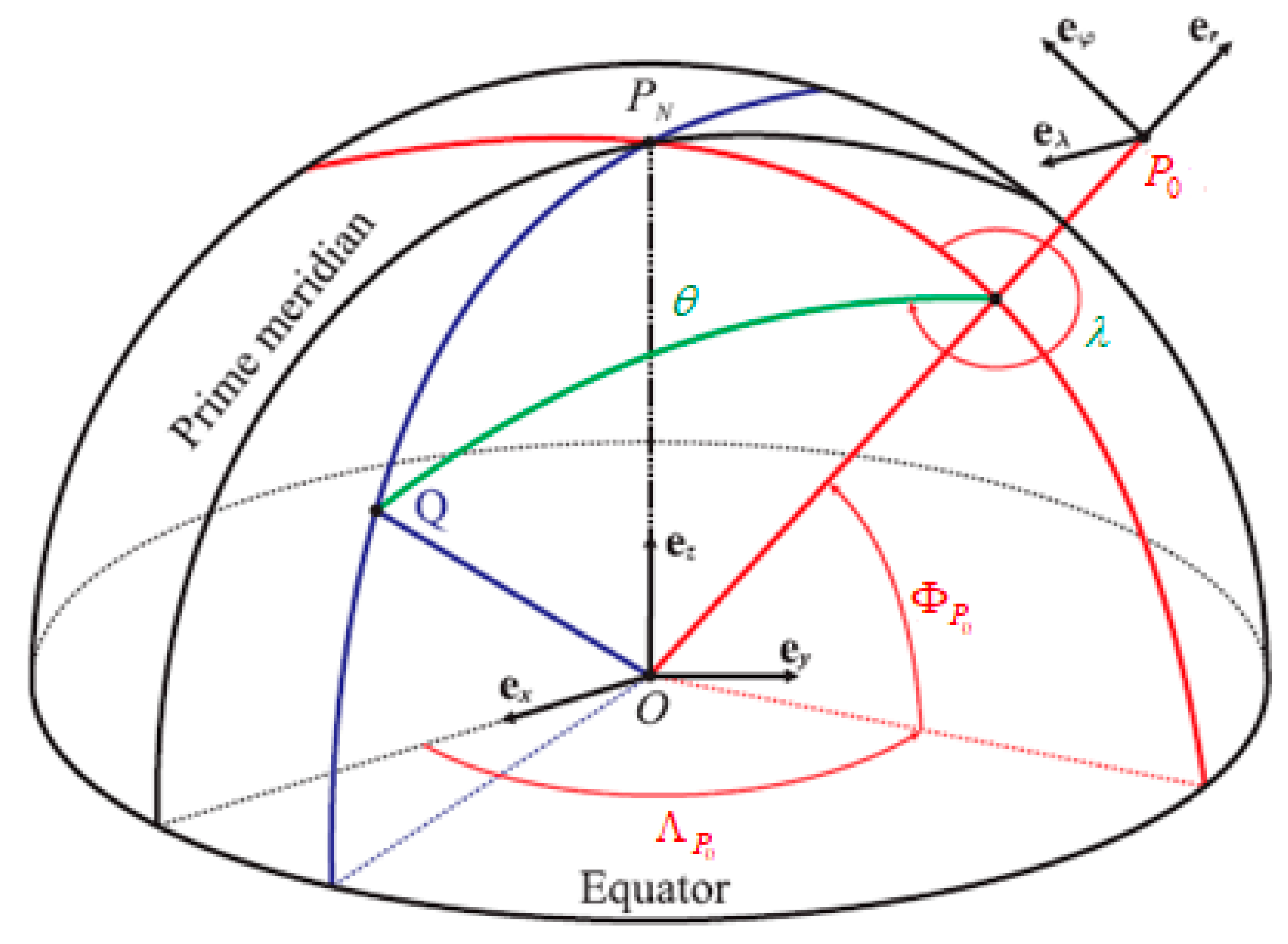
2. Spherical Cap Harmonics Analysis
3. Line-of-Sight Gravity Difference (LGD)
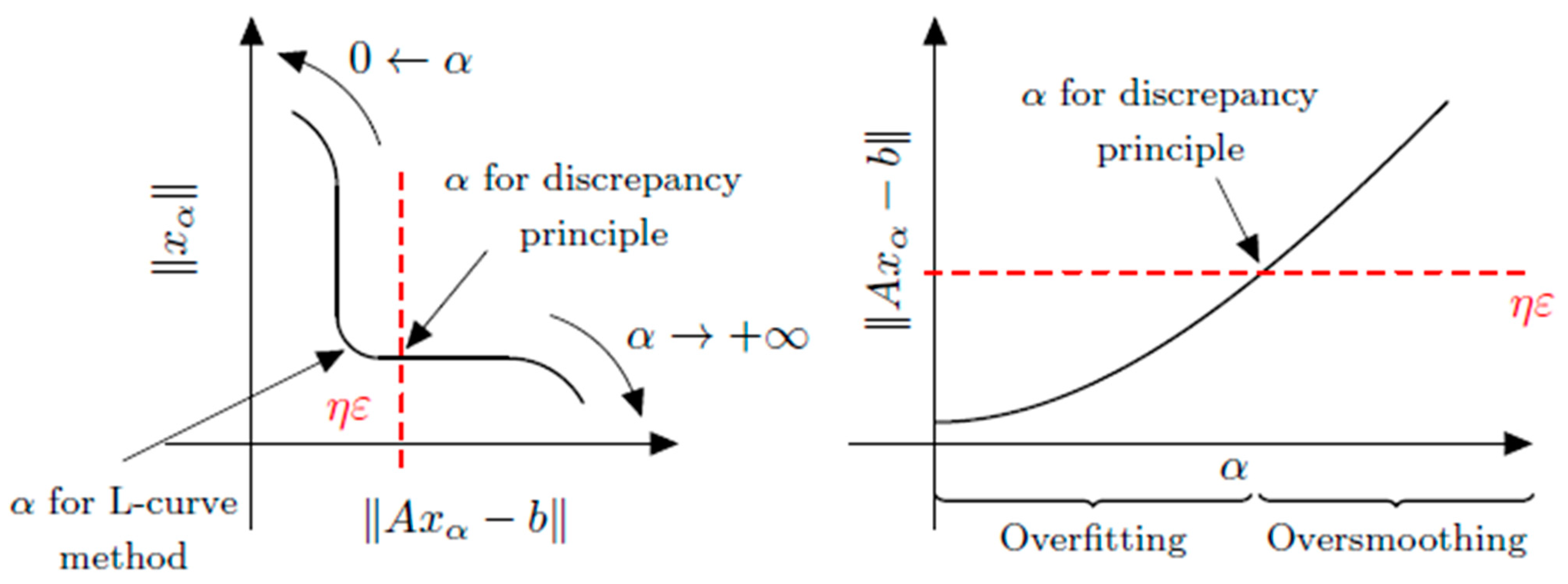
4. Numerical Analysis
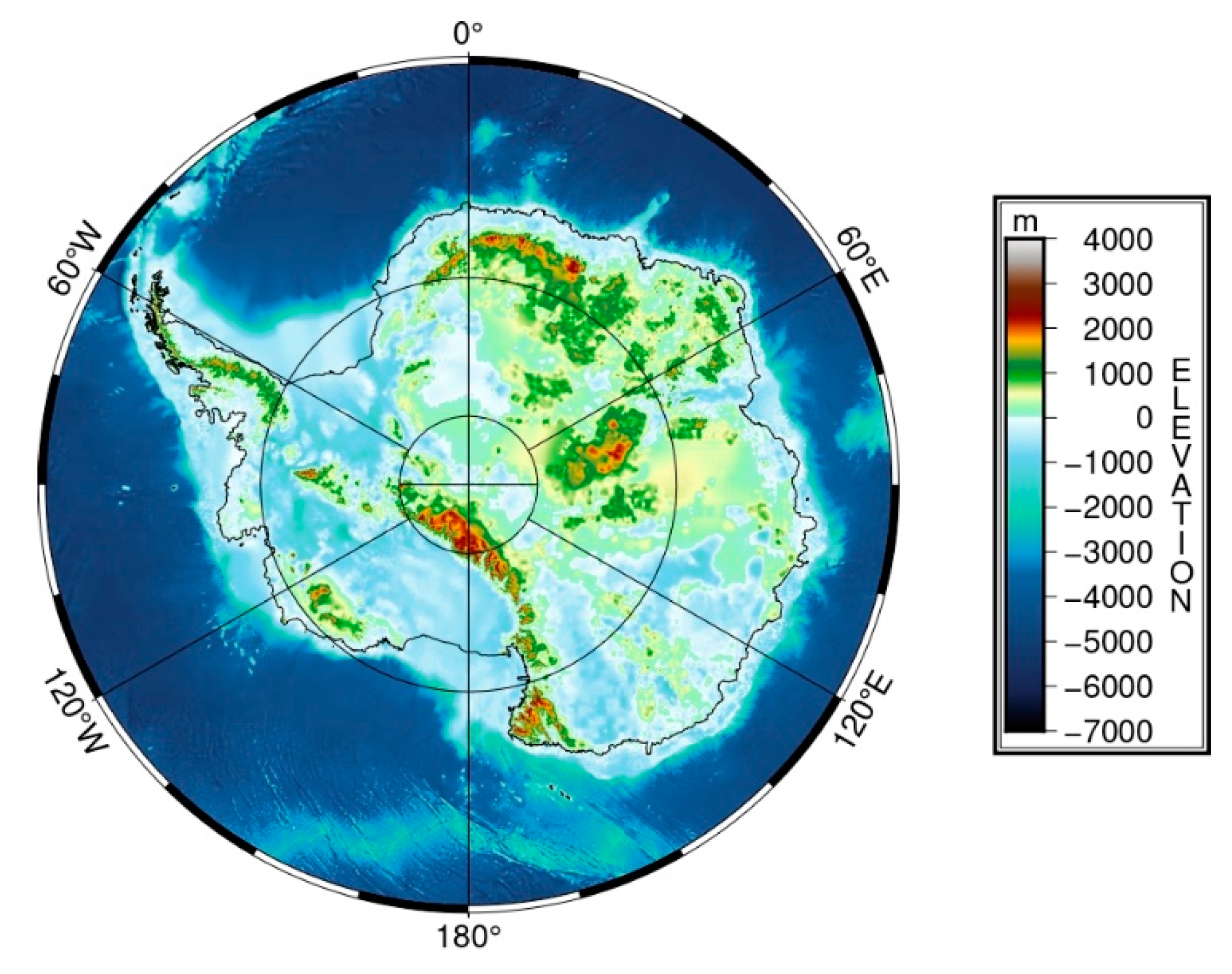
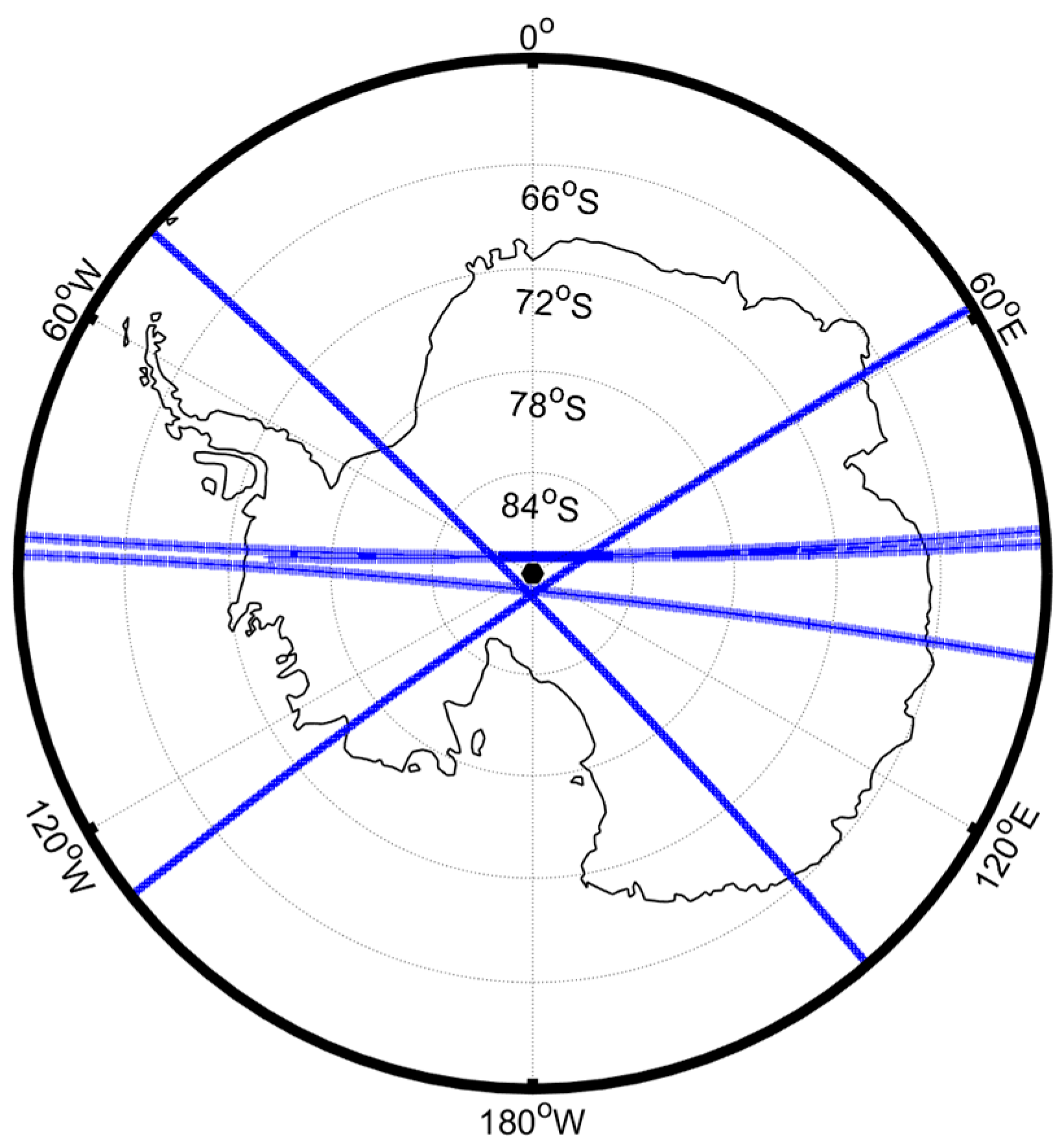
4.1. The Study Area
4.2. Antarctic Time-Variable Regional Gravity Field Model
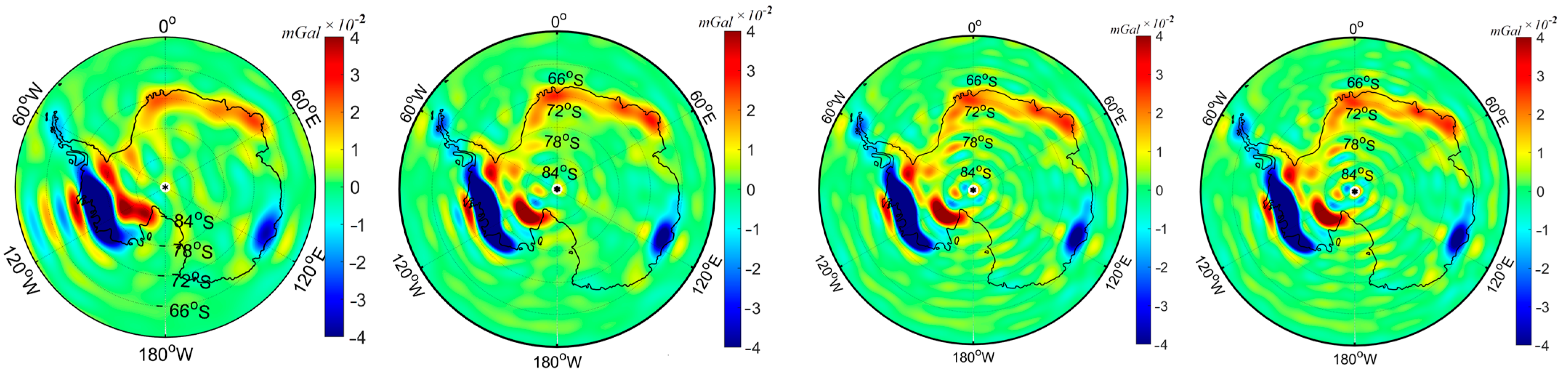
- In the first scenario, we first use the LGD data obtained from L2 JPL, and then we apply the SCHA basis function with capsize = and Kmax = 20. It corresponds to degree 60 in spherical harmonic and captures the majority of the time-variable gravity signal acquired during the GFO mission. This study discovers that by utilizing regional geo-potential coefficients, the radial component of the Earth’s gravitational field on the surface can be precisely determined, supporting the reliability of the regional harmonic basis functions in the study region.
- In the second scenario, after validation in the first scenario, the SCHA model is used to generate a local geo-potential model using LGD data from GFO Level 1B product to demonstrate the effectiveness of the regional harmonic basis function (SCHA) in providing more information about the gravity field of Antarctica, particularly in time-variable gravity fields. Moreover, we analyze the time-variable local geo-potential model using various degrees of harmonics. We calculate geo-potential coefficients of SCHA for different degrees of harmonics over Antarctica using LGD data to evaluate the performance of each degree in estimating the time-variable gravity field.
4.2.1. First Scenario: Antarctic Time-Variable Regional Gravity Field Model Using LGD Data Obtained from the L2 JPL
4.2.2. Second Scenario: Antarctic Time-Variable Regional Gravity Field Model Using LGD Data from GFO Level 1B Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eicker, A. Gravity Field Refinement by Radial Basis Functions from In-Situ Satellite Data; Citeseer: Princeton, NJ, USA, 2008. [Google Scholar]
- Schmidt, M.; Han, S.C.; Kusche, J.; Sanchez, L.; Shum, C.K. Regional high-resolution spatiotemporal gravity modeling from GRACE data using spherical wavelets. Geophys. Res. Lett. 2006, 33, L08403. [Google Scholar] [CrossRef]
- Yang, F.; Kusche, J.; Forootan, E.; Rietbroek, R. Passive-ocean radial basis function approach to improve temporal gravity recovery from GRACE observations. J. Geophys. Res. Solid Earth 2017, 122, 6875–6892. [Google Scholar] [CrossRef]
- Han, S.C.; Simons, F.J. Spatiospectral localization of global geopotential fields from the Gravity Recovery and Climate Experiment (GRACE) reveals the coseismic gravity change owing to the 2004 Sumatra-Andaman earthquake. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Klees, R.; Tenzer, R.; Prutkin, I.; Wittwer, T. A data-driven approach to local gravity field modelling using spherical radial basis functions. J. Geod. 2008, 82, 457–471. [Google Scholar] [CrossRef]
- Wittwer, T. Regional Gravity Field Modelling with Radial Basis Functions; Neighborhood Cinema Group: Owosso, MI, USA, 2009. [Google Scholar]
- Schmidt, M.; Fengler, M.; Mayer-Gürr, T.; Eicker, A.; Kusche, J.; Sánchez, L.; Han, S.C. Regional gravity modeling in terms of spherical base functions. J. Geod. 2007, 81, 17–38. [Google Scholar] [CrossRef]
- Bucha, B.; Bezděk, A.; Sebera, J.; Janák, J. Global and regional gravity field determination from GOCE kinematic orbit by means of spherical radial basis functions. Surv. Geophys. 2015, 36, 773–801. [Google Scholar] [CrossRef]
- Naeimi, M.; Flury, J.; Brieden, P. On the regularization of regional gravity field solutions in spherical radial base functions. Geophys. J. Int. 2015, 202, 1041–1053. [Google Scholar] [CrossRef]
- Pitoňák, M.; Šprlák, M.; Tenzer, R. Possibilities of inversion of satellite third-order gravitational tensor onto gravity anomalies: A case study for central Europe. Geophys. J. Int. 2017, 209, 799–812. [Google Scholar] [CrossRef]
- Naeimi, M.; Bouman, J. Contribution of the GOCE gradiometer components to regional gravity solutions. Geophys. J. Int. 2017, 209, 559–569. [Google Scholar] [CrossRef]
- Ghobadi-Far, K.; Han, S.-C.; Allgeyer, S.; Tregoning, P.; Sauber, J.; Behzadpour, S.; Mayer-Gürr, T.; Sneeuw, N.; Okal, E. GRACE gravitational measurements of tsunamis after the 2004, 2010, and 2011 great earthquakes. J. Geod. 2020, 94, 65. [Google Scholar] [CrossRef]
- Ghobadi-Far, K.; Han, S.; Weller, S.; Loomis, B.D.; Luthcke, S.B.; Mayer-Gürr, T.; Behzadpour, S. A transfer function between line-of-sight gravity difference and GRACE intersatellite ranging data and an application to hydrological surface mass variation. J. Geophys. Res. Solid Earth 2018, 123, 9186–9201. [Google Scholar] [CrossRef]
- Ghobadi-Far, K.; Han, S.C.; McCullough, C.M.; Wiese, D.N.; Ray, R.D.; Sauber, J.; Shihora, L.; Dobslaw, H. Along-orbit analysis of GRACE Follow-On inter-satellite laser ranging measurements for sub-monthly surface mass variations. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022983. [Google Scholar] [CrossRef]
- Müller, J.; Riedel, S.; Scheinert, M.; Howath, M.; Dietrich, R.; Steinhage, D.; Anschütz, H.; Jokat, W. Regional Geoid and Gravity Field from a Combination of Airborne and Satellite Data in Dronning Maud Land, East Antarctica. 2007. Proceedings of the 10th ISAES, hdl:10013/epic.26719. Available online: https://epic.awi.de/id/eprint/16885/ (accessed on 19 May 2023).
- Scheinert, M.; Müller, J.; Dietrich, R.; Damaske, D.; Damm, V. Regional geoid determination in Antarctica utilizing airborne gravity and topography data. J. Geod. 2008, 82, 403–414. [Google Scholar] [CrossRef]
- Scheinert, M. Progress and prospects of the antarctic geoid project (Commission Project 2.4). In Geodesy for Planet Earth: Proceedings of the 2009 IAG Symposium, Buenos Aires, Argentina, 31 August–4 September 2009; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Schwabe, J.; Ewert, H.; Scheinert, M.; Dietrich, R. Regional geoid modeling in the area of subglacial Lake Vostok, Antarctica. J. Geodyn. 2014, 75, 9–21. [Google Scholar] [CrossRef]
- Schwabe, J.; Scheinert, M. Regional geoid of the Weddell Sea, Antarctica, from heterogeneous ground-based gravity data. J. Geod. 2014, 88, 821–838. [Google Scholar] [CrossRef]
- Hirt, C.; Rexer, M.; Scheinert, M.; Pail, R.; Claessens, S.; Holmes, S. A new degree-2190 (10 km resolution) gravity field model for Antarctica developed from GRACE, GOCE and Bedmap2 data. J. Geod. 2016, 90, 105–127. [Google Scholar] [CrossRef]
- De Santis, A.; Kerridge, D.; Barraclough, D. A spherical cap harmonic model of the crustal magnetic anomaly field. Geomagn. Palaeomagnetism 2012, 261, 1–19. [Google Scholar]
- Nahayo, E.; Kotzé, P.; Webb, S. Application of Spherical Cap Harmonic Analysis on CHAMP satellite data to develop a lithospheric magnetic field model over southern Africa at satellite altitude. S. Afr. J. Geol. 2019, 122, 163–172. [Google Scholar] [CrossRef]
- Nevanlinna, H.; Rynö, J.; Haines, G.V.; Borg, K. Spherical cap harmonic analysis applied to the Scandinavian geomagnetic field 1985.0. Dtsch. Hydrogr. Z. 1988, 41, 177–186. [Google Scholar] [CrossRef]
- Ou, J.; Du, A.; Thébault, E.; Xu, W.; Tian, X.; Zhang, T. A high resolution lithospheric magnetic field model over China. Sci. China Earth Sci. 2013, 56, 1759–1768. [Google Scholar] [CrossRef]
- Pavon-Carrasco, F.J.; Osete, M.L.; Torta, J.M.; Gaya-Piqué, L.R.; Lanos, P. Initial SCHA. DI. 00 regional archaeomagnetic model for Europe for the last 2000 years. Phys. Chem. Earth Parts A/B/C 2008, 33, 596–608. [Google Scholar] [CrossRef]
- Stening, R.; Reztsova, T.; Ivers, D.; Turner, J.; Winch, D.E. Spherical cap harmonic analysis of magnetic variations data from mainland Australia. Earth Planets Space 2008, 60, 1177–1186. [Google Scholar] [CrossRef]
- Talarn, À.; Pavón-Carrasco, F.J.; Torta, J.M.; Catalán, M. Evaluation of using R-SCHA to simultaneously model main field and secular variation multilevel geomagnetic data for the North Atlantic. Phys. Earth Planet. Inter. 2017, 263, 55–68. [Google Scholar] [CrossRef]
- Taylor, P.; Kis, K.I.; Puszta, S.; Wittmann, G.; Kim, H.R. Interpretation of CHAMP magnetic anomaly data over the Pannonian Basin region using lower altitude and gradient data. In Proceedings of the International Association of Geomagnetism and Aeronomy IAGA 11. Scientific Assembly, Sopron, Hungary, 23–30 August 2009. [Google Scholar]
- Thébault, E.; Gaya-Piqué, L. Applied comparisons between SCHA and R-SCHA regional modeling techniques. Geochem. Geophys. Geosystems 2008, 9. [Google Scholar] [CrossRef]
- Thébault, E.; Mandea, M.; Schott, J. Modeling the lithospheric magnetic field over France by means of revised spherical cap harmonic analysis (R-SCHA). J. Geophys. Res. Solid Earth 2006, 111, B05102. [Google Scholar] [CrossRef]
- Torta, J.M.; Gaya-Piqué, L.R.; De Santis, A. Spherical Cap Harmonic Analysis of the Geomagnetic Field with Application for Aeronautical Mapping. In Geomagnetics for Aeronautical Safety: A Case Study in and Around the Balkans; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Walker, J.K. Spherical cap harmonic modelling of high latitude magnetic activity and equivalent sources with sparse observations. J. Atmos. Terr. Phys. 1989, 51, 67–80. [Google Scholar] [CrossRef]
- Haines, G.; Torta, J. Determination of equivalent current sources from spherical cap harmonic models of geomagnetic field variations. Geophys. J. Int. 1994, 118, 499–514. [Google Scholar] [CrossRef]
- Haines, G. Modelling the geomagnetic field by the method of spherical cap harmonic analysis. HHI Rep. 1987, 21, 27–34. [Google Scholar]
- Feng, Y.; Jiang, Y.; Jiang, Y.; Liu, B.-J.; Jiang, J.; Liu, Z.-W.; Ye, M.-C.; Wang, H.-S.; Li, X.-M. Spherical cap harmonic analysis of regional magnetic anomalies based on CHAMP satellite data. Appl. Geophys. 2016, 13, 561–569. [Google Scholar] [CrossRef]
- De Santis, A.; Kerridge, D.; Barraclough, D. A Spherical Cap Harmonic Model of the Crustal Magnetic Anomaly Field in Europe Observed by Magsat; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Haines, G.V. Spherical cap harmonic analysis. J. Geophys. Res. Solid Earth 1985, 90, 2583–2591. [Google Scholar] [CrossRef]
- Feizi, M.; Raoofian-Naeeni, M.; Han, S.-C. Comparison of spherical cap and rectangular harmonic analysis of airborne vector gravity data for high-resolution (1.5 km) local geopotential field models over Tanzania. Geophys. J. Int. 2021, 227, 1465–1479. [Google Scholar] [CrossRef]
- Wang, J.; Wu, K. Construction of regional geoid using a virtual spherical harmonics model. J. Appl. Geod. 2019, 13, 151–158. [Google Scholar] [CrossRef]
- De Santis, A.; Torta, J. Spherical cap harmonic analysis: A comment on its proper use for local gravity field representation. J. Geod. 1997, 71, 526–532. [Google Scholar] [CrossRef]
- Rummel, R. Determination of short-wavelength components of the gravity field from satellite-to-satellite tracking or satellite gradiometry. Manuscr. Geod. 1979, 4, 107–148. [Google Scholar]
- Šprlák, M.; Han, S.-C.; Featherstone, W. Integral inversion of GRAIL inter-satellite gravitational accelerations for regional recovery of the lunar gravitational field. Adv. Space Res. 2020, 65, 630–649. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization tools: A Matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 1994, 6, 1–35. [Google Scholar] [CrossRef]
- Schenkels, N.; Vanroose, W. Projected Newton method for a system of Tikhonov-Morozov equations. arXiv 2018, arXiv:1809.01627. [Google Scholar]
- Barriot, J.; Balmino, G. Estimation of local planetary gravity fields using line of sight gravity data and an integral operator. Icarus 1992, 99, 202–224. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Change 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Shi, T.; Fukuda, Y.; Doi, K.; Okuno, J. Extraction of GRACE/GRACE-FO observed mass change patterns across Antarctica via independent component analysis (ICA). Geophys. J. Int. 2022, 229, 1914–1926. [Google Scholar] [CrossRef]
- Harig, C.; Simons, F.J. Accelerated West Antarctic ice mass loss continues to outpace East Antarctic gains. Earth Planet. Sci. Lett. 2015, 415, 134–141. [Google Scholar] [CrossRef]




| RMSE | Mean | ||
|---|---|---|---|
| LGD | 1.5735 × 10−6 | 8.0426 × 10−7 | 20 |
| Radial component | 4.0089 × 10−4 | 2.0707 × 10−4 |
| Data Set | Reference Field | True Field | Filter | Altitude | Length |
|---|---|---|---|---|---|
| 1 | ITG GRACE 2010 (d/o 60) | CSR-R05b August 2002 (d/o 60) | DDK6 | 500 | 10 days |
| 2 | ITG GRACE 2010 (d/o 60) | CSR-R05 August 2002 (d/o 60) | DDK4 | 400 | 10 days |
| 3 | ITG GRACE 2010 (d/o 60) | CSR-R05 August 2002 (d/o 60) | DDK2 | 300 | 10 days |
| 4 | Static gravity and better-known geophysical signals such as ocean tide as for March 2004 | NASA GSFC mascon March 2004 (d/o 90) | - | 487 | 1 month |
| 5 | Static gravity and better-known geophysical signals such as ocean tide for March 2016 | NASA GSFC mascon March 2016 (d/o 90) | - | 377 | 1 month |
| Method | RMSE | Mean | |
|---|---|---|---|
| SCHA | 3.7133 × 10−4 | 2.2307 × 10−4 | 20 |
| L2 | 6.3598 × 10−4 | −2.9193 × 10−5 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feizi, M.; Raoofian Naeeni, M.; Flury, J. Antarctic Time-Variable Regional Gravity Field Model Derived from Satellite Line-of-Sight Gravity Differences and Spherical Cap Harmonic Analysis. Remote Sens. 2023, 15, 2815. https://doi.org/10.3390/rs15112815
Feizi M, Raoofian Naeeni M, Flury J. Antarctic Time-Variable Regional Gravity Field Model Derived from Satellite Line-of-Sight Gravity Differences and Spherical Cap Harmonic Analysis. Remote Sensing. 2023; 15(11):2815. https://doi.org/10.3390/rs15112815
Chicago/Turabian StyleFeizi, Mohsen, Mehdi Raoofian Naeeni, and Jakob Flury. 2023. "Antarctic Time-Variable Regional Gravity Field Model Derived from Satellite Line-of-Sight Gravity Differences and Spherical Cap Harmonic Analysis" Remote Sensing 15, no. 11: 2815. https://doi.org/10.3390/rs15112815
APA StyleFeizi, M., Raoofian Naeeni, M., & Flury, J. (2023). Antarctic Time-Variable Regional Gravity Field Model Derived from Satellite Line-of-Sight Gravity Differences and Spherical Cap Harmonic Analysis. Remote Sensing, 15(11), 2815. https://doi.org/10.3390/rs15112815






