Predict Seasonal Maximum Freezing Depth Changes Using Machine Learning in China over the Last 50 Years
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods
2.1.1. Selection of Feature Input Variables
2.1.2. Constructing a Reasonable Model
2.1.3. Predicting the Maximum Freezing Depth
2.2. Data
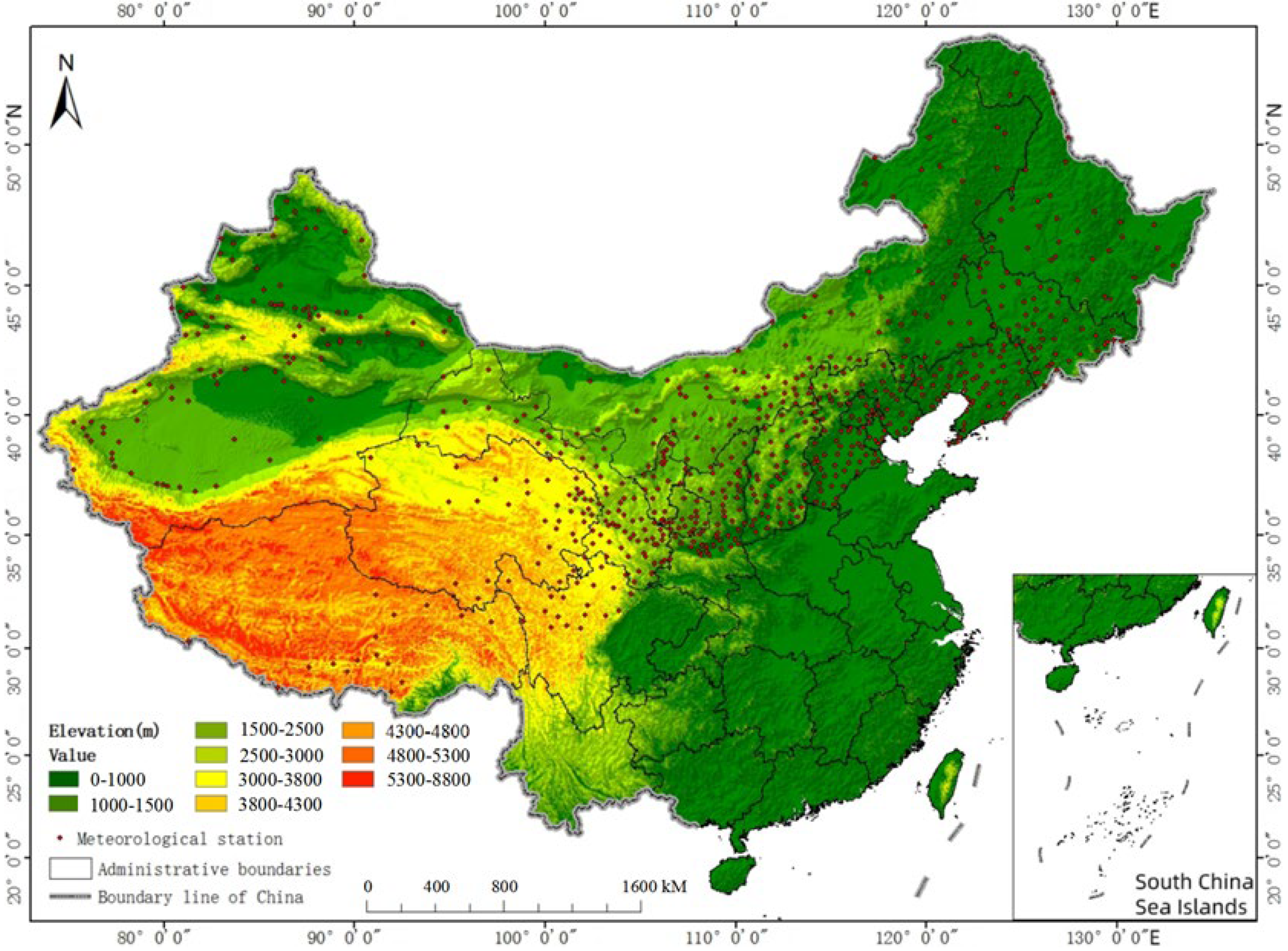
2.2.1. Maximum Freezing Depth Monitoring Data
2.2.2. Climate Data
- We processed the raw data in the temperature element file to form daily average data, and converted the unit of the data to Celsius and the file format to grid data.
- We distinguished between positive and negative values in the daily temperature grid data. The positive and negative values in the annual daily temperature grid data were separated. Finally, the annual positive accumulated temperature grid data and the annual negative accumulated temperature grid data were obtained.
- We added the negative accumulated temperature grid data in the second half of a year to the negative accumulated temperature grid data in the first half of the adjacent years. The cross year negative accumulated temperature grid data were thus obtained.
- We processed grid data such as precipitation, snow depth, and solar radiation into the annual average grid data.
2.2.3. Soil Data
2.2.4. Digital Elevation Model (DEM)
2.2.5. Data Aggregation and Preprocessing
3. Results
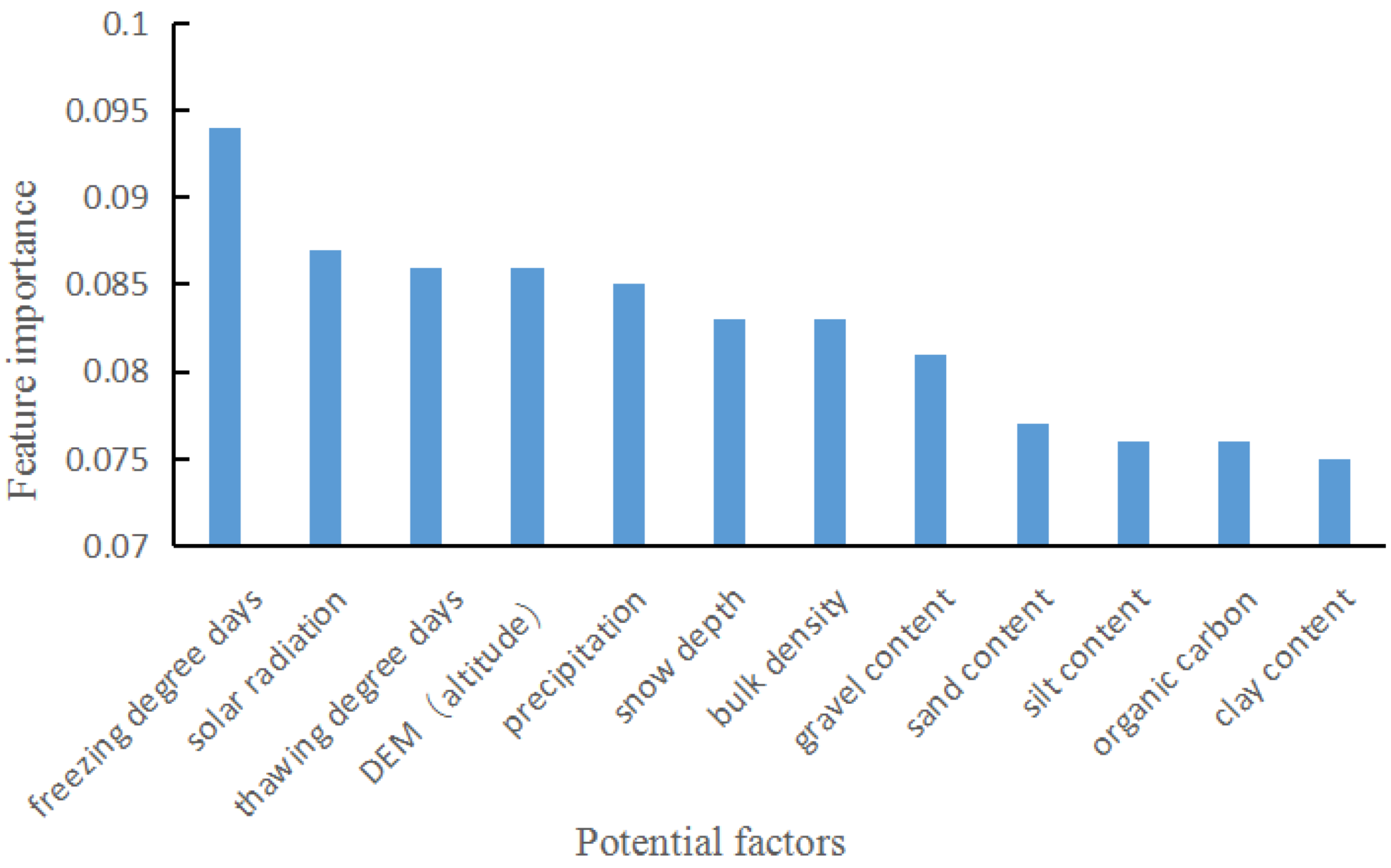
3.1. Optimization of Feature Input Variables
3.2. Comparison of Machine-Learning Models (MLMs)
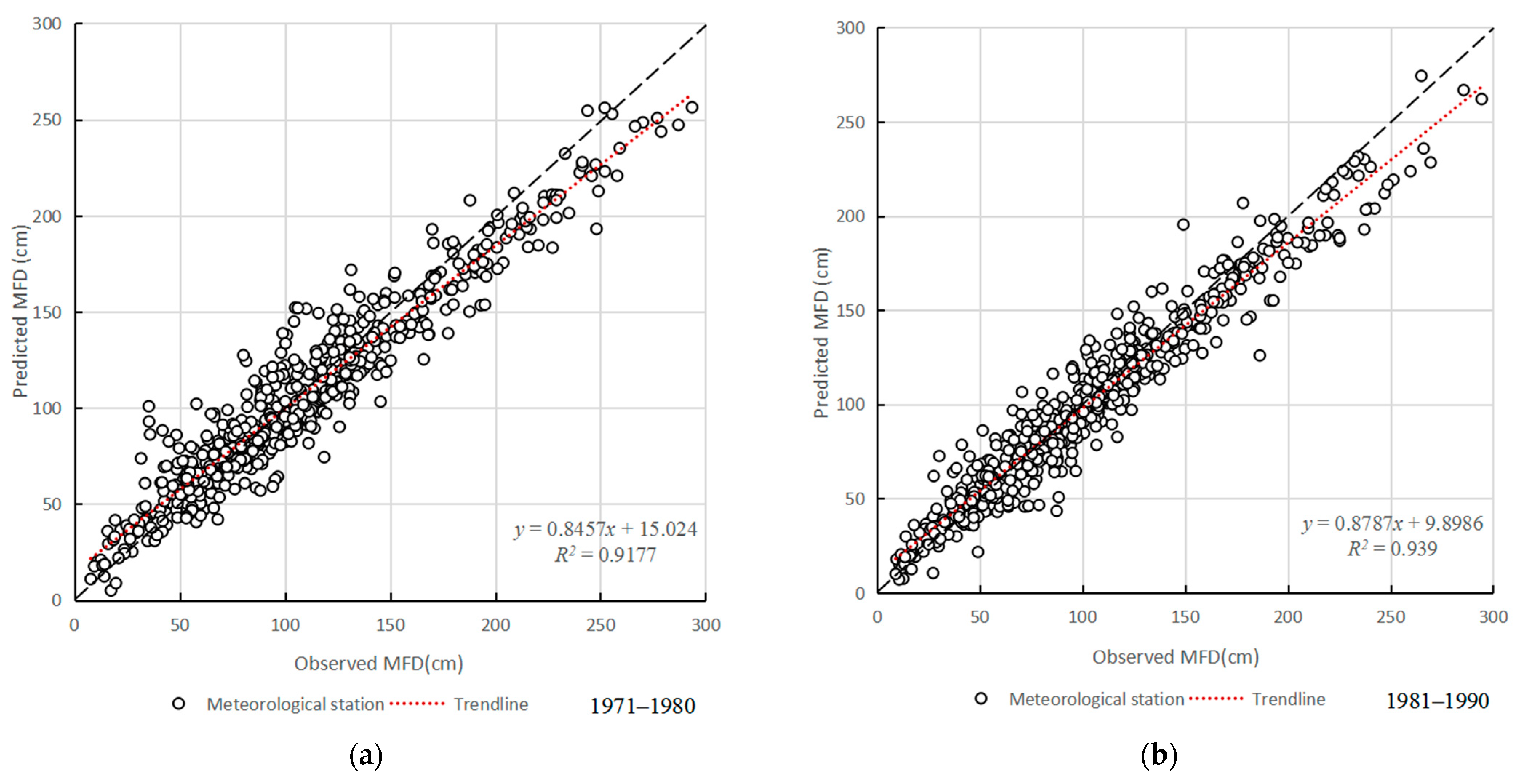
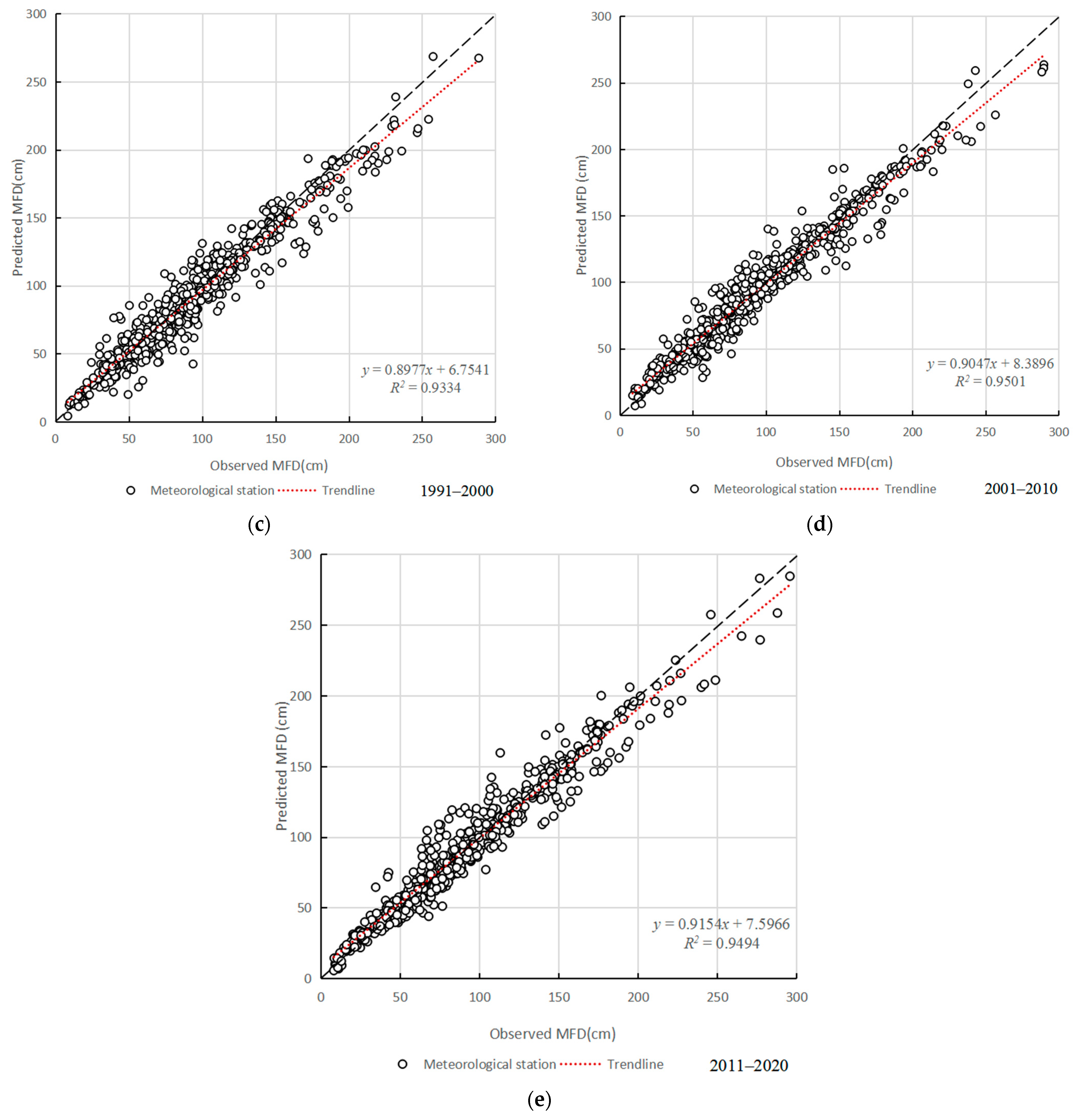
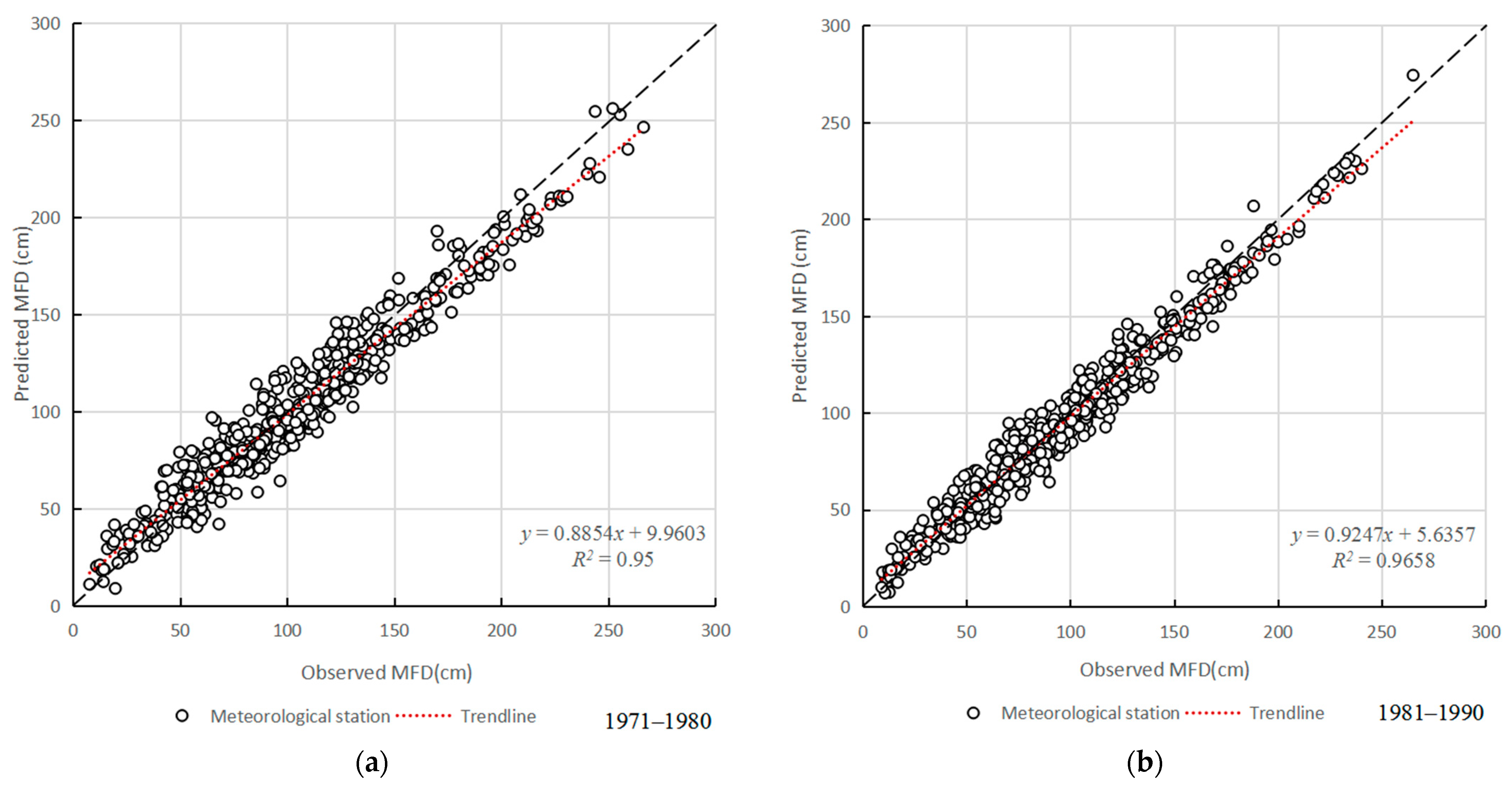
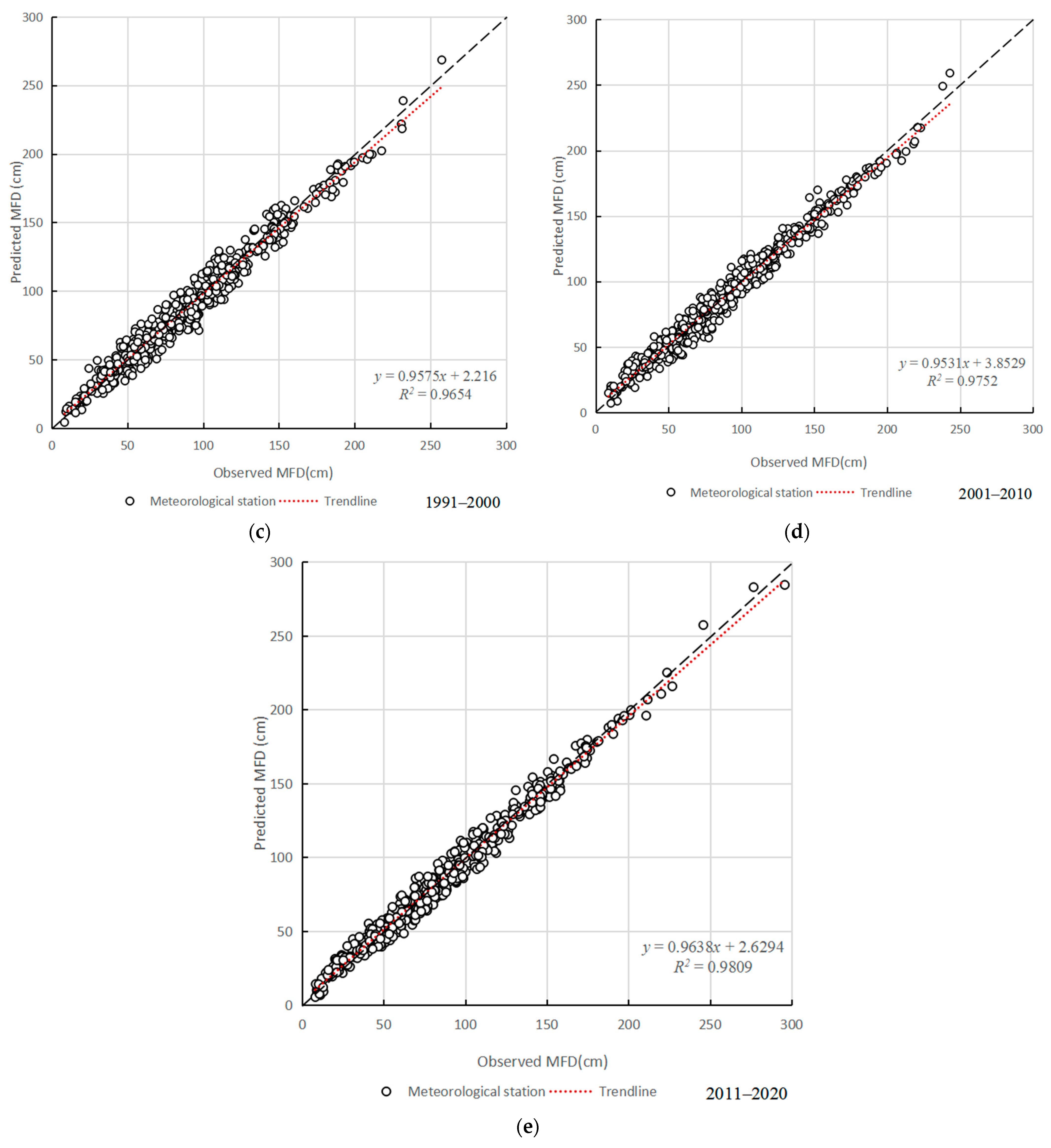
3.3. Evaluation of Machine-Learning Model Prediction Results
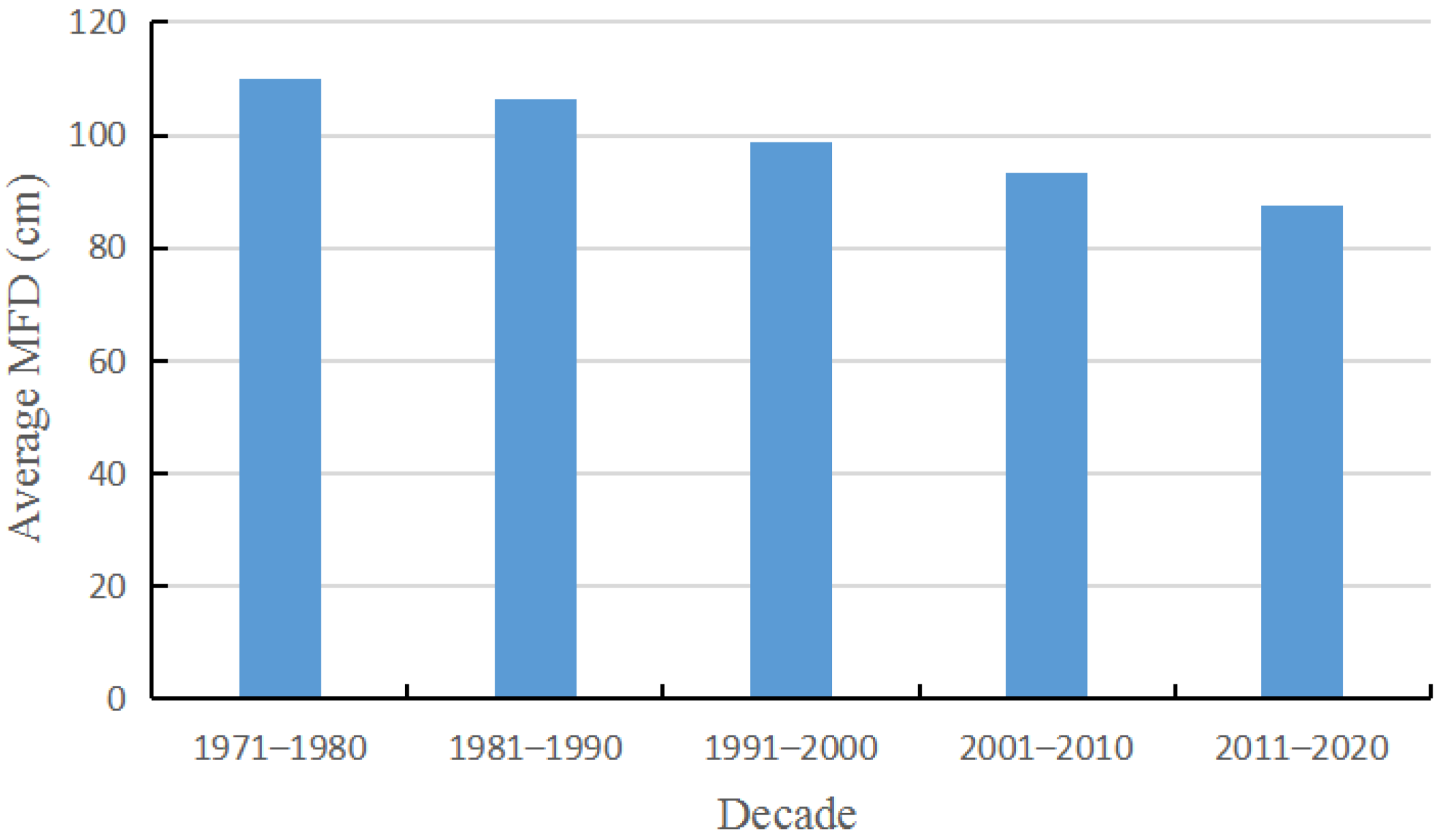
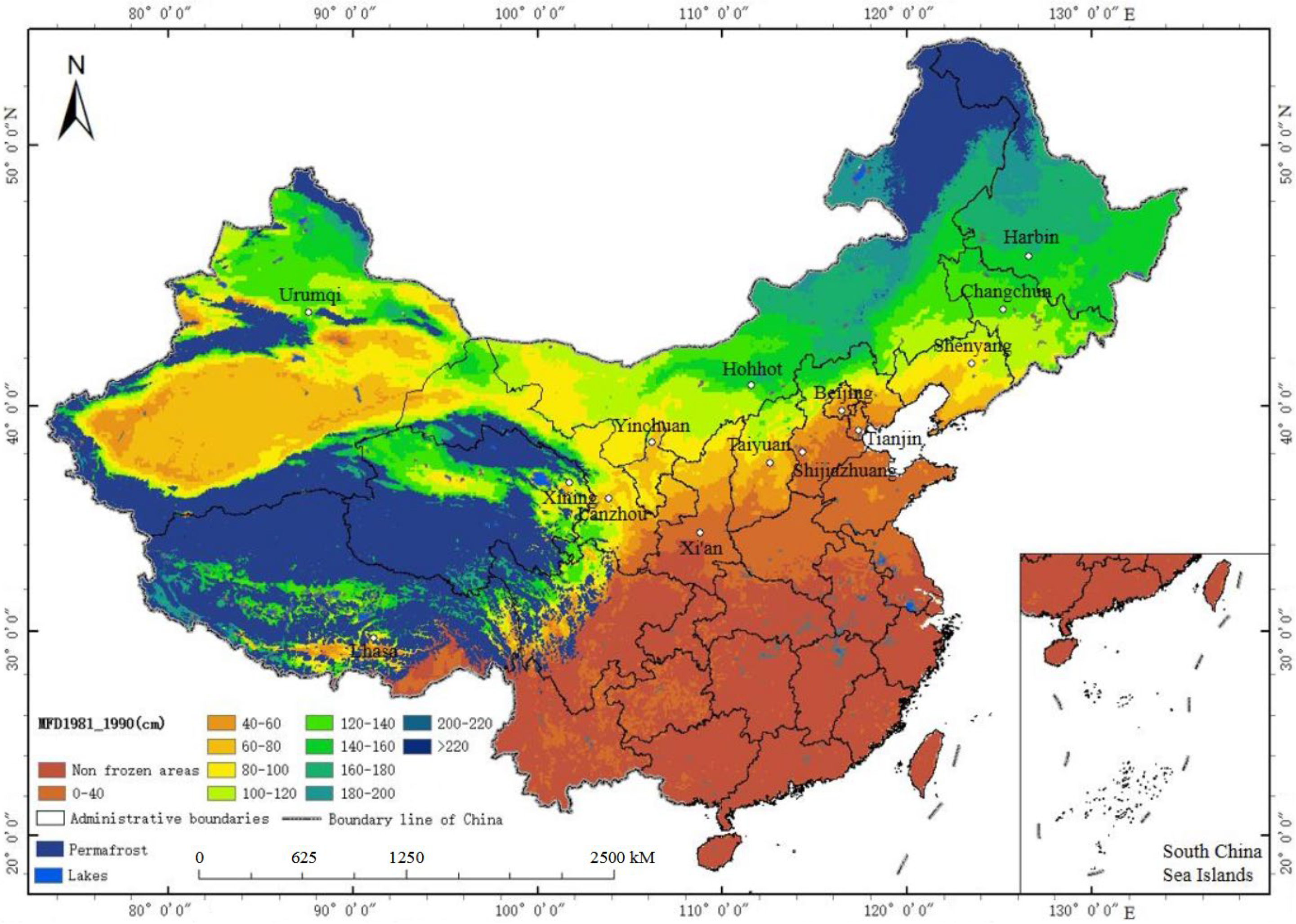
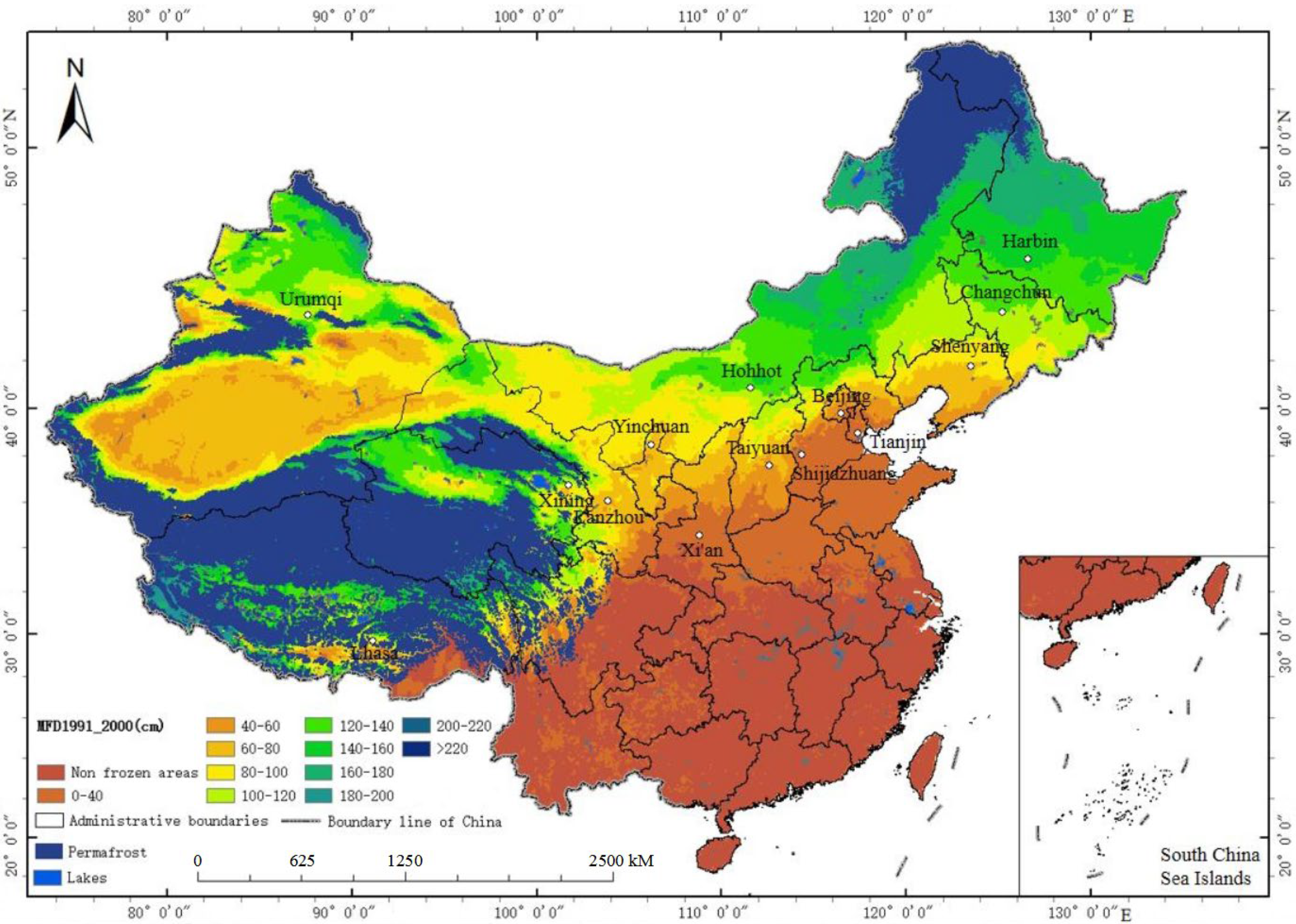
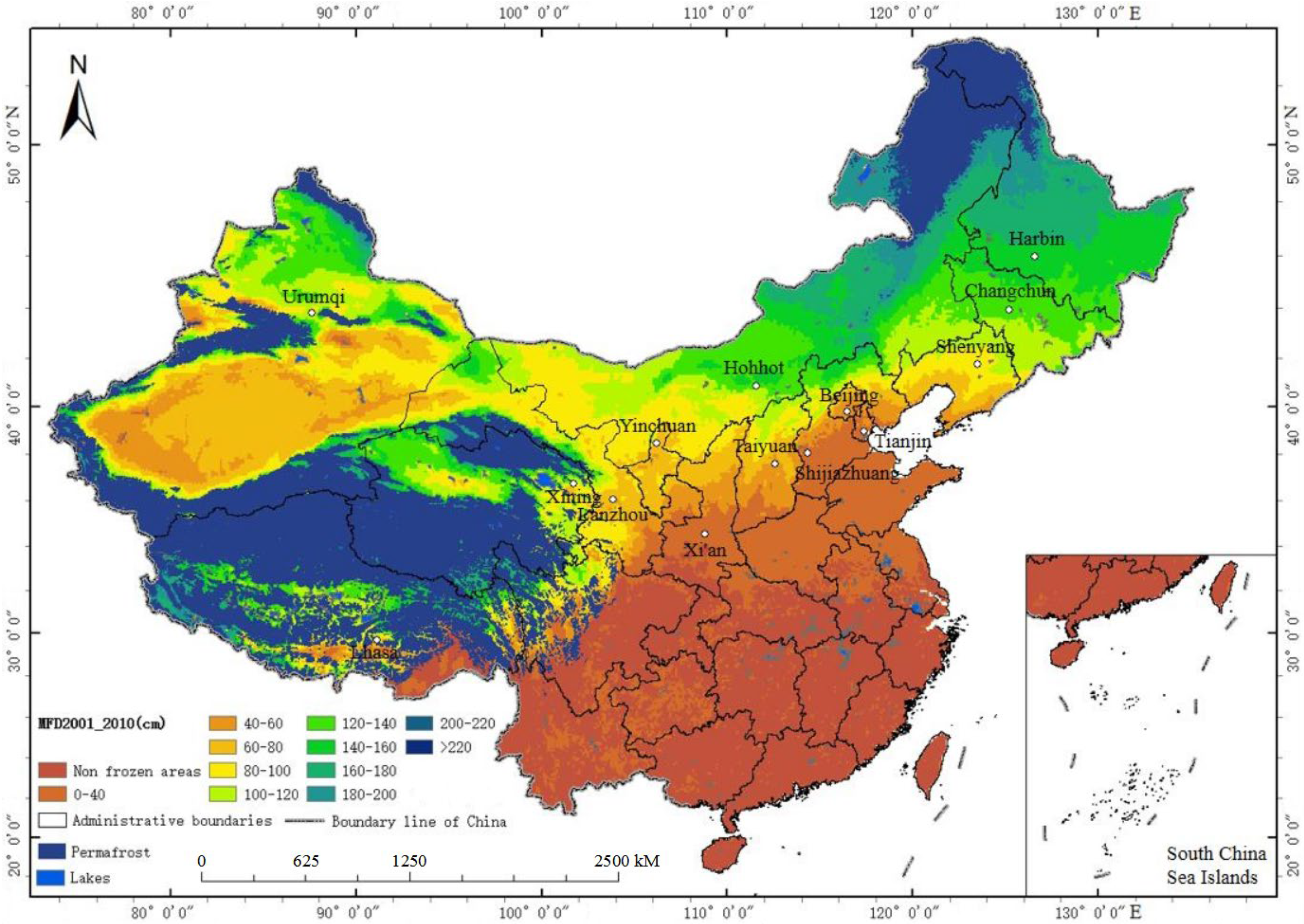
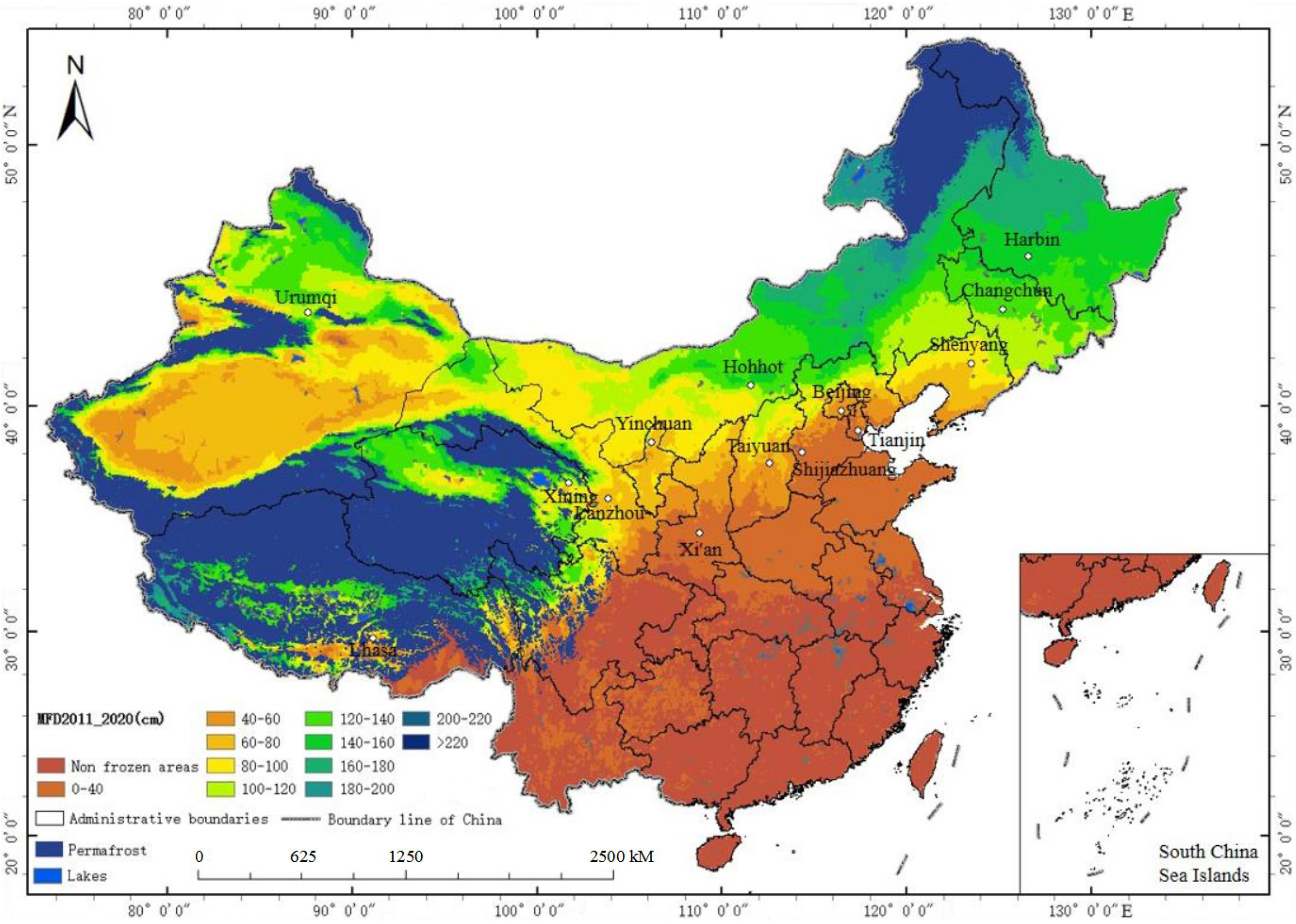
3.4. Overall Changing Trend of Maximum Freezing Depth
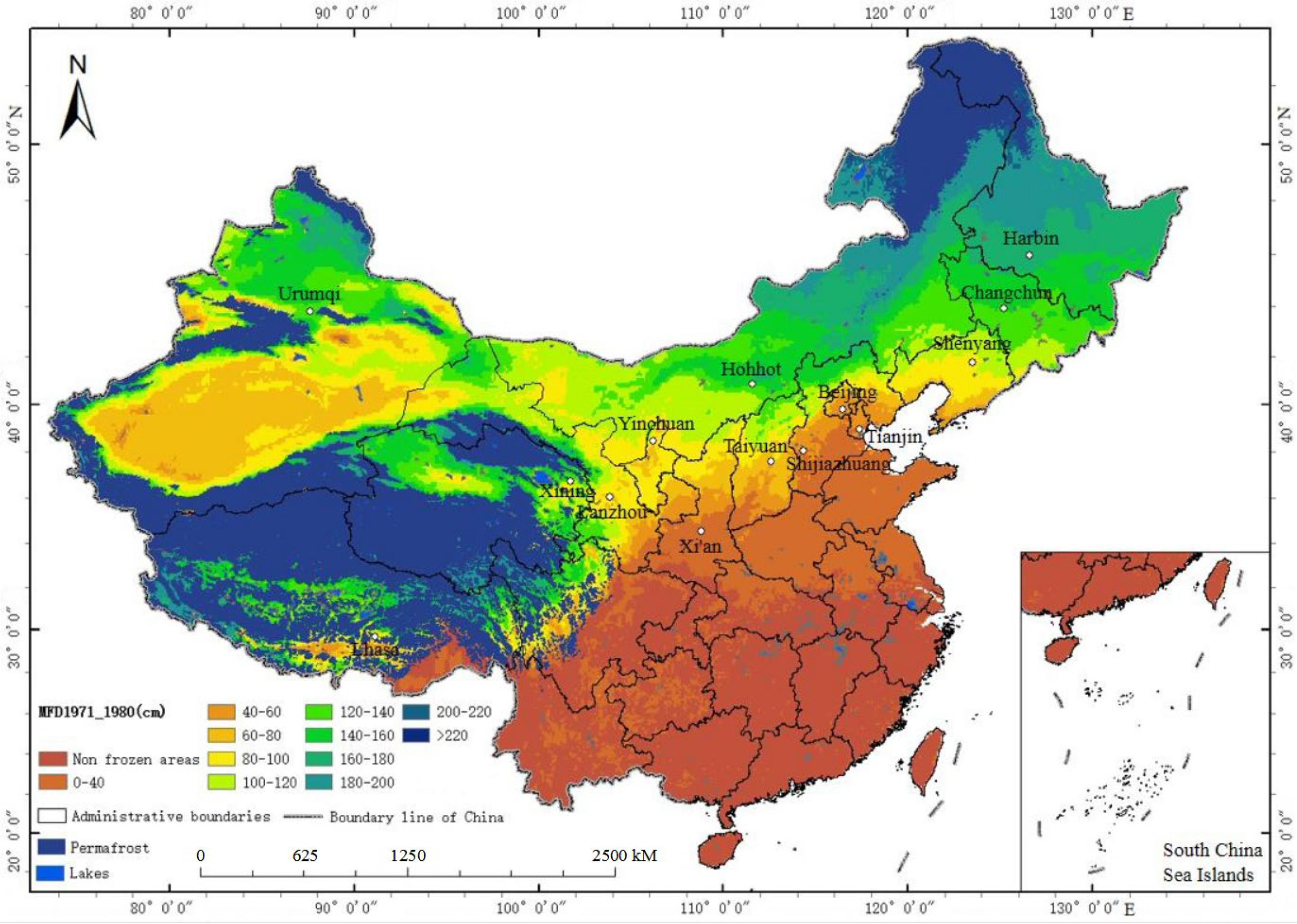
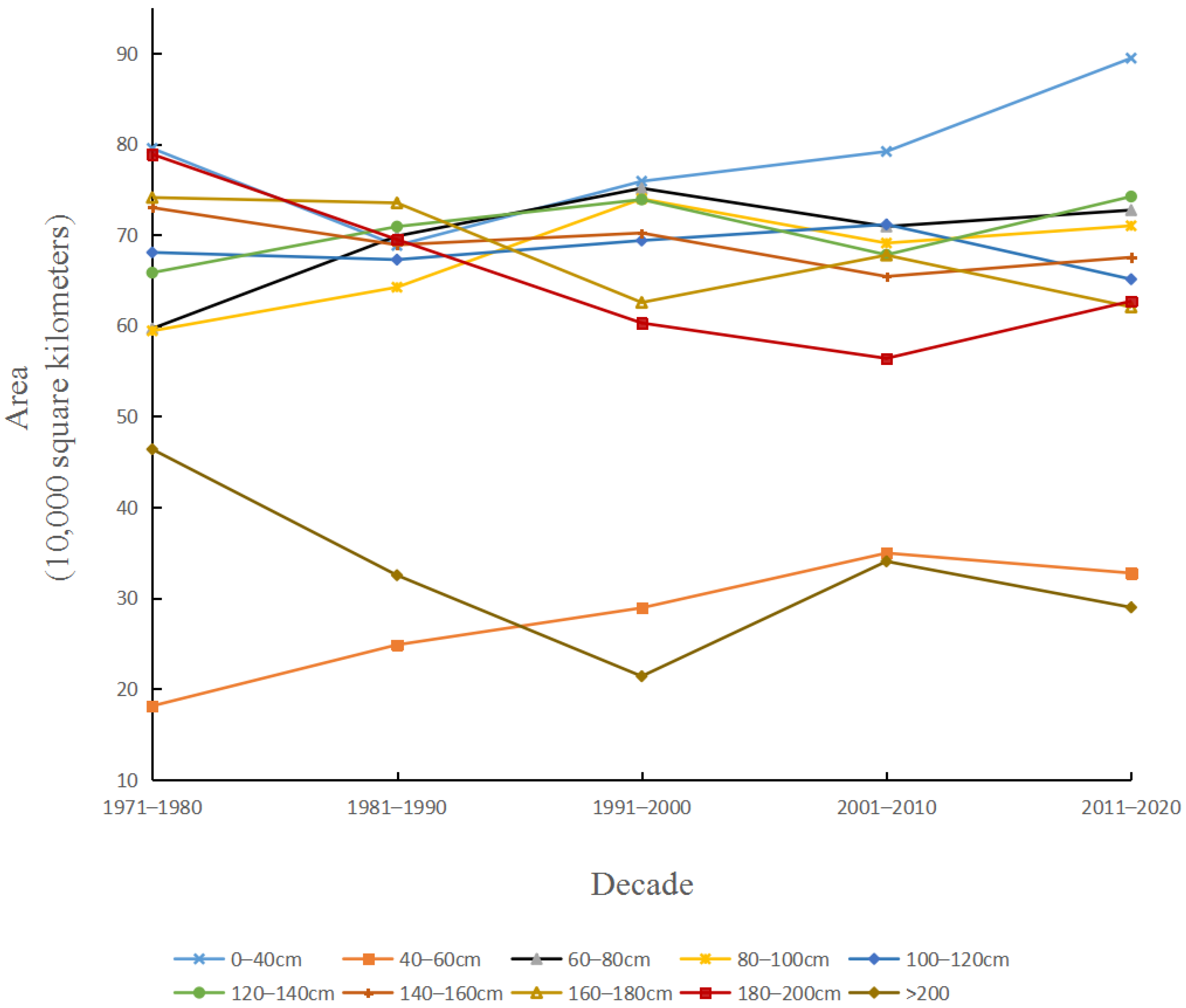
3.5. Changes in Maximum Freezing Depth in Different Regions
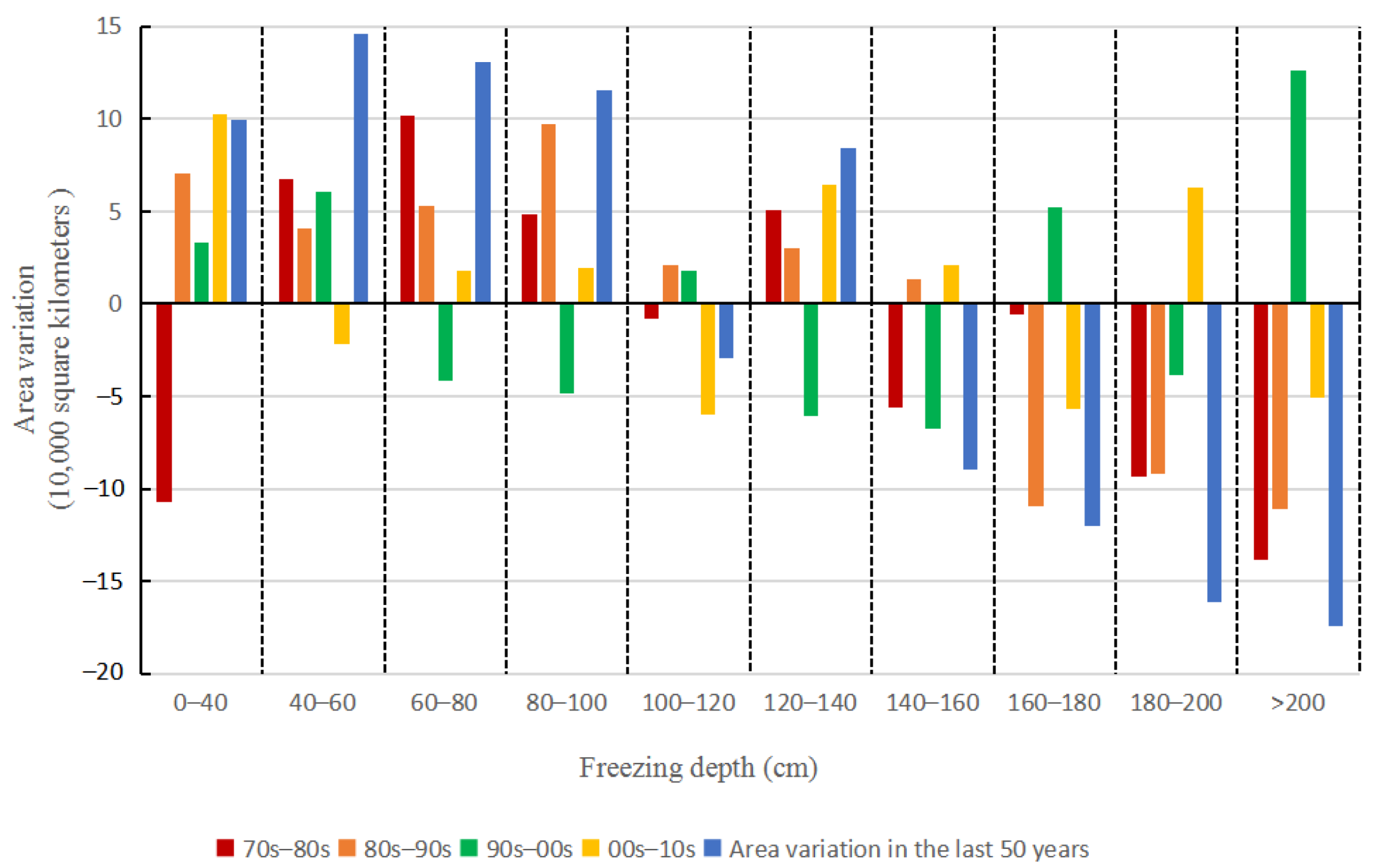
3.6. Area Variation of Seasonally Frozen Ground at Different Maximum Freezing Depths
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.W.; Guo, D.X.; Qiu, G.Q.; Cheng, G.; Li, S. Geocryology in China, 1st ed.; Science Press: Beijing, China, 2000; pp. 9–19. [Google Scholar]
- Yang, J.P.; Yang, S.Q.; Li, M. Vulnerability of permafrost to climate change in China. J. Glaciol. Geocryol. 2013, 35, 10–15. [Google Scholar]
- Zhao, L.; Cheng, G.D.; Ding, Y.J. Studies on frozen ground of China. J. Geogr. Sci. 2004, 14, 411–416. [Google Scholar]
- Qin, Y.; Chen, J.; Yang, D.; Wang, T. Estimating seasonally frozen ground depth from historical climate data and site measurements using a Bayesian model. Water Resour. Res. 2018, 54, 4361–4375. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, S.; Kim, Y.; Won, J. Predicting Frost Depth of Soils in South Korea Using Machine Learning Techniques. Sustainability 2022, 14, 9767. [Google Scholar] [CrossRef]
- Wang, B.; Ran, Y. Diversity of remote sensing-based variable inputs improves the estimation of seasonal maximum freezing depth. Remote Sens. 2021, 13, 4829. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Song, X.; Guo, L.F.; Rao, M.N. Machine learning approaches to multisource geospatial data classification: Application to CRP mapping in Texas County, Oklahoma. In IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data; IEEE: New York, NY, USA, 2003. [Google Scholar]
- Bhattacharya, B.; Solomatine, D.P. Machine learning in soil classification. Neural Netw. 2006, 19, 186–195. [Google Scholar] [CrossRef]
- Wang, B.Q.; Ran, Y.H. Decadal dataset of the seasonal maximum freezing depth with 1 km resolution from 1961 to 2020 in Northwest China, Tibet and surrounding area. Adv. Ear. Sci. 2021, 36, 1137–1145. [Google Scholar]
- Alizamir, M.; Kisi, O.; Ahmed, A.N.; Mert, C.; Fai, C.M.; Kim, S.; Kim, N.W.; El-Shafie, A. Advanced machine learning model for better prediction accuracy of soil temperature at different depths. PLoS ONE 2020, 15, e0231055. [Google Scholar] [CrossRef]
- Ran, Y.-H.; Li, X.; Che, T.; Wang, B.-Q.; Cheng, G.-D. Current state and past changes in frozen ground at the Third Pole: A research synthesis. Adv. Clim. Chang. Res. 2022, 13, 4–11. [Google Scholar] [CrossRef]
- Wang, B.Q.; Ran, Y.H. Machine learning-based forecasting of future maximum freezing depth over the Third Pole. J. Glaciol. Geocryol. 2023, 45, 1–10. [Google Scholar]
- Sha, L.; Zhang, Y.M. Research on automatic observation methods of freezing depth in Shenyang, China. Meteorol. Hydrol. Mar. Instrum. 2019, 36, 56–59. [Google Scholar]
- Liu, T.L. An overview of formulas for calculating freezing or thawing depth. J. Glaciol. Geocryol. 1983, 2, 85–95. [Google Scholar]
- DeGaetano, A.T.; Cameron, M.D.; Wilks, D.S. Physical simulation of maximum seasonal soil freezing depth in the United States using routine weather observations. J. Appl. Meteorol. 2001, 40, 546–555. [Google Scholar] [CrossRef]
- Godlewski, T.; Wodzyński, Ł.; Wszędyrówny-Nast, M. Probabilistic analysis as a method for ground freezing depth estimation. Appl. Sci. 2021, 11, 8194. [Google Scholar] [CrossRef]
- Jerzy, A.U.; Sobolewski, A. Probabilistic approach to the assessment of the depth of soil freezing. In Proceedings of the 13th Baltic Sea Region Geotechnical Conference, Vilnius, Lithuania, 22–24 September 2016. [Google Scholar]
- Kudriyatsev, B.A.; Guo, D.X.; Ma, S.M.; Ding, D.W. Principles of Frozen Soil Prediction in Engineering Geological Research, 1st ed.; Lanzhou University Press: LanZhou, China, 1992; pp. 112–123. [Google Scholar]
- Friedman, G.M.; Cheng, G.D.; Ding, D.W. Calculation Method for Temperature Conditions of Frozen Soil, 1st ed.; Science Press: Beijing, China, 1982; pp. 15–23. [Google Scholar]
- Institute of Frozen Soil Research, Siberian Branch of the Soviet Academy of Sciences. General Frozen Soil Science, 1st ed.; Science Press: Beijing, China, 1988; pp. 21–29. [Google Scholar]
- Degaetano, A.T.; Wilks, D.S. Extreme-value climatology of maximum soil freezing depths in contiguous United States. J. Cold Reg. Eng. 2002, 16, 51–71. [Google Scholar] [CrossRef]
- Guo, D. Simulation of permafrost and seasonally frozen ground conditions on the Tibetan Plateau, 1981–2010. J. Geophys. Res-Atmos. 2013, 118, 5216–5230. [Google Scholar] [CrossRef]
- Saito, K.; Emori, S.; Kimoto, M. Change in hydro-thermal regimes in the soil-freezing regions in the Global Warming simulation by a CGCM of moderate- and high-resolution. In Proceedings of the Asian Conference on Permafrost, Lanzhou, China, 7–9 August 2006. [Google Scholar]
- Lawrence, D.M.; Slater, A.G.; Swenson, S.C. Simulation of present-day and future permafrost and seasonally frozen ground conditions in CCSM4. J. Clim. 2012, 25, 2207–2225. [Google Scholar] [CrossRef]
- Duguay, R.; Pietroniro, A. Remote Sensing in Northern Hydrology: Measuring Environmental Change, 1st ed.; American Geophysical Union: Washington, DC, USA, 2005; Volume 163, pp. 91–118. [Google Scholar]
- Walter, G.R.; Stothoff, S.A.; Necsoiu, D.M.; Dinwiddie, C.L. Integrated methodology for mapping and monitoring permafrost and seasonally frozen ground. In Proceedings of the Society of Petroleum Engineers-Arctic Technology Conference, Houston, TX, USA, 7–9 February 2011. [Google Scholar]
- Rey, D.M.; Hinckley, E.L.S.; Walvoord, M.A.; Singha, K. Integrating observations and models to determine the effect of seasonally frozen ground on hydrologic partitioning in alpine hillslopes in the Colorado Rocky Mountains, USA. Hydrol. Process. 2021, 35, e14374. [Google Scholar] [CrossRef]
- Traczyk, A.; Migaa, K. Depth of seasonally frozen ground in the Karkonosze Mts (Sudetes, SW Poland) in the light of GIS modeling of topoclimate and geomorphic conditions. XI. In Proceedings of the International Conference on Permafrost, Potsdam, Germany, 3–5 June 2016. [Google Scholar]
- Gouttevin, I.; Krinner, G.; Ciais, P.; Polcher, J.; Legout, C. Multi-scale validation of a new soil freezing scheme for a land-surfacemodel with physically-based hydrology. Cryosphere 2012, 6, 407–430. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic impacts of thawing permafrost-a review. Vadose. Zone J. 2016, 15, 1–20. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X. Progress, Chanllenges and opportunities of permafrost mapping in China. Adv. Earth Sci. 2019, 34, 1015–1027. [Google Scholar]
- Sabaghy, S.; Walker, J.P.; Renzullo, L.J.; Jackson, T.J. Spatially enhanced passive microwave derived soil moisture: Capabilities and opportunities. Remote Sens. Environ. 2018, 209, 551–580. [Google Scholar] [CrossRef]
- Minha, C.; Yoomi, H. A microwave-optical/infrared disaggregation for improving spatial representation of soil moisture using AMSR-E and MODIS products. Remote Sens. Environ. 2012, 124, 259–269. [Google Scholar]
- Wang, L.; Fang, S.; Pei, Z.; Wu, D.; Zhu, Y.; Zhuo, W. Developing machine learning models with multisource inputs for improved land surface soil moisture in China. Comput. Electron. Agric. 2022, 192, 106623. [Google Scholar] [CrossRef]
- Mehmet, B. Prediction of soil temperature using regression and artificial neural network models. Meteorol. Atmos. Phys. 2010, 110, 59–70. [Google Scholar]
- Feng, Y.; Cui, N.B.; Hao, W.P.; Gao, L.L.; Gong, D.Z. Estimation of soil temperature from meteorological data using different machine learning models. Geoderma 2019, 338, 67–77. [Google Scholar] [CrossRef]
- Nahvi, B.; Habibi, J.; Mohammadi, K.; Shamshirband, S.; Al Razgan, O.S. Using self-adaptive evolutionary algorithm to improve the performance of an extreme learning machine for estimating soil temperature. Comput. Electron. Agric. 2016, 124, 150–160. [Google Scholar] [CrossRef]
- Kalyuzhny, I.L.; Lavrov, S.A. Effect of climate changes on the soil freezing depth in the Volga River basin. Led. Sneg. Ice Snow 2016, 56, 437–451. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, Y.; Wang, X.; Kang, S.; Chen, A.A.; Mao, W.; Zhong, X. Snow cover controls seasonally frozen ground regime on the southern edge of Altai Mountains. Agric. For. Meteorol. 2021, 297, 108271. [Google Scholar] [CrossRef]
- Qin, Y.; Lei, H.M.; Yang, D.W.; Gao, B.; Wang, Y.H.; Cong, Z.T.; Fan, W.J. Long-term change in the depth of seasonally frozen ground and its ecohydrological impacts in the Qilian Mountains, northeastern Tibetan Plateau. J. Hydrol. 2016, 9, 8–26. [Google Scholar] [CrossRef]
- Frauenfeld, O.W. Interdecadal changes in seasonal freeze and thaw depths in Russia. J. Geophys. Res. 2004, 109, D05101. [Google Scholar] [CrossRef]
- Nella, S. Specific features of distribution of the perennially and seasonally frozen ground in Transbaikalia. In Proceedings of the Asian Conference on Permafrost, Lanzhou, China, 7–9 August 2006. [Google Scholar]
- Sahbeni, G.; Pleynet, J.B.; Jarocki, K. A spatiotemporal analysis of precipitation anomalies using rainfall Gini index between 1980 and 2022. Atmos. Sci. Lett. 2023, 24, e1161. [Google Scholar] [CrossRef]
- Ceriani, L.; Verme, P. The origins of the Gini index: Extracts from variabilità e mutabilità (1912) by Corrado Gini. J. Econ. Inequal. 2012, 10, 421–443. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Wang, S.G.; Dai, Y.; Duan, Q.; Liu, B.; Yuan, H. A global soil data set for earth system modeling. J. Adv. Model. Earth Syst. 2014, 6, 249–263. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Awad, M.; Khanna, R. Support Vector Regression in Efficient Learning Machines; APress: Berkeley, CA, USA, 2015; pp. 25–31. [Google Scholar]
- Tong, B.L.; Xie, Y.Q.; Guo, D.X. Seasonal permafrost at the southern foot of Tanggula Mountain. Glacier Permafr. 1980, 2, 23–28. [Google Scholar]
- Wang, T. Distribution Map of Frozen Soil in China Based on the “Map of Glaciers, Frozen Soil, and Deserts in China”; National Glacier, Frozen Soil and Desert Science Data Center: Lanzhou China, 2019. [Google Scholar]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Liu, X.N.; Li, Q.X. Variation and preliminary interpretation of the maximum frozen soil depth in China. J. Appl. Meteorol. Sci. 2003, 14, 299–308. [Google Scholar]
- Chen, B. Temporal and Spatial Variation Characteristics of Frozen Soil in China and Its Relationship with East Asian Climate. Master’s Thesis, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China, 2007. [Google Scholar]
- Wang, X.; Chen, R.; Han, C.; Yang, Y.; Liu, J.; Liu, Z.; Guo, S. Estimation of soil freeze depth in typical snowy regions using reanalysis dataset: A case study in Heilongjiang province, China. Remote Sens. 2022, 14, 5989. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, T.; Frauenfeld, O.W.; Wang, K.; Cao, B.; Zhong, X.; Su, H.; Mu, C. Response of seasonal soil freeze depth to climate change across China. Cryosphere 2017, 11, 1059–1073. [Google Scholar] [CrossRef]
- Wang, T.; Yang, D.; Fang, B.; Yang, W.; Qin, Y.; Wang, Y. Data-driven mapping of the spatial distribution and potential changes of frozen ground over the Tibetan Plateau. Sci. Total Environ. 2019, 649, 515–525. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Nan, Z.; Che, J.; Sheng, Y.; Wu, Q.; Jin, H.; Luo, D.; Tang, Z.; et al. Mapping the permafrost stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2020, 64, 62–79. [Google Scholar] [CrossRef]
- Zhang, T.; Armstrong, R.; Smith, J. Investigation of the near-surface soil freeze-thaw cycle in the contiguous United States: Algorithm development and validation. J. Geophys. Res. 2003, 108, 8860. [Google Scholar] [CrossRef]
- Zimov, S.A.; Schuur, E.A.; Chapin, F.S., III. Permafrost and the global carbon budget. Science 2006, 312, 1612–1613. [Google Scholar] [CrossRef]
- Li, X.; Feng, M.; Ran, Y.H.; Su, Y.; Liu, F.; Huang, C.; Guo, H. Big Data in Earth system science and progress towards a digital twin. Nat. Rev. Earth Env. 2023, 5, 319–332. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
| Variable | Date Source and Reference | Spatial Resolution | Temporal Resolution and Time Span |
|---|---|---|---|
| Freezing degree days, °C·days | ERA5-Land, Muñoz-Sabater et al. [46] | 9 km | Daily, 1971–2020 |
| Thawing degree days, °C·days | ERA5-Land, Muñoz-Sabater et al. [46] | 9 km | Daily, 1971–2020 |
| Precipitation, m | ERA5-Land, Muñoz-Sabater et al. [46] | 9 km | Daily, 1971–2020 |
| Snow depth, m | ERA5-Land, Muñoz-Sabater et al. [46] | 9 km | Daily, 1971–2020 |
| Solar radiation, | ERA5-Land, Muñoz-Sabater et al. [46] | 9 km | Daily, 1971–2020 |
| Soil bulk density, | GSDE, Shangguan W et al. [47] | 1 km | - |
| Soil organic carbon, % of weight | GSDE, Shangguan W et al. [47] | 1 km | - |
| Sand content, % of weight | GSDE, Shangguan W et al. [47] | 1 km | - |
| Clay content, % of weight | GSDE, Shangguan W et al. [47] | 1 km | - |
| Silt content, % of weight | GSDE, Shangguan W et al. [47] | 1 km | - |
| Gravel content, % of volume | GSDE, Shangguan W et al. [47] | 1 km | - |
| DEM (altitude), m | ASTER GDEM 30 m | 30 m | - |
| Variable | Original Resolution | Resolution after Downscaling |
|---|---|---|
| Freezing degree days, °C·days | 9 km | 9 km (no change) |
| Thawing degree days,°C·days | 9 km | 9 km (no change) |
| Precipitation, m | 9 km | 9 km (no change) |
| Snow depth, m | 9 km | 9 km (no change) |
| Solar radiation, | 9 km | 9 km (no change) |
| Soil bulk density, | 1 km | 9 km |
| Soil organic carbon, % of weight | 1 km | 9 km |
| Sand content, % of weight | 1 km | 9 km |
| Clay content, % of weight | 1 km | 9 km |
| Silt content, % of weight | 1 km | 9 km |
| Gravel content, % of volume | 1 km | 9 km |
| DEM (altitude), m | 30 m | 9 km |
| Learning Times | Statistical Indicators | RF | SVMR | KNN | GLR |
|---|---|---|---|---|---|
| Mean Values/Standard Deviation | |||||
| 300 | R-squared | 0.856 ± 0.037 | 0.853 ± 0.032 | 0.774 ± 0.059 | 0.749 ± 0.394 |
| RMSE | 19.198 ± 2.704 | 19.556 ± 3.036 | 24.165 ± 4.062 | 23.024 ± 10.838 | |
| MAE | 13.413 ± 1.657 | 13.361 ± 1.702 | 16.826 ± 2.269 | 14.858 ± 2.391 | |
| bias | 0.061 ± 2.744 | 0.066 ± 2.698 | −1.154 ± 3.092 | −0.338 ± 3.533 | |
| 400 | R-squared | 0.853 ± 0.039 | 0.850 ± 0.038 | 0.765 ± 0.062 | 0.656 ± 0.645 |
| RMSE | 19.626 ± 2.923 | 19.985 ± 3.412 | 24.952 ± 4.260 | 25.958 ± 15.966 | |
| MAE | 13.643 ± 1.798 | 13.536 ± 1.847 | 17.164 ± 2.268 | 15.478 ± 3.164 | |
| bias | 0.117 ± 2.617 | 0.051 ± 2.636 | −1.200 ± 3.205 | −1.019 ± 4.016 | |
| 500 | R-squared | 0.855 ± 0.043 | 0.854 ± 0.037 | 0.775 ± 0.065 | 0.666 ± 0.751 |
| RMSE | 19.522 ± 2.780 | 19.649 ± 3.001 | 24.359 ± 4.146 | 25.006 ± 16.215 | |
| MAE | 13.595 ± 1.760 | 13.435 ± 1.708 | 17.009 ± 2.323 | 15.309 ± 3.252 | |
| bias | −0.097 ± 2.656 | 0.097 ± 2.569 | −1.391 ± 3.154 | −0.828 ± 3.951 | |
| 600 | R-squared | 0.856 ± 0.039 | 0.853 ± 0.039 | 0.768 ± 0.067 | 0.605 ± 0.770 |
| RMSE | 19.453 ± 2.791 | 19.709 ± 3.335 | 24.723 ± 4.206 | 26.897 ± 18.208 | |
| MAE | 13.566 ± 1.765 | 13.464 ± 1.860 | 17.188 ± 2.351 | 15.660 ± 3.513 | |
| bias | 0.081 ± 2.793 | 0.091 ± 2.792 | −1.332 ± 3.420 | −1.131 ± 4.258 | |
| 700 | R-squared | 0.854 ± 0.041 | 0.851 ± 0.037 | 0.771 ± 0.064 | 0.677 ± 0.592 |
| RMSE | 19.539 ± 2.994 | 19.825 ± 3.323 | 24.542 ± 4.282 | 25.351 ± 15.385 | |
| MAE | 13.584 ± 1.842 | 13.517 ± 1.778 | 17.011 ± 2.332 | 15.393 ± 3.034 | |
| bias | 0.132 ± 2.725 | 0.153 ± 2.806 | −1.225 ± 3.428 | −0.768 ± 4.017 | |
| 800 | R-squared | 0.852 ± 0.040 | 0.851 ± 0.035 | 0.770 ± 0.060 | 0.659 ± 0.703 |
| RMSE | 19.709 ± 2.851 | 19.912 ± 3.184 | 24.632 ± 4.031 | 25.452 ± 15.445 | |
| MAE | 13.784 ± 1.797 | 13.616 ± 1.753 | 17.104 ± 2.156 | 15.508 ± 3.099 | |
| bias | 0.034 ± 2.794 | 0.197 ± 2.874 | −1.332 ± 3.464 | −0.703 ± 4.030 | |
| 900 | R-squared | 0.856 ± 0.039 | 0.853 ± 0.037 | 0.767 ± 0.064 | 0.630 ± 0.788 |
| RMSE | 19.461 ± 2.861 | 19.792 ± 3.326 | 24.824 ± 4.263 | 25.994 ± 17.150 | |
| MAE | 13.552 ± 1.771 | 13.448 ± 1.819 | 17.202 ± 2.298 | 15.436 ± 3.377 | |
| bias | 0.051 ± 2.628 | 0.199 ± 2.620 | −1.258 ± 3.264 | −0.994 ± 4.021 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Sheng, Y.; Ran, Y.; Wang, B.; Cao, W.; Peng, E.; Peng, C. Predict Seasonal Maximum Freezing Depth Changes Using Machine Learning in China over the Last 50 Years. Remote Sens. 2023, 15, 3834. https://doi.org/10.3390/rs15153834
Wang S, Sheng Y, Ran Y, Wang B, Cao W, Peng E, Peng C. Predict Seasonal Maximum Freezing Depth Changes Using Machine Learning in China over the Last 50 Years. Remote Sensing. 2023; 15(15):3834. https://doi.org/10.3390/rs15153834
Chicago/Turabian StyleWang, Shuo, Yu Sheng, Youhua Ran, Bingquan Wang, Wei Cao, Erxing Peng, and Chenyang Peng. 2023. "Predict Seasonal Maximum Freezing Depth Changes Using Machine Learning in China over the Last 50 Years" Remote Sensing 15, no. 15: 3834. https://doi.org/10.3390/rs15153834
APA StyleWang, S., Sheng, Y., Ran, Y., Wang, B., Cao, W., Peng, E., & Peng, C. (2023). Predict Seasonal Maximum Freezing Depth Changes Using Machine Learning in China over the Last 50 Years. Remote Sensing, 15(15), 3834. https://doi.org/10.3390/rs15153834








