Hyperspectral Target Detection Methods Based on Statistical Information: The Key Problems and the Corresponding Strategies
Abstract
1. Introduction
- (1)
- Target detection based on spectral characteristics. When the target of interest has diagnostic absorption features, they can be detected directly based on these spectral bands or features [4]. Commonly used quantitative parameters for absorption-band features include the position, depth, width and asymmetry [5,6]. These parameters are widely used for determining the mineralogy of samples or analyze the chemical composition [7,8]. To eliminate the effects of atmosphere, lighting differences, and other factors, the continuum is often removed before spectral feature extraction [9]. Moreover, continuum removed spectra can highlight the absorption characteristics. In addition, spectral indices based on target spectral characteristics can also be designed for target detection, such as the normalized difference vegetation index (NDVI), soil-adjusted vegetation index, enhanced vegetation index for vegetation, normalized difference water index, and modified normalized difference water index for water [10,11,12,13,14,15,16]. These methods are developed by utilizing the spectral characteristics of targets, so they are physical-based. Generally, they are simple with low computational complexity. However, they typically only utilize a small portion of bands (usually bands with absorption features), and completely ignore background information, so their accuracy is often lower than needed.
- (2)
- Target detection based on spectral similarity matching. These methods aim to measure the spectral similarity of the target and each pixel in the image, so as to directly obtain the distribution of target in the image. Common methods include minimum distance method [17], spectral angle mapper [18,19], cross correlogram spectral matching [20], spectral similarity scale [21], and correlation simulating analysis model [22]. This kind of method is also simple and easy to implement, but they have not used background information either. As a result, their accuracy can not be well guaranteed in many cases.
- (3)
- Target detection based on spectral mixture analysis. This kind of method relies on the assumption of a linear mixing model, which means that each pixel in the image can be a linear combination of several pure spectral signatures (also named endmembers) weighted by the corresponding abundance fractions. Owing to the physical constraints, the abundances satisfy the abundance non-negative constraint and abundance sum-to-one constraint [23]. The commonly used procedure to extract the distribution of target is as follows: (a) extract endmembers from the image through endmember extraction methods [24,25]; (b) identify each endmember as target or background; and (c) perform spectral unmixing using the target endmember and background endmenbers [26]. Then the abundance map of the target endmember is the distribution of target. In addition, a simple spectral matching can also be used to detect target in the orthogonal subspace of the background endmembers. The most representative way to calculate the orthogonal subspace is to perform the orthogonal subspace projection [27]. Based on this algorithm, noise subspace projection [28], generalized orthogonal subspace projection [29], have also been developed. The above methods are all based on the assumption that there are pure pixels of all kinds of objects in the image. However, in real images, this assumption often does not hold. To address this issue, researchers have proposed endmember generation methods that can simultaneously obtain endmembers and abundance maps by proposing a reasonable objective function [30,31,32]. The algorithm based on spectral mixture analysis can effectively extract targets and suppress background in many cases, but its detection accuracy is easily to be affected by the errors in background endmember extraction. In addition, the linear mixing model is not always valid in some scenarios [33,34].
- (4)
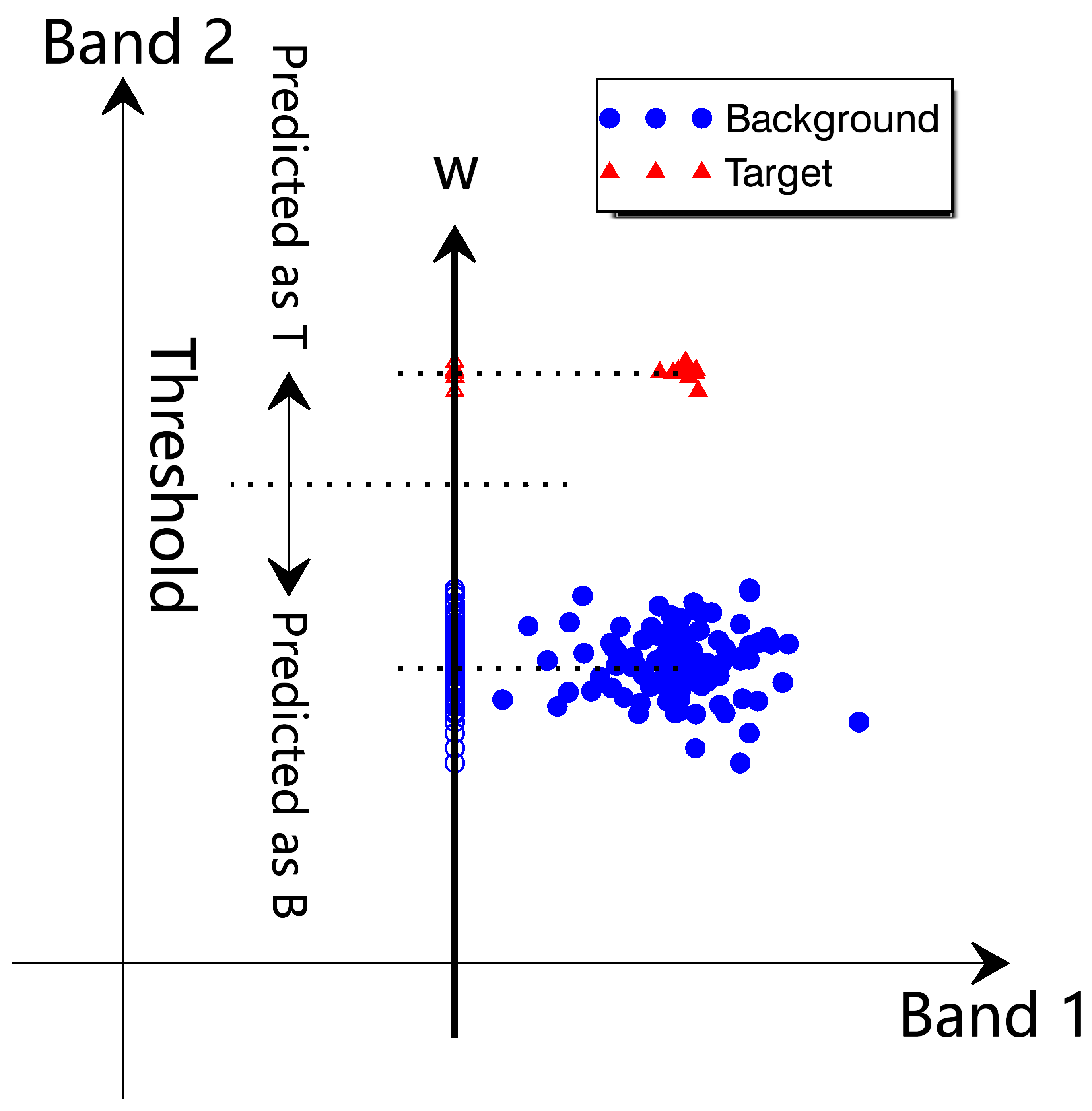
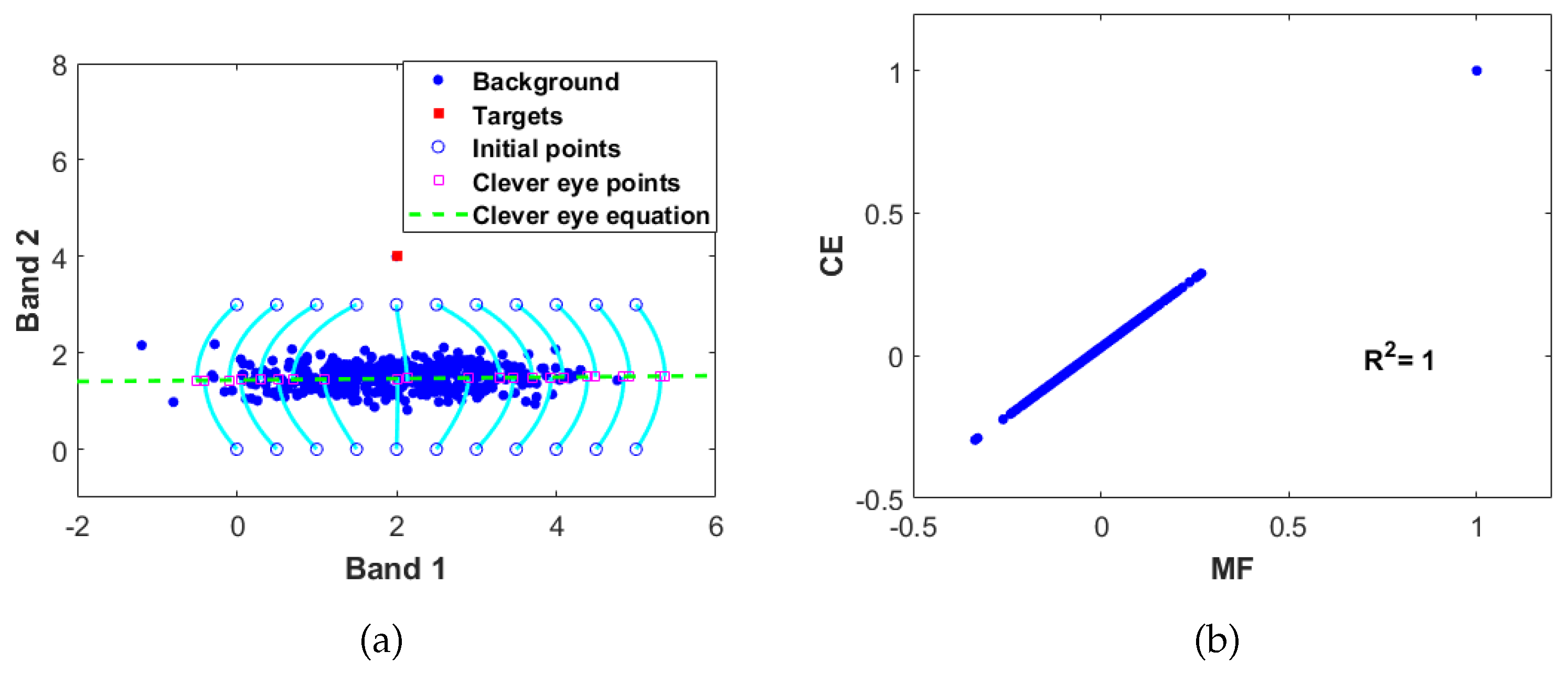
- Target detection based on image statistical information. This type of methods relies mainly on the statistical information of the hyperspectral data. Its aim is to suppress the background while matching the target. The most classical algorithms in this category are the Constrained Energy Minimization (CEM) algorithm [35] and the Matched Filter (MF) algorithm [36,37]. The former was proposed by Harsanyi in 1993, which was derived from a linearly constrained adaptive beamforming in the field of signal processing. CEM aims to minimize the average filter output energy while maintaining the output for the target as a constant. The latter is derived from the binary hypothesis testing problem in statistics, assuming that both the target and the background classes follow the Gaussian distribution. MF obtains the optimal target detector by maximizing the likelihood ratio under the Neyman–Pearson criterion. The detectors of MF and CEM have similar mathematical expressions, with the only difference being that MF requires the data to be centralized first. Many algorithms have been developed based on these two algorithms, such as the Mixed Tuned Matched Filter [38], General Constrained Energy Minimization [39], Adaptive Cosine Estimation [40], Multi-Objective Constrained Energy Minimization [41], Target-Constrained Interference Minimization Filtering [42], Kernel-based Constrained Energy Minimization/Matched Filtering [43], Weighted Constrained Energy Minimization [44], Clever Eye Algorithm [45], Augmented Constrained Energy Minimization [46], and Filtering Tensor Analysis [47,48]. In addition to second-order statistical quantities, higher-order statistics have also been introduced for hyperspectral target detection [49,50,51,52]. By making full use of the statistical information of the background, this kind of algorithms can achieve good target detection results even when the background spectrum is unknown. However, if there exist a large spectral variation in target pixels or the target’s spectra are close to that of the background, this kind of methods may fail to achieve a high target detection accuracy.
- (5)
- Target detection based on deep learning. In recent years, due to the strong data analysis capabilities, deep learning has been introduced to various hyperspectral applications [53,54,55,56,57,58,59], especially for classification [60,61,62]. Yet, unlike hyperspectral classification, there has been relatively less research on deep learning-based hyperspectral target detection algorithms [63,64]. There are two types of deep learning-based methods for hyperspectral target detection [65]. One way is to treat the task as a deep learning-based binary classification problem, by setting the target pixels as positive samples and the background pixels as negative samples [63,64,66,67]. Due to the the limited sample problem, this kind of methods usually require to perform training sample augmentation [63,64,68]. Another way is to use the deep learning model by combing the feature reconstruction and target detection together [69,70], and the generative models includes autoencoder [69], variational autoencoder [71], and generative adversarial networks [72]. Compared to the traditional methods, deep learning methods typically achieve a higher accuracy, yet they often lack interpretability. In addition, they usually require a higher computational complexity and more parameter tuning.
- We have theoretically analyzed the factors that affect the target detection, including the data origin, target size, target spectral variation, and the number of bands.
- We have theoretically proven that the impact of the target size mainly depends on the degree of spectral variation in the target. If all the target pixels have identical spectra, this factor will not impact the final output.
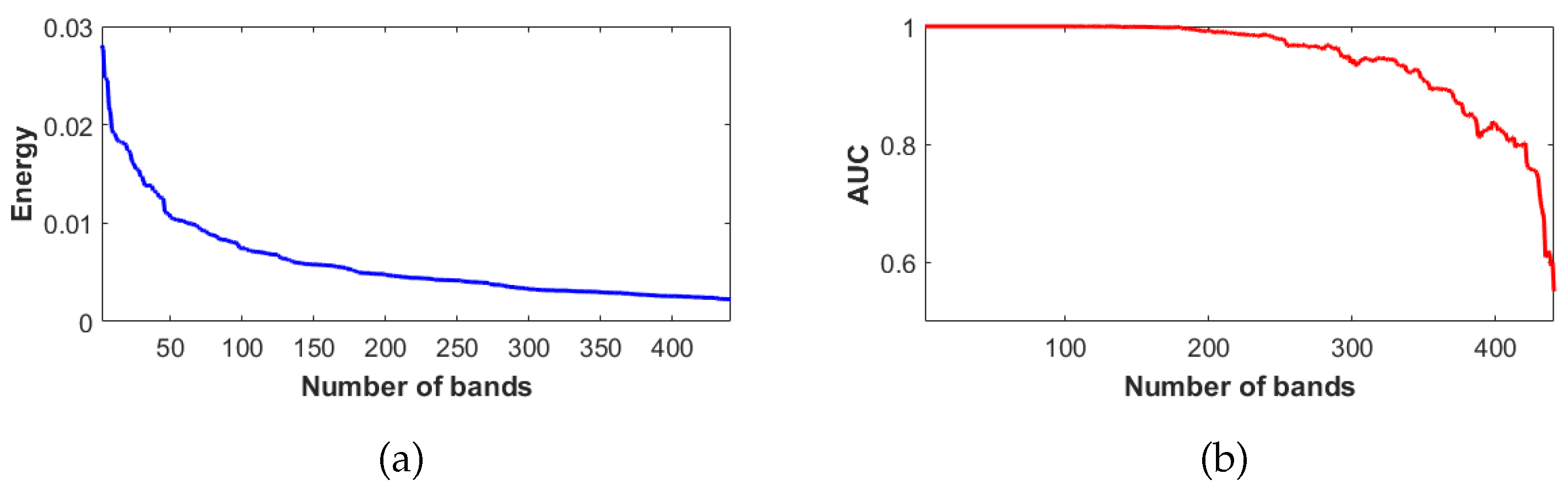
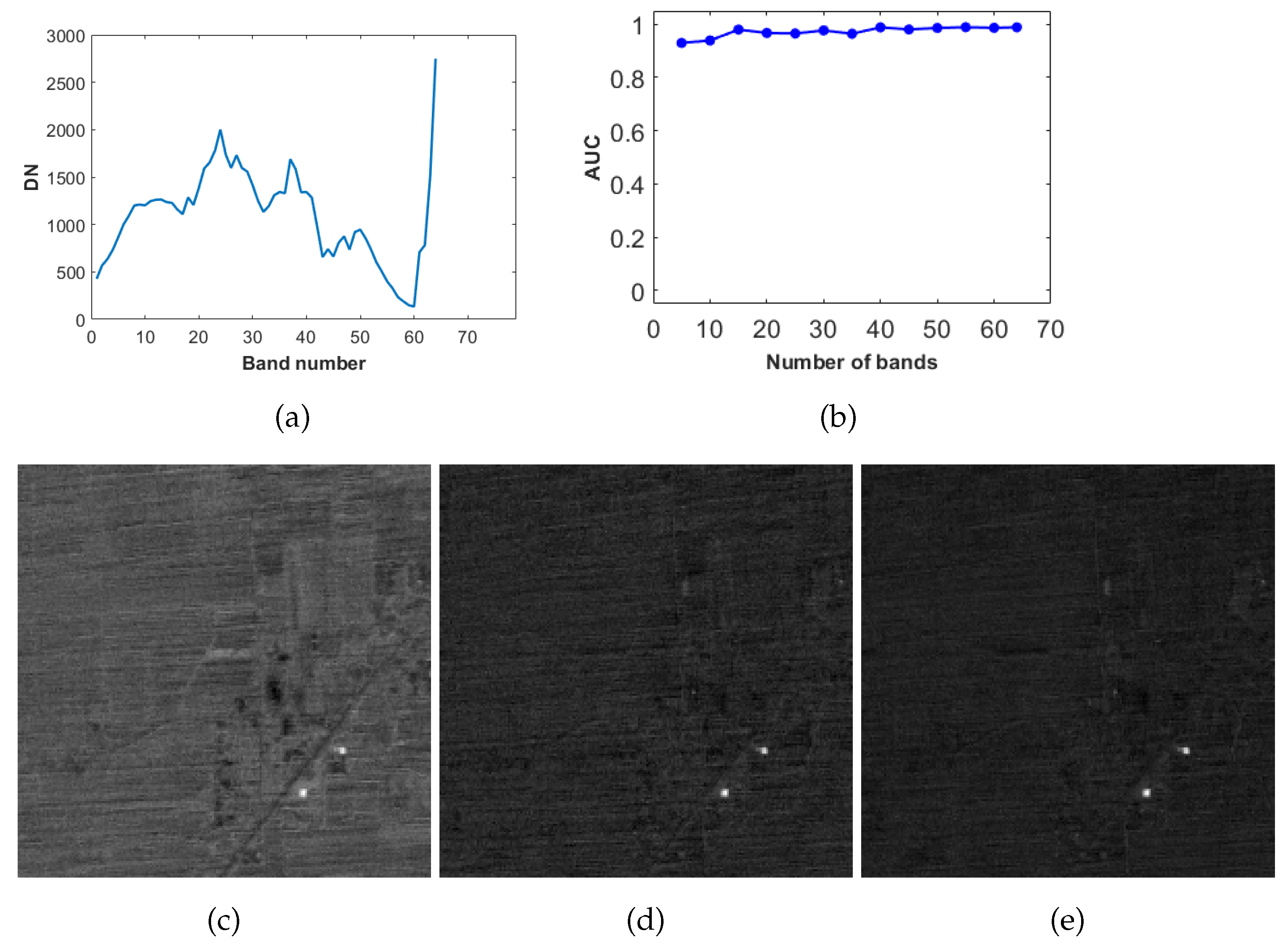
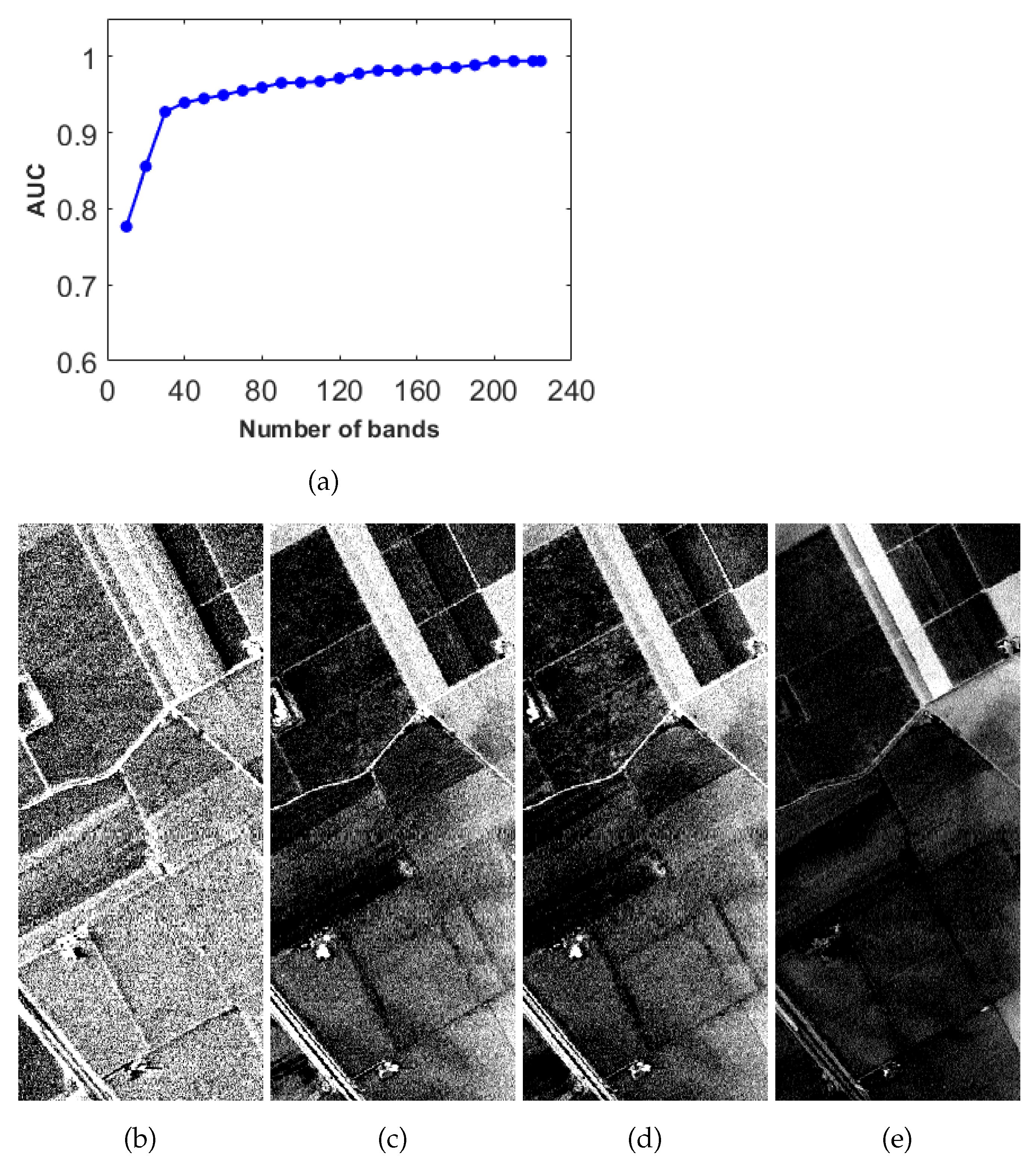
- Increase the number of bands can improve the performance of the detector from the perspective of average filter output energy. However, when there is significant variation in target’s spectra, an excessive number of bands will cause the detector to suppress other target pixels as well.
- In four different target extraction scenarios with varying levels of difficulty, the effects of selecting different target spectra, adding or removing bands, using single-target or multi-target detection algorithms, as well as the role of spatial filtering in target detection are demonstrated using multiple real hyperspectral datasets.
2. Problems in Hyperspectral Target Detection
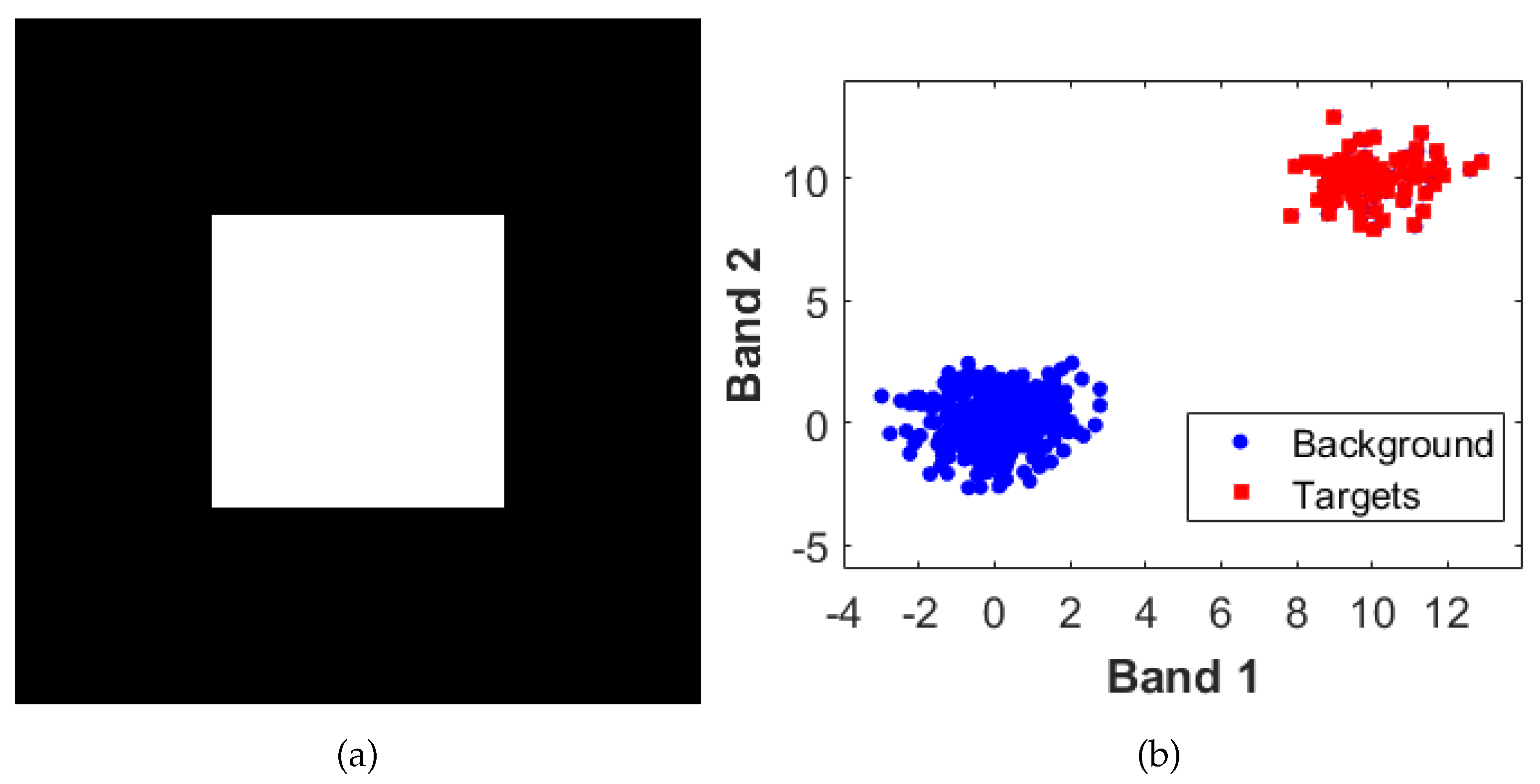
2.1. Data Origin
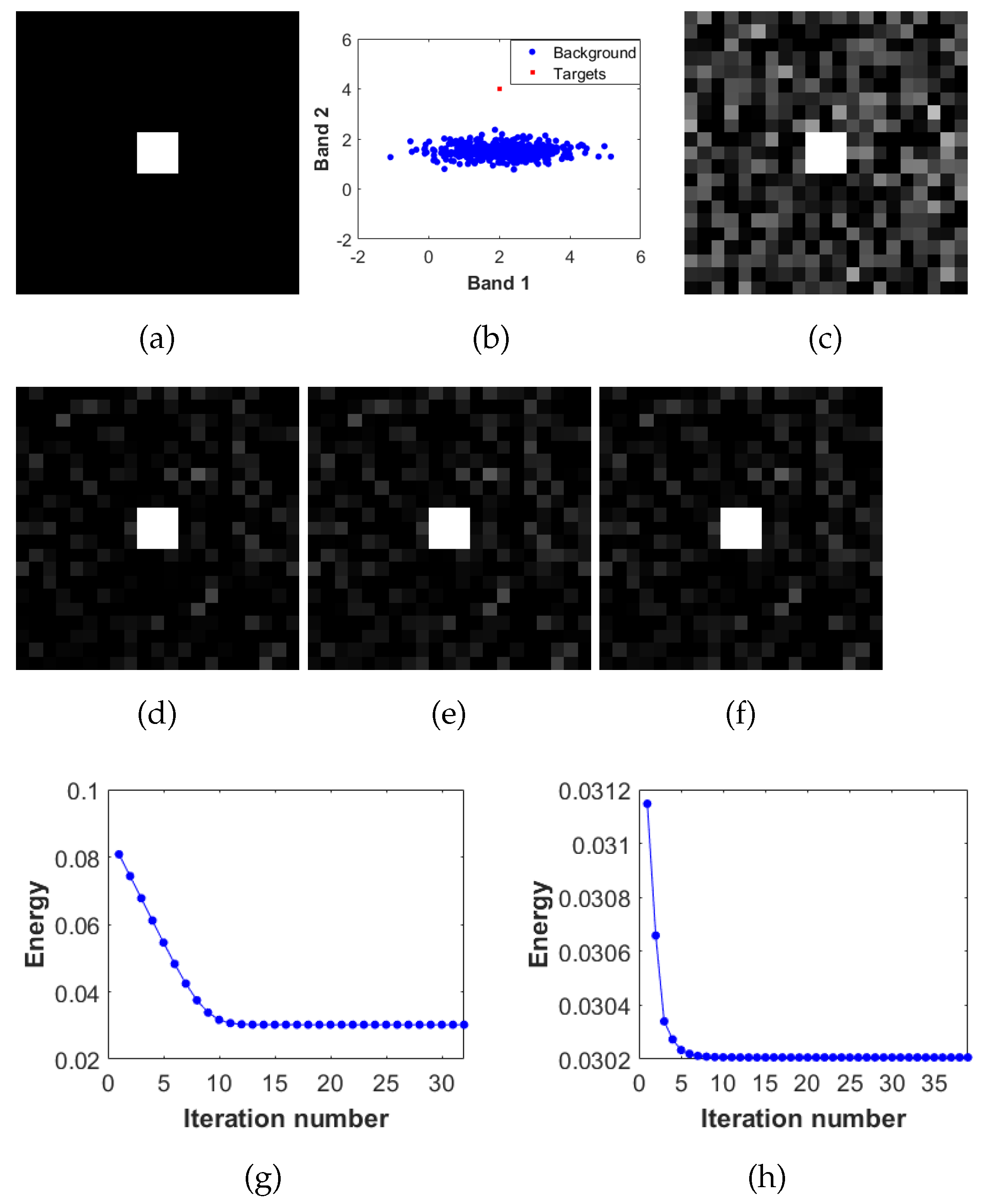
2.2. Target Size
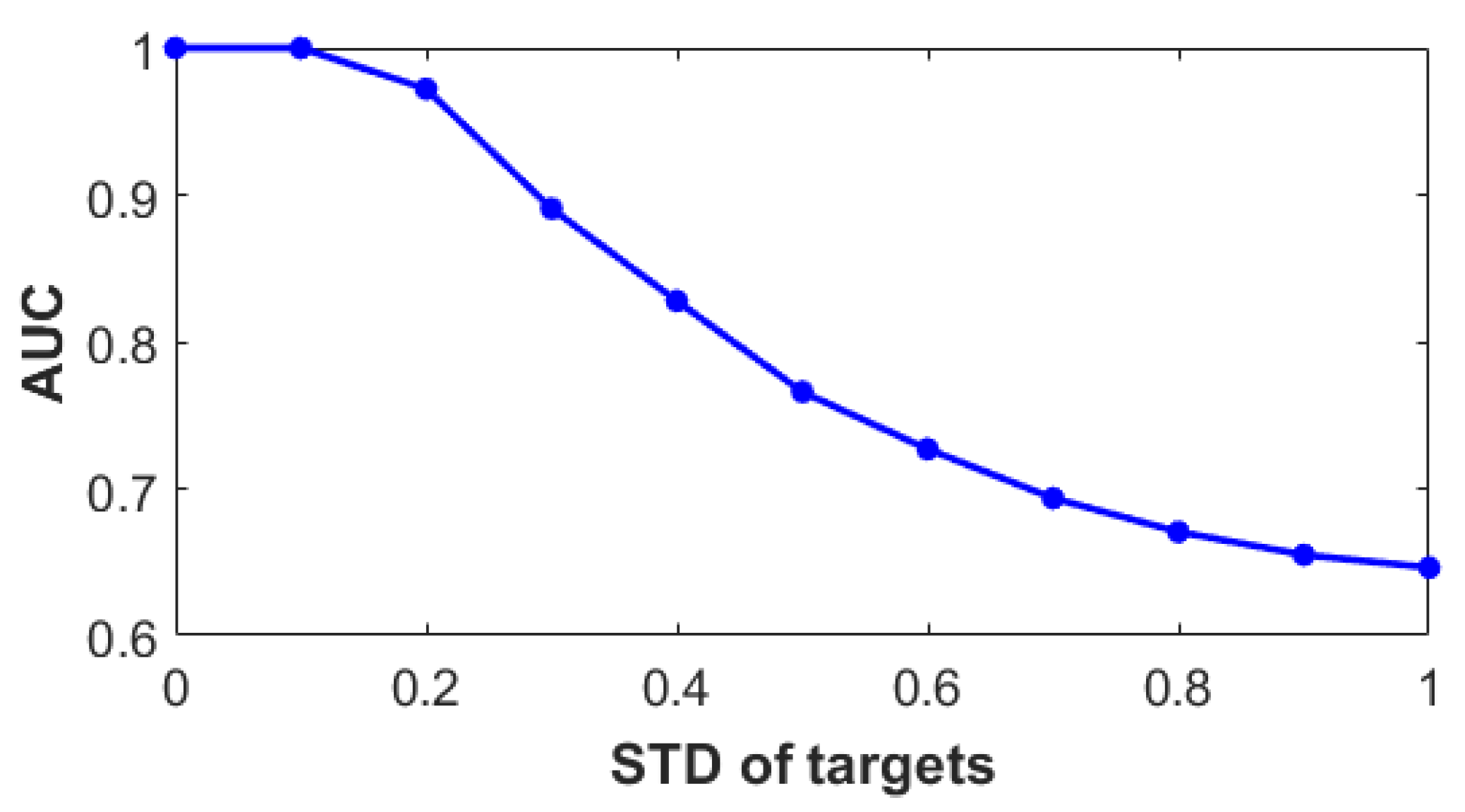
2.3. Target Spectral Variation
2.4. The Number of Bands
3. Strategies to Improve the Target Detection Accuracy under Different Conditions
- (1)
- The target spectral variation is small while the spectral difference between target and background is large;
- (2)
- The target spectral variation is small while the spectral difference between target and background is small;
- (3)
- The target spectral variation is large while the spectral difference between target and background is large;
- (4)
- The target spectral variation is large while the spectral difference between target and background is small.
- (1)
- Data origin: Since the issue of the data origin has already been solved theoretically (see Section 2.1), we suggest to centralize the data firstly (i.e., subtract the mean vector from the data firstly). Therefore, for the following experiments, all the data are centralized firstly.
- (2)
- Target size and target spectral variation: If the single-target detection method is chosen, the problem becomes how to select a proper spectrum to represent the target pixels. If the multiple-target detection method is chosen, the problem turns to how to choose a proper spectrum for each category of the target.
- (3)
- Number of bands: We mainly considers how to select proper bands and/or increase feature bands.
3.1. The Target Spectral Variation Is Small While the Spectral Difference between Target and Background Is Large
- (1)
- Selection of : Select the central pixel of the target region as the representative one, avoiding to select the spectral mixing pixels at the boundary of the target region as ; or select the mean spectrum of all target pixels as .
- (2)
- Band operation: If there is no requirement on computational efficiency, all the bands except for the noise or bad bands should be selected; otherwise, band selection methods can be used before the target detection to reduce the number of bands. Furthermore, if a higher target detection accuracy is required, one can add more feature bands which are helpful to differentiate the target from the background.
3.2. The Target Spectral Variation Is Small While the Spectral Difference between Target and Background Is Small
- (1)
- Selection of : Similar to Case 1, try to avoid selecting spectral mixing pixels at the target boundary as . Instead, pixels from the central region of the target or the mean spectrum can be chosen as .
- (2)
- Band operation: By adding useful bands, the difference between the target and background can be increased, so as to improve the accuracy of the target detection.
3.3. The Target Spectral Variation Is Large While the Spectral Difference between Target and Background Is Large
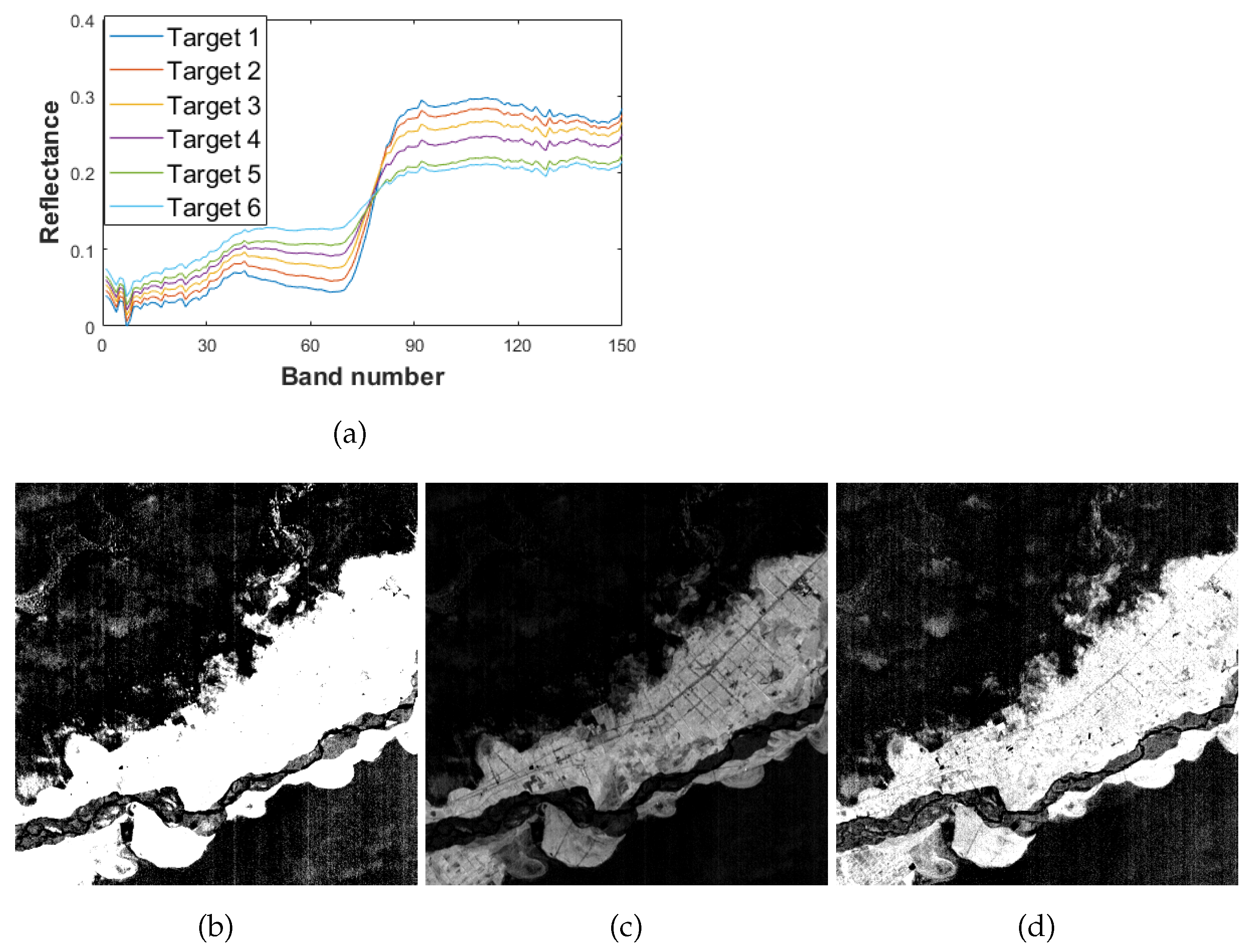
- Target 1: NDVI ;
- Target 2: NDVI ;
- Target 3: NDVI ;
- Target 4: NDVI ;
- Target 5: NDVI ;
- Target 6: NDVI .
- (1)
- If using a single-target detection algorithm, the number of bands can be reduced by using the band selection method to remove redundant bands. Since the target pixels’ spectra vary greatly, it is recommended to use the mean value of all target pixels as .
- (2)
- Multi-target detection algorithms can be used instead of the single-target detection algorithms, but it should be noted that the multiple representative spectra of target should cover all target categories. To improve computational efficiency, redundant bands can also be removed when using multi-target detection algorithms.
3.4. The Target Spectral Variation Is Large While the Spectral Difference between Target and Background Is Small
- (1)
- When using the single target detection method, the detection accuracy can be improved mainly by band operation. On one hand, we should reduce redundant bands and on the other hand, we should add useful feature bands that can increase the difference between target and background. The average spectrum should be selected for .
- (2)
- When using the multi-target detection method, the representative spectra should cover all types of target pixels. Moreover, it is also recommended to simultaneously conduct band selection before performing multi-target detection, so as to reduce redundant bands and increase useful feature bands, which can further improve the detection accuracy.
4. Conclusions
- (1)
- The data origin will affect the performance of target detection. However, there exist optimal data origins in terms of average filter output energy, named CE points. Yet the corresponding CE detector is equivalent to the MF detector, it is recommended to subtract the mean vector before conducting target detection.
- (2)
- As the target size increases, the detection of the target may deteriorate because the influence of target pixels on the auto-correlation matrix becomes more significant. However, Theorem 3 states that the target detection results will remain unaffected under the premise that the target pixels has the same spectrum.
- (3)
- The degree of target spectral variation is what actually affects the target detection result.
- (4)
- From the perspective of the average filter output energy, adding more bands can achieve a better target detection. However, from the perspective of detection accuracy, too many bands may not necessarily be beneficial for target detection. In particular, when the spectral variation of the target is large, the disadvantage of having more bands becomes more apparent. This is because with more bands, detectors are more likely to mislabel other target pixels as background.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Theorem 3
Appendix B. Proof of Theorem 5
References
- Goetz, A.F.H.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef]
- Stein, D.; Beaven, S.; Hoff, L.; Winter, E.; Schaum, A.; Stocker, A. Anomaly detection from hyperspectral imagery. IEEE Signal Process. Mag. 2002, 19, 58–69. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral Image Processing for Automatic Target Detection Applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Kruse, F.A.; Kierein-Young, K.S.; Boardman, J.W. Mineral mapping at Cuprite, Nevada with a 63-channel imaging spectrometer. Photogramm. Eng. Remote Sens. 1990, 56, 176–186. [Google Scholar]
- Clark Roger, N.; Gallagher Andrea, J.; Swayze Gregg, A. Material Absorption Band Depth Mapping of Imaging Spectrometer Data Using a Complete Band Shape Least-Squares Fit with Library Reference Spectra. In Proceedings of the Second Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop; JPL Publication: Pasadena, CA, USA, 1990; Volume 90–54, pp. 176–186. [Google Scholar]
- van der Meer, F. Analysis of spectral absorption features in hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 55–68. [Google Scholar] [CrossRef]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. Solid Earth 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- Kruse, F.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Sellers, P. Canopy reflectance, photosynthesis, and transpiration, II. The role of biophysics in the linearity of their interdependence. Remote Sens. Environ. 1987, 21, 143–183. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- McFEETERS, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Ji, L.; Gong, P.; Wang, J.; Shi, J.; Zhu, Z. Construction of the 500-m Resolution Daily Global Surface Water Change Database (2001–2016). Water Resour. Res. 2018, 54, 10270–10292. [Google Scholar] [CrossRef]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Kruse, F.; Lefkoff, A.; Dietz, J. Expert system-based mineral mapping in northern death valley, California/Nevada, using the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 1993, 44, 309–336. [Google Scholar] [CrossRef]
- Ren, Z.; Zhai, Q.; Sun, L. A Novel Method for Hyperspectral Mineral Mapping Based on Clustering-Matching and Nonnegative Matrix Factorization. Remote Sens. 2022, 14, 1042. [Google Scholar] [CrossRef]
- van der Meero, F.; Bakker, W. Cross correlogram spectral matching: Application to surface mineralogical mapping by using AVIRIS data from Cuprite, Nevada. Remote Sens. Environ. 1997, 61, 371–382. [Google Scholar] [CrossRef]
- Sweet, J. The spectral similarity scale and its application to the classification of hyperspectral remote sensing data. In Proceedings of the IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, MD, USA, 27–28 October 2003; pp. 92–99. [Google Scholar] [CrossRef]
- Zhao, Y.; Pu, R.; Bell, S.S.; Meyer, C.; Baggett, L.P.; Geng, X. Hyperion Image Optimization in Coastal Waters. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1025–1036. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 Site. J. Geophys. Res. Solid Earth 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Boardman, J.W. Automating Spectral Unmixing of AVIRIS Data Using Convex Geometry Concepts. In Fourth JPL Airborne Geoscience Workshop; JPL Publication: Pasadena, CA, USA, 1993. [Google Scholar]
- Geng, X.; Sun, K.; Ji, L.; Zhao, Y.; Tang, H. Optimizing the Endmembers Using Volume Invariant Constrained Model. IEEE Trans. Image Process. 2015, 24, 3441–3449. [Google Scholar] [CrossRef]
- Chang, C.I.; Heinz, D.C. Constrained subpixel target detection for remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1144–1159. [Google Scholar] [CrossRef]
- Harsanyi, J.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Tu, T.M.; Chen, C.H.; Chang, C.I. A noise subspace projection approach to target signature detection and extraction in an unknown background for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 171–181. [Google Scholar] [CrossRef]
- Ren, H.; Chang, C.I. A generalized orthogonal subspace projection approach to unsupervised multispectral image classification. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2515–2528. [Google Scholar] [CrossRef]
- Craig, M. Minimum-volume transforms for remotely sensed data. IEEE Trans. Geosci. Remote Sens. 1994, 32, 542–552. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember Extraction From Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Geng, X.; Xiao, Z.; Ji, L.; Zhao, Y.; Wang, F. A Gaussian elimination based fast endmember extraction algorithm for hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2013, 79, 211–218. [Google Scholar] [CrossRef]
- Nash, D.B.; Conel, J.E. Spectral reflectance systematics for mixtures of powdered hypersthene, labradorite, and ilmenite. J. Geophys. Res. 1974, 79, 1615–1621. [Google Scholar] [CrossRef]
- Somers, B.; Cools, K.; Delalieux, S.; Stuckens, J.; Van der Zande, D.; Verstraeten, W.W.; Coppin, P. Nonlinear Hyperspectral Mixture Analysis for tree cover estimates in orchards. Remote Sens. Environ. 2009, 113, 1183–1193. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences. Ph.D. Thesis, University of Maryland, Baltimore Country, MD, USA, 1993. [Google Scholar]
- North, D. An Analysis of the factors which determine signal/noise discrimination in pulsed-carrier systems. Proc. IEEE 1963, 51, 1016–1027. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A. Analysis of Imaging Spectrometer Data Using N -Dimensional Geometry and a Mixture-Tuned Matched Filtering Approach. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4138–4152. [Google Scholar] [CrossRef]
- Chang, C.I.; Liu, J.; Ren, B.C.H.; Wang, C.M.; Lo, C.; Chung, P.C.; Yang, C.W.; Ma, D. Generalized constrained energy minimization approach to subpixel target detection for multispectral imagery. Opt. Eng. 2000, 39, 5. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L. The CFAR adaptive subspace detector is a scale-invariant GLRT. IEEE Trans. Signal Process. 1999, 47, 2538–2541. [Google Scholar] [CrossRef]
- Ren, H.; Du, Q.; Chang, C.I.; Jensen, J.O. Comparison between constrained energy minimization based approaches for hyperspectral imagery. In Proceedings of the Advances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, DC, USA, 27–28 October 2003; pp. 244–248. [Google Scholar] [CrossRef]
- Chang, C.I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification; Springer Publishing Co.: New York, NY, USA, 2003. [Google Scholar]
- Kwon, H.; Nasrabadi, N.M. Kernel Spectral Matched Filter for Hyperspectral Imagery. Int. J. Comput. Vis. 2007, 71, 127–141. [Google Scholar] [CrossRef]
- Geng, X.; Zhao, Y. Principle of small target detection for hyperspectral imagery. Sci. China Ser. D Earth Sci. 2007, 037, 1081–1087. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Sun, K. Clever eye algorithm for target detection of remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2016, 114, 32–39. [Google Scholar] [CrossRef]
- Geng, X.; Yang, W.; Ji, L.; Wang, F.; Zhao, Y. The match filter (MF) is always superior to constrained energy minimization (CEM). Remote Sens. Lett. 2017, 8, 696–702. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Zhao, Y. Filter tensor analysis: A tool for multi-temporal remote sensing target detection. ISPRS J. Photogramm. Remote Sens. 2019, 151, 290–301. [Google Scholar] [CrossRef]
- Xi, Y.; Ji, L.; Yang, W.; Geng, X.; Zhao, Y. Multitarget Detection Algorithms for Multitemporal Remote Sensing Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Gu, Y. Target Detection For Hyperspectral Images Using ICA-Based Feature Extraction. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 850–853. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Sun, K. Principal Skewness Analysis: Algorithm and Its Application for Multispectral/Hyperspectral Images Indexing. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1821–1825. [Google Scholar] [CrossRef]
- Geng, X.; Wang, L.; Ji, L. Identify Informative Bands for Hyperspectral Target Detection Using the Third-Order Statistic. Remote Sens. 2021, 13, 1776. [Google Scholar] [CrossRef]
- Yang, S.; Song, Z.; Yuan, H.; Zou, Z.; Shi, Z. Fast high-order matched filter for hyperspectral image target detection. Infrared Phys. Technol. 2018, 94, 151–155. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Liu, M.; Pan, H.; Ge, H.; Wang, L. MS3Net: Multiscale stratified-split symmetric network with quadra-view attention for hyperspectral image classification. Signal Process. 2023, 212, 109153. [Google Scholar] [CrossRef]
- Pan, H.; Liu, M.; Ge, H.; Wang, L. One-Shot Dense Network with Polarized Attention for Hyperspectral Image Classification. Remote Sens. 2022, 14, 2265. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Zhao, X.; Siye, L.; Yang, N.; Cai, Y.; Zhan, Y. Multireceptive field: An adaptive path aggregation graph neural framework for hyperspectral image classification. Expert Syst. Appl. 2023, 217, 119508. [Google Scholar] [CrossRef]
- Medus, L.D.; Saban, M.; Francés-Víllora, J.V.; Bataller-Mompeán, M.; Rosado-Muñoz, A. Hyperspectral image classification using CNN: Application to industrial food packaging. Food Control 2021, 125, 107962. [Google Scholar] [CrossRef]
- Xie, T.; Li, X.; Zhang, X.; Hu, J.; Fang, Y. Detection of Atlantic salmon bone residues using machine vision technology. Food Control 2021, 123, 107787. [Google Scholar] [CrossRef]
- Li, J.; Hong, D.; Gao, L.; Yao, J.; Zheng, K.; Zhang, B.; Chanussot, J. Deep learning in multimodal remote sensing data fusion: A comprehensive review. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102926. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yang, N.; Wang, B. Multi-scale receptive fields: Graph attention neural network for hyperspectral image classification. Expert Syst. Appl. 2023, 223, 119858. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yu, C.; Yang, N.; Cai, W. Multi-feature fusion: Graph neural network and CNN combining for hyperspectral image classification. Neurocomputing 2022, 501, 246–257. [Google Scholar] [CrossRef]
- Ge, H.; Wang, L.; Liu, M.; Zhao, X.; Zhu, Y.; Pan, H.; Liu, Y. Pyramidal Multiscale Convolutional Network With Polarized Self-Attention for Pixel-Wise Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, S.; Li, W.; Du, Q.; Ran, Q.; Tao, R. HTD-Net: A Deep Convolutional Neural Network for Target Detection in Hyperspectral Imagery. Remote Sens. 2020, 12, 1489. [Google Scholar] [CrossRef]
- Zhu, D.; Du, B.; Zhang, L. Two-Stream Convolutional Networks for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6907–6921. [Google Scholar] [CrossRef]
- Chen, B.; Liu, L.; Zou, Z.; Shi, Z. Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges. Remote Sens. 2023, 15, 3223. [Google Scholar] [CrossRef]
- Freitas, S.; Silva, H.; Almeida, J.M.; Silva, E. Convolutional neural network target detection in hyperspectral imaging for maritime surveillance. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419842991. [Google Scholar] [CrossRef]
- Qin, H.; Xie, W.; Li, Y.; Du, Q. HTD-VIT: Spectral-Spatial Joint Hyperspectral Target Detection with Vision Transformer. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 1967–1970. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Y.; Yu, X. Hyperspectral Target Detection with an Auxiliary Generative Adversarial Network. Remote Sens. 2021, 13, 4454. [Google Scholar] [CrossRef]
- Shi, Y.; Lei, J.; Yin, Y.; Cao, K.; Li, Y.; Chang, C.I. Discriminative Feature Learning With Distance Constrained Stacked Sparse Autoencoder for Hyperspectral Target Detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1462–1466. [Google Scholar] [CrossRef]
- Xie, W.; Yang, J.; Lei, J.; Li, Y.; Du, Q.; He, G. SRUN: Spectral Regularized Unsupervised Networks for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1463–1474. [Google Scholar] [CrossRef]
- Xie, W.; Lei, J.; Yang, J.; Li, Y.; Du, Q.; Li, Z. Deep Latent Spectral Representation Learning-Based Hyperspectral Band Selection for Target Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2015–2026. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, J.; Lei, J.; Li, Y.; Jia, X. Self-spectral learning with GAN based spectral–spatial target detection for hyperspectral image. Neural Netw. 2021, 142, 375–387. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral Target Detection: An Overview of Current and Future Challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Yang, W. The Analytical Solution of the Clever Eye (CE) Method. IEEE Trans. Geosci. Remote Sens. 2021, 59, 478–487. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Sun, K.; Zhao, Y. CEM: More Bands, Better Performance. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1876–1880. [Google Scholar] [CrossRef]
- Ji, L.; Geng, X.; Sun, K.; Zhao, Y.; Gong, P. Target Detection Method for Water Mapping Using Landsat 8 OLI/TIRS Imagery. Water 2015, 7, 794–817. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Yang, M.; Zhang, Y.; Wang, J.; Marshall, S.; Han, J. Novel Folded-PCA for improved feature extraction and data reduction with hyperspectral imaging and SAR in remote sensing. ISPRS J. Photogramm. Remote Sens. 2014, 93, 112–122. [Google Scholar] [CrossRef]
- Chang, C.I.; Wang, S. Constrained band selection for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1575–1585. [Google Scholar] [CrossRef]
- Geng, X.; Sun, K.; Ji, L.; Zhao, Y. A Fast Volume-Gradient-Based Band Selection Method for Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7111–7119. [Google Scholar] [CrossRef]
- Ji, L.; Zhu, L.; Wang, L.; Xi, Y.; Yu, K.; Geng, X. FastVGBS: A Fast Version of the Volume-Gradient-Based Band Selection Method for Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2021, 18, 514–517. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A Novel Ranking-Based Clustering Approach for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 88–102. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, Y.; Zhang, P.; Ji, L. An automatic band selection algorithm based on connection centre evolution. Remote Sens. Lett. 2023, 14, 323–333. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X. Sparse Transfer Manifold Embedding for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1030–1043. [Google Scholar] [CrossRef]
- Ji, L.; Wang, L.; Geng, X. An Automatic Bad Band Pre-Removal Method for Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4985–4994. [Google Scholar] [CrossRef]
- Sherman, J.; Morrison, W.J. Adjustment of an Inverse Matrix Corresponding to a Change in One Element of a Given Matrix. Ann. Math. Stat. 1950, 21, 124–127. [Google Scholar] [CrossRef]






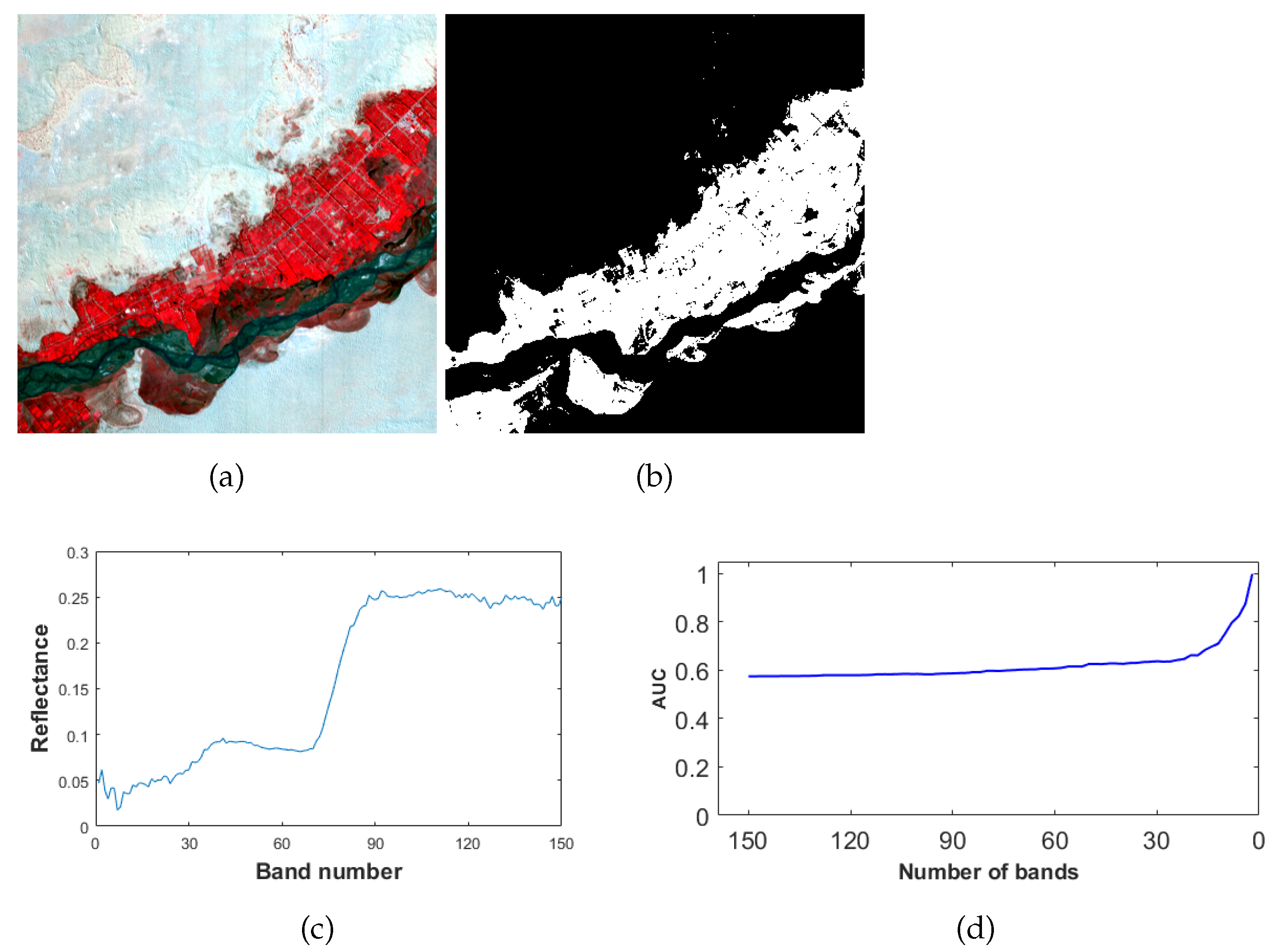


| Target Size | |||||
|---|---|---|---|---|---|
| AUC | 0.9996 | 0.8857 | 0.7250 | 0.6301 | 0.5940 |
| Target size | |||||
| AUC | 0.5669 | 0.5580 | 0.5369 | 0.5250 |
| L | Band Indices |
|---|---|
| 50 | 1 2 3 4 5 6 7 8 9 10 11 34 68 78 87 88 101 102 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 |
| 20 | 1 2 3 4 7 68 78 88 127 128 129 130 133 143 145 146 147 148 149 150 |
| 10 | 1 2 3 68 78 88 128 146 149 150 |
| 6 | 1 2 68 88 146 150 |
| 2 | 68 150 |
| Algorithm | CEM | SCEM | WTACEM | MTCEM |
|---|---|---|---|---|
| AUC | 0.5749 | 0.9988 | 0.9988 | 0.9841 |
| Class No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Original | 0.9985 | 0.9589 | 0.9191 | 0.9676 | 0.9487 | 0.9828 | 0.9992 | 0.9966 |
| Filtered | 0.9991 | 0.9706 | 0.9334 | 0.9738 | 0.9656 | 0.9883 | 0.9996 | 0.9976 |
| Class No. | ||||||||
| Original | 0.9994 | 0.9448 | 0.9417 | 0.9784 | 0.9992 | 0.9619 | 0.9667 | 0.9982 |
| Filtered | 0.9996 | 0.9613 | 0.9523 | 0.9829 | 0.9996 | 0.9689 | 0.9792 | 0.9990 |
| Case No. | Description (Difficulty Level) | Diagram | Strategies | |||
|---|---|---|---|---|---|---|
| Data Origin | Selection of Target Spectrum | Band Operation | Spatial Filter | |||
| 1 | The target spectral variation is small while the spectral difference between target and background is large (Easy) | 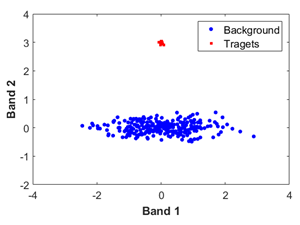 | Move the data to the mean vector of the data | Select the representative target spectrum or the mean vector of the target as . | Reduce redundant or bad bands to increase the computational efficiency. | |
| 2 | The target spectral variation is small while the spectral difference between target and background is small (Normal) | 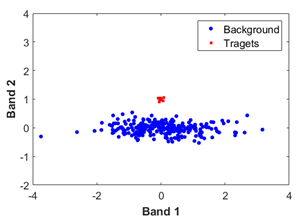 | Move the data to the mean vector of the data. | Select the representative target spectrum or the mean vector of the target as . | Add useful bands. | |
| 3 | The target spectral variation is large while the spectral difference between target and background is large (A bit challenging) |  | Move the data to the mean vector of the data. | Select the representative target spectrum or the mean vector of the target as . | Reduce redundant or bad bands to increase the computational efficiency. | |
| 4 | The target spectral variation is large while the spectral difference between target and background is small (Hard) | 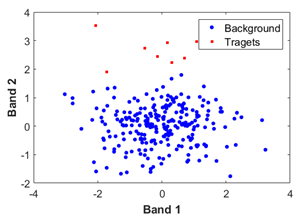 | Move the data to the mean vector of the data. | Select the representative target spectrum or the mean vector of the target as . | Reduce redundant or bad bands, and add useful bands. | Use the spatial filter to reduce the target spectral variation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, L.; Geng, X. Hyperspectral Target Detection Methods Based on Statistical Information: The Key Problems and the Corresponding Strategies. Remote Sens. 2023, 15, 3835. https://doi.org/10.3390/rs15153835
Ji L, Geng X. Hyperspectral Target Detection Methods Based on Statistical Information: The Key Problems and the Corresponding Strategies. Remote Sensing. 2023; 15(15):3835. https://doi.org/10.3390/rs15153835
Chicago/Turabian StyleJi, Luyan, and Xiurui Geng. 2023. "Hyperspectral Target Detection Methods Based on Statistical Information: The Key Problems and the Corresponding Strategies" Remote Sensing 15, no. 15: 3835. https://doi.org/10.3390/rs15153835
APA StyleJi, L., & Geng, X. (2023). Hyperspectral Target Detection Methods Based on Statistical Information: The Key Problems and the Corresponding Strategies. Remote Sensing, 15(15), 3835. https://doi.org/10.3390/rs15153835





