An ENSO Prediction Model Based on Backtracking Multiple Initial Values: Ordinary Differential Equations–Memory Kernel Function
Abstract
:1. Introduction
2. Materials and Methods
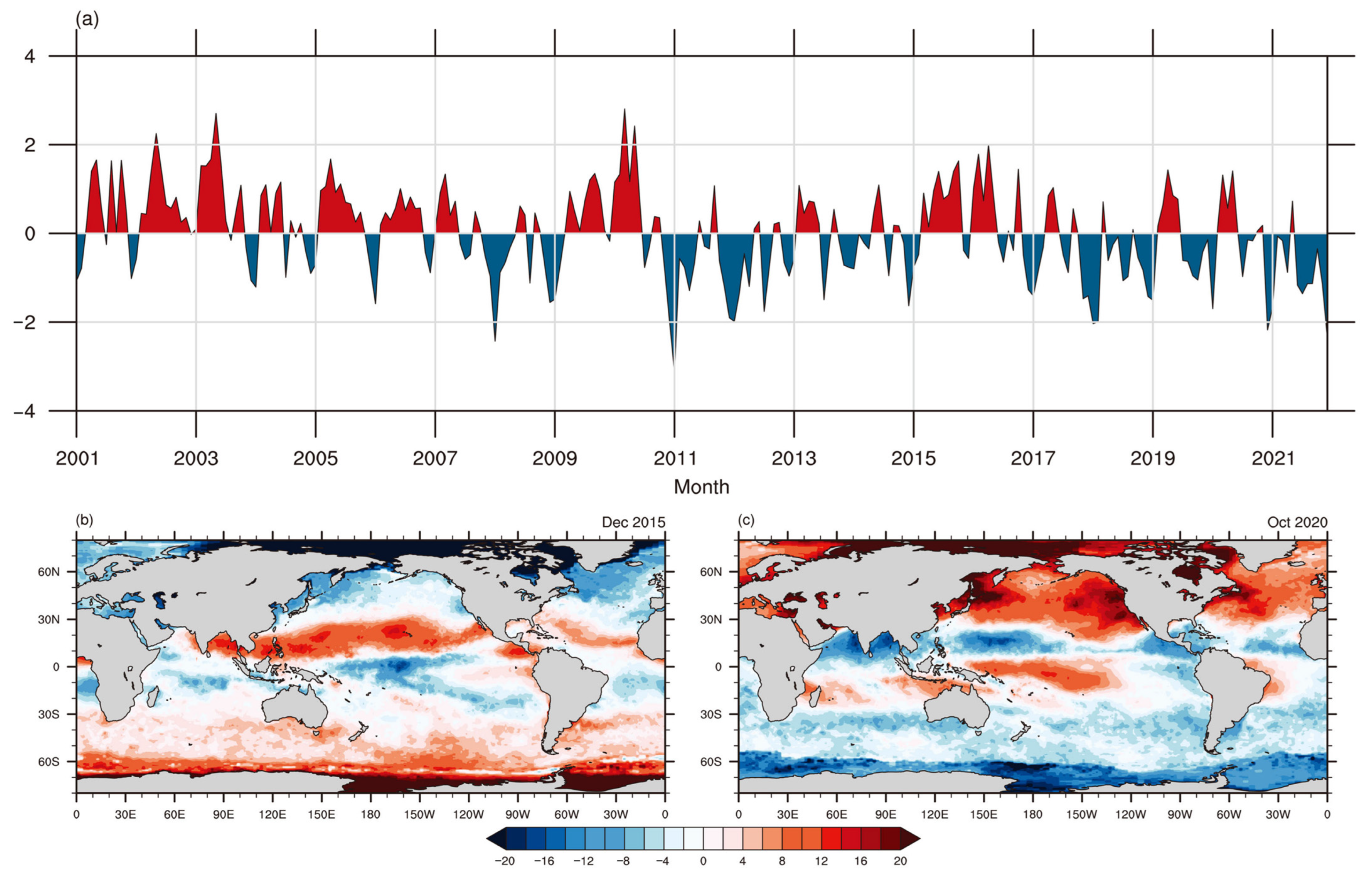
2.1. Materials
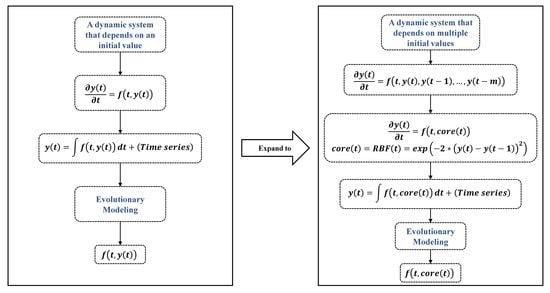
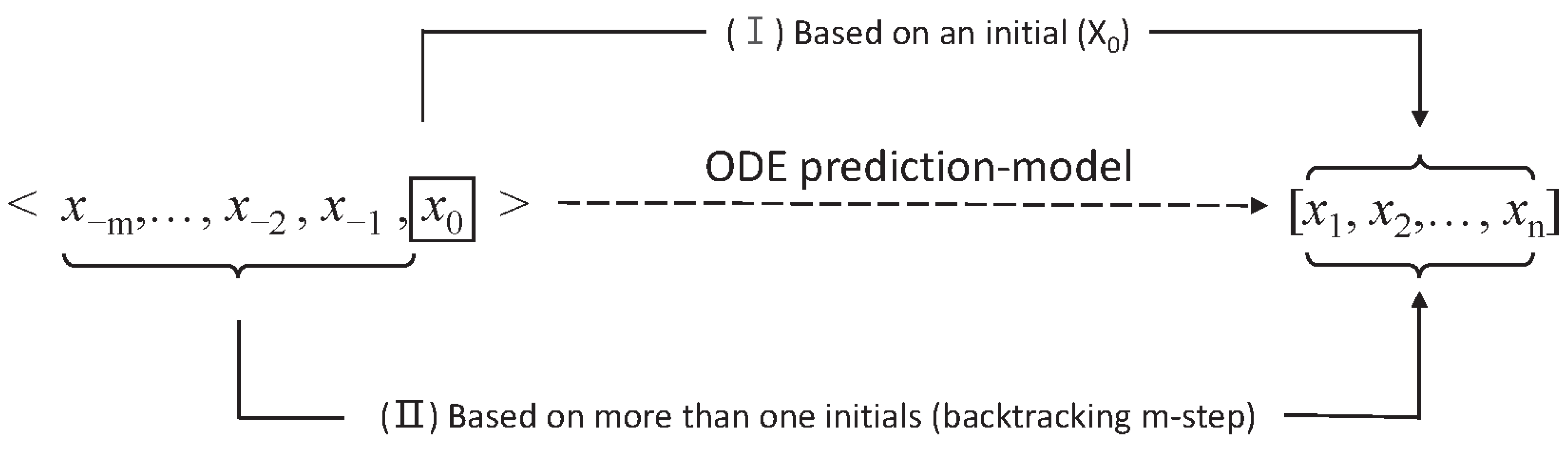
2.2. Backtracking Multiple-Initial-Values Differential Equation
2.3. Evolutionary Algorithm
3. Results
3.1. Local and Global Behaviors in a Complex System
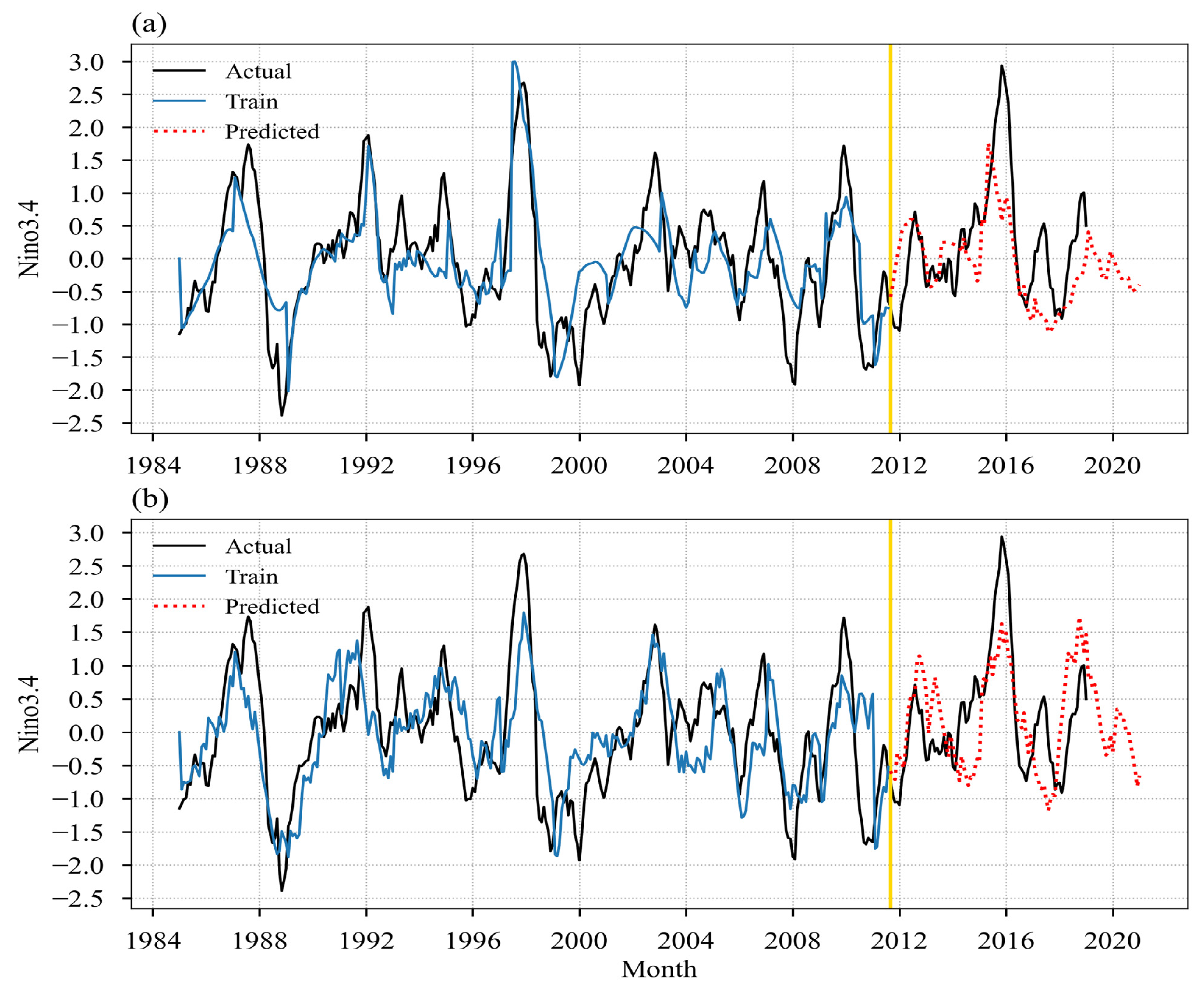
3.2. The ODE–MKF Model for Niño3.4
3.3. Influence of the Backtracking Scale
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thual, S.; Majda, A.J.; Chen, N.; Stechmann, S.N. Simple stochastic model for El Niño with westerly wind bursts. Proc. Natl. Acad. Sci. USA 2016, 113, 10245–10250. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Ling, X.; Zheng, H.; Chen, Z.; Xu, Y. Adaptive multi-kernel SVM with spatial–temporal correlation for short-term traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2001–2013. [Google Scholar] [CrossRef]
- Lorenz, E.N. A study of the predictability of a 28-variable atmospheric model. Tellus 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Y. Reconstruction of missing spring discharge by using deep learning models with ensemble empirical mode decomposition of precipitation. Environ. Sci. Pollut. Res. 2022, 29, 82451–82466. [Google Scholar] [CrossRef] [PubMed]
- Cuo, L.; Pagano, T.C.; Wang, Q.J. A review of quantitative precipitation forecasts and their use in short-to medium-range streamflow forecasting. J. Hydrometeorol. 2011, 12, 713–728. [Google Scholar] [CrossRef]
- Gil-Alana, L.A. Cyclical long-range dependence and the warming effect in a long temperature time series. Int. J. Climatol. 2008, 28, 1435–1443. [Google Scholar] [CrossRef]
- Hariharan, G.; Kannan, K. Review of wavelet methods for the solution of reaction–diffusion problems in science and engineering. Appl. Math. Model. 2014, 38, 799–813. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Tang, Z.; Jian, Z.; Xu, Y.; Zhang, H. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Franzke, C.L.E. Nonlinear climate change. Nat. Clim. Chang. 2014, 4, 423–424. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Snyder, R.D.; Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. Int. J. Forecast. 2002, 18, 439–454. [Google Scholar] [CrossRef] [Green Version]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Busuioc, A.; Tomozeiu, R.; Cacciamani, C. Statistical downscaling model based on canonical correlation analysis for winter extreme precipitation events in the Emilia-Romagna region. Int. J. Climatol. Quart. J. Roy. Meteor. Soc. 2008, 28, 449–464. [Google Scholar] [CrossRef]
- Rehana, S.; Mujumdar, P.P. Climate change induced risk in water quality control problems. J. Hydrol. 2012, 444, 63–77. [Google Scholar] [CrossRef]
- Hannachi, A.; Jolliffe, I.T.; Stephenson, D.B. Empirical orthogonal functions and related techniques in atmospheric science: A review. Int. J. Climatol. 2007, 27, 1119–1152. [Google Scholar] [CrossRef]
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 2005, 12, 345–356. [Google Scholar] [CrossRef] [Green Version]
- Cane, M.A.; Zebiak, S.E. A theory for El Niño and the Southern Oscillation. Science 1985, 228, 1085–1087. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vannitsem, S. Predictability of large-scale atmospheric motions: Lyapunov exponents and error dynamics. Chaos 2017, 27, 032101. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Maraun, D.; Shepherd, T.G.; Widmann, M.; Zappa, G.; Walton, D.; Gutiérrez, J.M.; Hagemann, S.; Richter, I.; Soares, P.M.; Hall, A.D.; et al. Towards process-informed bias correction of climate change simulations. Nat. Clim. Chang. 2017, 7, 764–773. [Google Scholar] [CrossRef] [Green Version]
- Hourdin, F.; Musat, I.; Bony, S.; Braconnot, P.; Codron, F.; Dufresne, J.L.; Fairhead, L.; Filiberti, M.A.; Friedlingstein, P.; Grandpeix, J.Y.; et al. The LMDZ4 General Circulation Model: Climate Performance and Equilibrium Climate Sensitivity. J. Clim. 2006, 24, 634–661. [Google Scholar]
- Held, I.M.; Winton, M.; Takahashi, K.; Delworth, T.; Zeng, F.; Vallis, G.K. Probing the Fast and Slow Components of Global Warming by Returning Abruptly to Preindustrial Forcing. J. Clim. 2010, 23, 2418–2427. [Google Scholar] [CrossRef] [Green Version]
- Rabier, F. Overview of global data assimilation developments in numerical weather-prediction centres. Q. J. R. Meteorol. Soc. J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2005, 131, 3215–3233. [Google Scholar] [CrossRef]
- Feng, G.; Cao, H.; Gao, X.; Dong, W.; Chou, J. Prediction of precipitation during summer monsoon with self-memorial model. Adv. Atmos. Sci. 2001, 18, 701–709. [Google Scholar]
- He, W.; Feng, G.; Wu, Q.; He, T.; Wan, S.; Chou, J. A new method for abrupt dynamic change detection of correlated time series. Int. J. Climatol. 2012, 32, 1604–1614. [Google Scholar] [CrossRef]
- Fischer, M.J. Investigating Nonlinear Dependence between Climate Fields. J. Clim. 2017, 30, 5547–5562. [Google Scholar] [CrossRef]
- Feng, G.; Yang, J.; Zhi, R.; Zhao, J.; Gong, Z.; Zheng, Z.; Xiong, K.; Qiao, S.; Yan, Z.; Wu, Y.; et al. Improved prediction model for flood-season rainfall based on a nonlinear dynamics-statistic combined method. Chaos Solitons Fractals 2020, 140, 110160. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Cheng, Z.; Wang, H. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 2018, 226, 408–422. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. Ensemble smoother with multiple data assimilation. Comput. Geosci. 2013, 55, 3–15. [Google Scholar] [CrossRef]
- Ballabrera-Poy, J.; Busalacchi, A.J.; Murtugudde, R. Application of a reduced-order Kalman filter to initialize a coupled atmosphere–ocean model: Impact on the prediction of El Nino. J. Clim. 2001, 14, 1720–1737. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, J.; Feng, G.; Chou, J. Forecast scheme and strategy for extended-range predictable components. Sci. China Earth Sci. 2013, 56, 878–889. [Google Scholar] [CrossRef]
- Feng, G.; Dong, W. Evaluation of the applicability of a retrospective scheme based on comparison with several difference schemes. Chin. Phys. 2003, 12, 1076. [Google Scholar]
- Chevallier, M.; Vrac, M.; Vautard, R. Nonlinear statistical downscaling for climate model outputs: Description and application to the French Mediterranean region. Clim. Dyn. 2013, 40, 709–735. [Google Scholar]
- Mazzola, L.; Laine, E.M.; Breuer, H.P.; Maniscalco, S.; Piilo, J. Phenomenological memory-kernel master equations and time-dependent Markovian processes. Phys. Rev. A 2010, 81, 062120. [Google Scholar] [CrossRef] [Green Version]
- Slingo, J.; Bates, P.; Bauer, P.; Belcher, S.; Palmer, T.; Stephens, G.; Stevens, B.; Stocker, T.; Teutsch, G. Ambitious partnership needed for reliable climate prediction. Nat. Clim. Chang. 2022, 12, 499–503. [Google Scholar] [CrossRef]
- Neelin, J.D.; Battisti, D.S.; Hirst, A.C.; Jin, F.-F.; Wakata, Y.; Yamagata, T.; Zebiak, S.E. ENSO theory. J. Geophys. Res. Ocean. 1998, 103, 14261–14290. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Jin, F.-F.; Turner, A. Increasing autumn drought over southern China associated with ENSO regime shift. Geophys. Res. Lett. 2014, 41, 4020–4026. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.-P.; Hu, K.; Hafner, J.; Tokinaga, H.; Du, Y.; Huang, G.; Sampe, T. Indian Ocean Capacitor Effect on Indo–Western Pacific Climate during the Summer following El Niño. J. Clim. 2009, 22, 730–747. [Google Scholar] [CrossRef]
- Choi, J.; Son, S.W. Seasonal-to-decadal prediction of El Niño–Southern Oscillation and Pacific Decadal Oscillation. NPJ Clim. Atmos. 2022, 5, 29. [Google Scholar] [CrossRef]
- Keppenne, C.L.; Ghil, M. Adaptive Filtering and Prediction of Noisy Multivariate Signals: AN Application to Subannual Variability in Atmospheric Angular Momentum. Int. J. Bifurcat Chaos 1993, 3, 625–634. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.; DeWitt, D.G. Skill of real-time seasonal ENSO model predictions during 2002–2011: Is our capability increasing? Bull. Am. Meteorol. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Seleznev, A.; Mukhin, D. Improving statistical prediction and revealing nonlinearity of ENSO using observations of ocean heat content in the tropical Pacific. Clim. Dyn. 2023, 60, 1–15. [Google Scholar] [CrossRef]
- Saha, M.; Nanjundiah, R.S. Prediction of the ENSO and EQUINOO indices during June–September using a deep learning method. Meteorol. Appl. 2020, 27, e1826. [Google Scholar] [CrossRef] [Green Version]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U.; Jebara, T.; Barnston, A.G. Statistical Prediction of ENSO from Subsurface Sea Temperature Using a Nonlinear Dimensionality Reduction. J. Clim. 2009, 22, 4501–4519. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y.; Paiement, J.F.; Vincent, P.; Delalleau, O.; Roux, N.L.; Ouimet, M. Out-of-sample extensions for LLE, Isomap, MDS, eigenmaps, and spectral clustering. In Proceedings of the 16th International Conference on Neural Information Processing Systems (NIPS’03), Whistler, BC, Canada, 9–11 December 2003; MIT Press: Cambridge, MA, USA, 2004; pp. 177–184. [Google Scholar]
- Loeb, N.G.; Doelling, D.R. CERES Energy Balanced and Filled (EBAF) from Afternoon-Only Satellite Orbits. Remote Sens. 2020, 12, 1280. [Google Scholar] [CrossRef] [Green Version]
- Jönsson, A.; Bender, F.A.M. Persistence and variability of Earth’s interhemispheric albedo symmetry in 19 years of CERES EBAF observations. J. Clim. 2022, 35, 249–268. [Google Scholar]
- Ragone, F.; Wouters, J.; Bouchet, F. Computation of extreme heat waves in climate models using a large deviation algorithm. Proc. Natl. Acad. Sci. USA 2018, 115, 24–29. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Wang, L.; Wan, S.; Liao, L.; He, T. Evolutionary modeling for dryness and wetness prediction. Acta Phys. Sin. 2012, 61, 119201. [Google Scholar]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Hidalgo, A.; Tello, L. Numerical approach of the equilibrium solutions of a global climate model. Mathematics 2020, 8, 1542. [Google Scholar] [CrossRef]
- Emanuel, K.A.; Živković-Rothman, M. Development and evaluation of a convection scheme for use in climate models. J. Atmos. Sci. 1999, 56, 1766–1782. [Google Scholar] [CrossRef]
- Kane, R.P. Prediction of southern oscillation index using spectral components. Mausam 2022, 53, 165–176. [Google Scholar] [CrossRef]
- Metzger, S.; Latif, M.; Fraedrich, K. Combining ENSO Forecasts: A Feasibility Study. Mon. Wea. Rev. 2004, 132, 456–472. [Google Scholar] [CrossRef]
- Keppenne, C.L.; Ghil, M. Adaptive filtering and prediction of the Southern Oscillation index. J. Geophys. Res. 1992, 97, 20449–20454. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; An, D.; Cai, Y. A Novel Evolution Kalman Filter Algorithm for Short-Term Climate Prediction. Asian J. Control 2016, 18, 400–405. [Google Scholar] [CrossRef]
- Mokhov, I.I.; Smirnov, D.A. El Niño–Southern Oscillation drives North Atlantic Oscillation as revealed with nonlinear techniques from climatic indices. Geophys. Res. Lett. 2006, 33, L03708. [Google Scholar] [CrossRef] [Green Version]
- Tao, W.; Huang, G.; Wu, G.; Hu, K.; Wang, P.; Gong, H. Origins of Biases in CMIP5 Models Simulating Northwest Pacific Summertime Atmospheric Circulation Anomalies during the Decaying Phase of ENSO. J. Clim. 2018, 31, 5707–5729. [Google Scholar] [CrossRef]
- Gong, H.; Wang, L.; Chen, W.; Nath, D.; Huang, G.; Tao, W. Diverse influences of ENSO on the East Asian-western Pacific winter climate tied to different ENSO properties in CMIP5 models. J. Clim. 2015, 28, 2187–2202. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Sun, Y.; Wan, S.; Gu, Y.; Bai, Y.; Mu, J. An ENSO Prediction Model Based on Backtracking Multiple Initial Values: Ordinary Differential Equations–Memory Kernel Function. Remote Sens. 2023, 15, 3767. https://doi.org/10.3390/rs15153767
Ma Q, Sun Y, Wan S, Gu Y, Bai Y, Mu J. An ENSO Prediction Model Based on Backtracking Multiple Initial Values: Ordinary Differential Equations–Memory Kernel Function. Remote Sensing. 2023; 15(15):3767. https://doi.org/10.3390/rs15153767
Chicago/Turabian StyleMa, Qianrong, Yingxiao Sun, Shiquan Wan, Yu Gu, Yang Bai, and Jiayi Mu. 2023. "An ENSO Prediction Model Based on Backtracking Multiple Initial Values: Ordinary Differential Equations–Memory Kernel Function" Remote Sensing 15, no. 15: 3767. https://doi.org/10.3390/rs15153767
APA StyleMa, Q., Sun, Y., Wan, S., Gu, Y., Bai, Y., & Mu, J. (2023). An ENSO Prediction Model Based on Backtracking Multiple Initial Values: Ordinary Differential Equations–Memory Kernel Function. Remote Sensing, 15(15), 3767. https://doi.org/10.3390/rs15153767