Abstract
There has been a severe shortage of water resources in Central Asia and agriculture has been highly dependent on irrigation because of the scarce precipitation in the croplands. Central Asia is also experiencing climate warming in the context of global warming; however, few studies have focused on changes in the amount of irrigation in Central Asia under future climate warming and their regional climate effects. In this study, we adopted the Weather Research and Forecasting (WRF) model to design three types of experiments: historical experiments (Exp01); warming experiments using future driving fields (Exp02); and warming experiments that involved increasing the surface energy (Exp03). In each type of experiment, two experiments (considering and not considering irrigation) were carried out. We analyzed the regional climate effects of irrigation under the warming of Central Asia by 2.0 °C through determining the differences between the two types of warming experiments and the historical experiments. For surface variables (irrigation amount; sensible heat flux; latent heat flux; and surface air temperature), the changes (relative to Exp01) in Exp03 were thought to be reasonable. For precipitation, the changes (relative to Exp01) in Exp02 were thought to be reasonable. The main conclusions were as follows: in Central Asia, after warming by 2.0 °C, the irrigation amount increased by 10–20%; in the irrigated croplands of Central Asia, the irrigation-caused increases (decreases) in latent heat flux (sensible heat flux) further expanded; and then the irrigation-caused decreases in surface air temperature also became enhanced; during the irrigation period, the irrigation-caused increases in precipitation in the mid-latitude mountainous areas were reduced. This study also showed that, in the WRF model, the warming experiments caused by driving fields were not suitable to simulate the changes in irrigation amount affected by climate warming.
1. Introduction
As an important source of energy and moisture in the atmosphere, land surface is an important component of the climate system [1,2]. In the past hundreds of years, 30–50% of the Earth’s land surface has been altered by human activities [3,4,5], and studies have shown that these changes in land surface exerted important impacts on climate through interactions between the land and atmosphere [6,7,8,9,10,11]. Therefore, the changes in land surface have become the important driving factors for local, regional, and global climate changes. Among the anthropogenic activities that alter the underlying surface characteristics, irrigation is an important land management practice. Through adding water to the soil, irrigation increases soil moisture and maintains the normal growth of crops. Irrigation accounts for 90% of the consumptive water usage and 70% of global freshwater withdrawals [12]. Irrigated croplands account for over 18% of global croplands, corresponding to approximately 2% of the total land surface [13]. Since irrigation can increase water vapor in the atmosphere and affect the partitioning of surface energy, irrigation has been recognized as an important anthropogenic factor that affects the local and regional climate [11,14,15,16,17,18,19].
Thus far, there have been many researchers who studied the climate effects of irrigation, in which most of the studies adopted numerical simulation means. For numerical simulations, the crucial part in the model is the irrigation scheme. In the past, default climate models did not consider irrigation processes, leading to irrigation schemes that were diverse in different studies. At the core of irrigation schemes is determining how to increase soil moisture in the model. Wu et al. [11] summarized three commonly used types of irrigation schemes: (a) the soil moisture of croplands being set to fixed values (such as saturation, field capacity) during an irrigation period [20,21,22,23,24]; (b) the estimated irrigation amount based on observations was applied into croplands during the irrigation period [25,26,27,28]; (c) the dynamic irrigation scheme, which basically regarded the soil moisture of the root zone as the irrigation trigger, has been adopted by increasing the number of studies [11,14,15,16,19,29,30,31,32,33,34]. In this dynamic irrigation scheme, the amount of each irrigation is calculated on the basis of the soil’s current moisture. The third scheme mentioned above considered the impacts of climatic conditions on the irrigation amount, but the first and second scheme did not. Obviously, the dynamic irrigation scheme was more in line with reality. The WRF (Weather Research and Forecasting) model has been widely adopted to study the regional climate effects of irrigation. In the official WRF model version 4.2 and above, Valmassoi et al. [35] developed and incorporated the irrigation schemes. However, these schemes did not consider well the impacts of climatic conditions on the irrigation amount. Global warming has become an indisputable fact, and it will continue; however, few studies have focused on the regional climate effects of irrigation under future climate warming. Since the dynamic irrigation scheme considered the effects of climatic conditions, this scheme was very suitable for simulating the changes in irrigation amount caused by future climate warming, including their regional climate effects.
Central Asia is in the hinterland of Eurasia, including Kazakhstan, Uzbekistan, Turkmenistan, Tajikistan, Kyrgyzstan, and Xinjiang province of China [36]. As the central area of the Silk Road Economic Belt, Central Asia has become a hot study area. The topography of Central Asia generally shows high in the southeast and low in the northwest, which is characterized with large contrast in elevation, from 154 m below the sea level to 8611 m above the sea level. The precipitation is less affected by the ocean due to Central Asia being far away from it. Therefore, precipitation was scarce in Central Asia (not including its mountainous region). However, affected by the orographic lifting in mountains, the high-value areas of precipitation in Central Asia were in the high-altitude mountainous regions [11]. For example, the annual precipitation is below 50 mm in the Tarim Basin, but the annual precipitation can be more than 800 mm in the Tianshan Mountains. Unfortunately, the croplands of Central Asia are widely distributed in low-altitude areas, where precipitation is scarce. Therefore, the agricultural production here was highly dependent on irrigation, and a large amount of water resources was inevitably consumed by irrigation. Due to water sources for irrigation, the major irrigation areas in Central Asia are mainly located near the rivers (such as Syr Darya, Amu Darya, and Yarkand River). Under global warming, Central Asia is also experiencing an area-averaged surface air temperature that had significantly increased by 0.18 °C per decade in the past century (1901–2003), an amount that was greater than the global averaged value [37]. From 1979 to 2011, the temperature in Central Asia increased by up to 0.36–0.42 °C per decade [38]. Climate warming in Central Asia was projected to continue [39]. Central Asia has been facing severe water stress, and irrigation consumes most of its water resources [40]. Therefore, in Central Asia, for the sustainable development of irrigated agriculture, it was very meaningful to study the influences of future climate warming on irrigation amount and their regional climate effects.
Wu et al. [11] have adopted the numerical simulation method to investigate the impacts of irrigation over Central Asia on regional climate during the historical period (1995–2014), and they drew some important conclusions. Compared to the official irrigation schemes in the WRF model, the advantage of the irrigation scheme constructed by Wu et al. [11] was obvious, which provided a more suitable irrigation scheme for this study. As mentioned above, although Central Asia has been facing a severe water crisis, irrigation consumes a large amount of water resources. However, in Central Asia, under climate warming, few studies have focused on the impacts of future climate warming on water resources use (such as irrigation). Therefore, the impacts of future climate warming on irrigation amount were unknown, and the impacts of future climate warming on irrigation-induced changes in the related physical variables were also unknown. The purpose of this study was to address these scientific questions. In addition, were the warming experiments caused by driving fields suitable to simulate the influences of climate warming on irrigation amount? This was also unclear. Therefore, based on the partial settings of Wu et al. [11], in this study, we designed three types of experiments (historical experiments, warming experiments using future driving fields, and warming experiments by increasing the surface energy), in order to analyze the impacts of irrigation on the regional climate under Central Asia warming by 2.0 °C, including changes caused by climate warming to irrigation amount.
2. Methods
2.1. WRF Setup and Irrigation Scheme
Wu et al. [11] have simulated the impacts of irrigation over Central Asia on regional climate via the WRF model. We also adopted the WRF model, with version 4.0.3 as the regional climate model in this study. The adopted physical parameterization schemes were the same as those selected by Wu et al. [11]. The schemes were as follows: the Thompson graupel microphysics scheme, the Tiedtke cumulus scheme, the RRTMG shortwave radiation and longwave radiation scheme, the Noah-mosaic land surface model, and the Yonsei University planetary boundary layer scheme.
Figure 1 showed the simulated region. The land use type used was MODIS 20-category (Figure 1a). The model domain and the settings of the 3D grid points were consistent with a previous study [11]. The center of model domain was (44.5°N, 67°E), and the horizontal grid points were 196 (meridional) × 146 (zonal) with a horizontal resolution of 20 km. In the vertical coordinates, 33 eta levels from the surface to 50 mb were used. The lateral boundary adopted an exponential relaxation scheme and the buffer set 10 grid points. The driving fields of the WRF model were the bias-corrected CMIP6 global dataset, which were constructed by Xu et al. [41]. The reference data required for bias correction were the ERA5 reanalysis data. The model data were the outputs of 18 models from CMIP6. This dataset contained the historical period (1979–2014) and future scenarios (2015–2100) with 1.25° × 1.25° grid spacing and 6-hourly intervals, and the future emission scenarios of this dataset were SSP2-4.5 and SSP5-8.5.

Figure 1.
(a) The altitude (unit: m) of the simulated region. (b) Land use type in the simulated domain. (c) Irrigation fraction (unit: %) in the simulated domain.
In the dynamic irrigation scheme, the irrigation trigger is the root-zone soil moisture, which was more realistic [11]. We also adopted the dynamic irrigation scheme in this study, and this scheme considered irrigation only in subgrid-scale. According to the irrigation fraction (Figure 1b), the irrigated areas consisted of the irrigated portions within each grid cell. Referred to the irrigation period of Wu et al. [11] and Zhang et al. [33], the irrigation period was also set from April 10 to September 10, while the other time of the year was the non-irrigation period. To avoid that the start day of irrigation every year was the same in the whole simulation region, the start day of irrigation in different croplands was determined according to the land surface temperature at 06:00 UTC on 10 April every year [11]. Since the core of the dynamic irrigation scheme is the irrigation trigger, we again exhibited the irrigation trigger (Equation (4)) and the calculation of irrigation amount each irrigation (Equation (5)) in this study. If the soil water content of the upper 0.6 m layers satisfies Equation (4) at 08:00 UTC on each day, croplands start irrigation, and irrigation continues for 4 h and ends at 12:00 UTC, in which the irrigation rate (IRATE, unit: mm s−1) is calculated by Equation (5).
where D(i) is the thicknesses of soil layers for layer i: D(1) = 0.1 m, D(2) = 0.3 m, and D(3) = 0.2 m (only taken from 0.4 to 0.6 m). SM(i) refers to the soil moisture for layer i; SWLT, SREF, and SMAX are the soil wilting point, field capacity, and saturated value, respectively, and their units are m3 m−3. ASM is the total soil water content of the three layers soil thickness (0.6 m); TSMCWLT and TSMCREF are the total soil water content of 0.6 m soil thickness when soil moisture is at the soil wilting point and field capacity, respectively, and their units are mm.
2.2. Experimental Design
We designed three types of experiments (Table 1). (a) The simulated period started at 00:00 UTC on 1 January 1994 and ended at 18:00 UTC on 31 December 2014, which was driven by the historical period (1994–2014) CMIP6 dataset. (b) The adopted driving fields were the CMIP6 SSP5-8.5 data of the future scenarios; the simulated experiments started from 00:00 UTC on 1 January 2035 and ended at 18:00 UTC on 31 December 2055. (c) The simulated period and driving fields were the same as those in (a), with the only difference being that the surface upward longwave radiation in the Noah land surface module was set to decrease by 8% in (c). The purpose of setting an 8% reduction rate was to increase the simulated surface air temperature by about 2.0 °C (mentioned in Section 3.2 later). The determination of the decrease rate had undergone a series of experiments with different reduction rates. The first type of experiments were historical experiments, which were referred to as Exp01; the second type of experiments were the warming experiments using future scenario (SSP5-8.5) data and were referred to as Exp02; the third type of experiments were the warming experiments with increasing surface energy, which were referred to as Exp03. For each type of experiment, two experiments were designed: the control experiment (CTL) that did not consider irrigation, and the sensitivity experiment (SEN) that considered irrigation. The adopted scheme was the dynamic irrigation scheme mentioned previously. The simulated results were outputted every 6 hrs. The first year (1994 or 2035) of each simulation was considered as spin-up time and was not used for analysis.

Table 1.
The experimental design.
3. Results
3.1. The Warming Experiments Using Driving Fields
The simulated results of the historical period were evaluated by adopting the validation data [11], which were not repeated in this study. For future simulations in Exp02, we adopted the high emission scenario (SSP5-8.5) data as the driving fields of the WRF model, and thus the simulated surface air temperature during the future period should be greater than that during the historical period. As shown in Figure 2a, the simulations indicated that the future multi-year (2036–2055) annual mean surface air temperature obviously increased, relative to the historical period (1995–2014), in which the regional averaged value of the increased temperature was about 2.0 °C. Therefore, in this study, based on the high emission scenario (SSP5-8.5), we treated 2035–2055 as the time period for future warming of Central Asia by 2.0 °C, and then, we simulated the impacts of irrigation over Central Asia on regional climate against the background of future warming. It should be noted that, in our study, the changes (increases or decreases) in the related variables in Exp02 and Exp03 were referred to as the results of Exp02 minus Exp01 and Exp03 minus Exp01, respectively.
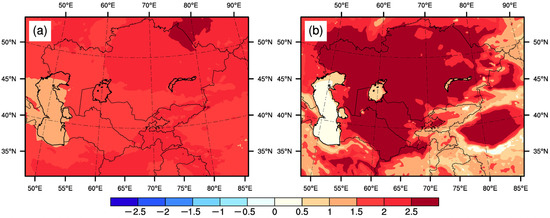
Figure 2.
Spatial differences ((a) CTL in Exp02 minus CTL in Exp01; (b) CTL in Exp03 minus CTL in Exp01) in multi-year (20 years) annual mean surface air temperature (unit: °C). The 20 years denoted were from 1995 to 2014 in Exp 01 and Exp03, and from 2036 to 2055 in Exp02 (the same below).
In Central Asia, the irrigation period was the warm season, and the non-irrigation period was the cold season, meaning that the temperatures of these two periods were totally different. However, the magnitude of precipitation in the non-irrigation period was roughly consistent with that in the irrigation period, with some areas where the former was greater than the latter (Figure 3a,b). Therefore, after warming by 2.0 °C in Central Asia, it was necessary to analyze the changes in precipitation during the non-irrigation period and the irrigation period, respectively. There was a very interesting phenomenon where the direction of warming-induced changes in precipitation in mid-latitude mountainous areas was opposite during the non-irrigation period and the irrigation period (Figure 3c,d). In mid-latitude mountainous areas, the precipitation affected by warming increased during the non-irrigation period (Figure 3c) and decreased during the irrigation period (Figure 3d).

Figure 3.
(a) Non-irrigation period mean and (b) irrigation period mean precipitation (unit: mm day−1) (CTL in Exp01). Spatial differences (CTL in Exp02 minus CTL in Exp01) in (c) non-irrigation period mean and (d) irrigation period mean precipitation (unit: mm day−1). Spatial differences (CTL in Exp03 minus CTL in Exp01) in (e) non-irrigation period mean and (f) irrigation period mean precipitation (unit: mm day−1). The results shown were all the multi-year (20 years) mean values.
Figure 4a,b showed the spatial characteristics of the annual mean latent heat flux and sensible heat flux, respectively. It could be seen that, in addition to mountainous and water areas, and high-latitude regions, the surface energy was mainly allocated to sensible heat flux (Figure 4a,b). Although the surface air temperature of Central Asia was raised by 2.0 °C under the future high emission scenario, our simulations showed that the changes in latent heat flux and sensible heat flux were small (Figure 4c,d). Obviously, in the simulations of Exp02, the increased surface air temperature was only induced by the driving fields and had nothing to do with the changes in surface energy. In Exp02, for the non-irrigation period mean and the irrigation period mean values, the changes in latent heat flux and sensible heat flux caused by warming were also small, which was the reason that we only analyzed the annual mean values here.
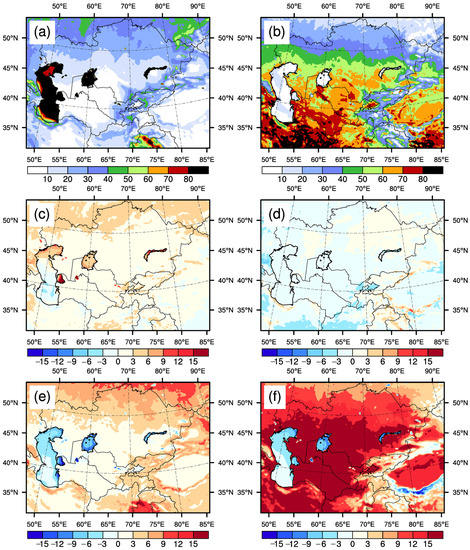
Figure 4.
Annual mean (a) latent heat flux and (b) sensible heat flux (unit: W m−2) (CTL in Exp01). Spatial differences (CTL in Exp02 minus CTL in Exp01) in annual mean (c) latent heat flux and (d) sensible heat flux (unit: W m−2). Spatial differences (CTL in Exp03 minus CTL in Exp01) in annual mean (e) latent heat flux and (f) sensible heat flux (unit: W m−2). The results shown were all the multi-year (20 years) mean values.
According to general knowledge, a rise in temperature should lead to increases in the amount of irrigation. However, the simulations showed that the irrigation amount (in Exp02) affected by warming did not increase, and even decreased slightly in the main irrigation areas except for Xinjiang province of China (Figure 5b), which was obviously unreasonable. From the physical point of view, the problem of global warming is actually an imbalance in the Earth’s energy budget. Since the greenhouse gases can absorb a large amount of longwave radiation, the increased greenhouse gases in the atmosphere reduce the energy emitted from the top of the atmosphere, which increases the energy on Earth, and eventually leads to increases in the surface air temperature. Unfortunately, in Exp02, the increased surface air temperature (relative to Exp01) was only caused by driving fields and had nothing to do with changes in surface energy (as previously mentioned, the changes in latent heat flux and sensible heat flux were small). Small changes in the surface energy were not conducive to increases in surface evapotranspiration, which was also the reason that the irrigation amount (in Exp02) affected by warming did not increase. Therefore, in the WRF model, it was not feasible to study the impacts of future climate warming on the irrigation amount through the warming experiments with future driving fields. The impacts of future climate warming on irrigation amount would be again analyzed in the warming experiments with increasing surface energy (Exp03).

Figure 5.
Spatial distributions of multi-year (20 years) irrigation period mean irrigation rate in (a) Exp01 (unit: mm day−1), (b) (Exp02 minus Exp01)/Exp01 (unit: %), and (c) (Exp03 minus Exp01)/Exp01 (unit: %).
For Exp01, in croplands after irrigation, the latent heat flux increased (Figure 6a), and the sensible heat flux and the surface air temperature decreased (Figure 6b,c), which was completely consistent with the results of study [11]. Although the differences (Exp02 minus Exp01) in the irrigation-caused changes in the latent heat flux, sensible heat flux, and surface air temperature were not obvious (Figure 6d–f), the latent heat flux affected by warming did not increase (even decreased) in the main irrigation areas (such as the Fergana basin) (Figure 6d), which was also unreasonable. Here, the non-increases in the latent heat flux affected by warming corresponded to the non-increases in the irrigation amount (Figure 5b and Figure 6d).
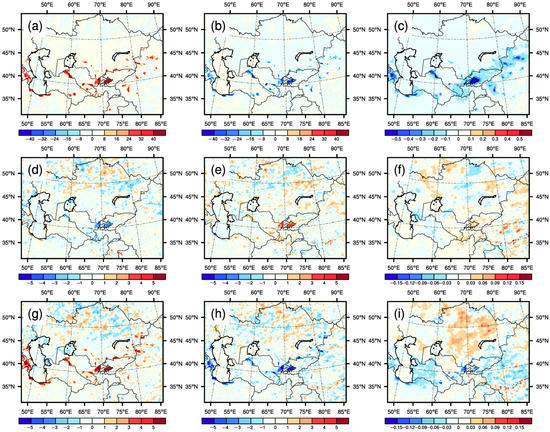
Figure 6.
Spatial differences (SEN in Exp01 minus CTL in Exp01) in (a) latent heat flux (unit: W m−2), (b) sensible heat flux (unit: W m−2), and (c) surface air temperature (unit: °C). Spatial differences ((SEN in Exp02 minus CTL in Exp02) minus (SEN in Exp01 minus CTL in Exp01)) in (d) latent heat flux (unit: W m−2), (e) sensible heat flux (unit: W m−2), and (f) surface air temperature (unit: °C). Spatial differences ((SEN in Exp03 minus CTL in Exp03) minus (SEN in Exp01 minus CTL in Exp01)) in (g) latent heat flux (unit: W m−2), (h) sensible heat flux (unit: W m−2), and (i) surface air temperature (unit: °C). The results shown were the multi-year (20 years) irrigation period mean values.
For Exp01, precipitation affected by irrigation obviously increased in the mountainous regions of the dotted box (Xinjiang province of China and Kyrgyzstan) (Figure 7a), which was completely consistent with a previous study [11]. As mentioned above, the precipitation affected by warming in the mid-latitude mountainous areas (dotted box) decreased during the irrigation period (Figure 3d), which led to that, in Exp02, the irrigation-caused increases in precipitation in the mountainous areas of the dotted box also decreased by 0.05–0.3 mm day−1, relative to Exp01 (Figure 7b).
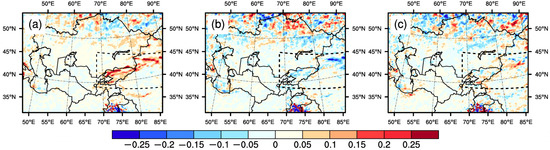
Figure 7.
(a) Spatial differences (SEN in Exp01 minus CTL in Exp01) in multi-year (20 years) irrigation period mean precipitation (unit: mm day−1). (b) Spatial differences ((SEN in Exp02 minus CTL in Exp02) minus (SEN in Exp01 minus CTL in Exp01)) in multi-year (20 years) irrigation period mean precipitation (unit: mm day−1). (c) Spatial differences ((SEN in Exp03 minus CTL in Exp03) minus (SEN in Exp01 minus CTL in Exp01)) in multi-year (20 years) irrigation period mean precipitation (unit: mm day−1).
3.2. The Warming Experiments by Increasing Surface Energy
As mentioned in Section 3.1, although the surface air temperature in Exp02 was increased by 2.0 °C (relative to Exp01), the changes in surface energy (latent heat flux, sensible heat flux) were small (Figure 4c,d), and the irrigation amount (in Exp02) affected by warming also did not increase (they even decreased in some irrigation areas) (Figure 5b). The main reason for climate warming is that the increased greenhouse gases can absorb more longwave radiation [42,43]. Therefore, the third type of experiments (referred to as Exp03) was designed by decreasing surface upward longwave radiation by 8% in the land surface model, with the purpose of more reasonably simulating the impacts of climate warming on the irrigation amount. As shown in Figure 2b, the multi-year (1995–2014) annual mean surface air temperature in Exp03 was obviously greater than that in Exp01, and the regional averaged value of their differences was also about 2.0 °C, which was the reason that the surface upward longwave radiation was set to decrease by 8% in Exp03. It should be mentioned that, in this study, the warming up of 2.0 °C in Exp03 referred to the mean surface air temperature of the whole simulation domain. The calculation of surface upward longwave radiation in the WRF model is proportional to the fourth power of land surface temperature. The surface upward longwave radiation in different areas was different because of the different land surface temperature. The same reduction rate (8%) led to the size of the decreased surface upward longwave radiation to be different in different areas. In the low-altitude areas, the difference in the mean surface air temperature between Exp03 and Exp01 was greater than 2.0 °C (Figure 2b) because of larger decreases in surface upward longwave radiation.
In contrast to the warming-induced changes in precipitation in Exp02, in Exp03, the precipitation affected by warming both increased in the irrigation period and the non-irrigation period (Figure 3e,f). In Exp03, the surface upward longwave radiation decreased by 8%, meaning that the surface net radiation was increased. The surface net radiation was mainly allocated to sensible heat flux and latent heat flux. Therefore, the differences showed that the latent heat flux and sensible heat flux in Exp03 were greater than those in Exp01 (Figure 4e,f). Due to the characteristics of drought in Central Asia, the increased surface net radiation was more allocated to sensible heat flux. Therefore, in Exp03, the warming-induced increases in sensible heat flux were obviously greater than those in latent heat flux (Figure 4e,f). Compared to the small changes in latent heat flux and sensible heat flux after warming by 2.0 °C in Exp02 (Figure 4c,d), the differences in latent heat flux and sensible heat flux between Exp03 and Exp01 were more obvious (Figure 4e,f), especially sensible heat flux (Figure 4f), whose reason was the increased surface net radiation in Exp03.
The increased surface energy was beneficial to increases in surface evapotranspiration, which affected soil moisture. If the irrigation amount remained unchanged with the increased surface energy, the increased surface evapotranspiration would reduce the soil moisture of croplands, which was not conducive to the growth of crops. To ensure the normal growth of crops, the amount of irrigation should be increased. As shown in Figure 5c, the irrigation amount in Exp03 increased by 10–20%, relative to Exp01. Therefore, the third type of experiments (Exp03) reasonably simulated the impacts of future climate warming on irrigation amount.
In correspondence to the increases in irrigation amount in Exp03, the irrigation-induced increases in latent heat flux were increased by 2–8 W m−2 (Figure 6g). According to the surface energy balance, the decreases in sensible heat flux caused by irrigation also increased (1–7 W m−2) (Figure 6h). Unlike Exp02, in Exp03, the changes in surface energy were thought to be reasonable, and the reason was that climate warming was caused by the increased energy of the climate system [42]. In other words, irrigation had a greater influence on the partitioning of surface energy after warming. The above changes in surface energy led to intensifying irrigation-induced decreases (0.03–0.12 °C) in surface air temperature in the irrigated croplands (Figure 6i), which indicated that the cooling effect of irrigation would enhance after warming. As mentioned above, in Exp03, the precipitation affected by warming increased during the irrigation period (Figure 3f), and the irrigation amount also increased (Figure 5c), both of which helped to increase the irrigation-caused increases in precipitation (Figure 7c). In Exp03, the surface net radiation increased because of the decreased surface upward longwave radiation, and the increased surface net radiation led to increases in surface air temperature. Therefore, the warming in Exp03 was only driven by decreasing surface upward longwave radiation, and then the temperature only increased in the lower atmosphere (discussed later). Based on the high emission scenario (SSP5-8.5), the future temperature increased in the whole atmosphere [44], which was consistent with our conclusion in Exp02 (Figure 8a). In this study, the whole atmosphere referred to 0–12km and mainly located in troposphere. The formation of precipitation is also mainly in the troposphere; thus, the temperature of the whole atmosphere should affect the precipitation. Therefore, the increased irrigation-induced increases in precipitation in Exp03 might not be reasonable.

Figure 8.
Height–longitude cross sections (averaged over the latitude range of simulation domain) of differences ((a) CTL in Exp02 minus CTL in Exp01; (b) CTL in Exp03 minus CTL in Exp01)) in multi-year (20 years) irrigation period mean temperature (unit: °C). Height–longitude cross sections (averaged over the latitude range of simulation domain) of differences ((c) CTL in Exp02 minus CTL in Exp01; (d) CTL in Exp03 minus CTL in Exp01)) in multi-year (20 years) irrigation period mean water vapor mixing ratio (unit: g kg−1).
4. Discussion
In Exp02, the surface air temperature obviously increased by about 2.0 °C because of future driving fields, but the changes in the simulated surface energy (latent heat flux and sensible heat flux) were very small. The small changes in surface energy would lead to changes in surface evapotranspiration that were also small. Therefore, in Exp02, the irrigation amount affected by warming did not increase. Obviously, in Exp02, the influences of warming on surface variables (latent heat flux, sensible heat flux, and irrigation amount) were unreasonable. To solve the shortage of Exp02, we designed other warming experiments (Exp03) by decreasing the surface upward longwave radiation. The surface net radiation increased because of the decreased surface upward longwave radiation, that is, the surface energy was increased by the experimental setup in Exp03. In Exp03, not only did the surface air temperature obviously increase by about 2.0 °C, but the simulated surface energy also obviously increased. The increased surface energy was favorable to increases in surface evapotranspiration; thus, in Exp03, the irrigation amount affected by warming (2.0 °C) increased by 10–20%, which was thought to be reasonable. In Exp03, the changes in latent heat flux and sensible heat flux were thought to be reasonable, indicating that the impacts of warming on irrigation-caused changes in surface variables were also reasonable. In the irrigated croplands of Central Asia, after warming by 2.0 °C, the irrigation-induced increases in latent heat flux and the irrigation-induced decreases in sensible heat flux both expanded further, and then the irrigation-induced decreases in surface air temperature became further enhanced.
Although the regional averaged values of the increased surface air temperature were both about 2.0 °C in Exp02 and Exp03 (Figure 2), the warming mechanisms of Exp02 and Exp03 were completely different. In Exp02, the warming was induced by adopting the future high emission scenario data (SSP5-8.5) to drive the WRF model; in Exp03, the warming was only driven by decreasing the surface upward longwave radiation. The different warming mechanisms leading to the changes in temperature of the whole atmosphere were also different. In Exp02, the temperature of the whole atmosphere increased (Figure 8a); however, in Exp03, the temperature only increased in the lower atmosphere (Figure 8b). Banerjee and Singh [44] also drew the cross sections of the differences (SSP5-8.5 minus Historical) in temperature, and the results indicated that the temperature increased in the whole atmosphere, which was consistent with our conclusion. Therefore, we thought that the warming-induced increases (Exp02 minus Exp01) in the temperature of the whole atmosphere were reasonable. The temperature affected the atmospheric water vapor content, and their changes were basically consistent [45,46,47]. Therefore, the increased temperature found in Exp02 and Exp03 should lead to increases in water vapor. As shown in Figure 8c, the water vapor in Exp02 obviously increased by more than 0.1 g kg−1 from the surface to a height of 7 km; however, in Exp03, the height range of obvious increases in water vapor was from approximately 2 km to 6 km (Figure 8d). These different changes in water vapor were caused by the aforementioned different warming mechanisms.
The warming-induced changes in temperature and water vapor of the whole atmosphere in Exp02 were thought to be reasonable from the above analysis. The changes in temperature and water vapor of the whole atmosphere affected the precipitation. During the irrigation period, although the water vapor affected by warming obviously increased from the surface to 7 km high (Figure 8c), the low cloud cover decreased (Figure 9a), which corresponded to decreases in precipitation after warming in the mid-latitude mountainous areas (Figure 3d). Obviously, in Exp02, the increased water vapor did not lead to increases in precipitation, and the reason was that the temperature increased by about 2.0 °C in the whole atmosphere, which was not conducive to the water vapor condensation and the formation of precipitation. The increased temperature of the whole atmosphere was also not favorable for the irrigation-caused increases in precipitation. Therefore, as mentioned in Section 3.1, the irrigation-induced increases in precipitation in the mid-latitude mountainous areas decreased (Figure 7b), which was thought to be reasonable. In Exp03, the warming of only the lower atmosphere favored the water vapor condensation; that is, the low cloud cover increased (Figure 9b), which could explain the changes in precipitation after warming during the irrigation period (Figure 3f and Figure 7c). However, in Exp03, the warming-induced changes in precipitation might not be reasonable.
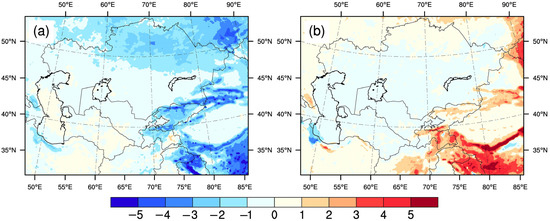
Figure 9.
Spatial differences ((a) CTL in Exp02 minus CTL in Exp01; (b) CTL in Exp03 minus CTL in Exp01) in multi-year (20 years) irrigation period mean low cloud cover (unit: %). Low cloud cover is for 0.8 < sigma < 1.0 (sigma = pressure/surface pressure).
In summary, in Exp03, the impacts of warming on irrigation amount and irrigation-induced changes in surface variables (latent heat flux, sensible heat flux, and surface air temperature) were reasonable; in Exp02, the influences of warming on precipitation and irrigation-induced changes in precipitation were reasonable. The advantages of these two types of experiments (Exp02 and Exp03) were complementary, which achieved the objective of running reasonable simulations.
5. Conclusions
In this study, we designed three types of experiments: historical experiments (Exp01), warming experiments using future driving fields (Exp02), and warming experiments that increased surface energy (Exp03). We analyzed the impacts of irrigation on the regional climate under Central Asia warming by 2.0 °C by drawing on the differences between two types of warming experiments and the historical experiments, respectively. For surface variables (irrigation amount, latent heat flux, sensible heat flux, and surface air temperature), the changes (relative to Exp01) were thought to be reasonable in Exp03. For precipitation, the changes (relative to Exp01) were thought to be reasonable in Exp02. The main conclusions were as follows: (1) in Central Asia, after warming by 2.0 °C, the irrigation amount of the croplands increased by 10–20%. (2) In the irrigated croplands of Central Asia, after warming by 2.0 °C, the irrigation-induced increases in latent heat flux and the irrigation-induced decreases in sensible heat flux both expanded further, and then the irrigation-induced decreases in surface air temperature became further enhanced. (3) After warming up by 2.0 °C, the irrigation-induced increases in precipitation during the irrigation period in the mid-latitude mountainous areas were reduced.
Before conducting this study, we intended to simulate the impacts of irrigation on regional climate under Central Asia warming by 2.0 °C by adopting the future high emission scenario data (SSP5-8.5) as the driving fields. However, things did not happen as we wished, and the simulated results of some surface variables were not reasonable. To achieve more reasonable simulations, we designed another warming experiment that involved decreasing the surface upward longwave radiation. Although the advantages of these two types of warming experiments were complementary, the most ideal warming experiments were those that increased the temperature by increasing greenhouse gases in the atmosphere. However, the increased surface air temperature was less than 0.9 °C in the experiment where the CO2 concentration was set to 1000 ppmv, relative to the experiment where the CO2 concentration was set to 400 ppmv. This simulation showed that the size of the increased surface air temperature was too low in the high CO2 concentration scenario. The reason for this might be that the WRF is a regional model, and the simulated results were affected by the lateral boundary conditions.
Author Contributions
Conceptualization, L.W. and H.Z.; methodology, L.W.; investigation, L.W. and H.Z.; visualization, L.W.; writing—original draft preparation, L.W.; data curation, L.W. and H.Z.; writing—review and editing, L.W. and H.Z.; supervision, L.W. and H.Z.; funding acquisition, L.W. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 42005031), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA20020201), and the Science and Technology Development Project of Henan Province China (Grant No. 222102110419).
Data Availability Statement
The irrigation fraction data are obtained from http://www.fao.org/nr/water/aquastat/irrigationmap/index10.stm (accessed on 11 June 2020). The Bias-corrected CMIP6 global dataset (historical and SSP585) are available at http://www.doi.org/10.11922/sciencedb.00487 (accessed on 20 May 2021). The WRF version 4.0.3 (Software) source codes are obtained from https://github.com/wrf-model/ (accessed on 30 October 2020).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schneider, N.; Eugster, W. Historical land use changes and mesoscale summer climate on the Swiss Plateau. J. Geophys. Res. Atmos. 2005, 110, D19102. [Google Scholar] [CrossRef]
- Feng, D.; Wang, G.; Wei, X.; Amankwah, S.O.Y.; Hu, Y.; Luo, Z.; Hagan, D.F.T.; Ullah, W. Merging and Downscaling Soil Moisture Data From CMIP6 Projections Using Deep Learning Method. Front. Environ. Sci. 2022, 10, 847475. [Google Scholar] [CrossRef]
- Crutzen, P. Geology of mankind. Nature 2002, 415, 23. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef]
- Bonan, G.B.; Doney, S.C. Climate, ecosystems, and planetary futures: The challenge to predict life in Earth system models. Science 2018, 359, eaam8328. [Google Scholar] [CrossRef] [PubMed]
- Pielke, R.A., Sr.; Marland, G.; Betts, R.A.; Chase, T.N.; Eastman, J.L.; Niles, J.O. The influence of land-use change and landscape dynamics on the climate system: Relevance to climate-change policy beyond the radiative effect of greenhouse gases. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2002, 360, 1705–1719. [Google Scholar] [CrossRef] [PubMed]
- Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Mearns, L.O.; Buja, L.E.; Meehl, G.A.; Washington, W.M. The importance of land-cover change in simulating future climates. Science 2005, 310, 1674–1678. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.M.; Wang, Y.L.; Ma, Z.G.; Liu, Y.H. Simulating the regional impacts of urbanization and anthropogenic heat release on climate across China. J. Clim. 2012, 25, 7187–7203. [Google Scholar] [CrossRef]
- Cao, Q.; Yu, D.; Georgescu, M.; Han, Z.; Wu, J. Impacts of land use and land cover change on regional climate: A case study in the agro-pastoral transitional zone of China. Environ. Res. Lett. 2015, 10, 124025. [Google Scholar] [CrossRef]
- Li, D.; Tian, P.; Luo, H.; Hu, T.; Dong, B.; Cui, Y.; Khan, S.; Luo, Y. Impacts of land use and land cover changes on regional climate in the Lhasa River basin, Tibetan Plateau. Sci. Total Environ. 2020, 742, 140570. [Google Scholar] [CrossRef]
- Wu, L.; Feng, J.; Qin, F.; Qiu, Y. Regional climate effects of irrigation over Central Asia using Weather Research and Forecasting model. J. Geophys. Res. Atmos. 2022, 127, e2021JD036210. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P. Groundwater use for irrigation-a global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Siebert, S.; Döll, P.; Hoogeveen, J.; Faures, J.M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Qian, Y.; Tang, J.; Liu, D. Climatic effects of irrigation over the Huang-Huai-Hai Plain in China simulated by the weather research and forecasting model. J. Geophys. Res. Atmos. 2016, 121, 2246–2264. [Google Scholar] [CrossRef]
- Yang, Z.; Dominguez, F.; Zeng, X.; Hu, H.; Gupta, H.; Yang, B. Impact of irrigation over the California Central Valley on regional climate. J. Hydrometeorol. 2017, 18, 1341–1357. [Google Scholar] [CrossRef]
- Wu, L.; Feng, J.; Miao, W. Simulating the impacts of irrigation and dynamic vegetation over the North China Plain on regional climate. J. Geophys. Res. Atmos. 2018, 123, 8017–8034. [Google Scholar] [CrossRef]
- Kang, S.; Eltahir, E.A.B. Impact of irrigation on regional climate over Eastern China. Geophys. Res. Lett. 2019, 46, 5499–5505. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, X.; Tang, Q. Irrigation cooling effect on land surface temperature across China based on satellite observations. Sci. Total Environ. 2020, 705, 135984. [Google Scholar] [CrossRef]
- Liu, G.; Wang, W.; Shao, Q.; Wei, J.; Zheng, J.; Liu, B.; Chen, Z. Simulating the Climatic Effects of Irrigation over China by Using the WRF-Noah Model System with Mosaic Approach. J. Geophys. Res. Atmos. 2021, 126, e2020JD034428. [Google Scholar] [CrossRef]
- Adegoke, J.O.; Pielke Sr, R.A.; Eastman, J.; Mahmood, R.; Hubbard, K.G. Impact of irrigation on midsummer surface fluxes and temperature under dry synoptic conditions: A regional atmospheric model study of the US High Plains. Mon. Weather Rev. 2003, 131, 556–564. [Google Scholar] [CrossRef]
- Lobell, D.B.; Bonfils, C.J.; Kueppers, L.M.; Snyder, M.A. Irrigation cooling effect on temperature and heat index extremes. Geophys. Res. Lett. 2008, 35, L09705. [Google Scholar] [CrossRef]
- Kanamaru, H.; Kanamitsu, M. Model diagnosis of nighttime minimum temperature warming during summer due to irrigation in the California Central Valley. J. Hydrometeorol. 2008, 9, 1061–1072. [Google Scholar] [CrossRef]
- Kueppers, L.M.; Snyder, M.A. Influence of irrigated agriculture on diurnal surface energy and water fluxes, surface climate, and atmospheric circulation in California. Clim. Dyn. 2012, 38, 1017–1029. [Google Scholar] [CrossRef]
- Huber, D.B.; Mechem, D.B.; Brunsell, N.A. The effects of Great Plains irrigation on the surface energy balance, regional circulation, and precipitation. Climate 2014, 2, 103–128. [Google Scholar] [CrossRef]
- Sacks, W.J.; Cook, B.I.; Buenning, N.; Levis, S.; Helkowski, J.H. Effects of global irrigation on the near-surface climate. Clim. Dyn. 2009, 33, 159–175. [Google Scholar] [CrossRef]
- Lo, M.H.; Famiglietti, J.S. Irrigation in California’s Central Valley strengthens the southwestern US water cycle. Geophys. Res. Lett. 2013, 40, 301–306. [Google Scholar] [CrossRef]
- Zou, J.; Xie, Z.; Yu, Y.; Zhan, C.; Sun, Q. Climatic responses to anthropogenic groundwater exploitation: A case study of the Haihe River Basin, Northern China. Clim. Dyn. 2014, 42, 2125–2145. [Google Scholar] [CrossRef]
- Zeng, Y.; Xie, Z.; Zou, J. Hydrologic and climatic responses to global anthropogenic groundwater extraction. J. Clim. 2017, 30, 71–90. [Google Scholar] [CrossRef]
- Qian, Y.; Huang, M.; Yang, B.; Berg, L.K. A modeling study of irrigation effects on surface fluxes and land–air–cloud interactions in the Southern Great Plains. J. Hydrometeorol. 2013, 14, 700–721. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Li, J. Influence of irrigation on land hydrological processes over California. J. Geophys. Res. Atmos. 2014, 119, 13137–13152. [Google Scholar] [CrossRef]
- Pei, L.; Moore, N.; Zhong, S.; Kendall, A.D.; Gao, Z.; Hyndman, D.W. Effects of irrigation on summer precipitation over the United States. J. Clim. 2016, 29, 3541–3558. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, Z.; Tang, Q. Modeled effects of irrigation on surface climate in the Heihe River Basin, Northwest China. J. Geophys. Res. Atmos. 2017, 122, 7881–7895. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, G.; Cao, X.; Hamdi, R.; Li, T.; Cai, P. Numerical simulation of the irrigation effects on surface fluxes and local climate in typical mountain-oasis-desert systems in the Central Asia arid area. J. Geophys. Res. Atmos. 2019, 124, 12485–12506. [Google Scholar] [CrossRef]
- Wang, W.; Liu, G.; Wei, J.; Chen, Z.; Ding, Y.; Zheng, J. The climatic effects of irrigation over the middle and lower reaches of the Yangtze River, China. Agric. For. Meteorol. 2021, 308, 108550. [Google Scholar] [CrossRef]
- Valmassoi, A.; Dudhia, J.; Di Sabatino, S.; Pilla, F. Evaluation of three new surface irrigation parameterizations in the WRF-ARW v3. 8.1 model: The Po Valley (Italy) case study. Geosci. Model Dev. 2020, 13, 3179–3201. [Google Scholar] [CrossRef]
- Li, C.; Zhang, C.; Luo, G.; Chen, X.; Maisupova, B.; Madaminov, A.A.; Han, Q.; Djenbaev, B.M. Carbon stock and its responses to climate change in Central Asia. Glob. Chang. Biol. 2015, 21, 1951–1967. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Wang, J.; Jin, L.; Zhang, Q.; Li, J.; Chen, J. Rapid warming in mid-latitude central Asia for the past 100 years. Front. Earth Sci. China 2009, 3, 42–50. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, C.; Hu, Q.; Tian, H. Temperature changes in Central Asia from 1979 to 2011 based on multiple datasets. J. Clim. 2014, 27, 1143–1167. [Google Scholar] [CrossRef]
- Ma, X.; Zhu, J.; Yan, W.; Zhao, C. Projections of desertification trends in Central Asia under global warming scenarios. Sci. Total Environ. 2021, 781, 146777. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, Y. Detecting changes in irrigation water requirement in Central Asia under CO2 fertilization and land use changes. J. Hydrol. 2020, 583, 124315. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Y.; Tam, C.Y.; Yang, Z.L.; Fu, C. Bias-corrected CMIP6 global dataset for dynamical downscaling of the historical and future climate (1979–2100). Sci. Data 2021, 8, 293. [Google Scholar] [CrossRef]
- Donohoe, A.; Armour, K.C.; Pendergrass, A.G.; Battisti, D.S. Shortwave and longwave radiative contributions to global warming under increasing CO2. Proc. Natl. Acad. Sci. USA 2014, 111, 16700–16705. [Google Scholar] [CrossRef] [PubMed]
- Kweku, D.W.; Bismark, O.; Maxwell, A.; Desmond, K.A.; Danso, K.B.; Oti-Mensah, E.A.; Quachie, A.T.; Adormaa, B.B. Greenhouse effect: Greenhouse gases and their impact on global warming. J. Sci. Res. Rep. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Banerjee, D.; Singh, C. An appraisal of seasonal precipitation dynamics over the North-West Himalayan region under future warming scenarios. Int. J. Climatol. 2022, 42, 2328–2350. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, A.; Wang, J. Trends in tropospheric humidity from 1970 to 2008 over China from a homogenized radiosonde dataset. J. Clim. 2012, 25, 4549–4567. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, T. Historical and future changes of atmospheric precipitable water over China simulated by CMIP5 models. Clim. Dyn. 2019, 52, 6969–6988. [Google Scholar] [CrossRef]
- He, W.; Meng, H.; Han, J.; Zhou, G.; Zheng, H.; Zhang, S. Spatiotemporal PM2.5 estimations in China from 2015 to 2020 using an improved gradient boosting decision tree. Chemosphere 2022, 296, 134003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).