GAN-Based Inversion of Crosshole GPR Data to Characterize Subsurface Structures
Abstract
1. Introduction
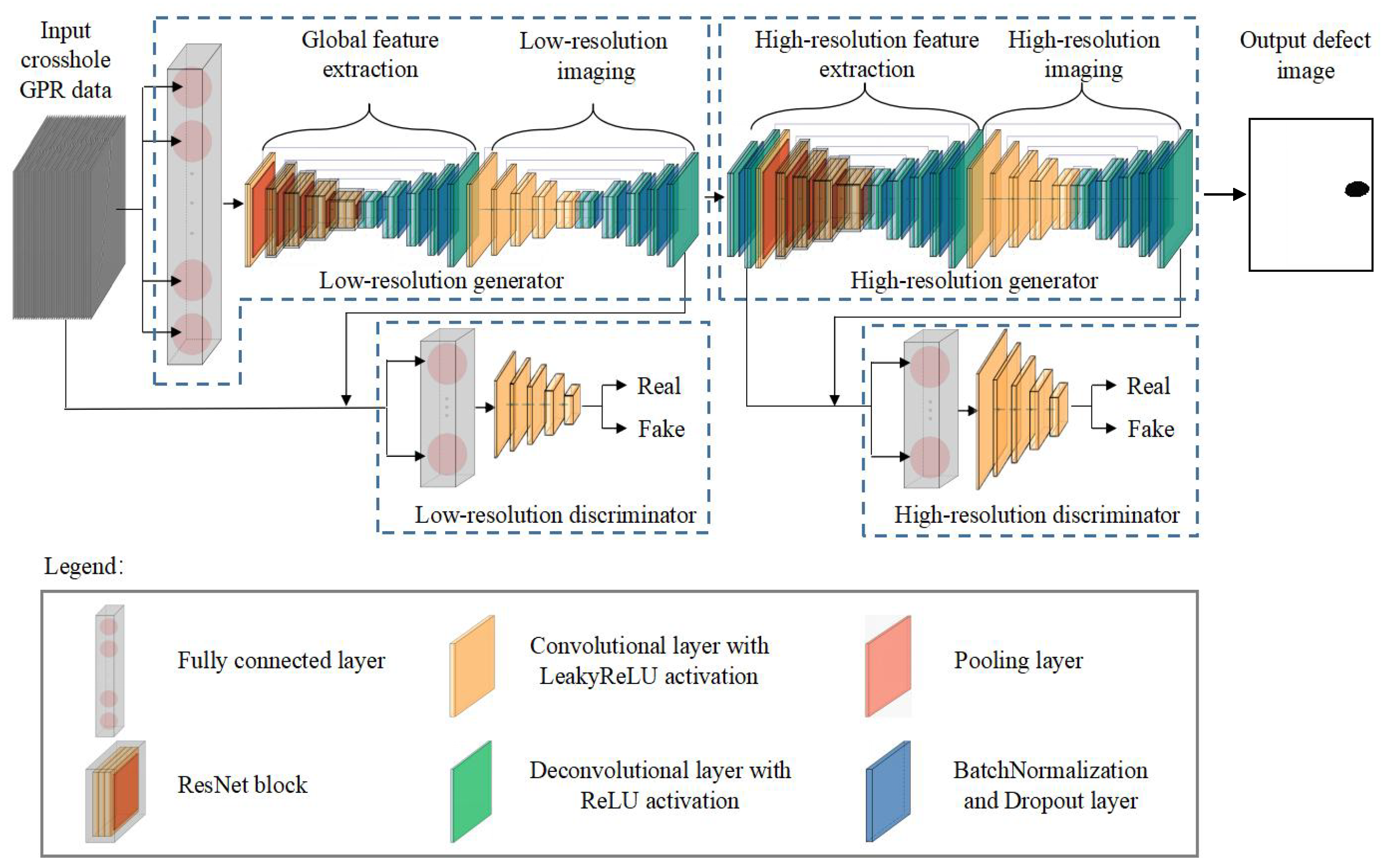
2. Methodology
2.1. Low-Resolution GAN
2.2. High-Resolution GAN
2.3. Network Performance Evaluation
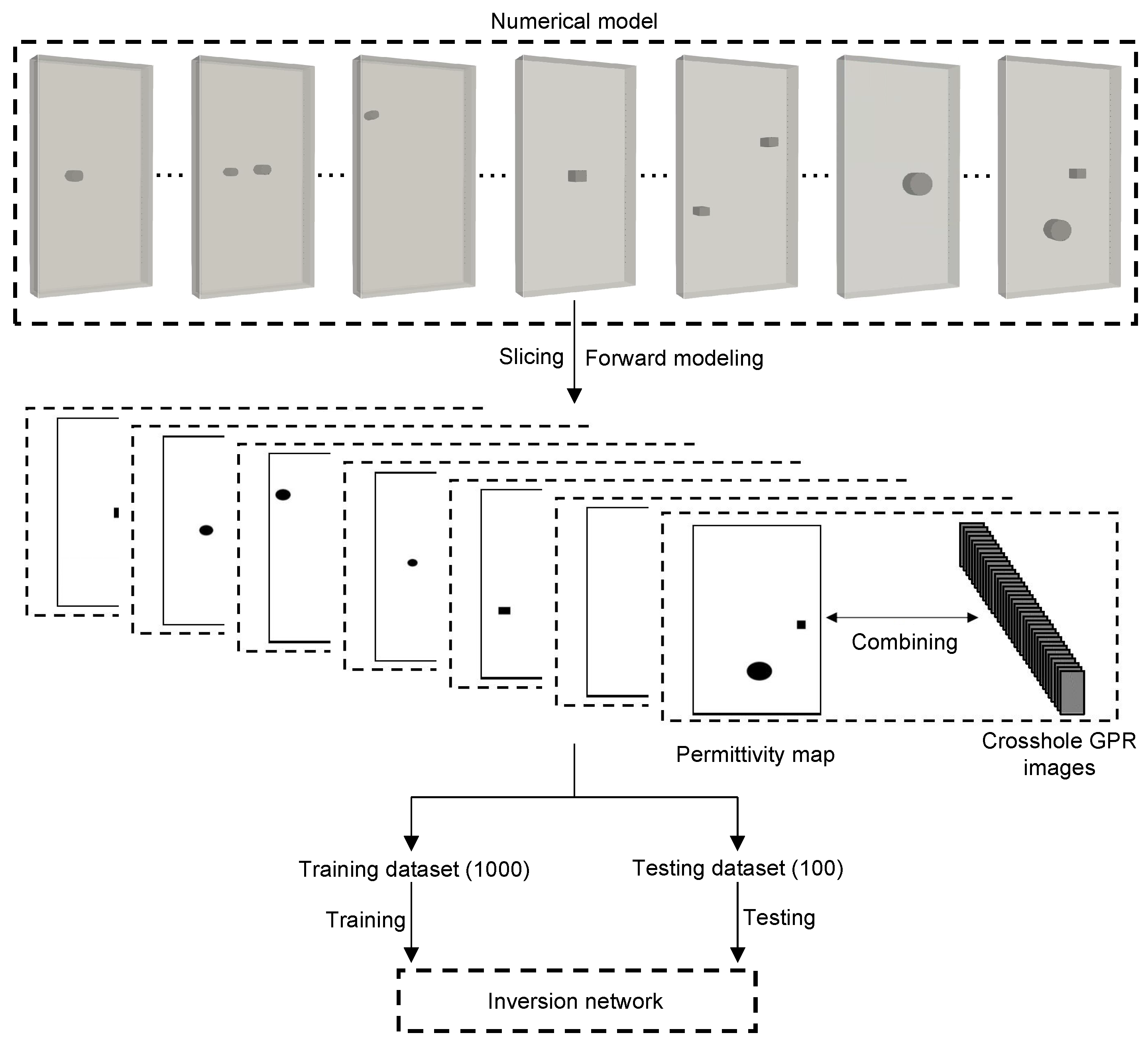
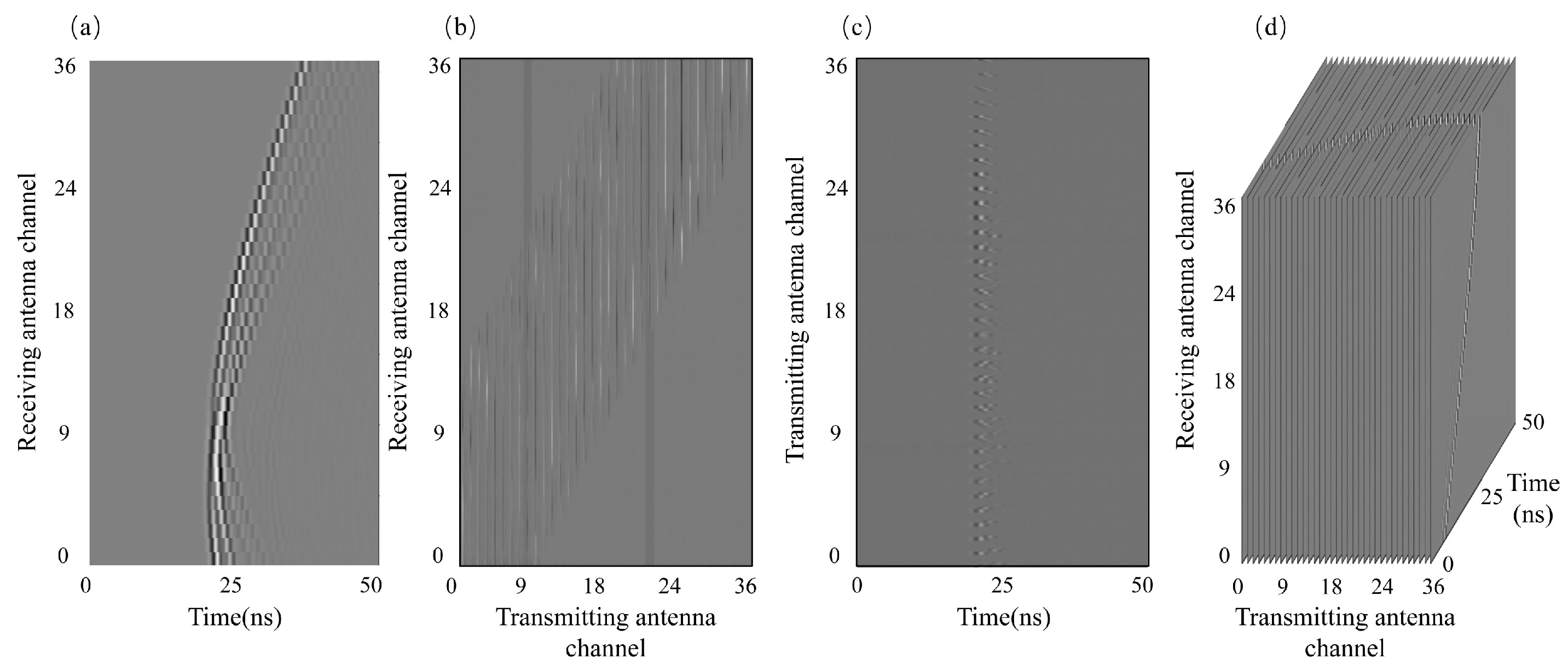
3. Dataset
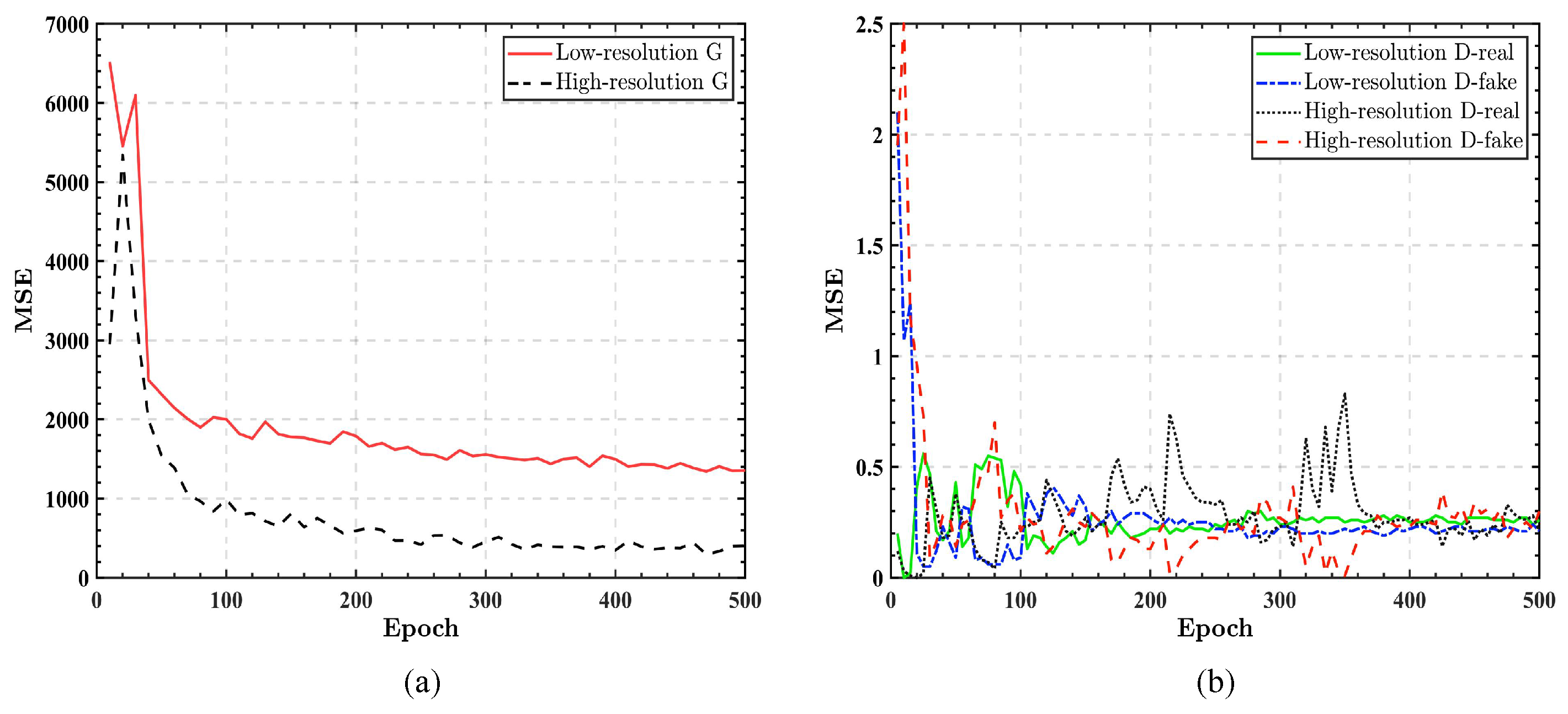
4. Network Training and Testing
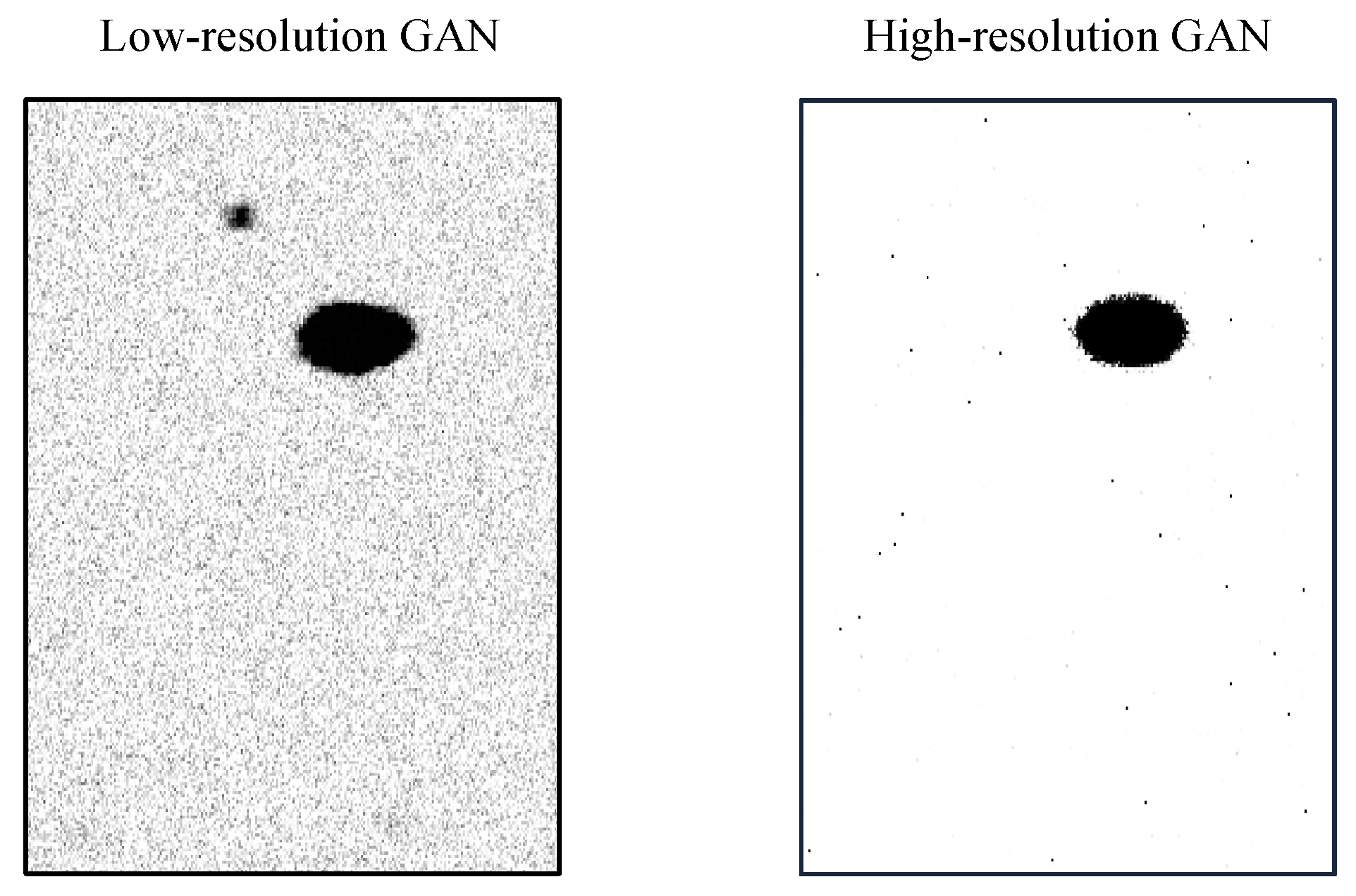
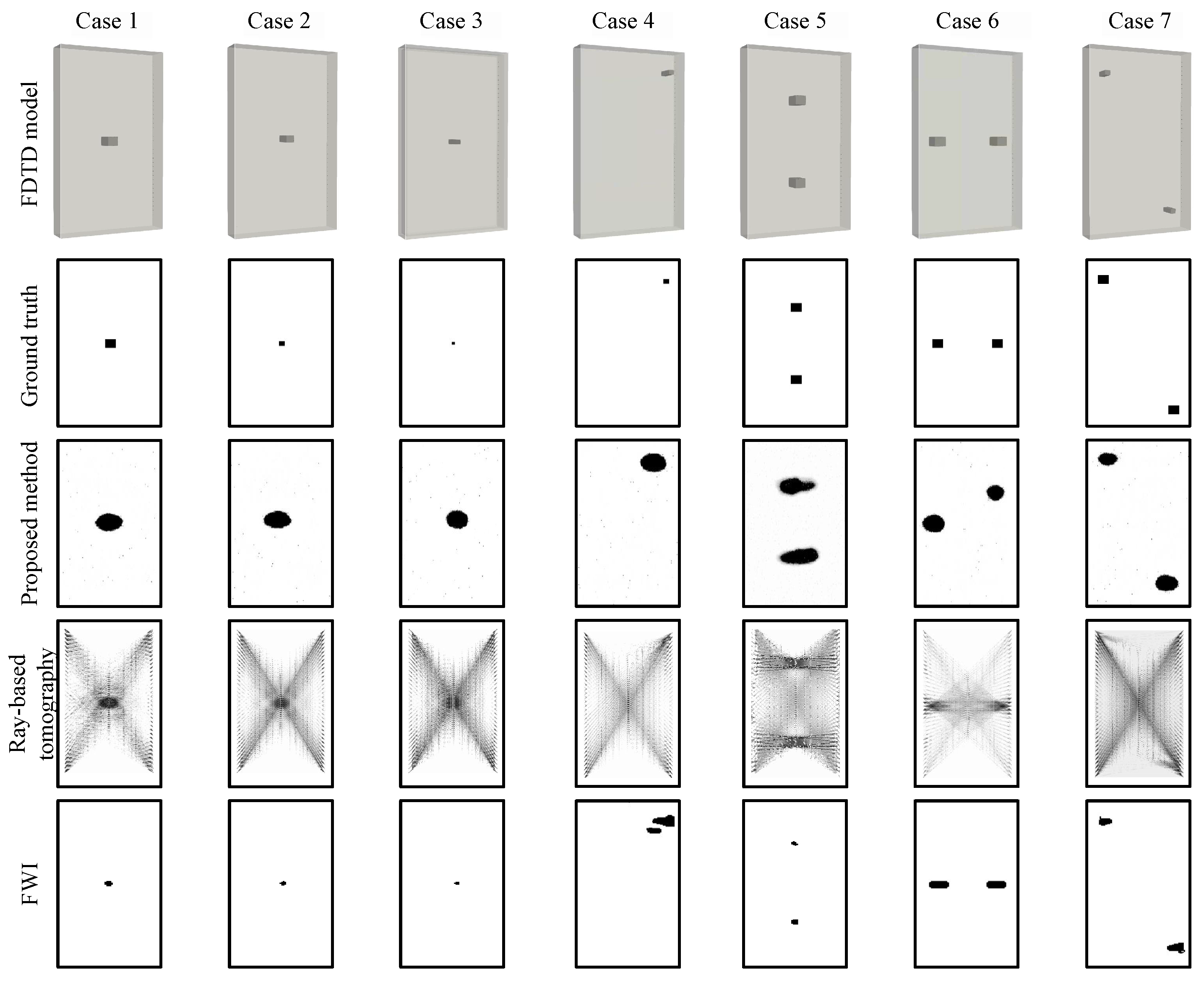
5. Inversion Results
5.1. Synthetic Data Inversion Results
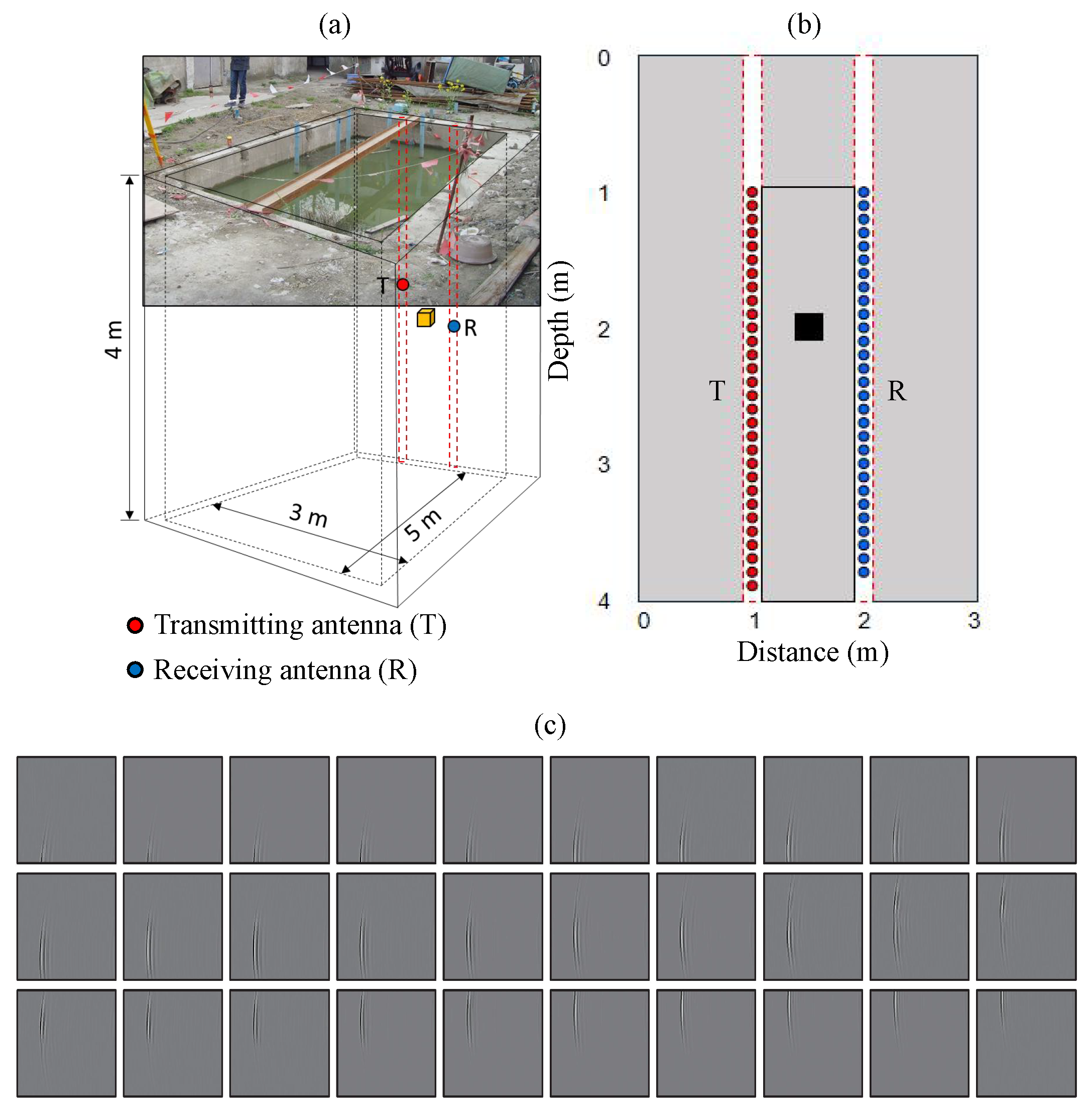
5.2. Experiment Data Inversion Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, X.; Qin, H.; Yao, R. Design of an improved dipole antenna for detecting enclosure structure defects by crosshole GPR. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 723–727. [Google Scholar] [CrossRef]
- Xie, P.; Wen, H.; Xiao, P.; Zhang, Y. Evaluation of ground-penetrating radar (GPR) and geology survey for slope stability study in mantled karst region. Environ. Earth Sci. 2018, 77, 122. [Google Scholar] [CrossRef]
- Kulich, J.; Bleibinhaus, F. Fault Detection with Crosshole and Reflection Geo-Radar for Underground Mine Safety. Geosciences 2020, 10, 456. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Cui, X.; Liu, Q.; Cao, X.; Chen, X. Measurement of soil water content using ground-penetrating radar: A review of current methods. Int. J. Digit. Earth 2019, 12, 95–118. [Google Scholar] [CrossRef]
- Gueting, N.; Vienken, T.; Klotzsche, A.; van der Kruk, J.; Vanderborght, J.; Caers, J.; Vereecken, H.; Englert, A. High resolution aquifer characterization using crosshole GPR full-waveform tomography: Comparison with direct-push and tracer test data. Water Resour. Res. 2017, 53, 49–72. [Google Scholar] [CrossRef]
- Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring soil water content with ground penetrating radar: A decade of progress. Vadose Zone J. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Hui, Z.; Sato, M. Subsurface cavity imaging by crosshole borehole radar measurements. IEEE Trans. Geosci. Remote Sens. 2004, 42, 335–341. [Google Scholar] [CrossRef]
- Qin, H.; Xie, X.; Tang, Y.; Wang, Z. Detection of diaphragm wall defects using crosshole GPR. In Proceedings of the 17th International Conference on Ground Penetrating Radar, Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Klotzsche, A.; Vereecken, H.; van der Kruk, J. Review of crosshole ground-penetrating radar full-waveform inversion of experimental data: Recent developments, challenges, and pitfalls. Geophysics 2019, 84, H13–H28. [Google Scholar] [CrossRef]
- Ernst, J.R.; Maurer, H.; Green, A.G.; Holliger, K. Full-waveform inversion of crosshole radar data based on 2-D finite-difference time domain solutions of Maxwell’s equations. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2807–2828. [Google Scholar] [CrossRef]
- Ernst, J.R.; Green, A.G.; Maurer, H.; Holliger, K. Application of a new 2D time-domain full-waveform inversion scheme to crosshole radar data. Geophysics 2007, 72, J53–J64. [Google Scholar] [CrossRef]
- Busch, S.; van der Kruk, J.; Bikowski, J.; Vereecken, H. Quantitative conductivity and permittivity estimation using full-waveform inversion of on-ground GPR data. Geophysics 2012, 77, H79–H91. [Google Scholar] [CrossRef]
- Meles, G.; Greenhalgh, S.; Van der Kruk, J.; Green, A.; Maurer, H. Taming the non-linearity problem in GPR full-waveform inversion for high contrast media. J. Appl. Geophys. 2012, 78, 31–43. [Google Scholar] [CrossRef]
- Hansen, T.M.; Cordua, K.S.; Jacobsen, B.H.; Mosegaard, K. Accounting for imperfect forward modeling in geophysical inverse problems-exemplified for crosshole tomography. Geophysics 2014, 79, H1–H21. [Google Scholar] [CrossRef]
- Linde, N.; Vrugt, J.A. Distributed soil moisture from crosshole ground-penetrating radar travel times using stochastic inversion. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
- Qin, H.; Xie, X.; Vrugt, J.A.; Zeng, K.; Hong, G. Underground structure defect detection and reconstruction using crosshole GPR and Bayesian waveform inversion. Autom. Constr. 2016, 68, 156–169. [Google Scholar] [CrossRef]
- Qin, H.; Vrugt, J.A.; Xie, X.; Zhou, Y. Improved characterization of underground structure defects from two-stage Bayesian inversion using crosshole GPR data. Autom. Constr. 2018, 95, 233–244. [Google Scholar] [CrossRef]
- Hunziker, J.; Laloy, E.; Linde, N. Bayesian full-waveform tomography with application to crosshole ground penetrating radar data. Geophys. J. Int. 2019, 218, 913–931. [Google Scholar] [CrossRef]
- Qin, H.; Xie, X.; Tang, Y. Evaluation of a straight-ray forward model for Bayesian inversion of crosshole ground penetrating radar data. Electronics 2019, 8, 630. [Google Scholar] [CrossRef]
- Qin, H.; Wang, Z.; Tang, Y.; Geng, T. Analysis of Forward Model, Data Type, and Prior Information in Probabilistic Inversion of Crosshole GPR Data. Remote Sens. 2021, 13, 215. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Computer Vision—ECCV 2014; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar] [CrossRef]
- Mahendran, A.; Vedaldi, A. Understanding deep image representations by inverting them. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5188–5196. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar] [CrossRef]
- Laloy, E.; Linde, N.; Ruffino, C.; Hérault, R.; Gasso, G.; Jacques, D. Gradient-based deterministic inversion of geophysical data with generative adversarial networks: Is it feasible? Comput. Geosci. 2019, 133, 104333. [Google Scholar] [CrossRef]
- Ni, Z.; Shi, C.; Pan, J.; Zheng, Z.; Ye, S.; Fang, G. Declutter-GAN: GPR B-scan data clutter removal using conditional generative adversarial nets. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023105. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, H.; Tang, Y.; Zhang, D.; Yang, D.; Qu, C.; Geng, T. RCE-GAN: A rebar clutter elimination network to improve tunnel lining void detection from GPR images. Remote Sens. 2022, 14, 251. [Google Scholar] [CrossRef]
- Qin, H.; Zhang, D.; Tang, Y.; Wang, Y. Automatic recognition of tunnel lining elements from GPR images using deep convolutional networks with data augmentation. Autom. Constr. 2021, 130, 103830. [Google Scholar] [CrossRef]
- Wang, B.; Chen, P.; Zhang, G. Simulation of GPR B-scan data based on dense generative adversarial network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3938–3944. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Zhang, H.; Sindagi, V.; Patel, V.M. Image de-raining using a conditional generative adversarial network. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3943–3956. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, B.; Wu, G. Canny edge detection based on Open CV. In Proceedings of the 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 53–56. [Google Scholar] [CrossRef]
- Hahn, J.; Hausman, J.; Kuersteiner, G. Estimation with weak instruments: Accuracy of higher-order bias and MSE approximations. Econom. J. 2004, 7, 272–306. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for ground penetrating radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Angelopoulos, C.; Scarfe, W.C.; Farman, A.G. A comparison of maxillofacial CBCT and medical CT. J. Comput. Commun. 2012, 20, 1–17. [Google Scholar] [CrossRef]
- Dines, K.; Lytle, R. Computerized geophysical tomography. Proc. IEEE 1979, 67, 1065–1073. [Google Scholar] [CrossRef]


| Low-Resolution Generator | High-Resolution Generator | ||
|---|---|---|---|
| Model Layer | Output Shape | Model Layer | Output Shape |
| (W, H, C) | (W, H, C) | ||
| FC_1 | (64, 64, 1024) | Deconv2d_16 | (128, 128, 8) |
| ResNet 101 | (2, 2, 2048) | Deconv2d_17 | (256, 256, 16) |
| Deconv2d_1 | (4, 4, 256) | ResNet 50 | (8, 8, 2048) |
| BN_1 and Dropout_1 | (4, 4, 256) | Deconv2d_18 | (8, 8, 256) |
| Deconv2d_2 | (4, 4, 256) | BN_14 and Dropout_14 | (8, 8, 256) |
| BN_2 and Dropout_2 | (4, 4, 256) | Deconv2d_19 | (16, 16, 128) |
| Deconv2d_3 | (8, 8, 64) | BN_15 and Dropout_15 | (16, 16, 128) |
| BN_3 and Dropout_3 | (8, 8, 64) | Deconv2d_20 | (16, 16, 128) |
| Deconv2d_4 | (8, 8, 64) | BN_16 and Dropout_16 | (16, 16, 128) |
| BN_4 and Dropout_4 | (8, 8, 64) | Deconv2d_21 | (32, 32, 64) |
| Deconv2d_5 | (16, 16, 64) | BN_17 and Dropout_17 | (32, 32, 64) |
| BN_5 and Dropout_5 | (16, 16, 64) | Deconv2d_22 | (32, 32, 64) |
| Deconv2d_6 | (16, 16, 64) | BN_18 and Dropout_18 | (32, 32, 64) |
| BN_6 and Dropout_6 | (16, 16, 64) | Deconv2d_23 | (64, 64, 32) |
| Deconv2d_7 | (32, 32, 64) | BN_19 and Dropout_19 | (64, 64, 32) |
| BN_7 and Dropout_7 | (32, 32, 64) | Deconv2d_24 | (64, 64, 32) |
| Deconv2d_8 | (32, 32, 64) | BN_20 and Dropout_20 | (64, 64, 32) |
| BN_8 and Dropout_8 | (32, 32, 64) | Deconv2d_25 | (128, 128, 16) |
| Deconv2d_9 | (64, 64, 32) | BN_21 and Dropout_21 | (128, 128, 16) |
| BN_9 and Dropout_9 | (64, 64, 32) | Deconv2d_26 | (128, 128, 16) |
| Deconv2d_10 | (64, 64, 32) | BN_22 and Dropout_22 | (128, 128, 16) |
| Conv2d_1 | (32, 32, 16) | Deconv2d_26 | (256, 256, 8) |
| Conv2d_2 | (16, 16, 32) | BN_23 and Dropout_23 | (256, 256, 8) |
| Conv2d_3 | (8, 8, 64) | Deconv2d_26 | (256, 256, 1) |
| Conv2d_4 | (4, 4, 128) | Conv2d_6 | (128, 128, 16) |
| Conv2d_5 | (4, 4, 256) | Conv2d_7 | (64, 64, 32) |
| Deconv2d_11 | (4, 4, 256) | Conv2d_8 | (32, 32, 64) |
| BN_10 and Dropout_10 | (4, 4, 256) | Conv2d_9 | (16, 16, 128) |
| Deconv2d_12 | (8, 8, 128) | Conv2d_10 | (16, 16, 256) |
| BN_11 and Dropout_11 | (8, 8, 128) | Deconv2d_27 | (16, 16, 256) |
| Deconv2d_13 | (16, 16, 64) | BN_24 and Dropout_24 | (16, 16, 256) |
| BN_12 and Dropout_12 | (16, 16, 64) | Deconv2d_28 | (16, 16, 128) |
| Deconv2d_14 | (32, 32, 32) | BN_25 and Dropout_25 | (16, 16, 128) |
| BN_13 and Dropout_13 | (32, 32, 32) | Deconv2d_29 | (32, 32, 64) |
| Deconv2d_15 | (64, 64, 1) | BN_26 and Dropout_26 | (32, 32, 64) |
| - | - | Deconv2d_30 | (64, 64, 32) |
| - | - | BN_27 and Dropout_27 | (64, 64, 32) |
| - | - | Deconv2d_31 | (128, 128, 16) |
| - | - | BN_28 and Dropout_28 | (128, 128, 16) |
| - | - | Deconv2d_32 | (256, 256, 1) |
| - | - | BN_29 and Dropout_29 | (256, 256, 1) |
| Low-Resolution Discriminator | High-Resolution Discriminator | ||
| Model Layer | Output Shape | Model Layer | Output Shape |
| (W, H, C) | (W, H, C) | ||
| FC_2 | (64, 64, 256) | FC_3 | (256, 256, 256) |
| Conv2d_11 | (32, 32, 64) | Conv2d_16 | (128, 128, 64) |
| Conv2d_12 | (16, 16, 128) | Conv2d_17 | (64, 64, 128) |
| Conv2d_13 | (8, 8, 256) | Conv2d_18 | (32, 32, 256) |
| Conv2d_14 | (4, 4, 512) | Conv2d_19 | (16, 16, 512) |
| Conv2d_15 | (4, 4, 1) | Conv2d_20 | (16, 16, 1) |
| Modeling Parameter | Value |
|---|---|
| Model size (width × depth × thickness) | 2.00 m × 4.00 m × 0.40 m |
| Discretized grid | 0.005 m × 0.005 m × 0.005 m |
| Antenna detection depth range | 0.2–3.8 m |
| Transmitting–receiving baseline distance | 1.8 m |
| Sampling interval | 0.1 m |
| Source wavelet | Ricker |
| Center frequency | 500 MHz |
| Time window | 50 ns |
| Sampling points for each A-scan | 5194 |
| Method | Indicator | Case Number | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Proposed method | MSE | 1024.29 | 1273.77 | 1167.94 | 1465.12 | 2543.65 | 1918.53 | 1640.71 |
| SSIM | 0.93 | 0.93 | 0.93 | 0.92 | 0.85 | 0.91 | 0.91 | |
| Time (s) | 2.4 | 2.3 | 2.5 | 2.5 | 2.7 | 2.5 | 2.5 | |
| Ray-based tomography | MSE | 2625.57 | 3063.00 | 4130.67 | 2178.10 | 4967.70 | 1440.1 | 5136.34 |
| SSIM | 0.34 | 0.33 | 0.30 | 0.30 | 0.25 | 0.43 | 0.23 | |
| Time (ns) | 4.5 | 4.6 | 4.6 | 4.7 | 4.6 | 4.8 | 4.7 | |
| FWI | MSE | 231.76 | 81.4 | 53.67 | 871.19 | 634.41 | 506.46 | 713.47 |
| SSIM | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 0.98 | 0.97 | |
| Time (s) | 29.3 | 29.5 | 29.5 | 29.6 | 30.0 | 29.9 | 29.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, Z.; Qin, H.; Geng, T.; Pan, S. GAN-Based Inversion of Crosshole GPR Data to Characterize Subsurface Structures. Remote Sens. 2023, 15, 3650. https://doi.org/10.3390/rs15143650
Zhang D, Wang Z, Qin H, Geng T, Pan S. GAN-Based Inversion of Crosshole GPR Data to Characterize Subsurface Structures. Remote Sensing. 2023; 15(14):3650. https://doi.org/10.3390/rs15143650
Chicago/Turabian StyleZhang, Donghao, Zhengzheng Wang, Hui Qin, Tiesuo Geng, and Shengshan Pan. 2023. "GAN-Based Inversion of Crosshole GPR Data to Characterize Subsurface Structures" Remote Sensing 15, no. 14: 3650. https://doi.org/10.3390/rs15143650
APA StyleZhang, D., Wang, Z., Qin, H., Geng, T., & Pan, S. (2023). GAN-Based Inversion of Crosshole GPR Data to Characterize Subsurface Structures. Remote Sensing, 15(14), 3650. https://doi.org/10.3390/rs15143650








