The LPR Instantaneous Centroid Frequency Attribute Based on the 1D Higher-Order Differential Energy Operator
Abstract
:1. Introduction
2. Methods
2.1. The Teager–Kaiser Energy Operator
2.2. The Higher-Order Differential Energy Operator (1D-HODEO)
2.3. Instantaneous Centroid Frequency Based on 1D-HODEO
3. Results
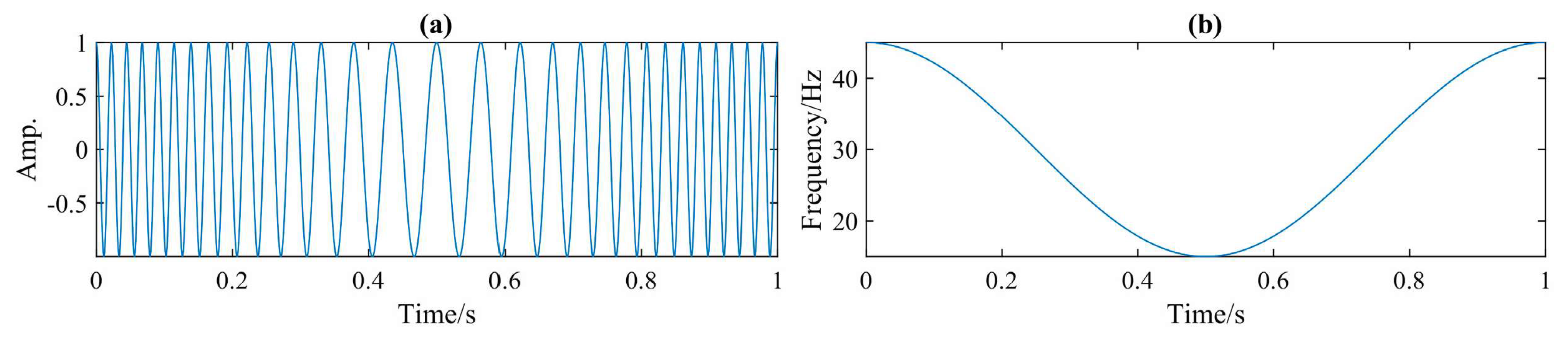
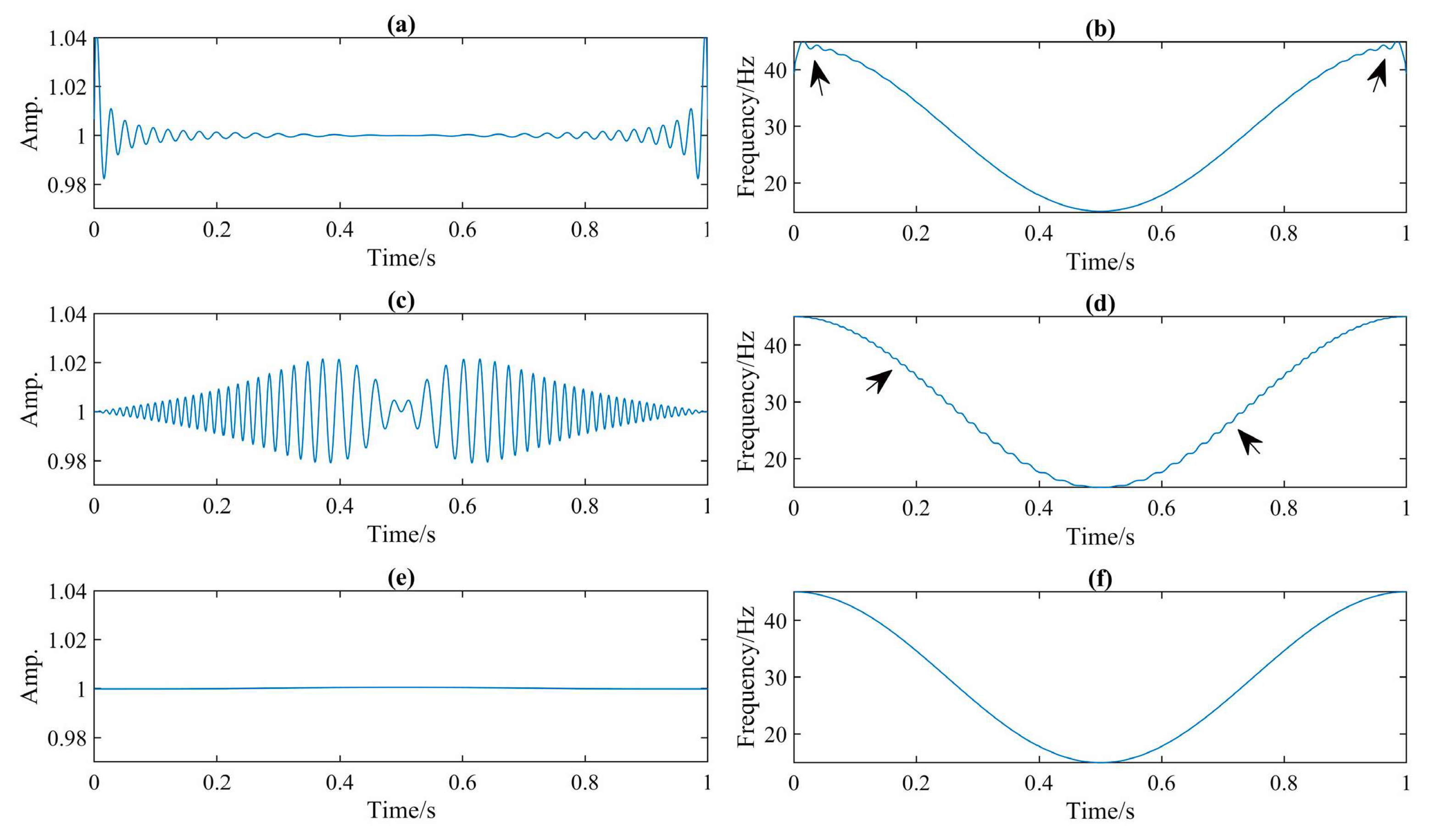
3.1. Benchmark Test (Chirp)
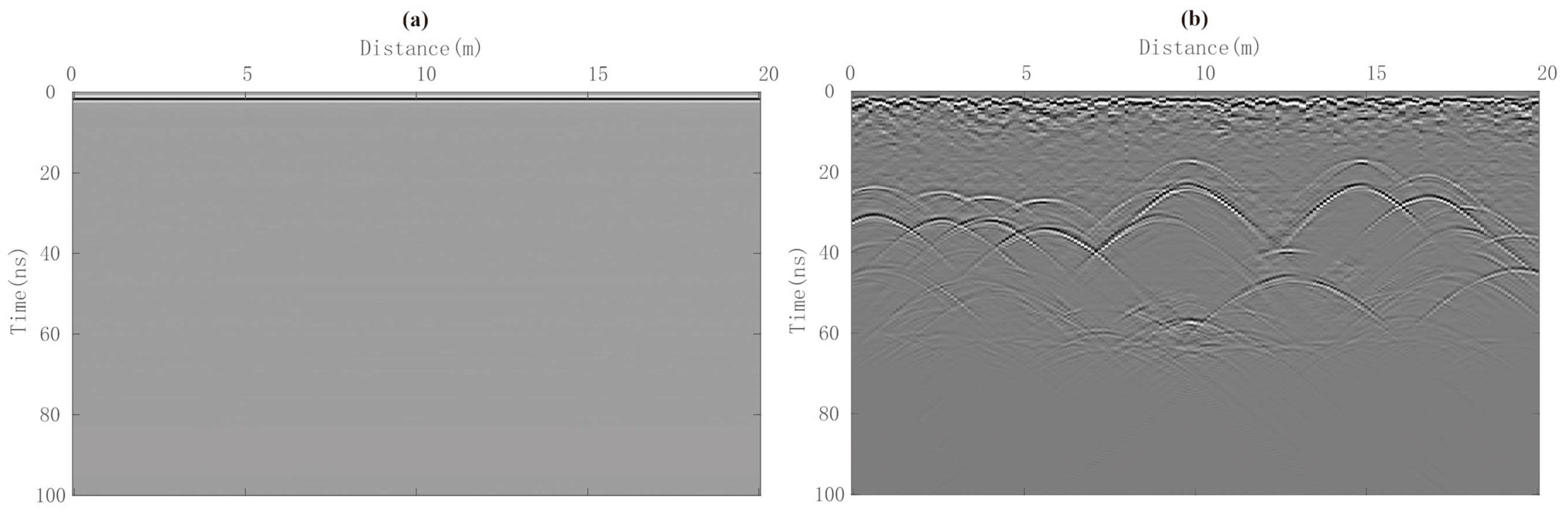
3.2. FDTD Model Test
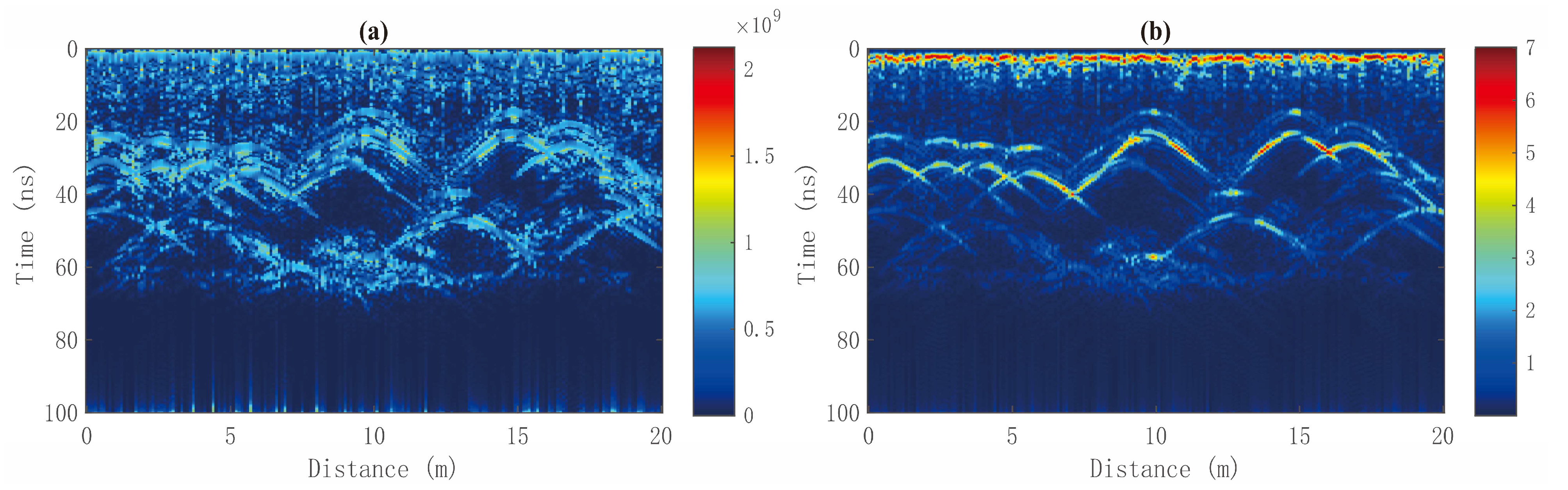
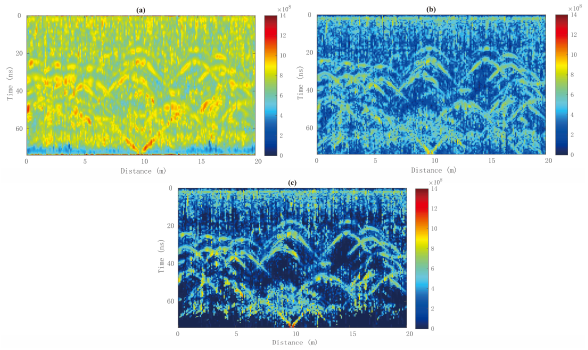
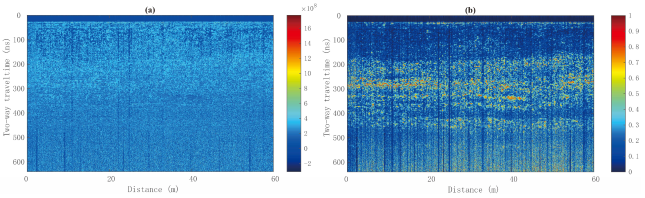
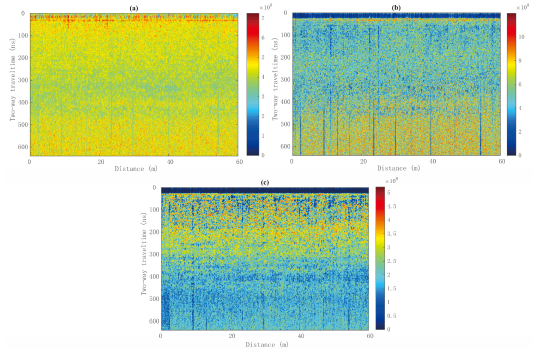
3.3. LPR Data Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dong, Z.; Feng, X.; Zhou, H.; Liu, C.; Liang, W. Properties Analysis of Lunar Regolith at Chang’E-4 Landing Site Based on 3D Velocity Spectrum of Lunar Penetrating Radar. Remote Sens. 2020, 12, 629. [Google Scholar] [CrossRef]
- Liu, Z.; Yeoh, J.K.; Gu, X.; Dong, Q.; Chen, Y.; Wu, W.; Wang, L.; Wang, D. Automatic pixel-level detection of vertical cracks in asphalt pavement based on GPR investigation and improved mask R-CNN. Autom. Constr. 2023, 146, 104689. [Google Scholar] [CrossRef]
- Li, C.; Xing, S.; Lauro, S.E.; Su, Y.; Dai, S.; Feng, J.; Cosciotti, B.; Di Paolo, F.; Mattei, E.; Xiao, Y.; et al. Pitfalls in GPR Data Interpretation: False Reflectors Detected in Lunar Radar Cross Sections by Chang’e-3. IEEE T. Geosci. Remote 2018, 56, 1325–1335. [Google Scholar] [CrossRef]
- Li, C.; Su, Y.; Pettinelli, E.; Xing, S.; Ding, C.; Liu, J.; Ren, X.; Lauro, S.E.; Soldovieri, F.; Zeng, X.; et al. The Moon’s farside shallow subsurface structure unveiled by Chang’E-4 Lunar Penetrating Radar. Sci. Adv. 2020, 6, eaay6898. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Feng, X.; Ding, C.; Dong, Z.; Liu, C.; Zhang, Y.; Meng, Z. Yutu-2 Radar Sounding Evidence of a Buried Crater at Chang’E-4 Landing Site. IEEE T. Geosci. Remote 2021, 60, 1–19. [Google Scholar] [CrossRef]
- Lai, J.; Xu, Y.; Zhang, X.; Xiao, L.; Yan, Q.; Meng, X.; Zhou, B.; Dong, Z.; Zhao, D. Comparison of Dielectric Properties and Structure of Lunar Regolith at Chang’e-3 and Chang’e-4 Landing Sites Revealed by Ground-Penetrating Radar. Geophys. Res. Lett. 2019, 46, 12783–12793. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Li, J.; Ling, H.; Huo, h.; Zhang, J.; Huai, N. A Story of Regolith Told by Lunar Penetrating Radar. Icarus 2018, 321, 148–160. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Zeng, Z.; Xu, Y.; Liu, C.; Chen, S. Stratigraphy of the Von Kármán Crater Based on Chang’E-4 Lunar Penetrating Radar Data. Geophys. Res. Lett. 2020, 47, e2020GL088680. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, L.; Jia, Z.; Zhao, X.; Lu, Q.; Liu, S. Stratification of Lunar Regolith Based on Attribute Analysis. IOP Conf. Ser. Earth Environ. Sci. 2021, 660, 012031. [Google Scholar] [CrossRef]
- Yurasov, N.I. Energy Level Quantization in the 1D Quantum Well in Case of Instantaneous Stationary State with the Non-Relativistic Wall and Particle Motion. Her. Bauman Mosc. State Tech. Univ. 2023, 4, 108–122. [Google Scholar] [CrossRef]
- Barnes, A. The calculation of instantaneous frequency and instantaneous bandwidth. Geophysics 1992, 57, 1520–1524. [Google Scholar] [CrossRef]
- Maragos, P.; Kaiser, J.F.; Quatieri, T.F. Energy separation in signal modulations with application to speech analysis. IEEE Trans. Signal Process. 1993, 41, 3024–3051. [Google Scholar] [CrossRef]
- Maragos, P.; Potamianos, A. Higher order differential energy operators. IEEE Signal Process. Lett. 1995, 2, 152–154. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Zhang, X.; Nilot, E.; Feng, X.; Ren, Q.; Zhang, Z. IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method. Remote Sens. 2018, 10, 476. [Google Scholar] [CrossRef]
- Xue, Y.; Du, H.; Cao, J.; Jin, D.; Chen, W.; Zhou, J. Application of a Variational Mode Decomposition-Based Instantaneous Centroid Estimation Method to a Carbonate Reservoir in China. IEEE Geosci. Remote Sens. Lett. 2018, 15, 364–368. [Google Scholar] [CrossRef]
- Quan, Y.; Harrist, J.M. Seismic attenuation tomography using the frequency shift method. Geophysics 1997, 62, 895–905. [Google Scholar] [CrossRef]
- Liu, G.; Fomel, S.; Chen, X. Time-frequency analysis of seismic data using local attributes. Geophysics 2011, 76, P23–P34. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Salzenstein, F.; Cexus, J.C. Two-dimensional continuous higher-order energy operators. Opt. Eng. 2005, 44, 117001. [Google Scholar]
- Kaiser, J.F. On a simple algorithm to calculate the ‘energy’ of a signal. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; pp. 381–384. [Google Scholar]
- Bouchikhi, A.; Boudraa, A.-O. Multicomponent AM–FM signals analysis based on EMD–B-splines ESA. Signal Process. 2012, 92, 2214–2228. [Google Scholar] [CrossRef]
- Fertig, L.B.; McClellan, J.H. Instantaneous frequency estimation using linear prediction with comparisons to the DESAs. IEEE Signal Process Lett. 1996, 3, 54–56. [Google Scholar] [CrossRef]
- Liu, L.; Lane, J.W.; Quan, Y. Radar attenuation tomography using the centroid frequency downshift method. J. Appl. Geophys. 1998, 40, 105–116. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, X.; Qiu, Z.; Feng, X.; Qin, Y. Extraction of the GPR instantaneous centroid frequency based on the envelope derivative operator and ICEEMDAN. Remote Sens. Lett. 2023, 14, 469–478. [Google Scholar] [CrossRef]
- Hou, T.Y.; Shi, Z. Data-driven time–frequency analysis. Appl. Comput. Harmon. Anal. 2013, 35, 284–308. [Google Scholar] [CrossRef]
- Zeng, Z.-F.; Chen, X.; Li, J.; Chen, L.-N.; Lu, Q.; Liu, F.-S. Recursive impedance inversion of ground-penetrating radar data in stochastic media. Appl. Geophys. 2015, 12, 615–625. [Google Scholar] [CrossRef]
- Li, J.; Zeng, Z.; Liu, C.; Huai, N.; Wang, K. A Study on Lunar Regolith Quantitative Random Model and Lunar Penetrating Radar Parameter Inversion. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1953–1957. [Google Scholar] [CrossRef]
- Irving, J.; Knight, R. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Comput. Geosci. 2006, 32, 1247–1258. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, C.; Feng, X.; Li, B.; Li, K.; You, Q. The attenuated Ricker wavelet basis for seismic trace decomposition and attenuation analysis. Geophys. Prospect. 2020, 68, 371–381. [Google Scholar] [CrossRef]
- Irving, J.D.; Knight, R.J. Removal of wavelet dispersion from ground-penetrating radar data. Geophysics 2003, 68, 960–970. [Google Scholar] [CrossRef]
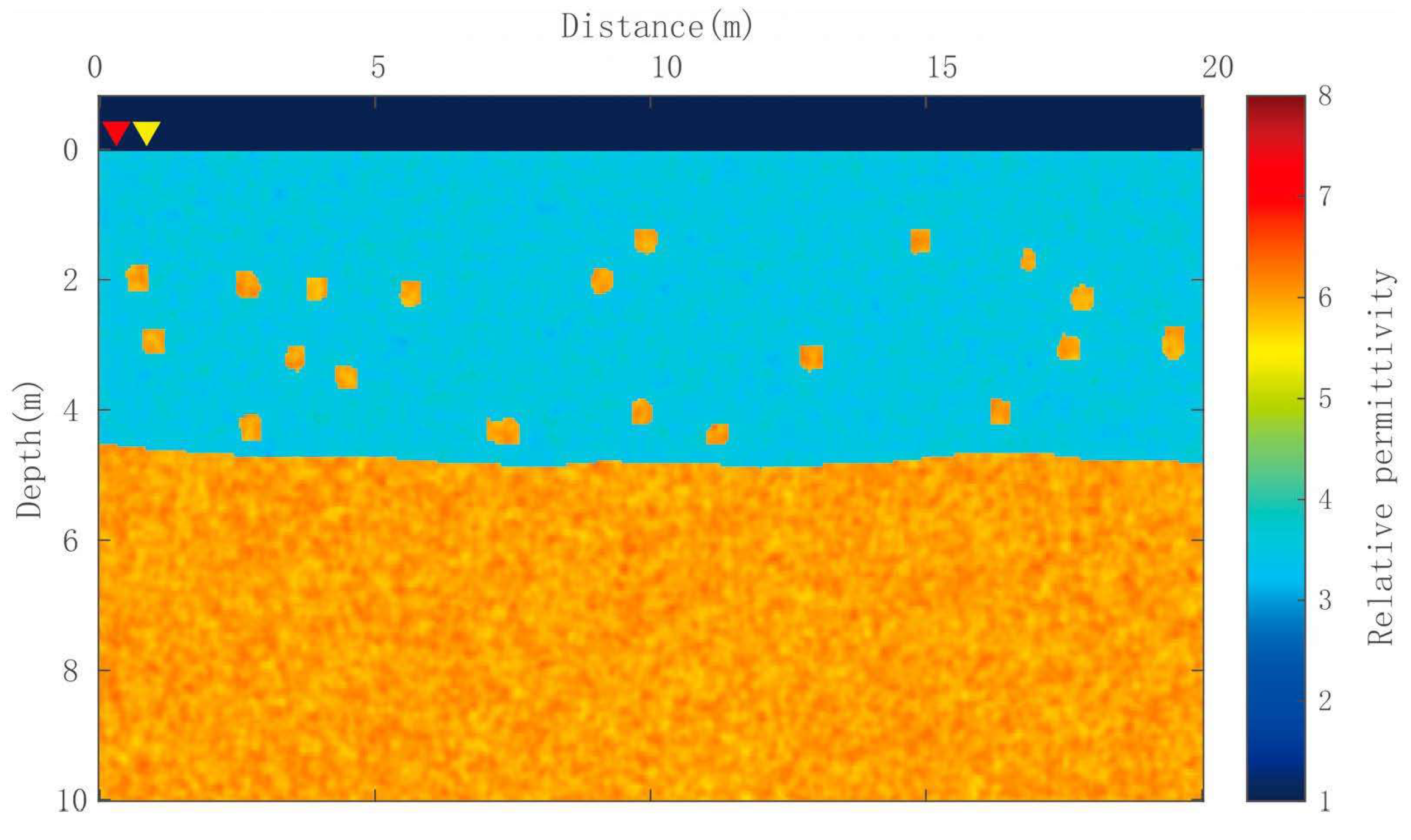


| Electrical Properties Components | Vacuum (≤0 m) | Lunar Regolith Layer (0~4.5 m) | Bedrock Layer (4.5~10 m) | Grains |
|---|---|---|---|---|
| 1 | 3~4 | 5.5~6.5 | 5.5~6.5 | |
| (S/m) | 0 | 0.001 | 0.01 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Song, Z.; Li, B.; Feng, X.; Zhou, J.; Yu, Y.; Hu, X. The LPR Instantaneous Centroid Frequency Attribute Based on the 1D Higher-Order Differential Energy Operator. Remote Sens. 2023, 15, 5305. https://doi.org/10.3390/rs15225305
Zhang X, Song Z, Li B, Feng X, Zhou J, Yu Y, Hu X. The LPR Instantaneous Centroid Frequency Attribute Based on the 1D Higher-Order Differential Energy Operator. Remote Sensing. 2023; 15(22):5305. https://doi.org/10.3390/rs15225305
Chicago/Turabian StyleZhang, Xuebing, Zhengchun Song, Bonan Li, Xuan Feng, Jiangang Zhou, Yipeng Yu, and Xin Hu. 2023. "The LPR Instantaneous Centroid Frequency Attribute Based on the 1D Higher-Order Differential Energy Operator" Remote Sensing 15, no. 22: 5305. https://doi.org/10.3390/rs15225305
APA StyleZhang, X., Song, Z., Li, B., Feng, X., Zhou, J., Yu, Y., & Hu, X. (2023). The LPR Instantaneous Centroid Frequency Attribute Based on the 1D Higher-Order Differential Energy Operator. Remote Sensing, 15(22), 5305. https://doi.org/10.3390/rs15225305







