A Graph Memory Neural Network for Sea Surface Temperature Prediction
Abstract
1. Introduction
2. Materials
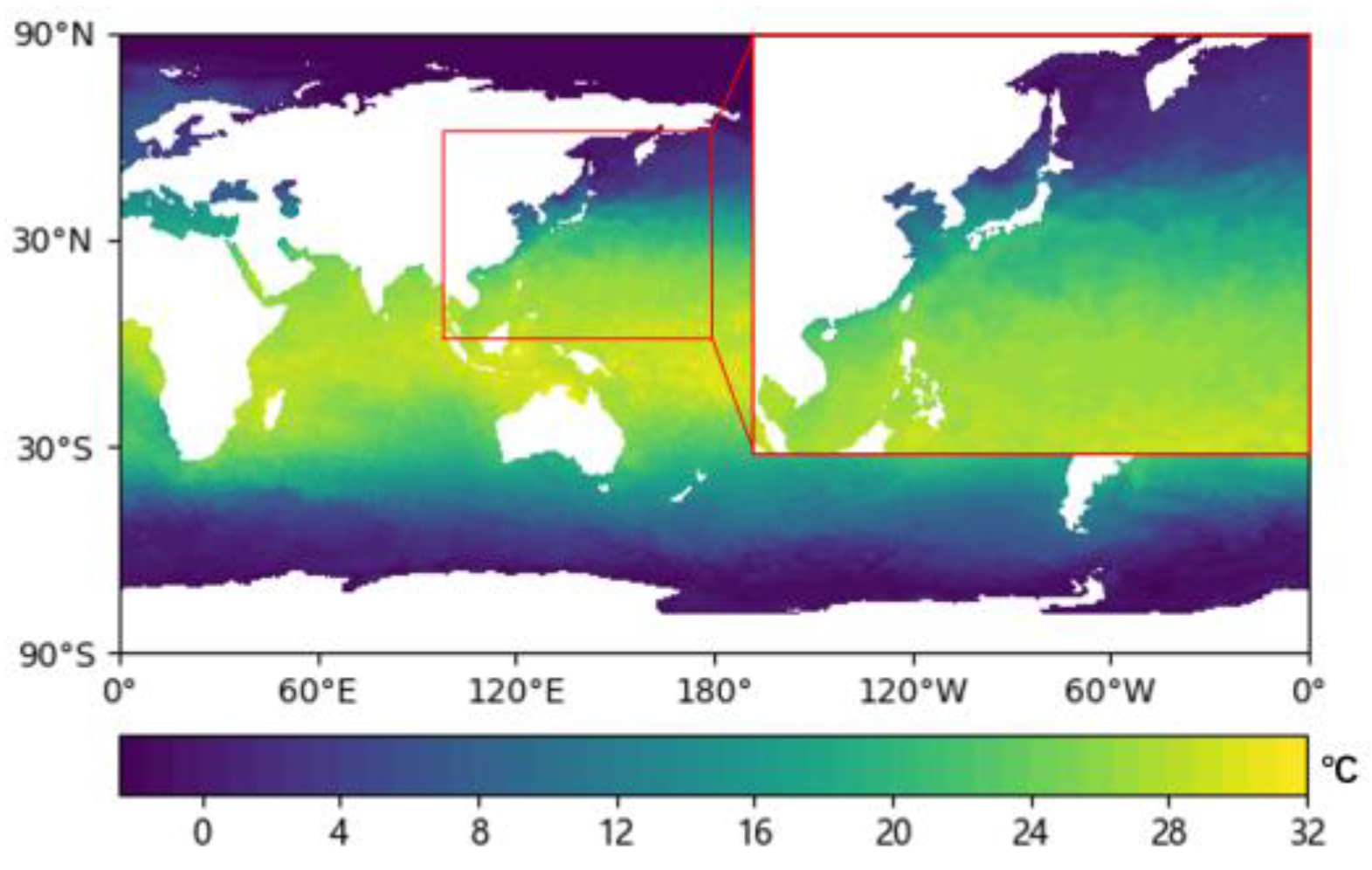
2.1. Datasets
2.2. Pre-Processing
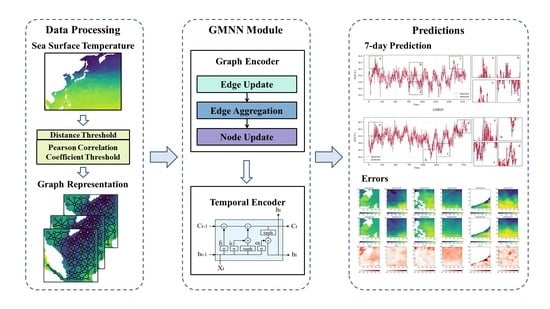
3. Methods
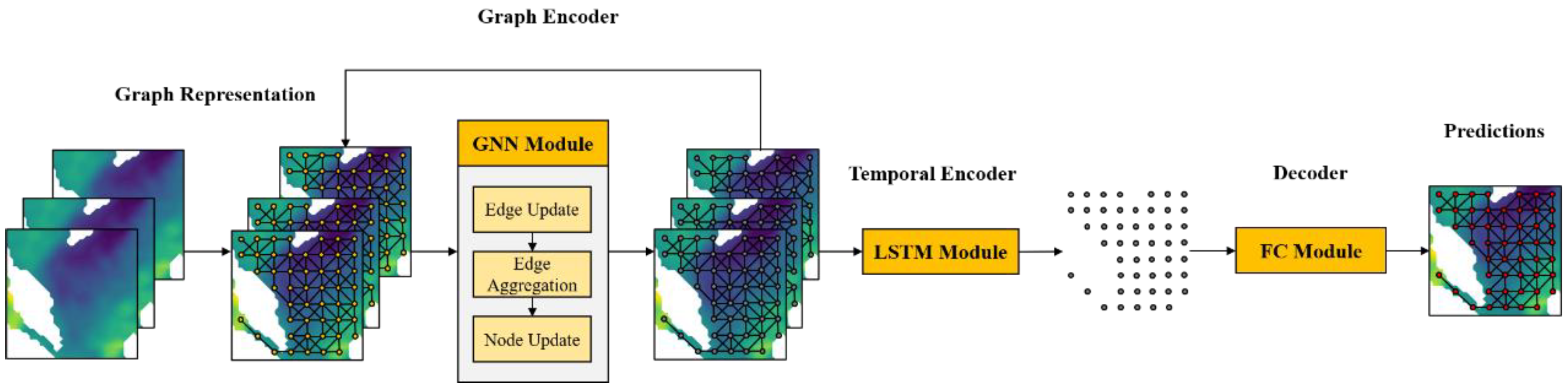
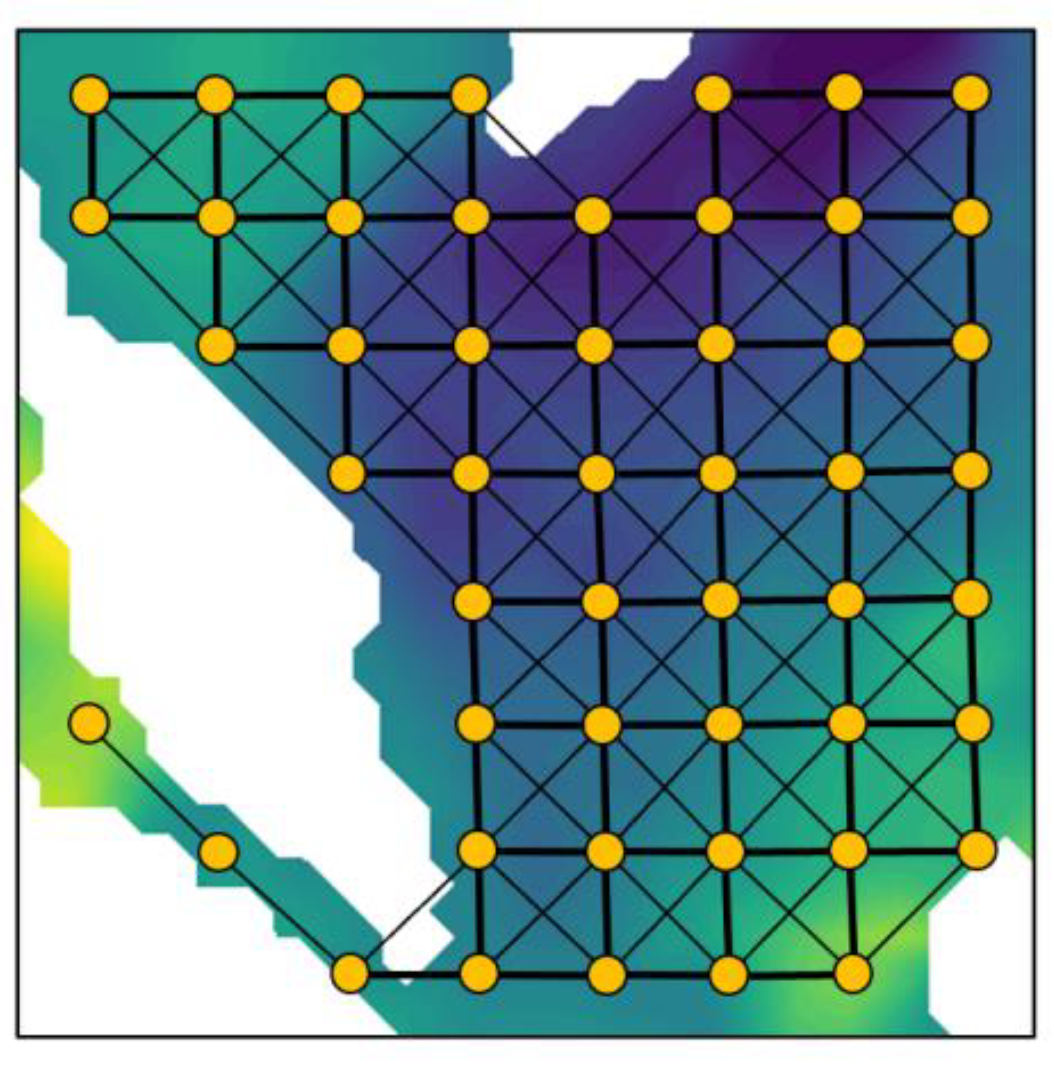
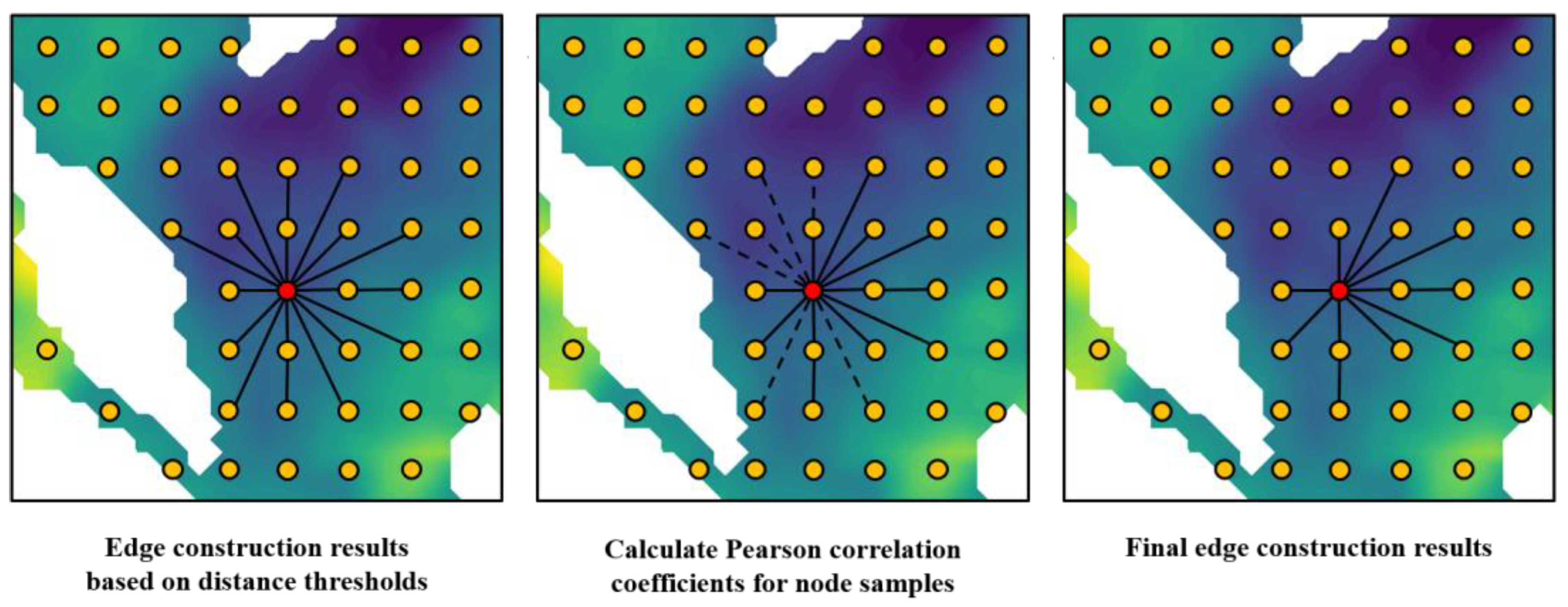
3.1. Graph Representation
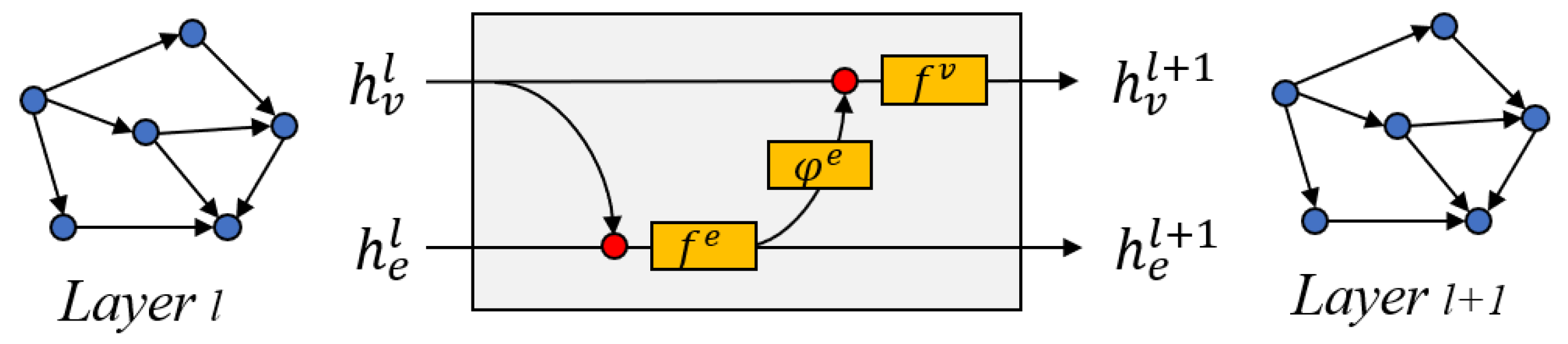
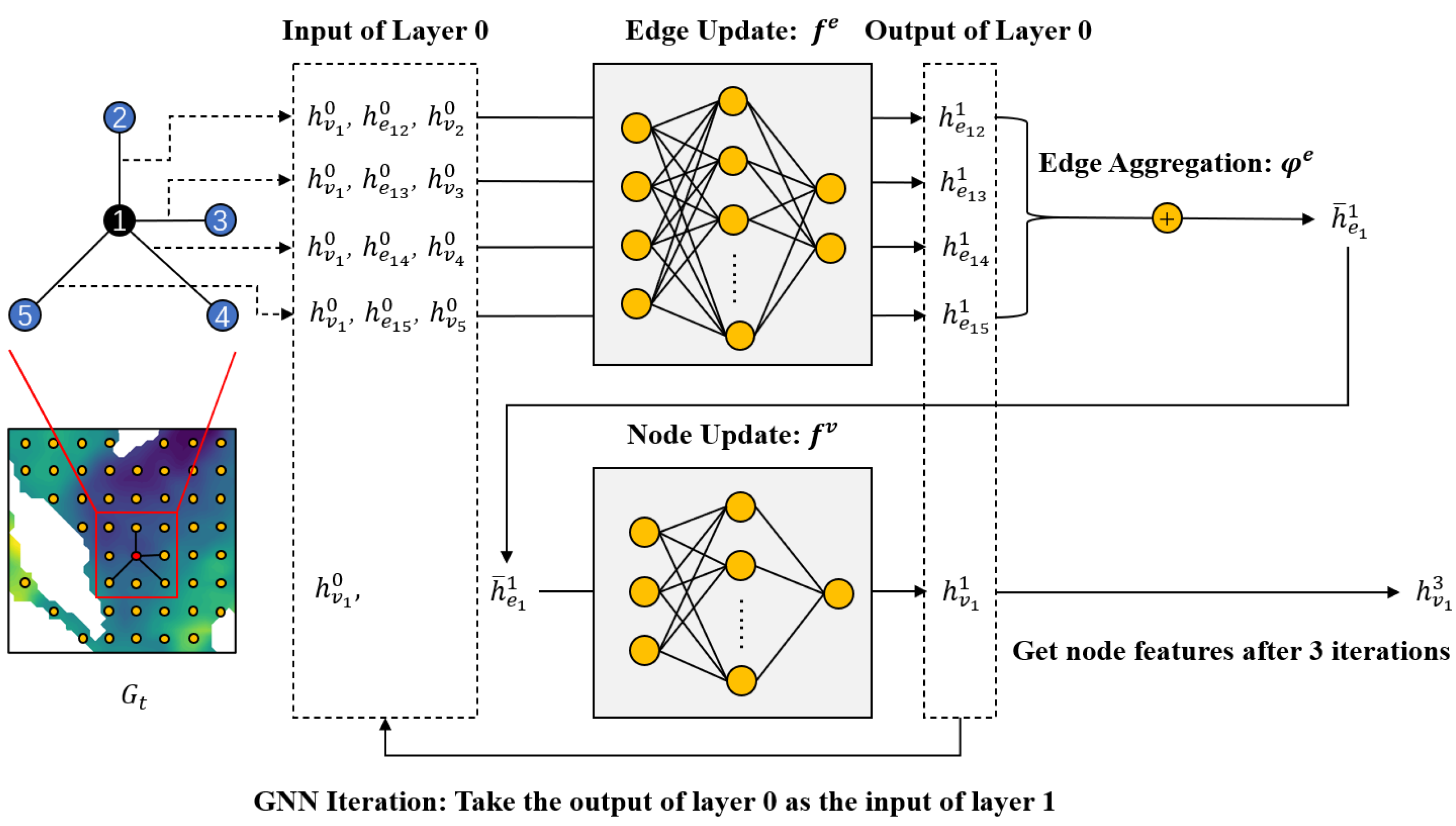
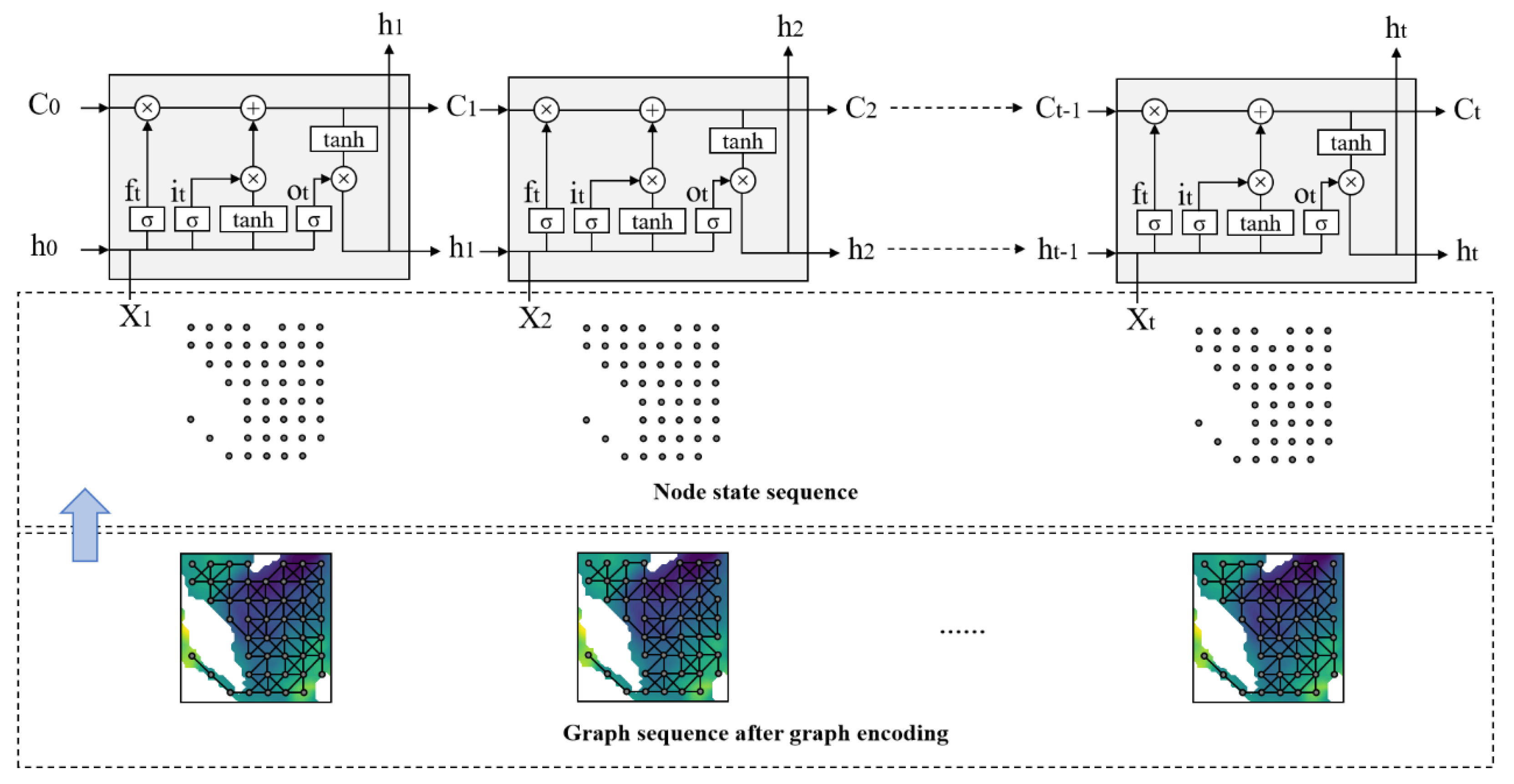
3.2. Graph Encoder
- Edge update: As shown in Equation (5), we gather the current edge state and the states of its adjacent nodes, and pass them through the edge update function to obtain the updated result. This output will be used in the edge aggregation and the next iteration. The is a multilayer perceptron and a ReLU activation function to capture nonlinear features.
- Edge aggregation: Next, as shown in Equation (6), we use the function to aggregate the updated edge states of all connected edges for each node. Common aggregation methods include sum, mean, and max. Considering that for a point on the sea surface, heat changes manifest as a convergence or dissipation process, we choose the sum aggregation method.
- Node update: Finally, we gather the previous aggregation outputs and their current states and put them into the update function . Similar to , is also a combination of a multilayer perceptron and a ReLU activation function.
3.3. Temporal Encoder
3.4. Decoder and Loss Function
4. Experiments
4.1. Metrics
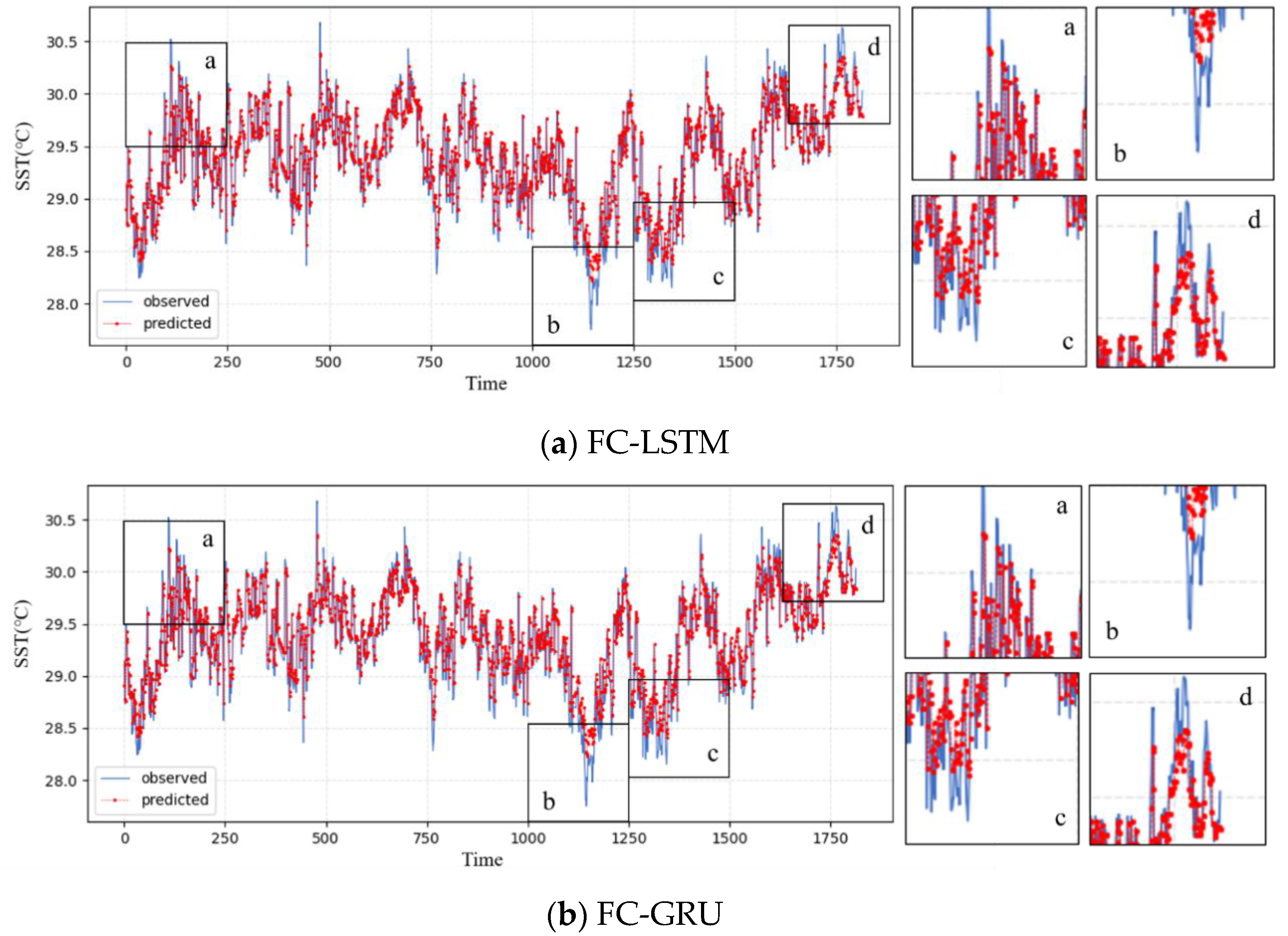
4.2. Compared Models
- FC-LSTM and FC-GRU: They are time series prediction models, which integrate LSTM or GRU layers with fully connected layers for feature extraction and improved representation capability.
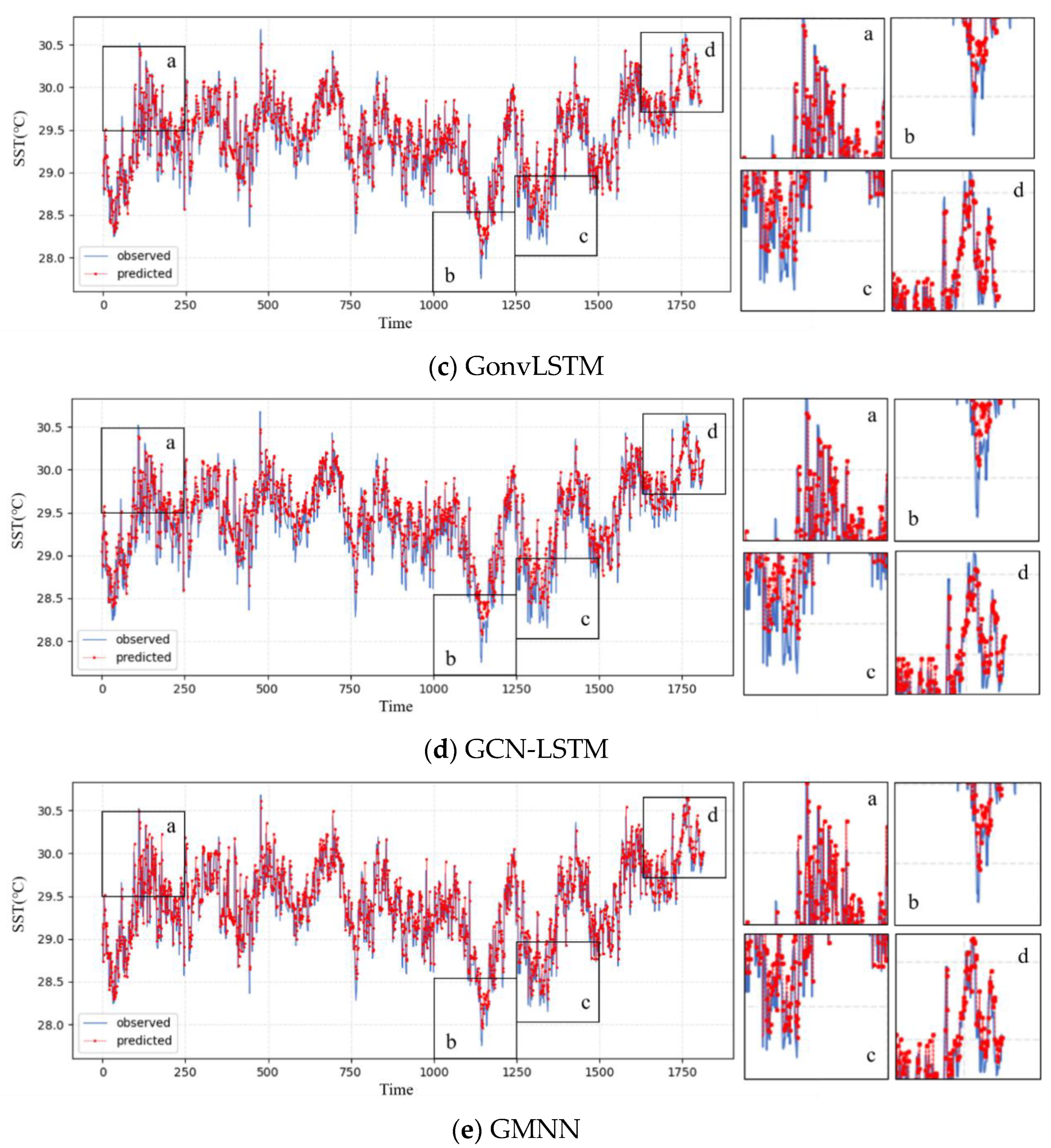
- ConvLSTM: This is a spatiotemporal model utilizing CNN idea with LSTM, which incorporates convolution operations into input data and hidden states, allowing for the capture of spatial information and complex spatiotemporal features.
- GCN-LSTM: This is a spatiotemporal model employing GNN idea, which combines graph convolutional networks (GCN) with LSTM for graph sequence prediction, effectively extracting features from nodes and their multi-order neighbors and integrating them into the LSTM layer for temporal information processing.
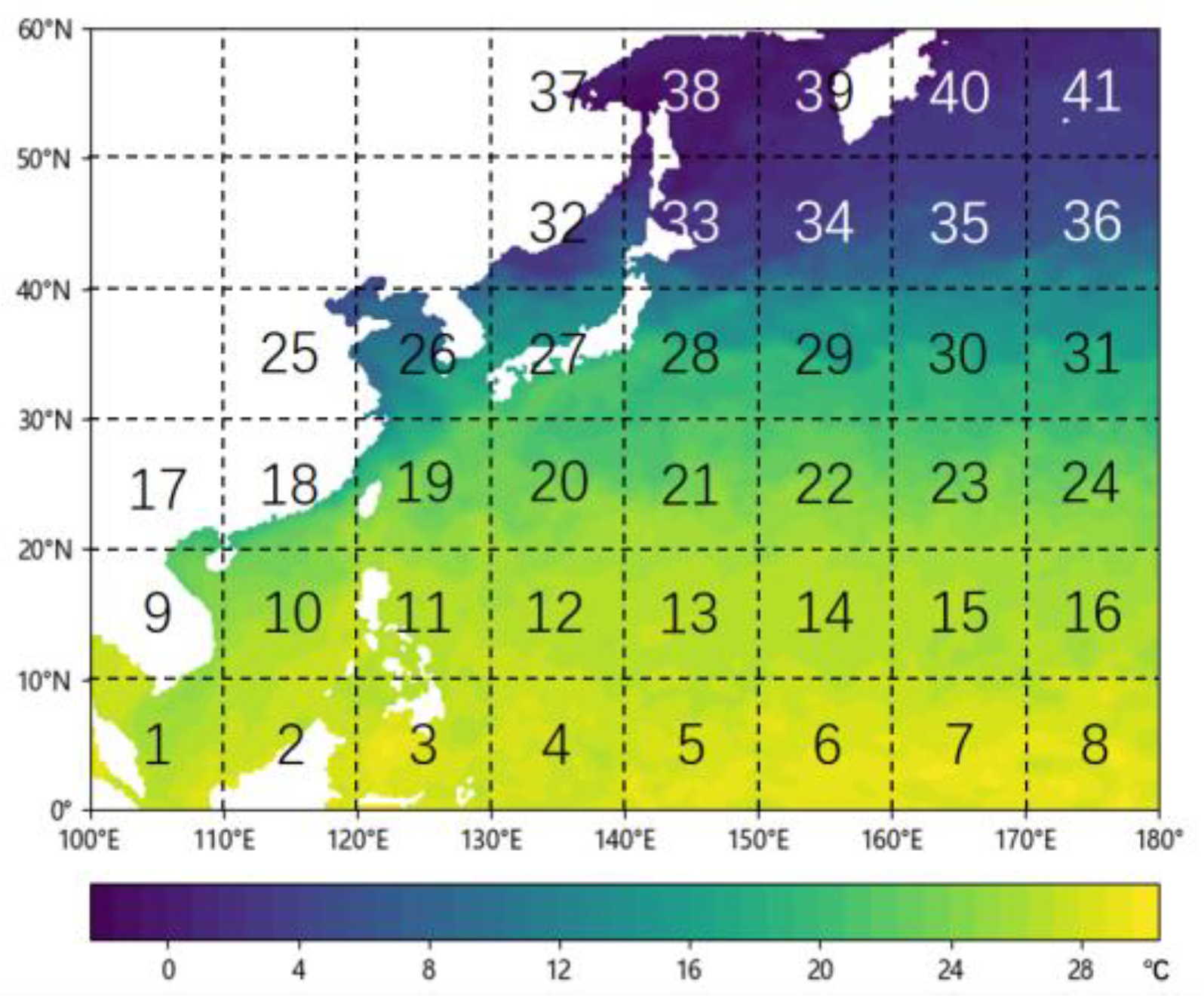
4.3. Results of Different Subregions
4.3.1. Results of Incomplete Sea Areas
4.3.2. Results of Complete Sea Areas
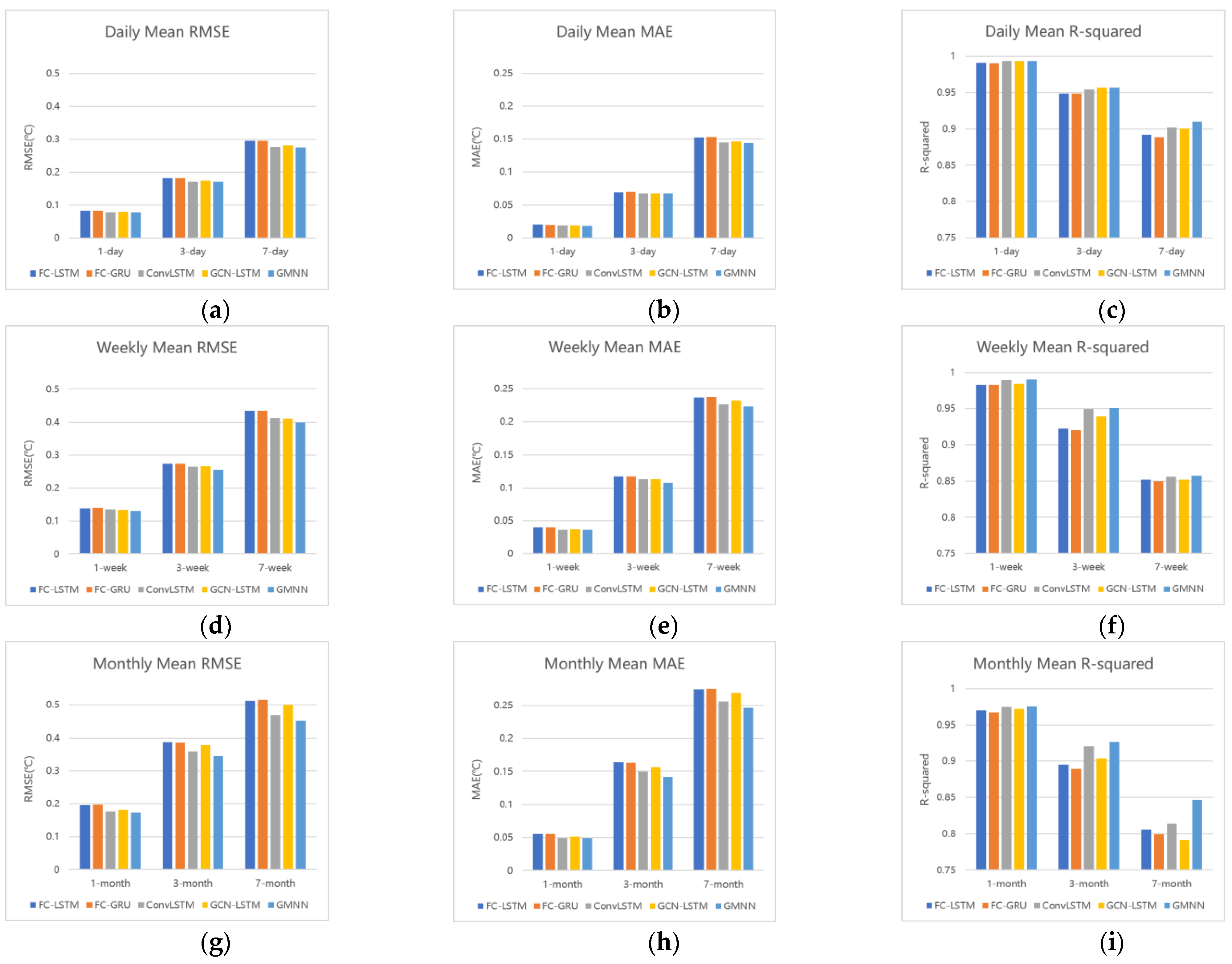
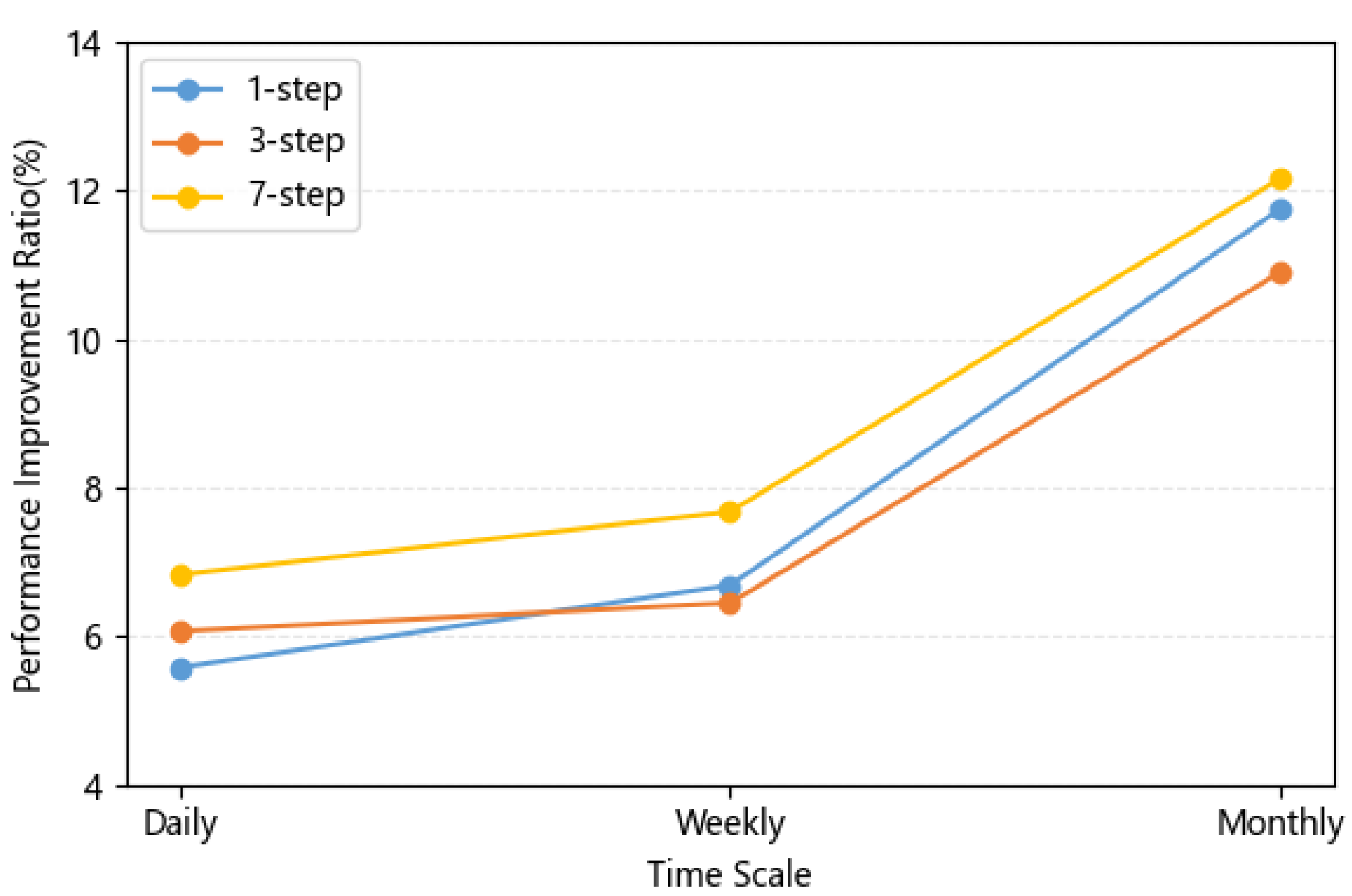
4.4. Results of Different Time Scales
5. Discussion
5.1. Model Comparison
5.2. Error Distribution
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Cheng, L.; Abraham, J.; Li, C. Consensuses and discrepancies of basin-scale ocean heat content changes in different ocean analyses. Clim. Dyn. 2018, 50, 2471–2487. [Google Scholar] [CrossRef]
- Ham, Y.; Kug, J.; Park, J.; Jin, F. Sea surface temperature in the north tropical Atlantic as a trigger for El Niño/Southern Oscillation events. Nat. Geosci. 2013, 6, 112–116. [Google Scholar] [CrossRef]
- Chen, Z.; Wen, Z.; Wu, R.; Lin, X.; Wang, J. Relative importance of tropical SST anomalies in maintaining the Western North Pacific anomalous anticyclone during El Niño to La Niña transition years. Clim. Dyn. 2016, 46, 1027–1041. [Google Scholar] [CrossRef]
- Andrade, H.A.; Garcia, C.A.E. Skipjack tuna fishery in relation to sea surface temperature off the southern Brazilian coast. Fish Oceanogr. 1999, 8, 245–254. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, C.; Shao, Q.; Mulla, D.J. Remote sensing of sea surface temperature and chlorophyll-a: Implications for squid fisheries in the north-west Pacific Ocean. Int. J. Remote Sens. 2010, 31, 4515–4530. [Google Scholar] [CrossRef]
- Khan, T.M.A.; Singh, O.P.; Rahman, M.S. Recent sea level and sea surface temperature trends along the Bangladesh coast in relation to the frequency of intense cyclones. Mar. Geod. 2000, 23, 103–116. [Google Scholar] [CrossRef]
- Emanuel, K.; Sobel, A. Response of tropical sea surface temperature, precipitation, and tropical cyclone-related variables to changes in global and local forcing. J. Adv. Model. Earth Syst. 2013, 5, 447–458. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlbert, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Bleck, R. Ocean prediction with the hybrid coordinate ocean model (HYCOM). In Ocean Weather Forecasting: An Integrated View of Oceanography; Springer: Berlin/Heidelberg, Germany, 2006; pp. 413–426. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Metzger, E.J.; Smedstad, O.M.; Cummings, J.A.; Halliwell, G.R. US GODAE: Global ocean prediction with the HYbrid Coordinate Ocean Model (HYCOM). Oceanography 2009, 22, 64–75. [Google Scholar] [CrossRef]
- Qian, C.; Huang, B.; Yang, X.; Chen, G. Data science for oceanography: From small data to big data. Big Earth Data 2022, 6, 236–250. [Google Scholar] [CrossRef]
- Kartal, S. Assessment of the spatiotemporal prediction capabilities of machine learning algorithms on Sea Surface Temperature data: A comprehensive study. Eng. Appl. Artif. Intell. 2023, 118, 105675. [Google Scholar] [CrossRef]
- Xue, Y.; Leetmaa, A. Forecasts of Tropical Pacific SST and Sea Level Using a Markov Model. Geophys. Res. Lett. 2000, 27, 2701–2704. [Google Scholar] [CrossRef]
- Collins, D.C.; Reason, C.J.C. Predictability of Indian Ocean Sea Surface Temperature Using Canonical Correlation Analysis. Clim. Dyn. 2004, 22, 481–497. [Google Scholar] [CrossRef]
- Neetu, S.R.; Basu, S.; Sarkar, A.; Pal, P.K. Data-Adaptive Prediction of Sea-Surface Temperature in the Arabian Sea. Ieee Geosci. Remote Sens. Lett. 2010, 8, 9–13. [Google Scholar] [CrossRef]
- Shao, Q.; Li, W.; Han, G.; Hou, G.; Liu, S.; Gong, Y.; Qu, P. A Deep Learning Model for Forecasting Sea Surface Height Anomalies and Temperatures in the South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2021JC017515. [Google Scholar] [CrossRef]
- Garcia-Gorriz, E.; Garcia-Sanchez, J. Prediction of Sea Surface Temperatures in the Western Mediterranean Sea by Neural Networks Using Satellite Observations. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Lee, Y.; Ho, C.; Su, F.; Kuo, N.; Cheng, Y. The Use of Neural Networks in Identifying Error Sources in Satellite-Derived Tropical SST Estimates. Sensors 2011, 11, 7530–7544. [Google Scholar] [CrossRef]
- Lins, I.D.; Araujo, M.; Moura, M.D.C.; Silva, M.A.; Droguett, E.L. Prediction of Sea Surface Temperature in the Tropical Atlantic by Support Vector Machines. Comput. Stat. Data Anal. 2013, 61, 187–198. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of Sea Surface Temperature Using Long Short-Term Memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef]
- Sun, T.; Feng, Y.; Li, C.; Zhang, X. High Precision Sea Surface Temperature Prediction of Long Period and Large Area in the Indian Ocean Based on the Temporal Convolutional Network and Internet of Things. Sensors 2022, 22, 1636. [Google Scholar] [CrossRef]
- Su, H.; Zhang, T.; Lin, M.; Lu, W.; Yan, X. Predicting subsurface thermohaline structure from remote sensing data based on long short-term memory neural networks. Remote Sens. Environ. 2021, 260, 112465. [Google Scholar] [CrossRef]
- Guo, H.; Xie, C. Multi-Feature Attention Based LSTM Network for Sea Surface Temperature Prediction. In Proceedings of the 3rd International Conference on Computer Information and Big Data Applications, Wuhan, China, 25–27 March 2022. [Google Scholar]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM Model for Sea Surface Temperature Prediction. IEEE Geosci. Remote Sens. Lett. 2018, 15, 207–211. [Google Scholar] [CrossRef]
- Yu, X.; Shi, S.; Xu, L.; Liu, Y.; Miao, Q.; Sun, M. A Novel Method for Sea Surface Temperature Prediction Based on Deep Learning. Math. Probl. Eng. 2020, 2020, 6387173. [Google Scholar] [CrossRef]
- Qiao, B.; Wu, Z.; Tang, Z.; Wu, G. Sea Surface Temperature Prediction Approach Based on 3D CNN and LSTM with Attention Mechanism. In Proceedings of the 23rd International Conference on Advanced Communication Technology (ICACT), PyeongChang, Republic of Korea, 7–10 February 2021. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Cai, Y.; Xu, L.; Chen, Z.; Gong, J. A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Environ. Modell. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- Jung, S.; Kim, Y.J.; Park, S.; Im, J. Prediction of Sea Surface Temperature and Detection of Ocean Heat Wave in the South Sea of Korea Using Time-series Deep-learning Approaches. Korean J. Remote Sens. 2020, 36, 1077–1093. [Google Scholar] [CrossRef]
- Zhang, K.; Geng, X.; Yan, X.H. Prediction of 3-D Ocean Temperature by Multilayer Convolutional LSTM. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1303–1307. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Frery, A.C.; Ren, P. Sea Surface Temperature Prediction With Memory Graph Convolutional Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. arXiv 2017, arXiv:1704.01212. [Google Scholar] [CrossRef]
- Sun, Y.; Yao, X.; Bi, X.; Huang, X.; Zhao, X.; Qiao, B. Time-Series Graph Network for Sea Surface Temperature Prediction. Big Data Res. 2021, 25, 100237. [Google Scholar] [CrossRef]
- Wang, T.; Li, Z.; Geng, X.; Jin, B.; Xu, L. Time Series Prediction of Sea Surface Temperature Based on an Adaptive Graph Learning Neural Model. Future Internet 2022, 14, 171. [Google Scholar] [CrossRef]
- Pan, J.; Li, Z.; Shi, S.; Xu, L.; Yu, J.; Wu, X. Adaptive graph neural network based South China Sea seawater temperature prediction and multivariate uncertainty correlation analysis. Stoch. Environ. Res. Risk Assess. 2022, 37, 1877–1896. [Google Scholar] [CrossRef]
- Xia, F.; Sun, K.; Yu, S.; Aziz, A.; Wan, L.; Pan, S.; Liu, H. Graph Learning: A Survey. IEEE Trans. Artif. Intell. 2021, 2, 109–127. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time-Series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995; pp. 255–258. [Google Scholar]
- Ye, Z.; Kumar, Y.J.; Sing, G.O.; Song, F.; Wang, J. A Comprehensive Survey on Graph Neural Networks for Knowledge Graphs. IEEE Access 2019, 10, 75729–75741. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Deep Locally Connected Networks on Graphs. arXiv 2014, arXiv:1312.6203. [Google Scholar] [CrossRef]
- Micheli, A. Neural Network for Graphs: A Contextual Constructive Approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]


| Temporal Resolution | Dataset | Time Range |
|---|---|---|
| Daily Mean | Training Set | 1 January 1993~31 December 2010 |
| Validation Set | 1 January 2011~31 December 2015 | |
| Testing Set | 1 January 2016~31 December 2020 | |
| Weekly Mean | Training Set | 3 January 1993~26 December 2010 |
| Validation Set | 2 January 2011~27 December 2015 | |
| Testing Set | 3 January 2016~27 December 2020 | |
| Monthly Mean | Training Set | January 1993~December 2010 |
| Validation Set | January 2011~December 2015 | |
| Testing Set | January 2016~December 2020 |
| Method | Metric | Daily | ||
|---|---|---|---|---|
| 1 | 3 | 7 | ||
| FC-LSTM | RMSE | 0.084 | 0.184 | 0.311 |
| MAE | 0.020 | 0.071 | 0.160 | |
| R-squared | 0.993 | 0.952 | 0.911 | |
| FC-GRU | RMSE | 0.084 | 0.186 | 0.312 |
| MAE | 0.209 | 0.074 | 0.163 | |
| R-squared | 0.994 | 0.933 | 0.909 | |
| GCN-LSTM | RMSE | 0.081 | 0.178 | 0.292 |
| MAE | 0.019 | 0.070 | 0.153 | |
| R-squared | 0.996 | 0.965 | 0.924 | |
| GMNN | RMSE | 0.080 | 0.177 | 0.288 |
| MAE | 0.019 | 0.070 | 0.152 | |
| R-squared | 0.999 | 0.968 | 0.924 | |
| Method | Metric | Daily | ||
|---|---|---|---|---|
| 1 | 3 | 7 | ||
| FC-LSTM | RMSE | 0.078 | 0.164 | 0.252 |
| MAE | 0.019 | 0.069 | 0.134 | |
| R-squared | 0.979 | 0.948 | 0.807 | |
| FC-GRU | RMSE | 0.076 | 0.169 | 0.252 |
| MAE | 0.019 | 0.070 | 0.134 | |
| R-squared | 0.979 | 0.949 | 0.798 | |
| ConvLSTM | RMSE | 0.079 | 0.154 | 0.241 |
| MAE | 0.018 | 0.062 | 0.127 | |
| R-squared | 0.982 | 0.940 | 0.834 | |
| GCN-LSTM | RMSE | 0.075 | 0.156 | 0.243 |
| MAE | 0.018 | 0.062 | 0.129 | |
| R-squared | 0.982 | 0.939 | 0.834 | |
| GMNN | RMSE | 0.073 | 0.154 | 0.238 |
| MAE | 0.018 | 0.062 | 0.127 | |
| R-squared | 0.983 | 0.956 | 0.855 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Zhao, A.; Qin, M.; Hu, L.; Wu, S.; Du, Z.; Liu, R. A Graph Memory Neural Network for Sea Surface Temperature Prediction. Remote Sens. 2023, 15, 3539. https://doi.org/10.3390/rs15143539
Liang S, Zhao A, Qin M, Hu L, Wu S, Du Z, Liu R. A Graph Memory Neural Network for Sea Surface Temperature Prediction. Remote Sensing. 2023; 15(14):3539. https://doi.org/10.3390/rs15143539
Chicago/Turabian StyleLiang, Shuchen, Anming Zhao, Mengjiao Qin, Linshu Hu, Sensen Wu, Zhenhong Du, and Renyi Liu. 2023. "A Graph Memory Neural Network for Sea Surface Temperature Prediction" Remote Sensing 15, no. 14: 3539. https://doi.org/10.3390/rs15143539
APA StyleLiang, S., Zhao, A., Qin, M., Hu, L., Wu, S., Du, Z., & Liu, R. (2023). A Graph Memory Neural Network for Sea Surface Temperature Prediction. Remote Sensing, 15(14), 3539. https://doi.org/10.3390/rs15143539