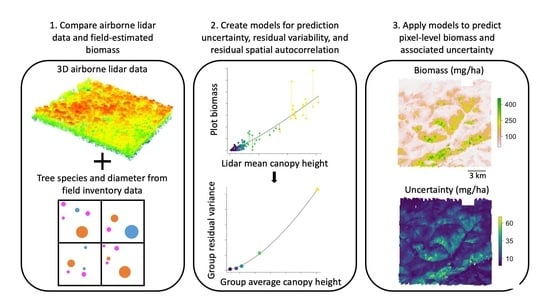
Small Field Plots Can Cause Substantial Uncertainty in Gridded Aboveground Biomass Products from Airborne Lidar Data
Abstract
1. Introduction
2. Methods
2.1. Study Sites
2.2. Field Estimates of AGB
2.3. ALS Data
2.4. AGB-ALS Model
- First, the plots were ordered by their MCH and sorted into equal-sized groups of at least 10 plots each;
- Next, the average MCH and biomass residual variance were calculated for each group;
- Finally, a model was fit describing the increase in residual variance as a power function of average MCH:
2.5. Predicted Gridded Biomass across Landscapes
2.6. Estimating AGB Uncertainty at 1 ha Resolution
2.7. The Effect of Plot Size on AGB Uncertainty
3. Results
3.1. Plot-Based Biomass Estimates
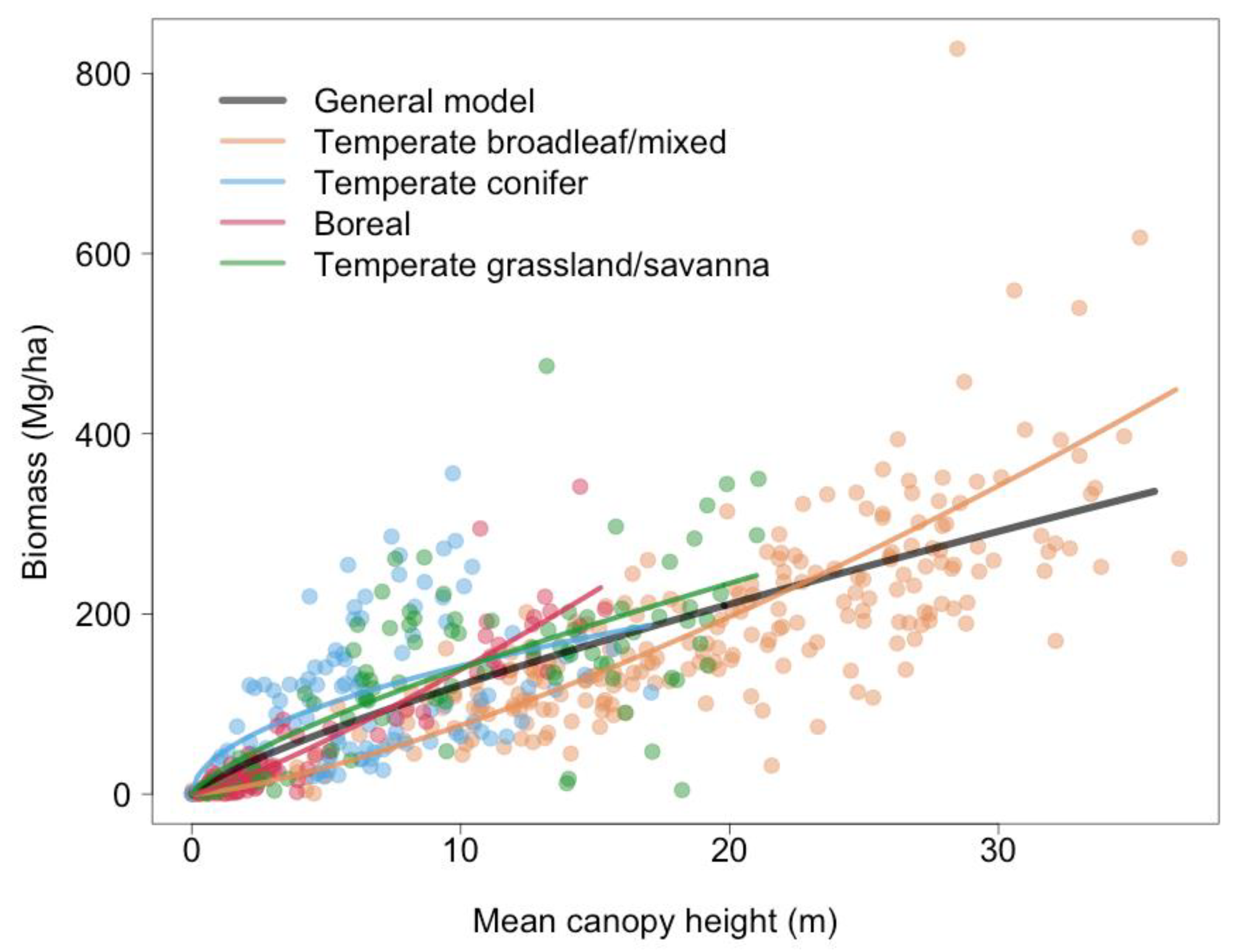
3.2. Plot-Based Model Performance
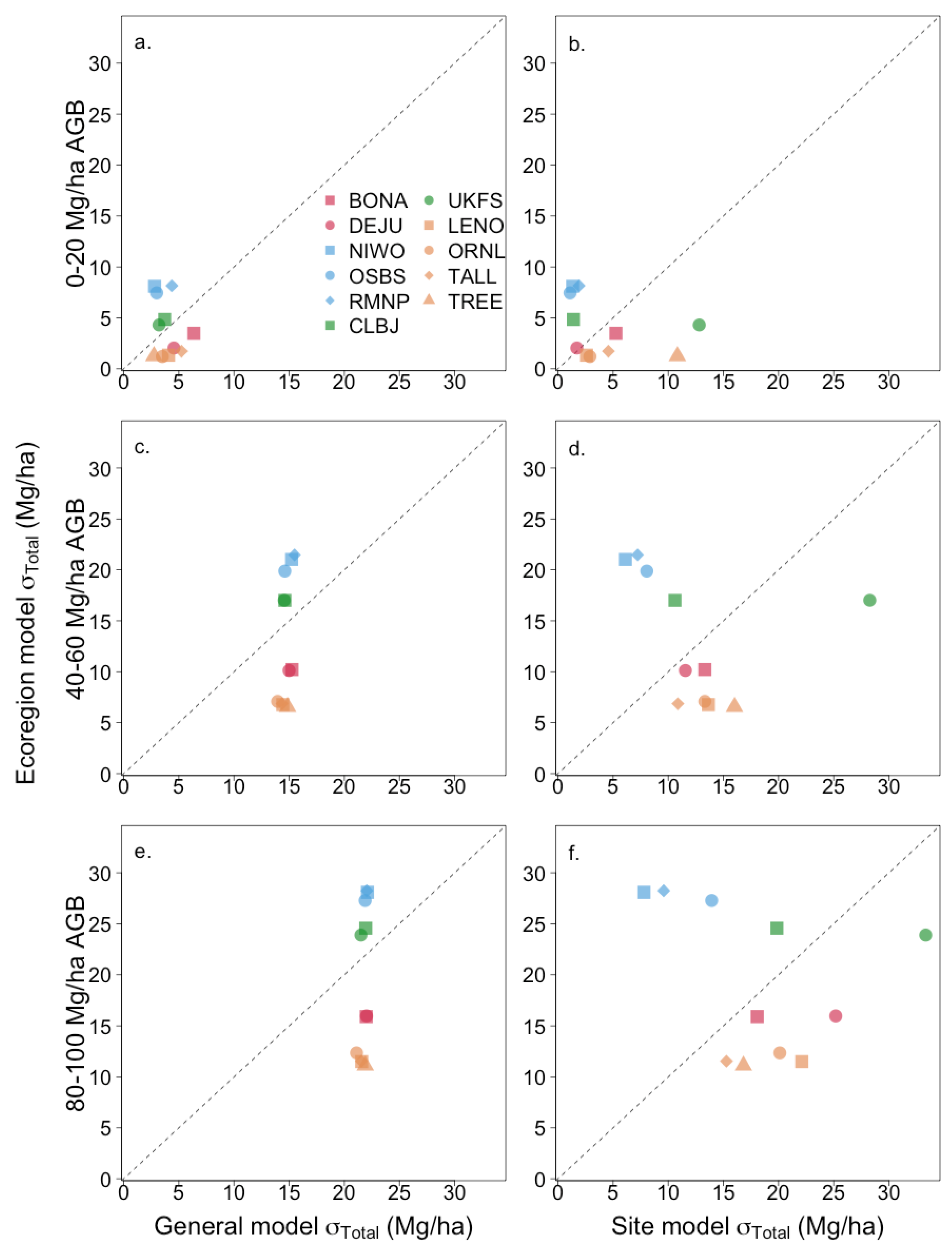
3.3. One-Hectare-Resolution Estimates of Uncertainty
3.4. Plot Size Effects on Gridded AGB Uncertainty
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Saatchi, S.S.; Yang, Y.; Yu, Y.; Pongratz, J.; Anthony Bloom, A.; Bowman, K.; Worden, J.; Liu, J.; Yin, Y.; et al. Changes in Global Terrestrial Live Biomass over the 21st Century. Sci. Adv. 2021, 7, eabe9829. [Google Scholar] [CrossRef]
- Dubayah, R.; Armston, J.; Healey, S.; Bruening, J.; Patterson, P.; Kellner, J.; Duncanson, L.; Saarela, S.; Ståhl, G.; Yang, Z.; et al. GEDI Launches a New Era of Biomass Inference from Space. Environ. Res. Lett. 2022, 17, 095001. [Google Scholar] [CrossRef]
- Quegan, S.; Le Toan, T.; Chave, J.; Dall, J.; Exbrayat, J.F.; Minh, D.H.T.; Lomas, M.; D’Alessandro, M.M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS Mission: Measuring Forest Above-Ground Biomass from Space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Rosen, P.A.; Kumar, R. NASA-ISRO SAR (NISAR) Mission Status. In Proceedings of the 2021 IEEE Radar Conference, Atlanta, GA, USA, 8–14 May 2021; Institute of Electrical and Electronics Engineers Inc.: Atlanta, GA, USA, 2021; pp. 1–6. [Google Scholar]
- Shugart, H.H.; Saatchi, S.; Hall, F.G. Importance of Structure and Its Measurement in Quantifying Function of Forest Ecosystems. J. Geophys. Res. Biogeosci 2010, 115, G00E13. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of Spatial Variability of Tropical Forest Structure on Radar Estimation of Aboveground Biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Xu, L.; Saatchi, S.S.; Shapiro, A.; Meyer, V.; Ferraz, A.; Yang, Y.; Bastin, J.F.; Banks, N.; Boeckx, P.; Verbeeck, H.; et al. Spatial Distribution of Carbon Stored in Forests of the Democratic Republic of Congo. Sci. Rep. 2017, 7, 15030. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Stefanoni, J.L.; Reyes-Palomeque, G.; Castillo-Santiago, M.Á.; George-Chacón, S.P.; Huechacona-Ruiz, A.H.; Tun-Dzul, F.; Rondon-Rivera, D.; Dupuy, J.M. Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests. Remote Sens. 2018, 10, 1586. [Google Scholar] [CrossRef]
- Chapman, B.; Rosen, P.; Joughin, I.; Siqueira, P.; Saatchi, S.; Meyer, V.; Borsa, A.; Meyer, F.; Simard, M.; Lohman, R.; et al. NISAR Calibration and Validation Plan V0.9, NASA Jet Propulsion Laboratory Document D-80829; California Institute of Technology: Pasadena, CA, USA, 2018. [Google Scholar]
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T. Estimation of Above- and Below-Ground Biomass across Regions of the Boreal Forest Zone Using Airborne Laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Meyer, V.; Saatchi, S.S.; Chave, J.; Dalling, J.; Bohlman, S.; Fricker, G.A.; Robinson, C.; Neumann, M. Detecting Tropical Forest Biomass Dynamics from Repeated Airborne Lidar Measurements. Biogeosci. Discuss. 2013, 10, 1957–1992. [Google Scholar] [CrossRef]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.W.; et al. The Importance of Consistent Global Forest Aboveground Biomass Product Validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated Impact of Sample Plot Size and Co-Registration Error on the Accuracy and Uncertainty of LiDAR-Derived Estimates of Forest Stand Biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.; Holm, S. Model-Assisted Estimation of Biomass in a LiDAR Sample Survey in Hedmark County, Norway. Canadian J. Forest Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for Lidar-Assisted Estimation of Forest Growing Stock Volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating Uncertainty in Mapping Forest Carbon with Airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; MacBean, N.; et al. Aboveground Woody Biomass Product Validation Good Practices Protocol. In Good Practices for Satellite Derived Land Product Validation; Duncanson, L., Disney, M., Armston, J., Nickeson, J., Minor, D., Camacho, F., Eds.; Land Product Validation Subgroup (WGCV/CEOS), 2021; p. 236. Available online: https://lpvs.gsfc.nasa.gov/PDF/CEOS_WGCV_LPV_Biomass_Protocol_2021_V1.0.pdf (accessed on 4 June 2023). [CrossRef]
- NISAR Science Team. NISAR Ecosystems Science Algorithms. Available online: https://gitlab.com/nisar-science-algorithms/ecosystems (accessed on 4 June 2023).
- McRoberts, R.E.; Næsset, E.; Saatchi, S.; Quegan, S. Statistically Rigorous, Model-Based Inferences from Maps. Remote Sens. Environ. 2022, 279, 113028. [Google Scholar] [CrossRef]
- Davies, S.J.; Abiem, I.; Salim, K.A.; Aguilar, S.; Allen, D.; Alonso, A.; Anderson-Teixeira, K.; Andrade, A.; Arellano, G.; Ashton, P.S.; et al. ForestGEO: Understanding Forest Diversity and Dynamics through a Global Observatory Network. Biol. Conserv. 2021, 253, 108907. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Davies, S.J.; Bennett, A.C.; Gonzalez-Akre, E.B.; Muller-Landau, H.C.; Joseph Wright, S.; Abu Salim, K.; Almeyda Zambrano, A.M.; Alonso, A.; Baltzer, J.L.; et al. CTFS-ForestGEO: A Worldwide Network Monitoring Forests in an Era of Global Change. Glob. Chang. Biol. 2014, 21, 528–549. [Google Scholar] [CrossRef]
- Bourg, N.A.; McShea, W.J.; Thompson, J.R.; McGarvey, J.C.; Shen, X. Initial Census, Woody Seedling, Seed Rain, and Stand Structure Data for the SCBI SIGEO Large Forest Dynamics Plot. Ecology 2013, 94, 2111–2112. [Google Scholar] [CrossRef]
- NEON (National Ecological Observatory Network). Vegetation Structure (DP1.10098.001); RELEASE-2022; NEON: Boulder, CO, USA, 2022. [Google Scholar]
- Gonzalez-Akre, E.; Piponiot, C.; Lepore, M.; Herrmann, V.; Lutz, J.A.; Baltzer, J.L.; Dick, C.W.; Gilbert, G.S.; He, F.; Heym, M.; et al. Allodb: An R Package for Biomass Estimation at Globally Distributed Extratropical Forest Plots. Methods Ecol. Evol. 2022, 13, 330–338. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Westfall, J.A. Effects of Uncertainty in Model Predictions of Individual Tree Volume on Large Area Volume Estimates. Forest Sci. 2014, 60, 34–42. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Westfall, J.A. Propagating Uncertainty through Individual Tree Volume Model Predictions to Large-Area Volume Estimates. Ann. For. Sci. 2016, 73, 625–633. [Google Scholar] [CrossRef]
- NEON (National Ecological Observatory Network). Discrete Return LiDAR Point Cloud (DP1.30003.001); NEON: Boulder, CO, USA, 2022. [Google Scholar]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D. LidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications, R. Package Version 3.1.2. 2021. Available online: https://cran.r-project.org/package=lidR (accessed on 4 June 2023).
- Liu, R.Y. Bootstrap Procedures under Some Non-I.I.D. Models. Ann. Stat. 1988, 16, 1696–1708. [Google Scholar] [CrossRef]
- Wu, C.F.J. Jackknife, Bootstrap and Other Resampling Methods in Regression Analysis. Ann. Stat. 1986, 14, 1261–1350. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Hou, Z.; Ståhl, G.; Saarela, S.; Esteban, J.; Travaglini, D.; Mohammadi, J.; Chirici, G. How Many Bootstrap Replications Are Necessary for Estimating Remote Sensing-Assisted, Model-Based Standard Errors? Remote Sens. Environ. 2023, 288, 113455. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling, R. Package Version 2.8-4. 2021. Available online: https://CRAN.R-project.org/package=raster (accessed on 4 June 2023).
- Bjornstad, O.N. ncf: Spatial Covariance Functions, R package version 1.3-2. 2022. Available online: https://CRAN.R-project.org/package=ncf (accessed on 4 June 2023).
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar Remote Sensing of Above-Ground Biomass in Three Biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef]
- Görgens, E.B.; Packalen, P.; da Silva, A.G.P.; Alvares, C.A.; Campoe, O.C.; Stape, J.L.; Rodriguez, L.C.E. Stand Volume Models Based on Stable Metrics as from Multiple ALS Acquisitions in Eucalyptus Plantations. Ann. For. Sci. 2015, 72, 489–498. [Google Scholar] [CrossRef]
- Pascual, A.; Guerra-Hernández, J.; Cosenza, D.N.; Sandoval-Altalerrea, V. Using Enhanced Data Co-Registration to Update Spanish National Forest Inventories (NFI) and to Reduce Training Data under LiDAR-Assisted Inference. Int. J. Remote Sens. 2021, 42, 106–127. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Walters, B.F.; Kaisershot, D.J. The Effects of Global Positioning System Receiver Accuracy on Airborne Laser Scanning-Assisted Estimates of Aboveground Biomass. Remote Sens. Environ. 2018, 207, 42–49. [Google Scholar] [CrossRef]
- Burt, A.; Calders, K.; Cuni-Sanchez, A.; Gomez-Dans, J.; Lewis, P.; Lewis, S.L.; Malhi, Y.; Phillips, O.L.; Disney, M. Assessment of Bias in Pan-Tropical Biomass Predictions. Front. For. Glob. Chang. 2020, 3, 1–20. [Google Scholar] [CrossRef]
- Demol, M.; Verbeeck, H.; Gielen, B.; Armston, J.; Burt, A.; Disney, M.; Duncanson, L.; Hackenberg, J.; Kükenbrink, D.; Lau, A.; et al. Estimating Forest Above-Ground Biomass with Terrestrial Laser Scanning: Current Status and Future Directions. Methods Ecol. Evol. 2022, 13, 1628–1639. [Google Scholar] [CrossRef]
- Labrière, N.; Davies, S.J.; Disney, M.I.; Duncanson, L.I.; Herold, M.; Lewis, S.L.; Phillips, O.L.; Quegan, S.; Saatchi, S.S.; Schepaschenko, D.G.; et al. Toward a Forest Biomass Reference Measurement System for Remote Sensing Applications. Glob. Chang. Biol. 2023, 29, 827–840. [Google Scholar] [CrossRef]
- Chave, J.; Davies, S.J.; Phillips, O.L.; Lewis, S.L.; Sist, P.; Schepaschenko, D.; Armston, J.; Baker, T.R.; Coomes, D.; Disney, M.; et al. Ground Data Are Essential for Biomass Remote Sensing Missions. Surv. Geophys. 2019, 40, 863–880. [Google Scholar] [CrossRef]
- Clark, D.A.; Asao, S.; Fisher, R.; Reed, S.; Reich, P.B.; Ryan, M.G.; Wood, T.E.; Yang, X. Reviews and Syntheses: Field Data to Benchmark the Carbon-Cycle Models for Tropical Forests. Biogeosciences 2017, 14, 4663–4690. [Google Scholar] [CrossRef]
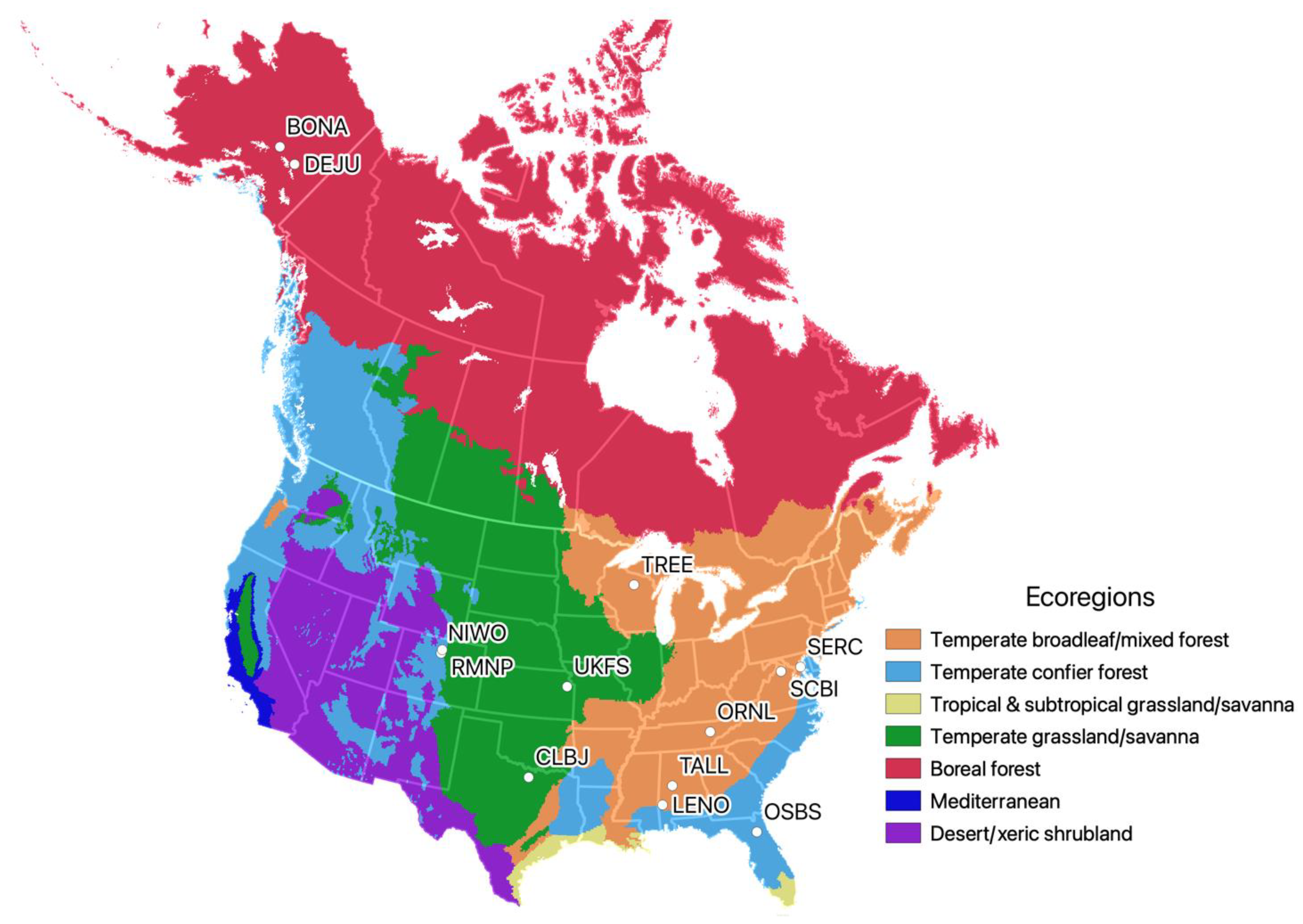

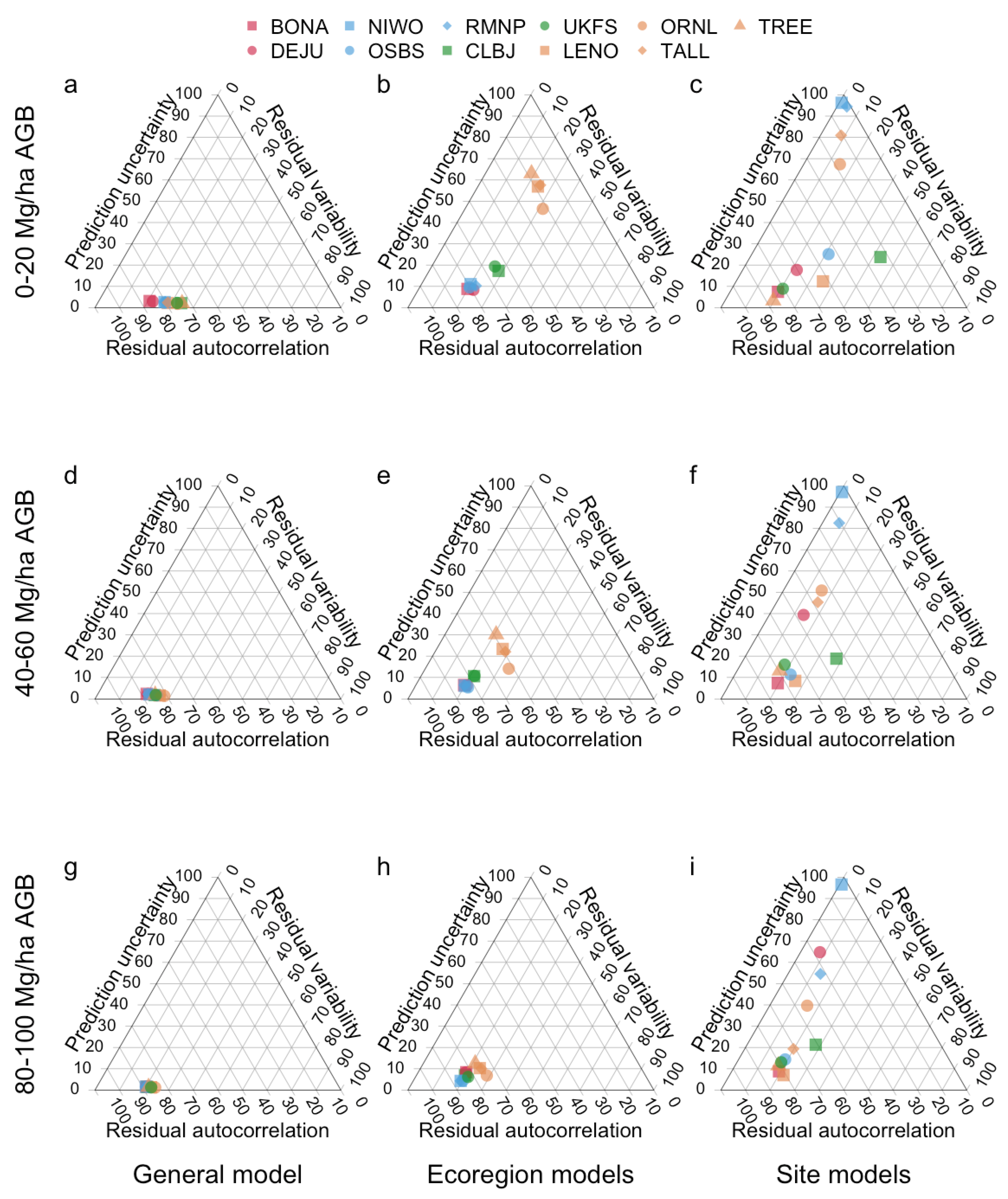
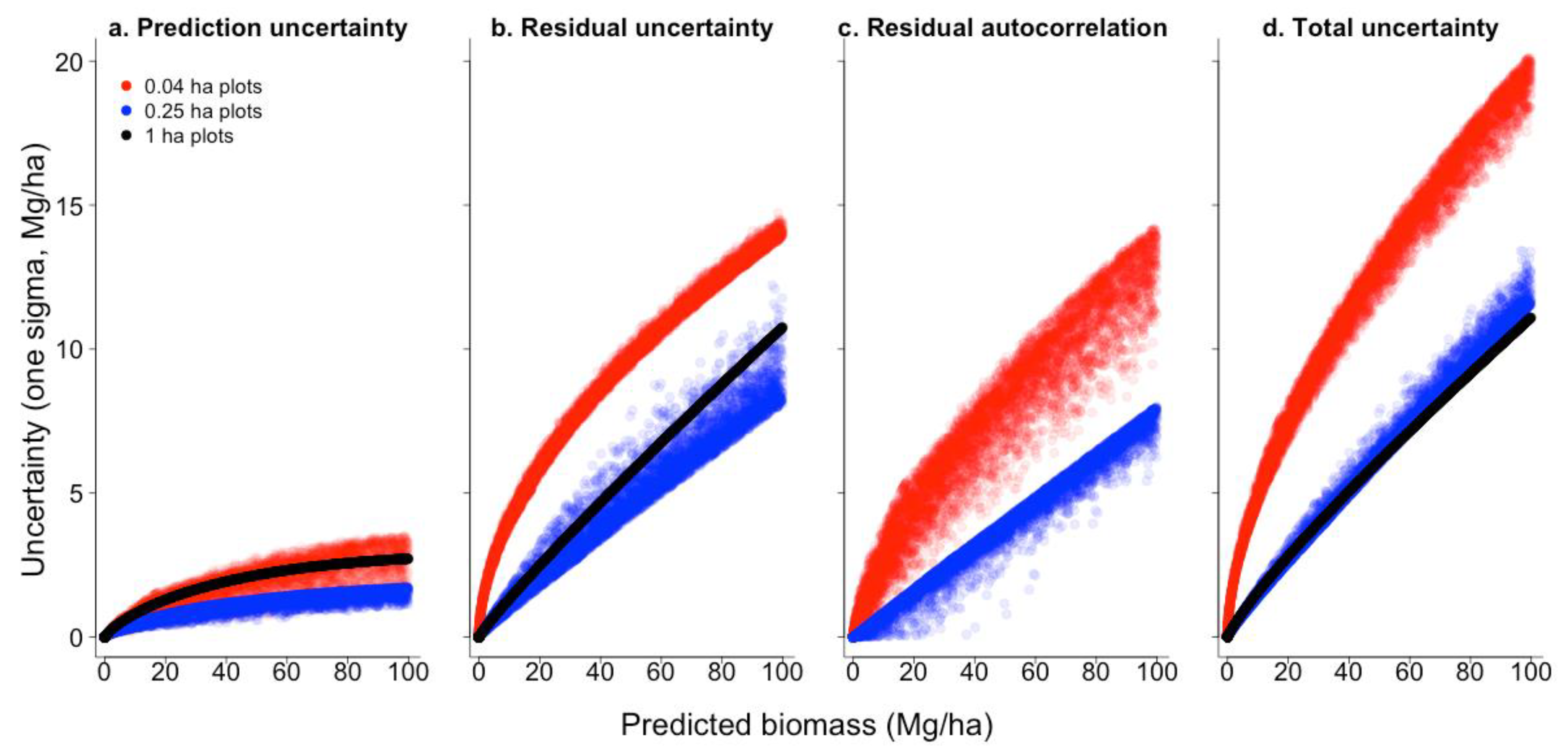
| NISAR Ecoregion | Site Name | Location | Plot Data | ALS Data | ||||
|---|---|---|---|---|---|---|---|---|
| Latitude | Longitude | Years | AGB Mean [Range] (Mg ha−1) | Area (ha) | Year | Density (pts m−2) | ||
| Boreal forests | Caribou–Poker Creeks Research Watershed (BONA) | 63.876 | −149.213 | 2016–2021 | 96.1 [1.5, 149.0] | 23,473 | 2021 | 16.9 |
| Delta Junction (DEJU) | 63.881 | −145.751 | 2016–2021 | 20.9 [0.2, 104.6] | 19,543 | 2021 | 8.2 | |
| Conifer forests | Ordway–Swisher Biological Station (OSBS) | 29.689 | −81.993 | 2016–2020 | 70.2 [16.3, 206.8] | 19,394 | 2021 | 13.6 * |
| Niwot Ridge (NIWO) | 40.054 | −105.582 | 2015–2020 | 124.7 [0.01, 346.3] | 13,688 | 2020 | 5.6 | |
| Rocky Mountain National Park (RMNP) | 40.276 | −105.546 | 2017–2020 | 149.3 [31.8, 275.6] | 19,796 | 2020 | 11.9 * | |
| Temperate broadleaf and mixed forests | Lenoir Landing (LENO) | 31.854 | −88.161 | 2017–2021 | 175.8 [0.4, 961.4] | 11,483 | 2019 | 5.2 |
| Oak Ridge (ORNL) | 35.964 | −84.283 | 2017–2018 | 247.6 [0.1, 441.3] | 23,910 | 2018 | 14.0 | |
| Smithsonian Conservation Biology Institute (SCBI) ‡ | 38.893 | −78.139 | 2018 | 306.4 [7.2, 758.5] | 11,243 | 2021 | 14.1 * | |
| Smithsonian Environmental Research Center (SERC) ‡ | 38.890 | −76.560 | 2014 | 326.6 [0.8, 1022.3] | 10,884 | 2021 | 12.8 * | |
| Talladega National Forest (TALL) | 32.950 | −87.393 | 2015–2020 | 150.6 [1.3, 328.9] | 13,616 | 2019 | 6.3 | |
| Treehaven (TREE) | 45.494 | −89.586 | 2018–2021 | 132.6 [7.9, 265.2] | 23,491 | 2020 | 13.1 * | |
| Temperate grasslands and savannas | Lyndon B. Johnson National Grassland (CLBJ) | 33.368 | −97.587 | 2016–2021 | 108.7 [0.1, 265.4] | 15,794 | 2021 | 12.0 |
| University of Kansas Field Station (UKFS) | 39.040 | −95.192 | 2016–2020 | 165.9 [10.3, 506.0] | 13,591 | 2020 | 10.7 | |
| Ecoregion | RMSE (Mg ha−1) [% of Mean AGB] | R2 | Number of Plots | ||
|---|---|---|---|---|---|
| General Model | Ecoregion Model | General Model | Ecoregion Model | ||
| Boreal forests | 34.7 [61.9] | 27.7 [49.5] | 0.77 | 0.85 | 92 |
| Temperate grasslands and savannas | 75.0 [53.2] | 74.0 [52.5] | 0.34 | 0.35 | 89 |
| Temperate broadleaf and mixed forests | 72.8 [41.7] | 68.9 [39.4] | 0.60 | 0.64 | 243 |
| Temperate conifer forests | 73.8 [68.4] | 68.4 [63.4] | 0.06 | 0.20 | 105 |
| Ecoregion | Site | RMSE (Mg ha−1) [% of Mean AGB] | R2 | Number of Plots | ||||
|---|---|---|---|---|---|---|---|---|
| General | Ecoregion | Site | General | Ecoregion | Site | |||
| Boreal forests | BONA | 48.6 [50.5] | 38.2 [39.7] | 39.5 [41.1] | 0.69 | 0.81 | 0.80 | 43 |
| DEJU | 13.7 [65.6] | 12.9 [61.7] | 11.2 [53.4] | 0.48 | 0.54 | 0.66 | 49 | |
| Temperate grasslands and savannas | CLBJ | 65.3 [60.1] | 55.1 [50.7] | 56.2 [51.7] | 0.35 | 0.54 | 0.52 | 39 |
| UKFS | 81.7 [49.3] | 85.9 [51.8] | 86.0 [51.8] | 0.21 | 0.13 | 0.13 | 50 | |
| Temperate broadleaf and mixed forests | LENO | 93.9 [53.4] | 88.4 [50.3] | 95.0 [54.0] | 0.64 | 0.68 | 0.63 | 75 |
| ORNL | 82.2 [33.2] | 83.3 [33.6] | 83.8 [33.8] | 0.25 | 0.23 | 0.23 | 52 | |
| TALL | 51.4 [34.1] | 48.1 [31.9] | 49.3 [32.8] | 0.48 | 0.55 | 0.52 | 57 | |
| TREE | 46.3 [34.9] | 35.8 [27.0] | 35.9 [27.0] | 0.34 | 0.61 | 0.61 | 59 | |
| Temperate conifer forests | NIWO | 95.4 [76.5] | 74.9 [60.1] | 31.2 [25.0] | 0.00 | 0.35 | 0.89 | 26 |
| OSBS | 40.2 [57.3] | 62.1 [88.5] | 23.9 [34.1] | 0.08 | 0.00 | 0.67 | 47 | |
| RMNP | 90.0 [60.2] | 71.5 [47.9] | 39.5 [26.4] | 0.00 | 0.06 | 0.71 | 32 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cushman, K.C.; Saatchi, S.; McRoberts, R.E.; Anderson-Teixeira, K.J.; Bourg, N.A.; Chapman, B.; McMahon, S.M.; Mulverhill, C. Small Field Plots Can Cause Substantial Uncertainty in Gridded Aboveground Biomass Products from Airborne Lidar Data. Remote Sens. 2023, 15, 3509. https://doi.org/10.3390/rs15143509
Cushman KC, Saatchi S, McRoberts RE, Anderson-Teixeira KJ, Bourg NA, Chapman B, McMahon SM, Mulverhill C. Small Field Plots Can Cause Substantial Uncertainty in Gridded Aboveground Biomass Products from Airborne Lidar Data. Remote Sensing. 2023; 15(14):3509. https://doi.org/10.3390/rs15143509
Chicago/Turabian StyleCushman, K. C., Sassan Saatchi, Ronald E. McRoberts, Kristina J. Anderson-Teixeira, Norman A. Bourg, Bruce Chapman, Sean M. McMahon, and Christopher Mulverhill. 2023. "Small Field Plots Can Cause Substantial Uncertainty in Gridded Aboveground Biomass Products from Airborne Lidar Data" Remote Sensing 15, no. 14: 3509. https://doi.org/10.3390/rs15143509
APA StyleCushman, K. C., Saatchi, S., McRoberts, R. E., Anderson-Teixeira, K. J., Bourg, N. A., Chapman, B., McMahon, S. M., & Mulverhill, C. (2023). Small Field Plots Can Cause Substantial Uncertainty in Gridded Aboveground Biomass Products from Airborne Lidar Data. Remote Sensing, 15(14), 3509. https://doi.org/10.3390/rs15143509