Investigation of Temperature Effects into Long-Span Bridges via Hybrid Sensing and Supervised Regression Models
Abstract
1. Introduction
1.1. Related Works and Challenges
1.2. Objectives
1.3. Contributions
2. Long-Span Bridges
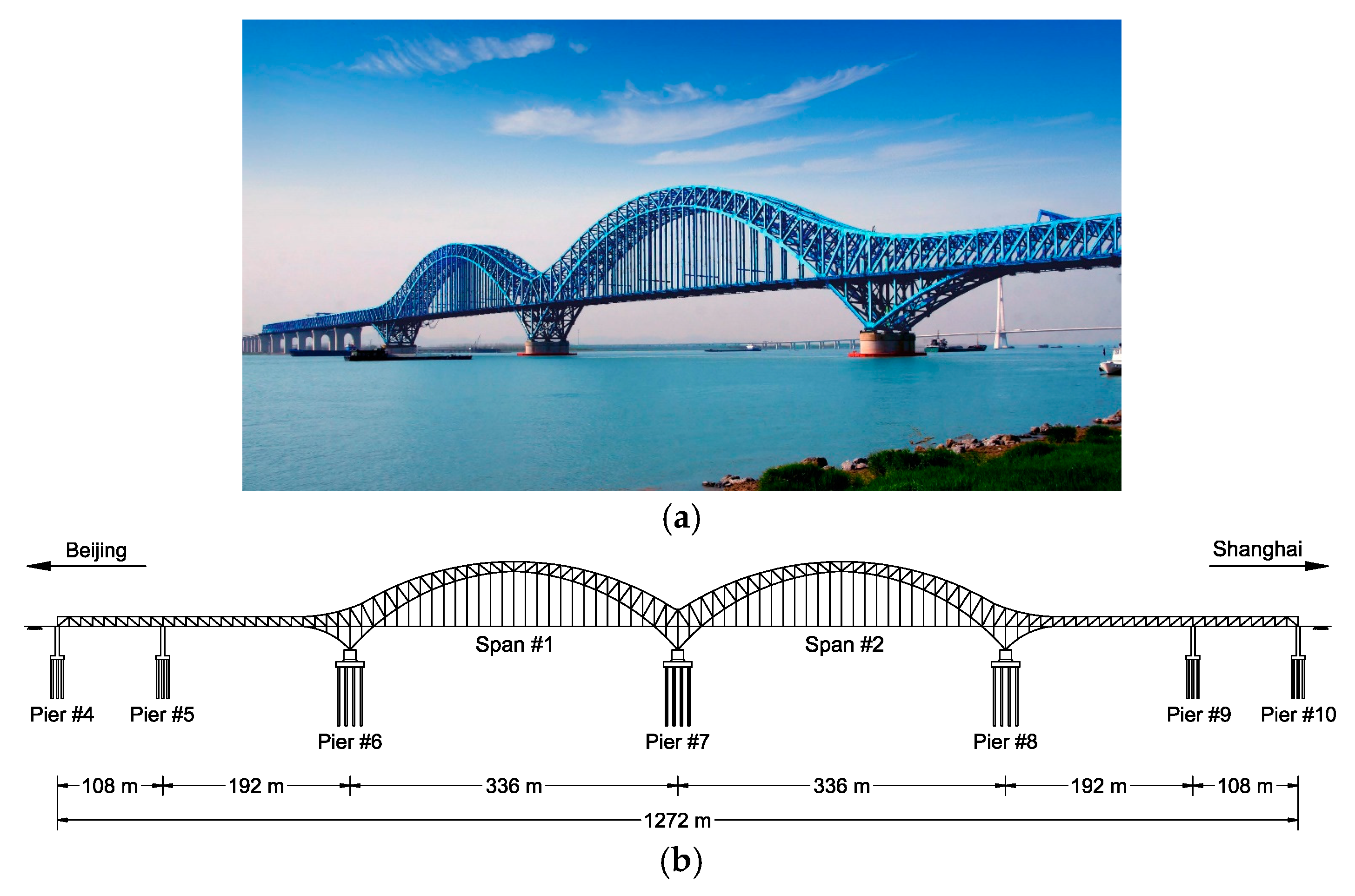
2.1. Dashengguan Bridge
2.2. Lupu Bridge
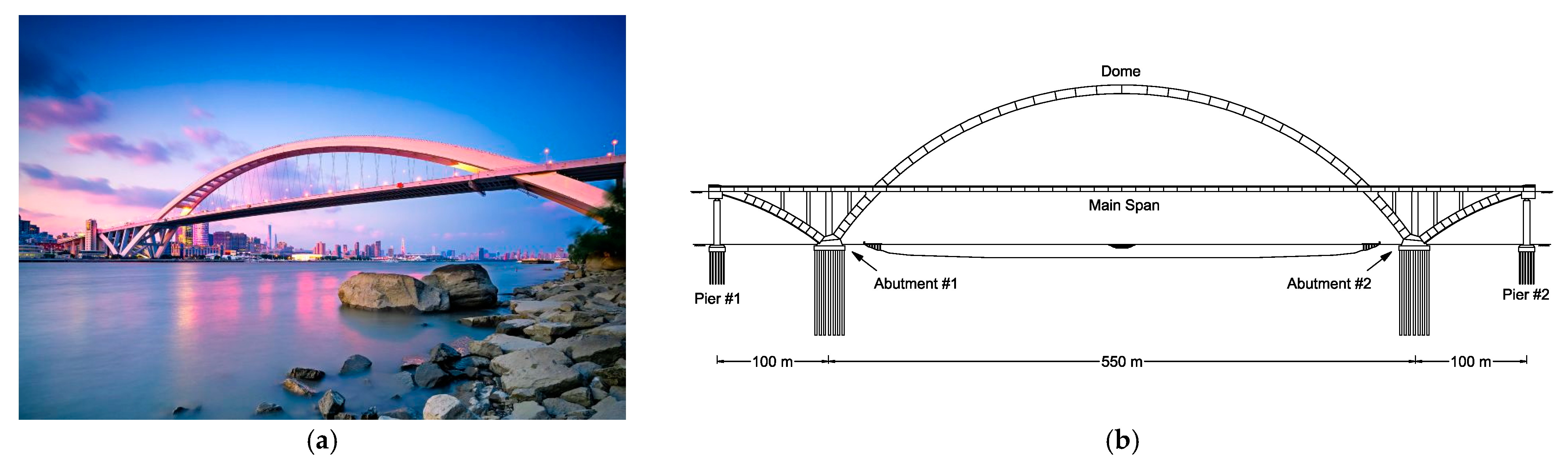
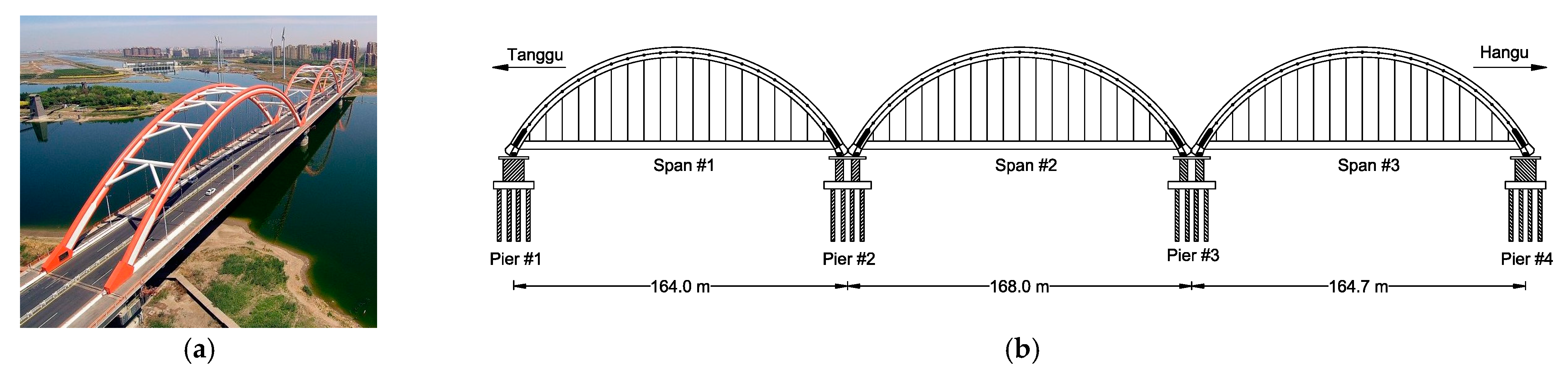
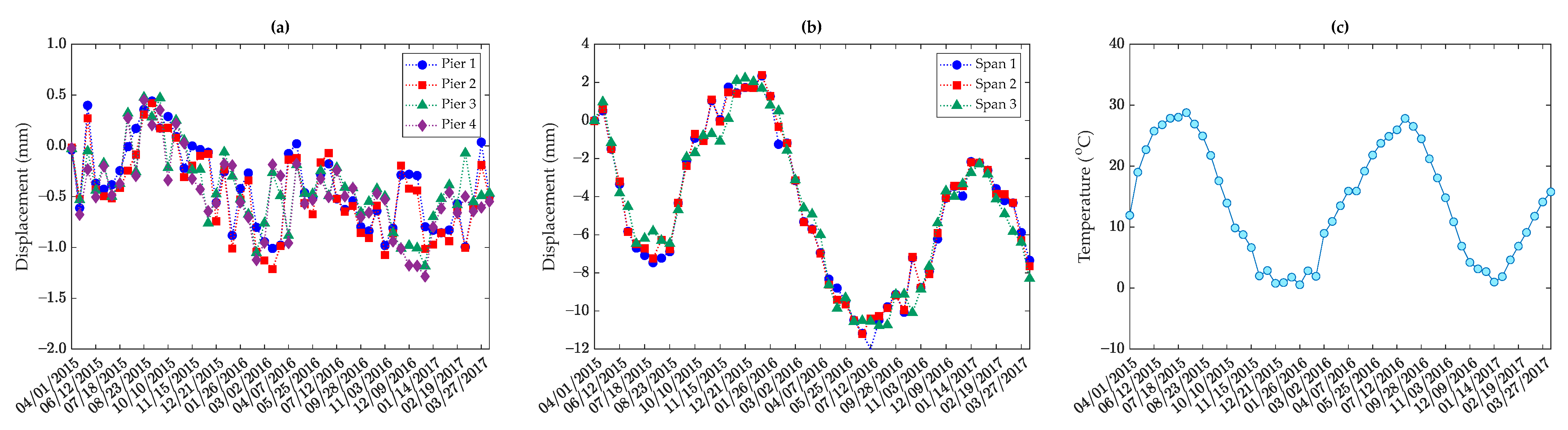
2.3. Rainbow Bridge
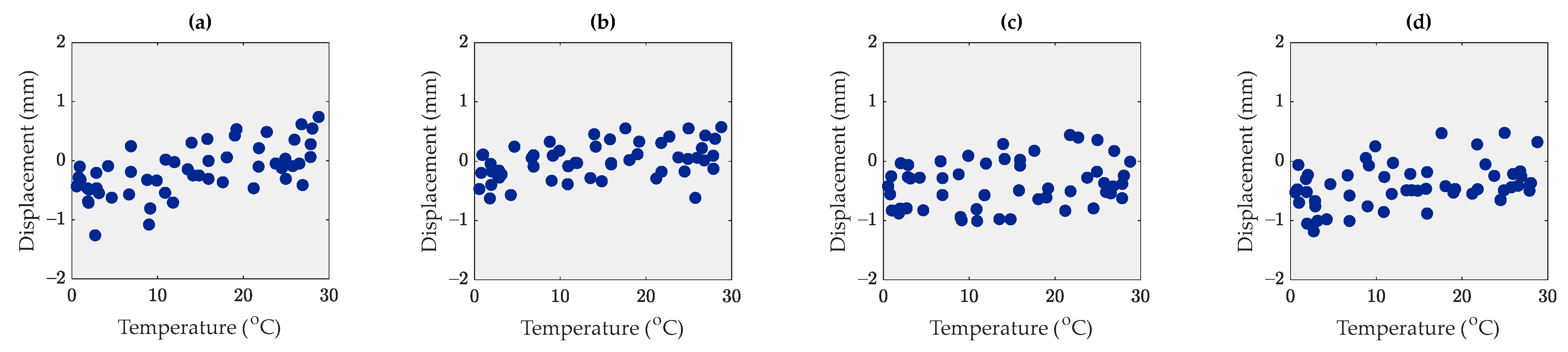
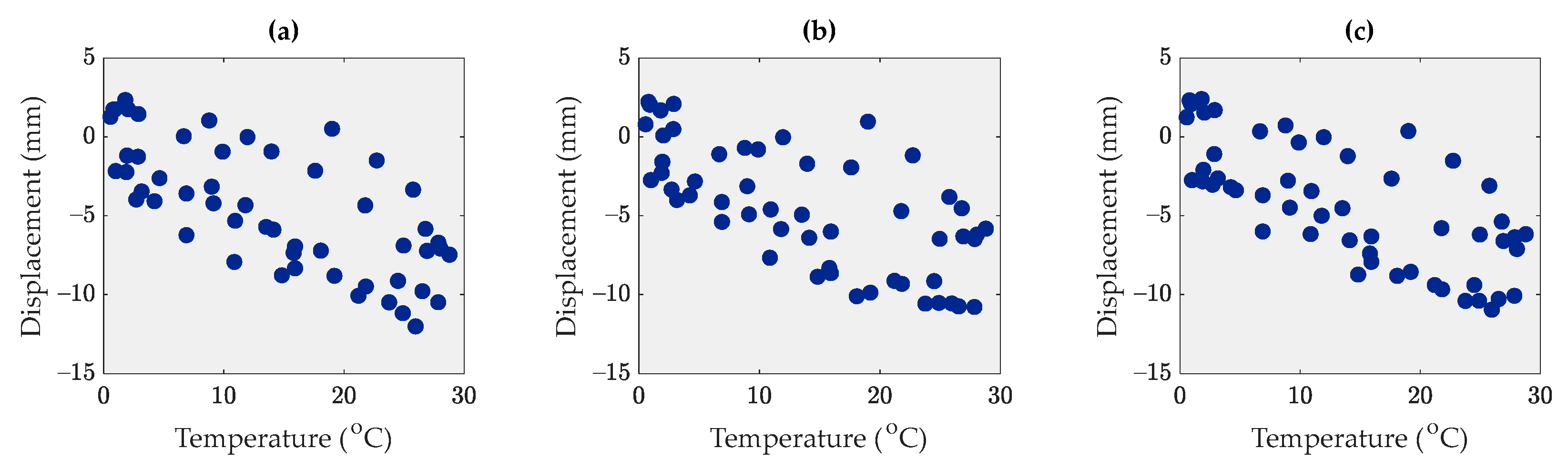
3. Correlation Analysis
4. Supervised Regression Models
4.1. Linear Regression Model
4.2. Gaussian Process Regression
4.3. Supervised Vector Regression
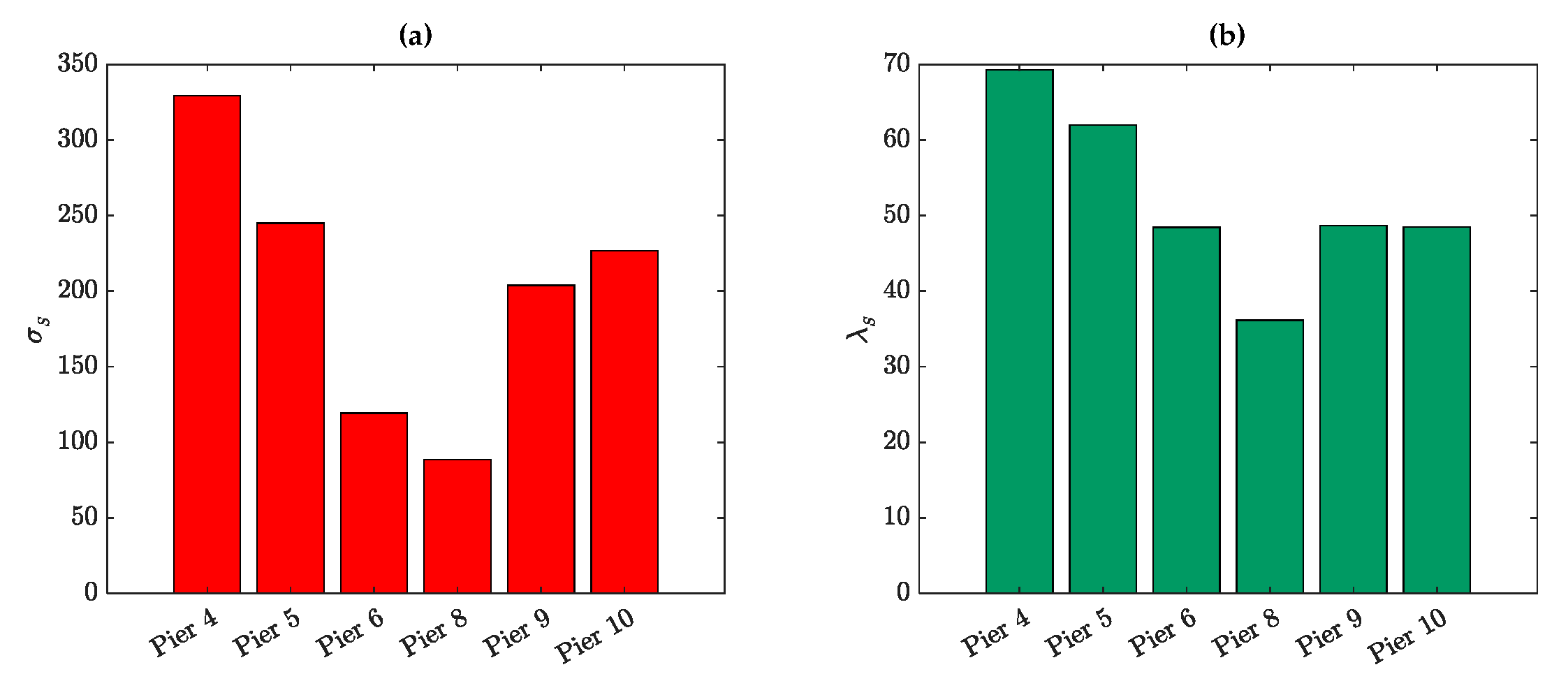
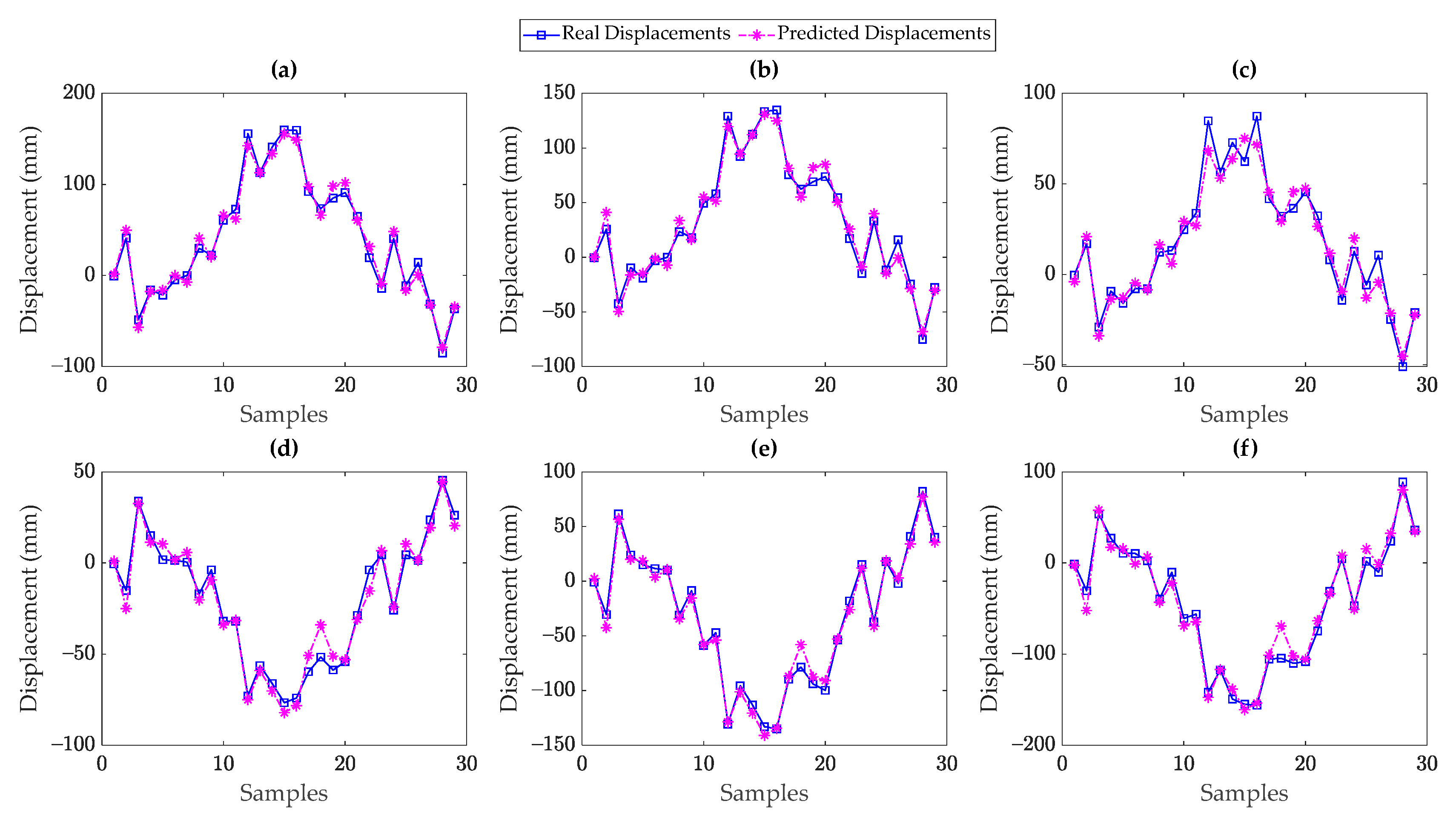
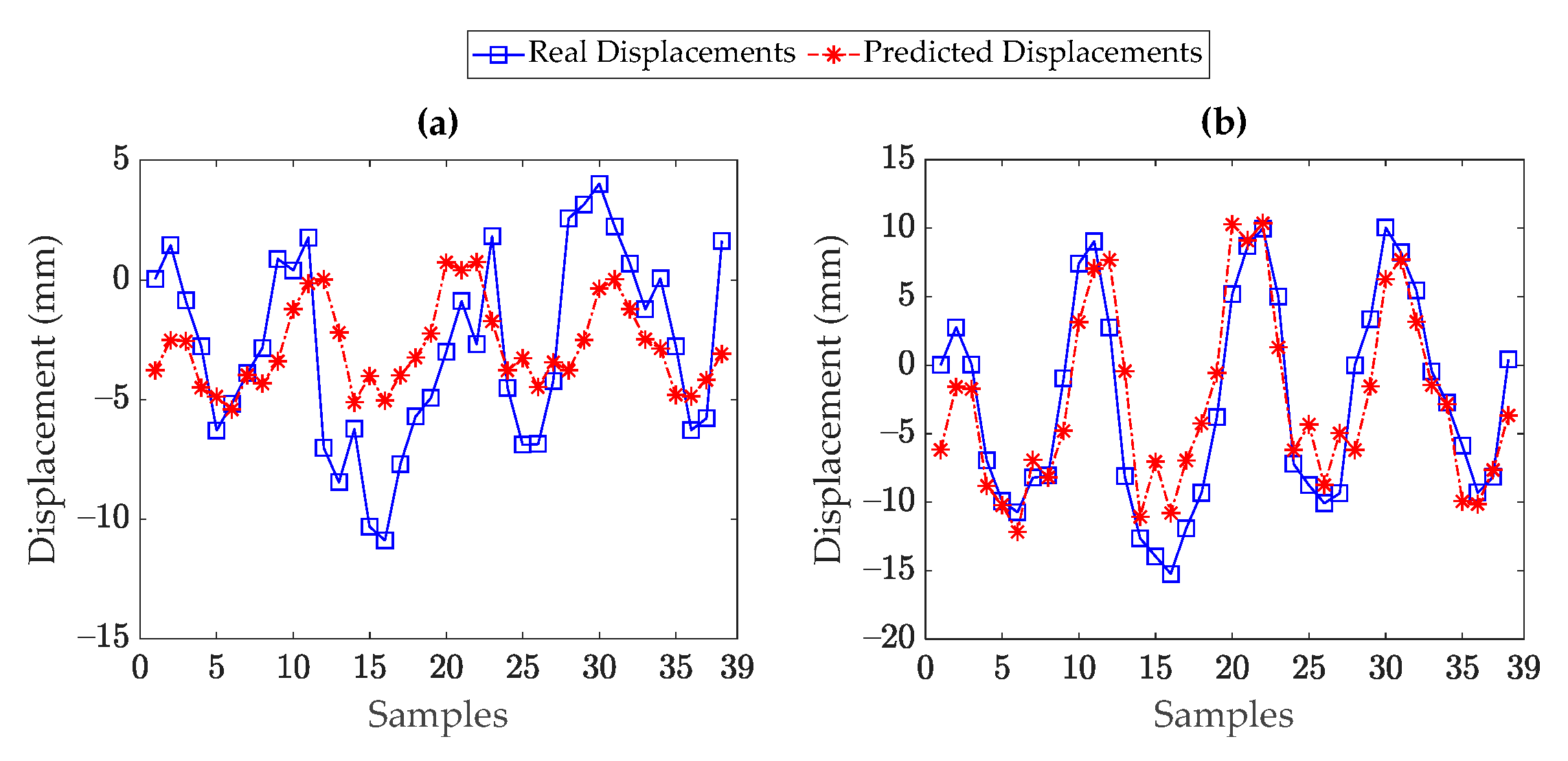
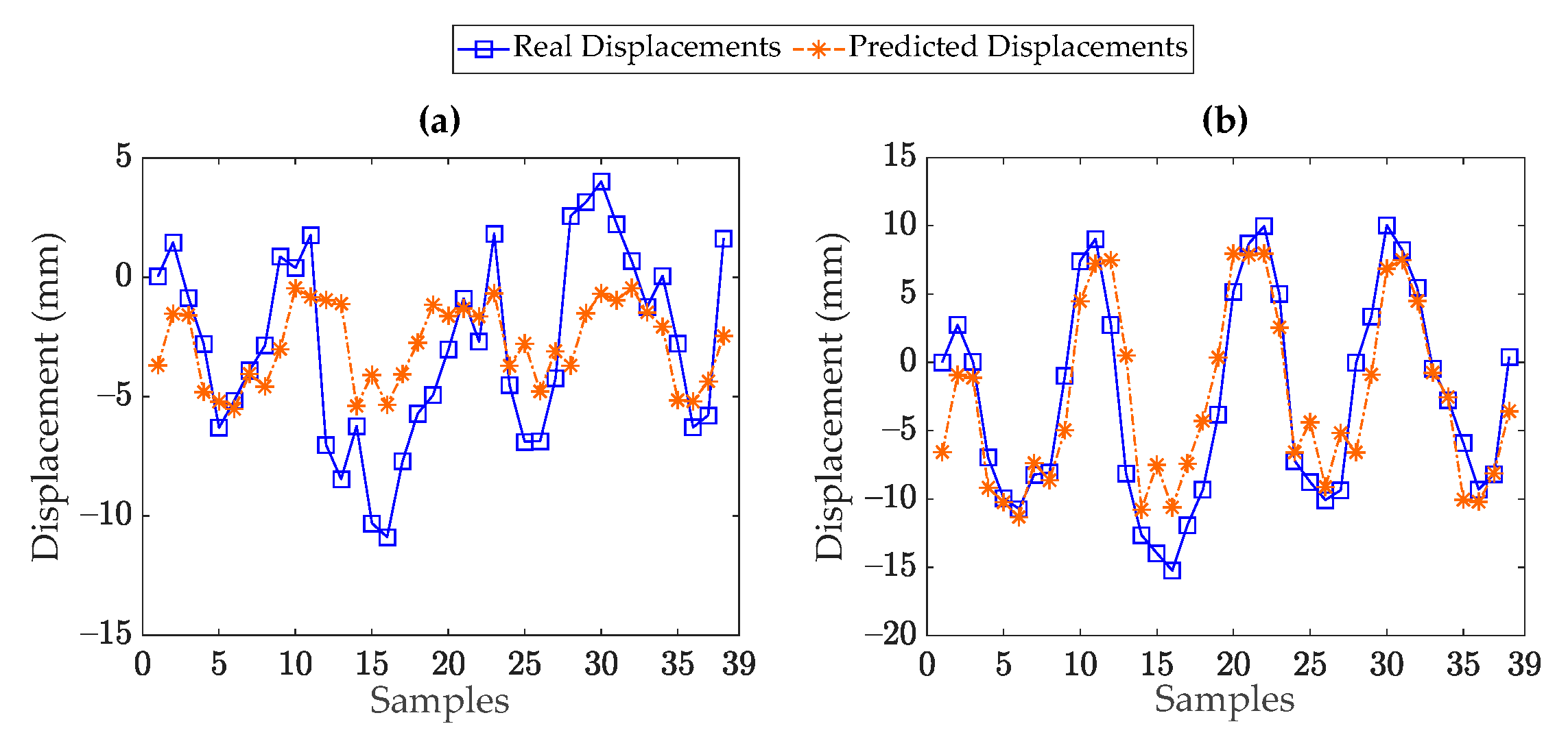
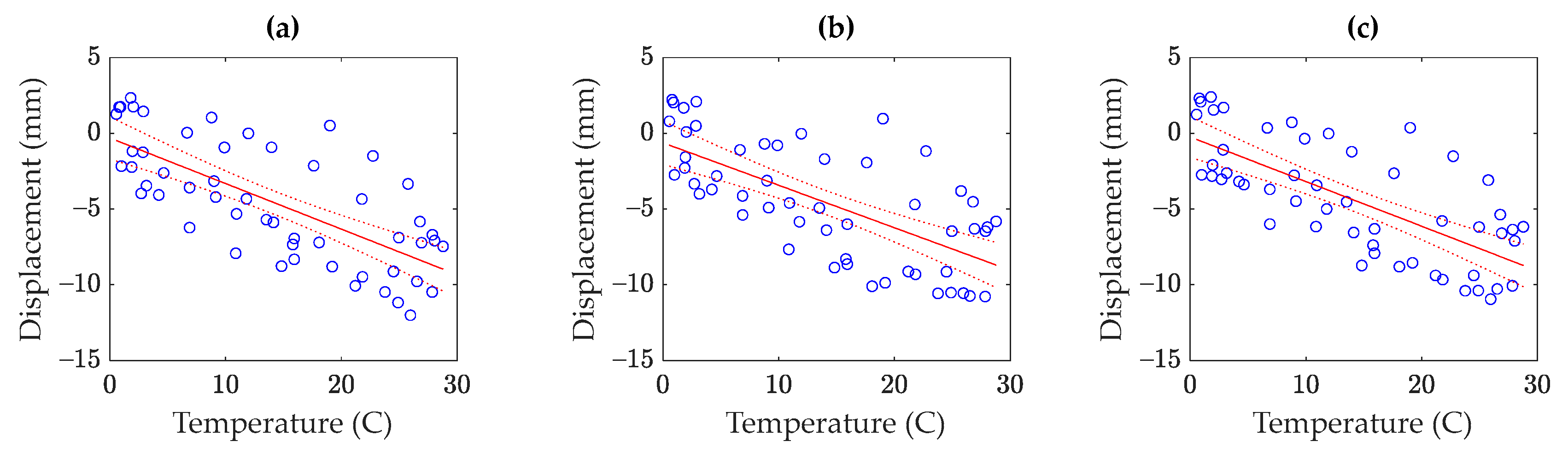
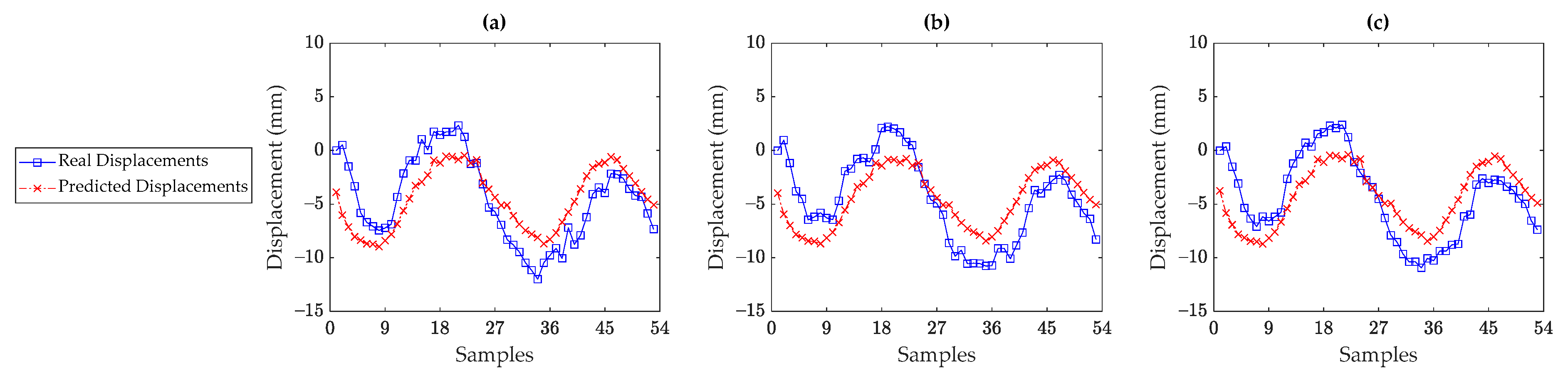
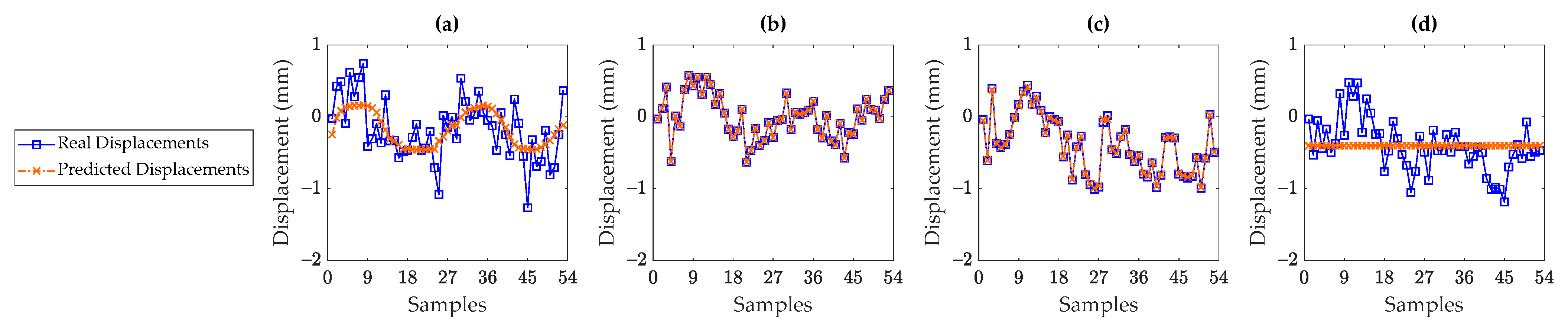
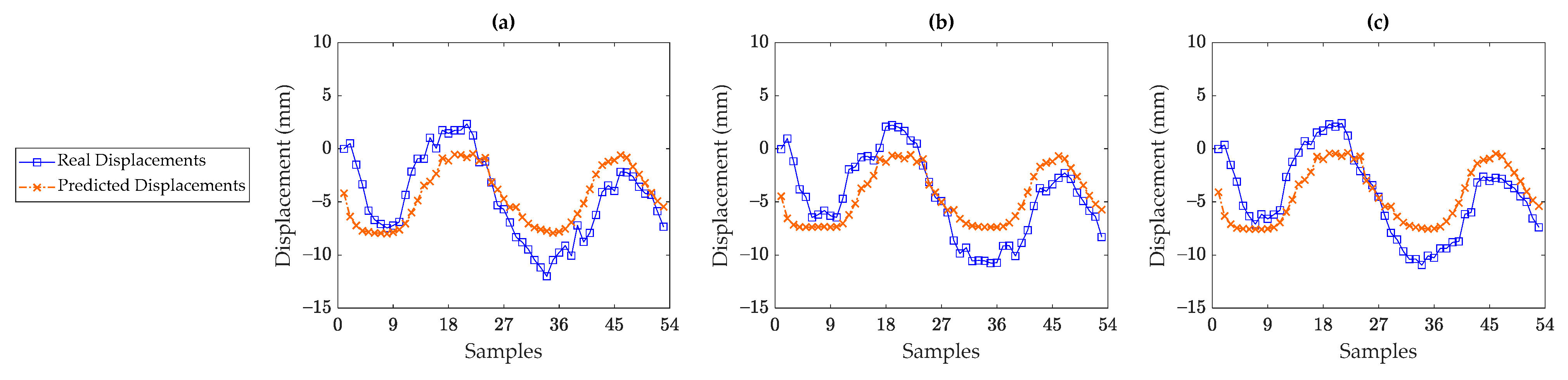
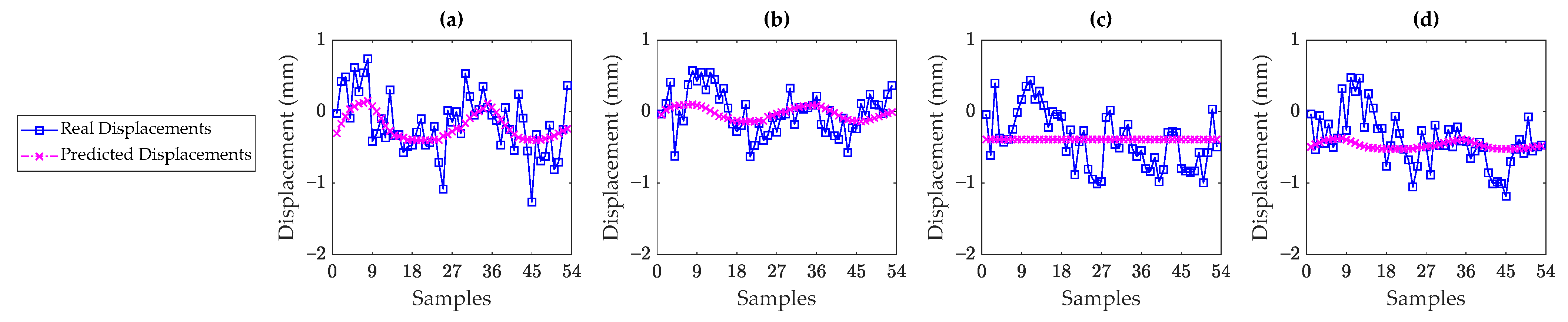
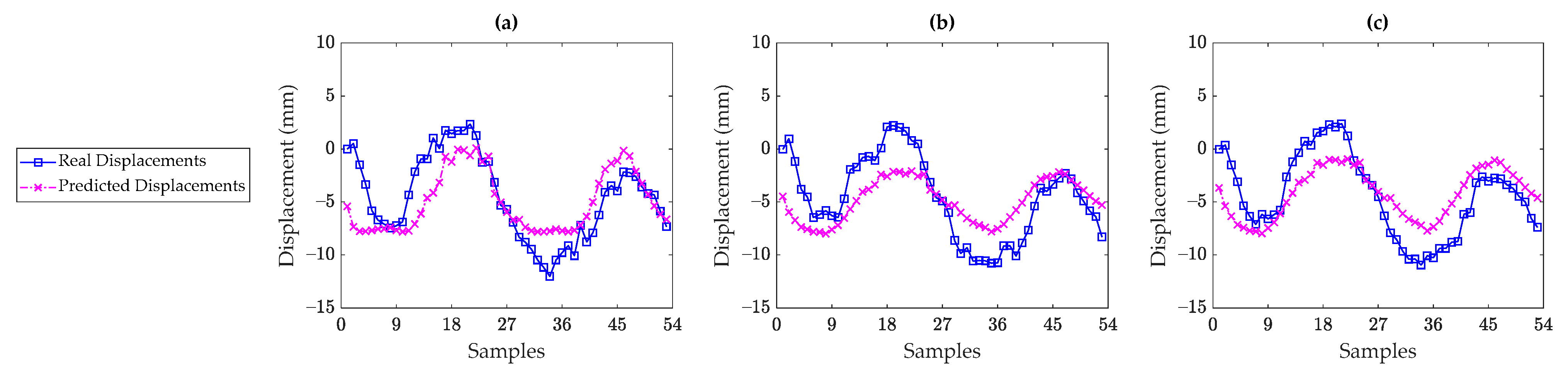
5. Results
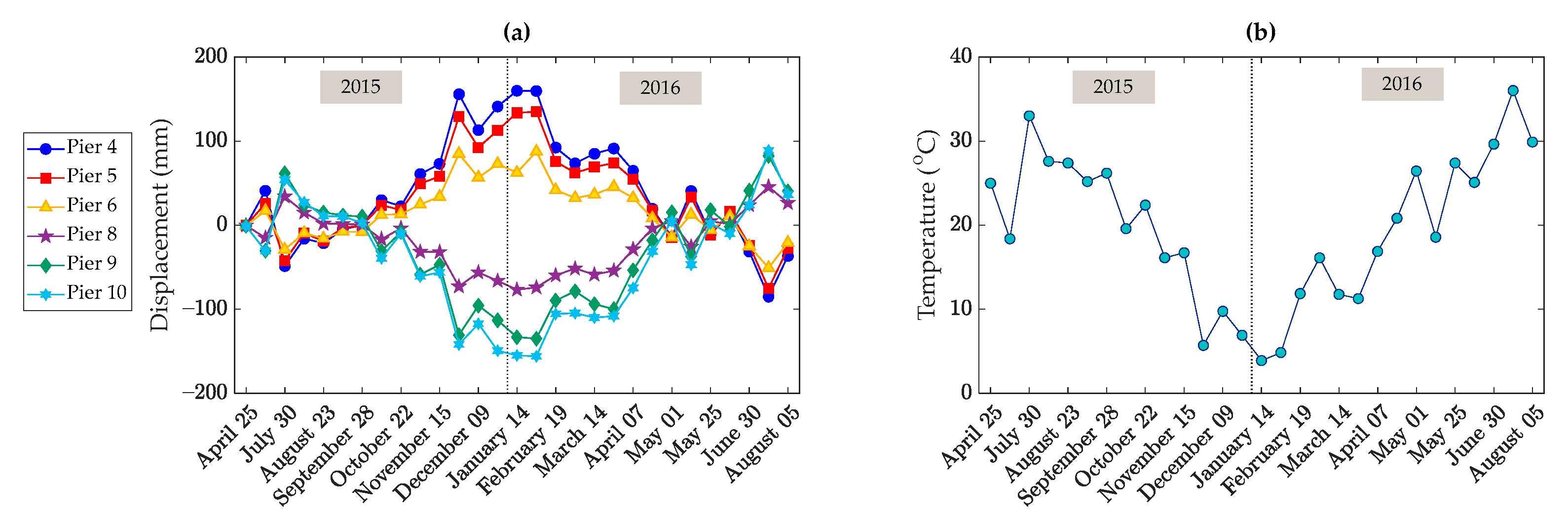
5.1. Dashengguan Bridge
5.2. Lupu Bridge
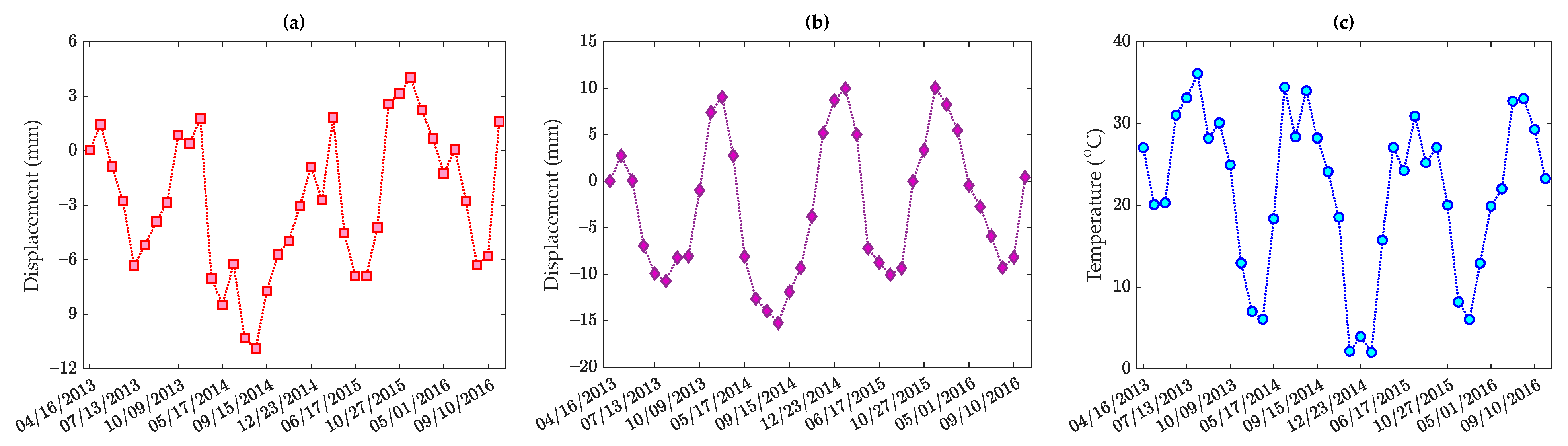
5.3. Rainbow Bridge
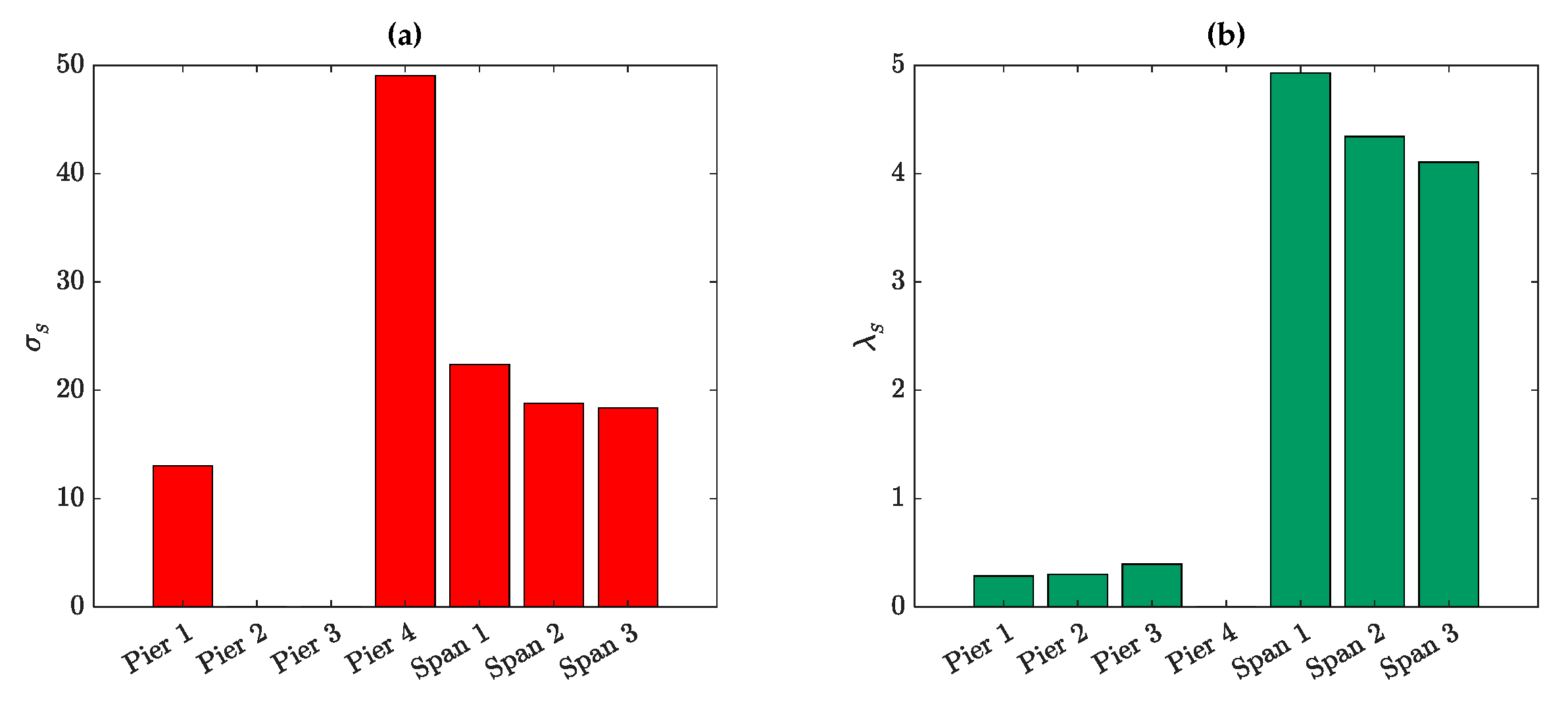
5.4. Discussions on Sufficiency of Environmental/Operational Sensors
6. Conclusions
- (1)
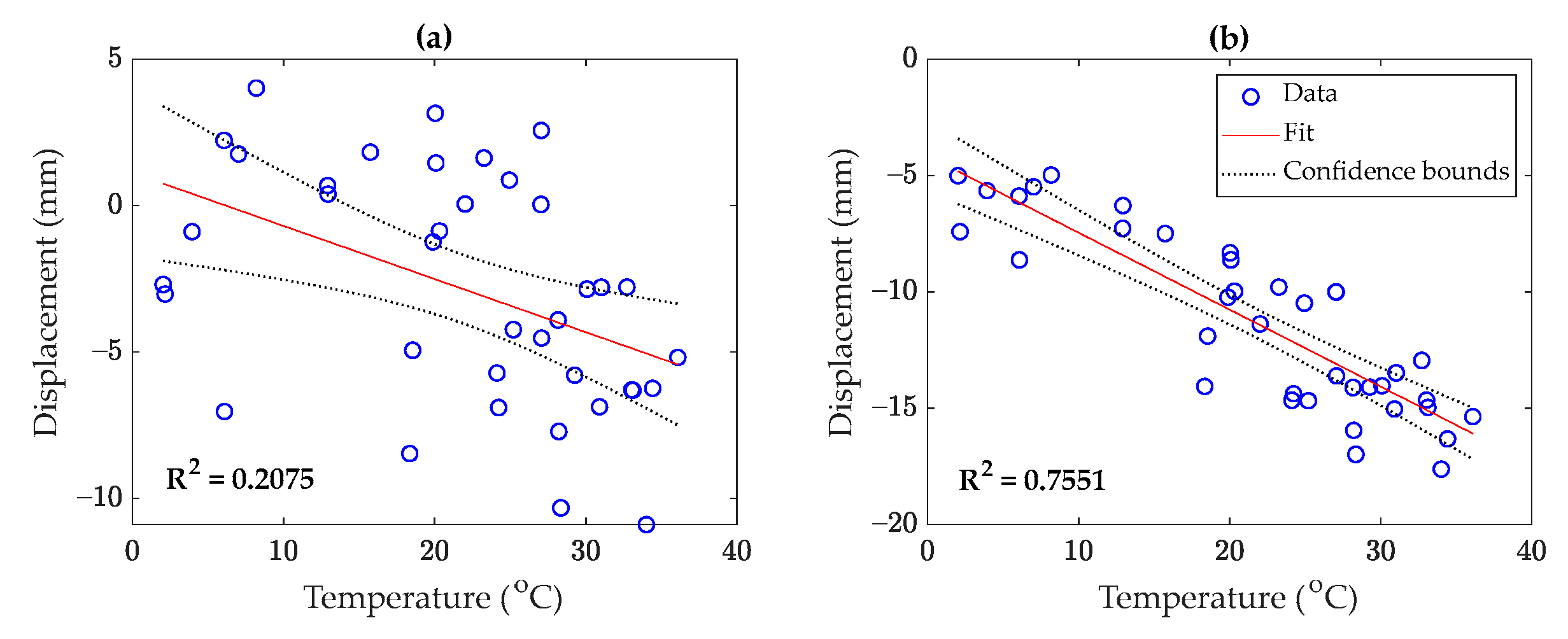
- When any environmental data are available, it is necessary to perform a correlation analysis to realize relationships between the structural responses. Based on the four correlation analysis methods investigated in this paper, the proposed MIC method provided more reasonable results than the other ones due to its consideration of both the linear and nonlinear correlation patterns.
- (2)
- In the problem of the Dashengguan Bridge, where the single measured environmental factor (temperature) and SAR-based displacement data had a strong linear correlation, Kendall’s correlation coefficient could not yield appropriate outputs as good as the MIC, Pearson’s, and Spearman’s correlation coefficient methods. Hence, this correlation measure can be disregarded in further applications.
- (3)
- The supervised regression techniques could perform well when there is a high correlation between the displacement and temperature data. These techniques failed in providing accurate and reliable results when the temperature and displacement data had a low correlation. This was most likely due to the fact that the other unmeasured environmental and/or operational conditions or even structural damage impacted the displacement data. Since such conditions were not incorporated into the supervised regression models, those could not properly predict the measured (real) displacement data.
- (4)
- The low correlation rates and poor prediction performances mean that the environmental/operational sensors (i.e., temperature sensors in this research) in a bridge structure are not sufficient, and one needs to consider further sensors for measuring other environmental and/or operational conditions such as humidity, wind speed and direction, traffic, etc. Moreover, it is important to investigate the possibility of existing any structural damage by visual inspection or tried-and-test techniques for early damage assessment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rizzo, P.; Enshaeian, A. Challenges in Bridge Health Monitoring: A Review. Sensors 2021, 21, 4336. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Jiang, W.; Meng, X.; Jiang, P.; Wang, K.; Xie, Y.; Ye, J. Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK. Remote Sens. 2018, 10, 364. [Google Scholar] [CrossRef]
- Gonen, S.; Erduran, E. A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sens. 2022, 14, 6054. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; De Michele, C. On continuous health monitoring of bridges under serious environmental variability by an innovative multi-task unsupervised learning method. Struct. Infrastruct. Eng. 2023, in press. [CrossRef]
- Daneshvar, M.H.; Sarmadi, H. Unsupervised learning-based damage assessment of full-scale civil structures under long-term and short-term monitoring. Eng. Struct. 2022, 256, 114059. [Google Scholar] [CrossRef]
- Gordan, M.; Sabbagh-Yazdi, S.-R.; Ismail, Z.; Ghaedi, K.; Carroll, P.; McCrum, D.; Samali, B. State-of-the-art review on advancements of data mining in structural health monitoring. Measurement 2022, 193, 110939. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-driven structural health monitoring and damage detection through deep learning: State-of-the-art review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Liu, J.; Wang, L.; Tao, T.; Wu, D.; Chen, R. A Review of Global Navigation Satellite System (GNSS)-Based Dynamic Monitoring Technologies for Structural Health Monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Machado, M.A.; Carvalho, M.S.; Vidal, C. Embedded Sensors for Structural Health Monitoring: Methodologies and Applications Review. Sensors 2022, 22, 8320. [Google Scholar] [CrossRef]
- Sony, S.; Laventure, S.; Sadhu, A. A literature review of next-generation smart sensing technology in structural health monitoring. Struct. Control Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Ullo, S.L.; Clemente, C.; Orlando, D. Perspectives on the Structural Health Monitoring of Bridges by Synthetic Aperture Radar. Remote Sens. 2020, 12, 3852. [Google Scholar] [CrossRef]
- Entezami, A.; Arslan, A.N.; De Michele, C.; Behkamal, B. Online hybrid learning methods for real-time structural health monitoring using remote sensing and small displacement data. Remote Sens. 2022, 14, 3357. [Google Scholar] [CrossRef]
- Cigna, F.; Lasaponara, R.; Masini, N.; Milillo, P.; Tapete, D. Persistent Scatterer Interferometry Processing of COSMO-SkyMed StripMap HIMAGE Time Series to Depict Deformation of the Historic Centre of Rome, Italy. Remote Sens. 2014, 6, 12593–12618. [Google Scholar] [CrossRef]
- Gama, F.F.; Mura, J.C.; Paradella, W.R.; de Oliveira, C.G. Deformations Prior to the Brumadinho Dam Collapse Revealed by Sentinel-1 InSAR Data Using SBAS and PSI Techniques. Remote Sens. 2020, 12, 3664. [Google Scholar] [CrossRef]
- Jänichen, J.; Schmullius, C.; Baade, J.; Last, K.; Bettzieche, V.; Dubois, C. Monitoring of Radial Deformations of a Gravity Dam Using Sentinel-1 Persistent Scatterer Interferometry. Remote Sens. 2022, 14, 1112. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; DeJong, M.J.; Perissin, D.; Milillo, G. Multi-Temporal InSAR Structural Damage Assessment: The London Crossrail Case Study. Remote Sens. 2018, 10, 287. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Pre-collapse space geodetic observations of critical infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sens. 2019, 11, 1403. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A. Structural Health Monitoring for Suspension Bridges: Interpretation of Field Measurements; Springer: Beijing, China, 2018. [Google Scholar]
- Ma, P.; Lin, H.; Wang, W.; Yu, H.; Chen, F.; Jiang, L.; Zhou, L.; Zhang, Z.; Shi, G.; Wang, J. Toward Fine Surveillance: A review of multitemporal interferometric synthetic aperture radar for infrastructure health monitoring. IEEE Geosci. Remote Sens. Mag. 2022, 10, 207–230. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, B.; Weng, S.; Ni, Y.-Q.; Xu, Y.-L. Temperature effect on vibration properties of civil structures: A literature review and case studies. J. Civ. Struct. Health Monit. 2012, 2, 29–46. [Google Scholar] [CrossRef]
- Han, Q.; Ma, Q.; Xu, J.; Liu, M. Structural health monitoring research under varying temperature condition: A review. J. Civ. Struct. Health Monit. 2020, 11, 149–173. [Google Scholar] [CrossRef]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Regression models for structural health monitoring of welded bridge joints based on temperature, traffic and strain measurements. Struct. Health Monit. 2015, 14, 648–662. [Google Scholar] [CrossRef]
- Maes, K.; Van Meerbeeck, L.; Reynders, E.P.B.; Lombaert, G. Validation of vibration-based structural health monitoring on retrofitted railway bridge KW51. Mech. Syst. Sig. Process. 2022, 165, 108380. [Google Scholar] [CrossRef]
- Laory, I.; Trinh, T.N.; Smith, I.F.C.; Brownjohn, J.M.W. Methodologies for predicting natural frequency variation of a suspension bridge. Eng. Struct. 2014, 80, 211–221. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, D.-H.; Yi, T.-H.; Zhang, G.-H.; Han, J.-G. Eliminating environmental and operational effects on structural modal frequency: A comprehensive review. Struct. Control Health Monit. 2022, 29, e3073. [Google Scholar] [CrossRef]
- Dervilis, N.; Worden, K.; Cross, E.J. On robust regression analysis as a means of exploring environmental and operational conditions for SHM data. J. Sound Vib. 2015, 347, 279–296. [Google Scholar] [CrossRef]
- Roberts, C.; Cava, D.G.; Avendaño-Valencia, L.D. Addressing practicalities in multivariate nonlinear regression for mitigating environmental and operational variations. Struct. Health Monit. 2022, 22, 1237–1255. [Google Scholar] [CrossRef]
- Entezami, A.; Mariani, S.; Shariatmadar, H. Damage detection in largely unobserved structures under varying environmental conditions: An autoregressive spectrum and multi-level machine learning methodology. Sensors 2022, 22, 1400. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; De Michele, C. Probabilistic data self-clustering based on semi-parametric extreme value theory for structural health monitoring. Mech. Syst. Sig. Process. 2023, 187, 109976. [Google Scholar] [CrossRef]
- Daneshvar, M.H.; Sarmadi, H.; Yuen, K.-V. A locally unsupervised hybrid learning method for removing environmental effects under different measurement periods. Measurement 2023, 208, 112465. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B. Long-term health monitoring of concrete and steel bridges under large and missing data by unsupervised meta learning. Eng. Struct. 2023, 279, 115616. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Magalhães, F. Unsupervised data normalization for continuous dynamic monitoring by an innovative hybrid feature weighting-selection algorithm and natural nearest neighbor searching. Struct. Health Monit. 2023, in press. [CrossRef]
- Sarmadi, H.; Yuen, K.-V. Structural health monitoring by a novel probabilistic machine learning method based on extreme value theory and mixture quantile modeling. Mech. Syst. Sig. Process. 2022, 173, 109049. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Ren, Y.; Zhao, D.-Y.; Yang, J.; Zhang, D.-Y. Modeling and Separation of Thermal Effects from Cable-Stayed Bridge Response. J. Bridge Eng. 2019, 24, 04019028. [Google Scholar] [CrossRef]
- Teng, J.; Tang, D.-H.; Hu, W.-H.; Lu, W.; Feng, Z.-W.; Ao, C.-F.; Liao, M.-H. Mechanism of the effect of temperature on frequency based on long-term monitoring of an arch bridge. Struct. Health Monit. 2021, 20, 1716–1737. [Google Scholar] [CrossRef]
- Murphy, B.; Yarnold, M. Temperature-driven structural identification of a steel girder bridge with an integral abutment. Eng. Struct. 2018, 155, 209–221. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, L. Effects of environmental and operational actions on the modal frequency variations of a sea-crossing bridge: A periodicity perspective. Mech. Syst. Sig. Process. 2019, 131, 505–523. [Google Scholar] [CrossRef]
- Mao, J.-X.; Wang, H.; Feng, D.-M.; Tao, T.-Y.; Zheng, W.-Z. Investigation of dynamic properties of long-span cable-stayed bridges based on one-year monitoring data under normal operating condition. Struct. Control Health Monit. 2018, 25, e2146. [Google Scholar] [CrossRef]
- Yang, D.-H.; Yi, T.-H.; Li, H.-N.; Zhang, Y.-F. Monitoring and analysis of thermal effect on tower displacement in cable-stayed bridge. Measurement 2018, 115, 249–257. [Google Scholar] [CrossRef]
- Xia, Q.; Zhang, J.; Tian, Y.; Zhang, Y. Experimental Study of Thermal Effects on a Long-Span Suspension Bridge. J. Bridge Eng. 2017, 22, 04017034. [Google Scholar] [CrossRef]
- Moser, P.; Moaveni, B. Environmental effects on the identified natural frequencies of the Dowling Hall Footbridge. Mech. Syst. Sig. Process. 2011, 25, 2336–2357. [Google Scholar] [CrossRef]
- Hu, W.H.; Cunha, Á.; Caetano, E.; Rohrmann, R.; Said, S.; Teng, J. Comparison of different statistical approaches for removing environmental/operational effects for massive data continuously collected from footbridges. Struct. Control Health Monit. 2016, 24, e1955. [Google Scholar] [CrossRef]
- Qin, Y.; Li, Y.; Liu, G. Separation of the Temperature Effect on Structure Responses via LSTM-Particle Filter Method Considering Outlier from Remote Cloud Platforms. Remote Sens. 2022, 14, 4629. [Google Scholar] [CrossRef]
- Jang, J.; Smyth, A.W. Data-driven models for temperature distribution effects on natural frequencies and thermal prestress modeling. Struct. Control Health Monit. 2020, 27, e2489. [Google Scholar] [CrossRef]
- Huang, Q.; Crosetto, M.; Monserrat, O.; Crippa, B. Displacement monitoring and modelling of a high-speed railway bridge using C-band Sentinel-1 data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 204–211. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, L.; Yang, M.; Luo, H.; Liao, M.; Ding, X. Mapping surface deformation and thermal dilation of arch bridges by structure-driven multi-temporal DInSAR analysis. Remote Sens. Environ. 2018, 216, 71–90. [Google Scholar] [CrossRef]
- Li, S.; Li, H.; Liu, Y.; Lan, C.; Zhou, W.; Ou, J. SMC structural health monitoring benchmark problem using monitored data from an actual cable-stayed bridge. Struct. Control Health Monit. 2014, 21, 156–172. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, X.W.; Guo, Y. Data set from wind, temperature, humidity and cable acceleration monitoring of the Jiashao bridge. J. Civ. Struct. Health Monit. 2023, 13, 579–589. [Google Scholar] [CrossRef]
- Fenerci, A.; Kvåle, K.A.; Petersen, Ø.W.; Rønnquist, A.; Øiseth, O. Data Set from Long-Term Wind and Acceleration Monitoring of the Hardanger Bridge. J. Struct. Eng. 2021, 147, 04721003. [Google Scholar] [CrossRef]
- Niu, Y.; Ye, Y.; Zhao, W.; Duan, Y.; Shu, J. Identifying Modal Parameters of a Multispan Bridge Based on High-Rate GNSS-RTK Measurement Using the CEEMD-RDT Approach. J. Bridge Eng. 2021, 26, 04021049. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.; Rosso, R. Extremes in Nature: An Approach Using Copulas; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Pisner, D.A.; Schnyer, D.M. Support vector machine. In Machine Learning; Mechelli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 101–121. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
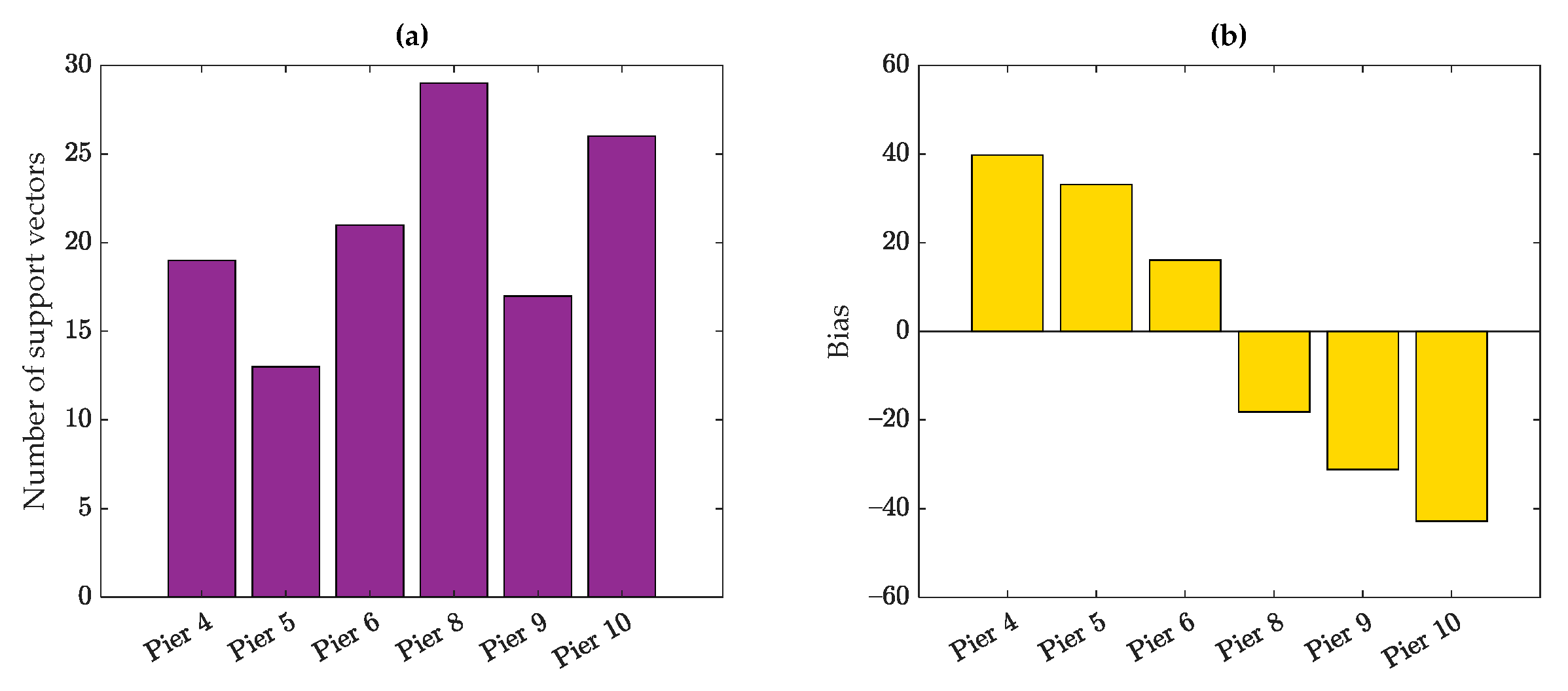






| Pier No. | MIC | Correlation Coefficient Metrics | ||
|---|---|---|---|---|
| Pearson | Spearman | Kendall | ||
| 4 | 1.00 | −0.9928 | −0.9931 | −0.9507 |
| 5 | 1.00 | −0.9899 | −0.9896 | −0.9310 |
| 6 | 1.00 | −0.9776 | −0.9822 | −0.9064 |
| 8 | 1.00 | 0.9850 | 0.9901 | 0.9359 |
| 9 | 1.00 | 0.9943 | 0.9940 | 0.9507 |
| 10 | 1.00 | 0.9877 | 0.9876 | 0.9211 |
| Component | Correlation Coefficient Metrics | |||
|---|---|---|---|---|
| MIC | Pearson | Spearman | Kendall | |
| Dome | 0.56 | −0.4555 | −0.4925 | −0.3285 |
| Span | 0.90 | −0.8689 | −0.8483 | −0.6557 |
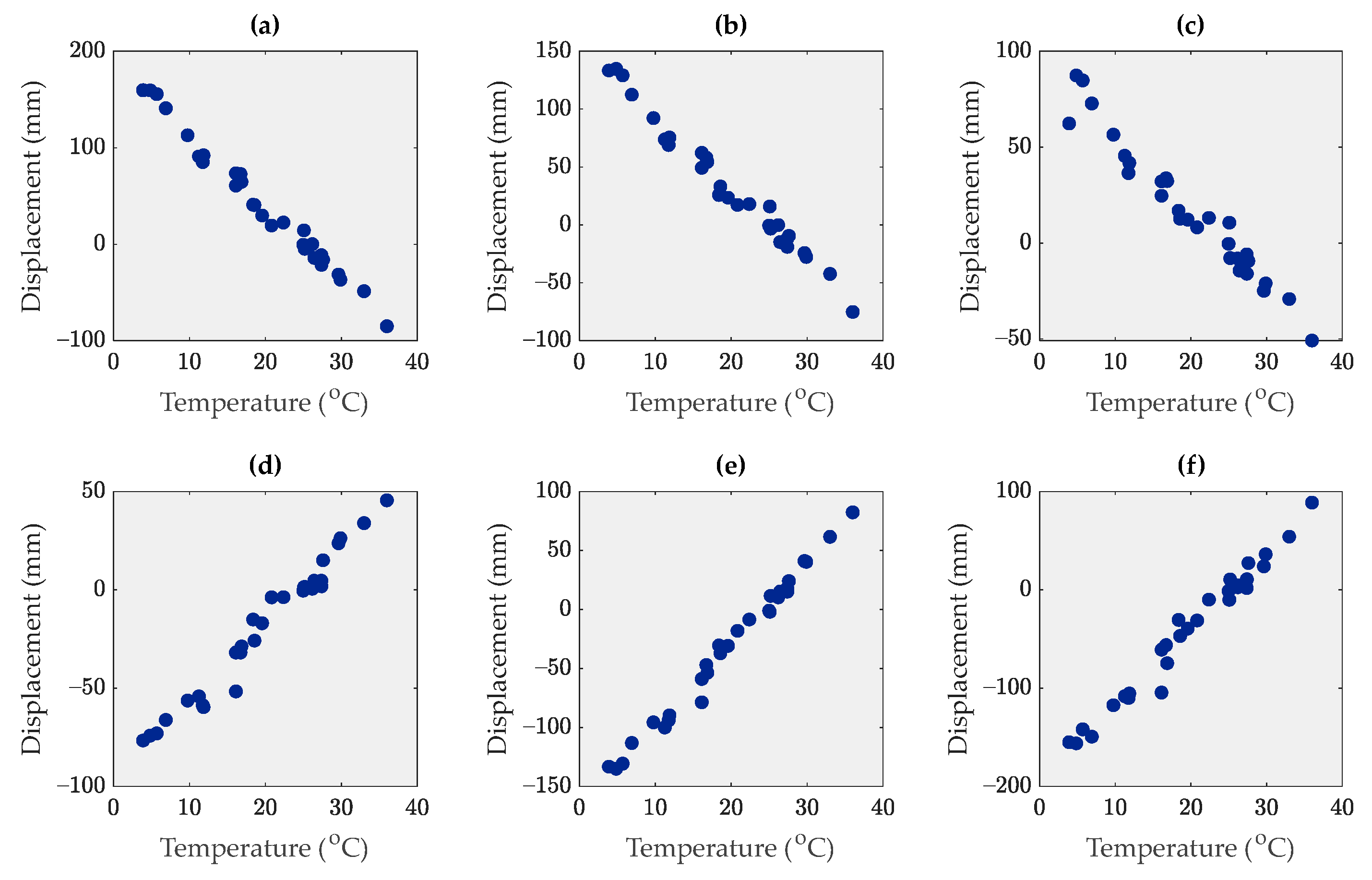
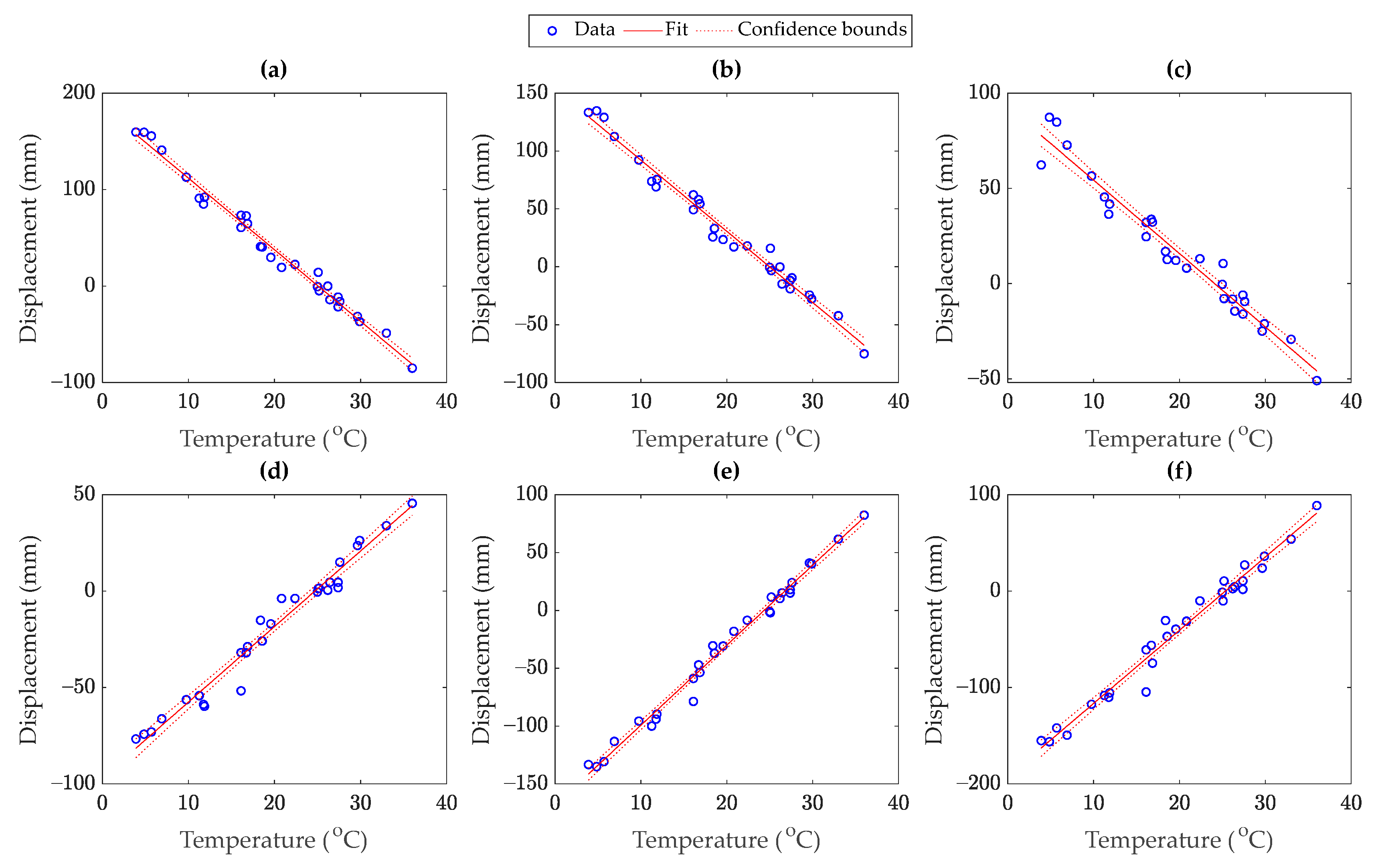
| Elements | MIC | Correlation Coefficient Metrics | ||
|---|---|---|---|---|
| Pearson | Spearman | Kendall | ||
| Pier 1 | 0.72 | 0.6081 | 0.6289 | 0.4296 |
| Pier 2 | 0.61 | 0.4194 | 0.4151 | 0.2946 |
| Pier 3 | 0.33 | 0.2521 | 0.2439 | 0.1625 |
| Pier 4 | 0.39 | 0.3745 | 0.3612 | 0.2481 |
| Span 1 | 0.75 | −0.7140 | −0.7184 | −0.5326 |
| Span 2 | 0.70 | −0.6793 | −0.7005 | −0.5195 |
| Span 3 | 0.74 | −0.7165 | −0.7281 | −0.5442 |
| Bridge Name | Elements | Correlation Rate | Prediction Accuracy | Decision | |
|---|---|---|---|---|---|
| Linear | Nonlinear | ||||
| Dashengguan | Piers 4–6 & 8–10 | High | High | High | Sufficient |
| Lupu | Dome | Low | Low | Low | Insufficient |
| Span | High | High | High | Sufficient | |
| Rainbow | Pier 1 | Low | Low | Low | Insufficient |
| Pier 2 | Low | Low | High * | Sufficient * | |
| Pier 3 | Low | Low | High * | Sufficient * | |
| Pier 4 | Low | Low | Low | Insufficient | |
| Span 1 | High | High | Low | Insufficient ** | |
| Span 2 | High | High | Low | Insufficient ** | |
| Span 3 | High | High | Low | Insufficient ** | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behkamal, B.; Entezami, A.; De Michele, C.; Arslan, A.N. Investigation of Temperature Effects into Long-Span Bridges via Hybrid Sensing and Supervised Regression Models. Remote Sens. 2023, 15, 3503. https://doi.org/10.3390/rs15143503
Behkamal B, Entezami A, De Michele C, Arslan AN. Investigation of Temperature Effects into Long-Span Bridges via Hybrid Sensing and Supervised Regression Models. Remote Sensing. 2023; 15(14):3503. https://doi.org/10.3390/rs15143503
Chicago/Turabian StyleBehkamal, Bahareh, Alireza Entezami, Carlo De Michele, and Ali Nadir Arslan. 2023. "Investigation of Temperature Effects into Long-Span Bridges via Hybrid Sensing and Supervised Regression Models" Remote Sensing 15, no. 14: 3503. https://doi.org/10.3390/rs15143503
APA StyleBehkamal, B., Entezami, A., De Michele, C., & Arslan, A. N. (2023). Investigation of Temperature Effects into Long-Span Bridges via Hybrid Sensing and Supervised Regression Models. Remote Sensing, 15(14), 3503. https://doi.org/10.3390/rs15143503









