A Novel Framework for Stratified-Coupled BLS Tree Trunk Detection and DBH Estimation in Forests (BSTDF) Using Deep Learning and Optimization Adaptive Algorithm
Abstract
1. Introduction
- (1)
- In light of the substantial volume of point cloud data in forest scenarios, we introduced a novel approach to constructing a deep learning tree trunk detection dataset, which is predicated on hierarchical coupling. This approach effectively curtails the data volume necessary during the tree trunk detection process;
- (2)
- To rectify the issue of uneven class accuracy in point cloud segmentation within the RandLA-Net model for tree trunk detection scenarios, we introduced an enhanced RandLA-Net semantic segmentation model with dual modules (WCF and CACL). By increasing the model’s attention towards the target classes and employing more flexible learning strategies, we improved the segmentation accuracy for the tree trunk class, ultimately leading to an elevated detection rate;
- (3)
- We enhanced the RANCAC algorithm by implementing an adaptive approach and a least squares optimization algorithm. These meticulously devised strategies served to optimize the fitting model parameters and boost the convergence of model error, thereby significantly elevating the accuracy of the DBH fitting within forest scenarios;
- (4)
- Lastly, having conducted a comparative analysis of the precision of tree trunk detection and DBH fitting at different MLS scanning distance levels, we proposed a recommended distance for MLS scanning, which offers a balance between data quality and scanning efficiency.
2. Materials and Methods
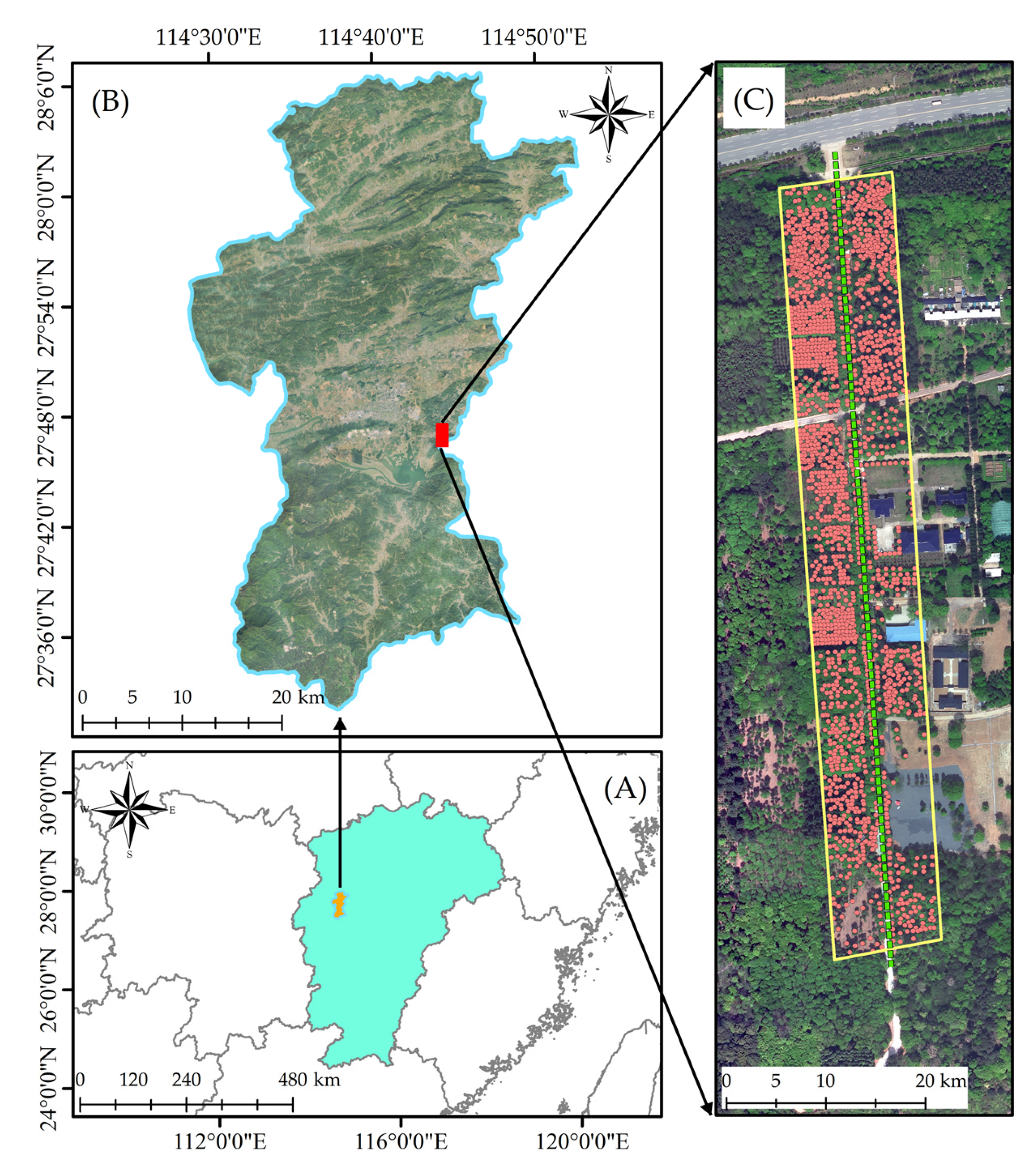
2.1. Study Area
2.2. Data
2.2.1. Field Survey Data
2.2.2. BLS Data
2.3. Methods
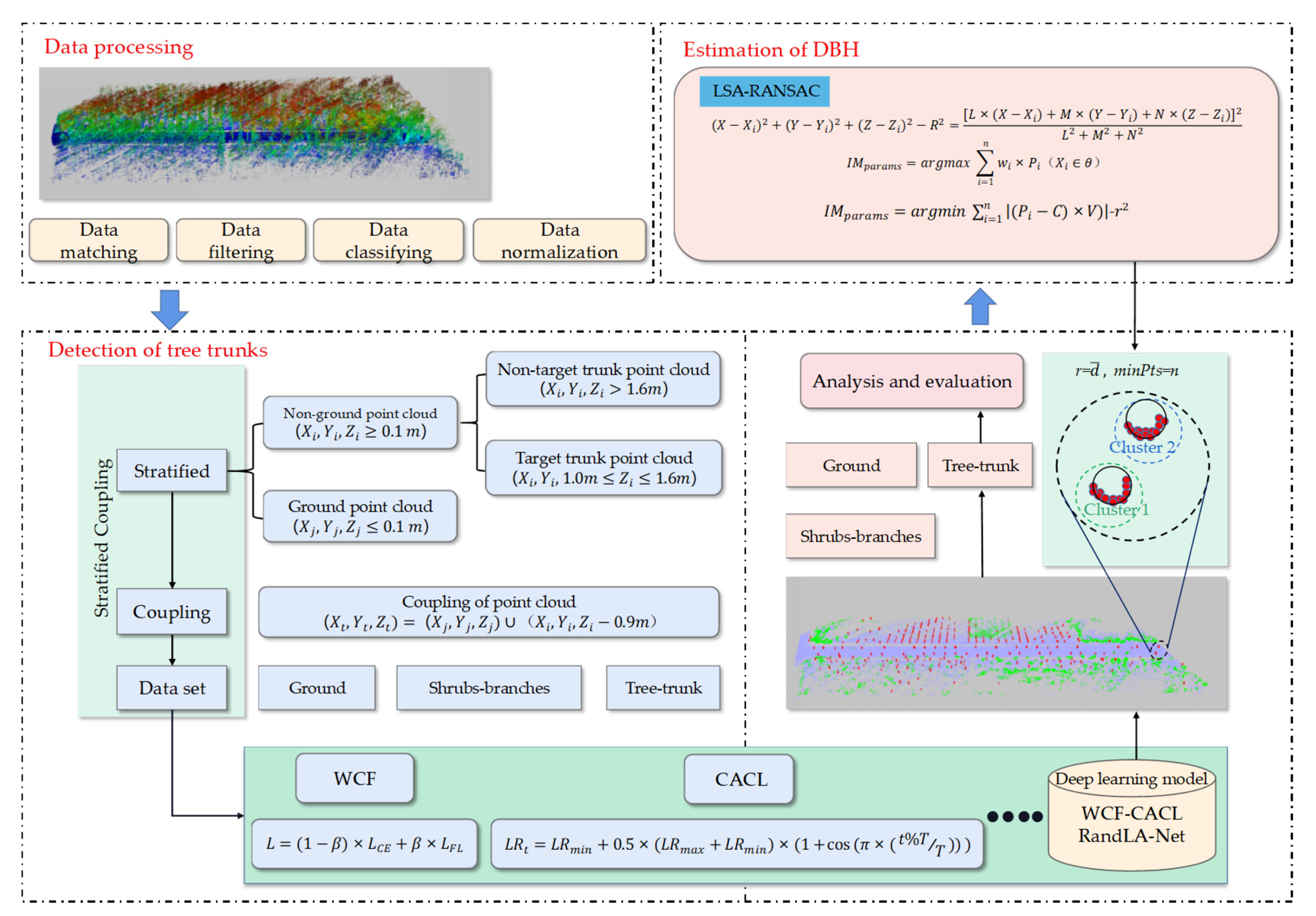
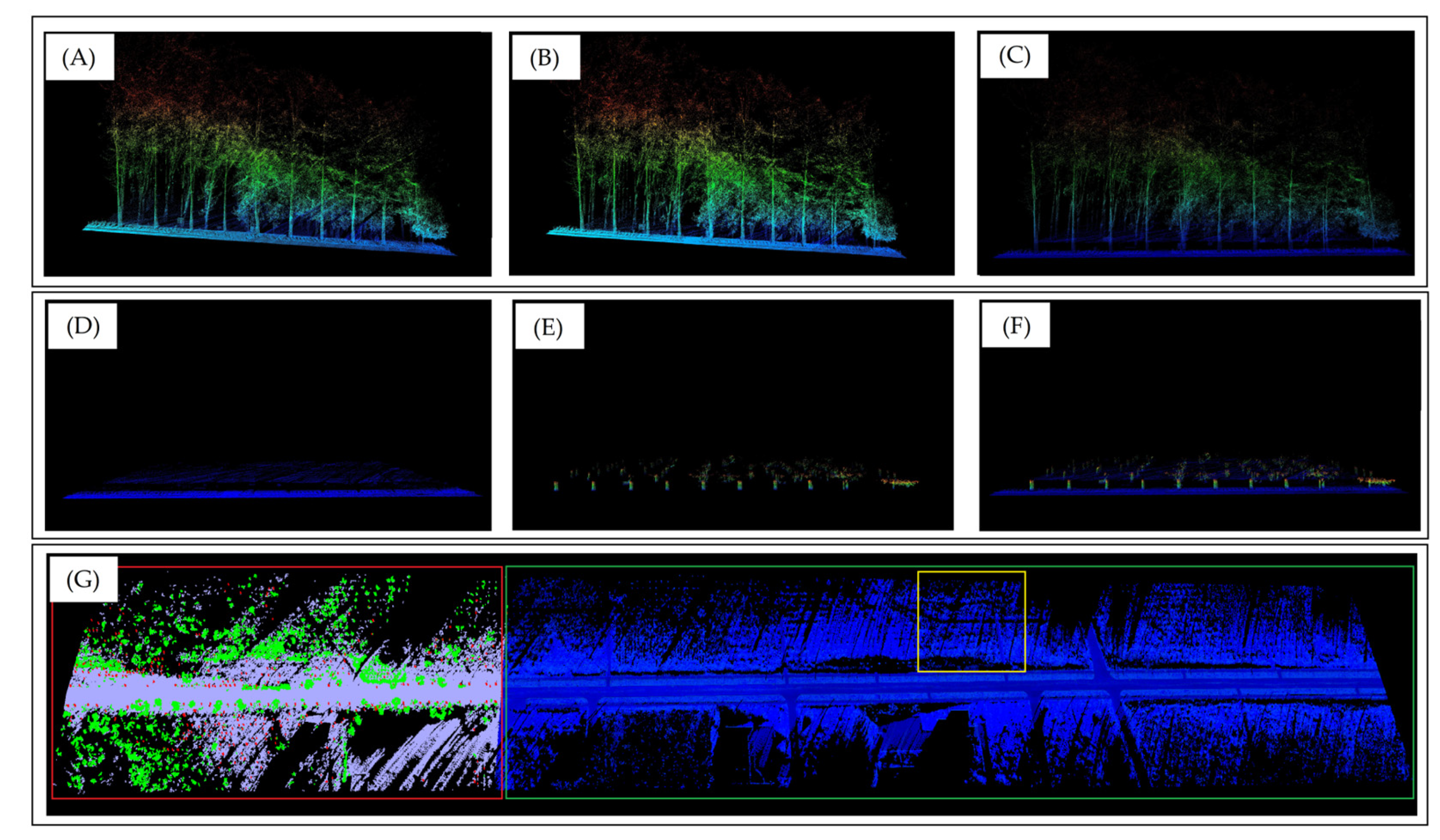
2.3.1. Creation of the Tree Trunk Detection Deep Learning Dataset Based on Stratified Coupling
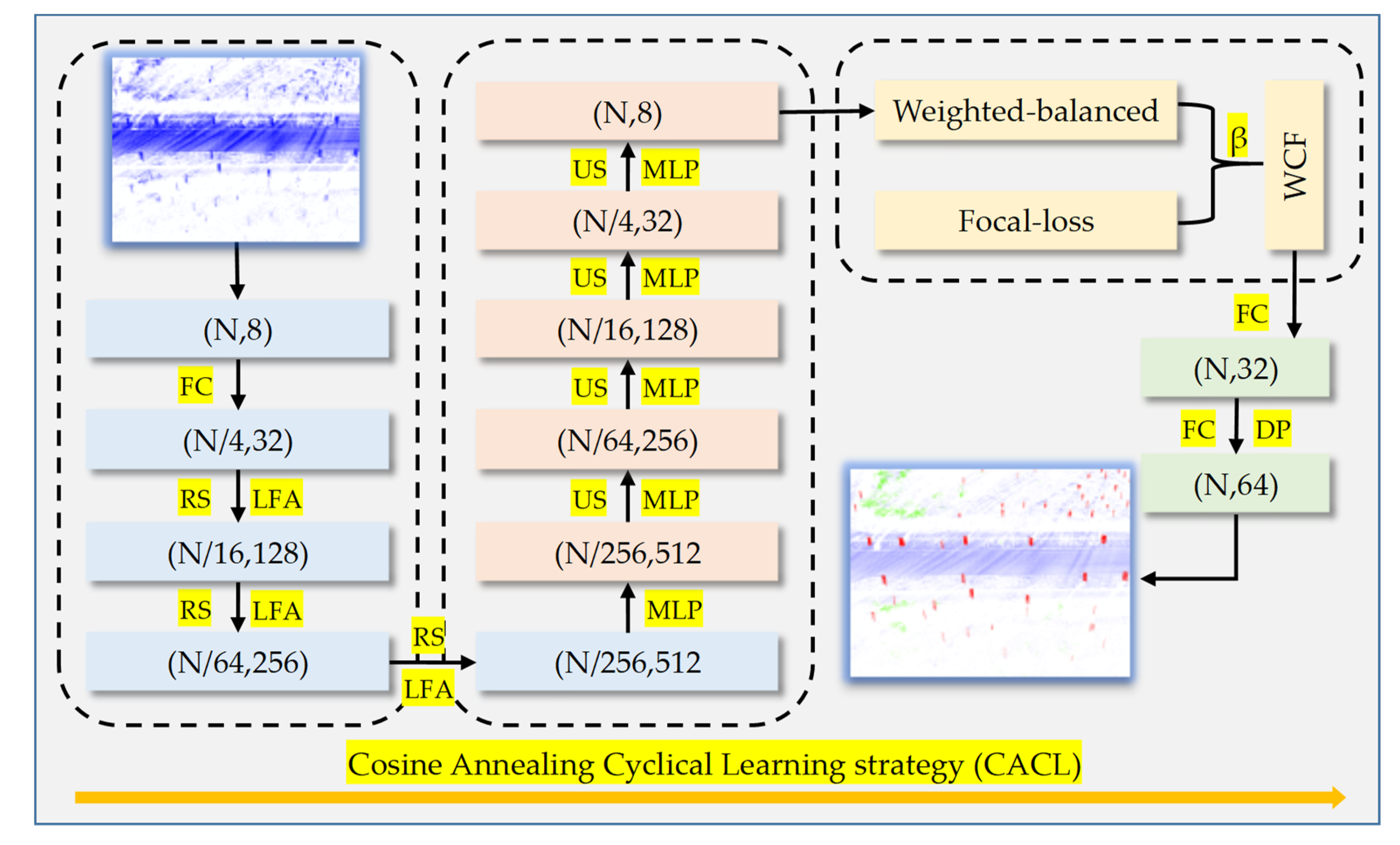
2.3.2. Construction of the WCF-CACL-RandLA-Net Model
- (1)
- Weighted Cross-Entropy Focal-Loss (WCF)
- (2)
- Cosine Annealing Cyclic Learning Strategy (CACL)
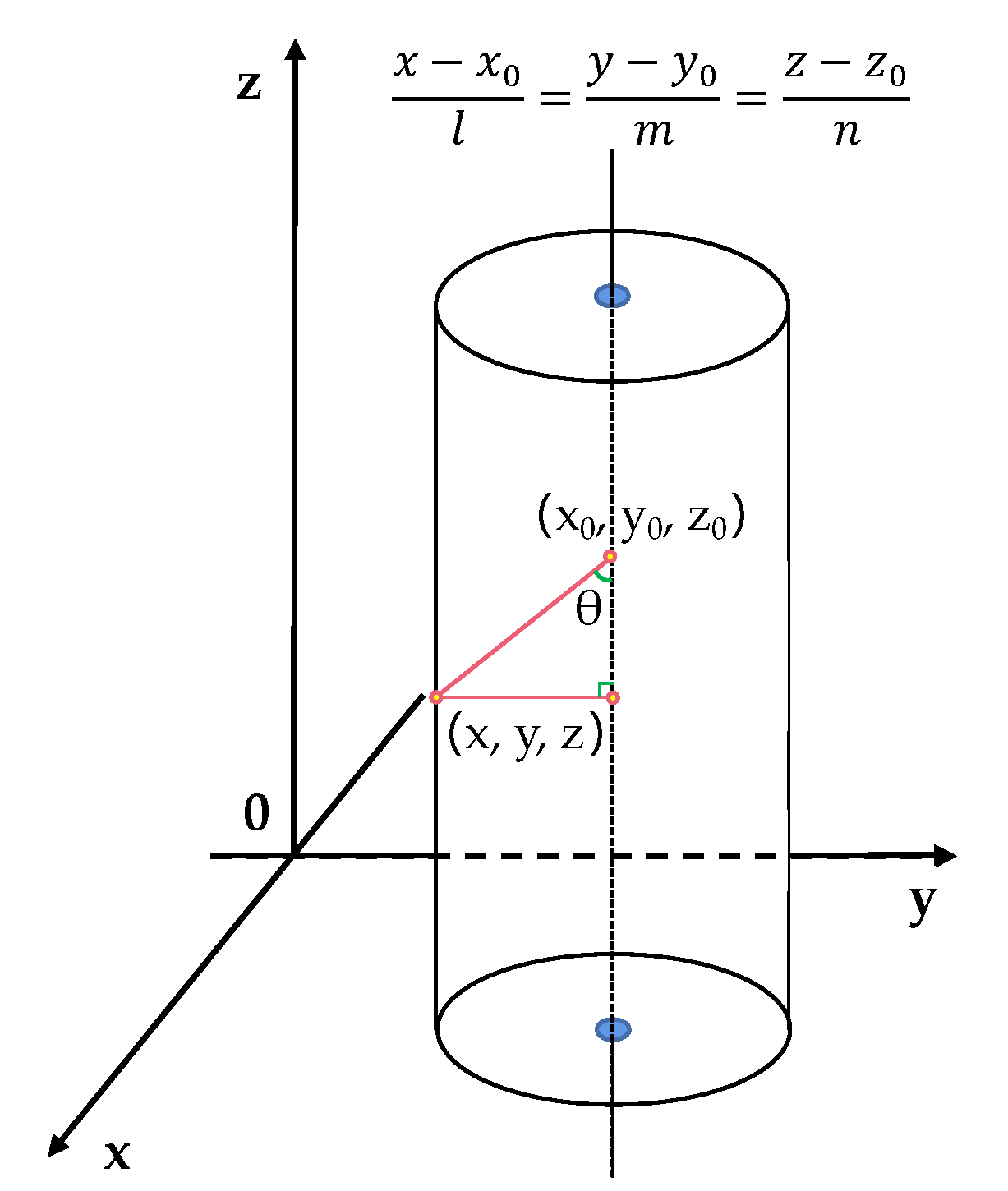
2.3.3. DBH Estimation Method Based on LSA-RANSAC
- (1)
- Initialize parameters: the maximum distance from the point cloud to the model, the desired inlier probability, maximum iterations, and minimum inlier count were set. The best initial inlier count and the best initial model were initialized;
- (2)
- Calculate the sample size based on the desired inlier probability;
- (3)
- Determine the best initial model parameters iteratively: randomly select a sample point cloud from the point cloud according to the current sample size. The cylindrical model was fit using the selected sample point cloud, returning the model parameters and inlier indices. The inlier count was calculated and compared with the current best initial inlier count. If the inlier count was greater than the current best initial inlier count, the best initial inlier count, the best initial model, sample size, and iteration count were updated. The adjustment process adaptively updated the sample size and iteration count based on the current inlier count;
- (4)
- Extract the best initial model parameters, : obtain the center point, axis direction, radius, and height of the cylinder from the best initial model acquired by the adaptive RANSAC algorithm;
- (5)
- Define the fitting error function by calculating the distance between the best initial model parameter and the point cloud data;
- (6)
- Perform nonlinear least-squares optimization on , using the Levenberg–Marquardt optimization method to solve for the minimum value of the fitting error function and obtain the best-fit cylindrical model parameters.
2.4. Comparison Method
3. Results
3.1. Segmentation Results of Point Cloud Based on WCF-CACL-RandLA-Net Model
3.1.1. Evaluation Metrics
3.1.2. Training Loss and Elapsed Time
3.1.3. Quantitative and Qualitative Evaluation
3.1.4. Comparative Studies
3.1.5. Ablation Experiments
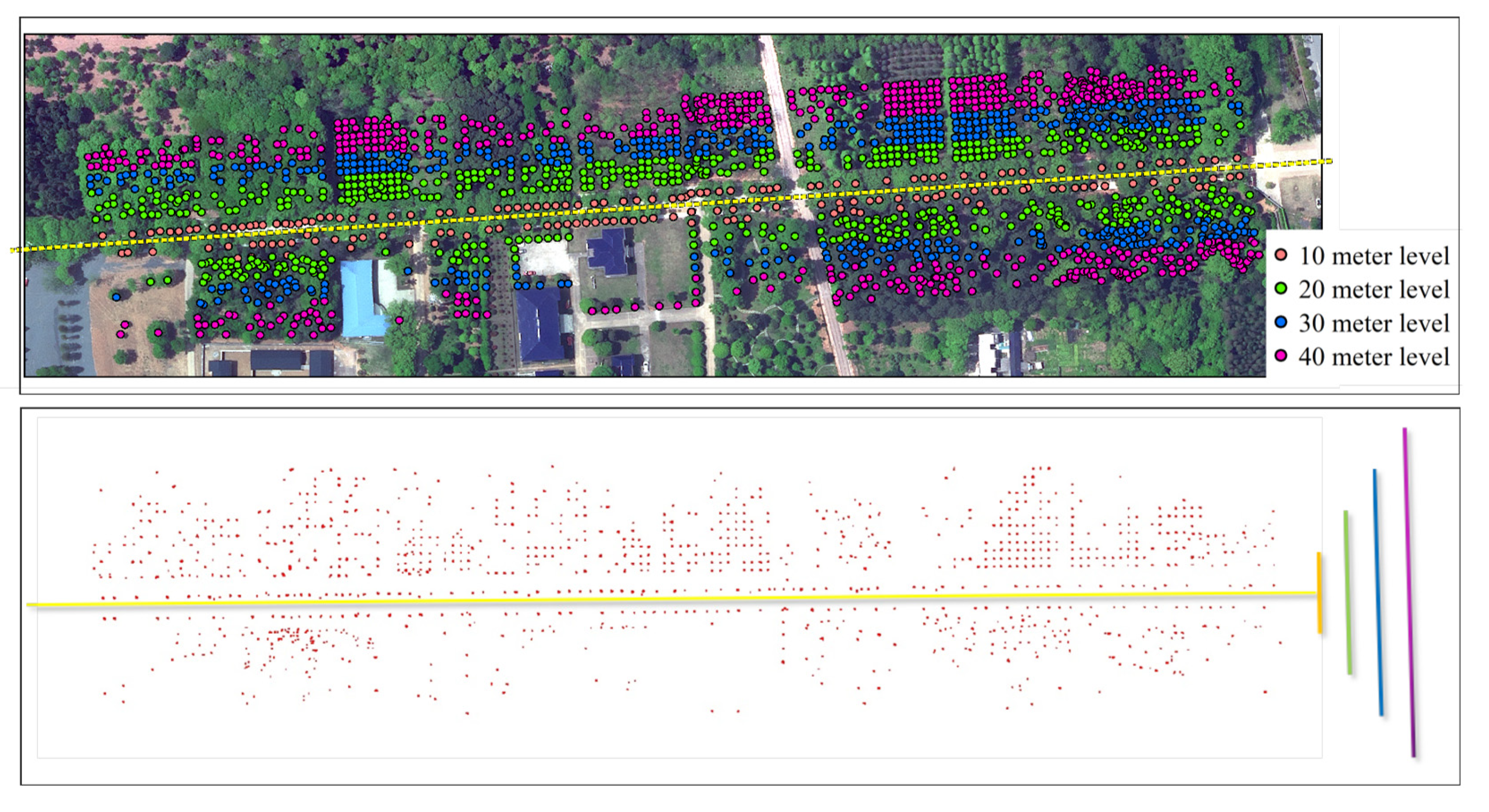
3.1.6. Impact of Laser Scanning Distance Level on Tree Trunk Detection Rate (ER)
3.2. DBH Estimation Results Based on LSA-RANSAC
3.2.1. Evaluation Metrics
3.2.2. Fitting Accuracy Comparison
3.2.3. Analysis of Tree Trunk Detection Accuracy Based on LiDAR Scanning Distance Level
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Xing, Y.; Duanmu, J.; Tian, X. Evaluating Different Methods for Estimating Diameter at Breast Height from Terrestrial Laser Scanning. Remote Sens. 2018, 10, 513. [Google Scholar] [CrossRef]
- Duanmu, J.; Xing, Y. Annular Neighboring Points Distribution Analysis: A Novel PLS Stem Point Cloud Preprocessing Algorithm for DBH Estimation. Remote Sens. 2020, 12, 808. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR Derived Canopy Height and DBH with Terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Oveland, I.; Hauglin, M.; Giannetti, F.; Schipper Kjørsvik, N.; Gobakken, T. Comparing Three Different Ground Based Laser Scanning Methods for Tree Stem Detection. Remote Sens. 2018, 10, 538. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, X.; An, F.; Zhou, L.; Wang, X.; Wang, Z.; Zhang, H.; Yun, T. Integrating Real Tree Skeleton Reconstruction Based on Partial Computational Virtual Measurement (CVM) with Actual Forest Scenario Rendering: A Solid Step Forward for the Realization of the Digital Twins of Trees and Forests. Remote Sens. 2022, 14, 6041. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Yu, X.; Jaakkola, A.; Wang, Y. Possibilities of a Personal Laser Scanning System for Forest Mapping and Ecosystem Services. Sensors 2014, 14, 1228–1248. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef]
- Pueschel, P.; Newnham, G.; Rock, G.; Udelhoven, T.; Werner, W.; Hill, J. The influence of scan mode and circle fitting on tree stem detection, stem diameter and volume extraction from terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 77, 44–56. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Trochta, J.; Krucek, M.; Vrska, T.; Kral, K. 3D forest: An application for descriptions of three-dimensional forest structures using terrestrial lidar. PLoS ONE 2017, 12, e0176871. [Google Scholar] [CrossRef]
- Sun, H.; Wang, G.; Lin, H.; Li, J.; Zhang, H.; Ju, H. Retrieval and accuracy assessment of tree and stand parameters for chinese fir plantation using terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1993–1997. [Google Scholar] [CrossRef]
- Del Perugia, B.; Giannetti, F.; Chirici, G.; Travaglini, D. Influence of Scan Density on the Estimation of Single-Tree Attributes by Hand-Held Mobile Laser Scanning. Forests 2019, 10, 277. [Google Scholar] [CrossRef]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J. Single Tree Stem Profile Detection Using Terrestrial Laser Scanner Data, Flatness Saliency Features and Curvature Properties. Forests 2016, 7, 207. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Cheng, X.; Stoter, J.; Xu, Z.; Wu, Z.; Nan, L. GlobalMatch: Registration of forest terrestrial point clouds by global matching of relative stem positions. ISPRS J. Photogramm. Remote Sens. 2023, 197, 71–86. [Google Scholar] [CrossRef]
- Li, J.; Cheng, X.; Xiao, Z. A branch-trunk-constrained hierarchical clustering method for street trees individual extraction from mobile laser scanning point clouds. Measurement 2022, 189, 110440. [Google Scholar] [CrossRef]
- Wang, P.; Tang, Y.; Liao, Z.; Yan, Y.; Dai, L.; Liu, S.; Jiang, T. Road-Side Individual Tree Segmentation from Urban MLS Point Clouds Using Metric Learning. Remote Sens. 2023, 15, 1992. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Cui, Z.; Lei, K.; Zuo, Y.; Wang, J.; Hu, X.; Qiu, H. Very High Resolution Images and Superpixel-Enhanced Deep Neural Forest Promote Urban Tree Canopy Detection. Remote Sens. 2023, 15, 519. [Google Scholar] [CrossRef]
- Armitage, S.; Awty-Carroll, K.; Clewley, D.; Martinez-Vicente, V. Detection and Classification of Floating Plastic Litter Using a Vessel-Mounted Video Camera and Deep Learning. Remote Sens. 2022, 14, 3425. [Google Scholar] [CrossRef]
- Ning, X.; Ma, Y.; Hou, Y.; Lv, Z.; Jin, H.; Wang, Y. Semantic Segmentation Guided Coarse-to-Fine Detection of Individual Trees from MLS Point Clouds Based on Treetop Points Extraction and Radius Expansion. Remote Sens. 2022, 14, 4926. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual Tree Crown Segmentation Directly from UAV-Borne LiDAR Data Using the PointNet of Deep Learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, R.; Deschaud, E.; Marcotegui, B.; Goulette, F.; Guibas, L. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Aloysius, N.; Geetha, M. A Review on Deep Convolutional Neural Networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP 2017), Chennai, India, 6–8 April 2017; pp. 588–592. [Google Scholar] [CrossRef]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P. Adaptive clustering of airborne LiDAR data to segment individual tree crowns in managed pine forests. Int. J. Remote Sens. 2010, 31, 117–139. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11105–11114. [Google Scholar]
- Ester, M.; Kriegel, P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; AAAI Press: Washington, DC, USA, 1996; Volume 34, pp. 226–231. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Demol, M.; Calders, K.; Krishna Moorthy, S.M.; Van den Bulcke, J.; Verbeeck, H.; Gielen, B. Consequences of vertical basic wood density variation on the estimation of aboveground biomass with terrestrial laser scanning. Trees 2021, 35, 671–684. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G.; Jing, W. A Single-Tree Point Cloud Completion Approach of Feature Fusion for Agricultural Robots. Electronics 2023, 12, 1296. [Google Scholar] [CrossRef]
- Luo, H.; Khoshelham, K.; Chen, C.; He, H. Individual tree extraction from urban mobile laser scanning point clouds using deep pointwise direction embedding. ISPRS J. Photogramm. Remote Sens. 2021, 175, 326–339. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Khalid, S.; Xiao, W.; Trigoni, N.; Markham, A. Towards Semantic Segmentation of Urban-Scale 3D Point Clouds: A Dataset, Benchmarks and Challenges. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 4977–4987. [Google Scholar]
- Liang, X.; Litkey, P.; Hyyppä, J.; Matikainen, L. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.; Onda, Y.; Hashimoto, A.; Gomi, T.; Chiu, C.; Inokoshi, S. A tree detection method based on trunk point cloud section in dense plantation forest using drone LiDAR data. For. Ecosyst. 2023, 10, 100088. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3D.Net: A New Large-Scale Point Cloud Classification Benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar] [CrossRef]
- Giannetti, F.; Puletti, N.; Quatrini, V.; Travaglini, D.; Bottalico, F.; Corona, P.; Chirici, G. Integrating terrestrial and airborne laser scanning for the assessment of single-tree attributes in Mediterranean forest stands. Eur. J. Remote Sens. 2018, 51, 795–807. [Google Scholar] [CrossRef]
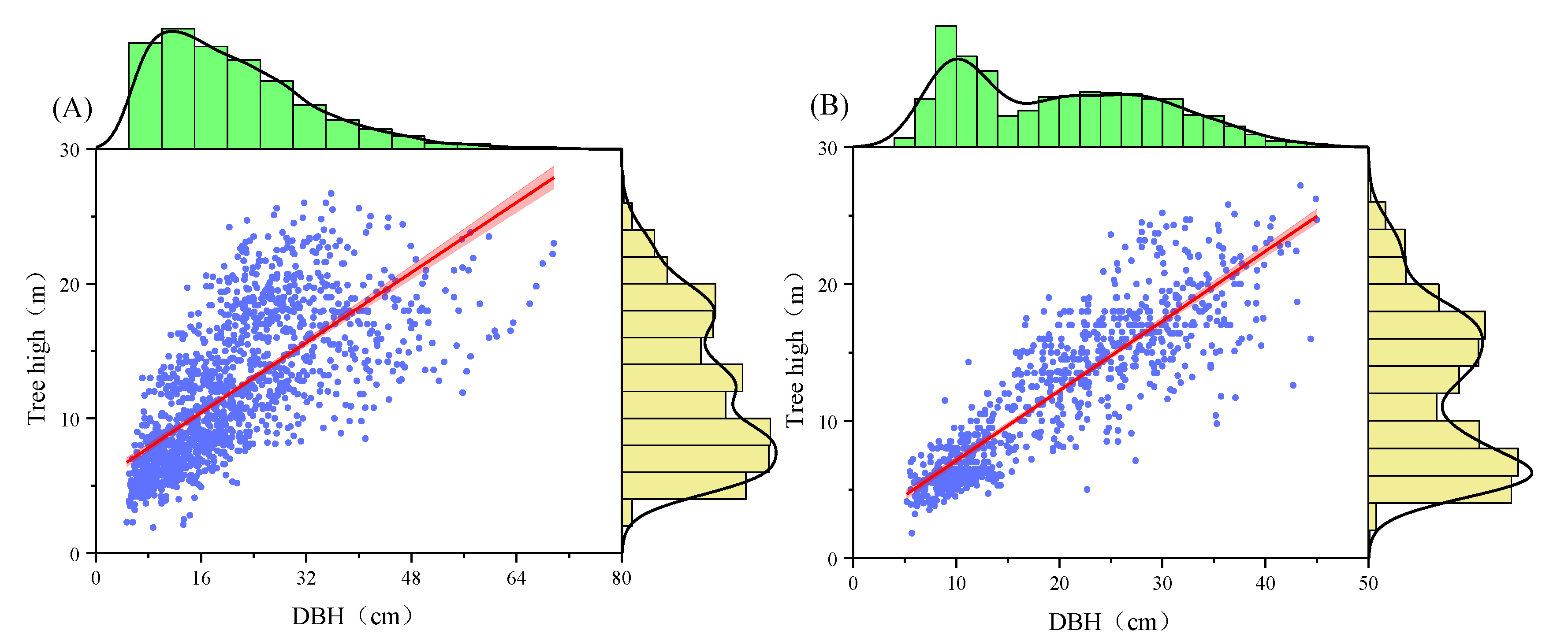



| Dataset Function Partition Type | Area (m2) | Species Name of Tree | Number of Trees | DBH (cm) | TH (m) | ||
|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||||
| Training sample area | 19,600 | Yulania denudata (Desrousseaux) D. L. Fu; Magnolia officinalis Rehd.et Wils., Michelia L.; Cupressus funebris Endl.; Pinus massoniana Lamb.; Cryptomeria japonica var. sinensis Miquel. | 453 | 21.34 | 9.83 | 11.28 | 3.68 |
| Validation sample area | 5000 | Betula luminifera H.Winkl.; Osmanthus sp., Michelia L.; Pinus massoniana Lamb.; Taxus wallichiana var. chinensis (Pilg.) Florin. | 220 | 19.24 | 9.52 | 12.33 | 6.17 |
| Experimental sample area | 45,400 | Michelia L., Osmanthus sp.; Cinnamomum camphora (L.) presl; Nageia nagi (Thunberg) Kuntze; Taxodium distichum (L.) Rich.; Taxodium distichum var. imbricatum (Nuttall) Croom. | 1851 | 20.78 | 11.20 | 12.39 | 6.13 |
| Total | 65,000 | Michelia L., Osmanthus sp.; Cinnamomum camphora (L.) presl; Cupressus funebris Endl.; Taxus wallichiana var.chinensis (Pilg.) Florin; Taxodium distichum (L.) Rich. | 2303 | 21.22 | 6.58 | 12.76 | 3.06 |
| Classification of the Point Cloud | ||||||
|---|---|---|---|---|---|---|
| WCF-CACL RandLA-Net | RandLA-Net | WCF-CACL RandLA-Net | RandLA-Net | WCF-CACL RandLA-Net | RandLA-Net | |
| Tree trunk | 0.99 | 0.99 | 0.84 | 0.78 | 0.88 | 0.85 |
| Shrub and branch | 0.98 | 0.98 | 0.86 | 0.81 | 0.90 | 0.87 |
| Ground | 0.96 | 0.96 | 0.97 | 0.97 | 0.97 | 0.98 |
| Total/Mean | 0.98 | 0.98 | 0.88 | 0.85 | 0.92 | 0.90 |
| References | Time of Train | Time of Test | IOU of Tree Trunk | IOU of Shrub-Branch | IOU of Ground | mIOU | mOA |
|---|---|---|---|---|---|---|---|
| KPconv | 2.9 | 0.80 | 0.71 | 0.79 | 0.98 | 0.83 | 0.97 |
| PointNet++ | 3.50 | 1.10 | 0.60 | 0.71 | 0.98 | 0.76 | 0.95 |
| Randlanet | 2.90 | 0.10 | 0.78 | 0.81 | 0.97 | 0.85 | 0.98 |
| VF | -- | -- | 0.36 | -- | -- | 0.36 | |
| Ours | 2.93 | 0.10 | 0.84 | 0.86 | 0.97 | 0.89 | 0.98 |
| Model | IOU of Tree Trunk | IOU of Shrub-Branch | IOU of Ground | Mean IOU | Step of Mean IOU ≥ 0.8 |
|---|---|---|---|---|---|
| RandLA-Net | 0.78 | 0.81 | 0.97 | 0.83 | 3500 |
| WCF-RandLA-Net | 0.82 | 0.84 | 0.97 | 0.87 | 3500 |
| CACL-RandLA-Net | 0.79 | 0.82 | 0.97 | 0.86 | 2000 |
| WCF-CACL-RandLA-Net | 0.84 | 0.86 | 0.97 | 0.88 | 2000 |
| Evaluating Indicator | ER at Different Distance Levels | |||
|---|---|---|---|---|
| 0–10 m | 10–20 m | 20–30 m | 30–45 m | |
| ER | 97.70% | 83.36% | 68.09% | 32.47% |
| Measured number of trees | 174 | 535 | 468 | 627 |
| Species Type of Foresty | Species Name of Tree | Number of Trees | LSA-RANSAC | RANSAC | CHA | LS | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |||
| Coniferous forest | Taxodium distichum (L.) Rich. andTaxodium distichum var. imbricatum (Nuttall) Croom | 129 | 0.77 | 6.37 | 0.60 | 7.10 | 0.39 | 10.58 | 0.53 | 10.23 |
| Broadleaf forest | Betula luminifera H.Winkl. and Liriodendron chinense (Hemsl.) Sargent. | 108 | 0.74 | 6.20 | 0.61 | 7.12 | 0.33 | 9.89 | 0.42 | 8.91 |
| Coniferous–broad forests | Cinnamomum camphora (Linn) Presl, Michelia maudiae Dunn, Cedrus deodara (Roxb.) G. Don and Abies fabri (Mast.) Craib | 106 | 0.73 | 6.92 | 0.59 | 8.53 | 0.20 | 11.19 | 0.23 | 13.70 |
| Total/Mean | 343 | 0.75 | 6.50 | 0.61 | 7.58 | 0.31 | 10.55 | 0.39 | 10.95 | |
| Species Type of Foresty | Evaluating Indicator | DBH Estimation Accuracy at Different Distance Levels | |||
|---|---|---|---|---|---|
| 0–10 m | 10–20 m | 20–30 m | 30–45 m | ||
| Coniferous forest | R2 | 0.97 | 0.83 | 0.81 | 0.67 |
| RMSE | 2.35 | 3.67 | 7.01 | 9.75 | |
| Nmber of tree | 10 | 51 | 43 | 25 | |
| Broad-leaved forest | R2 | 0.98 | 0.82 | 0.61 | 0.76 |
| RMSE | 2.53 | 5.04 | 8.56 | 6.99 | |
| Nmber of tree | 14 | 54 | 30 | 10 | |
| Coniferous–broad-leaved mixed forests | R2 | 0.83 | 0.75 | 0.58 | 0.47 |
| RMSE | 5.94 | 6.91 | 8.94 | 9.11 | |
| Nmber of tree | 42 | 48 | 9 | 7 | |
| Total/Mean | R2 | 0.93 | 0.80 | 0.67 | 0.63 |
| RMSE | 3.61 | 5.21 | 8.17 | 8.62 | |
| Nmber of tree | 66 | 153 | 82 | 42 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, H.; Xu, K.; Li, Y.; Wang, L.; Liu, R.; Qiu, H.; Yu, L. A Novel Framework for Stratified-Coupled BLS Tree Trunk Detection and DBH Estimation in Forests (BSTDF) Using Deep Learning and Optimization Adaptive Algorithm. Remote Sens. 2023, 15, 3480. https://doi.org/10.3390/rs15143480
Zhang H, Zhang H, Xu K, Li Y, Wang L, Liu R, Qiu H, Yu L. A Novel Framework for Stratified-Coupled BLS Tree Trunk Detection and DBH Estimation in Forests (BSTDF) Using Deep Learning and Optimization Adaptive Algorithm. Remote Sensing. 2023; 15(14):3480. https://doi.org/10.3390/rs15143480
Chicago/Turabian StyleZhang, Huacong, Huaiqing Zhang, Keqin Xu, Yueqiao Li, Linlong Wang, Ren Liu, Hanqing Qiu, and Longhua Yu. 2023. "A Novel Framework for Stratified-Coupled BLS Tree Trunk Detection and DBH Estimation in Forests (BSTDF) Using Deep Learning and Optimization Adaptive Algorithm" Remote Sensing 15, no. 14: 3480. https://doi.org/10.3390/rs15143480
APA StyleZhang, H., Zhang, H., Xu, K., Li, Y., Wang, L., Liu, R., Qiu, H., & Yu, L. (2023). A Novel Framework for Stratified-Coupled BLS Tree Trunk Detection and DBH Estimation in Forests (BSTDF) Using Deep Learning and Optimization Adaptive Algorithm. Remote Sensing, 15(14), 3480. https://doi.org/10.3390/rs15143480






