Sensing Mechanism and Real-Time Bridge Displacement Monitoring for a Laboratory Truss Bridge Using Hybrid Data Fusion
Abstract
:1. Introduction
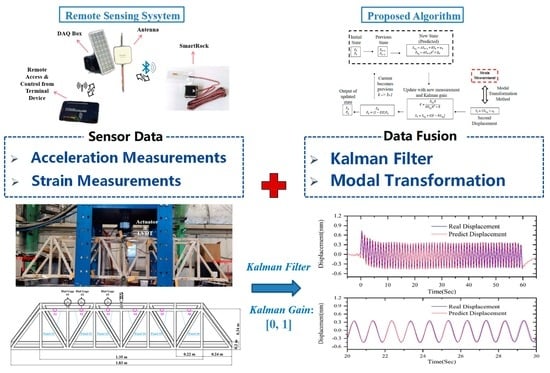
2. Objective, Novelty, and the General Framework
3. Instrumentation
4. Methodology
4.1. Formulation of Kalman Filter-Based Displacement Estimation Algorithm
- Time update
- a.
- Project the state ahead:
- b.
- Project the covariance ahead:
- Measurement update
- a.
- Compute the Kalman gain:
- b.
- Update state estimate:
- c.
- Update the covariance:
4.2. Strain–Displacement Transformation
4.3. Obtaining Full-Field Displacement
5. Implementation and Verification of the Algorithm
5.1. Experimental Setup and Sensing Units
5.2. Implementation of the Algorithm
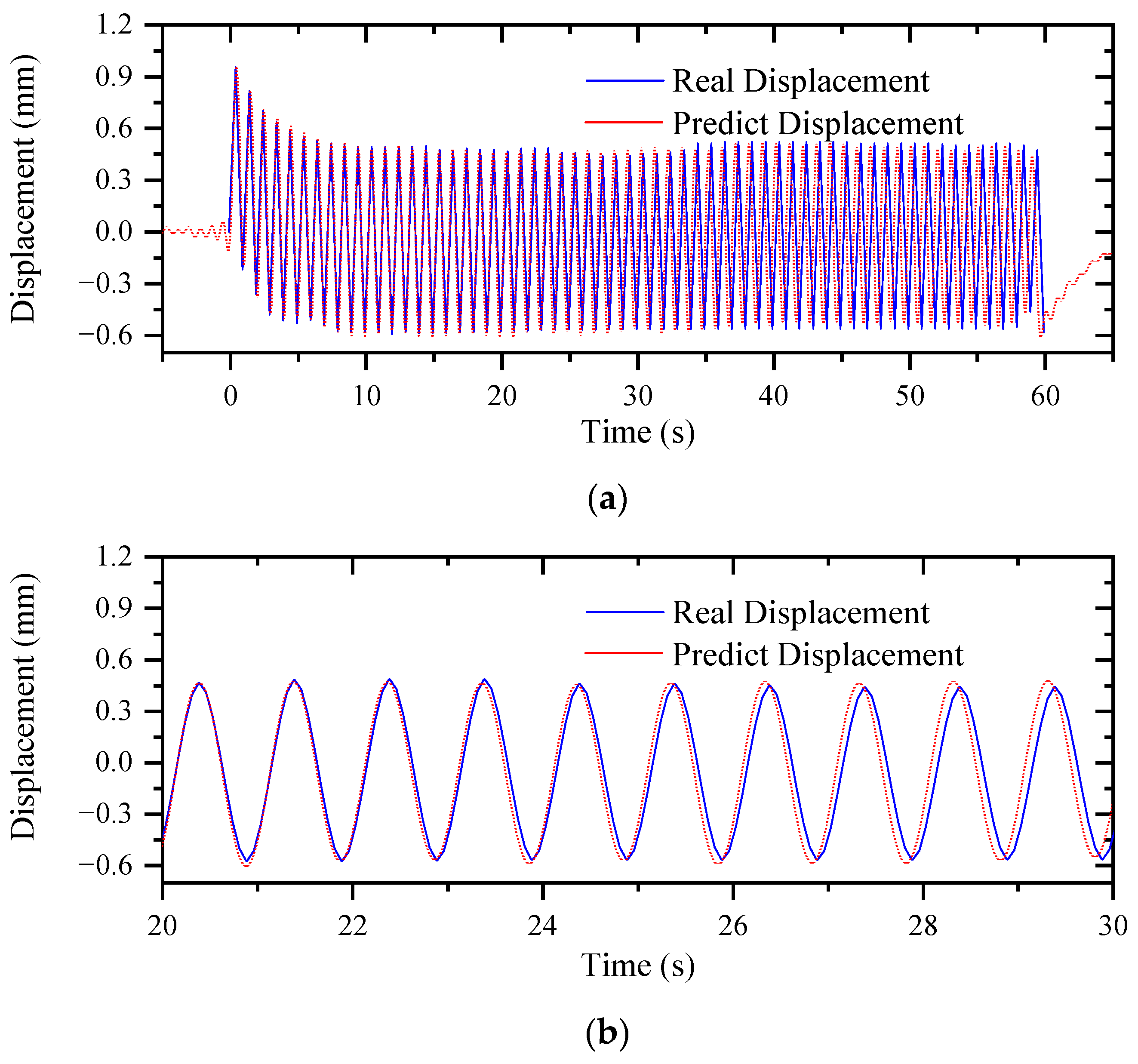
5.3. Displacement Prediction Using the Proposed Algorithm
5.3.1. Predicting Displacements at Sensor Locations
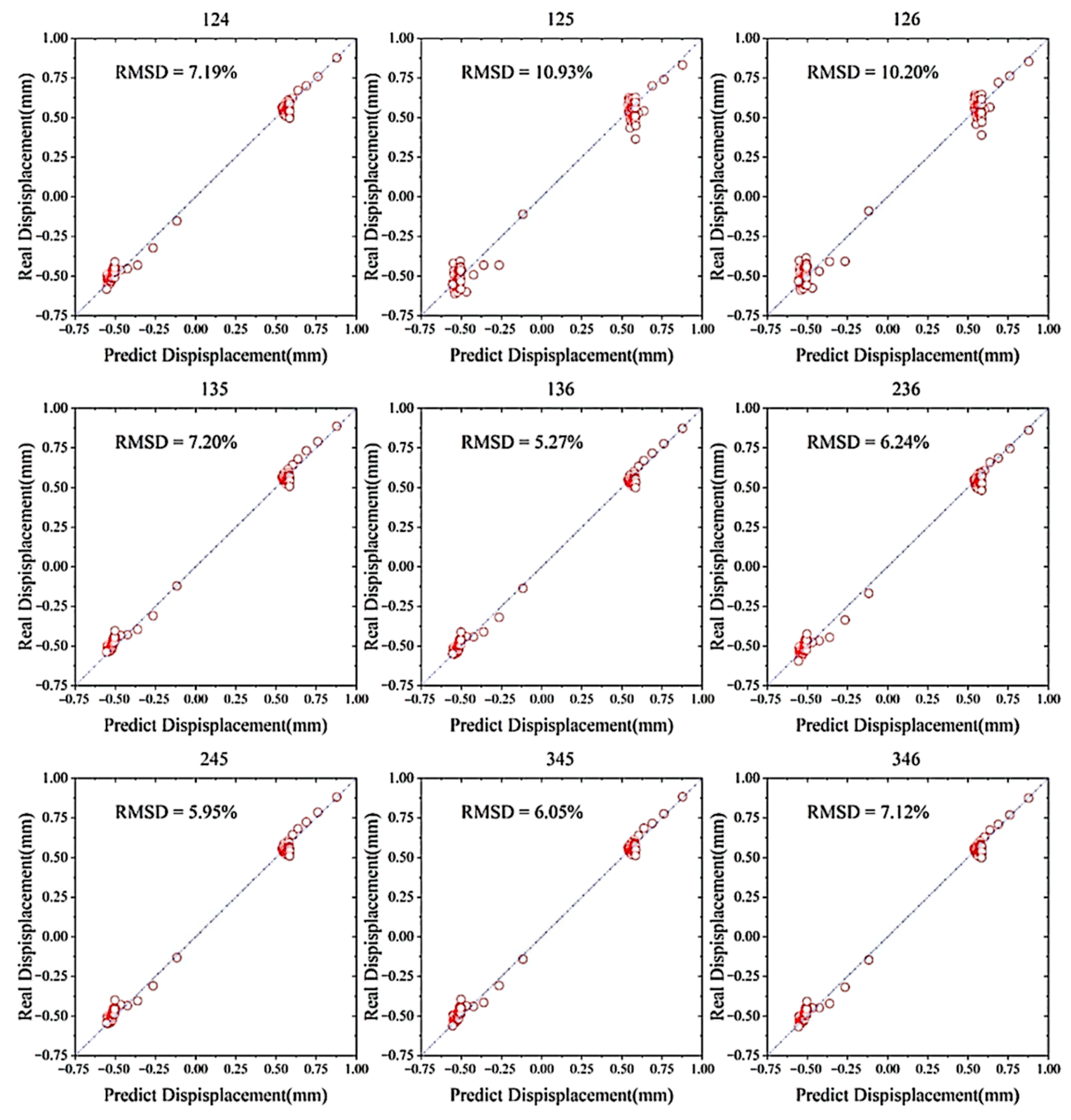
5.3.2. Predicting Displacements at the Location without a Sensor Installed
6. Conclusions
- (1)
- SmartRock with a built-in smart computing algorithm is capable of estimating bridge displacements in real time and can improve the accuracy compared to using only one type of sensor.
- (2)
- The predicted displacements using the proposed algorithm at the sensor locations (S1–S6) under a harmonic load showed a good match with the dial and gauge measured ‘real’ displacements in both harmonic trend and displacement magnitude. The RMSD of the predicted displacements were 4.91% and 4.25% at the two selected locations.
- (3)
- The modal expansion method was utilized to project the full-field displacements of the upper chord of the truss and yielded an excellent match with the real displacements.
- (4)
- The locations of the control nodes selected affected the accuracy of the displacement estimations when predicting the full-field displacements using three control nodes. The optimum combination of the control nodes for obtaining accurate displacement estimations of the upper chord was that two of the three control nodes should be symmetrical at about the middle of the upper chord and distributed at the extreme ends as much as possible, and the remaining one should be next to the center.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, J.J.; Shinozuka, M. Real-time displacement measurement of a flexible bridge using digital image processing techniques. Exp. Mech. 2006, 46, 105–114. [Google Scholar] [CrossRef]
- Huang, Q.; Monserrat, O.; Crosetto, M.; Crippa, B.; Wang, Y.; Jiang, J.; Ding, Y. Displacement monitoring and health evaluation of two bridges using Sentinel-1 SAR images. Remote Sens. 2018, 10, 1714. [Google Scholar] [CrossRef] [Green Version]
- Joshi, S.; Harle, S.M. Linear variable differential transducer (LVDT) & its applications in civil engineering. Int. J. Transp. Eng. Technol. 2017, 3, 62–66. [Google Scholar]
- Garg, P.; Nasimi, R.; Ozdagli, A.; Zhang, S.; Mascarenas, D.D.L.; Reda Taha, M.; Moreu, F. Measuring transverse displacements using unmanned aerial systems laser Doppler vibrometer (UAS-LDV): Development and field validation. Sensors 2020, 20, 6051. [Google Scholar] [CrossRef] [PubMed]
- Curt, J.; Capaldo, M.; Hild, F.; Roux, S. An algorithm for structural health monitoring by digital image correlation: Proof of concept and case study. Opt. Lasers Eng. 2022, 151, 106842. [Google Scholar] [CrossRef]
- Barros, F.; Aguiar, S.; Sousa, P.J.; Cachaço, A.; Tavares, P.J.; Moreira, P.M.; Ranzal, D.; Cardoso, N.; Fernandes, N.; Fernandes, R.; et al. Displacement monitoring of a pedestrian bridge using 3D digital image correlation. Procedia Struct. Integr. 2022, 37, 880–887. [Google Scholar] [CrossRef]
- Nasimi, R.; Moreu, F. A methodology for measuring the total displacements of structures using a laser–camera system. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 421–437. [Google Scholar] [CrossRef]
- Olaszek, P.; Świercz, A.; Boscagli, F. The integration of two interferometric radars for measuring dynamic displacement of bridges. Remote Sens. 2021, 13, 3668. [Google Scholar] [CrossRef]
- Lydon, D.; Lydon, M.; Taylor, S.; Del Rincon, J.M.; Hester, D.; Brownjohn, J. Development and field testing of a vision-based displacement system using a low cost wireless action camera. Mech. Syst. Signal Process. 2019, 121, 343–358. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lee, K.C.; Jeong, S.; Lee, Y.J.; Sim, S.H. Long-term displacement measurement of full-scale bridges using camera ego-motion compensation. Mech. Syst. Signal Process. 2020, 140, 106651. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Brownjohn, J. An accurate and distraction-free vision-based structural displacement measurement method integrating Siamese network based tracker and correlation-based template matching. Measurement 2021, 179, 109506. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, G.S.; Hulsey, J.L. Monitoring bridge dynamic responses using fiber Bragg grating tiltmeters. Sensors 2017, 17, 2390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, F.; Hulsey, J.L.; Balasubramanian, R. Fiber optic health monitoring and temperature behavior of bridge in cold region. Struct. Control Health Monit. 2017, 24, e2020. [Google Scholar] [CrossRef]
- Won, J.; Park, J.W.; Park, J.; Shin, J.; Park, M. Development of a reference-free indirect bridge displacement sensing system. Sensors 2021, 21, 5647. [Google Scholar] [CrossRef]
- Cai, C.; He, Q.; Zhu, S.; Zhai, W.; Wang, M. Dynamic interaction of suspension-type monorail vehicle and bridge: Numerical simulation and experiment. Mech. Syst. Signal Process. 2019, 118, 388–407. [Google Scholar] [CrossRef]
- Zhuge, S.; Xu, X.; Zhong, L.; Gan, S.; Lin, B.; Yang, X.; Zhang, X. Noncontact deflection measurement for bridge through a multi-UAVs system. Comput.-Aided Civ. Infrastruct. Eng. 2021, 37, 746–761. [Google Scholar] [CrossRef]
- Park, J.W.; Sim, S.H.; Jung, H.J. Development of a wireless displacement measurement system using acceleration responses. Sensors 2013, 13, 8377–8392. [Google Scholar] [CrossRef] [Green Version]
- Ozdagli, A.I.; Liu, B.; Moreu, F. Low-cost, efficient wireless intelligent sensors (LEWIS) measuring real-time reference-free dynamic displacements. Mech. Syst. Signal Process. 2018, 107, 343–356. [Google Scholar] [CrossRef]
- Thong, Y.K.; Woolfson, M.S.; Crowe, J.A.; Hayes-Gill, B.R.; Jones, D.A. Numerical double integration of acceleration measurements in noise. Measurement 2004, 36, 73–92. [Google Scholar] [CrossRef]
- Ozdagli, A.I.; Gomez, J.A.; Moreu, F. Real-time reference-free displacement of railroad bridges during train-crossing events. J. Bridge Eng. 2017, 22, 04017073. [Google Scholar] [CrossRef]
- Lee, H.S.; Hong, Y.H.; Park, H.W. Design of an FIR filter for the displacement reconstruction using measured acceleration in low-frequency dominant structures. Int. J. Numer. Methods Eng. 2010, 82, 403–434. [Google Scholar] [CrossRef]
- Moreu, F.; Li, J.; Jo, H.; Kim, R.E.; Scola, S.; Spencer, B.F., Jr.; LaFave, J.M. Reference-free displacements for condition assessment of timber railroad bridges. J. Bridge Eng. 2016, 21, 04015052. [Google Scholar] [CrossRef]
- Chan, W.S.; Xu, Y.L.; Ding, X.L.; Dai, W.J. An integrated GPS–accelerometer data processing technique for structural deformation monitoring. J. Geod. 2006, 80, 705–719. [Google Scholar] [CrossRef]
- Hong, Y.H.; Lee, S.G.; Lee, H.S. Design of the FEM-FIR filter for displacement reconstruction using accelerations and displacements measured at different sampling rates. Mech. Syst. Signal Process. 2013, 38, 460–481. [Google Scholar] [CrossRef]
- Kim, K.; Sohn, H. Dynamic Displacement Estimation for Long-Span Bridges Using Acceleration and Heuristically Enhanced Displacement Measurements of Real-Time Kinematic Global Navigation System. Sensors 2020, 20, 5092. [Google Scholar] [CrossRef] [PubMed]
- Zeng, K.; Huang, H.; Song, S. Displacement Measurement Based on Data Fusion and Real-Time Computing. J. Perform. Constr. Facil. 2020, 34, 04020118. [Google Scholar] [CrossRef]
- Zeng, K.; Qiu, T.; Bian, X.; Xiao, M.; Huang, H. Identification of ballast condition using SmartRock and pattern recognition. Constr. Build. Mater. 2019, 221, 50–59. [Google Scholar] [CrossRef]
- Liu, S.; Qiu, T.; Qian, Y.; Huang, H.; Tutumluer, E.; Shen, S. Simulations of large-scale triaxial shear tests on ballast aggregates using sensing mechanism and real-time (SMART) computing. Comput. Geotech. 2019, 110, 184–198. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Tran, N.H.; Wang, D.; Khatir, S.; Wahab, M.A. Artificial neural network combined with damage parameters to predict fretting fatigue crack initiation lifetime. Tribol. Int. 2022, 175, 107854. [Google Scholar] [CrossRef]
- Khatir, S.; Tiachacht, S.; Thanh, C.L.; Tran-Ngoc, H.; Mirjalili, S.; Wahab, M.A. A robust FRF damage indicator combined with optimization techniques for damage assessment in complex truss structures. Case Stud. Constr. Mater. 2022, 17, e01197. [Google Scholar] [CrossRef]
- Bishop, G.; Welch, G. An introduction to the kalman filter. In Proceedings of the SIGGRAPH, Los Angeles, CA, USA, 12–17 August 2001; Volume 8, p. 41. [Google Scholar]
- Li, Y.; Cao, M.; Tran-Ngoc, H.; Khatir, S.; Wahab, M.A. Multi-parameter identification of concrete dam using polynomial chaos expansion and slime mould algorithm. Comput. Struct. 2023, 281, 107018. [Google Scholar]
- Tran-Ngoc, H.; Khatir, S.; Le-Xuan, T.; Tran-Viet, H.; De Roeck, G.; Bui-Tien, T.; Wahab, M.A. Damage assessment in structures using artificial neural network working and a hybrid stochastic optimization. Sci. Rep. 2022, 12, 4958. [Google Scholar] [CrossRef] [PubMed]
- Foss, G.C.; Haugse, E.D. Using modal test results to develop strain to displacement transformations. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995; Volume 2460, p. 112. [Google Scholar]
- Kang, L.H.; Kim, D.K.; Han, J.H. Estimation of dynamic structural displacements using fiber Bragg grating strain sensors. J. Sound Vib. 2007, 305, 534–542. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape sensing methods: Review and experimental comparison on a wing-shaped plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Yu, M.; Guo, J.; Lee, K.M. A modal expansion method for displacement and strain field reconstruction of a thin-wall component during machining. IEEE/ASME Trans. Mechatron. 2018, 23, 1028–1037. [Google Scholar] [CrossRef]
- Bharadwaj, K.; Sheidaei, A.; Afshar, A.; Baqersad, J. Full-field strain prediction using mode shapes measured with digital image correlation. Measurement 2019, 139, 326–333. [Google Scholar] [CrossRef]
- Mathworks Partial Differential Equation Toolbox. Available online: https://www.mathworks.com/products/pde.html (accessed on 1 January 2021).
- Gonen, S.; Erduran, E. A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sens. 2022, 14, 6054. [Google Scholar] [CrossRef]
- Rapp, S.; Kang, L.H.; Han, J.H.; Mueller, U.C.; Baier, H. Displacement field estimation for a two-dimensional structure using fiber Bragg grating sensors. Smart Mater. Struct. 2009, 18, 025006. [Google Scholar] [CrossRef]
- Cara, F.J.; Juan, J.; Alarcón, E.; Reynders, E.; De Roeck, G. Modal contribution and state space order selection in operational modal analysis. Mech. Syst. Signal Process. 2013, 38, 276–298. [Google Scholar] [CrossRef] [Green Version]





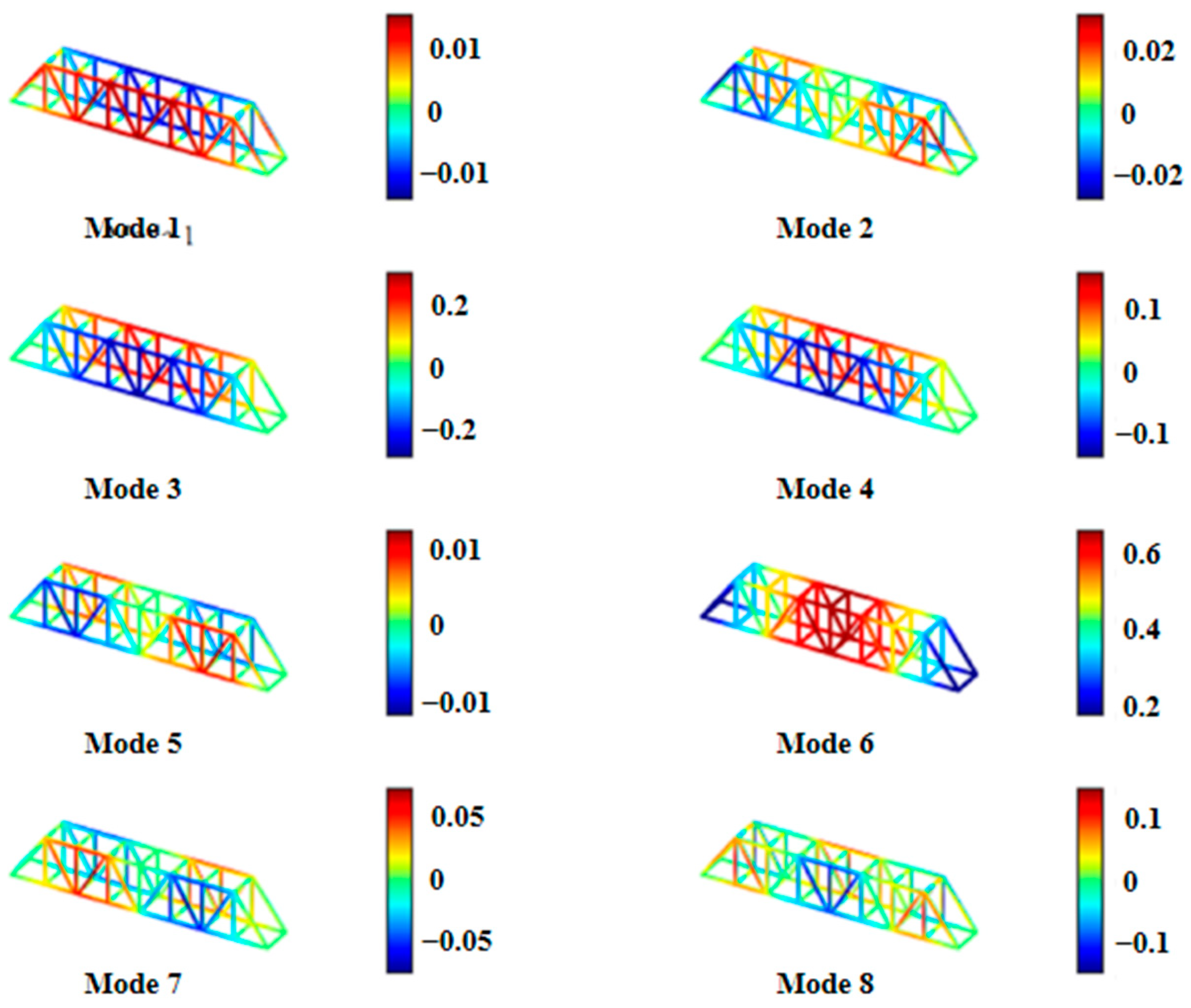




| Mode Number | Strain Energy (N·m) | Ratio | Mode # | Strain Energy (N·m) | Ratio |
|---|---|---|---|---|---|
| 1 | 1.70 × 108 | 10.1% | 11 | 4.85 × 104 | 0.0% |
| 2 | 8.20 × 104 | 0.0% | 12 | 1.22 × 105 | 0.0% |
| 3 | 4.90 × 105 | 0.0% | 13 | 8.45 × 107 | 5.0% |
| 4 | 4.66 × 106 | 0.3% | 14 | 1.35 × 103 | 0.0% |
| 5 | 3.18 × 104 | 0.0% | 15 | 5.41 × 105 | 0.0% |
| 6 | 1.32 × 109 | 78.6% | 16 | 9.86 × 105 | 0.1% |
| 7 | 5.80 × 105 | 0.0% | 17 | 5.24 × 106 | 0.3% |
| 8 | 5.31 × 104 | 0.0% | 18 | 1.28 × 105 | 0.0% |
| 9 | 1.52 × 106 | 0.1% | 19 | 4.13 × 106 | 0.2% |
| 10 | 3.41 × 106 | 0.2% | 20 | 3.74 × 107 | 2.2% |
| Location | RMSD | |
|---|---|---|
| Strain-Transferred Displacement | Predicted Displacement | |
| Dial gage #2 | 16.48% | 4.91% |
| Dial gage #3 | 14.53% | 4.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, K.; Zeng, S.; Huang, H.; Qiu, T.; Shen, S.; Wang, H.; Feng, S.; Zhang, C. Sensing Mechanism and Real-Time Bridge Displacement Monitoring for a Laboratory Truss Bridge Using Hybrid Data Fusion. Remote Sens. 2023, 15, 3444. https://doi.org/10.3390/rs15133444
Zeng K, Zeng S, Huang H, Qiu T, Shen S, Wang H, Feng S, Zhang C. Sensing Mechanism and Real-Time Bridge Displacement Monitoring for a Laboratory Truss Bridge Using Hybrid Data Fusion. Remote Sensing. 2023; 15(13):3444. https://doi.org/10.3390/rs15133444
Chicago/Turabian StyleZeng, Kun, Sheng Zeng, Hai Huang, Tong Qiu, Shihui Shen, Hui Wang, Songkai Feng, and Cheng Zhang. 2023. "Sensing Mechanism and Real-Time Bridge Displacement Monitoring for a Laboratory Truss Bridge Using Hybrid Data Fusion" Remote Sensing 15, no. 13: 3444. https://doi.org/10.3390/rs15133444
APA StyleZeng, K., Zeng, S., Huang, H., Qiu, T., Shen, S., Wang, H., Feng, S., & Zhang, C. (2023). Sensing Mechanism and Real-Time Bridge Displacement Monitoring for a Laboratory Truss Bridge Using Hybrid Data Fusion. Remote Sensing, 15(13), 3444. https://doi.org/10.3390/rs15133444