Elimination of Thermal Effects from Limited Structural Displacements Based on Remote Sensing by Machine Learning Techniques
Abstract
1. Introduction
1.1. Related Works
1.2. Objectives
1.3. Contributions
2. Data Normalization Frameworks
3. Supervised Data Normalization Methods
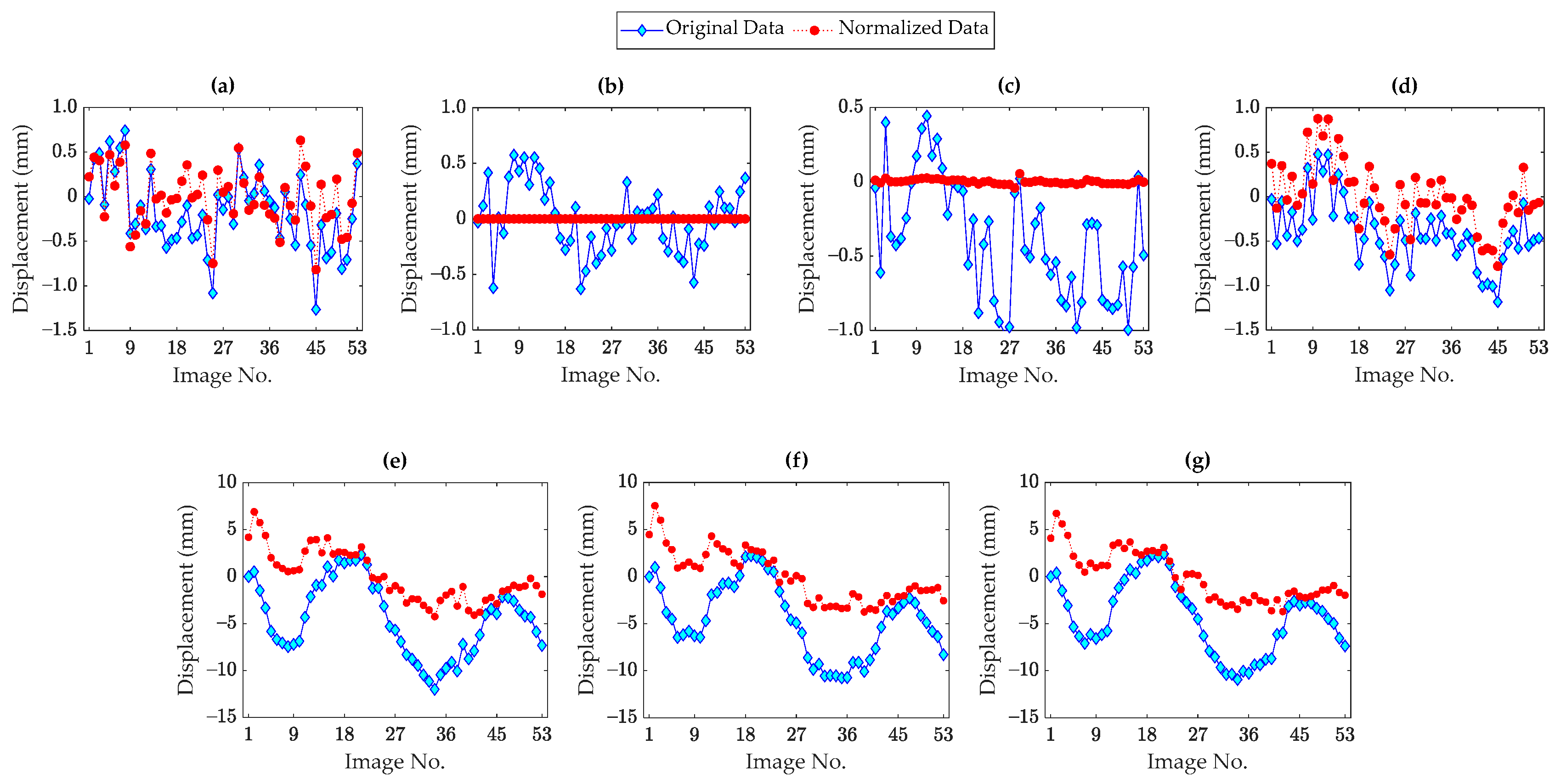
3.1. Gaussian Process Regression (GPR)
3.2. Support Vector Regression (SVR)
4. Unsupervised Data Normalization Methods
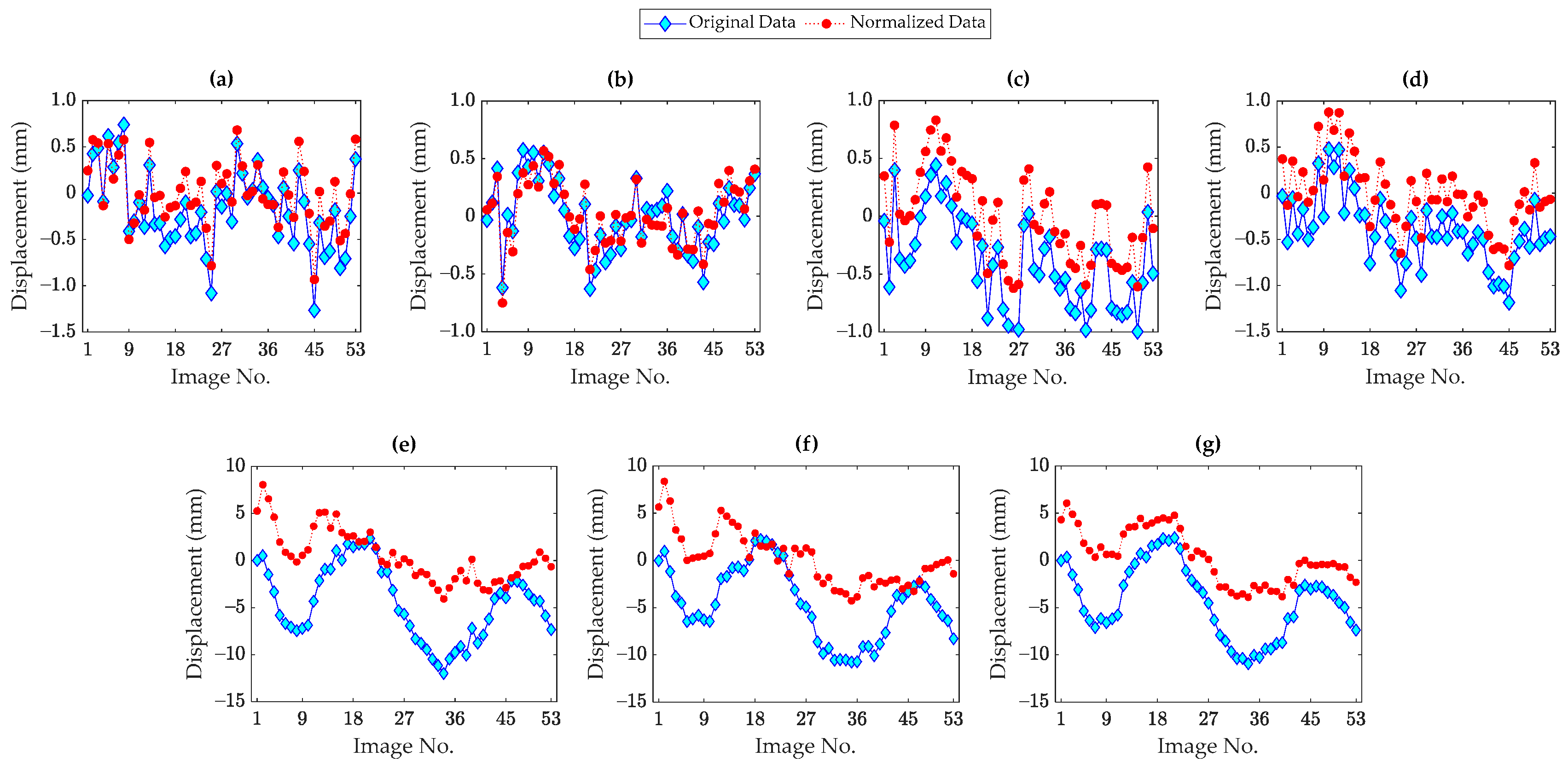
4.1. Principal Component Analysis (PCA)
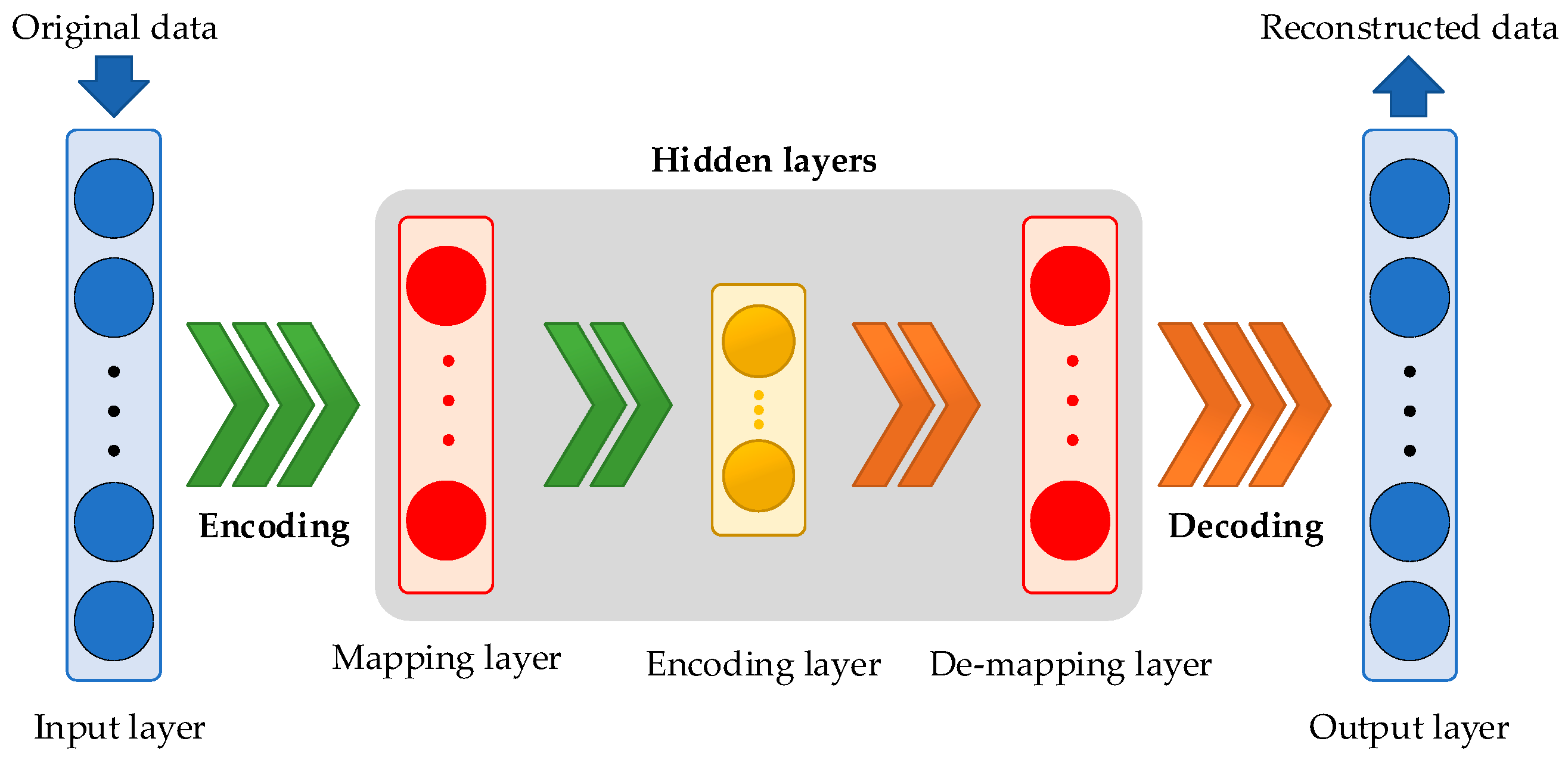
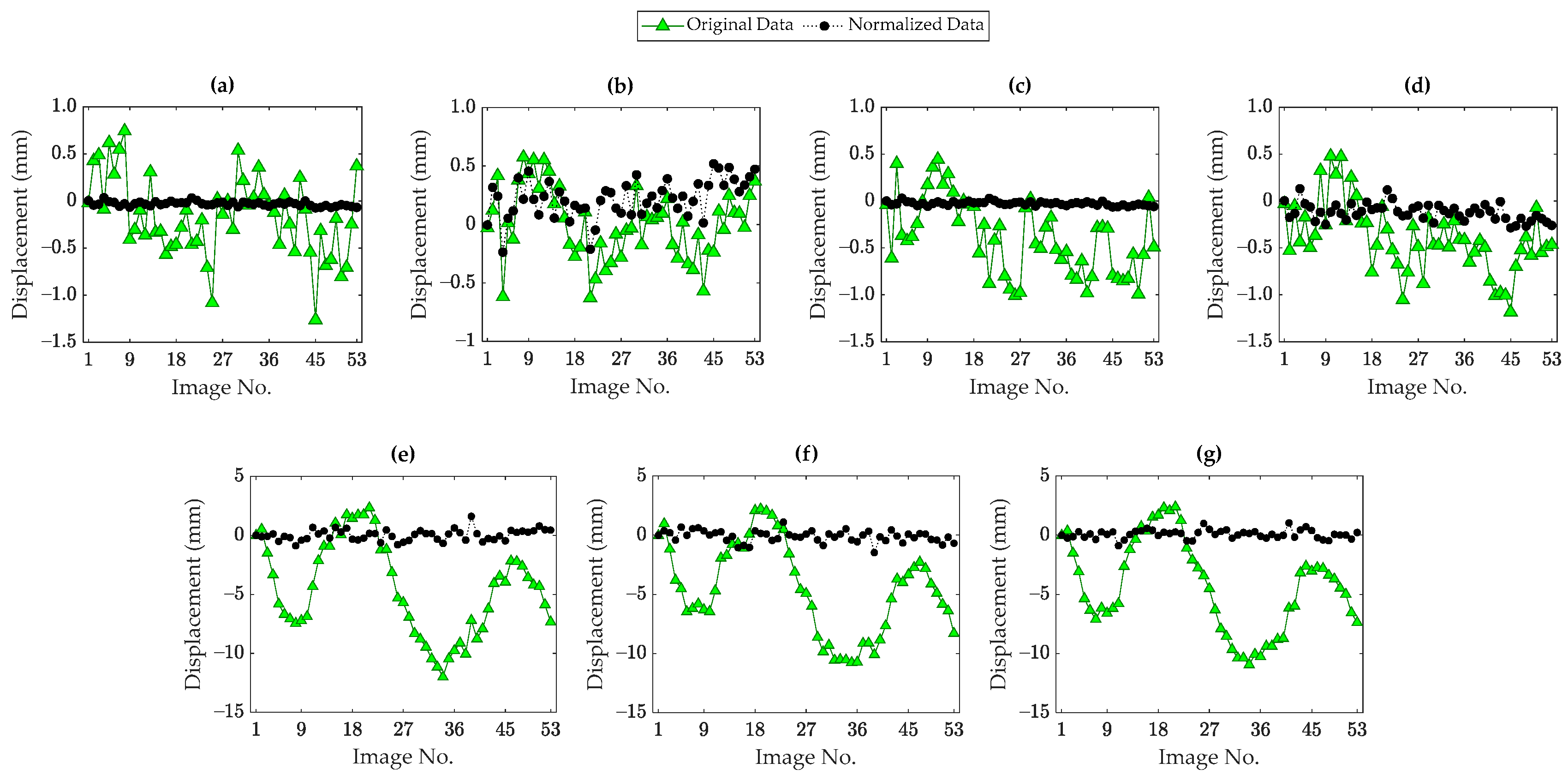
4.2. Deep Autoencoder (DAE)
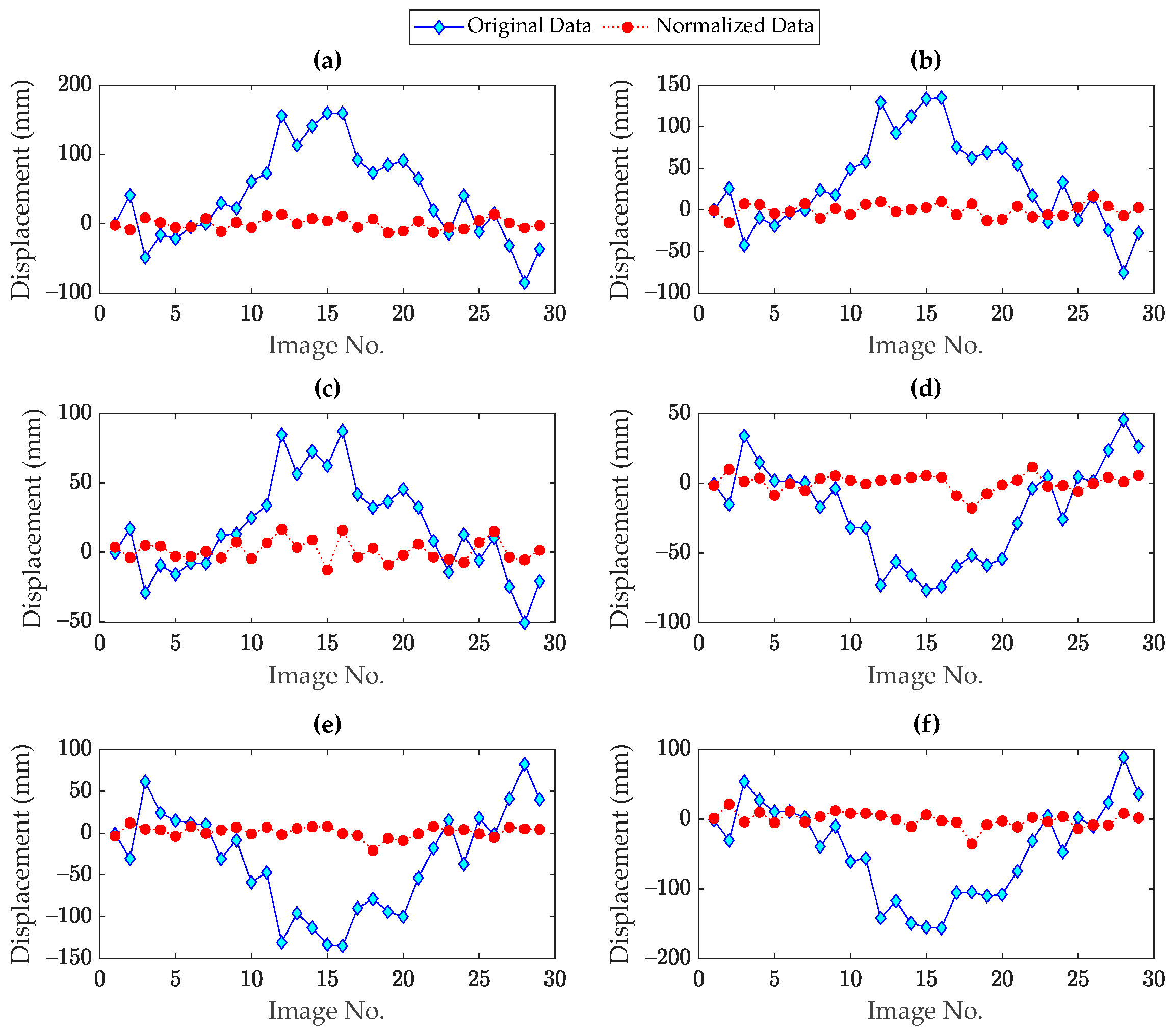
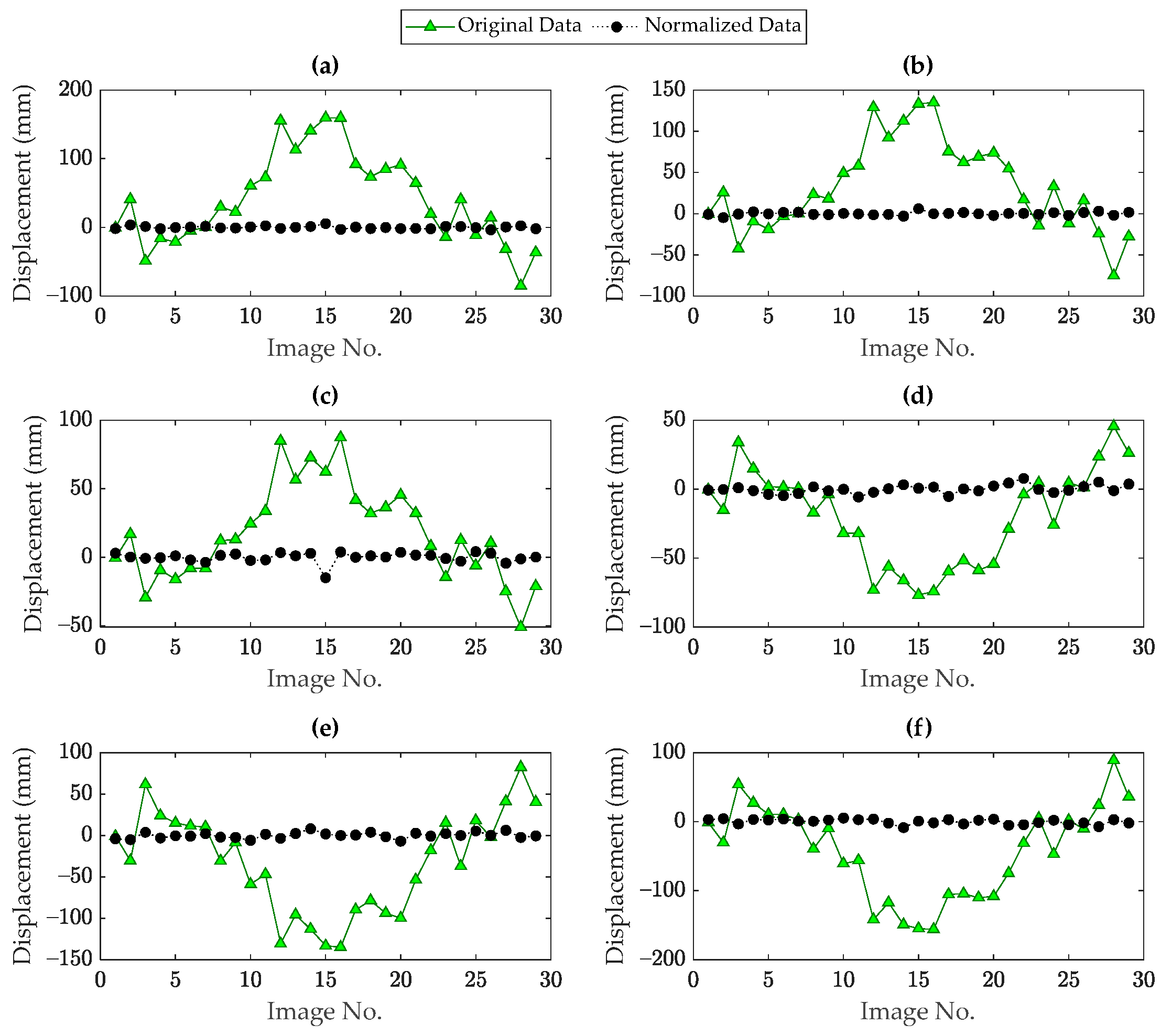
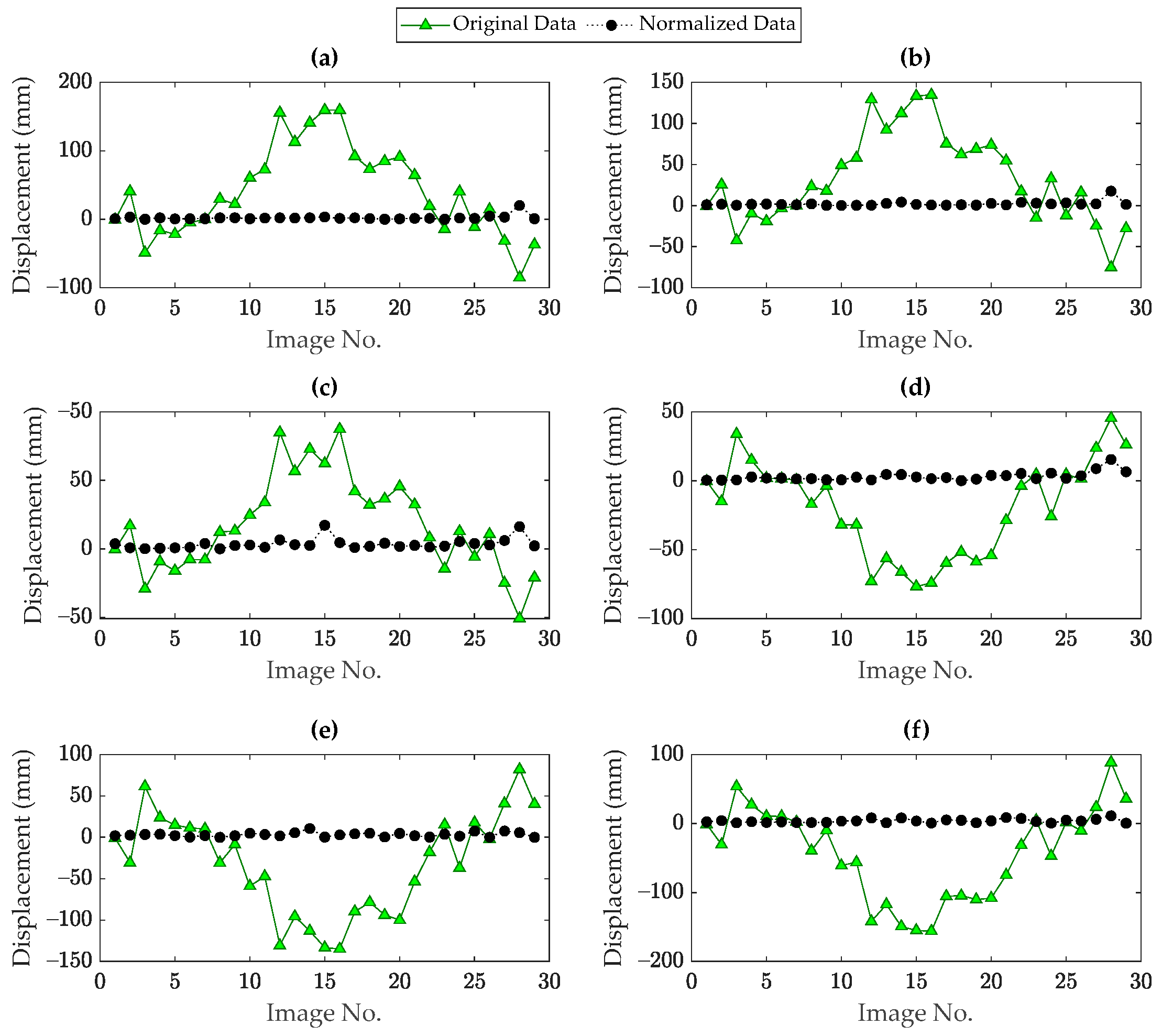
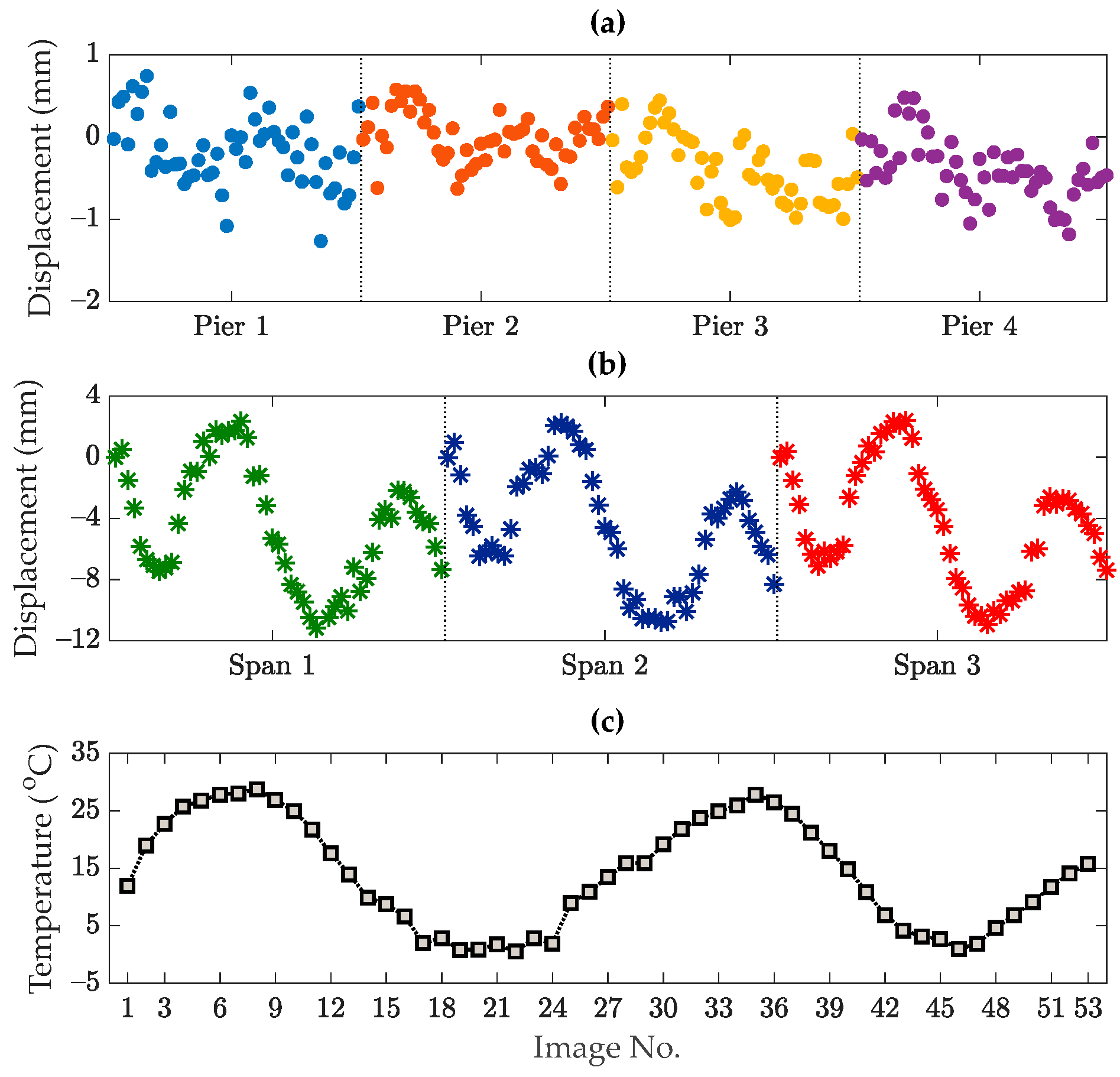
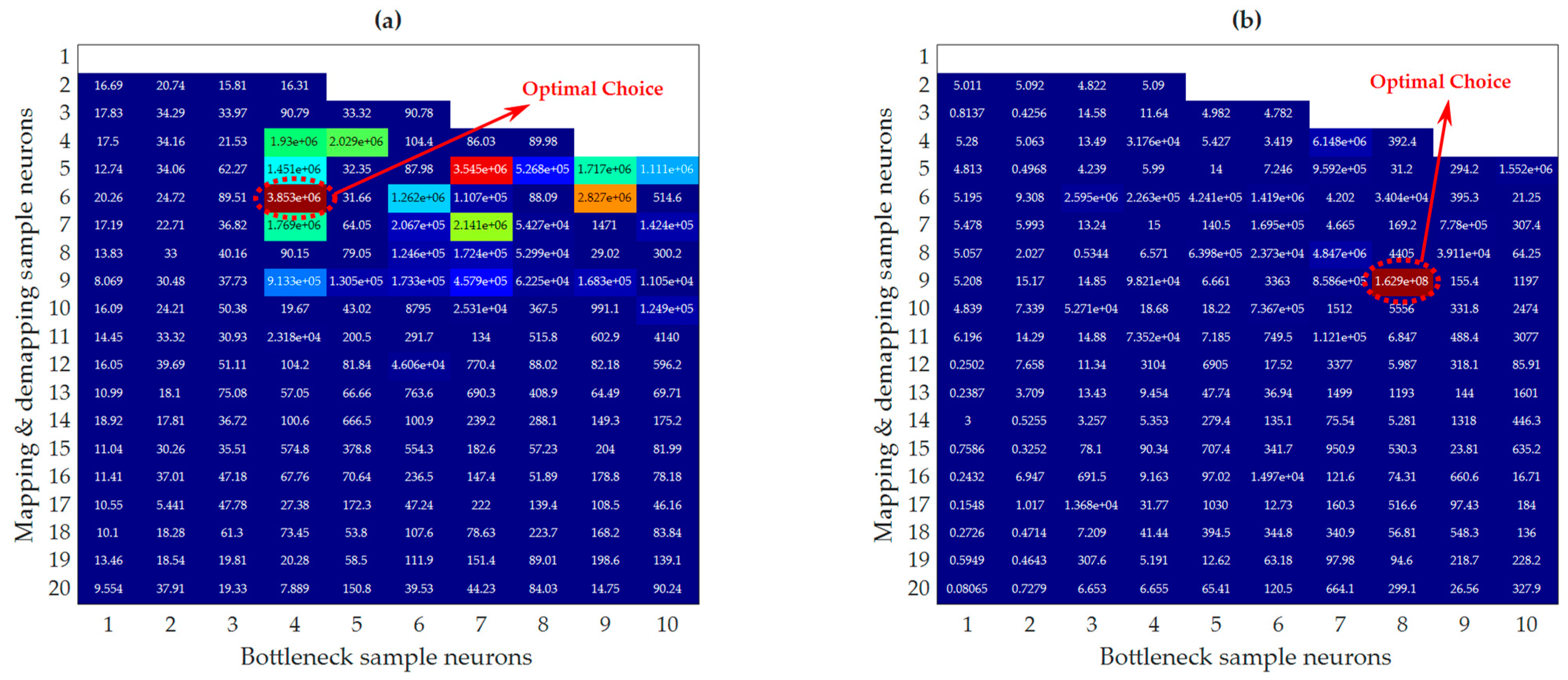
5. Applications
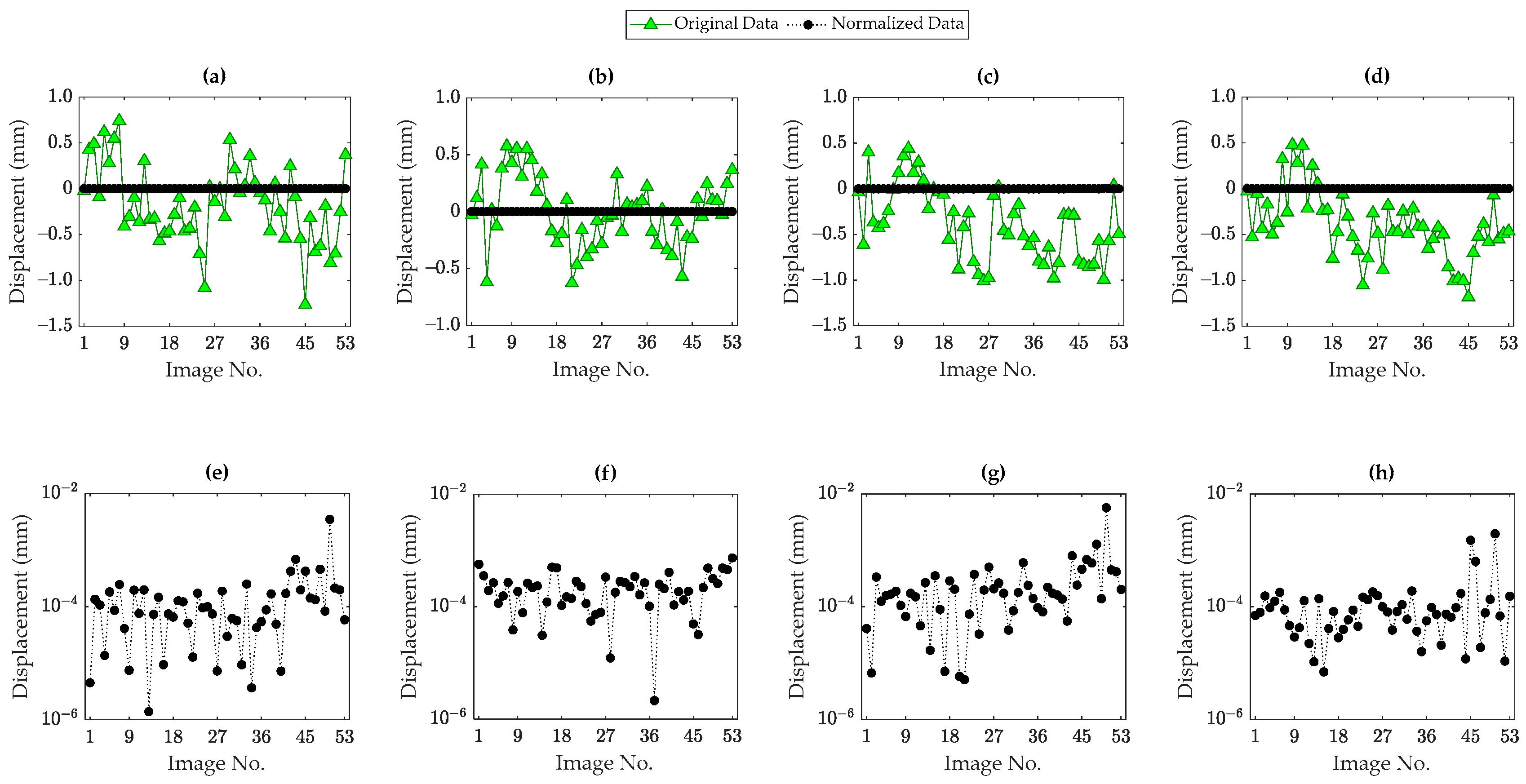
5.1. Dashengguan Bridge
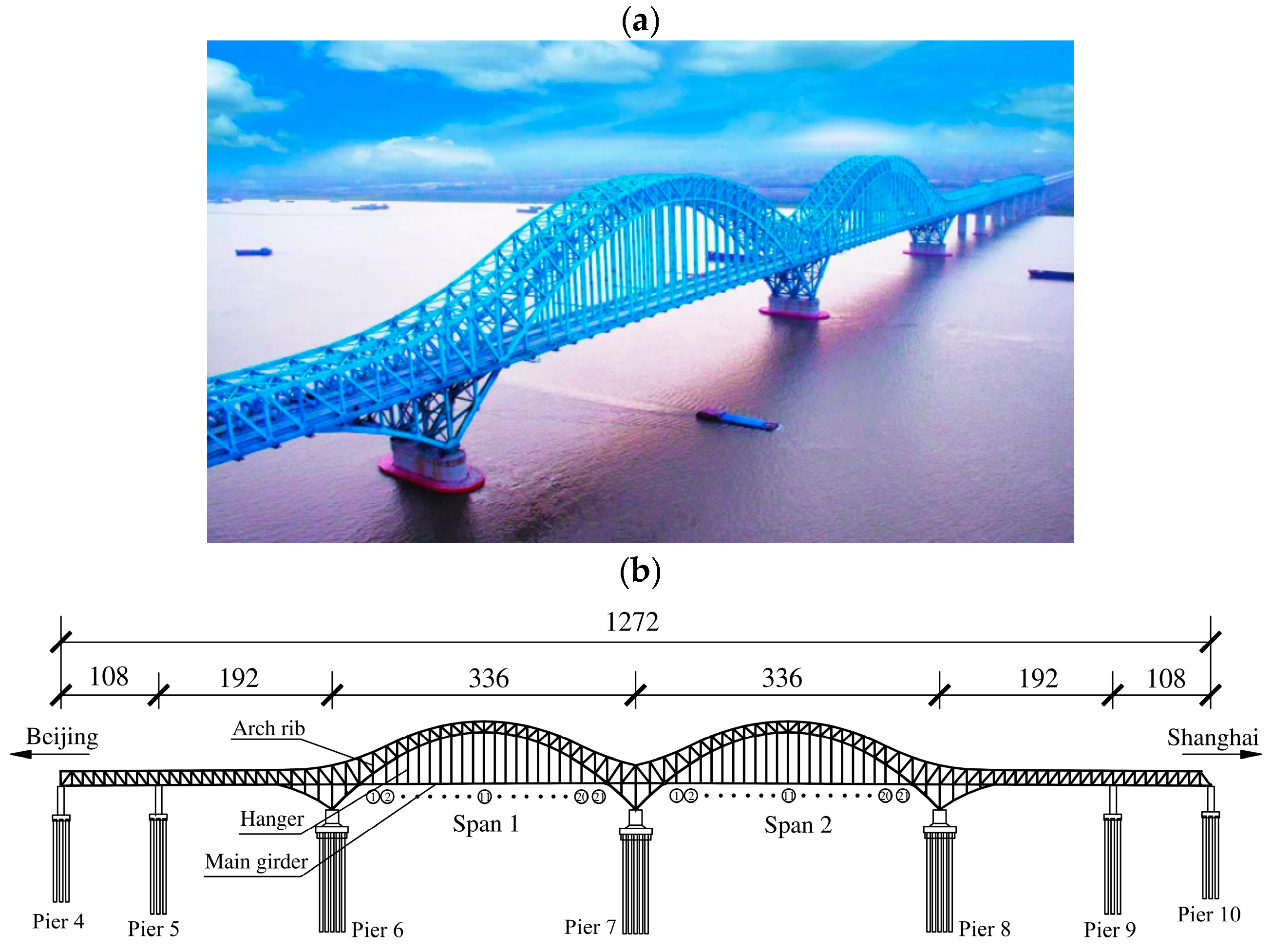
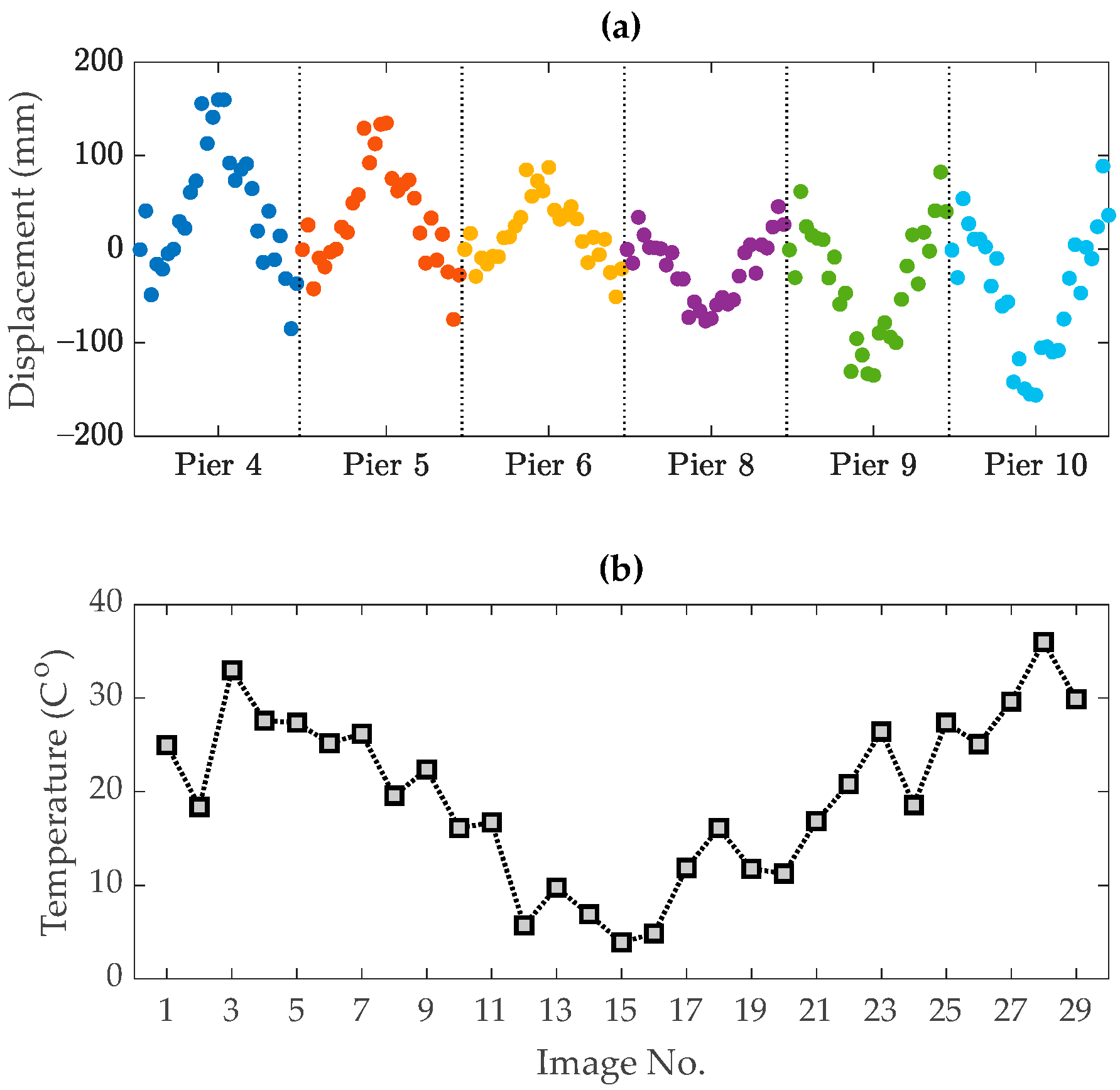
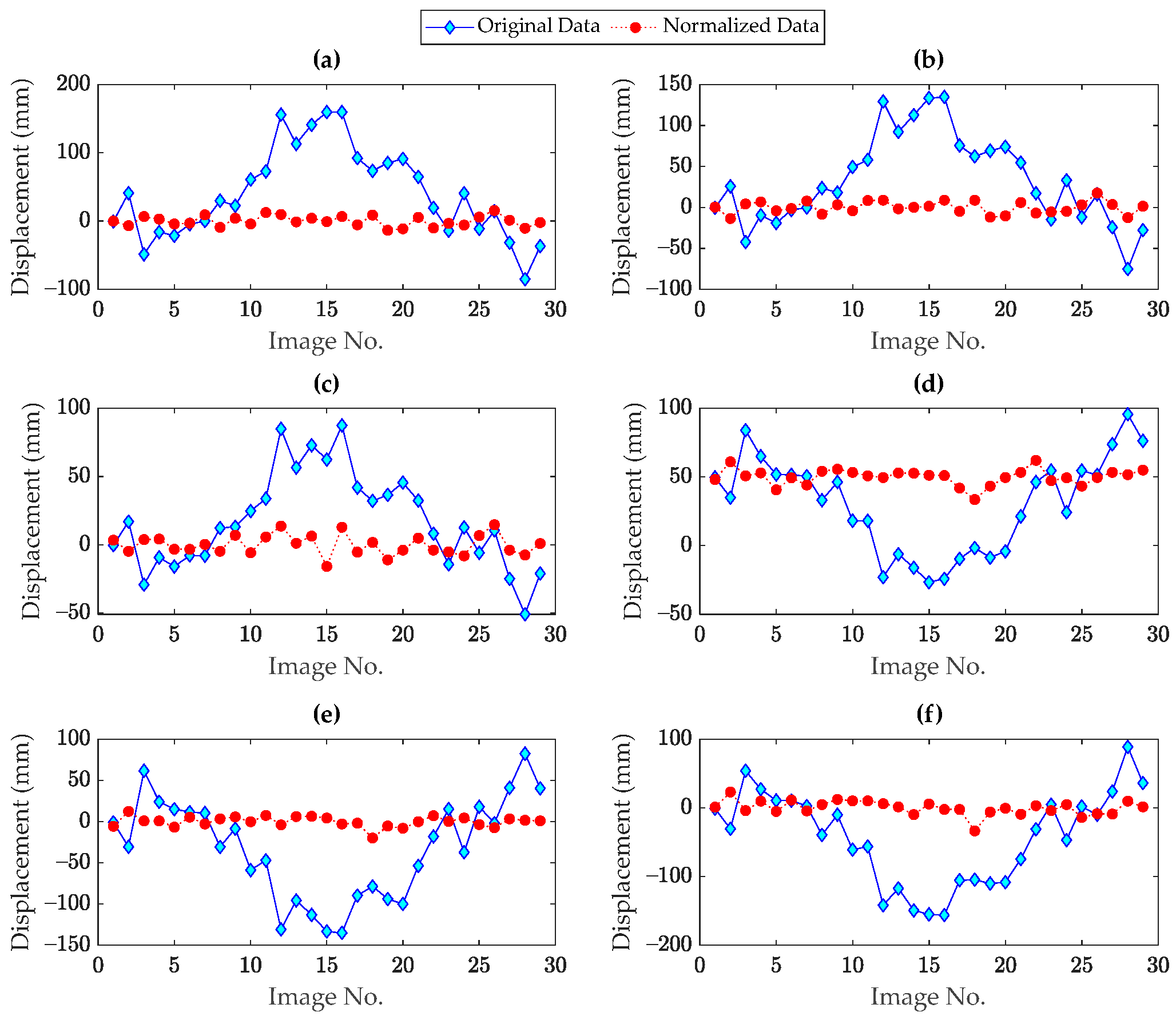
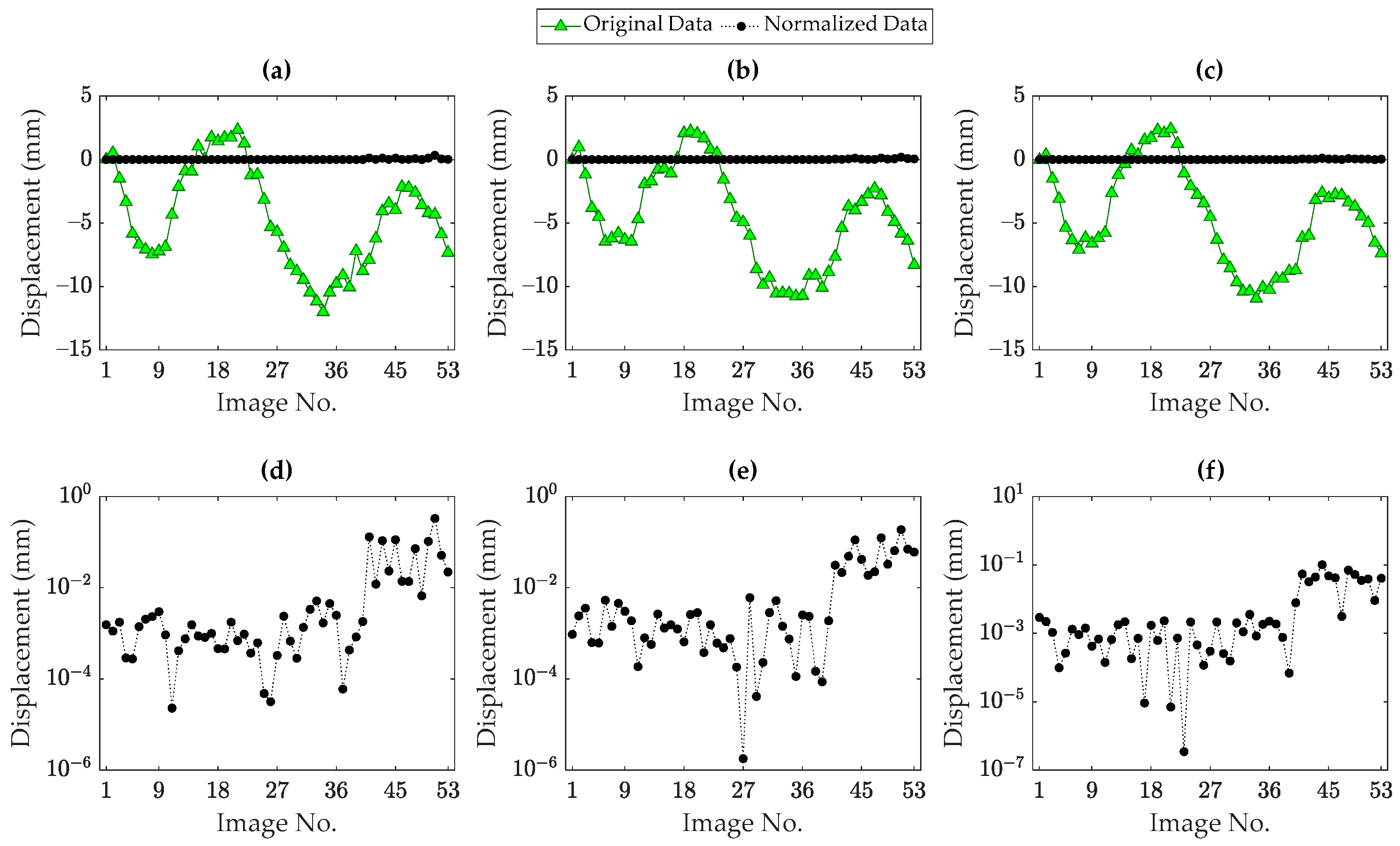
5.2. Rainbow Bridge
6. Conclusions
- i
- The input–output (supervised) data normalization techniques can perform well provided that the temperature is the main variability factor. When the other environmental and/or operational conditions influence the structure and these are not included in the supervised regression modeling, the input–output data normalization techniques fail in eliminating the variability sources. Under such circumstances, the residuals or normalized responses obtained from such techniques still contain the environmental and/or operational conditions leading to similarities in the forms of the original and normalized responses.
- ii
- Due to the importance of the input data in learning or developing input–output supervised models, it is essential to measure all possible environmental (e.g., humidity, wind speed and direction, etc.) and operational (e.g., traffic loads and volumes, live loads, etc.) conditions. When the measurements of such environmental and operational variability are not feasible, the best choice is to apply output-only (unsupervised) data normalization methods.
- iii
- In contrast to the input–output data normalization techniques, both the PCA and DAE models succeeded in accurately removing the thermal and other unmeasured variability conditions.
- iv
- In all cases of the influences of variability conditions and based on the R-squared values, especially in the problem of the Rainbow Bridge, the DAE-based data normalization yielded the best performance. Hence, it is preferred to apply this method to remove the environmental variability.
- v
- The findings of this research are suitable for long-term health monitoring of large-scale civil structures, particularly long-span bridges, with the aid of the remote sensing technology and providing normalized displacement responses insensitive to environmental and/or operational variability. However, it should be noted that a data normalization technique may be successful in removing a specific type of variability condition, but it might also hide changes due to damage, a sudden and critical event caused by an earthquake, and gradual variations due to a slow landslide or ageing. Hence, it is essential to evaluate the output of any data normalization technique based on a residual analysis based on some metrics, such as the R-squared statistic, and control charts for assessing anomalies in residual samples.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, J.; Xia, Y.; Weng, S. Review on field monitoring of high-rise structures. Struct. Contr. Health Monit. 2020, 27, e2629. [Google Scholar] [CrossRef]
- Scaioni, M.; Marsella, M.; Crosetto, M.; Tornatore, V.; Wang, J. Geodetic and Remote-Sensing Sensors for Dam Deformation Monitoring. Sensors 2018, 18, 3682. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.; La, H.M.; Gucunski, N. Review of Non-Destructive Civil Infrastructure Evaluation for Bridges: State-of-the-Art Robotic Platforms, Sensors and Algorithms. Sensors 2020, 20, 3954. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Jiang, W.; Meng, X.; Jiang, P.; Wang, K.; Xie, Y.; Ye, J. Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK. Remote Sens. 2018, 10, 364. [Google Scholar] [CrossRef]
- Gonen, S.; Erduran, E. A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sens. 2022, 14, 6054. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Liu, J.; Wang, L.; Tao, T.; Wu, D.; Chen, R. A Review of Global Navigation Satellite System (GNSS)-Based Dynamic Monitoring Technologies for Structural Health Monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Ullo, S.L.; Clemente, C.; Orlando, D. Perspectives on the Structural Health Monitoring of Bridges by Synthetic Aperture Radar. Remote Sens. 2020, 12, 3852. [Google Scholar] [CrossRef]
- Daneshvar, M.H.; Sarmadi, H. Unsupervised learning-based damage assessment of full-scale civil structures under long-term and short-term monitoring. Eng. Struct. 2022, 256, 114059. [Google Scholar] [CrossRef]
- Yang, H.; Xu, H.-C.; Jiao, S.-J.; Yin, F.-D. Semantic Image Segmentation Based Cable Vibration Frequency Visual Monitoring Using Modified Convolutional Neural Network with Pixel-wise Weighting Strategy. Remote Sens. 2021, 13, 1466. [Google Scholar] [CrossRef]
- Gardner, P.; Liu, X.; Worden, K. On the application of domain adaptation in structural health monitoring. Mech. Syst. Sig. Process. 2020, 138, 106550. [Google Scholar] [CrossRef]
- Sarmadi, H.; Yuen, K.-V. Early damage detection by an innovative unsupervised learning method based on kernel null space and peak-over-threshold. Comput. Aided Civ. Inf. 2021, 36, 1150–1167. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Saeedi Razavi, B.; Yuen, K.-V. Ensemble learning-based structural health monitoring by Mahalanobis distance metrics. Struct. Contr. Health Monit. 2021, 28, e2663. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; De Michele, C. Non-parametric empirical machine learning for short-term and long-term structural health monitoring. Struct. Health Monit. 2022, 21, 2700–2718. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B. Long-term health monitoring of concrete and steel bridges under large and missing data by unsupervised meta learning. Eng. Struct. 2023, 279, 115616. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; De Michele, C. On continuous health monitoring of bridges under serious environmental variability by an innovative multi-task unsupervised learning method. Struct. Infrastruct. Eng. 2023, 1–19. [Google Scholar] [CrossRef]
- Sarmadi, H.; Karamodin, A. A novel anomaly detection method based on adaptive Mahalanobis-squared distance and one-class kNN rule for structural health monitoring under environmental effects. Mech. Syst. Sig. Process. 2020, 140, 106495. [Google Scholar] [CrossRef]
- Entezami, A.; Arslan, A.N.; De Michele, C.; Behkamal, B. Online hybrid learning methods for real-time structural health monitoring using remote sensing and small displacement data. Remote Sens. 2022, 14, 3357. [Google Scholar] [CrossRef]
- Entezami, A.; De Michele, C.; Arslan, A.N.; Behkamal, B. Detection of partially structural collapse using long-term small displacement data from satellite images. Sensors 2022, 22, 4964. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Ren, Y.; Zhao, D.-Y.; Yang, J.; Zhang, D.-Y. Modeling and Separation of Thermal Effects from Cable-Stayed Bridge Response. J. Bridge Eng. 2019, 24, 04019028. [Google Scholar] [CrossRef]
- Sarmadi, H.; Yuen, K.-V. Structural health monitoring by a novel probabilistic machine learning method based on extreme value theory and mixture quantile modeling. Mech. Syst. Sig. Process. 2022, 173, 109049. [Google Scholar] [CrossRef]
- Kita, A.; Cavalagli, N.; Ubertini, F. Temperature effects on static and dynamic behavior of Consoli Palace in Gubbio, Italy. Mech. Syst. Sig. Process. 2019, 120, 180–202. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, D.-H.; Yi, T.-H.; Zhang, G.-H.; Han, J.-G. Eliminating environmental and operational effects on structural modal frequency: A comprehensive review. Struct. Contr. Health Monit. 2022, 29, e3073. [Google Scholar] [CrossRef]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Regression models for structural health monitoring of welded bridge joints based on temperature, traffic and strain measurements. Struct. Health Monit. 2015, 14, 648–662. [Google Scholar] [CrossRef]
- Roberts, C.; Cava, D.G.; Avendaño-Valencia, L.D. Addressing practicalities in multivariate nonlinear regression for mitigating environmental and operational variations. Struct. Health Monit. 2022, 22, 1237–1255. [Google Scholar] [CrossRef]
- Laory, I.; Trinh, T.N.; Smith, I.F.C.; Brownjohn, J.M.W. Methodologies for predicting natural frequency variation of a suspension bridge. Eng. Struct. 2014, 80, 211–221. [Google Scholar] [CrossRef]
- Jang, J.; Smyth, A.W. Data-driven models for temperature distribution effects on natural frequencies and thermal prestress modeling. Struct. Contr. Health Monit. 2020, 27, e2489. [Google Scholar] [CrossRef]
- Ma, K.-C.; Yi, T.-H.; Yang, D.-H.; Li, H.-N.; Liu, H. Nonlinear Uncertainty Modeling between Bridge Frequencies and Multiple Environmental Factors Based on Monitoring Data. J. Perform. Constr. Facil. 2021, 35, 04021056. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Zhou, H.F.; Ko, J.M. Generalization Capability of Neural Network Models for Temperature-Frequency Correlation Using Monitoring Data. J. Struct. Eng. 2009, 135, 1290–1300. [Google Scholar] [CrossRef]
- Coletta, G.; Miraglia, G.; Pecorelli, M.; Ceravolo, R.; Cross, E.; Surace, C.; Worden, K. Use of the cointegration strategies to remove environmental effects from data acquired on historical buildings. Eng. Struct. 2019, 183, 1014–1026. [Google Scholar] [CrossRef]
- Qin, Y.; Li, Y.; Liu, G. Separation of the Temperature Effect on Structure Responses via LSTM-Particle Filter Method Considering Outlier from Remote Cloud Platforms. Remote Sens. 2022, 14, 4629. [Google Scholar] [CrossRef]
- Yan, A.-M.; Kerschen, G.; De Boe, P.; Golinval, J.-C. Structural damage diagnosis under varying environmental conditions—Part II: Local PCA for non-linear cases. Mech. Syst. Sig. Process. 2005, 19, 865–880. [Google Scholar] [CrossRef]
- Reynders, E.; Wursten, G.; De Roeck, G. Output-only structural health monitoring in changing environmental conditions by means of nonlinear system identification. Struct. Health Monit. 2014, 13, 82–93. [Google Scholar] [CrossRef]
- Comanducci, G.; Magalhães, F.; Ubertini, F.; Cunha, Á. On vibration-based damage detection by multivariate statistical techniques: Application to a long-span arch bridge. Struct. Health Monit. 2016, 15, 505–524. [Google Scholar] [CrossRef]
- Figueiredo, E.; Park, G.; Farrar, C.R.; Worden, K.; Figueiras, J. Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 2011, 10, 559–572. [Google Scholar] [CrossRef]
- Sarmadi, H. Investigation of machine learning methods for structural safety assessment under variability in data: Comparative studies and new approaches. J. Perform. Constr. Facil. 2021, 35, 04021090. [Google Scholar] [CrossRef]
- Daneshvar, M.H.; Sarmadi, H.; Yuen, K.-V. A locally unsupervised hybrid learning method for removing environmental effects under different measurement periods. Measurement 2023, 208, 112465. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Behkamal, B.; De Michele, C. Partially online damage detection using long-term modal data under severe environmental effects by unsupervised feature selection and local metric learning. J. Civ. Struct. Health Monit. 2022, 12, 1043–1066. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; De Michele, C. Probabilistic data self-clustering based on semi-parametric extreme value theory for structural health monitoring. Mech. Syst. Sig. Process. 2023, 187, 109976. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Magalhães, F. Unsupervised data normalization for continuous dynamic monitoring by an innovative hybrid feature weighting-selection algorithm and natural nearest neighbor searching. Struct. Health Monit. 2023; in press. [Google Scholar] [CrossRef]
- Teng, J.; Tang, D.-H.; Hu, W.-H.; Lu, W.; Feng, Z.-W.; Ao, C.-F.; Liao, M.-H. Mechanism of the effect of temperature on frequency based on long-term monitoring of an arch bridge. Struct. Health Monit. 2021, 20, 1716–1737. [Google Scholar] [CrossRef]
- Yang, D.-H.; Yi, T.-H.; Li, H.-N.; Zhang, Y.-F. Monitoring and analysis of thermal effect on tower displacement in cable-stayed bridge. Measurement 2018, 115, 249–257. [Google Scholar] [CrossRef]
- Xia, Q.; Zhang, J.; Tian, Y.; Zhang, Y. Experimental Study of Thermal Effects on a Long-Span Suspension Bridge. J. Bridge Eng. 2017, 22, 04017034. [Google Scholar] [CrossRef]
- Giordano, P.; Turksezer, Z.; Previtali, M.; Limongelli, M. Damage detection on a historic iron bridge using satellite DInSAR data. Struct. Health Monit. 2022, 21, 2291–2311. [Google Scholar] [CrossRef]
- Huang, Q.; Crosetto, M.; Monserrat, O.; Crippa, B. Displacement monitoring and modelling of a high-speed railway bridge using C-band Sentinel-1 data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 204–211. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, L.; Yang, M.; Luo, H.; Liao, M.; Ding, X. Mapping surface deformation and thermal dilation of arch bridges by structure-driven multi-temporal DInSAR analysis. Remote Sens. Environ. 2018, 216, 71–90. [Google Scholar] [CrossRef]
- Farneti, E.; Cavalagli, N.; Costantini, M.; Trillo, F.; Minati, F.; Venanzi, I.; Ubertini, F. A method for structural monitoring of multispan bridges using satellite InSAR data with uncertainty quantification and its pre-collapse application to the Albiano-Magra Bridge in Italy. Struct. Health Monit. 2023, 22, 353–371. [Google Scholar] [CrossRef]
- Bianchini, S.; Pratesi, F.; Nolesini, T.; Casagli, N. Building Deformation Assessment by Means of Persistent Scatterer Interferometry Analysis on a Landslide-Affected Area: The Volterra (Italy) Case Study. Remote Sens. 2015, 7, 4678–4701. [Google Scholar] [CrossRef]
- Cavalagli, N.; Kita, A.; Falco, S.; Trillo, F.; Costantini, M.; Ubertini, F. Satellite radar interferometry and in-situ measurements for static monitoring of historical monuments: The case of Gubbio, Italy. Remote Sens. Environ. 2019, 235, 111453. [Google Scholar] [CrossRef]
- Zhu, M.; Wan, X.; Fei, B.; Qiao, Z.; Ge, C.; Minati, F.; Vecchioli, F.; Li, J.; Costantini, M. Detection of Building and Infrastructure Instabilities by Automatic Spatiotemporal Analysis of Satellite SAR Interferometry Measurements. Remote Sens. 2018, 10, 1816. [Google Scholar] [CrossRef]
- Drougkas, A.; Verstrynge, E.; Van Balen, K.; Shimoni, M.; Croonenborghs, T.; Hayen, R.; Declercq, P.-Y. Country-scale InSAR monitoring for settlement and uplift damage calculation in architectural heritage structures. Struct. Health Monit. 2021, 20, 2317–2336. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Hu, W.-H.; Cunha, Á.; Caetano, E.; Rohrmann, R.G.; Said, S.; Teng, J. Comparison of different statistical approaches for removing environmental/operational effects for massive data continuously collected from footbridges. Struct. Contr. Health Monit. 2017, 24, e1955. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Kung, S.Y. Kernel Methods and Machine Learning; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing enviroment. Mech. Syst. Sig. Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Worden, K. A comparison of linear approaches to filter out environmental effects in structural health monitoring. Mech. Syst. Sig. Process. 2018, 105, 1–15. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Singh, A.; Kushwaha, S.; Alarfaj, M.; Singh, M. Comprehensive Overview of Backpropagation Algorithm for Digital Image Denoising. Electronics 2022, 11, 1590. [Google Scholar] [CrossRef]
- Charte, D.; Charte, F.; García, S.; del Jesus, M.J.; Herrera, F. A practical tutorial on autoencoders for nonlinear feature fusion: Taxonomy, models, software and guidelines. Inf. Fusion 2018, 44, 78–96. [Google Scholar] [CrossRef]
- Niu, Y.; Ye, Y.; Zhao, W.; Duan, Y.; Shu, J. Identifying Modal Parameters of a Multispan Bridge Based on High-Rate GNSS-RTK Measurement Using the CEEMD-RDT Approach. J. Bridge Eng. 2021, 26, 04021049. [Google Scholar] [CrossRef]
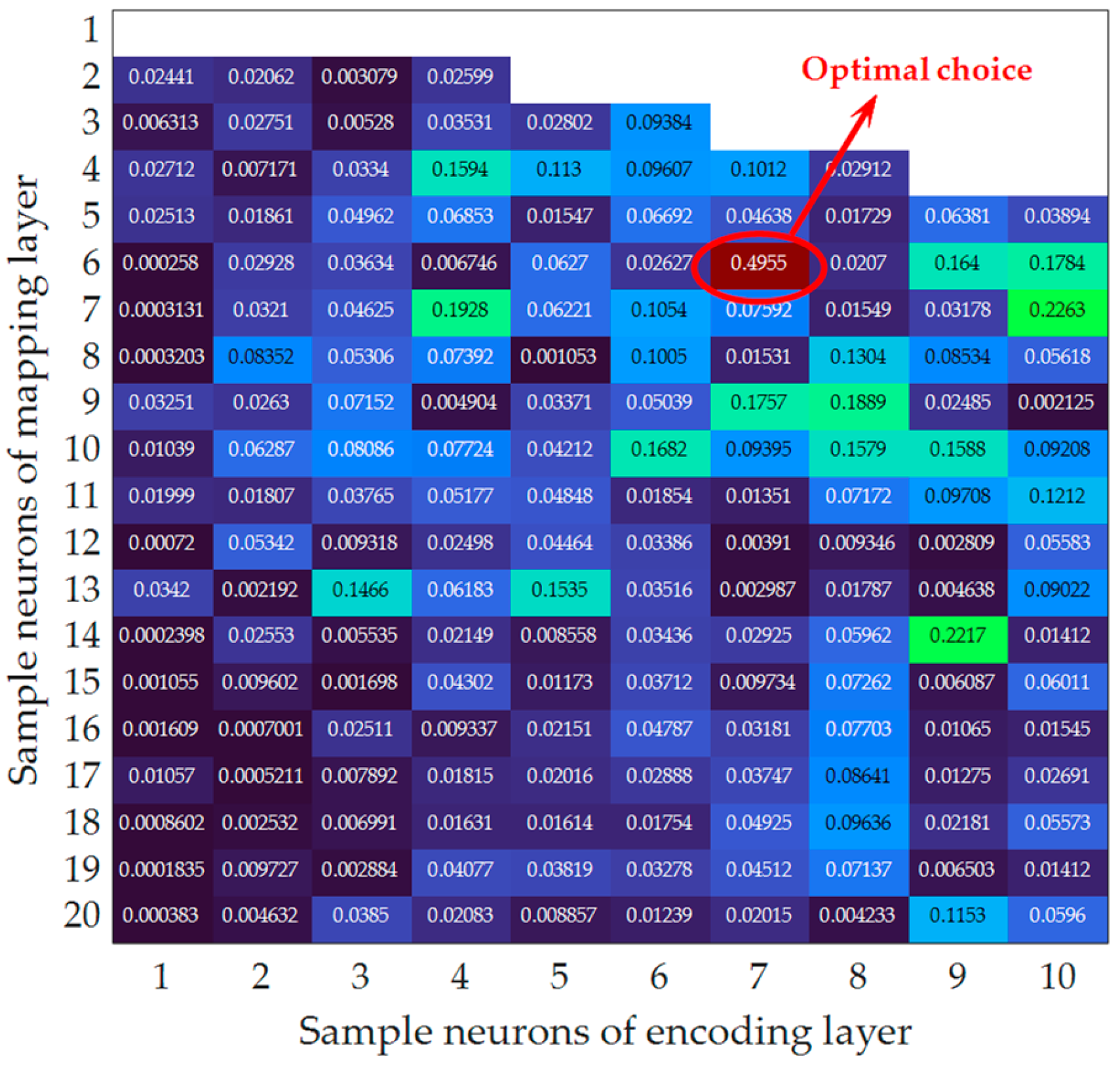

| Pier No. | Kernel Function | Kernel Parameters | α | |
|---|---|---|---|---|
| σf | l | |||
| 4 | KS | 329.15 | 69.34 | 120.10 |
| 5 | KS | 245.15 | 61.97 | 80.36 |
| 6 | KS | 119.28 | 48.44 | 28.26 |
| 8 | KS | 88.43 | 36.14 | −9.66 |
| 9 | KS | 203.83 | 48.69 | −10.49 |
| 10 | KS | 226.69 | 48.49 | −37.65 |
| Pier No. | Kernel Function | Kernel Parameters | Support Vectors | Bias | |
|---|---|---|---|---|---|
| s | q | ||||
| 4 | KL | 1 | - | 19 | 39.75 |
| 5 | KL | 1 | - | 13 | 33.14 |
| 6 | KL | 1 | - | 21 | 16.12 |
| 8 | KL | 1 | - | 29 | −18.15 |
| 9 | KL | 1 | - | 17 | −31.17 |
| 10 | KL | 1 | - | 26 | −42.81 |
| Pier No. | Data Normalization Models | |||
|---|---|---|---|---|
| GPR | SVR | PCA | DAE | |
| 4 | 0.9867 | 0.9854 | 0.9991 | 0.9957 |
| 5 | 0.9807 | 0.9798 | 0.9986 | 0.9950 |
| 6 | 0.9555 | 0.9541 | 0.9888 | 0.9762 |
| 8 | 0.9719 | 0.9701 | 0.9922 | 0.9842 |
| 9 | 0.9892 | 0.9877 | 0.9966 | 0.9955 |
| 10 | 0.9757 | 0.9754 | 0.9970 | 0.9951 |
| Element | Kernel Function | Kernel Parameters | α | |
|---|---|---|---|---|
| σf | l | |||
| Pier 1 | KS | 13.0332 | 0.2857 | −0.1380 |
| Pier 2 | KS | 0.0011 | 0.3029 | 0.0011 |
| Pier 3 | KS | 0.0052 | 0.3957 | −0.3946 |
| Pier 4 | KS | 49.0320 | 0.0001 | −0.4012 |
| Span 1 | KS | 22.4041 | 4.9274 | −3.1307 |
| Span 2 | KS | 18.7924 | 4.3413 | −2.7899 |
| Span 3 | KS | 18.3722 | 4.1048 | −3.2173 |
| Element | Kernel Function | Kernel Parameters | Support Vectors | Bias | |
|---|---|---|---|---|---|
| s | q | ||||
| Pier 1 | KP | - | 3 | 53 | −0.47 |
| Pier 2 | KP | - | 3 | 49 | −0.24 |
| Pier 3 | KP | - | 3 | 34 | −0.38 |
| Pier 4 | KP | - | 3 | 40 | −0.41 |
| Span 1 | KP | - | 3 | 53 | 0.31 |
| Span 2 | KP | - | 3 | 43 | 1.49 |
| Span 3 | KP | - | 3 | 52 | −1.87 |
| Elements | Data Normalization Models | |||
|---|---|---|---|---|
| GPR | SVR | PCA | DAE | |
| Pier 1 | 0.3727 | 0.3452 | 0.9911 | 0.9994 |
| Pier 2 | 0.9990 | 0.0507 | 0.1641 | 0.9996 |
| Pier 3 | 0.9975 | 0.0001 | 0.9924 | 0.9992 |
| Pier 4 | 0.0005 | 0.0003 | 0.8302 | 0.9994 |
| Span 1 | 0.5162 | 0.5113 | 0.9860 | 0.9998 |
| Span 2 | 0.4850 | 0.4575 | 0.9831 | 0.9994 |
| Span 3 | 0.5270 | 0.5051 | 0.9906 | 0.9995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behkamal, B.; Entezami, A.; De Michele, C.; Arslan, A.N. Elimination of Thermal Effects from Limited Structural Displacements Based on Remote Sensing by Machine Learning Techniques. Remote Sens. 2023, 15, 3095. https://doi.org/10.3390/rs15123095
Behkamal B, Entezami A, De Michele C, Arslan AN. Elimination of Thermal Effects from Limited Structural Displacements Based on Remote Sensing by Machine Learning Techniques. Remote Sensing. 2023; 15(12):3095. https://doi.org/10.3390/rs15123095
Chicago/Turabian StyleBehkamal, Bahareh, Alireza Entezami, Carlo De Michele, and Ali Nadir Arslan. 2023. "Elimination of Thermal Effects from Limited Structural Displacements Based on Remote Sensing by Machine Learning Techniques" Remote Sensing 15, no. 12: 3095. https://doi.org/10.3390/rs15123095
APA StyleBehkamal, B., Entezami, A., De Michele, C., & Arslan, A. N. (2023). Elimination of Thermal Effects from Limited Structural Displacements Based on Remote Sensing by Machine Learning Techniques. Remote Sensing, 15(12), 3095. https://doi.org/10.3390/rs15123095











