Hybrid-Scale Hierarchical Transformer for Remote Sensing Image Super-Resolution
Abstract
1. Introduction
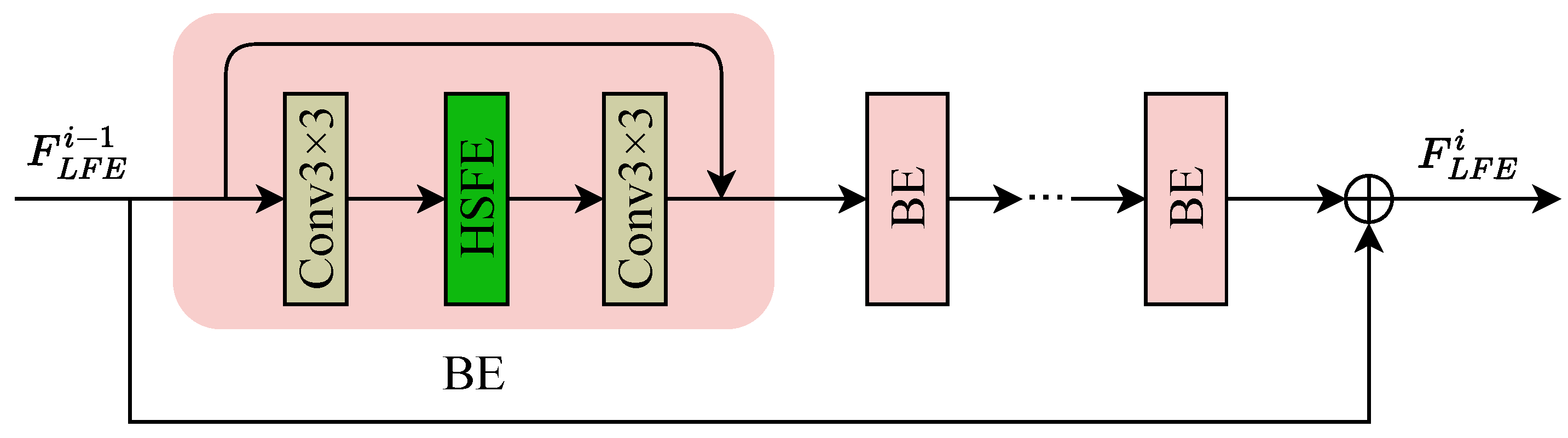
- We propose an HSFE module with two branches to leverage the internal recursive information from both single and cross scales within the images for enriching the feature representations for RSISR.
- We designed a CSET module to capture long-range dependencies and efficiently calculate the relevance between high-dimension and low-dimension features. It helps the network reconstruct SR images with rich edges and contours.
- Jointly incorporating the HSFE and CSET modules, we formed the HSTNet for RSISR. Extensive experiments on two challenging remote sensing datasets verify the superiority of the proposed model.
2. Related Literature
2.1. CNN-Based SR Models
2.2. Transformer-Based SR Models
3. Methodology
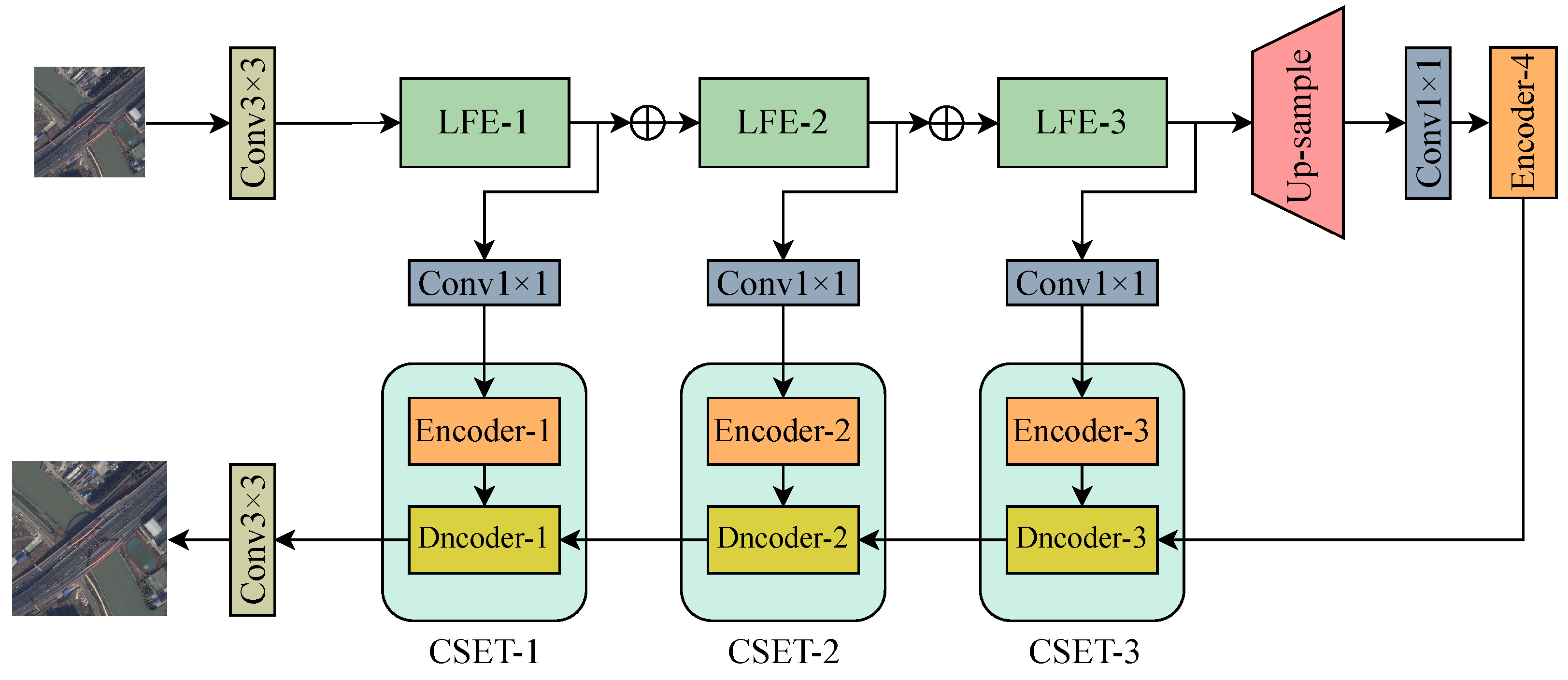
3.1. Overall Framework
3.2. Hybrid-Scale Feature Exploitation Module
3.3. Cross-Scale Enhancement Transformer Module
4. Experiments
4.1. Experimental Dataset and Settings
4.2. Implementation Details
4.3. Comparison with Other Methods
4.3.1. Quantitative Evaluation
4.3.2. Qualitative Evaluation
4.4. Results on Real Remote Sensing Data
4.5. Ablation Studies
4.5.1. Ablation Studies on the LFE Module
4.5.2. Ablation Studies on the CSET Module
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrie, L.; Oucheikh, R.; Nilsson, Å.; Oxenstierna, A.; Cederholm, P.; Wei, L.; Richter, K.F.; Olsson, P. Label Placement Challenges in City Wayfinding Map Production—Identification and Possible Solutions. J. Geovisualization Spat. Anal. 2022, 6, 16. [Google Scholar] [CrossRef]
- Kokila, S.; Jayachandran, A. Hybrid Behrens-Fisher- and Gray Contrast–Based Feature Point Selection for Building Detection from Satellite Images. J. Geovisualization Spat. Anal. 2023, 7, 8. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L.; Huang, B.; Li, P. A MAP Approach for Joint Motion Estimation, Segmentation, and Super Resolution. IEEE Trans. Image Process. 2007, 16, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Köhler, T.; Huang, X.; Schebesch, F.; Aichert, A.; Maier, A.K.; Hornegger, J. Robust Multiframe Super-Resolution Employing Iteratively Re-Weighted Minimization. IEEE Trans. Comput. Imaging 2016, 2, 42–58. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X. An edge-guided image interpolation algorithm via directional filtering and data fusion. IEEE Trans. Image Process. 2006, 15, 2226–2238. [Google Scholar] [CrossRef]
- Hung, K.W.; Siu, W.C. Robust Soft-Decision Interpolation Using Weighted Least Squares. IEEE Trans. Image Process. 2012, 21, 1061–1069. [Google Scholar] [CrossRef]
- Lu, X.; Yuan, H.; Yuan, Y.; Yan, P.; Li, L.; Li, X. Local learning-based image super-resolution. In Proceedings of the 2011 IEEE 13th International Workshop on Multimedia Signal Processing, Hangzhou, China, 17–19 October 2011; pp. 1–5. [Google Scholar]
- Zhang, K.; Gao, X.; Tao, D.; Li, X. Single Image Super-Resolution With Non-Local Means and Steering Kernel Regression. IEEE Trans. Image Process. 2012, 21, 4544–4556. [Google Scholar] [CrossRef]
- Schulter, S.; Leistner, C.; Bischof, H. Fast and accurate image upscaling with super-resolution forests. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3791–3799. [Google Scholar]
- Wang, L.; Guo, Y.; Liu, L.; Lin, Z.; Deng, X.; An, W. Deep Video Super-Resolution Using HR Optical Flow Estimation. IEEE Trans. Image Process. 2020, 29, 4323–4336. [Google Scholar] [CrossRef]
- Chang, K.; Ding, P.L.K.; Li, B. Single image super-resolution using collaborative representation and non-local self-similarity. Signal Process. 2018, 149, 49–61. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Li, Y.; Sixou, B.; Peyrin, F. A review of the deep learning methods for medical images super resolution problems. Irbm 2021, 42, 120–133. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Mo, W. Transformer-based Multi-Stage Enhancement for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–11. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Xu, J.; Zhang, L.; Zuo, W.; Zhang, D.; Feng, X. Patch Group Based Nonlocal Self-Similarity Prior Learning for Image Denoising. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 244–252. [Google Scholar]
- Michaeli, T.; Irani, M. Blind Deblurring Using Internal Patch Recurrence. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Freedman, G.; Fattal, R. Image and video upscaling from local self-examples. ACM Trans. Graph. 2011, 30, 12:1–12:11. [Google Scholar] [CrossRef]
- Yang, J.; Lin, Z.L.; Cohen, S.D. Fast Image Super-Resolution Based on In-Place Example Regression. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1059–1066. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. “Zero-Shot” Super-Resolution Using Deep Internal Learning. In Proceedings of the Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Pan, Z.; Yu, J.; Huang, H.; Hu, S.; Zhang, A.; Ma, H.; Sun, W. Super-Resolution Based on Compressive Sensing and Structural Self-Similarity for Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4864–4876. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11065–11074. [Google Scholar]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback network for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3867–3876. [Google Scholar]
- Lei, S.; Shi, Z.; Zou, Z. Super-Resolution for Remote Sensing Images via Local–Global Combined Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Fernández-Beltran, R.; Plaza, J.; Plaza, A.J.; Li, J. Remote Sensing Single-Image Superresolution Based on a Deep Compendium Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1432–1436. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Zhao, Y.; Yan, J.; Fan, L.; Chen, L. Lightweight Single-Image Super-Resolution Network with Attentive Auxiliary Feature Learning. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Ni, N.; Wu, H.; Zhang, L. Hierarchical Feature Aggregation and Self-Learning Network for Remote Sensing Image Continuous-Scale Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Chen, J. Multi-Scale Fast Fourier Transform Based Attention Network for Remote-Sensing Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2728–2740. [Google Scholar] [CrossRef]
- Liang, G.M.; KinTak, U.; Yin, H.; Liu, J.; Luo, H. Multi-scale hybrid attention graph convolution neural network for remote sensing images super-resolution. Signal Process. 2023, 207, 108954. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, Z.; Lu, T.; Wu, C.; Wang, J. Remote Sensing Image Super-Resolution via Multiscale Enhancement Network. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning Texture Transformer Network for Image Super-Resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5790–5799. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Gool, L.V.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Fang, J.; Lin, H.; Chen, X.; Zeng, K. A Hybrid Network of CNN and Transformer for Lightweight Image Super-Resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–24 June 2022; pp. 1102–1111. [Google Scholar]
- Lu, Z.; Li, J.; Liu, H.; Huang, C.; Zhang, L.; Zeng, T. Transformer for Single Image Super-Resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–24 June 2022; pp. 456–465. [Google Scholar]
- Yoo, J.; Kim, T.; Lee, S.; Kim, S.; Lee, H.S.; Kim, T.H. Enriched CNN-Transformer Feature Aggregation Networks for Super-Resolution. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 4945–4954. [Google Scholar]
- Ye, C.; Yan, L.; Zhang, Y.; Zhan, J.; Yang, J.; Wang, J. A Super-resolution Method of Remote Sensing Image Using Transformers. In Proceedings of the 2021 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Online, 22–25 September 2021; Volume 2, pp. 905–910. [Google Scholar]
- Tu, J.; Mei, G.; Ma, Z.; Piccialli, F. SWCGAN: Generative Adversarial Network Combining Swin Transformer and CNN for Remote Sensing Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5662–5673. [Google Scholar] [CrossRef]
- He, J.; Yuan, Q.; Li, J.; Xiao, Y.; Liu, X.; Zou, Y. DsTer: A dense spectral transformer for remote sensing spectral super-resolution. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102773. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z. Hybrid-Scale Self-Similarity Exploitation for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Wang, X.; Girshick, R.B.; Gupta, A.K.; He, K. Non-local Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Wang, S.; Zhou, T.; Lu, Y.; Di, H. Contextual Transformation Network for Lightweight Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. arXiv 2017, arXiv:abs/1706.03762. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Qin, M.; Mavromatis, S.; Hu, L.; Zhang, F.; Liu, R.; Sequeira, J.; Du, Z. Remote Sensing Single-Image Resolution Improvement Using A Deep Gradient-Aware Network with Image-Specific Enhancement. Remote. Sens. 2020, 12, 758. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the ACM SIGSPATIAL International Workshop on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010. [Google Scholar]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A Benchmark Data Set for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 3965–3981. [Google Scholar] [CrossRef]
- Muqeet, A.; Hwang, J.; Yang, S.; Kang, J.H.; Kim, Y.; Bae, S.H. Multi-attention Based Ultra Lightweight Image Super-Resolution. In Proceedings of the ECCV Workshops, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Zhang, D.; Shao, J.; Li, X.; Shen, H.T. Remote Sensing Image Super-Resolution via Mixed High-Order Attention Network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5183–5196. [Google Scholar] [CrossRef]







| Heads | Head Dim | Hidden Size D | MLP Dim | Layers | |
|---|---|---|---|---|---|
| Transformer Encoder | 6 | 32 | 512 | 512 | 8 |
| Transformer Decoder | 6 | 32 | 512 | 512 | 1 |
| Method | Scale | UCMerced Dataset | AID Dataset | ||
|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | ||
| Bicubic | 30.76 | 0.8789 | 32.39 | 0.8906 | |
| SC [12] | 32.77 | 0.9166 | 32.77 | 0.9166 | |
| SRCNN [22] | 32.84 | 0.9152 | 34.49 | 0.9286 | |
| FSRCNN [57] | 33.18 | 0.9196 | 34.11 | 0.9228 | |
| VDSR [24] | 33.47 | 0.9234 | 35.05 | 0.9346 | |
| LGCNet [30] | 33.48 | 0.9235 | 34.80 | 0.9320 | |
| DCM [31] | 33.65 | 0.9274 | 35.21 | 0.9366 | |
| CTNet [48] | 33.59 | 0.9255 | 35.13 | 0.9354 | |
| ESRT [40] | 33.70 | 0.9270 | 35.15 | 0.9358 | |
| ACT [41] | 33.88 | 0.9283 | 35.17 | 0.9362 | |
| TransENet [14] | 34.03 | 0.9301 | 35.28 | 0.9374 | |
| Ours | 34.19 | 0.9338 | 35.35 | 0.9387 | |
| Bicubic | 27.46 | 0.7631 | 29.08 | 0.7863 | |
| SC [12] | 28.26 | 0.7971 | 28.26 | 0.7671 | |
| SRCNN [22] | 28.66 | 0.8038 | 30.55 | 0.8372 | |
| FSRCNN [57] | 29.09 | 0.8167 | 30.30 | 0.8302 | |
| VDSR [24] | 29.34 | 0.8263 | 31.15 | 0.8522 | |
| LGCNet [30] | 29.28 | 0.8238 | 30.73 | 0.8417 | |
| DCM [31] | 29.52 | 0.8394 | 31.31 | 0.8561 | |
| CTNet [48] | 29.44 | 0.8319 | 31.16 | 0.8527 | |
| ESRT [40] | 29.52 | 0.8318 | 31.34 | 0.8562 | |
| ACT [41] | 29.80 | 0.8395 | 31.39 | 0.8579 | |
| TransENet [14] | 29.92 | 0.8408 | 31.45 | 0.8595 | |
| Ours | 30.07 | 0.8421 | 31.61 | 0.8613 | |
| Bicubic | 25.65 | 0.6725 | 27.30 | 0.7036 | |
| SC [12] | 26.51 | 0.7152 | 26.51 | 0.7152 | |
| SRCNN [22] | 26.78 | 0.7219 | 28.40 | 0.7561 | |
| FSRCNN [57] | 26.93 | 0.7267 | 28.03 | 0.7387 | |
| VDSR [24] | 27.11 | 0.7360 | 28.99 | 0.7753 | |
| LGCNet [30] | 27.02 | 0.7333 | 28.61 | 0.7626 | |
| DCM [31] | 27.22 | 0.7528 | 29.17 | 0.7824 | |
| CTNet [48] | 27.41 | 0.7512 | 29.00 | 0.7768 | |
| ESRT [40] | 27.41 | 0.7485 | 29.18 | 0.7831 | |
| ACT [41] | 27.54 | 0.7531 | 29.19 | 0.7836 | |
| TransENet [14] | 27.77 | 0.7630 | 29.38 | 0.7909 | |
| Ours | 27.89 | 0.7694 | 29.57 | 0.7983 | |
| Class | Bicubic | SC [12] | SRCNN [22] | FSRCNN [57] | LGCNet [30] | DCM [31] | CTNet [48] | ESRT [40] | ACT [41] | TransENet [14] | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 26.86 | 27.23 | 27.47 | 27.61 | 27.66 | 29.06 | 28.53 | 28.13 | 27.86 | 28.02 | 27.93 |
| 2 | 26.71 | 27.67 | 28.24 | 28.98 | 29.12 | 30.77 | 29.22 | 29.45 | 29.78 | 29.94 | 29.98 |
| 3 | 33.33 | 34.06 | 34.33 | 34.64 | 34.72 | 33.76 | 34.81 | 34.88 | 35.05 | 35.04 | 35.13 |
| 4 | 36.14 | 36.87 | 37.00 | 37.21 | 37.37 | 36.38 | 37.38 | 37.45 | 37.55 | 37.53 | 37.76 |
| 5 | 25.09 | 26.11 | 26.84 | 27.50 | 27.8 l | 28.51 | 27.99 | 28.18 | 28.66 | 28.81 | 29.12 |
| 6 | 25.21 | 25.82 | 26.11 | 26.21 | 26.39 | 26.81 | 26.40 | 26.43 | 26.62 | 26.69 | 26.78 |
| 7 | 25.76 | 26.75 | 27.41 | 28.02. | 28.25 | 28.79 | 28.42 | 28.53 | 28.97 | 29.11 | 29.27 |
| 8 | 27.53 | 28.09 | 28.24. | 28.35 | 28.44 | 28.16 | 28.48 | 28.47 | 28.56 | 28.59 | 28.65 |
| 9 | 27.36 | 28.28 | 28.69 | 29.27 | 29.52 | 30.45 | 29.60 | 29.87 | 30.25 | 30.38 | 30.65 |
| 10 | 35.21 | 35.92 | 36.15 | 36.43 | 36.51 | 34.43 | 36.46 | 36.54 | 36.63 | 36.68 | 36.69 |
| 11 | 21.25 | 22.11 | 22.82 | 23.29 | 23.63 | 26.55 | 23.83 | 23.87 | 24.42 | 24.72 | 24.91 |
| 12 | 26.48 | 27.20 | 27.67 | 28.06 | 28.29 | 29.28 | 28.38 | 28.53 | 28.85 | 29.03 | 29.32 |
| 13 | 25.68 | 26.54 | 27.06 | 27.58 | 27.76 | 27.21 | 27.87 | 27.93 | 28.30 | 28.47 | 28.64 |
| 14 | 22.25 | 23.25 | 23.89 | 24.34 | 24.59 | 26.05 | 24.87 | 24.92 | 25.32 | 25.64 | 25.74 |
| 15 | 24.59 | 25.30 | 25.65 | 26.53 | 26.58 | 27.77 | 26.89 | 27.17 | 27.76 | 27.83 | 28.31 |
| 16 | 21.75 | 22.59 | 23.11 | 23.34 | 23.69 | 24.95 | 23.59 | 23.72 | 24.11 | 24.45 | 24.53 |
| 17 | 28.12 | 28.71 | 28.89 | 29.07 | 29.12 | 28.89 | 29.11 | 29.14 | 29.28 | 29.25 | 29.32 |
| 18 | 29.30 | 30.25 | 30.61 | 31.01 | 31.15 | 32.53 | 30.60 | 30.98 | 31.21 | 31.25 | 31.21 |
| 19 | 28.34 | 29.33 | 29.40 | 30.23 | 30.53 | 29.81 | 31.25 | 31.35 | 31.55 | 31.57 | 31.71 |
| 20 | 29.97 | 30.86 | 31.33 | 31.92 | 32.17 | 29.02 | 32.29 | 32.42 | 32.74 | 32.71 | 32.98 |
| 21 | 29.75 | 30.62 | 30.98 | 31.34 | 31.58 | 30.76 | 31.74 | 31.99 | 32.40 | 32.51 | 32.77 |
| AVG | 27.46 | 28.23 | 28.66 | 29.09 | 29.28 | 29.52 | 29.41 | 29.52 | 29.80 | 29.92 | 30.07 |
| Class | Bicubic | SRCNN [22] | FSRCNN [57] | VDSR [24] | LGCNet [30] | DCM [31] | CTNet [48] | ESRT [40] | ACT [41] | TransENet [14] | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 27.03 | 28.17 | 27.70 | 28.82 | 28.39 | 28.99 | 28.80 | 28.98 | 29.01 | 29.23 | 29.29 |
| 2 | 34.88 | 35.63 | 35.73 | 35.98 | 35.78 | 36.17 | 36.12 | 36.15 | 36.15 | 36.20 | 36.45 |
| 3 | 29.06 | 30.51 | 29.89 | 31.18 | 30.75 | 31.36 | 31.15 | 31.35 | 31.37 | 31.59 | 31.69 |
| 4 | 31.07 | 31.92 | 31.79 | 32.29 | 32.08 | 32.45 | 32.40 | 32.47 | 32.45 | 32.55 | 32.61 |
| 5 | 28.98 | 30.41 | 29.83 | 31.19 | 30.67 | 31.39 | 31.17 | 31.42 | 31.42 | 31.63 | 31.75 |
| 6 | 25.26 | 26.59 | 25.96 | 27.48 | 26.92 | 27.72 | 27.48 | 27.73 | 27.75 | 28.03 | 28.23 |
| 7 | 22.15 | 23.41 | 22.74 | 24.12 | 23.68 | 24.29 | 24.10 | 24.29 | 24.32 | 24.51 | 24.56 |
| 8 | 25.83 | 27.05 | 26.65 | 27.62 | 27.24 | 27.78 | 27.63 | 27.78 | 27.79 | 27.97 | 28.06 |
| 9 | 23.05 | 24.13 | 23.69 | 24.70 | 24.33 | 24.87 | 24.70 | 24.88 | 24.89 | 25.13 | 25.32 |
| 10 | 38.49 | 38.84 | 38.84 | 39.13 | 39.06 | 39.27 | 39.25 | 39.25 | 39.24 | 39.31 | 39.45 |
| 11 | 32.30 | 33.48 | 32.95 | 34.20 | 33.77 | 34.42 | 34.25 | 34.41 | 34.43 | 34.58 | 34.59 |
| 12 | 27.39 | 28.15 | 28.19 | 28.36 | 28.20 | 28.47 | 28.47 | 28.53 | 28.47 | 28.56 | 28.76 |
| 13 | 24.75 | 26.00 | 25.49 | 26.72 | 26.24 | 26.92 | 26.71 | 26.93 | 26.94 | 27.21 | 27.19 |
| 14 | 32.06 | 32.57 | 32.50 | 32.77 | 32.65 | 32.88 | 32.84 | 32.89 | 32.87 | 32.94 | 33.26 |
| 15 | 26.09 | 27.37 | 26.84 | 28.06 | 27.63 | 28.25 | 28.06 | 28.25 | 28.25 | 28.45 | 28.54 |
| 16 | 28.04 | 28.90 | 28.70 | 29.11 | 28.97 | 29.18 | 29.15 | 29.20 | 29.18 | 29.28 | 29.42 |
| 17 | 26.23 | 27.25 | 26.98 | 27.69 | 27.37 | 27.82 | 27.69 | 27.84 | 27.84 | 28.01 | 28.34 |
| 18 | 22.33 | 24.01 | 23.47 | 25.21 | 24.40 | 25.74 | 25.27 | 25.80 | 25.75 | 26.40 | 26.38 |
| 19 | 27.27 | 28.72 | 28.09 | 29.62 | 29.04 | 29.92 | 29.66 | 29.96 | 29.96 | 30.30 | 30.52 |
| 20 | 28.94 | 29.85 | 29.50 | 30.26 | 30.00 | 30.39 | 30.25 | 30.39 | 30.38 | 30.53 | 30.79 |
| 21 | 24.69 | 25.82 | 25.40 | 26.43 | 26.02 | 26.62 | 26.41 | 26.62 | 26.61 | 26.91 | 27.18 |
| 22 | 26.31 | 27.55 | 27.12 | 28.19 | 27.76 | 28.38 | 28.19 | 28.40 | 28.40 | 28.61 | 28.76 |
| 23 | 25.98 | 27.12 | 26.77 | 27.71 | 27.32 | 27.88 | 27.72 | 27.90 | 27.89 | 28.08 | 28.22 |
| 24 | 29.61 | 30.48 | 30.22 | 30.82 | 30.60 | 30.91 | 30.83 | 30.92 | 30.92 | 31.00 | 31.27 |
| 25 | 24.91 | 26.13 | 25.66 | 26.78 | 26.34 | 26.94 | 26.75 | 26.96 | 26.99 | 27.22 | 27.43 |
| 26 | 25.41 | 26.16 | 25.88 | 26.46 | 26.27 | 26.53 | 26.46 | 26.55 | 26.54 | 26.63 | 26.87 |
| 27 | 26.75 | 28.13 | 27.62 | 28.91 | 28.39 | 29.13 | 28.94 | 29.17 | 29.15 | 29.39 | 29.72 |
| 28 | 24.81 | 26.10 | 25.50 | 26.88 | 26.37 | 27.10 | 26.86 | 27.14 | 27.10 | 27.41 | 27.68 |
| 29 | 24.18 | 25.27 | 24.73 | 25.86 | 25.48 | 26.00 | 25.82 | 26.01 | 26.02 | 26.20 | 26.43 |
| 30 | 25.86 | 27.03 | 26.54 | 27.74 | 27.26 | 27.93 | 27.67 | 27.92 | 27.95 | 28.21 | 28.48 |
| AVG | 27.3 | 28.4 | 28.03 | 28.99 | 28.61 | 29.17 | 29.03 | 29.18 | 29.19 | 29.38 | 29.57 |
| Scale | Numbers of LFE | Numbers of HSFE | PSNR | SSIM | Params | Multi-Adds |
|---|---|---|---|---|---|---|
| 2 | 2 | 27.57 | 0.7546 | 30.2M | 73.6G | |
| 2 | 5 | 27.72 | 0.7603 | 31.9M | 135.9G | |
| 2 | 8 | 27.61 | 0.7566 | 33.6M | 205.1G | |
| 3 | 2 | 27.58 | 0.7542 | 40.8M | 95.5G | |
| 3 | 5 | 27.89 | 0.7694 | 43.4M | 194.4G | |
| 3 | 8 | 27.73 | 0.7608 | 46.0M | 292.8G |
| Scale | RCAB | CTB | CB | SSEM | HSFE | PSNR | SSIM | Params | Multi-Adds |
|---|---|---|---|---|---|---|---|---|---|
| ✓ | ✗ | ✗ | ✗ | ✗ | 26.33 | 0.7010 | 41.2M | 112.0G | |
| ✗ | ✓ | ✗ | ✗ | ✗ | 27.36 | 0.7451 | 40.3M | 75.1G | |
| ✗ | ✗ | ✓ | ✗ | ✗ | 27.51 | 0.7510 | 45.7M | 275.2G | |
| ✗ | ✗ | ✗ | ✓ | ✗ | 27.61 | 0.7561 | 42.5M | 160.0G | |
| ✗ | ✗ | ✗ | ✗ | ✓ | 27.89 | 0.7694 | 43.4M | 194.4G |
| Scale | Transformer-3 | Transformer-2 | Transformer-1 | Transformer-0 | PSNR | SSIM |
|---|---|---|---|---|---|---|
| ✗ | ✗ | ✗ | ✗ | 27.54 | 0.7522 | |
| ✓ | ✗ | ✗ | ✗ | 27.61 | 0.7562 | |
| ✓ | ✓ | ✗ | ✗ | 27.73 | 0.7618 | |
| ✓ | ✓ | ✓ | ✗ | 27.89 | 0.7694 | |
| ✓ | ✓ | ✓ | ✓ | 27.50 | 0.7509 |
| Transformer | PSNR | SSIM |
|---|---|---|
| MHSA + FFN | 27.77 | 0.7630 |
| MHSA + FFN + CSTA | 27.89 | 0.7694 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, J.; Gao, M.; Li, Q.; Pan, J.; Zou, G.; Jeon, G. Hybrid-Scale Hierarchical Transformer for Remote Sensing Image Super-Resolution. Remote Sens. 2023, 15, 3442. https://doi.org/10.3390/rs15133442
Shang J, Gao M, Li Q, Pan J, Zou G, Jeon G. Hybrid-Scale Hierarchical Transformer for Remote Sensing Image Super-Resolution. Remote Sensing. 2023; 15(13):3442. https://doi.org/10.3390/rs15133442
Chicago/Turabian StyleShang, Jianrun, Mingliang Gao, Qilei Li, Jinfeng Pan, Guofeng Zou, and Gwanggil Jeon. 2023. "Hybrid-Scale Hierarchical Transformer for Remote Sensing Image Super-Resolution" Remote Sensing 15, no. 13: 3442. https://doi.org/10.3390/rs15133442
APA StyleShang, J., Gao, M., Li, Q., Pan, J., Zou, G., & Jeon, G. (2023). Hybrid-Scale Hierarchical Transformer for Remote Sensing Image Super-Resolution. Remote Sensing, 15(13), 3442. https://doi.org/10.3390/rs15133442










