An Effective Imputation Method Using Data Enrichment for Missing Data of Loop Detectors in Intelligent Traffic Control Systems

Abstract

In intelligent traffic control systems, the features extracted by loop detectors are insufficient to accurately impute missing data. Most of the existing imputation methods use only these extracted features, which leads to the construction of data models that cannot fulfill the required accuracy. This deficiency is the main motivation to propose an enrichment imputation method for loop detectors namely EIM-LD, in which the imputation accuracy is increased for different missing patterns and ratios by introducing a data enrichment technique using statistical multi-class labeling. It first enriches the clean data by adding a statistical multi-class label, including C₁…C_n classes. Then, the class of samples in the missed-volume data is labeled using the best data model constructed from the labeled clean data by five different classifiers. Experts of the traffic control department in Isfahan city determined classes of the statistical multi-class label for n = 5 (class labels), and we also developed subclass labels (n = 20) since the number of samples in the subclass labels was sufficient. Next, the enriched data are divided into n datasets, each of them is imputed independently using various imputation methods, and their results are finally merged. To evaluate the impact of using the proposed method, the original data, including missing volumes, are first imputed without our enrichment method. Then, the proposed method’s accuracy is evaluated by considering two class labels and subclass labels. The experimental and statistical results prove that the proposed EIM-LD method can enrich the real data collected by loop detectors, by which the comparative imputation methods construct a more accurate data model. In addition, using subclass labels further enhances the imputation method’s accuracy.

1. Introduction

Traffic control of intersections in metropolises is essential, and has remained a constant consideration with the expansion and development of urbanization. Many intelligent traffic control systems, such as Sydney coordinated adaptive traffic system (SCATS), split cycle offset optimization technique (SCOOT), InSync, and urban traffic optimization by integrated automation (UTOPIA) have been proposed using artificial intelligence methods to control intersections efficiently [1,2,3,4]. These intelligent systems control the traffic of intersections using vehicle traffic count data referred to as volume, generated by loop detectors. Although loop detectors are useful in generating traffic volume using a simple magnetic field embedded in the roadway, they are not entirely accurate and are prone to errors [5].

Data preprocessing, which is a crucial step in data analysis [6], becomes particularly important when dealing with inaccurate data, including incorrect and outlier data that arises when the actual value does not correspond to the calculated value by the detector in a certain period. Inaccurate data could lead to suboptimal traffic control decisions and longer wait times at intersections, which can cause frustration for drivers and increase air pollution due to idling cars. Additionally, inaccurate data could lead to safety concerns, such as increased risk of accidents due to congested intersections or incorrect signal timing [7,8]. The data of traffic loop detectors were tested using video data, and the results show that these detectors incorrectly count the number of vehicles, and in some cases, the number of vehicles is more than the actual number. The transmitted data from 25% of loop detectors include more than 20% error [9]. Furthermore, the detected errors for moving lines are usually less than theirs for mixed lines and rotation directions [7].

Effective imputation methods have been developed to increase the data quality in different applications [10,11]. Some imputation methods use the time relationship of single detectors regardless of their technique, such as probabilistic principal component analysis (PPCA), an autoregressive integrated moving average (ARIMA), Markov chain Monte Carlo (MCMC), multiple imputation, and k-nearest neighbors (KNN) [12,13,14,15,16,17,18,19]. Common methods in pattern-neighboring interpolation include the KNN model [14,20,21,22,23] and the local least squares model (LLS) [24,25]. Nguyen et al. [26] used the average values of historical data to estimate the missing data. These methods do not enrich features extracted by loop detectors, and most of them cannot fulfill the need of an accurate data model especially, when the missing ratio is high or the missing time is more than a few days or months. Some other imputation methods simultaneously utilize both temporal and spatial relationships of single and neighbor detectors, such as kernel PPCA (KPPCA), kernel regression, and mean matching multiple imputation method [27,28,29,30,31,32]. Smith et al. [33] applied historical data or data from surrounding periods or places to calculate missing data. Tang et al. [34] utilized the traffic flow hypothesis of similar distribution patterns at time intervals and spatial relationships with other upstream and downstream detectors. In the mentioned study, the fuzzy C-means (FCM) method is used, in which a genetic algorithm is applied to optimize the parameters. Pattern neighboring-based methods neglect the stochastic variation of traffic flow. As a result, once there is no record of a proper pattern, the chosen pattern is not similar enough to the original one and their shapes cannot match well [5].

Within intelligent traffic control systems, the extracted features are deemed inadequate for building an accurate data model to impute missing data. Many currently available imputation methods rely solely on these extracted features, resulting in the construction of data models that fail to meet the necessary level of accuracy. The motivation of this study is to propose an effective imputation method by introducing data enrichment technique for missing data of loop detectors named EIM-LD in intelligent traffic control systems. This article critically assesses the limitations of the existing imputation methods in handling missing data and highlights the need for a more accurate approach. The EIM-LD method is distinguished by two unique features that set it apart from other approaches. The first details using statistical labeling, to add and assign a specific traffic class to each sample. By precisely tagging each sample with a traffic class using this method, the data model in the imputation process can be trained more accurately. The data can be divided into n datasets depending on the assigned label or traffic class, and a data model is constructed for each dataset as the second innovative element of the EIM-LD method. Constructing the data model of each traffic class individually can enhance the overall accuracy of imputation. For statistical labeling, first, EIM-LD splits the original data into the clean and missed-volume datasets. The missed-volume dataset includes all samples with missing, incorrect, and noisy volumes detected using the Chebyshev inequality. The labeled clean dataset is then built by adding a statistical multi-class label, including C₁…C_n. First, five (n = 5) traffic classes known as class labels consisting of very low (VL), low (L), medium (M), high (H), and very high (VH) are determined by experts of the traffic control department in Isfahan city. Next, the traffic class of samples in the missed-volume dataset is also labeled using the best data model constructed by five different classifiers from the labeled clean dataset. After that, the labeled clean and labeled missed-volume datasets are merged to build the enriched dataset. Finally, the enriched dataset is divided into n datasets D_c1…D_cn and each of them is imputed independently using various imputation methods, and their results are merged to build the most accurate imputed datasets. Since the number of samples collected in this study is sufficient to consider small classes in statistical labeling step, we also develop statistical labeling with n = 20 traffic classes named subclass labels expectantly to reduce the imputation error.

To validate the main contribution in Section 5, the required experiments are designed to assess the proposed EIM-LD method and the impact of its introduced data enrichment technique. Initially, the original data, which includes missing volumes, is imputed without data enrichment. Subsequently, the missing volumes are imputed using the data enrichment technique, considering both class labels and subclass labels. The data imputation is performed using the best data model with the highest accuracy.

The remainder of this study is organized as follows: The state-of-the-art is discussed in Section 2. The preliminaries are presented in Section 3. The proposed method is described and evaluated in Section 4 and Section 5, respectively. Ultimately, discussion, conclusions and future works are given in Section 6 and Section 7.

2. State-of-the-Art

In the field of urban traffic, missing traffic data poses a major challenge for intelligent traffic control systems, as incomplete data can lead to inaccurate traffic models and poor management decisions. To address this issue, researchers have proposed a variety of methods, ranging from simple interpolation techniques to complex statistical models and machine learning algorithms, to impute missing traffic data. This section provides a comprehensive overview of the state-of-the-art research in this field, examining the challenges of missing traffic data and the various proposed solutions.

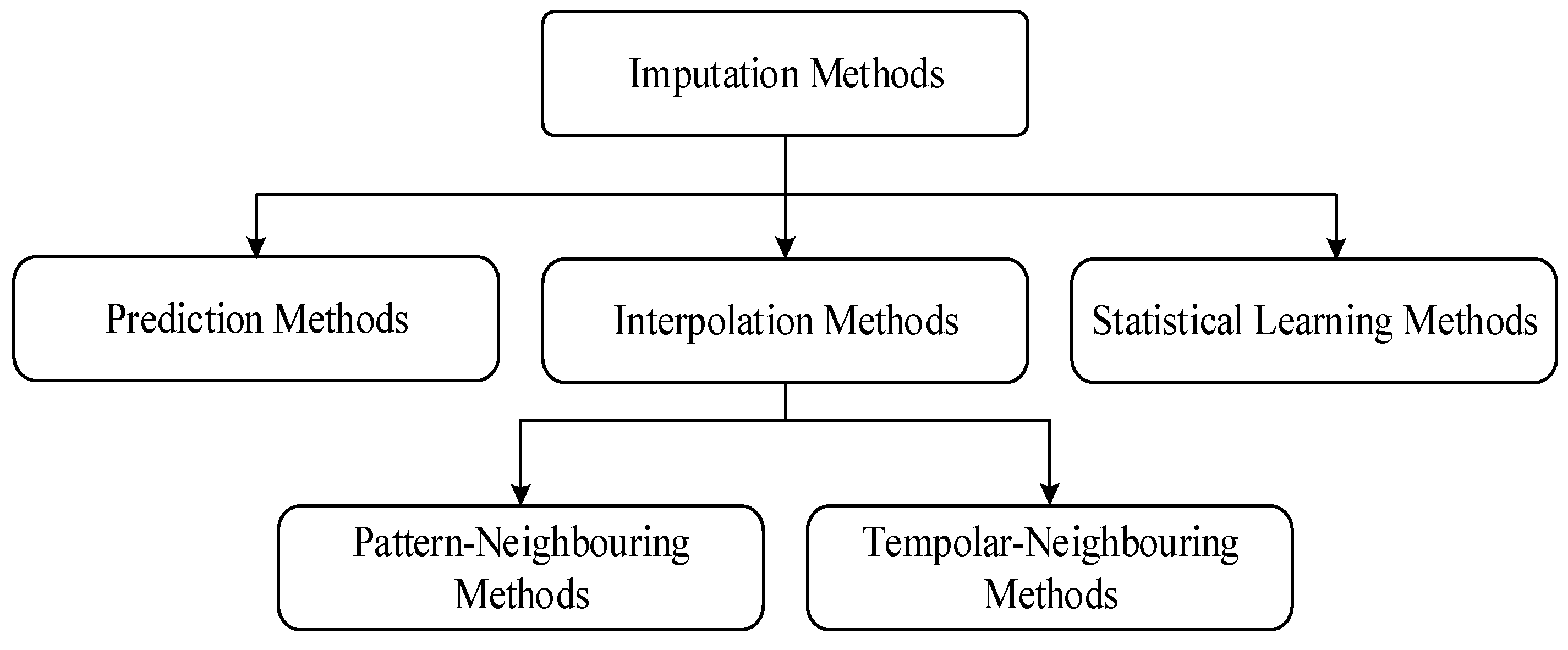
Reviewing the previous missing data imputation methods shows that there have been many methods proposed, and as shown in Figure 1 they can be classified into three categories: prediction methods, statistical learning methods, and interpolation methods [12,29]. In the prediction imputation methods, the missing data are imputed with their predicted values using data modeling and traffic volume forecasting methods such as autoregressive integrated moving average (ARIMA) [35], feed-forward neural network (FFNN) [36,37,38], support vector regression [39,40], and Bayesian network (BN) [41,42]. These methods predict the amount of missing data based on the relationships between past historical data [15,43]. Each missing data point is imputed in a time series based on previous data. Despite the acceptable accuracy of most of these methods, if a large part of consecutive data is lost, their imputation accuracy decreases. On the other hand, in these types of methods the collected data are not entirely used to impute the missing data.

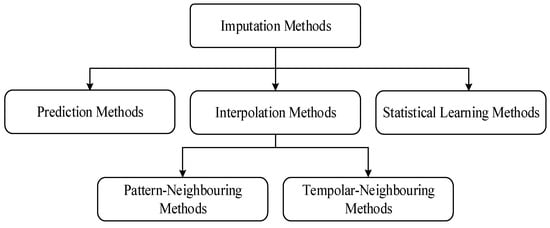
Figure 1. Categorization of missing data imputation methods.

Tekler et al. [44] introduces the ROBOD dataset, which focuses on room-level occupancy and building operation data. The authors propose a method to collect and curate this dataset, which includes gathering real-world data from sensors installed in buildings. The dataset provides detailed information on occupancy patterns, such as occupancy counts, duration, and activities performed in each room. Additionally, it includes data on HVAC system performance, such as temperature, humidity, and energy consumption. Its availability can facilitate the development of more accurate and efficient building simulation models. Briedis et al. [8] investigated the factors that affect the accuracy of loop detectors at 10 intersections in Canberra, Australia. In order to check the accuracy of the data, field statistics of intersections were compared with the results of the SCATS system, and then, using statistical methods, the average percentage of change and standard deviation of the data were obtained. Li et al. [45] investigated loop detector error using vehicle GPS data at 13 intersections in Changsha, China. Their study investigated the validity and accuracy of the performance of loop detectors by analyzing the percentage of vehicles in adjacent lanes. According to the results of studies, the data sent from 25% of loop detectors had more than 20% error.

In statistical learning methods, such as probabilistic principal component analysis (PPCA) [12,46,47], Bayesian principal component analysis (BPCA) [48], Markov chain monte carol (MCMC) [19], and ANN method [49] use iterative methods to impute probability distribution parameters by considering the probability distribution of traffic data. These methods use the observed data to impute the missing data with acceptable values. Although imputing with statistical learning methods is simple and can be used for missing data in most applications, estimating traffic data’s temporal–spatial dependence is the main challenge [48]. Li et al. [50] imputed missing values of Santa Clara traffic data over 43 days using different imputation methods. In their study, the participant methods were compared in terms of statistical behaviors, execution speed, and reconstruction errors. The obtained results show that when the percentage of missing data is high, the PPCA method is more efficient than the nearest neighbor and LLS method in terms of execution speed. In addition, since the nearest neighbor methods, LLS, and PPCA methods have good statistical features, they are recommended more than predictive methods and MCMC when the percentage of missing data is high.

Stekhoven and Buhlmann [51] introduces MissForest, a non-parametric approach for imputing missing values in datasets with mixed data types. MissForest employs a random forest algorithm to estimate missing values based on observed values and other features in the dataset. This method offers a robust solution to handle missing data, allowing for accurate and reliable analysis. The authors demonstrate the effectiveness of MissForest through experimental evaluations and comparisons with other imputation techniques. The paper by Yoon et al. [52] presents a method called GAIN for imputing missing data. GAIN utilizes generative adversarial networks (GANs) to impute missing data. It consists of two main components: an imputation network and a discriminator network. The imputation network estimates missing values, while the discriminator network evaluates the quality of the imputed data. The proposed approach achieves promising results in imputing missing data and demonstrates the potential of GANs in this task. Low et al. [53] propose a novel approach to estimate parking durations. The authors employ a generative adversarial network to impute missing values and improve the accuracy of predictions. This approach offers a reliable solution for estimating parking durations and enhances the overall performance of transportation system management.

In the third categorization, using interpolation methods, the missing data are replaced by the average or weighted average of known data related to similar patterns in two ways: temporal-neighboring method and the pattern-neighboring method [5,54,55]. In the temporal-neighboring method, data are collected from the same detector in the same time period on neighboring days [39,48,55]. In the pattern-neighboring method, data are collected from the same time interval of similar detectors on other days with the same pattern of daily flow change [18,54]. The historical mean model is a temporal-neighboring interpolation-based method that imputes missing data using the average historical data collected from the same place over the same time period in few days [56]. Pattern-neighboring interpolation methods often estimate missing data using the mean weighted average of known data from neighboring detectors [16]. Chen et al. [30] investigated, detected, and corrected data related to California loop detectors. They used data from thousands of loop detectors in six districts of California. In the mentioned study, in addition to a more accurate estimation of lost data rather than historical data, the relationship between volume and occupancy of neighboring detectors is shown using linear regression. The results show that after the implementation of the algorithm, the determined data does not have suitable accuracy. Weijermars et al. [57] proposed a method for detecting inaccurate data of loop detectors in the city of Almelo in the Netherlands. Data quality assessment at both microscopic and macroscopic levels based on the minimum and maximum flow thresholds has led to the identification of incorrect data. According to the results of studies in assessing the quality of microscopic data, 8% of the correct data were introduced as incorrect. The results show that 47% of the errors reported by the detectors of each station were equal to the data quality reports.

Liu et al. [14] have examined the compatibility of existing imputation methods for the holidays in Alberta, Canada, and according to the results, the nearest neighbor method shows sustainable performance for the holidays. The results of the comparison between methods show that the nearest neighbor method has the lowest rate of traffic forecasting error. Lu et al. [58] developed a portable error correction tool in California. This system can detect errors by identifying the type of error and analyzing the available data. In the proposed system, the instrument produced at the level of intersections was used to detect any types of inductive detector error. Tang et al. [34], in Harbin, China, have endeavored to impute missing data from loop detector using the FCM method. First, the data structure is transformed into a matrix structure, and then using a genetic algorithm, the parameters related to the weight factor and cluster sizes are optimized. Their study worked on data with MR algorithm. The existing correlation between traffic flow data was analyzed, then the parameters were optimized using genetic algorithm. To evaluate the efficiency of imputation methods, four methods, ARIMA, MLR, FCMGA, and Historical method, were compared with each other, and the accuracy of the methods was investigated. According to the results, the FCMGA method had the best performance in imputing data during weekdays compared to other methods.

Xiao et al. [59], in Changsha, China, with the SCATS data and GPS taxis, developed a methodology for estimating missing flow rates. Their proposed methodology was divided into three methods based on historical patterns, schedule, and location of the identifier, as well as FCD data. According to the results of the first and second methods in the east and west approaches, in contrast to the southern approach, they showed good performance, which could be due to the uncertainty and fluctuation of the flow pattern of the southern approach. Tak et al. [32] have attempted to impute the missing data by considering spatial–temporal correlation with the nearest neighbor method. This method differs from the previous conventional methods due to the selection of routes with similar traffic characteristics by correlation analysis. The efficiency of the nearest neighbor method is compared with Bootstrap-based Expectation (B-EM) and Nearest History (NH) methods, and using statistical methods; each has been measured separately in terms of loss pattern, percentage of loss, type of day, and traffic situation. Bae et al. [60] used cokriging to imputed data on traffic flow velocity. They used the distance-temporal cokriging method; imputation data on RTMS and HERE data sources were performed, and different missing data patterns were investigated. According to the results, in the MCAR data model, SK and OK methods, and MNAR data model, the SCK method had better performance than other methods. Table 1 summarizes the comparison of previous works in terms of advantages and disadvantages, volume of data, and accuracy calculation method.

Table 1. Comparison of the previous missing data imputation methods.

Ref	Method Used for IMPUTING	Volume of Data	Volume of Missing Data	Advantages	Disadvantages
Tekler et al. [44]	Random Forest-based imputation algorithm	52,128	2684	The ROBOD dataset helps building managers save energy, reduce waste, and cut expenses by providing detailed usage and operation information.	Room-level occupancy and building operation data are the only focus of the ROBOD data set. Sensor location, adjustment, and upkeep can affect data reliability, resulting in potentially incorrect or incomplete results.
Briedis et al. [8]	Comparison of field statistics with statistics obtained from SCATS system Using statistical methods and graphing.	800	-	Analyzing the inductive detector’s performance involves comparing field results with SCATS and assessing factors such as lane count, traffic type, asphalt condition, vehicle volume, and movement mode.	The simultaneous effect of two factors on the inductive detector accuracy and the lack of its examination.
Li et al. [45]	Comparison of field data with system data-error detection algorithm	408,960	-	25% of the tested inductive detectors had an error over 20%. This method measures vehicle flow, monitors queue length, and estimates GPS-equipped vehicles.	The routes need to be reconstructed to reduce the driver’s disorder, which improves the accuracy of the flow estimation on the route.
Li et al. [50]	Prediction methods, interpolation methods and statistical learning methods	12,384	-	PPCA yields best performance in all aspects and numerical tests demonstrate that it can be used to impute data online before making further and is robust to weather changes.	From a statistical perspective, prediction and MCMC methods are not advisable.
Stekhoven et al. [51]	Iterative imputation method (MissForest) based on a random forest algorithm	10 datasets	10, 20 or 30%	Miss-Forest is a reliable method for imputing high proportions of missing data in large datasets with many variables and observations. It generates multiple imputations, enabling consideration of imputation uncertainty in subsequent analyses.	Limitations for dealing with some kinds of mixed data. Imputed values from MissForest can be distorted with varying missing data patterns. The quality of imputed values in MissForest depends on parameters such as tree number and convergence criterion, making optimal settings challenging to determine.
Yoon et al. [52]	A machine learning technique for imputing missing data using Generative Adversarial Nets (GANs)	5 datasets	-	The GAIN method utilizes GANs to accurately impute missing data, handles diverse data types (continuous, categorical, mixed), and is robust against outliers and noise, making it suitable for real-world datasets.	GAIN requires ample data for effective GAN training and may struggle with complex data, resulting in inaccurate imputations. Training GAN is time-consuming, a drawback for time-sensitive data. Biased training or inadequate model adjustments in GAIN may introduce bias in imputed data.
Low et al. [53]	Missing data imputation using generative adversarial multiple imputation algorithm	-	0.000 to 0.980	Develop a regression model to predict the parking duration of commercial vehicles at the loading bays of retail malls and identify significant factors that contribute to this dwell time.	Training GANs is expensive and time-consuming. GAMIN can overfit, leading to poor generalization on new datasets.
Chen et al. [30]	DSA algorithm for error detection–linear regression algorithm	42 million sample	15%	By applying the linear regression algorithm, it can estimate the missing data more accurately than using historical data. This way, all the sensors that have a good neighbor will have their data completed in after running the algorithm once.	Linear regression fills most of the fields in the first run, but the accuracy of the filled fields decreases with each subsequent run.
Weijermars et al. [57]	Data quality check method to identify invalid data generated by inductive detector and Macroscopic quality checks Microscopic	3000	3.4%	Minimum and maximum flow thresholds are used to detect erroneous data. Macroscopic quality checks are a useful addition to the microscopic quality checks.	Microscopic data quality check does not detect many erroneous data. Flows are inconsistent between upstream detectors mutually in some cases, it is not always clear whether the results of this quality check are reliable.
Liu et al. [14]	Non-Parametric regression-the K-NN method	25,200	-	The proper performance of K-NN method in correcting lost data during holidays.	The ARIMA model fails to work properly when the traffic conditions vary across seasons.
Lu et al. [58]	Spatial and Temporal Correlation	2880	-	This method works well for highways or intersections where we can get the upstream and downstream volume or estimate the error by comparing the camera data and the hardware data.	Analyzing aggregated data at the macroscopic level is not an effective method for fault detection. This approach fails for intersections that lack data from both upstream and downstream sources.
Tang et al. [34]	Fuzzy C-means(FCM)	77,760	25,920	This research analyzes the data for weekdays and weekends separately, which improves the accuracy of measuring the methods’ efficiency.	NMR, MCR data patterns are not used.
Xiao et al. [59]	Historical Pattern- Timing Plan- FCD	3744	-	The methods show reliable results after several iterations.	In different conditions and approaches, the desired results and efficiency may not be achieved.
Tak et al. [32]	Data Driven method based on Spatial and Temporal Correlation using a modified knn method	135,936	-	The health vector enables the optimal computation of the Euclidean distance between the historical and subject data. KNN performance does not differ for weekday and weekend data.	B-EM is more effective for single identifier data than multiple neighboring identifiers. NH performance varies based on weekdays or weekends.
Bae et al. [60]	Cokriging method- spatial–temporal	8064	1113	The SK and OK methods excel on the MCAR data pattern. The SCK method is effective on the MNAR data pattern.	The OCK method results may become less accurate if there is no data from neighboring.

3. Preliminaries

This section provides background information on the preliminaries required for the study of urban traffic volume data analysis. It includes a detailed description of the loop detectors data and different missing data patterns.

Loop detectors can measure various variables such as traffic volume/count, speed, occupancy, and presence. Traffic volume/count refers to the number of vehicles that traverse the loop within a specified time interval. The speed of vehicles passing over the loop can also be measured. Occupancy, on the other hand, refers to the percentage of time that a vehicle occupies the loop. Finally, loop detectors can determine whether a vehicle is present or not on the loop at a given time, which is known as presence [61]. Furthermore, the components of loop detectors are described in Appendix A.

Loop detectors generate non-stationary time series data including accurate, incorrect, and outlier data. Particularly, in SCATS intelligent traffic control system, incorrect data consist of “BAD”, “DA”, “-” which are considered as missing data. Missing data occurs when no amount of data is observed for the traffic volume variable and its record is not stored in the desired time interval. “DA” stands for detector alarm, which is generated when the system detects a fault or malfunction. “BAD” is an error that occurs when the sensor is in a saturated state, typically caused by being parked or obstructed by a physical object for an extended period. Finally, “-” indicates missing data when the sensor fails to transmit any data within a specific time interval. Researchers use different methods to detect missing values, including standard procedures in statistical software such as SPSS, or using specialized procedures provided in SPSS Missing Value Analysis (MVA) module [62]. Outlier data is an observation that lies at an abnormal distance from other values in a random sample of a population. Outliers include global, contextual, and collective data [63]. A global outlier is out of line with the rules of analysis of all traffic volume data for a detector. According to the existing and special conditions, contextual outliers are considered outliers. These data are only for a specific time period. A collective outlier is not generally considered out of data, but the dataset is outdated for the existing system.

According to the missing pattern, missing data are divided into three categories: missing completely at random (MCR), missing at random (MR), and missing not at random (NMR) [64,65]. In the MCR category, the missing data appear completely independent as isolated points and are randomly distributed. In the MR category, the data are related to their neighboring points, so the missing data appear as a small set of consecutive points and at a particular time, which is a random distribution. In the NMR category, the missing data occur non-randomly throughout the dataset due to long-term errors in the detectors [65].

4. Proposed Method (EIM-LD)

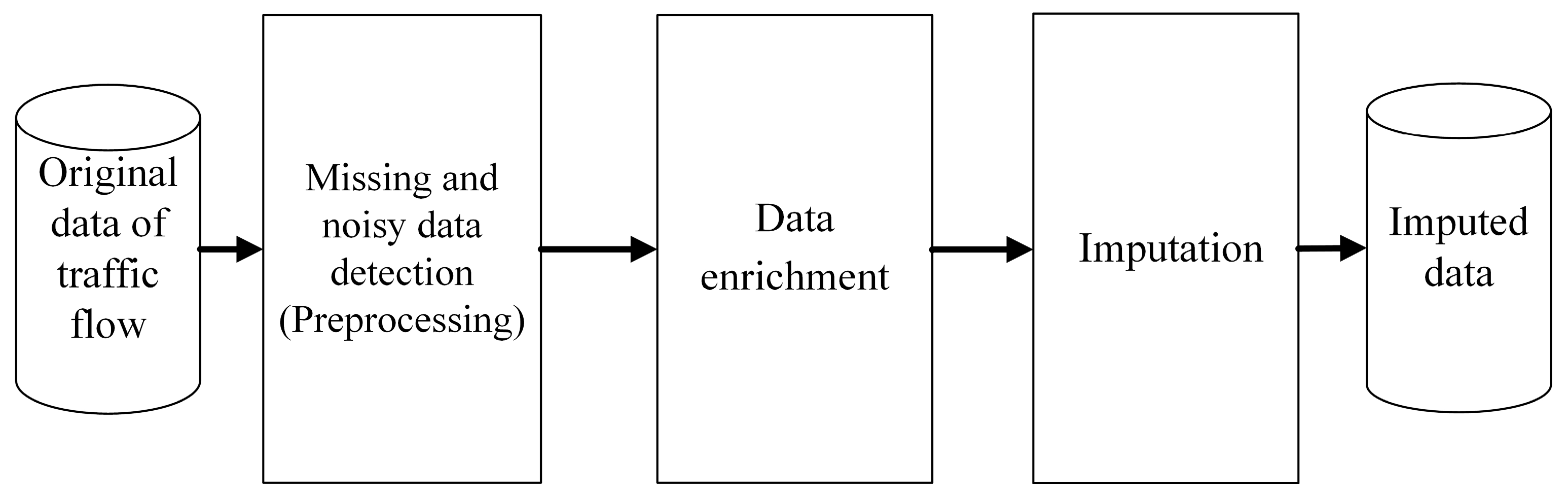
This section proposes an effective imputation method for the missing volume of loop detectors named EIM-LD, based on the model introduced in Figure 2. This model consists of three main phases. The first phase is data preprocessing to detect missing and noisy data from the original data. An effective data enrichment technique is introduced in the second phase to enrich the original data using statistical multi-class labeling, consisting of five different steps as shown in Figure 3. The enriched data are divided into n labeled datasets, which makes individual missing data imputation possible for each labeled dataset. In the final phase, the missing data of each labeled dataset are imputed using five different imputation algorithms and their results are finally merged to construct the most accurate imputed dataset.

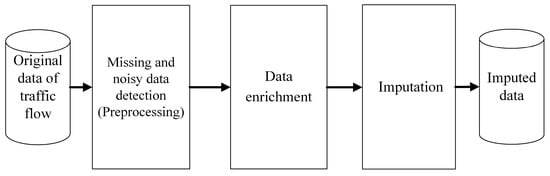
Figure 2. The introduced model consists of three main phases.

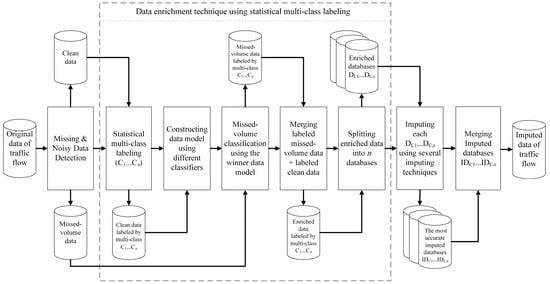
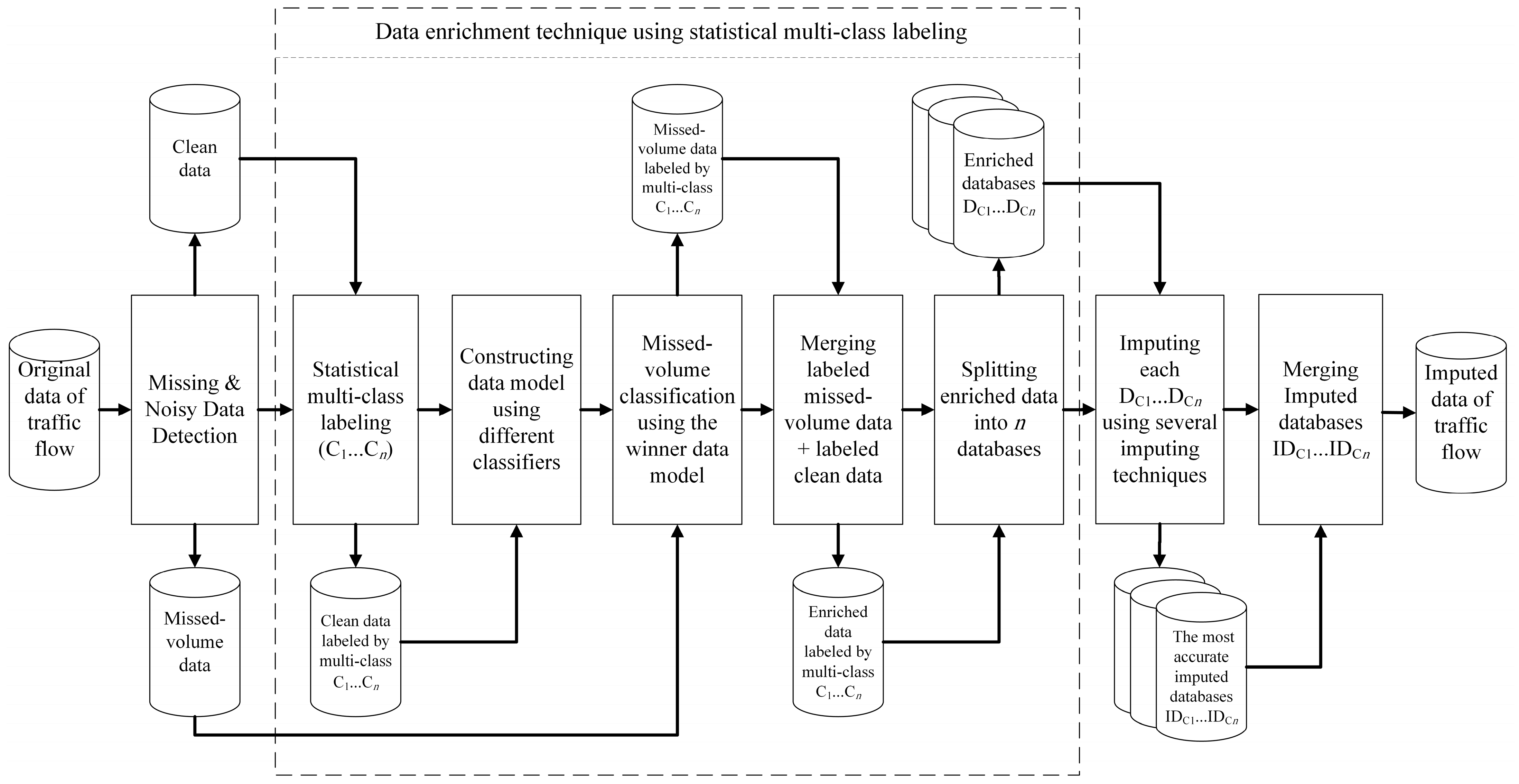
Figure 3. The proposed method including steps of the introduced data enrichment technique shown in the dashed-line rectangle.

In fact, the proposed EIM-LD method enriches the original data by adding an informative indicator using statistical multi-class labeling. The following subsections describe three phases of the model for developing the proposed EIM-LD method.

4.1. Phase 1: Missing and Noisy Data Detection (Preprocessing)

In this phase, the original data are split into two datasets, clean and missed-volume. First, we use SPSS statistical software package to detect missing values and also the incorrect data, which are tagged as missing data. Then, the proposed EIM-LD method uses Chebyshev inequality defined in Equation (1) [66] for different values of K to detect noisy data, because data distribution is abnormal,

$$P(|X-\mu |\ge k\sigma )\le \frac{1}{k^2}$$

(1)

where X and μ are random variable and expected value, respectively. $\sigma$ and K show standard deviation and number of standard deviations from the mean. To detect the noisy data of each interval that through which the data are collected from the loop detectors, the mean and standard deviation of each interval are calculated. Then, different values of k in the Chebyshev inequality are examined to identify values that exceed the boundaries for each specific interval as outliers. This approach is commonly used in statistical analysis to detect noisy data and remove them from the dataset. By setting boundaries for each interval based on its mean and standard deviation, the identification of outliers can be performed in a systematic manner, leading to a more accurate and reliable analysis of the data. Ultimately, this phase forms the clean dataset and also the missed-volume dataset by considering all samples with missing and noisy data.

4.2. Phase 2: Data Enrichment

In this phase, data are enriched by introducing an effective data enrichment technique shown in the dashed-line rectangle in Figure 3, in which the clean dataset is statistically labeled using class labels and subclass labels. Then, data models are constructed and assessed for accuracy. Missed-volume classification and merging of labeled datasets improve imputation accuracy. Finally, the enriched data are then split into datasets based on traffic classes for better data modeling in the imputation phase.

−

Statistical labeling: The clean dataset formed in the previous phase is statistically labeled using multi-class C₁…C_n. First, similar that of other studies [67,68], we consider five (n = 5) traffic classes named class labels consisting of very low (VL), low (L), medium (M), high (H), and very high (VH). These class labels had been determined by experts of the traffic control department in Isfahan city based on their experiences and historical traffic data.

−

Since smaller volume ranges provide specific subclass labels within each of the five class labels and can result in reducing the imputation error, therefore we consider the statistical labeling with subclass labels, for instance, 10 or 20 labels. It is expected that the data model constructed using the subclass labels will provide superior results compared to class labels, if the number of samples in smaller classes of the subclass labels have also sufficient samples to train the data model accurately. Table 2 shows the class labels and a subdivision the subclass labels of them including their ranges used in this study. In this table, µ and σ are the mean and the standard deviation distance.

Table 2. Class labels recommended by experts and considered subclass labels based on traffic volume.

Row	Range	Class Labels	Volume	Subclass Labels	Sub-Volume
1	[0, (µ − 1.5σ))	Very Low (VL)	0–19	VL1	0–4
				VL2	5–9
				VL3	10–14
				VL4	15–19
2	[(µ − 1.5σ), (µ − 1/2σ))	Low (L)	20–48	L1	20–27
				L2	28–34
				L3	35–41
				L4	42–48
3	[(µ − 1/2σ), (µ + 1.5σ))	Medium (M)	49–105	M1	49–63
				M2	64–77
				M3	78–91
				M4	92–105
4	[(µ + 1.5σ), (µ + 3σ))	High (H)	106–147	H1	106–115
				H2	116–126
				H3	127–137
				H4	138–147
5	[(µ + 3σ), max]	Very High (VH)	148 to (max)	VH1	148–173
				VH2	174–198
				VH3	199–223
				VH4	224–max

−

Data Model construction: The EIM-LD method constructs data models of the clean dataset, using both class labels and subclass labels. The data models are built using k-fold and different classifiers: k-nearest neighbor (KNN), artificial neural network (ANN), Naïve Bayesian (NB), decision tree (DT), and support vector machines (SVM). The accuracy of each data model is assessed to determine the candidate data model with the highest accuracy.

−

Missed-volume classification: In this step, the candidate data model is used to label the samples of the missed-volume dataset to construct the labeled missed-volume dataset. The label added to the missed-volume dataset is an informative indicator which can increase the accuracy of the data model that is used in the imputation step.

−

Constructing the labeled dataset: In this step, the missed-volume dataset labeled in the previous step is merged with the labeled clean dataset to build the enriched data, including multi-class C₁…C_n. It is expected that the imputation accuracy will be increased using this enriched data instead of using the original dataset because of adding the label to each sample.

−

Splitting enriched data: In this step, the enriched data are split into n enriched databases D_C1 to D_Cn. Dividing the enriched data into n databases, each representing specific traffic classes C₁…C_n, is anticipated to yield a refined data model. This approach holds the potential to construct more precise data models for split databases.

4.3. Phase 3: Imputation

In this phase, missing data are imputed using various methods and the most accurate imputed datasets are selected and merged.

−

Data Imputation: Missing data in databases D_C1 to D_Cn are imputed using five commonly used methods: ARIMA, KF, BN, PPCA, and KNN, as suggested in the literature. This comprehensive approach ensures a more accurate estimation of missing data.

Then, the most accurate imputed databases are selected as ID_c1…ID_cn.

−

Merging imputed databases: Finally, the EIM-LD merges imputed databases of ID_c1…ID_cn by concatenating them to build the imputed data of traffic flow.

According to the steps mentioned above, the pseudocode of the proposed method (EIM-LD) is shown in Algorithm 1.

Algorithm 1. Effective imputation method for missing volume of loop detectors (EIM-LD)
	Input: Original traffic flow data, n.
	Output: Imputed traffic flow data.
1.	Begin
2.	Splitting the original data into clean and missed-volume datasets by detecting missing and noisy data using Equation (1).
3.	Building the labeled clean dataset using statistical multi-class labeling C1…Cn.
4.	Selecting the candidate data model constructed by several classifiers for the labeled clean dataset.
5.	Determining the class of samples of the missed-volume dataset using the candidate data model.
6.	Merging labeled missed-volume and labeled clean datasets to build the enriched data.
7.	Splitting the enriched data into n databases DC1 to DCn.
8.	For i:1 to n
9.	Imputing DCi using several imputation techniques.
10.	Considering imputed results with the highest accuracy as IDCi.
11.	End
12.	Merging imputed databases IDc1…IDcn to build ID.
13.	Return ID as the imputed traffic flow data.
14.	End

5. Evaluation of the Proposed Method (EIM-LD)

In order to evaluate the proposed EIM-LD method and its introduced data enrichment technique in missing data imputation, a comprehensive experimental design consisting of four experiment sets is considered. The evaluation is conducted on one-year traffic flow data collected from the SCATS intelligent traffic control system of Isfahan city. The first experiment set is to assess the imputation without data enrichment, in which the original data, including different missing patterns with different missing ratio is imputed using different algorithms. The second and third experiment sets are to evaluate the proposed method with data enrichment using two different class labels and subclass labels. Finally, the fourth experiment set is to analyze the impact of using our innovative data enrichment technique, based on multi-class labeling against clustering. In these experiments, we consider some scenarios with different missing data ratios and missing patterns. In each scenario, the considered ratio of missing data is randomly selected by a missingness mechanism, and three different missing patterns NMR, MR, and MCR are considered. In all experiment sets, the proposed method is compared with other comparative algorithms regarding the root mean square error (RMSE). The experimental and statistical results prove that the proposed EIM-LD method using the introduced data enrichment technique, especially with subclass labels, can construct a more accurate data model, and the missing volumes can be imputed with less RMSE.

5.1. Experimental Environment

All experiments were intently executed under fair conditions. Thus, all algorithms were implemented on MATLAB 2018a and Rapid miner 5, and experiments were executed on a Windows 7 operating system by an Intel Core (TM) i7-10520U 1.8 GHz processor and 12.00 GB RAM. We have used k-nearest neighbor (KNN), artificial neural network (ANN), Naïve Bayesian (NB), decision tree (DT), and support vector machines (SVM) to learn the data.

5.2. Data Description

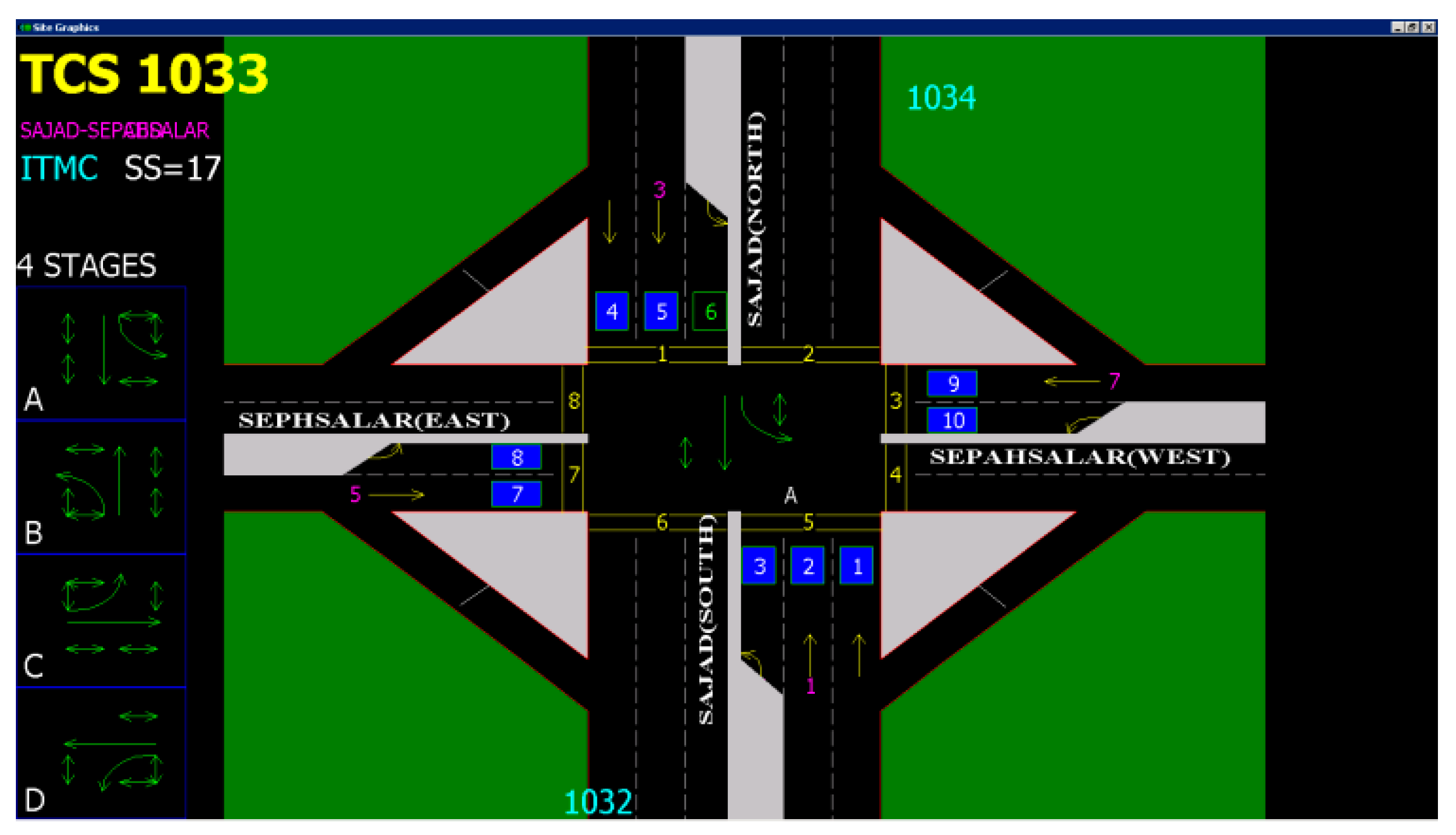
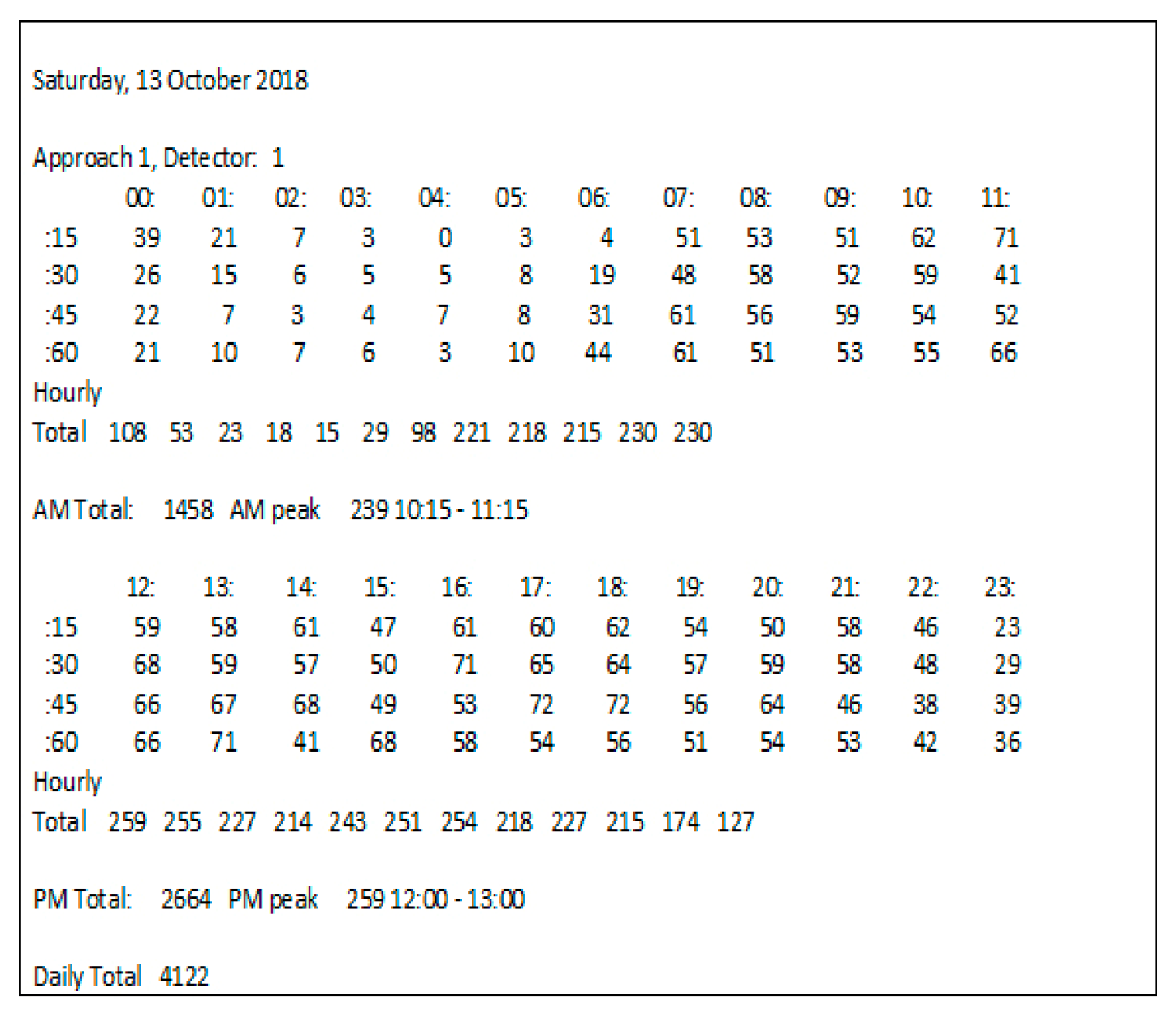
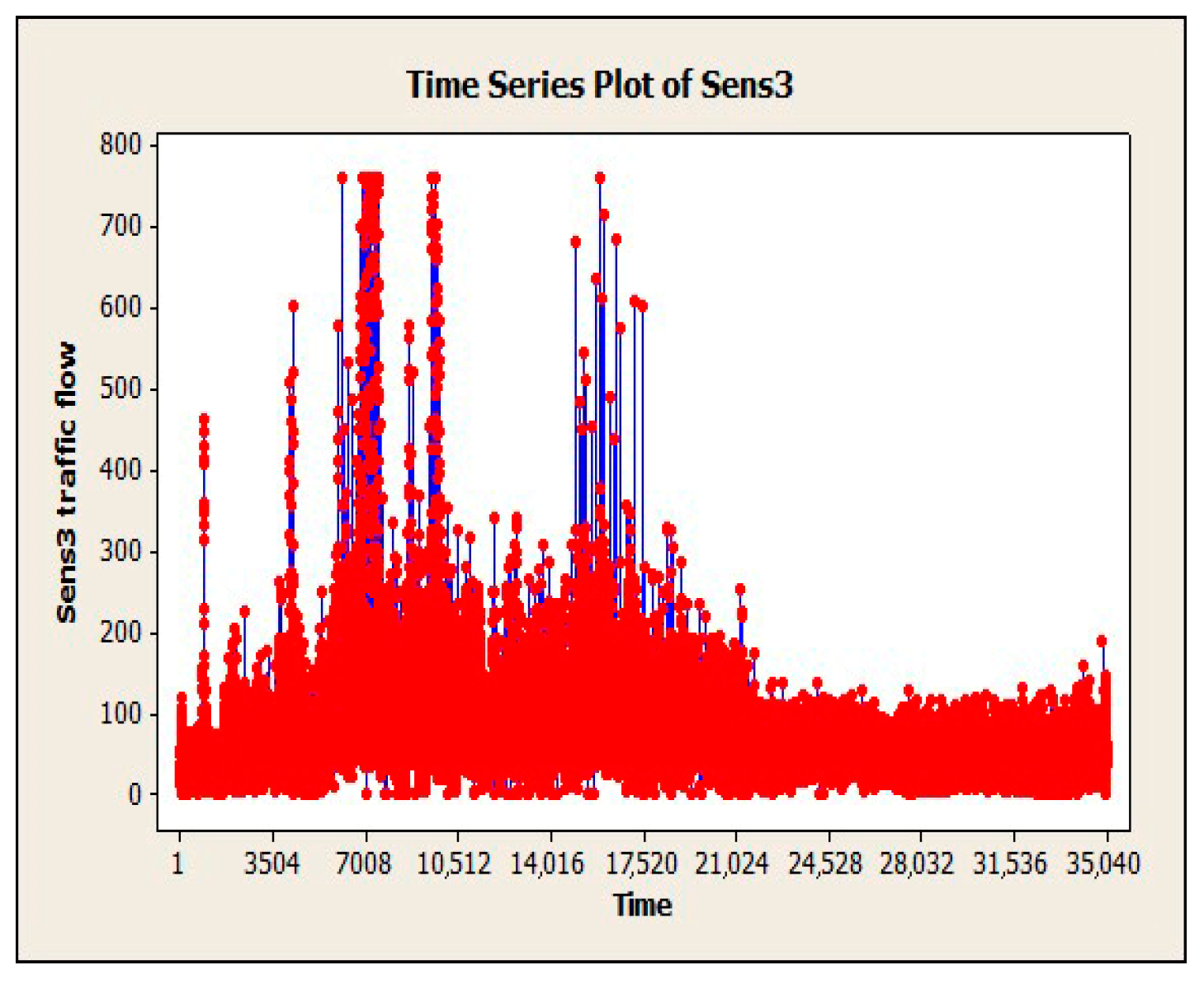
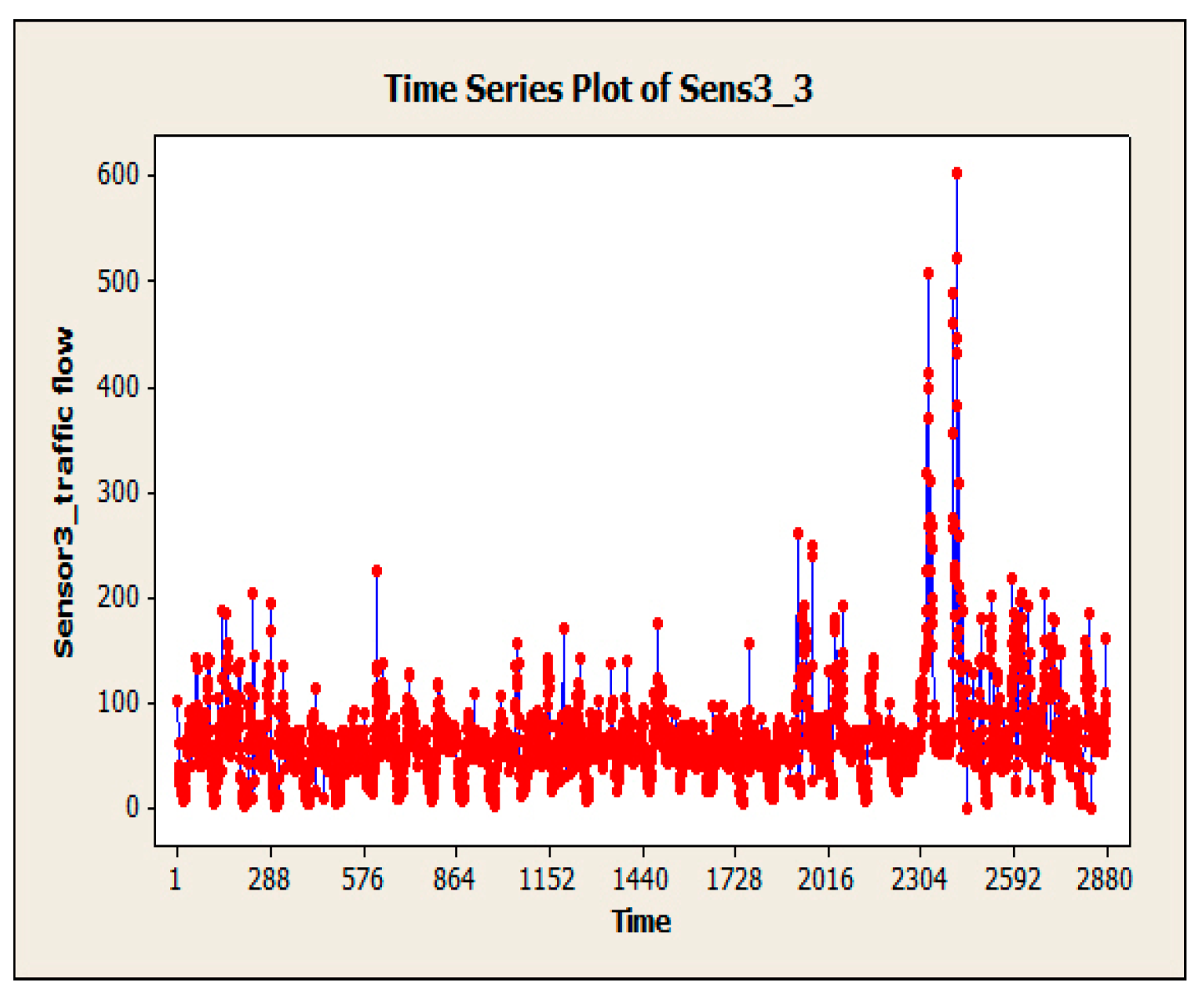
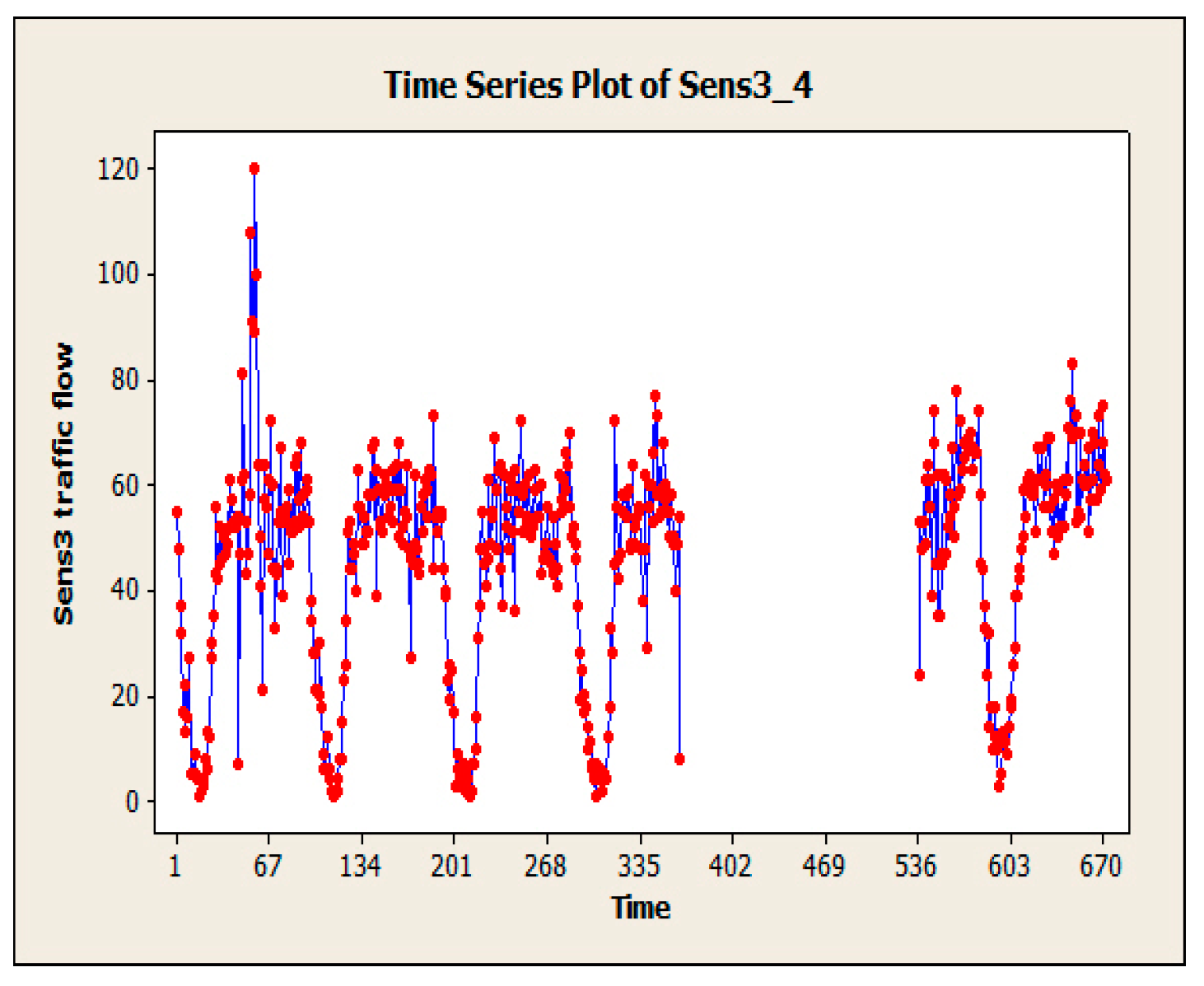
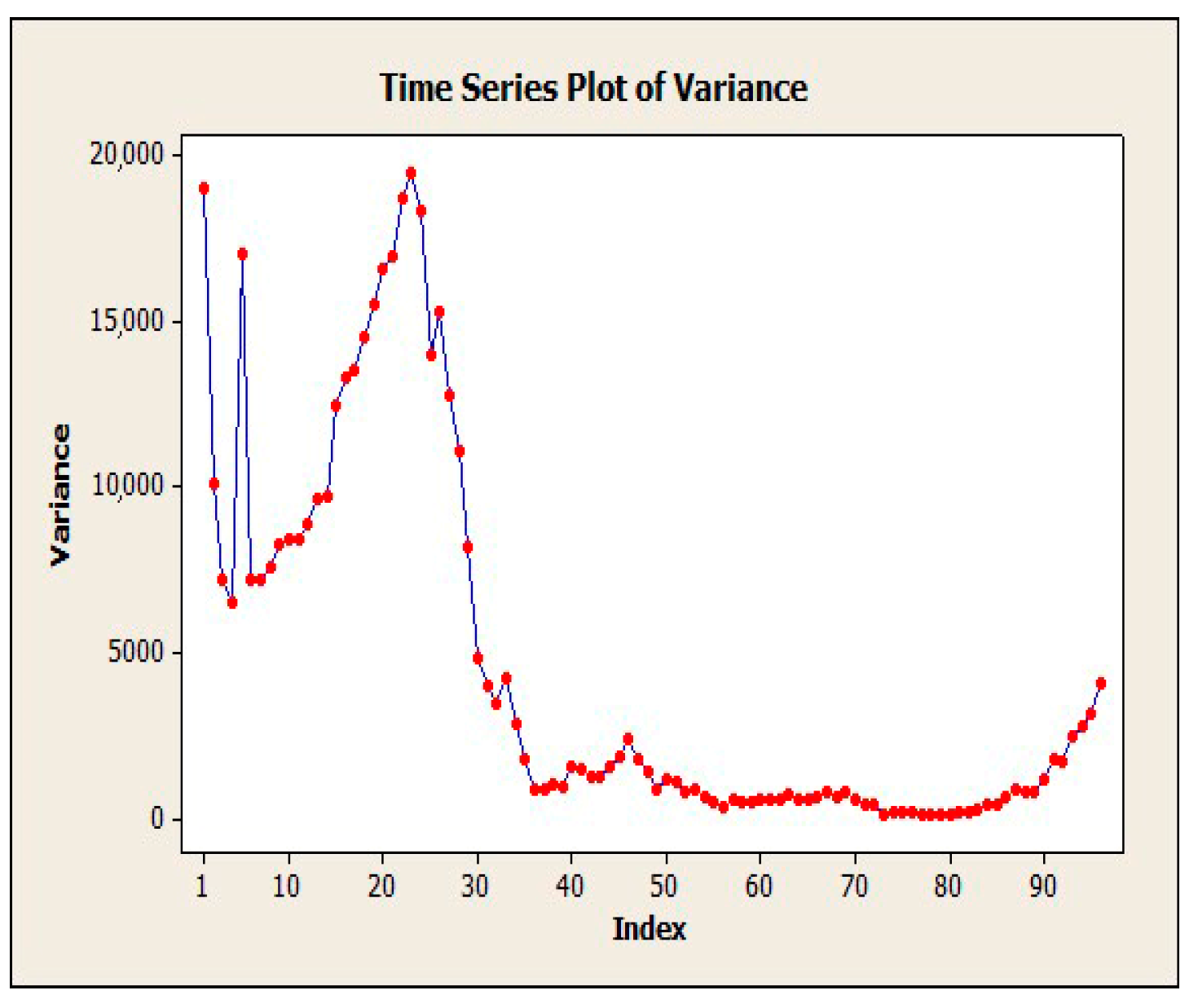
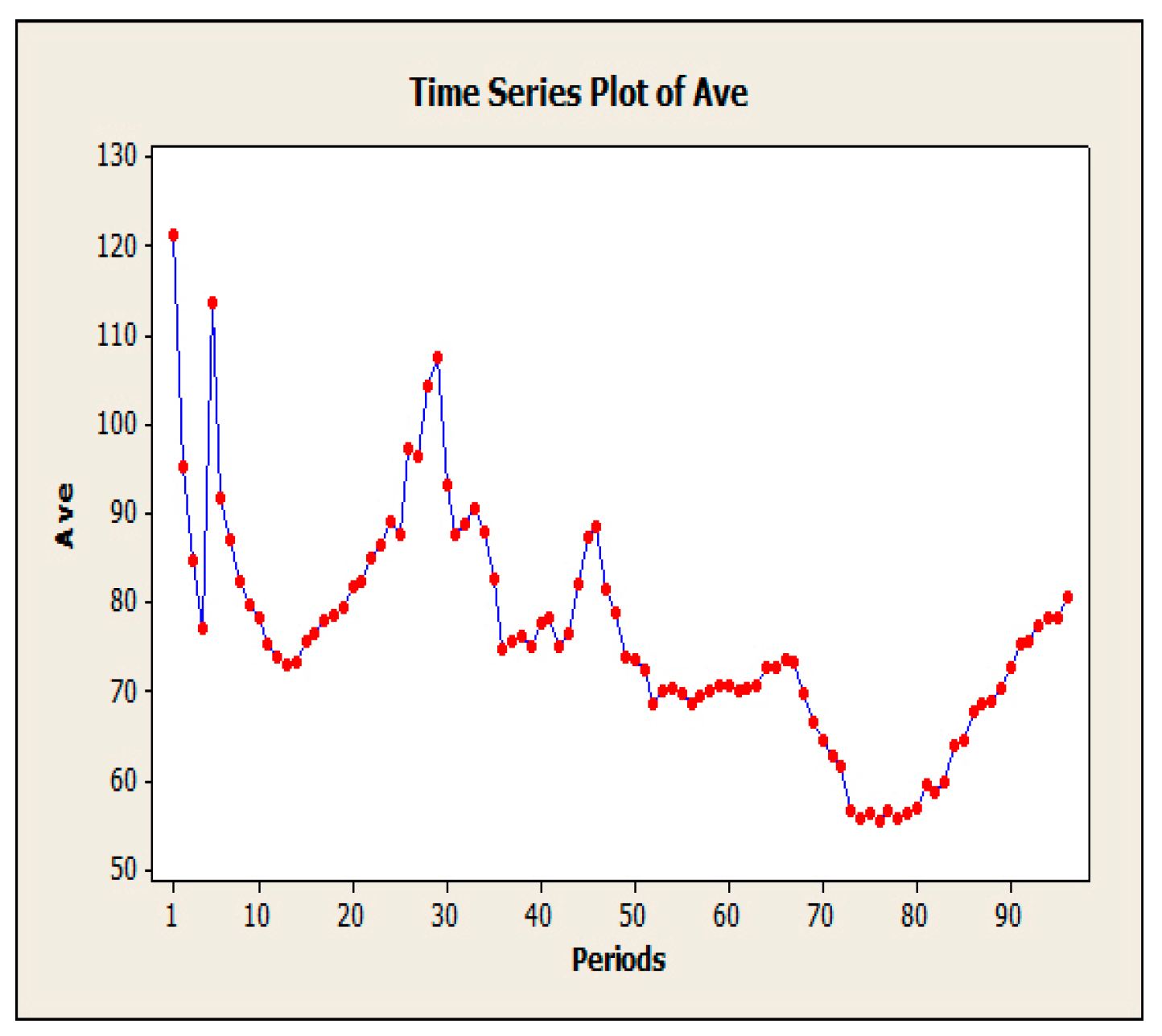
To evaluate the EIM-LD method, one-year data of the SCATS intelligent traffic control system of Isfahan megacity in Iran has been collected. The data were categorized into four approaches: north, south, west, and east. Related detectors in each approach can be seen in Figure 4, where numbers 1–10 denote 10 different detectors. Detectors 1 to 3 are in the south approach, detectors 4 to 6 are in the north approach, detectors 7 and 8 are in the west approach, and detectors 9 and 10 are in the east approach. This study exclusively examines the data obtained from detector No. 3, with the aim of utilizing the proposed methodology to address the issue of missing volume data imputation for this specific detector. The raw data received from SCATS software are shown in Figure 5. The traffic volume data obtained from the detectors of this intersection in intervals of 15 min during a day and night were 96 times and 35,040 as data recorded during a year. Figure 6, Figure 7 and Figure 8 show the time series diagrams of the one-year, one-month, and one-week detectors. As can be seen in Figure 9 and Figure 10, according to the changing mean and variance of data over one year, the time series are considered non-stationary.

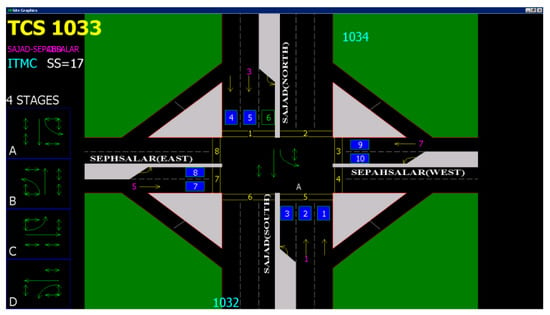
Figure 4. Location of detectors based on intersection approaches (Taken from SCATS software).

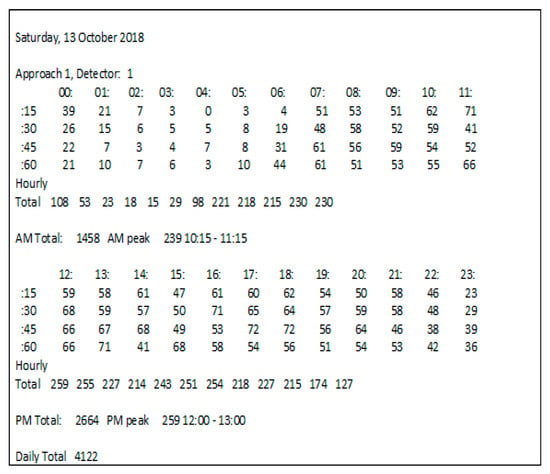
Figure 5. Raw data output from SCATS software.

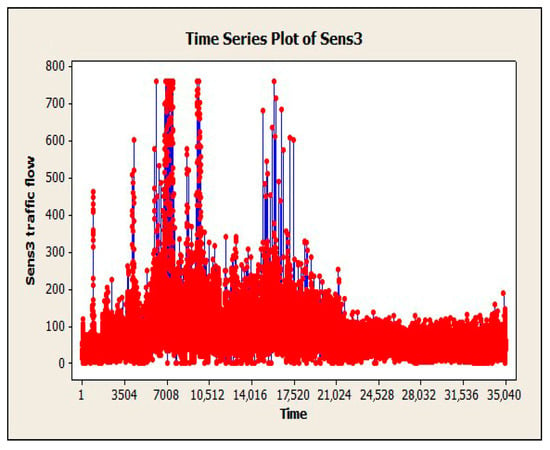
Figure 6. One-year time series diagram of detector 3.

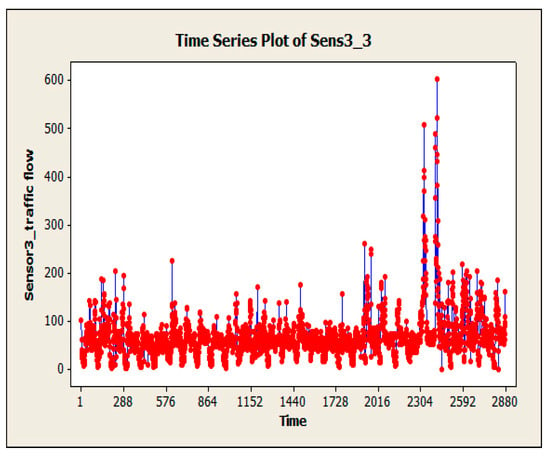
Figure 7. One-month time series diagram of detector 3.

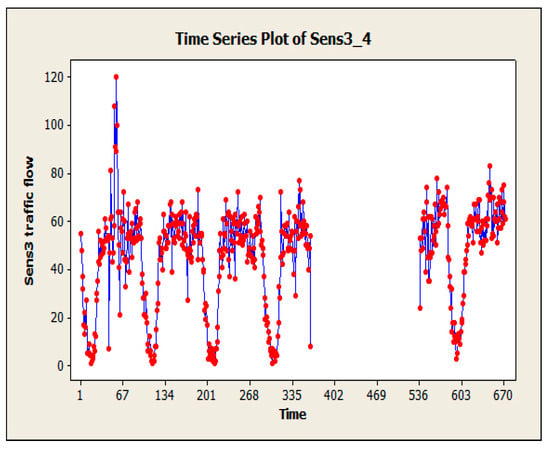
Figure 8. One-week time series diagram of detector 3.

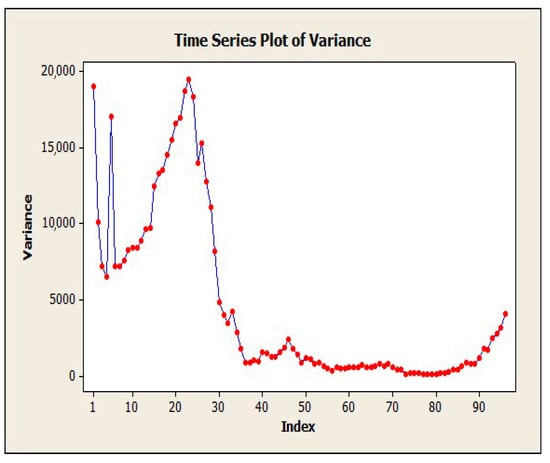
Figure 9. Evaluation of data non-stationary with an average of 365 days.

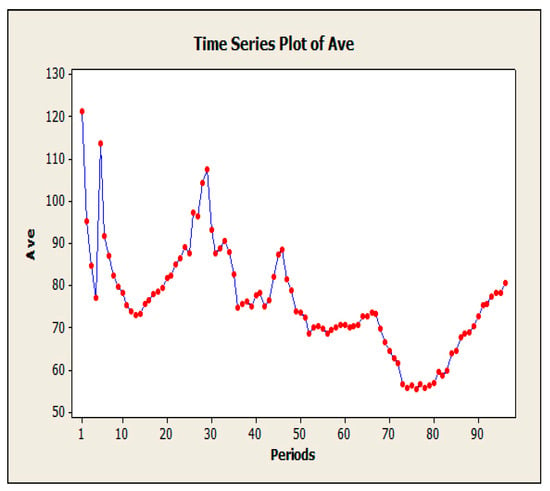
Figure 10. Evaluation of data non-stationary using 365 days variance.

The collected traffic flow data includes different features: volume, time, season, month, day of week, day of month, the holiday status, and rainy status. To illustrate, given record #27 (35, 6:30, Autumn, OCT, Saturday, 13, 0, 0), in which volume, time, season, month, day of week, and day of month are extracted from one-year data of the SCATS intelligent traffic control system of Isfahan city. The holiday status is obtained from the official calendar, and the rainy status is obtained from the city weather database. The traffic volume sensed by each detector is periodically sent in 15 min periods; therefore, the traffic volume sent by each detector is 35,040 records during a year. In the collected data, volumes received in the forms of “BAD”, “DA”, and “-”, are identified as missing values. The collected dataset has 621 records or 2.2% with missing values.

Table 3 shows features used for data model construction in statistical labeling and their information gain. The time and rainy features have the highest and the lowest information gain in the collected dataset. In the EIM-LD method, test data are separated from training data for both class labels and subclass labels data using 10-fold division.

Table 3. Features of dataset and their information ratio.

Feature	Info. Gain	Gain Ratio	Gini
Time	0.381	0.058	0.094
Month	0.158	0.044	0.027
Season	0.098	0.049	0.016
Weekday	0.004	0.001	0.001
Date	0.003	0.002	0.001
Holiday	0.002	0.003	0.001
Rainy	0.001	0.002	0.000

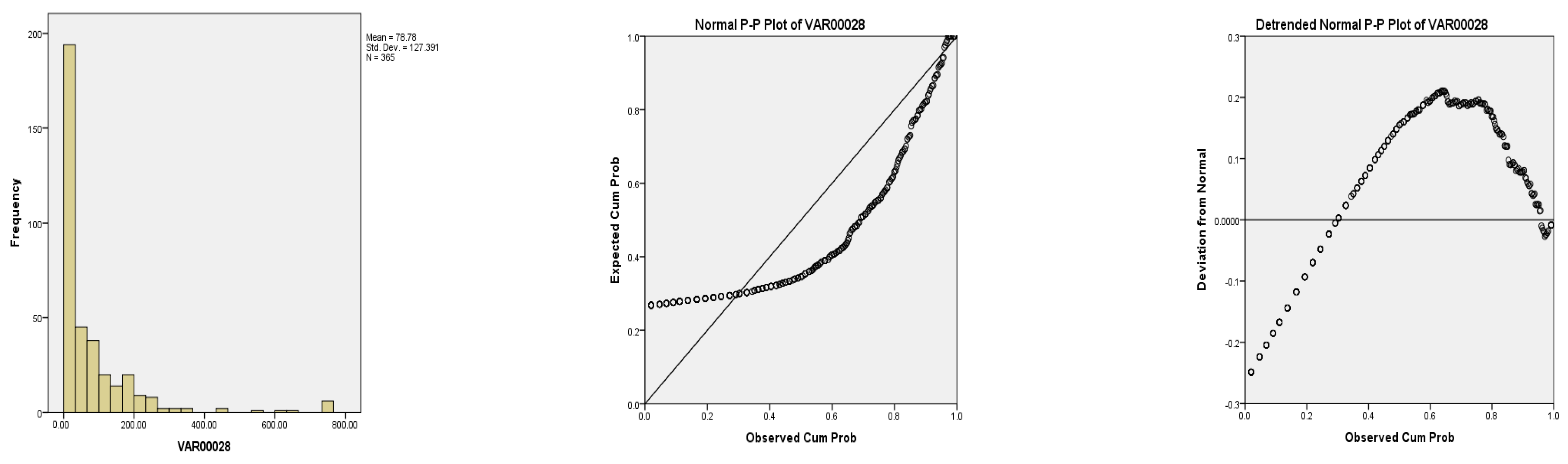
To determine noisy data, the data distribution was examined in different intervals of 96 per day. According to the histogram diagram and P-P detector plot No. 3 in Figure 11, the data distribution is uncommon between 5:00 to 5:15. By observing the results in Figure 11, the plotted points have deviated from the diagonal line, which suggests that the observed data did not follow a normal distribution.

Figure 11. Investigation of data distribution status of No. 3 traffic volume in the period from 5:00 to 5:15.

The Chebyshev inequality, as defined in Equation (1), is used to detect noisy data for different values of K. In the EIM-LD method, the mean and standard deviation of each interval differ from the yearly averages. Table 4 presents the total noise data detected for each K value within 96-day intervals over 365 days, along with separate calculations for each interval. For instance, when K = 1, the Chebyshev inequality identifies 3864 noise data points, which accounts for 14.097% of the dataset. Additionally, the table showcases the accuracy achieved by various classifiers for each K value in relation to the Chebyshev inequality. The results show that the highest accuracy of the models was associated to k = 1 in the Chebyshev inequality through which more accurate samples are considered to form the clean dataset that can construct a more accurate data model.

Table 4. The results of noise detection using Chebyshev inequality.

K	Outlier (n)	Outlier (%)	Acc. KNN	Acc. ANN	Acc. NB	Acc. DT	Acc. SVM
1	3864	14.097	71.40%	80.48%	79.46%	78.32%	70.64%
sqrt(2)	2221	8.103	68.84%	75.84%	75.59%	72.72%	68.19%
1.5	2028	7.399	68.30%	75.36%	75.17%	72.46%	68.10%
2	1230	4.488	66.30%	73.74%	73.51%	70.65%	66.83%
3	639	2.332	65.24%	72.99%	72.32%	69.32%	65.52%
4	388	1.416	64.67%	72.35%	71.71%	68.94%	64.96%
5	251	0.916	64.31%	72.54%	71.50%	68.56%	64.54%
6	148	0.54	64.22%	72.28%	71.42%	68.42%	64.41%
7	105	0.384	64.08%	72.04%	71.38%	68.35%	64.37%
8	90	0.329	64.08%	71.75%	71.36%	68.35%	64.41%
9	77	0.281	64.06%	72.20%	71.32%	68.33%	63.92%
10	70	0.256	64.06%	71.83%	71.31%	68.14%	64.39%

5.3. Imputation without Data Enrichment (IWDE)

In this experiment set, the original data, including missing volumes, is imputed without data enrichment using ARIMA, KF, BN, PPCA, and KNN algorithms. Table 5 shows RMSE of the imputation using these algorithms for different missing data ratio and missing patterns. The highest imputation error rate was observed for ARIMA algorithm with 76.15 for 50% missing ratio in MCR missing pattern. The results show that the PPCA algorithm has the lowest imputation error rate for all patterns and missing ratio compared to all other algorithms.

Table 5. Average square error of imputation using different algorithms without data enrichment for different types of missing patterns.

Missing Ratio	ARIMA			KF			BN			PPCA			KNN
	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR
10%	61.33	60.07	63.33	50.33	48.32	52.23	46.32	44.10	48.32	42.23	41.59	45.15	58.83	55.15	60.06
20%	64.19	63.65	65.89	53.15	51.32	53.91	47.50	45.81	51.03	44.51	43.51	46.71	60.32	58.09	62.04
30%	67.32	65.59	69.00	55.55	54.00	55.03	49.17	47.32	52.51	47.03	44.91	48.19	63.23	61.02	65.59
40%	69.04	67.25	72.17	58.91	56.61	59.17	52.02	50.00	54.05	48.92	47.05	51.32	65.00	62.88	68.32
50%	73.15	71.10	76.15	60.01	58.17	61.39	54.15	52.15	56.17	50.17	48.15	53.15	67.19	65.39	69.99

5.4. EIM-LD Using Data Enrichment with Macro Classification (EMAC)

In this experiment set, as the proposed method explained in Section 4, the original dataset is enriched by adding an informative label to each sample and constructing the enriched dataset using the class labels statistical labeling, which we refer to as enrichment with macro classification (EMAC). In the class labels, experts recommended five classes, including, very low (VL), low (L), medium (M), high (H), and very high (VH) based on the volume range existing in the collected real data. Then, this enriched dataset is split into five datasets D_C1 to D_C5 and each of them is imputed using different imputation methods, including ARIMA, KF, BN, PPCA, and KNN. The most accurate imputed datasets are then selected as ID_c1…ID_c5 and are merged to construct the final imputed data of traffic flow. As explained in Section 4, to enrich the original data, first samples with missing volume must be detected to build the clean and missed-volume datasets. Considering different kinds of incorrect data in the missed-volume dataset can affect the data model accuracy in the statistical labeling. Table A1 in Appendix B shows the impact of considering different kinds of missing data on the accuracy of the data models using class labels.

Table 6 shows the imputation RMSE for different missing patterns using the class labels (n = 5). Each imputation method is applied for datasets D_C1 to D_C5 individually, and the average of RMSE gained for all datasets is shown in Table 6. The results show that the PPCA algorithm in the MR missing pattern has the lower imputation RMSE for different missing ratios. The results also indicate that EMAC reduces RMSE compared to IWDA in all algorithms and all missing patterns.

Table 6. The average of imputation RMSE of different imputation methods using class labels C₁…C₅ for different missing patterns.

Missing Ratio	ARIMA			KF			BN			PPCA			KNN
	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR
10%	50.95	47.73	52.58	48.59	46.29	50.16	44.77	43.20	46.82	41.22	39.47	42.89	49.48	45.59	51.15
20%	52.60	49.43	54.34	50.05	48.42	51.75	46.52	45.08	48.83	42.64	40.13	44.76	51.18	48.07	52.90
30%	55.25	52.11	56.70	52.44	50.47	54.25	48.65	47.12	50.68	44.45	42.07	46.73	53.72	50.48	54.90
40%	57.33	54.57	59.03	54.48	52.98	59.19	51.47	49.33	53.03	46.33	43.68	48.76	55.58	52.77	56.91
50%	58.94	57.26	59.22	56.21	54.61	58.33	53.07	51.19	55.35	48.27	44.82	51.85	57.62	54.50	59.39

5.5. EIM-LD Using Data Enrichment with Micro Classification (EMIC)

In this subsection, similar to the previous subsection, the initial steps are performed to construct the enriched dataset using subclass labels, which we refer to as statistical labeling with enrichment through micro classification (EMIC). In the proposed method, we anticipated that due to the high volume of data, dividing the data into subclass labels with smaller ranges shown in Table 2 would result in higher accuracy and lower error rates for each small interval. Thus, in the second step, splitting the enriched data into labeled subclass labels with n = 10 and n = 20 was considered. Since the results obtained by the subclass labels with n = 20 were better than those with n = 10, Table 7 shows the average RMSE of different missing ratios for different imputation methods and missing patterns using subclass labels C₁…C₂₀ including traffic classes: VL1...VL4, L1…L2, M1…M4, H1…H4, VH1…VH4. To illustrate the results in different missing ratios, Table 8 outlines the average of RMSE gained by each imputation method. The experimental results show that the PPCA imputation algorithm in the MR missing pattern has less imputation RMSE for different missing ratios. Moreover, the results prove that using a subclass labels with 20 classes can reduce the RMSE and impute the missing volumes more effectively for all algorithms and the missing ratio. This is because the data model can be trained more accurately when the class range is smaller and sufficient samples are available.

Table 7. RMSE comparison of different imputation methods using subclass labels C1…C20 for different missing patterns.

Micro Class	ARIMA			KF			BN			PPCA			KNN
	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR
VL1	47.38	45.15	49.79	44.17	43.47	46.38	43.83	41.74	46.36	42.50	39.47	44.49	45.92	44.17	47.54
VL2	46.11	44.68	49.57	44.81	43.28	46.88	44.34	41.43	46.90	42.97	39.85	44.75	46.65	44.65	47.40
VL3	47.18	44.73	49.18	44.50	43.59	46.44	44.45	42.77	40.25	42.70	40.08	43.90	47.10	44.40	48.10
VL4	47.63	44.80	50.92	45.54	43.59	48.14	44.94	43.37	46.79	43.25	41.18	45.56	46.89	44.41	48.79
L1	48.59	47.03	51.56	44.91	43.91	47.28	44.39	41.42	46.93	41.40	39.22	43.70	46.20	43.35	49.31
L2	48.98	47.53	51.00	44.38	42.37	48.08	44.14	42.26	46.15	41.57	39.16	43.99	46.59	44.38	49.30
L3	49.58	46.12	51.76	46.00	44.51	48.40	44.22	42.92	46.78	41.35	38.24	42.88	47.30	44.39	49.57
L4	48.38	46.76	51.84	45.12	43.48	48.59	42.62	41.50	45.01	40.80	38.30	42.79	46.64	44.13	49.94
M1	51.92	50.21	53.64	47.61	46.17	50.60	46.89	45.14	49.82	44.31	42.42	45.74	49.61	46.58	52.67
M2	52.63	49.24	54.30	50.24	48.58	52.03	48.00	46.79	50.51	43.77	41.60	46.28	50.90	49.92	53.94
M3	52.10	49.97	54.79	48.75	46.56	51.04	48.14	45.80	50.44	45.49	42.76	46.99	49.67	47.73	52.46
M4	51.62	49.25	54.80	48.87	45.34	49.50	46.57	45.66	48.88	43.69	41.06	46.95	49.32	46.91	52.07
H1	50.99	48.89	54.24	48.76	46.30	51.20	37.01	45.34	49.94	43.88	41.93	46.53	49.15	47.86	52.05
H2	51.28	49.64	53.99	48.49	46.11	51.45	47.49	45.39	49.03	44.23	41.63	47.78	49.09	47.07	51.66
H3	52.50	50.40	55.62	47.48	45.51	50.31	45.96	44.50	49.04	44.13	41.42	46.02	50.20	48.72	52.72
H4	53.94	50.90	56.35	48.75	46.95	52.04	47.95	45.78	50.71	43.92	40.93	46.81	51.92	49.67	54.86
VH1	52.82	52.57	55.02	47.46	44.77	50.69	46.14	44.95	47.06	42.91	40.79	45.09	49.77	46.86	51.95
VH2	52.83	50.50	55.39	47.75	46.22	49.82	46.16	42.95	47.78	44.44	43.04	46.33	51.02	48.45	53.27
VH3	51.68	49.55	55.01	48.48	45.56	51.22	46.87	45.15	48.60	43.37	42.14	46.52	50.10	48.19	52.94
VH4	52.65	49.94	55.21	49.16	47.19	52.15	48.82	46.16	51.06	45.99	43.66	48.14	50.98	49.03	54.46

Table 8. The average of imputation RMSE of different imputation methods using subclass labels for different missing patterns and missing ratio.

Missing Ratio	ARIMA			KF			BN			PPCA			KNN
	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR
10%	45.75	43.70	48.29	42.71	40.95	44.92	41.23	39.55	43.18	38.64	36.53	40.68	43.91	42.06	46.43
20%	48.01	45.59	50.57	44.82	42.84	47.32	43.57	41.80	45.78	41.22	38.67	43.35	46.12	43.98	48.85
30%	50.34	48.50	52.99	46.93	45.04	49.97	46.04	44.08	48.59	43.31	40.87	45.90	48.49	46.37	51.59
40%	53.04	50.74	55.80	49.09	47.25	51.85	48.42	46.29	50.75	45.65	43.27	47.91	51.30	48.97	53.50
50%	55.56	53.44	58.33	51.75	49.78	54.00	50.50	48.52	51.22	47.85	45.37	49.97	53.94	51.35	55.88

5.6. Impact Analysis of Using EIM-LD vs. Clustering

In the previous experiment sets, we proved that using EIM-LD can decrease the imputation RMSE, which may benefit from splitting the original dataset. However, the main reason behind this gain is our innovative statistical multi-class labeling that can enrich the original dataset and arm the data model training. To prove this claim, we cluster the original dataset using the k-means algorithm with k = 5 and k = 20. Each cluster is then imputed using all imputation methods, ARIMA, KF, BN, PPCA, and KNN used in the previous experiments. The best-imputed datasets are merged in the same fashion. Table 9 compares the results gained from this experiment with previous approaches IWDE, EMAC, and EMIC. The experimental results in Table 9 prove that the proposed method using subclass labels is superior to other methods. The descriptive statistical results, including minimum, maximum, mean, and deviation of this experiment, are shown in Table A2 in Appendix C, in which the proposed method has the lowest RMSE imputation.

Table 9. Comparison of imputation methods without using data enrichment, using data enrichment with class labels and subclass labels, and clustering.

Method	Missing Ratio	ARIMA			KF			BN			PPCA			KNN
		NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR	NMR	MR	MCR
IWDE	10%	61.33	60.07	63.33	50.33	48.32	52.23	46.32	44.10	48.32	42.23	41.59	45.15	58.83	55.15	60.06
	20%	64.19	63.65	65.89	53.15	51.32	53.91	47.50	45.81	51.03	44.51	43.51	46.71	60.32	58.09	62.04
	30%	67.32	65.59	69.00	55.55	54.00	55.03	49.17	47.32	52.51	47.03	44.91	48.19	63.23	61.02	65.59
	40%	69.04	67.25	72.17	58.91	56.61	59.17	52.02	50.00	54.05	48.92	47.05	51.32	65.00	62.88	68.32
	50%	73.15	71.10	76.15	60.01	58.17	61.39	54.15	52.15	56.17	50.17	48.15	53.15	67.19	65.39	69.99
K-means K = 5	10%	55.32	54.14	57.15	49.12	47.73	51.12	45.12	45.80	47.32	42.50	41.00	43.00	53.19	51.19	54.15
	20%	57.19	56.39	60.85	52.13	50.05	52.80	46.99	46.00	49.12	43.91	42.19	44.51	54.85	52.80	56.19
	30%	59.32	58.18	62.15	54.95	52.19	55.00	48.80	48.01	51.52	45.95	44.00	46.51	57.15	54.82	58.83
	40%	61.87	60.15	64.40	56.32	54.14	57.32	51.50	49.12	53.70	47.81	45.93	48.19	59.63	56.63	60.38
	50%	63.50	62.15	66.15	58.12	57.88	60.69	53.39	51.32	55.85	49.99	47.13	51.90	61.62	58.19	64.25
K-means K = 20	10%	49.15	46.61	52.15	46.60	45.60	49.60	45.90	44.40	48.70	40.19	38.10	42.12	46.32	44.61	48.89
	20%	51.55	48.39	54.50	48.17	47.11	50.19	47.05	45.81	50.50	42.00	40.05	45.61	47.73	45.41	50.50
	30%	53.91	51.85	55.12	49.59	48.81	51.81	48.89	47.90	52.20	44.59	41.73	47.79	50.05	48.31	52.30
	40%	56.61	53.30	57.89	51.59	50.19	53.70	51.32	49.05	53.15	46.61	44.50	49.60	52.15	51.00	54.19
	50%	57.32	55.55	59.69	53.32	51.18	55.10	52.05	51.00	54.15	48.20	47.60	53.00	54.72	52.51	57.32
EMAC	10%	50.95	47.73	52.58	48.59	46.29	50.16	44.77	43.20	46.82	41.22	39.47	42.89	49.48	45.59	51.15
	20%	52.60	49.43	54.34	50.05	48.42	51.75	46.52	45.08	48.83	42.64	40.13	44.76	51.18	48.07	52.90
	30%	55.25	52.11	56.70	52.44	50.47	54.25	48.65	47.12	50.68	44.45	42.07	46.73	53.72	50.48	54.90
	40%	57.33	54.57	59.03	54.48	52.98	56.19	51.47	49.33	53.03	46.33	43.68	48.76	55.58	52.77	56.91
	50%	58.94	57.26	59.22	56.21	54.61	58.33	53.07	51.19	55.35	48.27	44.82	51.85	57.62	54.50	59.39
EMIC	10%	45.75	43.70	48.29	42.71	40.95	44.92	41.23	39.55	43.18	38.64	36.53	40.68	43.91	42.06	46.43
	20%	48.01	45.59	50.57	44.82	42.84	47.32	43.57	41.80	45.78	41.22	38.67	43.35	46.12	43.98	48.85
	30%	50.34	48.50	52.99	46.93	45.04	49.97	46.04	44.09	48.59	43.31	40.87	45.90	48.49	46.37	51.59
	40%	53.04	50.74	55.80	49.09	47.25	51.85	48.42	46.29	50.75	45.65	43.27	47.91	51.30	48.97	53.50
	50%	55.56	53.44	58.33	51.75	49.78	54.00	50.54	48.52	51.22	47.85	45.37	49.97	53.94	51.35	55.88

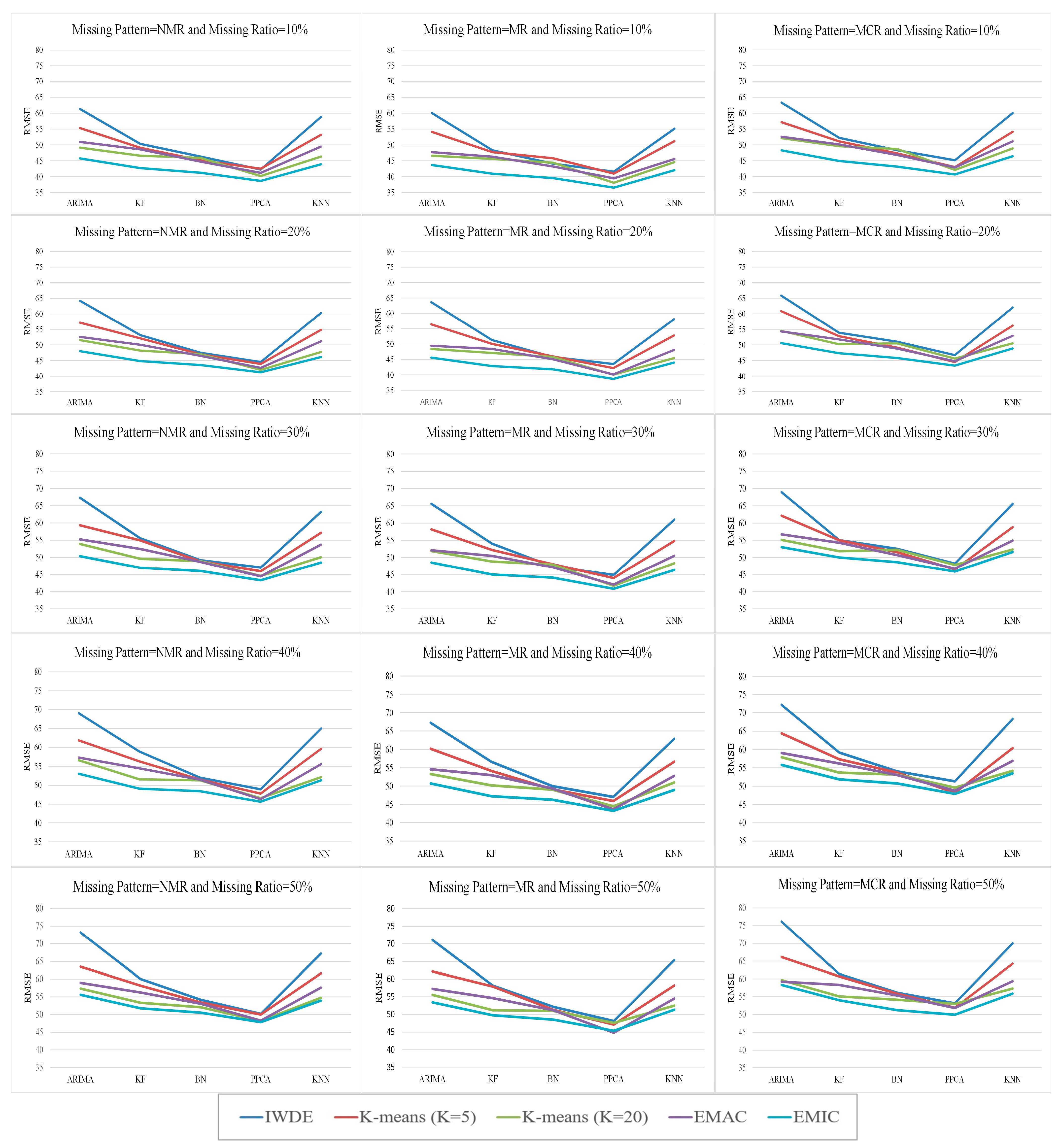
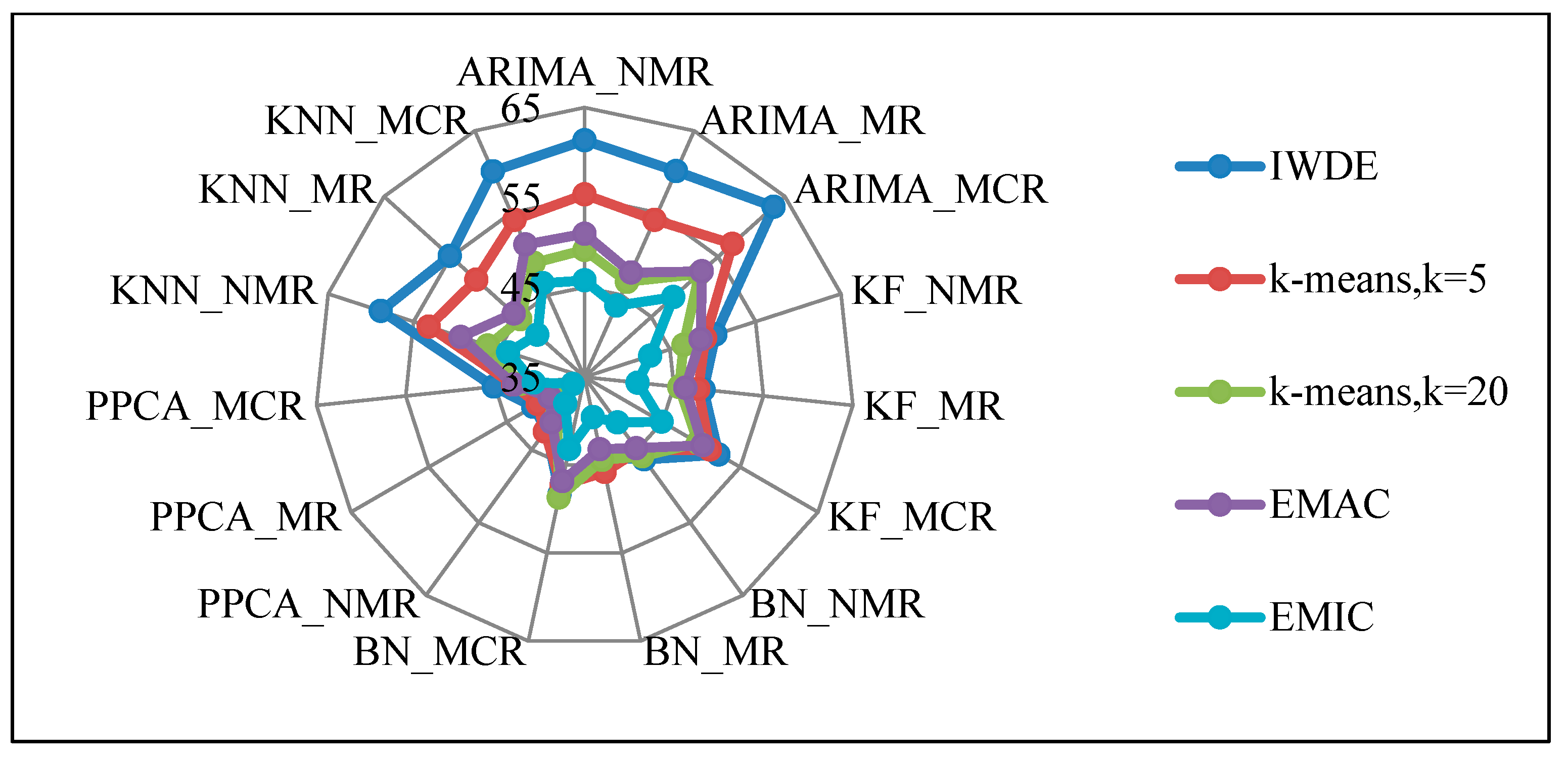
Curves shown in Figure 12 indicate that the proposed method with subclass labels (n = 20) or EMIC outperformed other methods in all experiments using KNN, PPCA, BN, and KF classifiers with different missing patterns, including ARIMA, NMR, MR, and MCR with missing ratio ranging from 10% to 50%. Moreover, it shows that the proposed method using subclass labels with the PPCA imputation method is very competitive with other approaches using PPCA. These curves also indicate that the lowest estimation error was observed in the PPCA algorithm for the MR missing pattern with a missing ratio of 10%. The highest estimation error was associated with the ARIMA and KNN algorithms in all experiments. Increasing the missing ratio in all missing patterns led to an increase in the estimation error for all algorithms.

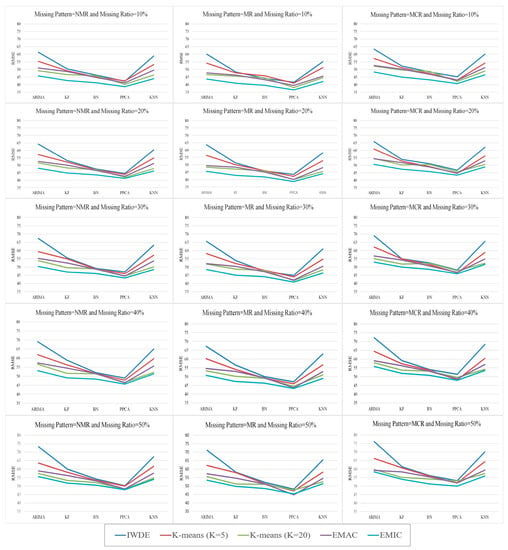
Figure 12. Comparison of imputation RMSE results obtained by different methods with different missing patterns and ratio.

Table 10 shows the mean rank of comparative methods for different missing ratios. The results indicate that the proposed EIM-LD method using subclass labels (EMIC) gains the first rank for all missing ratios. Table 11 shows the mean rank of imputation algorithms used in the EIM-LD method with subclass labels for different missing patterns on missing ratio = 10%. The results show that the PPCA algorithm for MR missing patterns achieves a better rank than other imputation algorithms. In addition, Figure 13 shows the overall ranking of comparative methods using different imputation algorithms for missing patterns on missing ratio = 10%.

Table 10. Mean rank of comparative methods for different missing ratios.

Ranks
Missing Ratio	Method	Mean Rank
	EMIC	1
	K-means, k = 20	2
10%	EMAC	3
	K-means, k = 5	4
	IWDE	5
	EMIC	1
	K-means, k = 20	2
20%	EMAC	3
	K-means, k = 5	4
	IWDE	5
30%	EMIC	1
	K-means, k = 20	2
	EMAC	3
	K-means, k = 5	4
	IWDE	5
40%	EMIC	1
	K-means, k = 20	2
	EMAC	3
	K-means, k = 5	4
	IWDE	5
50%	EMIC	1
	K-means, k = 20	2
	EMAC	3
	K-means, k = 5	4
	IWDE	5

Table 11. Mean rank of imputation algorithms used in the proposed method with subclass labels for different missing patterns on missing ratio = 10%.

Ranks
Algorithm	Mean Rank
PPCA_MR	1
PPCA_NMR	2
BN_MR	3
PPCA_MCR	4
BN_NMR	5
KF_MR	6
KNN_MR	7
BN_MCR	8
KF_NMR	9
KNN_NMR	10
KF_MCR	11
ARIMA_MR	11
KNN_MCR	12
ARIMA_NMR	13
ARIMA_MCR	14

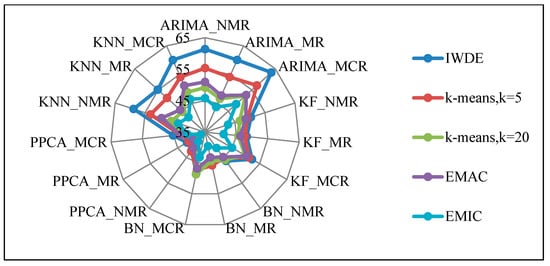
Figure 13. Overall ranking of comparative methods using different imputation algorithms for missing patterns on missing ratio = 10%.

6. Discussion

The experimental results shown in Table 7 indicate the proposed EIM-LD method can impute all missing data patterns, including NMR, MR, and MCR, with missing ratios from 10% to 50% more accurately than other comparative methods. In Section 5.6, we prove that the main reason is using our innovative statistical multi-class labeling that can enrich the original dataset and arm the data model training. However, determining the proper classes is challenging and a limitation. We determined the number of classes and their volume ranges using several pretests. Table A1 indicates that labeling the missed-volume data can be more accurate by removing all missing, incorrect, and noisy data from the clean data in the multi-class labeling step. Moreover, the ANN classifier outperforms other classification methods in the multi-class labeling step with the subclass labels. In contrast, the SVM had the highest classification error rate. This is because the smaller number of samples in the subclass labels is insufficient for model training by SVM.

The EIM-LD method involves an initial enrichment step where data are enriched with an additional feature. This feature is segmented into five classes from VL to VH based on the experts of the traffic control department in Isfahan city recommendation before data model training and subsequent fine-tuning. Following the results, subdividing the class labels into smaller or subclass labels yields more accurate data models. This process enriches the data models, imputing missing data within their specific intervals using data models trained by their specific split dataset. The obtained results demonstrate that fine-tuning using subclass labels yields superior outcomes.

The mean ranks of RMSE in Table 10 and the overall ranks in Figure 13 indicate that the proposed EIM-LD method using subclass labels (EMIC) is superior to other comparative methods for all missing ratios. In addition, the mean ranks in Table 11 show that the PPCA algorithm for MR missing patterns overcomes different imputation algorithms used in this stud. Moreover, the results shown in Table 8 reveal that the method proposed in this study exhibited greater accuracy in predicting records associated with traffic classes, VL1…VL4, L1…L2, M1…M4, and H1…H4 compared to those with VH1…VH4 labels. The inferior performance of the data model in the latter patterns could be attributed to the adverse effects of the higher rate of missing data, coupled with the inadequacy of the available samples for model training. As such, the resulting model failed to perform optimally and lagged behind its counterparts in other traffic classes.

7. Conclusions and Future Work

Intelligent traffic control systems rely heavily on accurate traffic volume data from loop detectors. However, missing data in the traffic volumes collected by these detectors hinders the effectiveness of these systems. Real data collected by the loop detectors have no sufficient features and most of the existing imputation methods do not enrich these data, which leads to constructing data models that cannot fulfill the required accuracy. In this study, an effective imputation method using a data enrichment technique for missing data of loop detectors employed in intelligent traffic control systems (EIM-LD) was proposed. At first, noisy and missing data are separated to construct two clean and missed-volume datasets. The clean dataset is statistically labeled using subclass labels. Then, the missed-volume dataset is labeled using the best data model constructed by different classifiers. The labeled missed-volume dataset is merged with the labeled clean dataset and the merged labeled dataset is split into n datasets to be separately imputed using different imputation methods. Finally, the most accurate imputed datasets are merged to build the imputed traffic volume data sent by the loop detector. The effectiveness of the proposed method was evaluated using four different experiment sets on one-year traffic flow data collected from the SCATS intelligent traffic control system of Isfahan city. The following findings can be concluded from the obtained results:

• The proposed EIM-LD method using data enrichment technique with subclass labels is superior to other comparative methods.
• The ANN classifier is more powerful than other classifiers to estimate the missing volumes of traffic flow data.
• Adding the statistical label to the original flow data can increase the training accuracy of data models in the imputing process.

In the statistical multi-class labeling step, the determining process of the classes is challenging. In this study, the number of classes and their volume ranges were manually determined by doing several pretests. As part of future works, the optimal classes can be determined automatically using continuous and binary metaheuristic algorithms [69,70] to construct better data models with lower error. In addition, the proposed method can be used to impute missing data in different applications, such as weather, medicine, and engineering. In this regard, each application can specifically consider the multi-class labeling method to achieve high imputation accuracy.