Landslide Hazard Assessment in Highway Areas of Guangxi Using Remote Sensing Data and a Pre-Trained XGBoost Model
Abstract
1. Introduction
2. Study Area and Data Sources
2.1. Study Area
2.2. Remote Sensing and Terrain Data
- Slope (1) and aspect (2) are important terrain factors that affect landslide occurrence. Steep terrain and slopes with different orientations can influence soil stability and the risk of soil erosion.
- Daily (3) and antecedent rainfall (4) (7 days in this paper) are important climate factors that affect soil saturation and pore water pressure. The amount and distribution of rainfall can both affect soil stability. In addition, to avoid overfitting the pre-trained models on the training set, this study further incorporated daily accumulated precipitation information for the past 10 years (5) in the region, which could help reduce biases caused by differences in regional precipitation distribution.
- Soil moisture (6) is another important soil factor, and excessive moisture can make soil unstable and increase the risk of landslides.
- The Normalized Difference Vegetation Index (NDVI) (7), as a vegetation index, can reflect the density of vegetation. Dense vegetation can reduce soil erosion and improve soil stability.
- Land cover type is a key factor that influences soil stability and affects its physical and chemical properties. We used two kinds of classification from the Moderate Resolution Imaging Spectroradiometer (MODIS) in this paper. The first one is the International Geosphere-Biosphere Programme (IGBP) (8), which consists of 17 classes defined by the IGBP. These data indicate the dominant land cover type for each pixel every year. The second one is the annual Leaf Area Index (LAI) (9) based on land cover type, which is an important variable for estimating photosynthesis, evapotranspiration, and crop growth. Moreover, by combining annual LAI with the latest NDVI, we can capture the heterogeneity and dynamics of land surface properties in our model.
- Lithology (10) is one of the important factors affecting soil stability, and different types of rocks can affect the properties and stability of the soil.
- 7.
- Distance to faults (11) and rivers (12) are also important factors influencing landslide occurrence. Faults can weaken the rock mass and make it vulnerable to sliding. Rivers can erode the toe of slopes and cause bank collapse. In addition, river erosion and undercutting on the outside bends of meandering rivers can also trigger landslides.
3. Methodology
3.1. Landslide Hazard Assessment (LHA) Framework
- Define the study area and objectives of the assessment.
- Collect and review existing data on landslide inventory, causative factors, and consequences.
- Select and apply appropriate methods and techniques for landslide susceptibility, hazard, and risk analysis.
- Validate and evaluate the results of the analysis using historical records, field observations, or expert opinions.
- Prepare and present landslide hazard maps and reports with recommendations for mitigation measures and further studies.
3.2. XGBoost Algorithm
3.2.1. Sample Preparation
3.2.2. Model Training, Evaluation, and Validation
4. Results and Discussion
4.1. Evaluation of Pre-Trained Model in the Contiguous United States
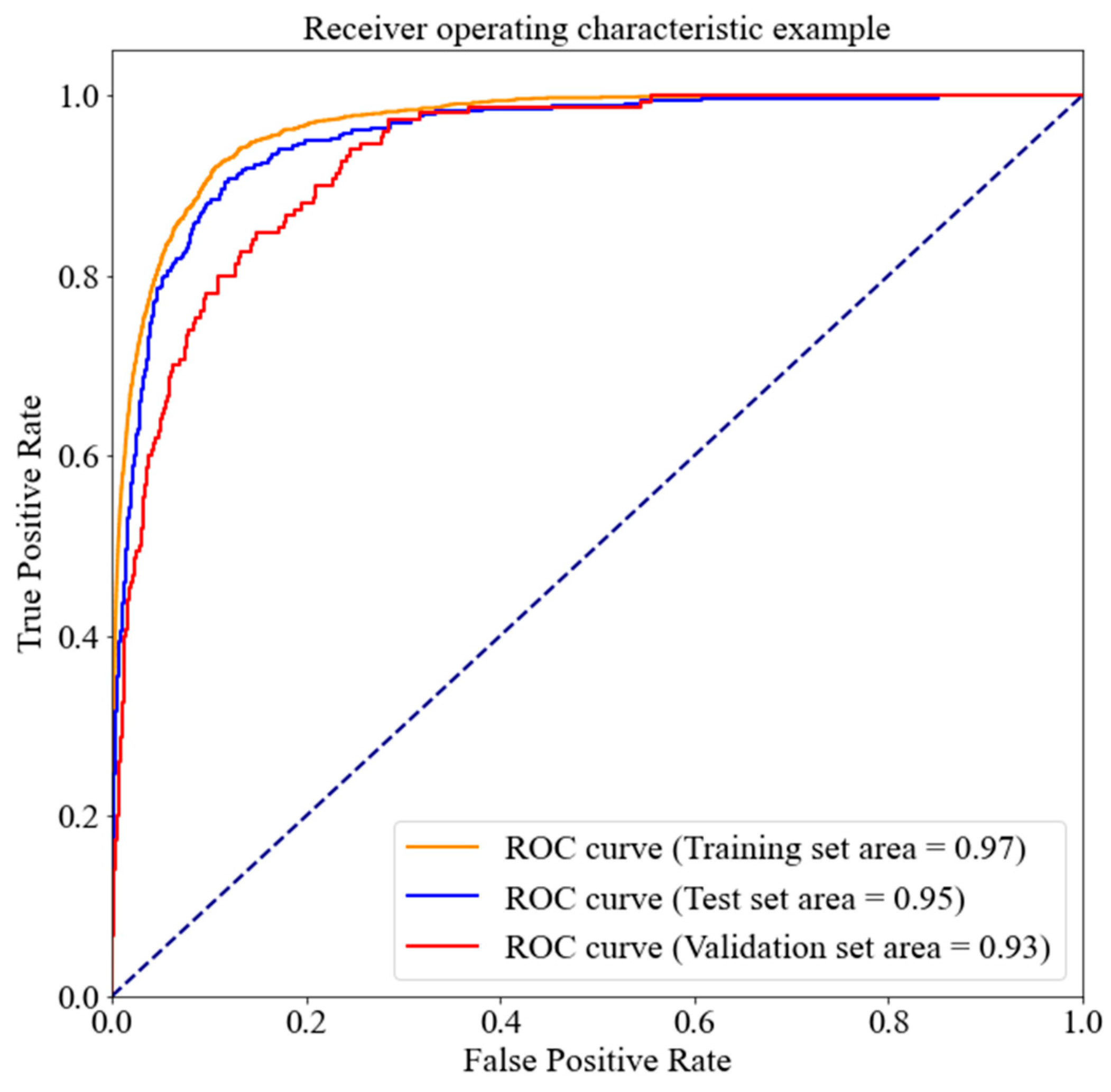
- The XGBoost-2 model achieved the best performance in most of the metrics, especially in F1-score, recall, FPR, and overall accuracy, which represent the overall classification ability and precision. However, it also had a significant drop in kappa and TPR on the validation set, which means it was less consistent and sensitive in LHA.
- MLP-3 showed similar performance to XGBoost-2, ranking second in most of the metrics. Compared to XGBoost-2, MLP-3 was slightly inferior, especially on the test and validation sets. There was a steep decline in metrics from training sets to test and validation sets, indicating a more serious overfitting problem.
- XGBoost-1 and MLP-2 also share similar performances in most metrics. In general, XGBoost-1 was slightly better than MLP-2 as all metrics ranked 1–3 among seven models. As for MLP-2, most values ranked third but with small gaps (1–2%) with XGBoost-1. It should be noted that both XGBoost-1 and MLP-2 had an obvious improvement in TPR but a slight loss in FPR on validation sets compared to XGBoost-2 and MLP-3. A higher TPR with a relatively low FPR is more valuable for balancing the accuracy and management cost in engineering applications for LHA.
- Finally, the SVM and LR models did not outperform XGBoost and MLP models. The classification performance and generalization ability were relatively poor. However, the LR model was the most robust one when tested on three datasets. The difference in metrics only ranged from 2 to 3%.
- The slope is the most important factor affecting landslide occurrence in the region, according to the ranking analysis. Aspect also influences landslides but to a lesser degree. Generally, slope stability decreases when slope and aspect are unfavorable, as they increase the driving forces. However, when the slope exceeds a certain threshold, collapse becomes more likely than a landslide. Therefore, setting an optimal maximum slope value to distinguish between landslide and collapse could further improve the performance of the LHA model.
- Climatic factors (daily rainfall, antecedent rainfall, and extreme rainfall) are also important features of the model. The importance of daily rainfall and antecedent rainfall (7 days) ranks third and fourth, respectively, indicating that the amount and distribution of rainfall are important reasons for soil instability in the region. For example, as rainwater infiltrates into the soil, it fills up the pore spaces and exerts pressure on soil particles. When the pore pressure builds up rapidly due to intense daily rainfall, it reduces the effective stress between soil particles that provide shear strength. This can quickly destabilize the slope and trigger landslides. In contrast, antecedent rainfall has already had time to drain from the soil, so it contributes less to elevated pore pressures on the specific day of landslide occurrence. In addition, sudden heavy rains will also increase the risk of landslides as excessive rainfall can increase soil saturation and pore water pressure, thus reducing soil shear strength and stability.
- Land cover factors (LAI land cover and IGBP land cover) also account for a relatively large weight in the important features of the model. The importance of LAI and IGBP classification ranks second and fifth, respectively, reflecting that land use type has a great influence on slope stability. This is because different land covers have different impacts on vegetation coverage, soil structure, and hydrological processes, thus affecting slope stability.
- Vegetation factors (NDVI) are also one of the features considered in the model. Their importance ranks ninth, indicating that vegetation cover is also a factor affecting landslide occurrence, but relatively less than other factors such as terrain, climate, and land use type. In general, dense vegetation can improve slope stability by reinforcing soil shear strength through its root system.
- Geological factors (lithology) and distance to faults and rivers also account for a certain weight in the model features. The importance of rock type, fault distance, and river distance ranks 7th, 10th, and 12th, respectively. These factors can weaken the rock mass and trigger slope collapse.
- Soil properties (soil moisture) matter because weaker, more porous soils with low shear strength saturate more easily and provide less resistance to sliding. Pore pressures rise quickly in these soils during intense rain, reducing stability.
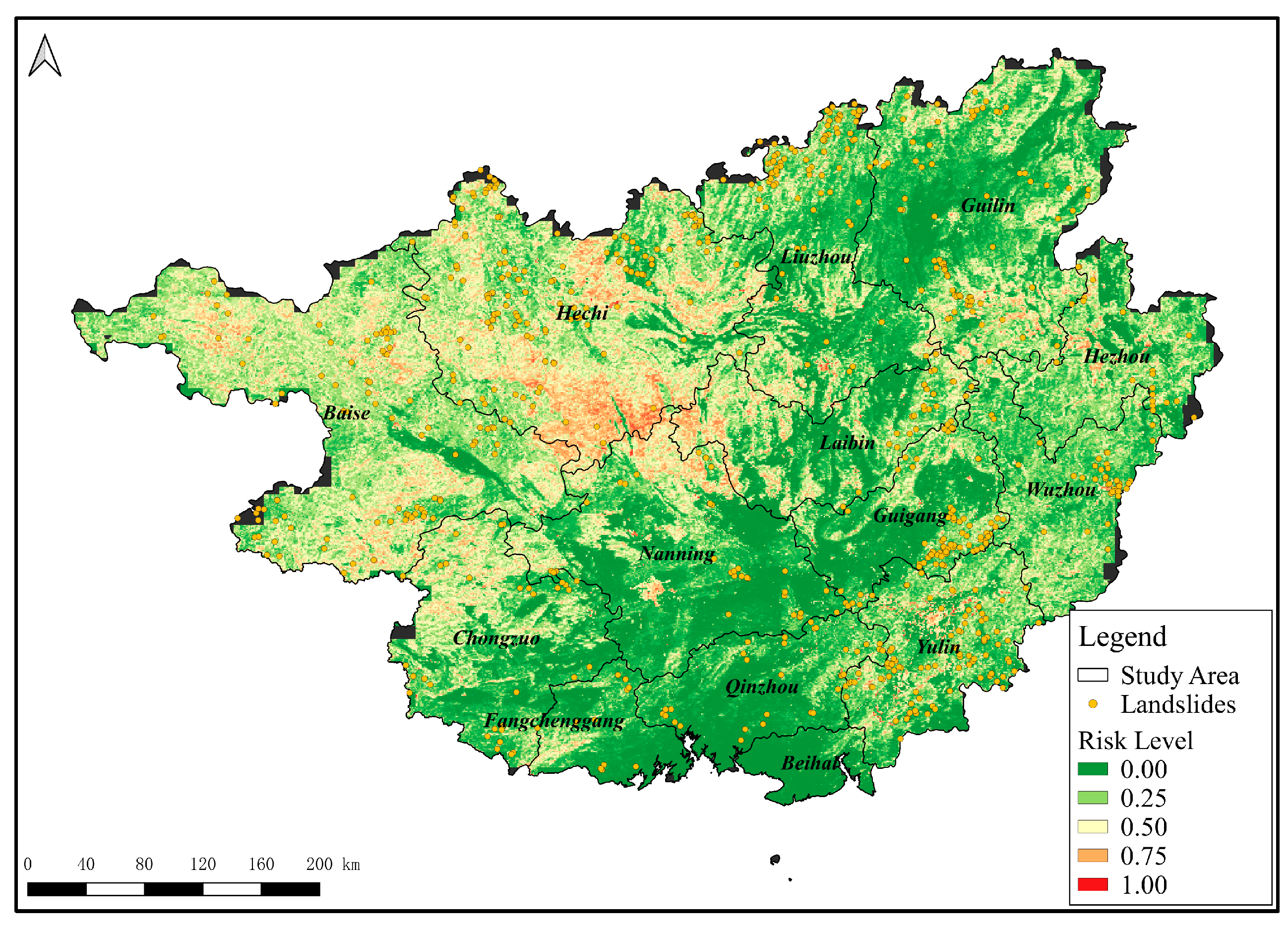
4.2. Evaluation of Pre-Trained Model Performance in Guangxi
4.2.1. Calibrating the Pre-Trained Model for LHA across Guangxi
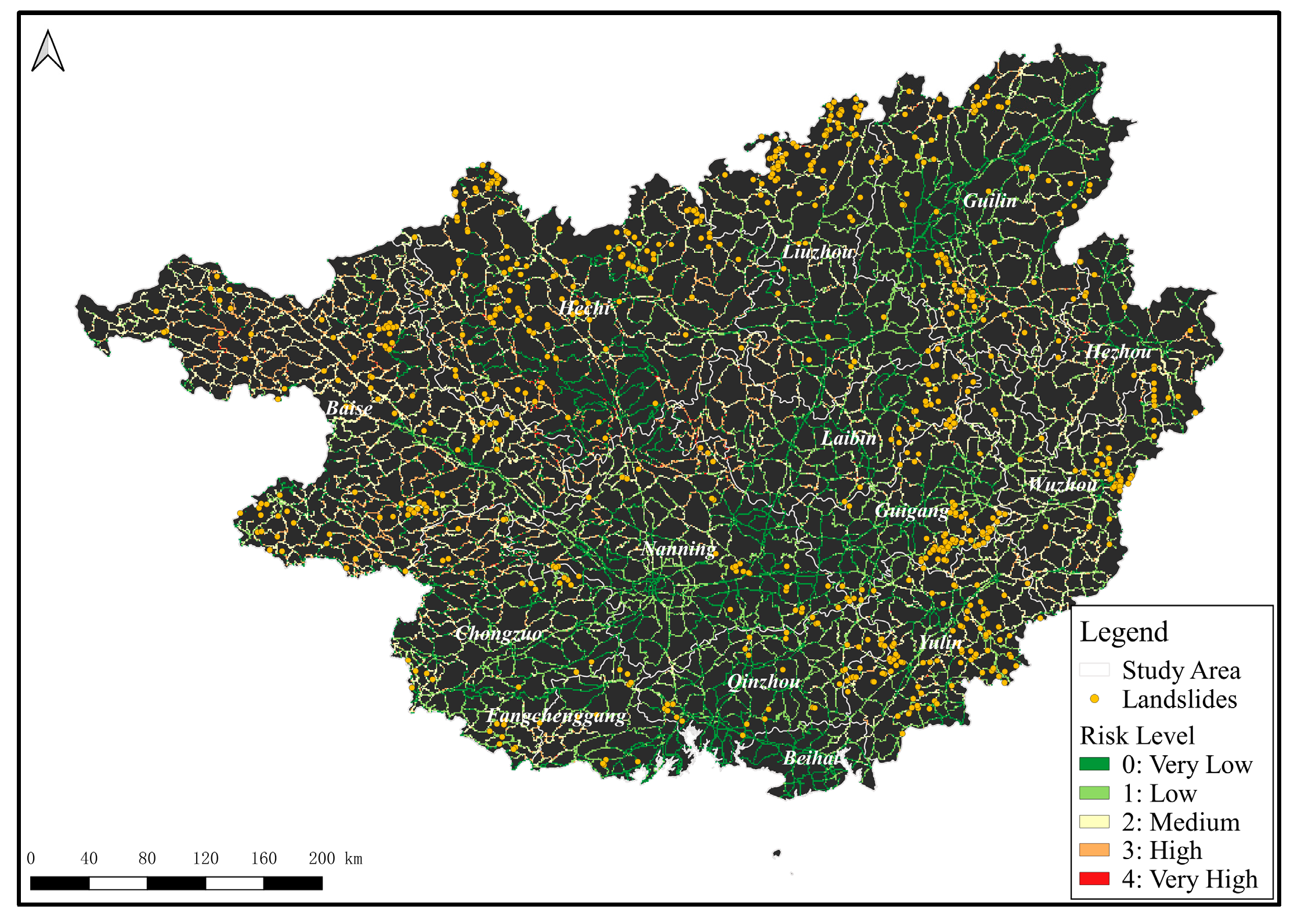
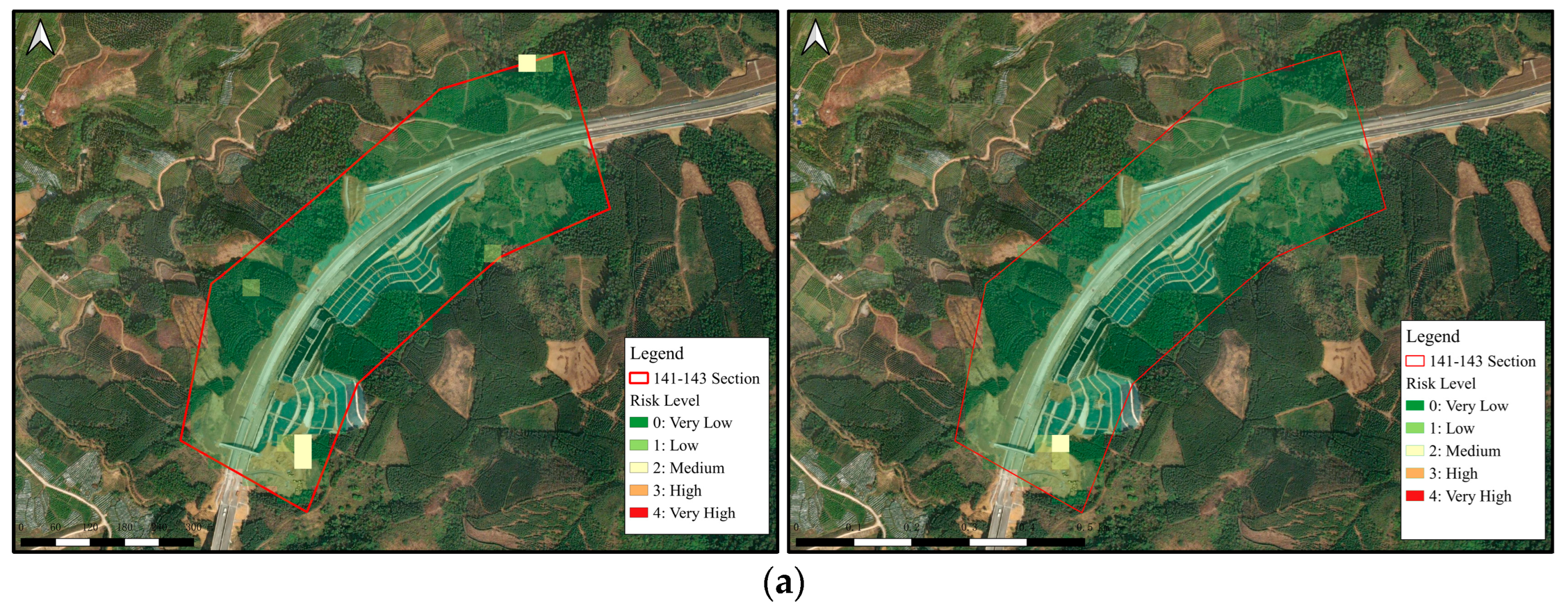
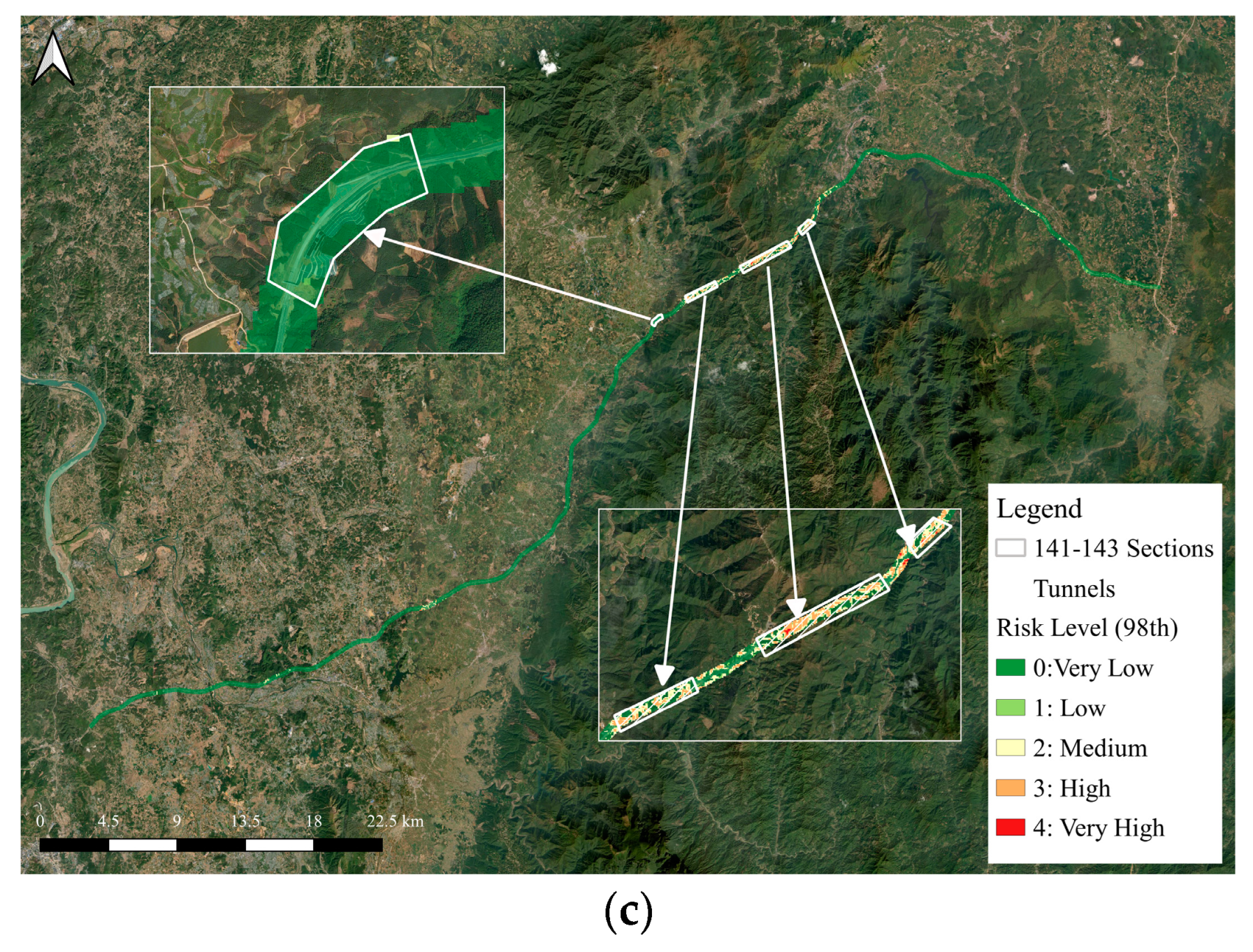
4.2.2. Validating Localized Landslide Hazard Assessment at High Resolution
- First, we set an 8-day data collection cycle and fused the collected data of the same type to achieve a gap-filled and high-quality image for driving the model. According to the data illustration in Table 2, using 8 days as a cycle can ensure at least two images of the same type are obtained within the cycle for data fusion. The cycle length can be adjusted according to the needs, as long as the main data features of the model are not empty.
- Next, we used the cycle-synthesized data to predict the landslide risk for each day within the cycle and took the maximum value as the output of the cycle’s risk probability. The reason for this process is that we assume that the landslide risk is mainly influenced by the cumulative effects of rainfall and soil moisture. Therefore, taking the maximum value can capture the highest risk level within a cycle.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schuster, R.L. Socioeconomic Significance of Landslides. In Landslides: Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board Special Report 247; National Academy Press: Washington, DC, USA, 1996. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide Risk Assessment and Management: An Overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Crozier, M.J. Deciphering the Effect of Climate Change on Landslide Activity: A Review. Geomorphology 2010, 124, 260–267. [Google Scholar] [CrossRef]
- Petley, D.N. Global Patterns of Loss of Life from Landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Varnes, D.J. Landslide Hazard Zonation: A Review of Principles and Practice; UNESCO: Paris, France, 1984. [Google Scholar]
- Guzzetti, F. Landslide Hazard and Risk Assessment. PhD. Thesis, University of Bonn, Bonn, Germany, 2006. [Google Scholar]
- Pardeshi, S.D.; Autade, S.E.; Pardeshi, S.S. Landslide Hazard Assessment: Recent Trends and Techniques; Springer Plus: Berlin/Heidelberg, Germany, 2013; Volume 2, p. 523. [Google Scholar]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Hungr, O. A model for the runout analysis of rapid flow slides, debris flows, and avalanches. Can. Geotech. J. 1995, 32, 610–623. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; Wiley: Chichester, UK, 2003. [Google Scholar]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Ado, M.; Wang, R.-Y.; Lv, G.-A.; Jiao, L. Landslide Susceptibility Mapping Using Machine Learning: A Literature Survey. Remote Sens. 2022, 14, 3029. [Google Scholar] [CrossRef]
- Yu, H.; Li, S.; Ruan, W.; Yao, J.; Liu, Y.; Zhang, L. Landslide Susceptibility Mapping and Driving Mechanisms in a Vulnerable Region Based on Multiple Machine Learning Models. Remote Sens. 2023, 15, 1886. [Google Scholar] [CrossRef]
- Chen, S.; Abd Razak, K.I.; Shi, X.; Huang, R. Landslide susceptibility mapping using machine learning algorithms and multi-source remote sensing data. J. Mt. Sci. 2020, 17, 1897–1914. [Google Scholar]
- Chen, Z.; Shahabi, H.; Shirzadi, A.; Chien, S.-F.; Koufos, G.D.; Yu, M.; Alipour, S.; Zhang, Y.; Yang, T.; Xu, C.; et al. Landslide susceptibility mapping using multi-source remote sensing data and an ensemble machine learning algorithm. Remote Sens. Environ. 2020, 246, 111853. [Google Scholar]
- Alvioli, M.; Melillo, M.; Baum, R.L. A comparison of machine learning algorithms for regional landslide susceptibility mapping. Landslides 2020, 17, 1059–1078. [Google Scholar]
- Hong, S.-H.; Park, J.; Lee, J.-S.; Kim, K.-S.; Yi, M.-J. Landslide susceptibility mapping using deep learning-based convolutional neural networks with high-resolution satellite imagery. Remote Sens. Lett. 2020, 11, 725–734. [Google Scholar]
- Maji, A.K.; Martha, T.R.; Kerle, N.; van Westen, C.J. Landslide susceptibility mapping using deep convolutional neural network with multi-source remote sensing data. Geomat. Nat. Hazards Risk 2020, 11, 2336–2355. [Google Scholar]
- Lissak, C.; Bartsch, A.; Michele, M.D.; Gomez, C.; Maquaire, O.; Raucoules, D.; Roulland, T. Remote Sensing for Assessing Landslides and Associated Hazards. Surv. Geophys. 2020, 41, 1391–1435. [Google Scholar] [CrossRef]
- Casagli, N.; Intrieri, E.; Tofani, V.; Gigli, G.; Raspini, F. Landslide detection, monitoring and prediction with remote-sensing techniques. Nat. Rev. Earth Environ. 2023, 4, 51–64. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Wang, J. Landslide identification using machine learning. J. Mt. Sci. 2020, 17, 1379–1392. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Althuwaynee, M.A.; Pradhan, B.; Lee, S.; Buchroithner, M.F. Landslide susceptibility mapping using XGBoost machine learning algorithm. Geomat. Nat. Hazards Risk 2020, 11, 2829–2854. [Google Scholar]
- Pradhan, S.; Devkar, G.; Singh, U.K.; Kumari, P.; Singh, R. Landslide susceptibility assessment using XGBoost machine learning model: A case study of Uttarakhand state in India. Geocarto Int. 2020, 35, 1788–1813. [Google Scholar]
- Rahmati, S.; Moumenifar, U.; Monavari, S.M.; Jolaei, S.A.; Shahabi, H. A novel hybrid machine learning model based on XGBoost and MARS for landslide susceptibility assessment. Catena 2020, 187, 104352. [Google Scholar]
- Zhang, Y.; Takara, K.; Tachikawa, T. Landslide susceptibility mapping using an improved XGboost algorithm: A case study in the Kii Peninsula, Japan. Remote Sens. 2020, 12, 3413. [Google Scholar]
- Breiman, L. Bagging predictors. Machine Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Paudel, U.; Oguchi, T.; Hayakawa, Y. Multi-resolution landslide susceptibility analysis using a DEM and random forest. Int. J. Geosci. 2016, 7, 726–743. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, R.Q.; Xiang, X.Q. Time and Spacial Predicting of Geological Hazards Occurrence. J. Mt. Sci. 2000, S1, 112–117. [Google Scholar]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Chen, T.; Zhong, Z.Y.; Niu, R.Q.; Liu, T.; Chen, S.Y. Mapping landslide susceptibility based on deep belief network. Geomatics Inf. Sci. Wuhan Univ. 2020, 45, 1809–1817. [Google Scholar]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. An uncertainty and sensitivity analysis approach for GIS-based multicriteria landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 610–638. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Vanwalleghem, T.; Poesen, J.; Govers, G.; Verstraeten, G.; Vandekerckhove, L. Prediction of landslide susceptibility using rare events logistic regression: A case-study in the Flemish Ardennes (Belgium). Geomorphology 2006, 76, 392–410. [Google Scholar] [CrossRef]
- Blahut, J.; Van Westen, C.J.; Sterlacchini, S. Analysis of landslide inventories for accurate prediction of debris-flow source areas. Geomorphology 2010, 119, 36–51. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2012, 10, 175–189. [Google Scholar] [CrossRef]
- Chen, T.; He, T. Higgs boson discovery with boosted trees. In Proceedings of the NIPS 2014 Workshop on High-energy Physics and Machine Learning 2015, Montreal, QC, Canada, 8–13 December 2014; PMLR: New York, NY, USA, 2015; Volume 42. [Google Scholar]
- James, G.M.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2018; Volume 103, p. 18. [Google Scholar]
- Molnar, C. Interpretable Machine Learning; Lulu Press: Morrisville, NC, USA, 2019. [Google Scholar]
- Lv, L.; Chen, T.; Dou, J.; Plaza, A. A hybrid ensemble-based deep-learning framework for landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102713. [Google Scholar] [CrossRef]
- He, Y.; Zhao, Z.; Yang, W.; Yan, H.; Liu, T. A unified network of information considering superimposed landslide factors sequence and pixel spatial neighbourhood for landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102508. [Google Scholar] [CrossRef]
- Gao, X.; Chen, T.; Niu, R.; Plaza, A. Recognition and mapping of landslide using a fully convolutional densenet and influencing factors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7881–7894. [Google Scholar] [CrossRef]


| Landslide Catalog | Time Range | Landslide Events | Reference |
|---|---|---|---|
| United States | 2009–2020 | 1963 | https://www.gislounge.com/using-nasas-global-landslide-catalog-for-landslide-risk-management/ (accessed on 13 May 2023) |
| Guangxi | 1950–2020 | 4229 | / |
| Heba Expressway | 2021.01–2022.03 | 7 | / |
| Indicator | Source | Dataset | Time Resolution | Spatial Resolution | Reference |
|---|---|---|---|---|---|
| Slope and Aspect | ASTGTM3 DEM | DEM | / | 30 m | https://lpdaac.usgs.gov/products/astgtmv003/ (accessed on 13 May 2023) |
| Rainfall | GPM Level 3 IMERG Late Daily | Precipitation | 1 day | 10 km | https://gpm.nasa.gov/data/directory (accessed on 13 May 2023) |
| Soil Moisture | SMAP L4 | Root zone soil moisture percentile | 1 day | 9000 m | https://grace.jpl.nasa.gov/data/get-data/ (accessed on 13 May 2023) |
| NDVI | MODIS Surface Reflectance Daily L2G | Surface Reflectance | 1 day | 500 m | https://lpdaac.usgs.gov/products/mod09gav061/ (accessed on 13 May 2023) |
| Harmonized Landsat Sentinel-2 (HLS) | 2–3 days | 30 m | https://lpdaac.usgs.gov/products/hlsl30v002/ (accessed on 13 May 2023) | ||
| Land Cover Types | MODIS Land Cover Type | LC_Type1(IGBP) and 3(LAI) | 1 year | 250 m | https://lpdaac.usgs.gov/products/modis_products_table/mcd12q1 (accessed on 13 May 2023) |
| China Land Cover Dataset (CLCD) | / | 30 m | https://essd.copernicus.org/articles/13/3907/2021/ (accessed on 13 May 2023) | ||
| Lithology | Global Lithological Map (GLiM) | / | / | / | https://www.earthdoc.org/content/papers/10.3997/2214-4609.201802924 (accessed on 13 May 2023) |
| Dataset | Total | Time Range | Positive Samples |
|---|---|---|---|
| Training | 145,738 | 2009–2017 | 1478 |
| Test | 36,435 | 335 | |
| Validation | 15,258 | 2018–2020 | 150 |
| Total | 197,431 | - | 1963 |
| Parameter Name | Parameter Content | Value Range |
|---|---|---|
| Learning Rate | The rate at which the model learns | 0.001, 0.05, 0.1 |
| Max Depths | The maximum depth of the tree | 3, 4, 5, |
| Subsamples | The subsample ratio of the training instances | 0.5, 0.8, 1.0 |
| Gamma | The minimum loss reduction. The larger it is, the more conservative the algorithm will be. | 0, 0.01, 0.1 |
| Minimum Child Weight | The minimum sum of instance weight (hessian) needed in a child | 1, 2, 3 |
| Estimators | Number of gradient-boosted trees | 100, 200, 300 |
| Metrics | Datasets | XGBoost-1 | XGBoost-2 | MLP-1 (8 × 8) | MLP-2 (16 × 16) | MLP-3 (32 × 32) | SVM | LR |
|---|---|---|---|---|---|---|---|---|
| AUC (%) | Training | 97 | 97 | 95 | 96 | 98 | 88 | 92 |
| Test | 95 | 96 | 94 | 95 | 93 | 87 | 92 | |
| Validation | 93 | 93 | 94 | 91 | 90 | 86 | 91 | |
| Kappa (%) | Training | 81 | 80 | 76 | 79 | 85 | 61 | 68 |
| Test | 78 | 78 | 74 | 77 | 70 | 57 | 70 | |
| Validation | 68 | 63 | 72 | 68 | 64 | 55 | 67 | |
| Weighted F1-Score (%) | Training | 94 | 95 | 93 | 93 | 94 | 91 | 91 |
| Test | 94 | 95 | 93 | 94 | 94 | 91 | 91 | |
| Validation | 93 | 94 | 92 | 92 | 93 | 88 | 89 | |
| Weighted Recall (%) | Training | 89 | 91 | 88 | 89 | 91 | 85 | 84 |
| Test | 89 | 91 | 88 | 89 | 90 | 85 | 85 | |
| Validation | 88 | 90 | 86 | 88 | 89 | 79 | 82 | |
| Overall Accuracy (%) | Training | 89 | 91 | 88 | 89 | 91 | 85 | 84 |
| Test | 89 | 91 | 88 | 89 | 90 | 85 | 85 | |
| Validation | 88 | 90 | 86 | 88 | 89 | 79 | 82 | |
| FPR (%) | Training | 11 | 9 | 12 | 11 | 10 | 15 | 16 |
| Test | 11 | 9 | 12 | 11 | 10 | 15 | 15 | |
| Validation | 12 | 10 | 14 | 12 | 11 | 21 | 18 | |
| TPR (%) | Training | 92 | 89 | 88 | 90 | 95 | 76 | 84 |
| Test | 88 | 87 | 86 | 88 | 79 | 72 | 86 | |
| Validation | 80 | 73 | 86 | 80 | 75 | 75 | 85 |
| Parameter Name | Values |
|---|---|
| Learning Rate | 0.1 |
| Max Depths | 4 |
| Subsamples | 0.5 |
| Gamma | 0.1 |
| Minimum Child Weight | 2 |
| Estimators | 200 |
| Tree Method | exact |
| Classified Number | Risk Level | Percentile Thresholds |
|---|---|---|
| 0 | Very Low | <2nd% |
| 1 | Low | [2nd%, 39th%) |
| 2 | Medium | [39th%, 89th%) |
| 3 | High | [89th%, 99th%) |
| 4 | Very High | ≥99th% |
| ICLD Values | IGBP Values | LAI Values |
|---|---|---|
| 1 | 12 | 3 |
| 2 | 5 | 5 |
| 3 | 6 | 2 |
| 4 | 10 | 1 |
| 5 | 17 | 0 |
| 6 | 15 | 9 |
| 7 | 16 | 9 |
| 8 | 13 | 10 |
| 9 | 11 | 9 |
| Prediction Cycle | Start Date | End Date | Landslide Occurrence | Predicted Risk Pixels (≥Medium) | ||
|---|---|---|---|---|---|---|
| XGBoost-1 | MLP-2 | LR | ||||
| 1 | 4 July 2021 | 11 July 2021 | 11 July 2021 | 3 | 1 | 0 |
| 4 July 2021 | 11 July 2021 | 12 July 2021 | ||||
| 2 | 24 October 2021 | 31 October 2021 | 25 October 2021 | 0 | 0 | 0 |
| 3 | 17 November 2021 | 24 November 2021 | 24 November 2021 | 0 | 0 | 0 |
| 4 | 17 January 2022 | 24 January 2022 | 18 January 2022 | 1 | 2 | 1 |
| 17 January 2022 | 24 January 2022 | 23 January 2022 | ||||
| 5 | 30 March 2022 | 6 April 2022 | 31 March 2022 | 14 | 30 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Deng, L.; Han, Y.; Sun, Y.; Zang, Y.; Zhou, M. Landslide Hazard Assessment in Highway Areas of Guangxi Using Remote Sensing Data and a Pre-Trained XGBoost Model. Remote Sens. 2023, 15, 3350. https://doi.org/10.3390/rs15133350
Zhang Y, Deng L, Han Y, Sun Y, Zang Y, Zhou M. Landslide Hazard Assessment in Highway Areas of Guangxi Using Remote Sensing Data and a Pre-Trained XGBoost Model. Remote Sensing. 2023; 15(13):3350. https://doi.org/10.3390/rs15133350
Chicago/Turabian StyleZhang, Yuze, Lei Deng, Ying Han, Yunhua Sun, Yu Zang, and Minlu Zhou. 2023. "Landslide Hazard Assessment in Highway Areas of Guangxi Using Remote Sensing Data and a Pre-Trained XGBoost Model" Remote Sensing 15, no. 13: 3350. https://doi.org/10.3390/rs15133350
APA StyleZhang, Y., Deng, L., Han, Y., Sun, Y., Zang, Y., & Zhou, M. (2023). Landslide Hazard Assessment in Highway Areas of Guangxi Using Remote Sensing Data and a Pre-Trained XGBoost Model. Remote Sensing, 15(13), 3350. https://doi.org/10.3390/rs15133350






